Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound

Abstract

Four very low birth weight, very premature infants were monitored during a 12° postural elevation using diffuse correlation spectroscopy (DCS) to measure microvascular cerebral blood flow (CBF) and transcranial Doppler ultrasound (TCD) to measure macrovascular blood flow velocity in the middle cerebral artery. DCS data correlated significantly with peak systolic, end diastolic, and mean velocities measured by TCD (p_A =0.036, 0.036, 0.047). Moreover, population averaged TCD and DCS data yielded no significant hemodynamic response to this postural change (p>0.05). We thus demonstrate feasibility of DCS in this population, we show correlation between absolute measures of blood flow from DCS and blood flow velocity from TCD, and we do not detect significant changes in CBF associated with a small postural change (12°) in these patients.

1. Introduction

Between 1990 and 2005 the percentage of preterm births in the United States rose by 20% [1]. Preterm births now account for almost half of children with cerebral palsy, as well as a significant portion of children with cognitive, visual, and hearing impairments [2]. Three forms of acquired brain injury affect the likelihood of mortality and neurodevelopmental deficits in very low birthweight (< 1500 g), very preterm (< 32 weeks gestation age) neonates: hypoxicischemic insult, periventricular leukomalacia (PVL) and intraventricular hemorrhage (IVH) [3,4]. PVL is a specific form of necrosis of the cerebral white matter adjacent to the lateral ventricles that is often associated with impaired motor development and is a major cause of cerebral palsy. During the early stages of brain development, this region of white matter is highly susceptible to injury from lack of blood flow and oxygen delivery due to the maturation stage of the supporting cells (oligodendrocytes) [5]. IVH refers to hemorrhaging from the germinal matrix, an immature bed of vascular tissue along the ventricular wall that is typically present only in preterm infants less than 32 weeks gestation age. Such hemorrhages are caused by fluctuations in cerebral blood flow (CBF) and may induce profound cognitive and physical handicaps. A continuous monitor of CBF at the bedside could therefore be a valuable supplement for gathering information about a patient’s condition [6] and for guiding treatment. Microvascular information about cerebral perfusion, in particular, is attractive because the microvasculature controls oxygen and nutrient delivery to relevant tissues.

Currently, transcranial Doppler ultrasound (TCD) and near-infrared spectroscopy (NIRS) are the only techniques deemed feasible for the estimation of CBF in this clinical population. TCD measures cerebral blood flow velocity (CBFV) in the cerebral arteries by monitoring the frequency shift of acoustic waves that scatter from moving red blood cells [7,8]. With additional information about the cross-sectional area of the insonated vessel, CBFV permits calculations of arterial CBF. However, cerebral vessels are small in size, making their diameter difficult to measure [9]. To avoid this source of error, one could focus on relative changes in flow. However, these blood vessels can change caliber over time, leading to large errors in calculations of relative change, which in turn cause errors in estimates of the amount of oxygen and nutrients delivered to the surrounding tissue [10–12].

Near-infrared spectroscopy measures tissue oxy- and deoxyhemoglobin concentrations, taking advantage of the tissue absorption “window” in the near-infrared [13]. A comprehensive review of near-infrared spectroscopy in the neonate was recently published by Wolfberg and du Plessis [14]. Although NIRS measurements of tissue oxygenation and total hemoglobin concentration are increasingly more common in the clinic, the calculation of CBF from NIRS data is indirect and relies on the Fick principle, which states that the total uptake of a tracer by tissue is proportional to the difference between the rates of inflow and outflow of the tracer to and from the tissue [15]. This calculation requires the use of a tracer, typically oxygen or indocyanine green, and requires certain assumptions to be valid, namely that cerebral blood volume, CBF, and cerebral oxygen extraction must remain constant.

In this paper we employ another recently developed optical technique to measure CBF: diffuse correlation spectroscopy (DCS). DCS [16–21] has shown promise as a monitor of relative changes in blood flow [21–35]. Like NIRS, DCS also employs near-infrared light to probe the dynamics of deep tissues. However, DCS detects changes in CBF directly by monitoring temporal fluctuations of scattered light. It does not rely on tracers to indirectly infer information about CBF, and it can be employed continuously. Finally, in contrast to TCD, DCS provides information about microvascular hemodynamics.

In the present investigation, diffuse correlation spectroscopy and transcranial Doppler ultrasound monitor the hemodynamics of four very low birthweight, very preterm neonates during a 0° to 12° postural change. Because this study is a feasibility test, we limited head of bed elevation to values within the range of the clinical isolette beds. Many studies have been conducted to determine the physiological response of preterm infants to postural manipulations [12,36–44]. Most of this work has focused on changes in vitals signs, such as heart rate, blood pressure, and/or arterial oxygen saturation, although some groups have also used near-infrared spectroscopy to probe cerebrovascular oxygenation during postural change [42–44]. To this author’s knowledge, only one study by Anthony et al. has been done with Doppler ultrasound to monitor the effects of HOB elevation to cerebral blood flow velocity in the main arteries [12], and no experiment has examined the resulting changes in microvascular cerebral blood flow. Anthony et al. defined four classifications of peak systolic velocity response within 30 seconds of a 20° HOB elevation: (1) a sudden change within 5 seconds, (2) a sudden change within 5 seconds, followed by a corrective change, (3) no change, (4) cycling or no discernible trace. Responses 2 and 3 were the most common. Two major questions raised by this finding are: what relationships exist between these large-vessel changes and the microvascular cerebral blood flow, and what impact, if any, does postural manipulation have on this microvascular flow. Our present study aims to address both of these questions by examining the use of diffuse correlation spectroscopy on preterm neonates.

Our results indicate that on a measurement by measurement basis, significant correlations were found between absolute values of the blood flow index (BFI) measured by DCS and peak systolic velocity (PSV) and mean velocity (MV) measured by TCD; a weaker but still significant correlation was found between BFI and end diastolic velocity (EDV) measured by TCD. As per the entire patient population, both modalities found no significant relative changes in hemodynamics during this relatively small (12°) postural intervention. Thus we demonstrate the use of DCS on this population of preterm infants, we show agreement between DCS and TCD for the first time, and we suggest that such small postural changes do not significantly affect cerebral blood flow in this population.

2. Methods and materials

In DCS, coherent near-infrared light is introduced into a highly scattering medium such as tissue wherein it travels deeply and scatters multiple times before detection at some distance from the light source. During each scattering event, the phase of the scattered light is changed. At the detector, the superposition of multiple light fields with different phases creates a speckle pattern. If the scattering particles move, the speckle pattern fluctuates in time. The intensity fluctuations of the speckles thus contain information about the motion of the scatterers [16,17]. In the case of tissue, the primary moving scatterers are red blood cells. Therefore, by characterizing the fluctuations in speckle intensity over time, we gather information about blood flow in tissue.

In order to monitor speckle fluctuations in time, we measure the normalized intensity autocorrelation function, g ₂(r, τ) = 〈I(r,t)I(r, t + τ)〉 / 〈I(r, t)〉², and calculate the normalized electric field temporal autocorrelation function, g ₁(r, τ) = G ₁(r, τ)/ 〈E ^*(r, t)E(r, t)〉, using the Siegert relation, g ₂(r, τ) = 1 + β |g ₁(r, τ)|². Here I(r, t) is the intensity at time t and position r, E(r, t) is the electric field at time t and position r, 〈〉 denotes the ensemble or time average, and β is a constant that depends on the source coherence, detection optics, ambient light and other external factors. G ₁(r, τ) is the unnormalized electric field autocorrelation function, equal to 〈E ^*(r,t)E(r, t + τ)〉, which obeys a correlation diffusion equation [18,19]. In this study we assume a homogeneous tissue-air interface geometry in the plane z = 0. The semi-infinite solution of G ₁(r, τ) to the correlation diffusion equation for a point source of the form S(r) = S ₀δ(r) [19,29] is

$$G_1(\mathbf{r},\tau )=\frac{3{\mu }_s^{\prime }{S}_0}{4\pi }\left(\frac{e^{-\kappa (\tau )r_1}}{r_1}-\frac{e^{-\kappa (\tau )r_2}}{r_2}\right).$$ (1)

Here ${\kappa }^2(\tau )=3{\mu }_s^{\prime }({\mu }_a+\frac{1}{3}\alpha {\mu }_s^{\prime }{k}_0^2〈\Delta r^2(\tau )〉)$; μ_a (cm⁻¹) and ${\mu }_s^{\prime }({\text{cm}}^{-1})$ are the tissue absorption and reduced scattering coefficients, respectively; k ₀ (cm⁻¹) is the magnitude of the optical wave vector, 2πn/λ, where n is the index of refraction of tissue and λ is the wavelength of incident light; α represents the percentage of light scattering events that come from moving scatterers; $〈\mathrm{\Delta }{r}_s^2(\tau )\rangle ({\text{cm}}^2)$ is the mean squared displacement of the moving scatterers in time τ, assumed to have the form 6D_Bτ where D_B is an effective Brownian diffusion coefficient; r ₁ and r ₂ (cm) are the distances between the detector and the source/image source, respectively, i.e. $r_1={[r^2+z_0^2]}^{1/2}$ and $r_2={[r^2+{(z_0+2z_b)}^2]}^{1/2}$; $z_0=1/{\mu }_s^{\prime }(\text{cm})$ is the depth at which a collimated source on the tissue surface can be approximated as a point source; $z_b=2.17/{\mu }_s^{\prime }(\text{cm})$ in the case of refraction indices of tissue and air (equal to 1.4 and 1.0, respectively). The decay rate of this autocorrelation function is dictated by blood flow. We define a blood flow index, BFI ≡ αD_B, with units of cm²/s, to quantify this decay rate. BFI reflects CBF, and changes in BFI relative to baseline measurements (rBFI) reflect analogous changes in CBF (rCBF) [30]. Although this analysis approach is empirical, numerous studies have validated it as a measure of relative blood flow, including comparisons to literature [21–23], to Doppler ultrasound in murine tumors [26], to laser Doppler flowmetry in rat brain [21–23,28], to fluorescent microspheres in piglet brains [35], and to arterial spin-labeled perfusion MRI in human brain and calf muscle [24,32].

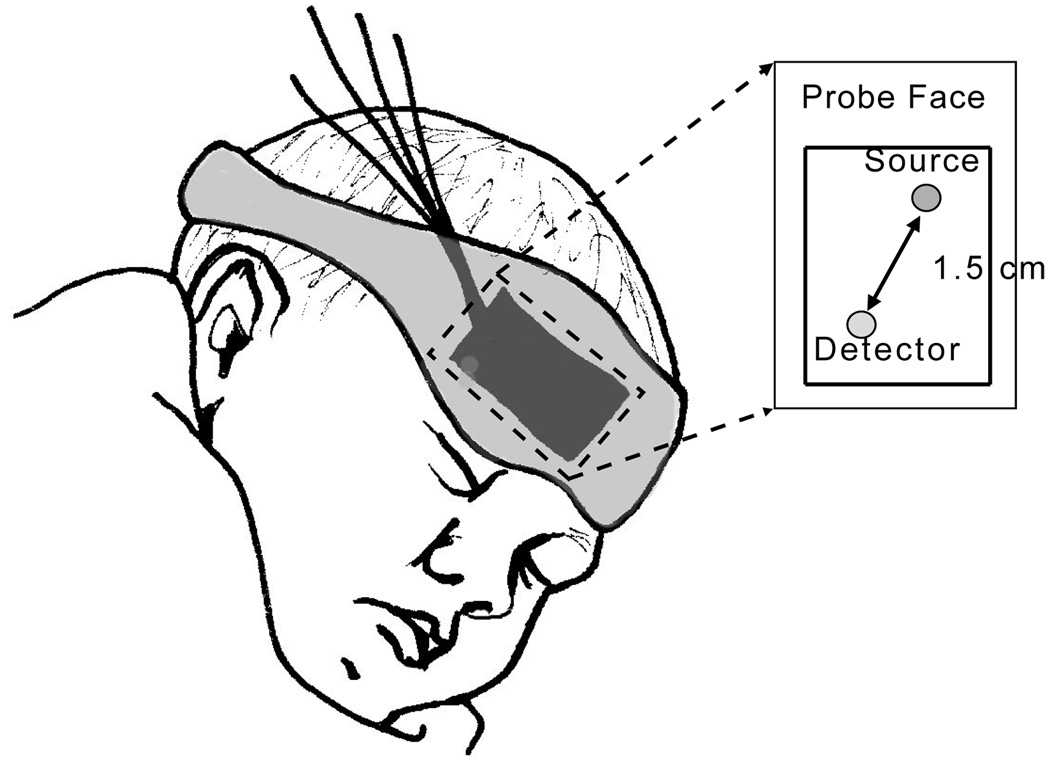
The DCS instrument uses a long-coherence-length laser (CrystaLaser, RCL-080-785S) operating at 785 nm to deliver light to the tissue. A single mode fiber secured by a black foam pad detects light 1.5 cm from the source. The fiber is custom designed with a 90° bend on the patient end, permitting the probe to rest adjacent to the forehead. Light is detected by a fast photon counting avalanche photodiode that outputs a TTL signal for every photon received. This TTL signal is transmitted to a custom built 2-channel correlator board (FLEX03OEM2CH, correlator.com, Bridgewater, NJ) derives the intensity autocorrelation function based on the photon arrival times [45]. Figure 1 shows a sketch of the probe on the infant’s head.

Fig. 1.

The fibers used to deliver and detect light are secured to the infant’s forehead using a soft black pad. The pad is held in place with a mask that wraps around the head.

Protocols for both DCS and TCD measurements are shown in Figure 2. Head of bed (HOB) angle manipulations were limited by the range of the isolette beds (Ohio Care, Ohmeda Isolette). These beds easily adjust from an angle of 0° to approximately 12° in seconds.

Fig. 2.

Diagram of the protocol used for DCS (top) and TCD (bottom) measurements. DCS and TCD measurements were NOT taken at the same time. For DCS, data was taken continuously (8 data points per minute) for 5 minutes at each head of bed angle adjustment. The head of bed 0° to 12° elevation was repeated 3 times, making the total study time 35 minutes. By comparison, for TCD only 3 data points were taken at each HOB angle before the bed was repositioned, and the HOB angle was only elevated twice.

For DCS, data were acquired for 30 minutes: three 5 minute HOB=0° sessions, alternating with three 5 minute HOB=12° sessions. Intensity autocorrelation curves were averaged over a period of 3 seconds and were acquired every 7 seconds, resulting in around 300 BFI data points per study. These curves were then converted to electric field autocorrelation functions using the Siegert relation with a fitted value for β of approximately 0.5. Theoretically, we expect β to be approximately equal to the inverse of the number of modes allowed to pass through the detection optics. In our case of single mode detection fibers, the number of modes is two. For analysis, we solved the correlation diffusion equation analytically, assuming the sample geometry was a homogeneous, semi-infinite medium. We used the semi-infinite solution (Equation 1) to fit our data for BFI. This fit is made possible by assuming constant values for μ_a and ${\mu }_s^{\prime }$ (0.1 cm⁻¹ and 10 cm⁻¹, respectively, at 785 nm) for the whole population and throughout the study. These values were chosen from literature references [47,48].

A mean relative change in CBF was calculated after each HOB= 12° event using the preceding HOB= 0° event for a baseline, i.e. for the i^th repetition, $\overline{rCB{F}_i}=\overline{BF{I}_i({12}^{°})}/\overline{BF{I}_i(0^{°})}\times 100$, where $\overline{BF{I}_i({\theta }^{°})}$ indicates the mean BFI over all data points taken at the i^th HOB= θ° event. After $\overline{rCB{F}_i}$ was calculated for each HOB change (3 total per day of study), a mean relative change in cerebral blood flow, 〈rCBF〉, was determined for each day. Here 〈〉 denotes the mean value over all $\overline{rCB{F}_i}$ measured on a given day. Additionally, to compare absolute measurements of BFI to the velocities found from TCD, a mean blood flow index, $\overline{BFI}$, was calculated for each day of study. For the purposes of this analysis, we used the initial HOB= 0° data to calculate $\overline{BFI}$, i.e. $\overline{BFI}=\overline{BF{I}_{i=1}(0°)}$, since the baby was most peaceful during this time period.

The protocol for TCD measurements differed slightly from the DCS protocol. Only two or three measurements of peak systolic velocity (PSV), end diastolic velocity (EDV), and mean velocity (MV = (PSV − EDV)/PI, where PI is the pulsatility index measured by the ultrasound scanner), were obtained at each head of bed angle. A Philips ATL HDI 5000 ultrasound scanner (Philips Medical Systems, Bothell, WA) with a C8-5 MHz broadband curved array transducer was used for data acquisition. Typically this process was repeated twice. As in the case of the mean rCBF calculation, mean relative changes of each parameter for the i^th repetition $(\overline{rPS{V}_i},\overline{rED{V}_i},\overline{rM{V}_i})$ comparing the responses at elevated HOB to lying flat were computed after each HOB change, i.e. $\overline{rPS{V}_i}=\overline{PS{V}_i(12°)}/\overline{PS{V}_i(0°)}\times 100$. Daily mean changes in velocities, 〈rPSV〉, 〈rEDV〉, 〈rMV〉, were calculated in the same manner as 〈rCBF〉. For comparison to DCS, mean velocities at the initial HOB= 0° event ($\overline{PSV}=\overline{PS{V}_{i=1}(0°)}$, $\overline{EDV}=\overline{ED{V}_{i=1}(0°)}$, and $\overline{MV}=\overline{M{V}_{i=1}(0°)}$) were calculated for each day of study. Unfortunately TCD and DCS data could not be collected at the same time due to the size of the infant’s head. However, the data were acquired on the same day by both modalities.

For the purpose of this analysis, we considered each of the nine days of data acquisition to be independent observations. To test for an association between $\overline{BFI}$ and each of $\overline{PSV}$, $\overline{EDV}$, and $\overline{MV}$, as well as between 〈rCBF〉 and each of 〈rPSV〉, 〈rEDV〉, and 〈rMV〉, we used Spearman’s rank-based non-parametric approach [49]. Rejection of the null hypothesis in this case implies a positive or negative, and possibly non-linear, association between the variables. Pearson’s correlation coefficient was used to estimate a linear association between $\overline{BFI}$, and each of $\overline{PSV}$, $\overline{EDV}$, and $\overline{MV}$. To test the hypothesis that each of the four relative variables differed from baseline during HOB elevation, we conducted a Wilcoxon signed rank test [50]. Analyses were carried out using R 2.8 [51]; hypotheses tests and associated p-values (p) were two-sided. A family-wise error rate of 0.05 was maintained using Hochberg’s method [52] to adjust for multiple comparisons within each of the three sets of analyses (associations with $\overline{BFI}$, associations with 〈rCBF〉, and comparison with baseline); adjusted p-values, p_A, are also reported.

3. Results

In total, we acquired nine days of data sets on four preterm infants with both DCS and TCD. The mean gestation age of our population was 26.3 weeks (range = 25–27 weeks) and the mean birthweight was 896 g (range = 640–1150 g). At the time of the study, the mean weight was 1185 g (range = 650–1900 g), and the mean corrected gestational age, defined as gestational age plus the time since birth, was 29.2 weeks (range = 26–34 weeks).

3.1. Results-DCS

Diffuse light signals (~ 100,000–500,000 photons/sec) were sufficient for all patients. Autocorrelation curves were averaged over a period of 3 s, leading to fairly smooth data and good signal-to-noise ratio. Sample autocorrelation curves are shown in Figure 3. The solid black line is the raw data. The dotted black line shows the fit to the data. The median (range) $\overline{BFI}$ for all nine days of measurement at the initial HOB=0° position was 1.62 × 10⁻⁸ (0.98 – 3.31 × 10⁻⁸) cm²/s. Median 〈rCBF〉 over the nine days of measurements was 93.4 (87.3 to 112.8) % (see Table 1).

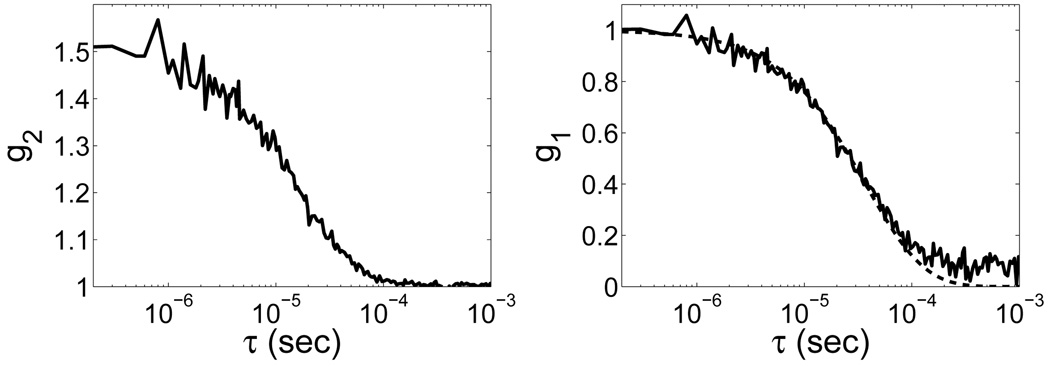
Fig. 3.

(Left) Typical normalized intensity autocorrelation curve derived directly from the correlator board as a function of time, τ (data measured on the forehead of a preterm infant). (Right) The corresponding normalized electric field autocorrelation curve, g ₁(r, τ), calculated using the Siegert relation with a fitted value for β. The solid line shows the raw data. The dotted line is the best fit curve to a Brownian motion model, which we use to derive the blood flow index (BFI).

Table 1.

Median and range of average daily hemodynamic response to postural elevation

	Median (%)	Range (%)	p-value
〈rCBF〉	93.4	87.3 to 112.8	0.12*
〈rPSV〉	103.0	91.1 to 128	0.34†
〈rEDV〉	104.0	61 to 138	0.9l†
〈rMV〉	100.1	80 to 125	0.53†

^*(p_A = 0.48

^†p_A = 0.91.)

3.2. Results-TCD

The TCD data at the initial HOB=0° event revealed a median (range) $\overline{PSV}$ of 44.1 (20.9 to 70.3) cm/s; median $\overline{EDV}$ was 8.3 (5.1 to 12.8) cm/s; median $\overline{MV}$ was 21.3 (11.4 to 30.6) cm/s. Median relative changes in these parameters (〈rPSV〉, 〈rEDV〉, and 〈rMV〉) after the postural intervention are shown in Table 1. A Wilcoxon signed rank test on these relative parameters revealed no significant changes from baseline values during HOB elevation.

3.3. Comparison of DCS and TCD

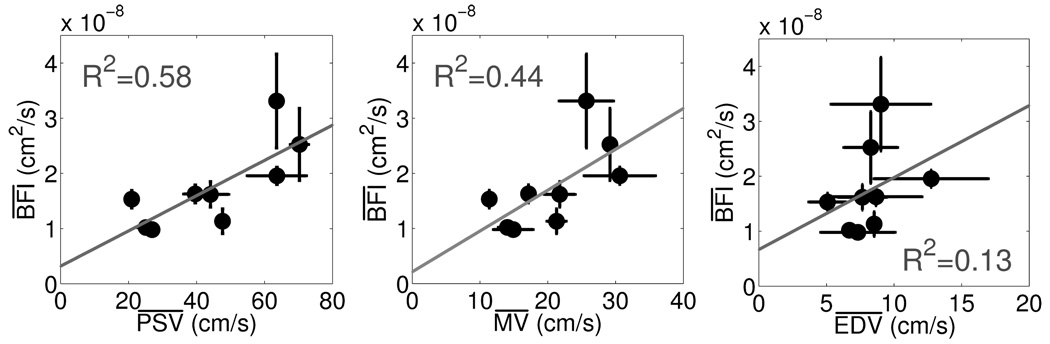
Figure 4 (left) shows the relationship between baseline $\overline{PSV}$ and $\overline{BFI}$ for TCD and DCS. The error bars in the horizontal and vertical directions represent the standard deviation in the mean value of the given parameter over all data points recorded at the first HOB=0° event. The estimated Spearman rank correlation coefficient, r_s, was 0.76, indicating a significant positive correlation (p = 0.018, p_A = .036) between $\overline{PSV}$ and $\overline{BFI}$. Baseline $\overline{MV}$ and $\overline{BFI}$ (Figure 4, center) revealed a significant correlation as well with r_s = 0.78 (p = 0.013, p_A = .036). As seen in Figure 4 (right), the relationship between $\overline{BFI}$ and $\overline{EDV}$ also achieved significance (r_s = 0.67, p = 0.047, p_A = .047).

Fig. 4.

(Left) Correlation between population averaged mean TCD PSV taken at the initial HOB=0° $(\overline{PSV})$ and population averaged mean DCS BFI also taken at the initial HOB=0° $(\overline{BFI})$. (Center) Correlation between population averaged mean TCD MV taken at the initial HOB=0° $(\overline{MV})$ and DCS $\overline{BFI}$. (Right) Correlation between population averaged mean TCD EDV taken at first HOB=0° event $(\overline{EDV})$ and DCS $\overline{BFI}$. The solid line in each plot shows the best linear fit between the two variables. Both Pearson’s and Spearman’s correlation coefficients (R² and r_s, respectively) were calculated. The R ² Pearson values are displayed for each plot.

The solid grey lines in Figure 4 depict the best linear fit to the data. Pearson’s correlation coefficient, R ², was calculated, and modest positive linear correlations between $\overline{PSV}$ and $\overline{BFI}$, $\overline{MV}$ and $\overline{BFI}$, and $\overline{EDV}$ and $\overline{BFI}$ were detected (R ² =0.58, 0.44, 0.13).

Both techniques showed no significant hemodynamic population-averaged changes during HOB elevation as compared to HOB flat (Table 1). In addition, correlations between 〈rCBF〉 and relative ultrasound parameters did not reach statistical significance for the HOB perturbation (i.e., 〈rCBF〉 and 〈rPSV〉, r_s = 0.52, p = 0.15, p_A = 0.19; 〈rCBF〉 and 〈rEDV〉, r_s = 0.55, p = 0.12, p_A = 0.19; 〈rCBF〉 and 〈rMV〉, r_s = 0.49, p = 0.19, p_A = 0.19).

4. Discussion

The study was conducted to demonstrate the feasibility of diffuse correlation spectroscopy (DCS) for continuous monitoring of cerebral blood flow (CBF) in preterm infants and to compare measurements of DCS with transcranial Doppler ultrasound (TCD); the latter technique is used routinely for this population. A priori, the two modalities need not be strongly correlated since they measure different quantities: TCD measures flow in primary arteries, and DCS measures flow in tissue microvasculature. Our results show that a correlation exists between TCD measurements of peak systolic and mean velocities in the middle cerebral artery and DCS measurements of blood flow index, and that this correlation is statistically significant in this population. Furthermore, a weak but significant correlation exists between BFI and end diastolic velocity. The relative weakness of this correlation is due primarily to the low signal-to-noise ratio (SNR) of the EDV measurements for this population. Intuitively, one might expect BFI to correlate most strongly with MV, given that BFI is extracted from an autocorrelation curve which is averaged over three seconds (approximately 7 cardiac cycles). However, since MV is derived from EDV, it is strongly influenced by the low SNR of the EDV data.

While absolute values of BFI from DCS and velocities from TCD correlate significantly, correlations between relative changes in these parameters did not achieve significance. It is not entirely clear why the absolute velocity measurements correlate well with BFI, while relative changes do not correlate with rCBF. We hypothesize that there may have been insufficient statistical power given the limited sample size and relatively large physiological and measurement noise as well as inter- and intra-subject variability. Future experiments would benefit from concurrent TCD and DCS data acquisition.

Our TCD results of relative velocity changes concur with Anthony et al. [12], who showed that most infants showed little or no middle cerebral artery velocity response to postural changes. However, a direct comparison between the studies is difficult because Anthony et al. used a larger bed elevation (20°) and monitored continuously before and after the bed tilt for only 30 seconds.

For the future, DCS quantification can be improved. For example, a semi-infinite model was used to fit DCS data. This model simplifies the head geometry of the infants. In reality, the scalp, skull, cerebral spinal fluid, grey matter, and white matter possess different optical properties that can be accounted for, at least partially, in calculations [21,27,46]. Although the semi-infinite model can be improved upon, it provides a sufficient approximation for this pilot study.

Finally, throughout our measurements we have assumed a constant absorption and reduced scattering coefficient (μ_a and ${\mu }_s^{\prime }$) for all patients and for the duration of the study [47,48]. The exact values used, however, had little affect on our results. For example, a tenfold change in μ_a and tripling ${\mu }_s^{\prime }$ (0.01–0.15 cm⁻¹ and 5–15 cm⁻¹ respectively) did not significantly affect 〈rCBF〉 or the correlations between $\overline{BFI}$ and $\overline{PSV}$, $\overline{MV}$, and $\overline{EDV}$. Of course, individual deviations of μ_a and ${\mu }_s^{\prime }$ from the population average could effect the strength of these correlations. Because our population of preterm infants was fairly homogeneous, i.e. clinically stable with no life threatening conditions and of approximately the same gestational age, we felt some justification in assuming μ_a and ${\mu }_s^{\prime }$ to have little variation (i.e. less than 15%) across subjects, as is the case for full term neonates [53,54]. Future work would, however, benefit from the use of a hybrid DCS/NIRS instrument [21,22,24,28] to gather absolute optical properties from NIRS for each patient individually and then employ them when fitting for BFI.

5. Conclusion

We have demonstrated the feasibility of diffuse correlation spectroscopy to continuously monitor changes in cerebral blood flow in very low birthweight preterm infants. The skull anatomy of preterm infants enables us to probe a significant amount of the cortex, making them an attractive patient population for bedside DCS measurements.

Physiologically, we also showed that when posed with a small head of bed angle challenge of 12°, the infants maintained a constant blood flow on the microvascular scale. This result was corroborated in the macrovasculature by findings from transcranial Doppler ultrasound measurements. Measurements of blood flow index as measured by DCS were found to correlate significantly with measurements of peak systolic, end diastolic, and mean velocities of the middle cerebral artery calculated with TCD. These results further validate diffuse correlation spectroscopy as an accurate monitor of cerebral blood flow.