Assays with lower detection limits: implications for epidemiological investigations

Summary

Epidemiological investigations of health effects related to chronic low-level exposures or other circumstances often face the difficult task of dealing with levels of biomarkers that are hard to detect and/or quantify. In these cases instrumentation may not adequately measure biomarker levels. Reasons include a failure of instruments to detect levels below a certain value or, alternatively, interference by error or ‘noise’. Current laboratory practice determines a ‘limit of detection (LOD)’, or some other detection threshold, as a function of the distribution of instrument ‘noise’. Although measurements are produced above and below this threshold in many circumstances, rather than numerical data, all points observed below this threshold may be reported as ‘not detected’. The focus of this process of determination of the LOD is instrument noise and avoiding false positives. Moreover, uncertainty is assumed to apply only to the lowest values, which are treated differently from above-threshold values, thereby potentially creating a false dichotomy.

In this paper we discuss the application of thresholds to measurement of biomarkers and illustrate how conventional approaches, though appropriate for certain settings, may fail epidemiological investigations. Rather than automated procedures that subject observed data to a standard threshold, the authors advocate investigators to seek information on the measurement process and request all observed data from laboratories (including the data below the threshold) to determine appropriate treatment of those data.

Introduction

Biomarkers are commonly used for biological assessments in a variety of settings. Clinically, medical tests use biomarkers for diagnosis (e.g. blood glucose for gestational diabetes), and for risk stratification (e.g. age and chorionic villi sampling for genetic disorders) at the subject level. Biomarkers are also commonly utilised in population studies for surveillance. Epidemiological investigations increasingly rely on laboratory tests for assessment of biomarkers of exposure and/or outcome. Population studies often aggregate individual levels to estimate summary statistics of interest, such as mean and variance or median and range, or regression parameters (e.g. estimated odds or hazard ratios).

When a biomarker is subject to a detection limit that affects measurement, decisions are required concerning how to handle values at or below the threshold in order to avoid biasing parameter estimates. Such low biomarker levels are likely to be encountered in various settings including investigations of health effects from chronic low-level exposures, or when study subjects are infants or children, whose levels of some biomarkers are inherently low. Alternatively, this difficulty can occur as a result of the biological specimen type used for testing. For example, serum levels of lipophilic xenobiotics have been observed at substantially lower levels than are found in adipose tissue samples from the same individuals.¹

Possible reasons for failures of instrumentation to adequately measure low biomarker levels include an inability to detect levels below a certain value – false negatives. Alternatively, when instrumentation fails to differentiate the biomarker of interest from ‘noise’, a false positive signal may obscure measurement. Current laboratory practice experimentally determines a lower ‘limit of detection (LOD)’ and rather than numerical data, results observed below that value may be reported as ‘not detected’.

Thresholds such as the LOD or limit of quantification (LOQ) are determined as a function of the error or ‘noise’ involved in the measurement process. Generally, samples with known biomarker levels (usually 0, or ‘blanks’) are measured in series. From these measurements the standard deviation of the instrument noise (σ_ε) is estimated. Importantly, variation does not only occur when a true signal is absent, as in a zero blank. In some cases estimation of σ_ε utilises samples spiked with a known biomarker level in the expected range for study samples, suggesting that error is not constrained to only the lowest values of the biomarker. ² The International Union of Pure and Applied Chemistry (IUPAC) definition for the LOD is the concentration or quantity ‘… derived from the smallest measure, X_L, that can be detected with reasonable certainty for a given analytical procedure’, where X_L equals the mean of the blanks plus k times the standard deviation of the blanks; for the LOD, IUPAC suggests k equal to 3, and generally the LOQ is set with k equal to 10.^3,4

The LOD can be seen as a random variable itself, and may be calculated for each use of an assay, although information supplied by the manufacturer is sometimes used as a fixed threshold. Although the LOD is used for decision making regarding biomarker measurements, determination of the LOD is performed explicitly without any biomarker present in samples. This approach narrowly focuses on not assigning a biomarker value where there is only noise, and may fail the purposes of epidemiological investigations. Biomarker assessment in epidemiological studies entails a more complete treatment of error that includes consideration of false positives as well as false negatives.

Sources of error in lab tests

For many laboratory assays, the LOD is determined as previously described, using serial blank measures to describe measurement error.² All assays include a number of possible sources of reproducibility and/or measurement error. With antibody-based assays, pipetting errors, incomplete mixing of samples and/or reagents, contamination, non-specific binding, and random instrument processes may contribute to both inconsistency and inaccuracy. The possible sources of test–retest variability and/or measurement error in chromatography/spectrometry primarily include sample preparation, contamination and random instrument processes.

These sources of error may be broadly placed into two bins. First consider all observations, Z_i, represented as

$$Z_i=X_i+{\mathrm{\epsilon }}_i,$$

where X_i are the true biomarker values, and the ε_i are sums of all sources of error influencing the measurement of the biomarker. Traditional measurement error models consider a mean-zero distribution for ε_i and rather focus on its variance, whereas bias in measurement will cause a shift in ε_i from the origin. The error may be either a function of the biomarker value whereby error exists only when X_i is less than some value (e.g. the LOD), or it may apply across biomarker levels. The amount of error may be related to the biomarker level or it may occur regardless of biomarker level. For many of the previously described sources of error, the latter is likely to be the case and error will apply across biomarker levels. For example, it is not reasonable to believe that contamination only exists when the biomarker is scarce. Use of spiked blanks to set the LOD indicates an implicit acknowledgement that test–retest variability exists even at elevated biomarker levels.

Traditionally, discussions of detection limits in analytical chemistry have focused on the decreasing precision of measurements as the true signal decreases, as reflected by the relative standard deviation. However, this does not imply error constrained to low biomarker levels, but rather that error will be higher relative to signal towards the left tail of the distribution. Conventional application of the LOD suggests a belief that the separation between signal and noise is important only for low biomarker levels. Diagnosis based on an individual’s biomarker level when the signal to noise ratio is very low is ill-advised, but these data points may be important for epidemiological investigations of population parameters.

Impact of traditional detection limit methods on estimation

When laboratory data are presented to investigators as a combination of ‘nondetects’ and numerical data for observations below and above the threshold, respectively, a false dichotomy may be created. If an error that occurs in the measurement process is independent of the true biomarker level, then all observations should be similarly considered. The substantial body of work regarding left-truncated data has largely considered a differential error that exists only below some threshold. As a result, data with a detection threshold are cast as a missing data issue, and solutions are aimed at whether and how to replace these missing data. Suggested methodologies include truncation of the data at the threshold or imputation of a constant – zero or a function of the LOD is commonly employed – for below-threshold observations, which are attractive in their simplicity. More complex approaches model the missing data, generally under some distributional assumptions, and include maximum likelihood estimations of below-threshold observations or Tobit regression.^2,5–9 These methods are appropriately employed when the error is a function of the biomarker level and is indeed applicable to data only below the threshold. However, blanket use of any of these approaches may be an oversimplification of the situation and may lead to biased estimates when used for epidemiological studies.

Addressing the problem

In the situations we have discussed, numerical data can be observed below the established detection threshold. Conventional approaches for determining the threshold treat observations below this threshold as unreliable. As a result, these data may not reach the data analyst of the epidemiological study. In turn, the data analysts may believe that the LOD is related to sensitivity and that no data can be observed below that threshold. In truth, observations at all biomarker levels are subject to measurement error or background noise.

Appropriate treatment of biomarker data depends upon the nature of the background noise. It should be established whether the same amount of error exists across the whole distribution of the biomarker of interest. This is not unlike a test for heteroscedasticity in linear regression. If error is subject to a threshold such that

$$Z_i=\{\begin{array}{cc}{X}_i\hfill & \text{if}x\ge \mathit{\text{LOD}}\hfill \\ X_i+{\mathrm{\epsilon }}_i\hfill & \text{if}x<\mathit{\text{LOD}}\hfill \end{array}$$

then it is appropriate to treat below-threshold data one way and those above the threshold another. Conversely, if the error is equally distributed, then all the data may be treated similarly with regard to error. For conventional determination of the LOD, use of true blanks in combination with blanks of mid- and high-range known values may serve as a ‘validation set’, and provide information regarding the error distribution. In order to make this determination, one should compare measures of error variance (standard deviation, relative standard deviation, coefficient of variation) across the range of standards. Generally, information regarding the measurement of standards is not provided by laboratories – a request would need to be made in order to have access to this information.

However, a simpler approach is available without deviating from current laboratory practice; replicates are frequently utilised and can be included in datasets to provide the same information at all relevant biomarker levels. If the error (the variance of replicates) is primarily constrained to low biomarker levels, then traditional LOD methods should be used; if it is the same across levels, then techniques for addressing measurement error are more appropriately employed. Many such methods are available and have been extensively described in the literature.^5,6,8,9 In the case that measurement error (i.e. variance of replicates) is unconstrained but varies with biomarker levels, nonlinear calibration function models can be used to address bias.¹⁰ Common imputations applied to data below the threshold result in minimally biased estimates when the distribution of data can be accurately described. Caution should be taken, as available data must be sufficient to allow for correct distributional specification; discrepancies between the assumed and actual distributions may give rise to bias dependent upon the accuracy of the assumed distribution.^2,5–7,9

By the same token, biomarkers measured with an upper measurement threshold may be considered. In such situations, there is less uncertainty regarding the presence of biomarker information, but the exact value is not established owing to issues with quantification. Although not explicitly discussed herein, the approaches for dealing with left-censored biomarker data can be used for biomarker data that are right censored.

Examples

Table 1 and Fig. 1 illustrate two circumstances of data subject to a lower measurement threshold. Example 1 illustrates the use of a calibration series to assess the distribution of error, and uses data from a study evaluating the risk of pregnancy outcomes associated with certain immunological biomarkers.^11,12 Serum samples from the Collaborative Perinatal Project¹³ were selected and multiplex ELISA assays used for measurement. Table 1 displays assay results for the standards used to generate the calibration curve for the protein, granulocyte colony stimulating factor. As per protocol, from a standard of known high concentration, threefold serial dilutions were added in replicates to the first 14 wells of a 96-well plate; a diluent-only blank was also measured in replicate. The manufacturer-determined lower threshold for this assay is 0.57 pg/mL, which was determined as the mean plus 2 standard deviations from measurements of analyte levels in 20 blank samples. The data shown in Table 1 display a source of error that applies across all levels of the protein, suggesting that non-constrained error techniques, such as regression calibration, be employed rather than censoring and imputation.

Table 1.

Serial dilution calibration set for multiplex assay of granulocyte colony stimulating factor measurements in serum, measured by Luminex-100

		Observed optical density (RFU)
Standard/concentration		Replicate 1	Replicate 2	Mean (SD)	CV (%)
1	6000.0 pg/mL	7604.0	7086.0	7345.0 (366.3)	5.0
2	2000.0 pg/mL	4016.0	3957.5	3986.8 (41.4)	1.0
3	666.7 pg/mL	1661.0	1566.5	1613.8 (66.8)	4.1
4	222.2 pg/mL	620.5	602.0	611.2 (13.1)	2.1
5	74.1 pg/mL	245.0	222.0	233.5 (16.3)	7.0
6	24.7 pg/mL	109.5	101.0	105.3 (6.0)	5.7
7	8.2 pg/mL	61.5	56.0	58.8 (3.9)	6.6
Blank	0.0 pg/mL	26.0	27.5	26.8 (1.1)	3.9

RFU, relative fluorescence units; SD, standard deviation; CV, coefficient of variation; pg/mL, picograms per millilitre (LOD = 0.57 pg/mL).

Figure 1.

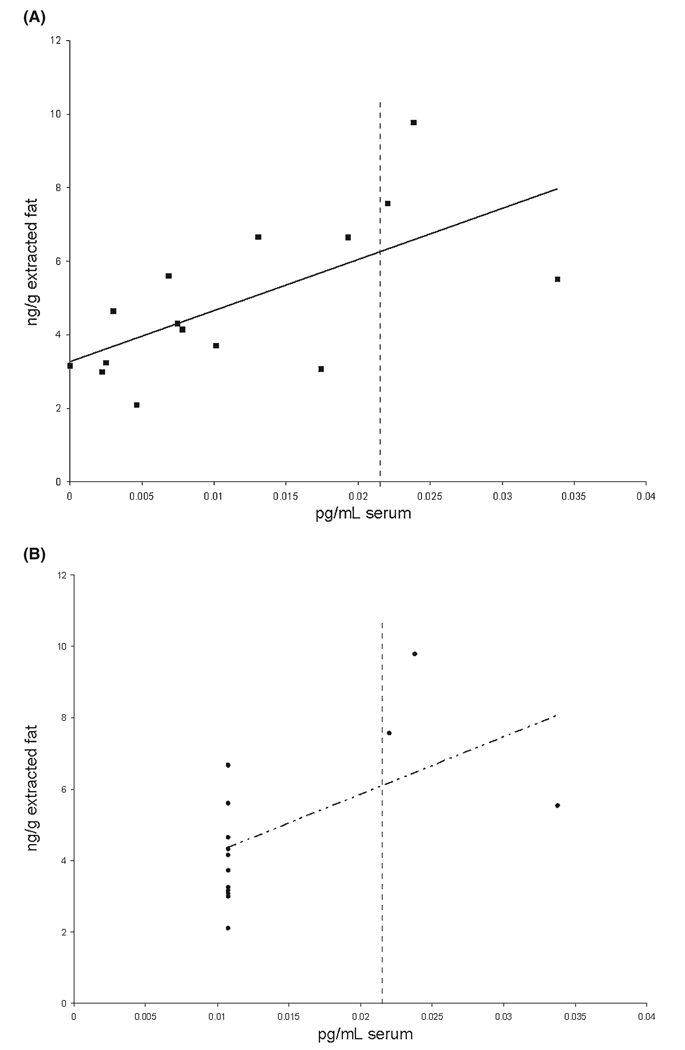
The data as observed and after imputation for below-threshold values – polychlorinated biphenyl congener number 105 in paired serum and adipose tissue samples as measured by gas chromatography-mass spectrometry, and after blank subtraction and recovery adjustment. ■, observations; ——, estimated regression line; •, observations after imputation; - -·- -, estimated regression line after imputation; ┋, limit of detection (LOD). Most data points are below the LOD at 0.02159 pg/mL serum. Utilising all observed data points regardless of the LOD results in an estimated regression line with intercept equal to 3.3 and slope equal to 139.3. The estimated regression line after imputation of 0.01080 (LOD/2) for below-threshold points has intercept equal to 2.6 and slope equal to 161.0.

The data for Example 2 are from a study of the effect of exposure to polychlorinated biphenyls (PCBs) on the risk of endometriosis as determined by laparoscopy.¹⁴ In a subset of study participants, serum samples and adipose tissue samples were taken, and PCB levels measured by gas chromatography-mass spectrometry (GC-MS). Owing to their lipophilic nature, PCBs are concentrated in fat; however, they are often measured in more easily attainable biological matrices such as blood. A correlation between values obtained in different specimens is required for these matrices to be used interchangeably, and was the subject of a small methodological sub-study.¹ Figure 1 shows data produced by GC-MS. When all observations are unaltered, shown in panel A, there is a clear relationship between serum and adipose tissue values, with a correlation coefficient equal to 0.65, and a 95% confidence interval [CI] of [0.21, 0.87]. Panel B illustrates the result of following a common practice for treatment of data below the detection threshold – imputing half the LOD for all such data – and the correlation coefficient drops to 0.54 [95% CI 0.03, 0.82]. In this case, the linear relationship differs only somewhat and 95% CIs overlap between the two approaches, and the same conclusions would be reached. This is not the case had investigators used (99% CIs [0.03, 0.91] in panel A; [−0.14, 0.87] in panel B); use of all observations results in a statistically significant correlation, whereas substitution does not. Moreover, there has been reluctance to evaluate congeners measured below the LOD in a large proportion of samples.^15,16 In this case 75% of serum values were less than the LOD and were those observations to be considered as missing; PCB 105 might not be considered for investigation.

Conclusions

Many measurement protocols entail experimental determination of an LOD and will yield numerical observations above and below the LOD. Elimination of data points below a LOD may be appropriate in some settings, such as clinically when providing diagnoses to patients, or in surveillance studies focused on establishing the presence or absence of a biomarker. However, in epidemiological studies a more nuanced approach to measurement error should be utilised to avoid biasing estimates. Rather than automated procedures that subject observed data to a standard threshold, investigators are encouraged to seek information on the measurement process and request all observed data from laboratories (including generation of the standard curve and the data below the threshold). Laboratory personnel should provide these data in order to determine appropriate treatment of these data cooperatively. Given this information, it is elementary to determine if error exists only below a threshold, above and below the threshold as a function of the true biomarker value, or completely independently of the biomarker values. When error is constrained to apply only to a certain range of biomarker levels (i.e. below the LOD), then conventional methods that differentiate between data above and below a threshold as previously described for handling left-censored data are appropriate. However, an error that exists across all biomarker levels suggests use of other measurement error approaches, familiar to epidemiologists.^10,17–20