Thermodynamic Dissection of Progesterone Receptor Interactions at the Mouse Mammary Tumor Virus Promoter: Monomer Binding and Strong Cooperativity Dominate the Assembly Reaction

Abstract

Progesterone receptors (PRs) play critical roles in eukaryotic gene regulation, yet the mechanisms by which they assemble at their promoters are poorly understood. One of the few promoters amenable to analysis is the mouse mammary tumor virus gene regulatory sequence. Embedded within this sequence are four progesterone response elements (PREs) corresponding to a palindromic PRE and three half-site PREs. Early mutational studies indicated that the presence of all four sites generated a synergistic and strong transcriptional response. However, DNA binding analyses suggested that receptor assembly at the promoter occurred in the absence of significant cooperativity. Taken together, the results indicated that cooperative interactions among PREs could not account for the observed functional synergy. More broadly, the studies raised the question of whether cooperativity was a common feature of PR-mediated gene regulation. As a step toward obtaining a quantitative and, thus, predictive understanding of receptor function, we have carried out a thermodynamic dissection of PR A-isoform interactions at the mouse mammary tumor virus promoter. Utilizing analytical ultracentrifugation and quantitative footprinting, we have resolved the microscopic energetics of PR A-isoform binding, including cooperativity terms. Our results reveal a model contrary to that inferred from previous biochemical investigations. Specifically, the binding unit at a half-site is not a receptor dimer but is instead a monomer; monomers bound at half-sites are capable of significant pairwise cooperative interactions; occupancy of all three half-sites is required to cooperatively engage the palindromic-bound dimer; and finally, large unfavorable forces accompany assembly. Overall, monomer binding accounts for the majority of the intrinsic binding energetics and cooperativity contributes an approximately 1000-fold increase in receptor–promoter stability. Finally, the partitioning of cooperativity suggests a framework for interpreting in vivo transcriptional synergy. These results highlight the insight available from rigorous analysis and demonstrate that receptor–promoter interactions are considerably more complex than typically envisioned.

Introduction

Progesterone receptors (PRs) are members of the nuclear receptor superfamily of ligand-activated transcription factors.¹ The traditional understanding of PR function is that the receptors dimerize in solution, bind to progesterone response elements (PREs) at upstream promoter sites, and recruit an array of coactivating proteins in order to remodel chromatin and activate transcription. This model is based upon an enormous number of biochemical and molecular biological studies, and it has lent great insight into the qualitative and semiquantitative aspects of receptor-mediated gene regulation. However, for PR and all other nuclear receptors, a quantitative and, thus, truly predictive understanding of function is still lacking. Even the seemingly straightforward basis by which receptors assemble at multisite promoter sequences is not understood from any physicochemical perspective. This absence of knowledge has limited our insight into the basic principles responsible for higher eukaryotic gene regulation and likely hindered the development of new drugs and therapeutics.

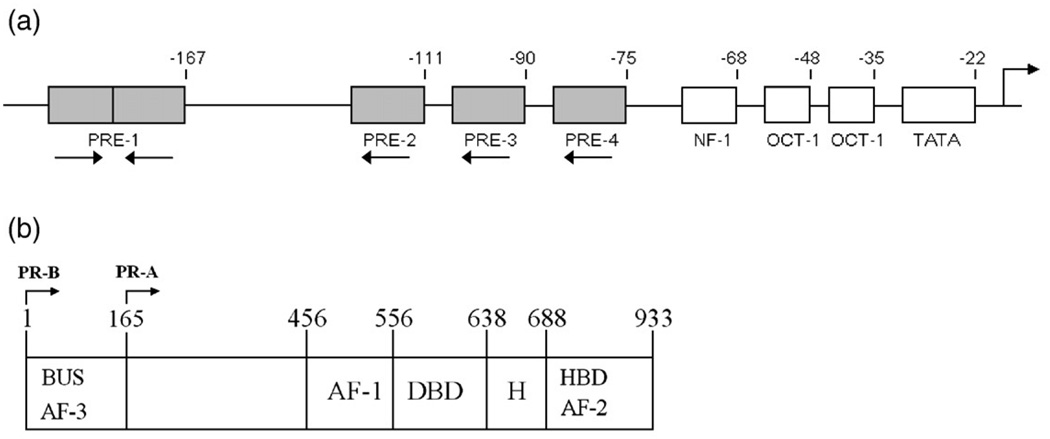
One of the very few (and perhaps only) PR-regulated promoters amenable to detailed analysis is the mouse mammary tumor virus (MMTV) gene regulatory sequence. This promoter has long been known to be regulated by PR and its closely related homolog, the glucocorticoid receptor (GR).² As shown in Fig. 1a, the sequence contains a number of cis-acting elements including a TATA box, two Oct-1 sites, an NF-1 site, and multiple response elements for PR or GR binding. More specifically, there are at least four clearly recognizable receptor binding sequences—a palindromic PRE (site 1) and three identical half-site PREs (sites 2–4). Semiquantitative footprinting and filter binding studies indicated that receptors bound at all four of the PREs,^2–4 and glycerol gradient centrifugation studies⁴ suggested that dimers assembled at each site.⁵ Finally, mutational studies indicated that loss of any one site decreased the level of transcriptional activity up to 10-fold,⁶ demonstrating that transcriptional activation was synergistic in character and, thus, suggestive of communication among the sites.

Fig. 1.

Schematic representations of the MMTV promoter and the two human PR isoforms. (a) Functional binding sites located within the MMTV promoter. PREs are indicated by shaded rectangles and labeled 1–4. Site 1 corresponds to the palindromic PRE (GTTACAAACTGTTCT); sites 2–4 correspond to the three half-site PREs of identical sequence (TGTTCT). Binding sites for cofactors are indicated by open rectangles and labeled as NF-1, OCT-1, and TATA. The numbers above the schematic indicate base-pair position relative to the transcriptional start site. Orientation of each PRE is indicated by an arrow below the site. The location of the transcriptional start site is as indicated by the arrow above the schematic. (b) PR-A and PR-B domain structure. Functional regions are as indicated: DBD, DNA binding domain; HBD, hormone binding domain; H, hinge; AF, activation function; BUS, B-unique sequence. PR-B is defined as amino acids 1–933, and PR-A is defined as amino acids 165–933.

It had been reasonably hypothesized that MMTV promoter functional synergy could arise through receptor-mediated cooperative interactions.³ However, the results of the footprinting studies noted above suggested that receptor assembly at the promoter was accompanied by little to no cooperativity. This conclusion was based on the observation that mutation of individual response elements changed receptor half-saturation values at the remaining sites by only two- to threefold.^3,4 This was despite the fact that, at least for GR, the binding transitions at each response element were extremely steep,⁴ indicating that additional reactions were somehow coupled to DNA binding (e.g., cooperative assembly or solution dimerization). Furthermore, the results were in contrast to concurrent studies of a synthetic PR-regulated promoter, which indicated the presence of highly cooperative interactions between adjacently bound PR dimers.⁷ This discordance thus left unanswered the mechanism of receptor-mediated transcriptional synergy and raised the broader question of whether cooperativity was a common feature of PR (and GR) function. These elementary and essential issues have never been resolved for any nuclear receptor, even as current research has now moved toward addressing the even more complex phenomena of coactivator recruitment and chromatin remodeling.

Any attempt to quantitatively understand PR function must first take into account the presence of two distinct isoforms: an 83-kDa PR A-isoform (PR-A) and a 99-kDa PR B-isoform (PR-B) (Fig. 1b).⁸ The two proteins are identical in primary structure except for the addition of 164 amino acids located at the N-terminus of PR-B. These residues define the B-unique sequence or BUS. Despite their high degree of sequence identity, the two isoforms exhibit a number of unique functional properties, including differences in transcriptional activity,^9,10 ligand response,¹¹ gene regulation,¹² and tissue-specific physiological effects.^13,14 We have previously analyzed the thermodynamics of PR-A and PR-B binding to synthetic promoters containing either one or two palindromic response elements and have found that a role for BUS is to allosterically enhance the cooperative binding energetics of PR-B relative to PR-A.^15,16 As a functional consequence, the increased affinity seen for the B-isoform predicts promoter occupancies that accurately correlate with its increased transcriptional activation properties relative to PR-A. Since this difference in activation is also maintained on the natural, nonsynthetic MMTV promoter,¹⁷ we hypothesized that PR-A should be capable of assembling at the promoter via high-affinity binding but with moderate cooperative interactions. Furthermore, since our work on the self-association energetics of PR-A found that there are few receptor dimers present upon initiation of DNA binding and that dimer binding is penalized relative to monomer binding,^15,16,18,19 we anticipated that monomers rather than dimers should assemble at individual half-sites. This issue of cooperative assembly is of particular interest in light of our work on steroid receptor coactivator-2 (SRC2), which demonstrated that efficient coactivator recruitment to the promoter is dependent upon cooperativity between tandemly linked PREs.²⁰

As a step toward a quantitative understanding of PR function, we present here a thermodynamic dissection of PR-A interactions with the MMTV promoter sequence. Using analytical ultracentrifugation and quantitative footprint titrations, we have resolved the stoichiometries of binding, the intrinsic DNA binding energetics, and the microstate cooperativity terms for PR-A assembly at this promoter. Our analysis of the data reveals that, in contrast to previous reports, the binding unit at a half-site is not a receptor dimer but is instead a monomer. Moreover, monomers bound at half-sites are capable of significant pairwise cooperative interactions, and occupancy of all three half-sites is required to cooperatively engage the palindromic-bound dimer. Each of these cooperative interactions is of moderate free energy, but as a whole, they translate into an approximately 1000-fold increase in receptor promoter stability. Somewhat unexpectedly, the large amount of cooperative free energy is balanced by unfavorable forces that penalize both monomer and dimer assembly reactions at the promoter. Finally, the distribution of the cooperative binding energetics may lend insight into the functional synergy observed in early mutational analyses. This study represents the first rigorous dissection of the interactions between a full-length nuclear receptor and any natural promoter and may serve as a template for dissecting and understanding other newly identified PR-regulated promoter sequences.

Results

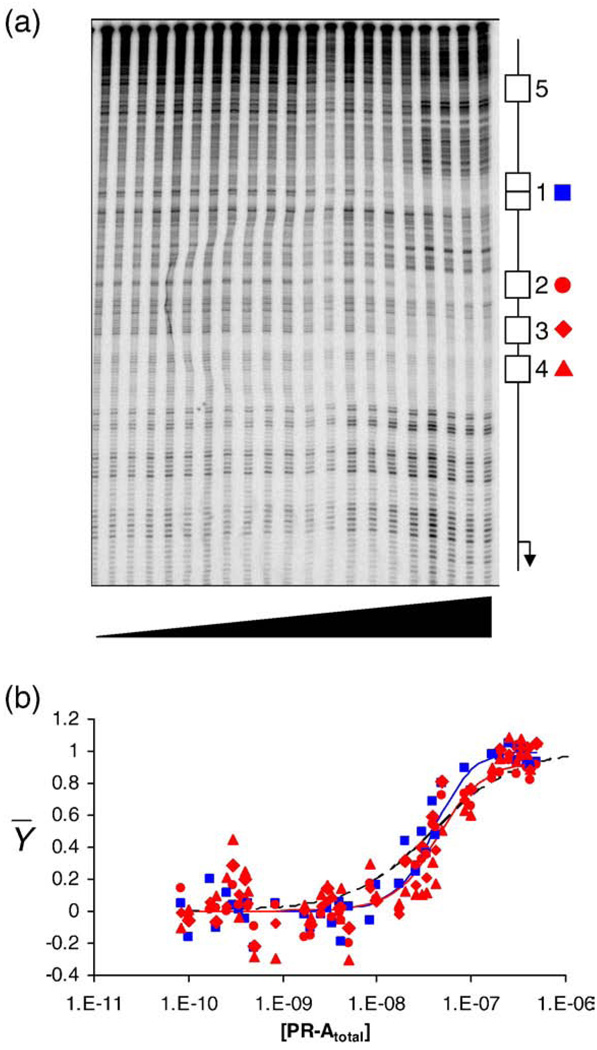
Shown in Fig. 2a is a quantitative DNase footprint titration of the wild-type MMTV promoter. It is evident that PR-A binding is specific for five regions, labeled here as sites 1–5. Dideoxy sequencing analysis reveals that the first four sites correspond to the palindromic site 1 and half-sites 2–4, respectively. Close inspection of the sequencing results indicates that only one or two additional nucleotides flanking each of the four PREs are also protected (data not shown). We also identified a fifth, cryptic binding site present on all MMTV promoter templates (site 5) located at least 149 bp upstream of site 1. We were unable to definitively identify the sequence of this site due to its distance from the 3′ label, but it likely corresponds in part to TGTTGT, given the close agreement to the consensus half-site binding sequence TGTTCT. Finally, seen only at the highest concentrations of receptor are hypersensitive bands surrounding many of the binding sites. The exact basis for this phenomenon is unclear, but previous observations suggest that it is due to receptor-induced distortion of the DNA.^15,16,21,22

Fig. 2.

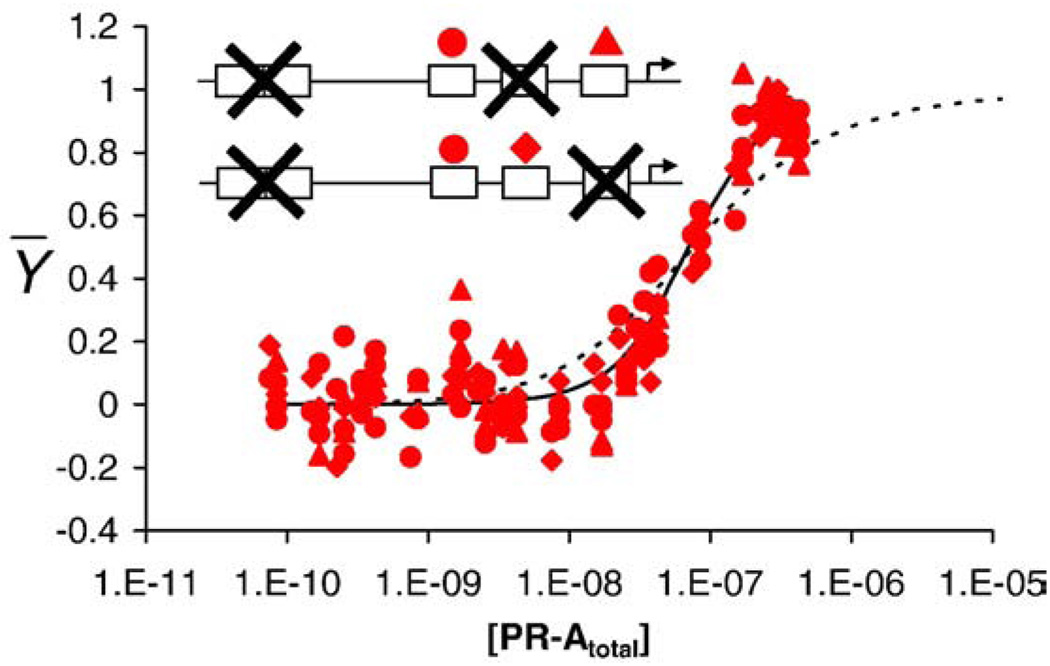
Quantitative footprint titration of the wild-type MMTV promoter and individual-site binding isotherms. (a) Representative footprint titration of the MMTV_wt promoter. PR-A concentration increases from left to right. A schematic of the canonical PRE binding sites (sites 1–4) and the cryptic site (site 5) is shown on the right. Symbols used to represent binding to each site in all footprints are as follows: blue squares, site 1; red circles, site 2; red diamonds, site 3; red triangles, site 4. (b) Fractional saturation of sites 1–4 on the wild-type promoter as a function of total PR-A concentration. Symbols are as described in (a). Continuous lines represent a global analysis of all seven MMTV templates using the microscopic model described in the text. The blue line represents binding to the palindromic site 1. The red line represents binding to a single half-site; only one line is shown since the energetics of binding to each half-site are identical. The black broken line represents a noncooperative, Langmuir binding isotherm.

Quantitation of sites 1–4 (Fig. 2b, plotted in units of total protein concentration) generated steep individual-site binding isotherms indicative of cooperative interactions among all the sites. The extent of cooperativity can be appreciated by comparison to a noncooperative, Langmuir binding isotherm overlaid on the data. By contrast, analysis of binding isotherms from site 5 (as collected from the wild-type promoter and six mutated promoters) revealed that the curve shape was noncooperative in nature and the affinity was independent of promoter type. Thus, PR-A binding to the cryptic site does not appear to be linked to binding at sites 1–4 and is not included in our subsequent analyses. However, these results do not preclude the possibility that site 5 plays a functional role in promoter regulation.

A simple molecular interpretation of the data in Fig. 2 is that a PR-A dimer is binding to the palindromic DNA sequence, whereas PR-A monomers are binding at the three half-sites. Additionally, for both monomers and dimers, the steep binding isotherms suggest that cooperative interactions are contributing significant stabilization to receptor–promoter interactions. Unfortunately, as useful as this interpretation may be, it offers no quantitative framework for describing receptor–promoter interaction mechanisms. Toward this end, we have developed a statistical thermodynamic model for PR-A assembly at the MMTV promoter. We have tested and validated this model by carrying out global analyses of the individual-site binding isotherms from the wild-type promoter in conjunction with isotherms generated from six mutated or “reduced-valency” promoter templates. The analysis confirms the qualitative interpretation presented above but more importantly reveals a specific code for cooperative assembly unobtainable from visual inspection of the data. Below, we present the microscopic rules and states that define the model and then describe its validation by addressing each of the prominent features in turn.

Statistical thermodynamic formulation of PR-A:MMTV promoter interactions

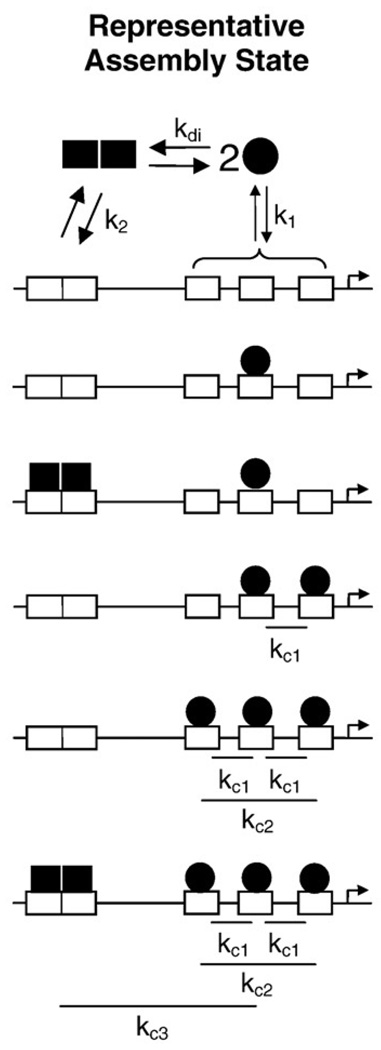
Listed in Table 1 are the 16 microstates and associated energetic terms predicted by our model. Shown in Fig. 3 is a schematic of representative ligation states. The rules that define this model are summarized as follows:

1. PR-A monomers bind at each individual half-site with an intrinsic affinity defined as ΔG₁. (Since the sequence of each half-site is identical, binding to each site is described by the same free-energy term.) The relevant microstates as shown in Table 1 are species 2–4.

2. A preformed PR-A dimer binds at the palindromic site with an affinity of ΔG₂ (species 5).

3. Pairwise cooperativity exists between monomers bound at half-sites (ΔG_c1, species 6–8) but not between individual monomers and the dimer bound at the palindrome (species 9–14).

4. Nonadditive cooperativity associated with complete occupancy of the half-sites is accounted for by ΔG_c2 (species 15).

5. Cooperative interactions between bound monomers and the dimer at the palindrome only arise when the three half-sites are fully occupied (ΔG_c3, species 16).

6. PR-A undergoes monomer–dimer self-association in the absence of DNA. This rule can be taken as fact in light of our previous analysis of the energetics of PR-A dimerization (ΔG_di) under conditions identical with those of the current study.¹⁵

Taken together, these rules define the 16-species model, which will also be referred to as the “microscopic” model for the purposes of discussion.

Table 1.

Model configurations and free energies for PR-A:MMTV binding

	Species binding configurationa
Species (s)	1	2	3	4	Free energy contributionb
1	–	–	–	–	Reference state
2	–	x	–	–	ΔG1
3	–	–	x	–	ΔG1
4	–	–	–	x	ΔG1
5	xx	–	–	–	ΔGdi+ΔG2
6	–	X	X	–	2*ΔG1+ΔGc1
7	–	X	–	X	2*ΔG1+ΔGc1
8	–	–	X	X	2*ΔG1+ΔGc1
9	xx	x	–	–	ΔGdi+ΔG2+ΔG1
10	xx	–	x	–	ΔGdi+ΔG2+ΔG1
11	xx	–	–	x	ΔGdi+ΔG2+ΔG1
12	xx	X	X	–	ΔGdi+ΔG2+2*ΔG1+ΔGc1
13	xx	X	–	X	ΔGdi+ΔG2+2*ΔG1+ΔGc1
14	xx	–	X	X	ΔGdi+ΔG2+2*ΔG1+ΔGc1
15	–	X	X	X	3*ΔG1+2*ΔGc1+ΔGc2
16	XX	X	X	X	ΔGdi+ΔG2+3*ΔG1+2*ΔGc1+ ΔGc2+ΔGc3
17	XX	–	–	–	2*ΔG1+ΔGc4
18	–	X	X	X	3*ΔG1+ΔGc234
19	XX	X	X	X	ΔGdi+ΔG2+3*ΔG1+ΔGc1234

^aEach site on the MMTV_wt promoter is indicated as sites 1–4. Each diagram represents one of the possible microscopic configurations. A PR-A protomer bound to a site is indicated by an “x.” Cooperative PR-A binding is indicated by an “X.”

^bThe free-energy change is related to each binding constant through the standard relationship ΔG_i=−RT ln(k_i), where R is the gas constant and T is the temperature in kelvin.

Fig. 3.

Schematic of selected assembly states for PR-A interactions at the MMTV promoter. MMTV promoter structure is as described in Fig. 1a. PR-A monomers (filled circle) can either dimerize in solution (k_di) or bind at a half-site (k₁). A solution dimer can bind at the palindromic site (k₂). Two monomers bound at half-sites cooperatively interact in a pairwise fashion (k_c1). Non-additive cooperativity induced by addition of a third monomer to the half-sites is accounted for by k_c2. Saturation of the MMTV promoter is linked to a third cooperative interaction between the palindrome and the three half-sites (k_c3).

We additionally tested the possibility that assembly at the palindromic site 1 occurs via a successive monomer binding and DNA-induced dimerization, rather than via a preformed dimer intermediate. This analysis was carried out by simply substituting all ΔG₂+ΔG_di terms in Table 1 for a ΔG₁+ΔG₁+ΔG_c4 term (species 17), where ΔG₁ is the free energy of binding to a half-site and ΔG_c4 is an intrasite cooperativity term describing the DNA-induced dimerization reaction.

In order to verify that all cooperative interactions are accounted for in the model, we describe two macroscopic cooperativity terms, ΔG_c234 and ΔG_c1234. The first term accounts for the entire cooperative free energy associated with saturating the three half-sites (species 18), and the second term accounts for the entire cooperative free energy for saturating the wild-type promoter (species 19). Species 18 and 19 thus substitute for species 15 and 16 in Table 1, respectively, and allow for an alternative formulation of the 16-species model. For the purposes of discussion, this will be referred to as the “macroscopic” model.

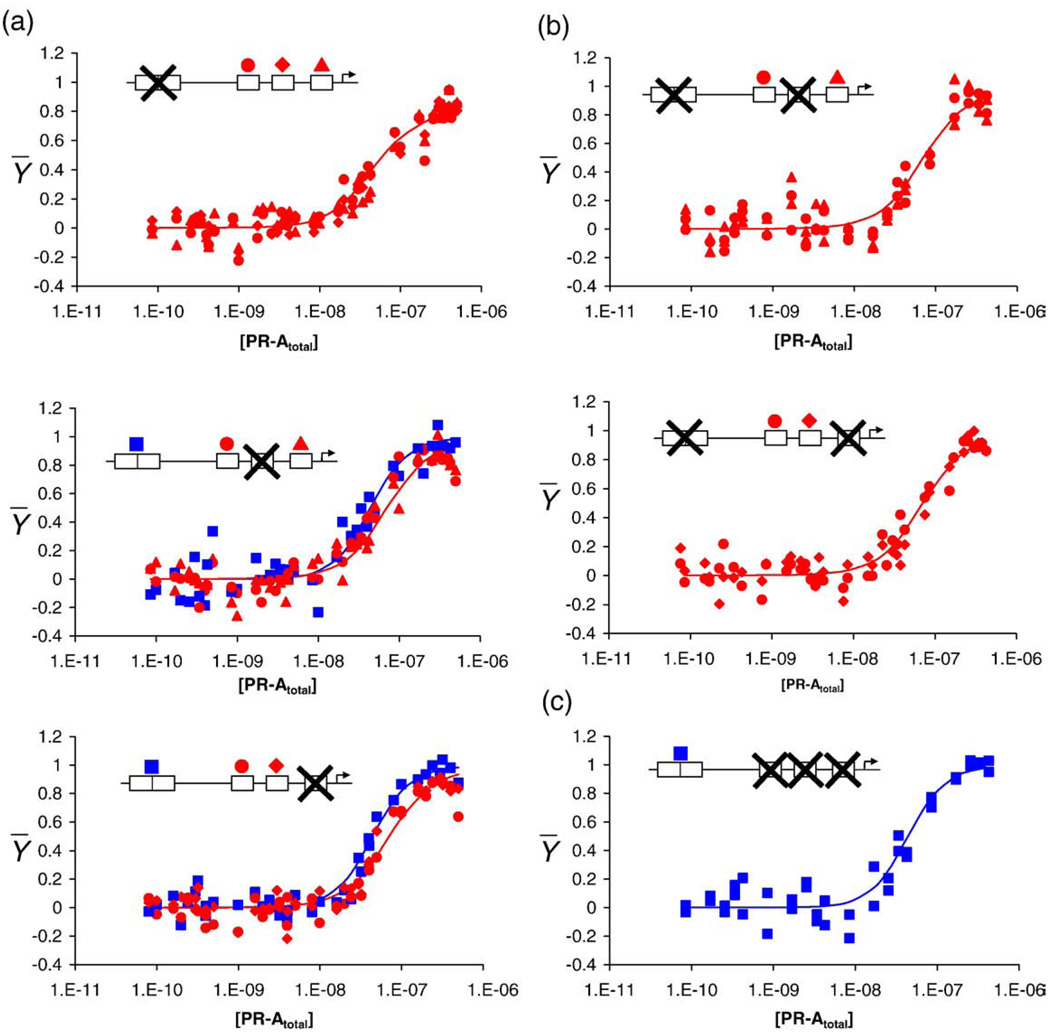
In order to resolve the microscopic energetics of PR-A binding to the MMTV promoter (i.e., the intrinsic and cooperative free-energy terms in Table 1), it is necessary to globally analyze the binding isotherms generated from the wild-type promoter with those obtained from the reduced-valency promoter templates. These latter templates can be divided into three classes. The first class (Class 1) is made up of three templates, each having a single mutated binding site (MMTV₁₋, MMTV₃₋, and MMTV₄₋). The individual-site binding isotherms for each of these templates are shown in Fig. 4a. The second class (Class 2) is made up of two templates, each containing two mutated binding sites (MMTV_1−,3− and MMTV_1−,4−). The binding isotherms resolved from each of these templates are shown in Fig. 4b. The third class (Class 3) is made up of a single template that contains a mutation at each of the three half-sites and, thus, represents binding to the isolated palindrome (MMTV_{2−,3−,4−}). The relevant binding isotherm is shown in Fig. 4c. Visual comparison of the wild-type binding data to that of the six reduced-valency templates indicates that, just as seen in earlier biochemical investigations,^2,3 the loss of a viable binding site changes the apparent binding affinity at the remaining sites only slightly.

Fig. 4.

Individual-site binding isotherms for MMTV promoter reduced-valency templates. The fractional saturation of each promoter template is shown as a function of total PR-A concentration. Each panel contains an inset depicting the specific mutant. “X” indicates a nonfunctional site. Shown above the functional sites is the symbol (as described in Fig. 2) used to depict binding to that specific site. Blue lines represent best fit to site 1 from the global analysis. Red lines represent best fit to individual half-sites from the global analysis. (a) Class 1 isotherms (MMTV₁₋, MMTV₃₋, and MMTV₄₋). (b) Class 2 isotherms (MMTV_1−,3− and MMTV_1−,4−). (c) Class 3 isotherm (MMTV_{2−,3−,4−}).

PR-A monomers and dimers bind with nanomolar intrinsic affinities

For all 18 isotherms, the continuous lines through the data points (Fig. 2 and Fig 4) represent the results of the global analysis using the microscopic 16-species model described in Table 1. It is evident that the model describes well all the binding transitions (standard deviation of 0.082 apparent fractional saturation units), capturing both their apparent affinities and curve shapes. The resolved energetics are presented in Table 2—the accompanying error estimates represent 68% confidence intervals as determined by Monte Carlo analysis. As shown, the affinity of monomer binding (ΔG₁) was determined to be −8.1 kcal/mol (68% confidence interval of −7.9 to −8.2 kcal/mol), which translates to a dissociation constant of 200 nM. By contrast, the preformed dimer binds with a free-energy change (ΔG₂) of −11.2 kcal/mol (68% confidence interval of −11.2 to −11.3 kcal/mol), which translates to a K_d of 1.5 nM. These values are statistically identical with those found previously for our analysis of a synthetic promoter containing nearly identical response elements,¹⁵ lending credence to our results and to the validity of our approach.

Table 2.

Resolved parameters from each of the microscopic, DNA-induced dimer, and macroscopic models

Microscopic modela			DNA-induced dimer modelb		Macroscopic modelb
ΔGi	kcal mol−1	68% Confidence (kcal mol−1)	ΔGi	kcal mol−1	ΔGi	kcal mol−1
ΔG1	−8.1	−7.9 to −8.2	ΔG1	−8.1	ΔG1	−8.1
ΔG2	−11.2	−11.2 to −11.3	ΔGc4	−2.5±0.1	ΔG2	−11.3±0.1
ΔGc1	−2.0	−1.9 to −2.5	ΔGc1	−2.1±0.1	ΔGc1	−2.1±0.1
ΔGc2	+1.3	+0.8 to +2.3	ΔGc2	+1.3±0.9	ΔGc234	−3.0±0.7
ΔGc3	−0.9	−0.1 to −1.9	ΔGc3	−1.5±1.0	ΔGc1234	−3.9±0.2

Values were calculated using the standard relationship ΔG_i=−RT ln(k_i).

^aErrors represent 68% confidence intervals established from Monte Carlo analysis.

^bErrors represent 68% confidence intervals reported from the program Scientist.

With regard to binding at the palindrome, we also analyzed the data assuming that the reaction occurred via successive and cooperative monomer binding (species 17) rather than via a preformed dimer. Unfortunately, the addition of another cooperativity term (ΔG_c4) made it impossible to simultaneously float all parameters. However, if the intrinsic monomer binding parameter was fixed at −8.1 kcal/mol, the intrasite cooperativity term was determined to be −2.5±0.1 kcal/mol, statistically identical with our previous work on the PRE₂ promoter.¹⁵ Moreover, the values of the remaining cooperativity terms were identical with those resolved using the 16-species model (see Table 2).

Noting these results, one might ask whether footprint titrations of isolated half-sites would enhance the analyses. Unfortunately, it is impossible to carry out these experiments because the intrinsic binding affinity of a monomer is so weak that one cannot obtain a complete titration curve. As a consequence, the partial isotherm cannot be rigorously analyzed and is, thus, of limited utility. With that said, we have carried out footprinting studies using an isolated half-site and have observed partial binding curves that are in phenomenological agreement with the results of the 16-species model, both in terms of apparent affinity and noncooperative curve shape (data not shown). Likewise, the Monte Carlo analysis demonstrates that all the parameters are well resolved (Table 2), despite the fact that we did not include binding data for isolated half-sites. This appealing result reflects the great power of global analysis. For other models, however, complete resolution of all parameters is not always possible, either due to the addition of parameters such as ΔG_c4 or due to the lack of data such as the half-site titrations. We highlight these concerns in the following discussion.

Pairwise cooperativity exists between monomers bound at half-sites

As seen in Table 2, the 16-species model resolved a pairwise cooperativity term of −2.0 kcal/mol (68% confidence interval of −1.9 to −2.5 kcal/mol), corresponding to an ~40-fold increase in stability relative to a noncooperative analog. In order to verify that pairwise cooperative interactions indeed exist between monomers bound at half-sites, we analyzed a subset of the Class 2 promoters. MMTV_1−,3− and MMTV_1−,4− were globally fit to a simple two-site binding model while keeping the monomer intrinsic affinity fixed at −8.1 kcal/mol. Under these conditions, the fit resolved a cooperative free energy of −1.8±0.1 kcal/mol. The results are shown as the continuous line through the data points in Fig. 5. By comparison, as seen by the dotted line, fitting the data to a noncooperative, two-site model generated a binding isotherm clearly inconsistent with the data.

Fig. 5.

MMTV_1−,3− and MMTV_1−,4− isotherms fit to cooperative and noncooperative binding models. Shown are data from the MMTV_1−,3− and MMTV_1−,4− promoter templates. The black continuous line represents a global fit to a pairwise cooperative model by locking ΔG₁ at −8.1 kcal/mol and allowing ΔG_c1 to float. The black broken line represents the MMTV_1−,3− and MMTV_1−,4− data fit to a noncooperative two-site model. Insets are as described previously.

One of the assumptions of our model is that a single cooperativity term, ΔG_c1, is capable of accounting for the pairwise cooperativity on all promoters containing at least two viable half-sites. In order to test this assumption, we individually fit the binding isotherms from the MMTV_1−,3− and MMTV_1−,4− promoters using separate pairwise cooperativity parameters. The resolved values were −1.7±0.2 and −1.9±0.1 kcal/mol, respectively. We thus conclude that pairwise cooperative interactions are (within error) independent of distance and phasing of the half-sites. Furthermore, given the identical trends in the data for each of the three MMTV₁₋ half-sites (Fig. 4a), we assume that the pairwise interaction between sites 3 and 4 (for a putative MMTV_1−,2− template) is identical with the interaction between sites 2 and 3 and that between sites 2 and 4^†.

Anticooperativity is associated with complete occupancy of the half-sites

It is clear that pairwise cooperative interactions occur upon receptor binding at the half-sites. Left unanswered is whether the cooperativity associated with saturation, or complete occupancy, of the three half-sites is simply an additive function of the two ΔG_c1 terms or whether there are additional favorable or unfavorable contributions to binding. In order to address this, we included a second cooperativity term, ΔG_c2. As seen in Table 2, this parameter was determined to be +1.3 kcal/mol (68% confidence interval of +0.8 to +2.3), thus demonstrating that saturation of the half-sites is accompanied by an approximately 10-fold decrease in binding stability. By contrast, attempts to analyze the data when ΔG_c2 was fixed at zero resulted in a poor quality of fit and a 7% increase in the standard deviation (to 0.088 apparent fractional saturation units). These results indicate that “anticooperativity” is a real aspect of PR-A function, and thus, saturation of the three half-sites is not a simple, additive polymerization reaction.

In order to provide a further test of the above result, we also fit all data to the macroscopic model, which replaces the 2*ΔG_c1+ΔG_c2 terms with a single ΔG_c234 term (species 18), thus accounting for the total cooperative free energy associated with complete occupancy of the half-sites. However, the macroscopic model was poorly constrained due to strong parameter correlation between the monomer intrinsic affinity and the remaining cooperativity terms. This poor resolution is due in part to the lack of any isolated half-site binding isotherms. In the absence of these data, the relevant parameters were resolved by fixing the intrinsic affinity of a monomer (ΔG₁) at the value obtained from the microscopic model. The resolved value of ΔG_c234 was then determined to be −3.0±0.7 kcal/mol. This total free-energy change, less the sum of the two pairwise interactions, is equal to +1.2 kcal/mol and is statistically identical with the ΔG_c2 determined by the microscopic analysis. Thus, again, the analysis strongly suggests that cooperative saturation of the half-sites occurs by a mechanism other than additive pairwise interactions (i.e., 2*ΔG_c1).

Cooperativity between the palindrome and the half-sites only occurs upon complete occupancy of sites 2–4

As seen in Table 1, we have assumed that cooperativity between site 1 and the half-sites occurs only when the three half-sites are ligated. The resolved parameter, ΔG_c3, was found to be equal to −0.9 kcal/mol (68% confidence interval of −0.1 to −1.9), thus contributing an approximately fivefold increase in receptor–promoter stability. In order to provide additional support for our assumption, we individually fit the MMTV₃₋ and MMTV₄₋ templates to a model allowing for cooperativity between the palindrome and the two viable half-sites (data not shown). In both cases, when the intrinsic affinities (ΔG₁ and ΔG₂) and the half-site cooperativity term (ΔG_c1) were fixed at their resolved values in Table 2, the returned parameter was statistically equal to zero. We thus conclude that, at least within the error of the data, a PR-A dimer bound at site 1 does not communicate with pairs of monomers bound at half-sites. This conclusion is in line with our previous work on a synthetic promoter that revealed no evidence in support of a palindromic-bound dimer interacting with a single monomer bound at a half-site.^15,16

Finally, we globally analyzed all data sets using the second macroscopic cooperativity term ΔG_c1234 (i.e., the macroscopic model). This term accounts for all excess free-energy contributions beyond the sum of the three monomer intrinsic binding free energies and the single dimer binding intrinsic free energy (thus substituting species 19 for 16 in Table 1). As discussed earlier, the absence of a half-site titration curve made it necessary to lock the monomer affinity at the previously resolved value of −8.1 kcal/mol in order to reach convergence. However, as seen in Table 2, the fit resolved a macroscopic cooperativity term of −3.9±0.2 kcal/mol—thus, the total cooperativity associated with complete ligation contributes over a 1000-fold increase in stability. Moreover, this value is statistically identical with the sum of microscopic cooperativity terms 2*ΔG_c1+ΔG_c2+ΔG_c3 (−3.6 kcal/mol, 68% confidence interval of −3.3 to −4.4 kcal/mol). Just as importantly, the difference between ΔG_c1234 and ΔG_c234 (−0.9 kcal/mol) is equal to the microscopic cooperative free energy between the palindrome and the saturated half-sites (ΔG_c3). Thus, the cooperativity associated with saturation of the MMTV promoter is energetically identical regardless of model. This concordance strongly suggests that we have accounted for all major energetic contributions to cooperativity.

PR-A monomers assemble at individual half-sites

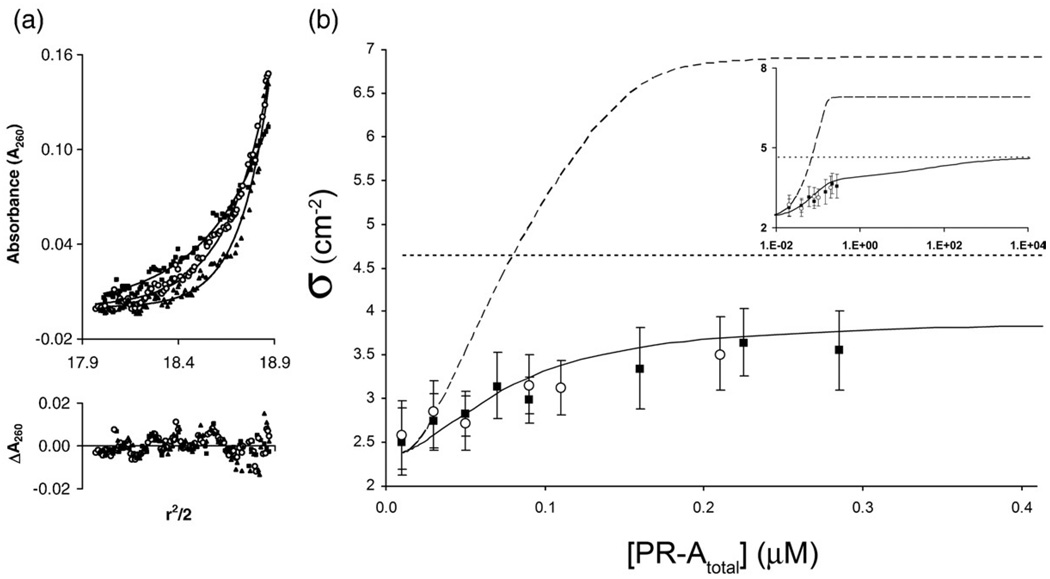
Despite early biochemical evidence suggesting that PR dimers are the only active binding species, ^23,24 the number of base pairs afforded protection at sites 2–4 (Fig. 2a) indicates that monomers rather than dimers assemble at each half-site. In order to directly determine the stoichiometry of this interaction, we measured the average molecular weight of PR-A:DNA complexes using a range of PR-A concentrations and a promoter fragment containing only PRE sites 2–4. Seen in Fig. 6a is a representative set of sedimentation equilibrium data carried out at one such PR-A concentration, equilibrated at three rotor speeds. The three data sets were globally fit to a noninteracting, single-species model in order to resolve sigma [σ; see Eq. (10) in Materials and Methods]. σ is defined as the reduced molecular mass and, in this example, is directly proportional to the average mass of all DNA species in solution. This procedure was carried out for PR-A concentrations ranging from 0 to 0.275 µM, and the results are shown in Fig. 6b. It is evident that in the absence of receptor, the experimentally determined σ for the isolated DNA fragment is 2.5±0.4 cm⁻², in close agreement with the calculated value of 2.4 cm⁻². However, as the amount of PR-A is increased in each sample, there is a gradual increase in the reduced apparent molecular mass toward the predicted plateau value (4.6 cm⁻²) for a monomer-saturated MMTV₁₋ fragment.

Fig. 6.

Sedimentation equilibrium analysis of PR-A binding stoichiometry to the MMTV₁₋ promoter (a) Representative sedimentation equilibrium data set plotted as A₂₆₀ versus r²/2. Shown is a loading concentration of 0.02 µM MMTV₁₋ in the presence of 0.06 µM PR-A equilibrated at three rotor speeds (filled squares, 8500 rpm; open circles, 10,500 rpm; filled triangles, 12,500 rpm). Lines represent a best fit to an ideal single-species model. Residuals of the fit are shown below the raw data and are plotted as ΔA₂₆₀ versus r²/2. (b) Plot of the resolved σ values from two independent experiments (filled squares and open circles) covering a range of 0 to 0.275 µMPR-A. Error bars represent 68% confidence intervals. Shown as a continuous line is the predicted σ value for monomers binding to each half-site. Shown as a broken line is the predicted σ value for dimers binding to each half-site. The dotted line represents calculated σ for monomers saturated at the three half-sites. The inset presents the identical plot in logarithmic scale covering a broader concentration range.

In order to better emphasize the rigor of these results, we also calculated the predicted σ as a function of receptor concentration based upon the model and energetics shown in Table 1 and Table 2, respectively. As seen in Fig. 6b, the average σ value as calculated over a range of receptor concentrations is in excellent agreement with the experimentally determined values. (Shown in the inset of Fig. 6b is the predicted σ over a much greater concentration range, showing the gradual increase in the predicted value until the curve plateaus at 4.6 cm^{− 2}.) By contrast, amodel in which PR-A dimers assemble at half-sites (determined by globally fitting the MMTV¹⁻, MMTV_1−,3−, and MMTV_1−,4− templates to a cooperative, dimer binding model) is seen to predict a concentration-dependent σ entirely at odds with the experimental data. In fact, we were unable to predict a concentration-dependent change in σ consistent with the experimental data whenever we invoked dimer interactions at the half-sites, regardless of assumed PR-A_dimer:MMTV₁₋ energetic values (data not shown). Finally, since the sedimentation experiments were carried out under identical solution conditions as the footprinting studies, where only site-specific protection was observed (Fig. 2a), we interpret the approach to a 3:1 monomer-to-DNA binding stoichiometry as arising from a single monomer at each half-site, rather than nonspecific receptor binding or nucleation of receptors at a single site.

Determination of statistical error

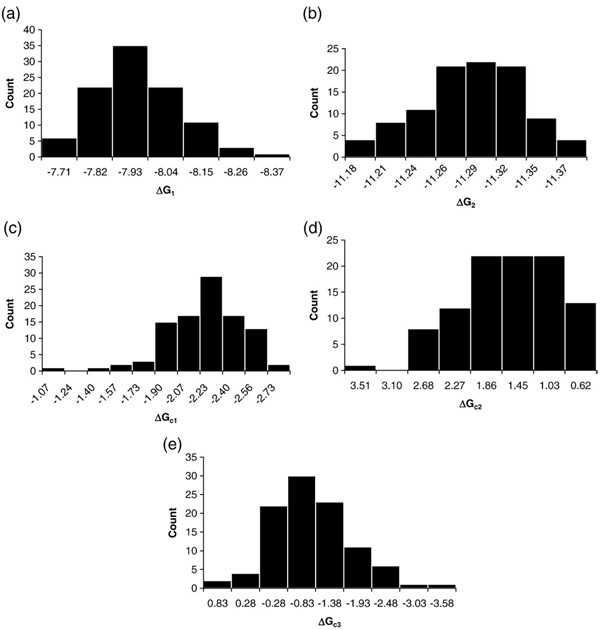
We have so far addressed whether the 16-species model is consistent with the data and whether other interpretations might also be consistent. We now address the third issue of whether the interaction parameters are well resolved. That is, whether the experimental data can support the level of model complexity, particularly in the absence of isolated half-site titration curves. The most rigorous method for making this determination is Monte Carlo analysis (see Materials and Methods), the results of which are presented in Fig. 7. It is evident that most parameters are well constrained as evidenced by the obvious grouping about a peak value. Additionally, as judged by the 68% confidence interval, none of the parameters in the model is statistically equal to zero, thus providing support for the existence of each interaction. Moreover, the error estimates on many of the parameters are small (below 15%), with the obvious exceptions being ΔG_c2 and ΔG_c3. The non-Gaussian, asymmetric distributions for these two parameters are due to parameter correlation. Correlation is a common problem in nonlinear least-squares analysis; we have largely overcome it through the global analysis of the wild-type and the reduced-valency promoter templates here and in our earlier work on PR–promoter interactions. ^15,16 Finally, as seen in Fig. 7e, the histogram distribution for ΔG_c3 crosses zero and contains values corresponding to a positive free-energy change. However, integration of the histogram shows that 93% of the values represent a negative free-energy change.

Fig. 7.

Histogram distributions of each resolved parameter as determined by Monte Carlo analysis. x-Axes represent the range of values resolved for each parameter; y-axes show the number of counts for each value. (a) Monomer intrinsic affinity (ΔG₁). (b) Dimer intrinsic affinity (ΔG₂). (c) Pairwise cooperativity (ΔG_c1). (d) Nonadditive cooperativity term (ΔG_c2). (e) Palindrome:half-site cooperativity (ΔG_c3).

Discussion

As noted in the Introduction, the long-accepted picture for PR interactions at the MMTV promoter is that only preformed dimers are capable of binding, that binding appears to be coupled to weak or non-existent cooperative interactions, and that the functional synergy observed for this promoter cannot be accounted for by cooperative assembly. This understanding was based upon a number of pioneering investigations that focused on elucidating the molecular origins of receptor–promoter interactions.^2–4 Unfortunately, at the time of these studies, it was only feasible to use unpurified or partially purified receptor fractions and qualitative or semiquantitative techniques. Furthermore, data interpretation was carried out largely by visual inspection rather than by theoretical or computational approaches. The shortcomings of this methodology can be seen in the results of the current study. For example, contrary to the traditional point of view, the stoichiometric and energetic majority of DNA binding is mediated by monomers rather than dimers. Likewise, despite the fact that visual inspection suggests that there is little cooperativity associated with receptor–promoter interactions, the present analysis reveals enormous cooperative stabilization. Finally, and as we will discuss in more detail below, the observed cooperativity may lend insight into the functional synergy seen at the MMTV promoter and for other PR-regulated genes. We note that these conclusions could not easily be reached (or even anticipated) by traditional biochemical or molecular biological approaches.

PR-A monomer interactions at the MMTV promoter

As shown in Fig. 6, sedimentation equilibrium analysis conclusively demonstrates that monomers rather than dimers assemble at MMTV promoter half-sites. This result is entirely consistent with the footprint titration data indicating that receptor-induced DNase protection is limited to the canonical half-sites and one or two flanking base pairs (Fig. 2a). Additionally, the intrinsic energetics of monomer binding to the half-sites sum to −24.0 kcal/mol, which is enormously more favorable relative to the −11.3 kcal/mol associated with dimer binding to the palindromic site. Thus, monomer rather than dimmer binding energetics dominate assembly at the MMTV promoter.

Although these results seemingly clash with the traditional understanding that only receptor dimmers are functionally active,^23,24 they are not unexpected based on our earlier analyses. Briefly summarized, analytical ultracentrifugation studies demonstrated that PR self-association does not occur in the nanomolar range as originally thought²⁵ but instead occurs in the micromolar range.^18,19 As a consequence, at the low nanomolar concentrations where DNA binding is initiated, the hormone-bound receptor is almost entirely monomeric in solution. Furthermore, our analysis of receptor interactions at synthetic promoters revealed that preformed dimmer binding to a palindromic response element was heavily disfavored by +5.4 to +6 kcal/mol.^15,16 Similar results are seen in the current study: Receptor binding to the MMTV promoter is again initiated at the low nanomolar range (Fig. 2b) under conditions in which little free dimer is present. Additionally, the difference between preformed dimer binding (−11.2±0.1 kcal/mol) at the palindromic site 1 versus a predicted successive monomer binding reaction (−16.2±0.2 kcal/mol) once again generates a large penalty (+5.0±0.2 kcal/mol), nearly identical with that observed in our previous work. Thus, for both synthetic and natural promoters, successive monomer binding is thermodynamically favored over dimer binding at palindromic response elements. Moreover, for the MMTV promoter, monomer binding at the three half-sites is stoichiometrically favored over the single dimmer binding event at the palindrome. Whether monomer binding is favored kinetically has not yet been established, although the present results clearly suggest that this is a possibility. Detailed transient-state kinetic studies are currently underway in order to quantitatively determine the time-dependent pathways associated with PR-A promoter binding.

Left unclear is what functional purpose might be served in allowing PR monomers to bind DNA. Typically, site-specific DNA binding proteins self-associate during or prior to binding at their response elements. This coupled reaction may serve as an additional means to regulate functional activity, either by more tightly controlling the concentration of the active species or by generating a high-affinity binding product via quaternary assembly. Since PR monomers are competent to bind DNA half-sites (and computational analysis indicates that natural PR-regulated promoters appear to contain an abundance of half-sites²⁶), there must be as yet unknown evolutionary pressures that favor monomer activity. However, since monomers have only moderate affinity for individual response elements, the strong cooperativity between and among the half-sites would appear to be critical for function. Later in the discussion, we speculate on how highly cooperative monomer binding reactions may contribute to PR-mediated gene regulation.

PR-A:MMTV binding is coupled to strong cooperativity

As seen in Table 2, there is an enormous amount of cooperativity associated with PR-A binding at the MMTV promoter. Specifically, the total amount of cooperative free energy associated with saturating the promoter corresponds to −3.6 to −3.9 kcal/mol or a 670- to 1189-fold increase in overall stability. Thus, an immediate question is why this contribution is not revealed by visual comparison of the binding isotherms between wild-type and mutated promoters. Several reasons explain this apparent paradox: Most specific to the MMTV promoter is that mutation of any one binding site eliminates only a portion of the total cooperativity. As a consequence, the half-saturation values for each site change only slightly. A more general reason is that the data presented in Fig. 2 and Fig 4 are plotted in units of total protein concentration rather than in units of a presumed active binding species (e.g., monomer concentration). Thus, the data as presented visually do not take into account the linked solution dimerization reaction. Finally, from basic theory, it can be demonstrated that cooperative binding free energies partition asymmetrically between nonidentical binding sites²⁷; thus, mutation of a single half-site associated with modest receptor binding affinity (−8.1 kcal/mol) will generate only negligible changes in apparent affinity at the remaining high-affinity sites. An example of this phenomenon can be seen in Fig. 4a: Loss of a functional site 3 only changes the apparent affinities of sites 2–4 by less than 2-fold in comparison to binding to the wild-type promoter, despite having lost ~55% of the cooperative free energy.

The energetics of pairwise cooperative interactions between monomers at the palindromic site 1 (ΔG_c4) and between monomers bound at half-sites (ΔG_c1) are nearly identical (see Table 2). However, the differing orientations, spacing, and phasing for the two classes of sites make it unlikely that cooperativity occurs through similar mechanisms. For example, receptor assembly at site 1 occurs in the context of a palindromic or “head-to-head” half-site orientation (see Fig. 1a), whereas interactions between sites 2 and 4 occur in the context of direct repeats or “head-to-tail” orientations. Furthermore, the palindromic site contains a short 3-bp spacer between half-sites whereas the half-sites 2–4 are separated by anywhere from 9 to 30 bp. Yet, analysis of each interaction using independent pairwise cooperativity terms showed all to be statistically identical, suggesting that these distances do not play an obvious role in pairwise polymerization. Moreover, the phasing of the three half-sites is different for each combination, suggesting that PR-mediated cooperativity occurs through a mechanism different from phase-dependent proteins such as λ cI repressor.²⁸

As seen in Table 2, the total cooperativity associated with saturating the three half-sites (ΔG_c234) is significantly less than what would be predicted by a simple additive polymerization reaction (2*ΔG_c1 or −4.0 to −4.2 kcal/mol). Thus, there is an apparent anticooperative contribution of +1.2 to +1.3 kcal/mol to binding at the MMTV promoter. With the current results, we are not in a position to discern the exact origin for this effect. However, one explanation is that the results reflect true anticooperativity. For example, upon binding the third monomer to the promoter, there may be a structural transition within the protein complex and/or DNA promoter, and ΔG_c2 represents the energetic cost of carrying out this transition. Alternatively, it is possible that cooperativity at the half-sites occurs via a mechanism entirely different from that outlined in Table 1. For example, there may be only alternate pairwise interactions (e.g., cooperative interactions between monomers bound at sites 2 and 3 preclude an interaction between sites 3 and 4) as seen in the classic λ repressor:right operator system. It is not possible to definitively rule out either of these possibilities in part because binding isotherms for the isolated half-sites were not included in the analysis. However, we do not favor the alternate pairwise model due to the dependence of the ΔG_c3 interaction on complete occupancy of the half-sites: It seems unlikely that cooperative interactions with the palindrome do not occur when a third half-site is unligated yet somehow commence when the half-site is occupied by a noncooperatively bound monomer.

The third level of cooperativity, ΔG_c3, describes the interaction between a dimer at the palindrome and monomers at the half-sites. Our analysis demonstrates that this interaction occurs only when the three half-sites are saturated with PR-A. As noted in our discussion regarding the “anticooperativity” ΔG_c2 term, it may be that complete ligation of the half-sites is coupled to formation of an active PR-A conformation, thus permitting an interaction with the palindromic-bound dimer. By contrast, the lack of observed cooperativity when the half-sites are partially ligated suggests that the interaction is not simply correlated with the number of response elements. Additionally, visual inspection of the promoter landscape shows no correlation between ΔG_c3 cooperativity and the phasing of the half-sites, their directionality, or their distance from the palindrome. Nonetheless, these aspects of promoter structure will require further exploration.

Functional implications of cooperative binding energetics

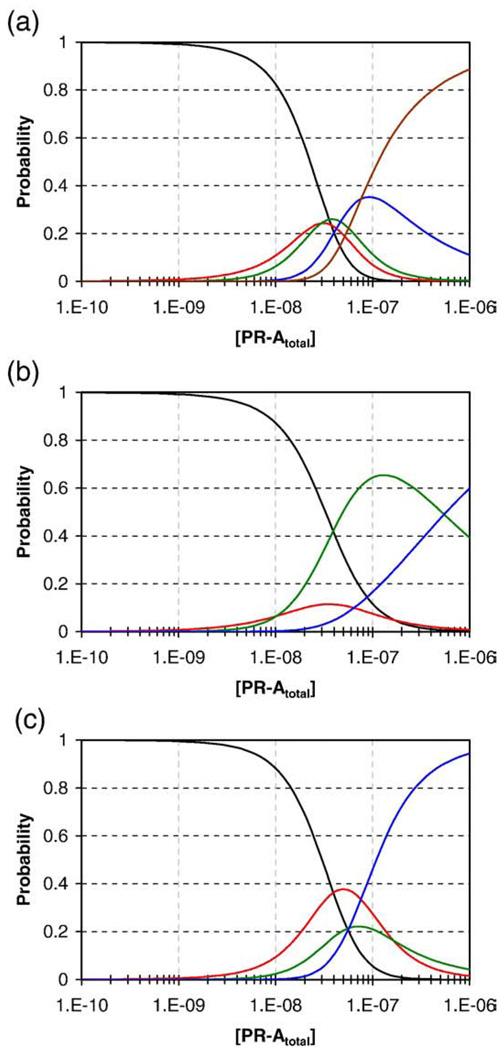
The results presented here demonstrate that cooperativity clearly exists, but does it shed any light on the functional properties of the MMTV promoter? Shown in Fig. 8 are the probability distributions of each macroscopic PR-A:promoter ligation state as a function of receptor concentration using the resolved energetics presented in Table 2. Calculations were carried out for the MMTV_wt, MMTV₁₋, and the MMTV₃₋ promoter templates. As seen in Fig. 8a, for even the highly cooperative wild-type promoter, the intermediate species are significantly populated. For example, the singly ligated state maximally reaches 24% of the population and the triply ligated state reaches 34% of the population (despite the large favorable cooperativity associated with saturation of the entire promoter). The second interesting result is the shallow slope of the curve describing the probability of the fully saturated promoter. These effects arise due to the modest +1.3 kcal/mol of anticooperativity associated with saturation of the half-sites.

Fig. 8.

Simulated species distributions for the MMTV_wt, MMTV₁₋, and the MMTV₃₋ promoter templates. The probability of each DNA species was calculated utilizing the 16-species model (Table 1) and resolved parameter values (Table 2). Populations are grouped by the number of binding sites occupied: Black line, free DNA; red line, one site occupied; green line, two sites occupied; blue line, three sites occupied; maroon line, four sites occupied. (a) MMTV_wt. (b) MMTV₁₋. (c) MMTV₃₋.

Shown in Fig. 8b is the population distribution for the MMTV₁₋ promoter. As expected, the loss of site 1 and the small −0.9 kcal/mol of cooperative free energy (ΔG_c3) greatly decrease the probability of fully populating the remaining three half-sites. However, the doubly ligated population is increased enormously, well beyond that predicted by a simple loss of cooperativity. This latter result is due to the energetically more prominent role of the anticooperative term. Shown in Fig. 8c is the predicted population distribution of the MMTV₃₋ promoter. Unlike in the previous example, the loss of a single site does not greatly reduce the population of the fully (now triply) ligated state as seen on the MMTV₁₋ template. This is the specific result of losing the unfavorable anticooperative term. Thus, an important conclusion of these studies is that loss of a binding site within a cooperatively interacting system is not a reliable predictor of decreased occupancy at the remaining sites.

The original basis for cooperativity within the MMTV promoter was to explain receptor-mediated functional synergy.³ This hypothesis was based on the notion that cooperatively induced stability at the promoter should translate into a synergistic increase in transcriptional activity. This interpretation was consistent with our understanding of classical gene regulatory switches such as the λ cI repressor:right operator system. However, unlike cI repressor, PR and other nuclear receptors do not function as sole regulators of transcriptional activation. Rather, the receptors must interact with more than 50 different proteins in order to properly activate gene expression.^29,30 Given these observations and the results presented herein, it may be worth asking whether cooperativity in higher eukaryotic systems plays the same functional role as it does in viral or bacterial systems. Recent work from this laboratory has revealed that at least one role for PR-mediated cooperativity is to allow efficient recruitment of coactivating proteins.²⁰ Briefly summarized, thermodynamic analysis of SRC2 coactivator recruitment found that PR-A interactions at individual response elements were coupled to a near-negligible, <2-fold increase in coactivator binding. By contrast, PR-A-mediated cooperative interactions were coupled to an additional 6- to 10-fold increase in SRC2 recruitment. As a consequence, these results offered a potential framework for explaining the synergistic increase in the transcriptional activity seen for multisite promoters. Specifically, the substantial increase in coactivator recruitment is not due to a simple increase in the number of receptors bound at the promoter; rather, it is almost exclusively due to cooperative interactions between bound receptors.

How the above results might translate into a molecular code for MMTV promoter function will clearly require analysis of PR binding in the presence of coactivator(s). In the meantime, it may be worth speculating that the code of cooperativity discovered here serves as the basis for promoter-specific coactivator recruitment. Specifically, if a synergistic loss of activity cannot be explained by a simple loss of cooperativity (Fig. 8), perhaps it is the type of cooperativity that is critical to transcriptional activation. For example, mutation of site 1 in the MMTV promoter is known to greatly diminish transcriptional activation⁶ despite cooperativity remaining among the half-sites (see Table 2). Similarly, loss of site 3 (or 2 or 4) results in a large decrease in transcriptional activity even though pairwise cooperative interactions are maintained. It may be that only certain higher-level interactions (e.g., ΔG_c3) are coupled to coactivator recruitment and, thus, gene activation. We are currently testing this hypothesis by analyzing the energetics of recruiting full-length SRC3 coactivator to wild-type and reduced-valency MMTV promoter templates.

Finally, why is it necessary for both monomers and dimers to bind DNA? Given that receptors such as PR regulate an enormous number of genes and over a large range of transcriptional levels,¹² perhaps both binding species are necessary to generate enough combinatorial control for promoter-specific cooperative binding, coactivator recruitment, and transcriptional activation. How these events might occur structurally is unknown. However, the results from the present study suggest that it is the ability of monomers or dimers to bind at these sites, the types of cooperativity that are then allowed, and possibly the directional and spatial orientation of response elements that dictate function. Clearly, more quantitative analyses of full-length receptors and their interactions with natural promoters, as well as a more mechanistic understanding of chromatin structure and function, will be necessary to explore these ideas.

Materials and Methods

Purification and hydrodynamic characterization of PR-A

An expression vector encoding full-length human PR-A (residues 165–933) fused to an N-terminal hexahistidine sequence was a generous gift from Dr. Dean Edwards (Baylor College of Medicine, Houston, TX). A detailed description of the PR-A purification process and a quantitative analysis of its hydrodynamic solution properties were published previously.¹⁸ Briefly summarized, PR-A expressed in Sf9 insect cells can be purified to at least 95% homogeneity. As judged by sedimentation velocity analysis, the purified protein exists as a homogeneous distribution of 3.50 s monomers in rapid equilibrium with 7.15 s dimers. By sedimentation equilibrium analysis, the free-energy change for dimerization (ΔG_di) was determined to be −7.6±0.6 kcal/mol. Statistically identical results were found in the footprinting buffer defined below,¹⁵ consistent with our observation that the weight-average sedimentation coefficient of PR-A is independent of NaCl concentrations ranging from 0.1 to 1.0 M NaCl.¹⁸

DNA preparation for DNase I footprinting

A vector containing the MMTV promoter region was a generous gift from Dr. Steven Nordeen (University of Colorado Denver). The wild-type promoter (MMTV_wt) contains a palindromic PRE (site 1) corresponding to the sequence GTTACAAACTGTTCT and three half-site PREs (sites 2–4) containing the binding sequence TGTTCT. Generated “in-house” were six reduced-valency promoter templates containing a G-to-T point mutation in the palindrome (MMTV₁₋), in the half-sites (MMTV₃₋ and MMTV₄₋), or in combinations thereof (MMTV_1−,4−, MMTV_1−,3−, and MMTV_{2−,3−,4−}). The point mutations completely eliminated PR-A binding to the respective response elements.³¹ Each template was excised from its respective vector with an XhoI/HindIII digestion and ³²P-end-labeled on both strands using a Klenow fill-in reaction.³² A subsequent BglII digestion generated a 984-bp fragment labeled only at the 3′ end of the sense strand. The most proximal half-site (site 4) was positioned 100 bp from the label.

Individual-site binding experiments

Experiments were carried out using quantitative DNase I footprint titrations as originally described by Brenowitz et al.,^33,34 with the following modifications. All reactions were carried out in an assay buffer containing 20 mM Hepes, pH 8.0, 50 mM NaCl, 1 mM DTT, 1 mM CaCl₂, 2.5 mM MgCl₂, 1×10⁻⁵ M progesterone, 100 µg/mL bovine serum albumin (BSA), and 2 µg/mL salmon sperm DNA. Each reaction contained 20,000 cpm of freshly labeled DNA containing either the MMTV_wt promoter or one of the mutated reduced-valency templates. DNA concentrations (maximally 5 pM) were estimated to be well below PR-A binding affinity, thus justifying the assumption that PR-A_free is approximately equal to PR-A_total. PR-A was added to each reaction mix, spanning a concentration range from subnanomolar to micromolar, and allowed to equilibrate at 4 °C for at least 45 min. DNase I (Invitrogen) was diluted to a concentration of 0.0058 units/µL in assay buffer, less BSA and salmon sperm DNA. After the samples reached equilibrium, 5 µL of the DNase I solution was added to each 200-µL reaction and digestion was allowed to proceed for exactly 2 min. Experiments were carried out using DNase concentrations that approximated “single-hit kinetics.”³³ Digestion products were electrophoresed on 6% acrylamide–urea gels and visualized using phosphorimaging. Individual-site binding isotherms were calculated as described by Brenowitz et al.³³ using the program ImageQuant (Molecular Dynamics).

Resolution of microscopic interaction free energies

The interactions of PR-A at the MMTV promoter were described using the following model, composed of the pathway represented in Fig. 3. The ligation state configurations and free-energy changes associated with this pathway are shown in Table 1. The model makes the following assumptions:

1. PR-A exists in a monomer–dimer equilibrium (ΔG_di) under the stated solution conditions.

2. PR-A binds the palindrome as a preformed dimmer (ΔG₂), whereas the receptor binds the half-sites as a monomer (ΔG₁).

3. A monomer bound to a half-site can cooperatively interact with another monomer at a half-site in a pairwise fashion (ΔG_c1).

4. Saturation at the three half-sites is accompanied by an additional cooperativity term (ΔG_c2) to account for any nonadditive behavior in the cooperative interactions.

5. Cooperativity arises between the palindrome and the half-sites (ΔG_c3) only upon complete occupancy of the half-sites.

The data were also analyzed using a model in which monomers sequentially bind at the palindromic site 1 (ΔG₁) and then dimerize on the DNA (ΔG_c4). Thus, all terms containing ΔG₂+ΔG_di were replaced with 2*ΔG₁+ΔG_c4. This model assumes that monomer binding at the two half-sites of the palindrome is energetically identical (and therefore identical with binding at sites 2–4 given their sequence identity of one of the palindromic half-sites). This assumption has been extensively explored previously.¹⁵ Briefly summarized, computer simulations demonstrate that the affinities between the half-sites in the palindrome can maximally differ by 1.3 kcal/mol. This large a difference is seen only when the cooperativity term between half-sites is fixed at a rarely observed value of −4.5 kcal/mol (corresponding to a 3000-fold increase in overall stability). The simulations thus suggest that any difference in monomer–half-site binding energetics is likely to be considerably less than 1.3 kcal/mol and, therefore, within the error of our data.

Finally, in order to assess types of cooperativity not explicitly accounted for in the above model, we also describe two macroscopic terms,ΔG_c234 and ΔG_c1234. These parameters account for any excess free energy beyond the sum of intrinsic binding affinities for the MMTV₁₋ promoter and the wild-type template, respectively:

$$\mathrm{\Delta }{G}_{\mathrm{c}134}=\mathrm{\Delta }{G}_{\text{total}1-}-3^{*}\mathrm{\Delta }{G}_1$$ (1)

$$\mathrm{\Delta }{G}_{\mathrm{c}1234}=\mathrm{\Delta }{G}_{\text{total}\text{wt}}-(3^{*}\mathrm{\Delta }{G}_1+\mathrm{\Delta }{G}_2)$$ (2)

where ΔG_{total 1−} and ΔG_{total wt} are the total free-energy changes associated with saturating the respective promoter. The relationships between the macroscopic cooperativity terms and the model-dependent microscopic terms are then defined as:

$$\mathrm{\Delta }{G}_{\mathrm{c}234}=2^{*}\mathrm{\Delta }{G}_{\mathrm{c}1}+\mathrm{\Delta }{G}_{\mathrm{c}2}$$ (3)

$$\mathrm{\Delta }{G}_{\mathrm{c}1234}=2^{*}\mathrm{\Delta }{G}_{\mathrm{c}1}+\mathrm{\Delta }{G}_{\mathrm{c}2}+\mathrm{\Delta }{G}_{\mathrm{c}3}$$ (4)

The DNase I footprint titration technique measures the fractional occupancy of individual binding sites. Thus, the statistical thermodynamic expressions that describe the binding isotherm for each site are constructed by summing the probabilities of each microscopic species that contributes to binding at that particular site (see Table 1). A detailed approach for constructing each mathematical formulation has been presented previously.³⁵ Briefly, the probability (f_s) of each microscopic species is defined as³⁶:

$$f_s=\frac{e^{(-\mathrm{\Delta }{G}_s/RT)}·{[x]}^j}{{\displaystyle \sum _{s=1}^j{e}^{(-\mathrm{\Delta }{G}_s/RT)}·{[x]}^j}}$$ (5)

where ΔG_s is the free energy of configuration s relative to the unliganded reference state, x is the PR-A monomer concentration (calculated from the dimerization constant, k_di), and j is the stoichiometry of PR-A protomers bound to the DNA template. R is the gas constant, and T is the temperature in kelvin. As an example, the fractional saturation (Y̅) for the palindromic site of the MMTV_wt promoter is the sum of probabilities for each species (see Table 1) where a dimer is bound to site 1:

$$f_{\text{site}1}=f_5+f_9+f_{10}+f_{11}+f_{12}+f_{13}+f_{14}+f_{16}$$ (6)

By contrast, if site 3 were rendered nonfunctional, the fractional saturation for site 1 would be:

$$f_{\text{site}1}=f_5+f_9+f_{11}+f_{13}$$ (7)

In order to resolve the microscopic interaction free energies defined in Table 1, we globally analyzed the binding isotherms generated from the wild-type template and the reduced-valency templates using the program Scientist 3.0 (MicroMath, Inc.). Subsets of data were analyzed using a similar approach in order to test and validate alternative binding models. The independently determined dimerization free energy, ΔG_di,^15,18 was used as a fixed parameter in all analyses. Finally, because protein interactions at specific DNA binding sites do not afford complete protection from DNase activity, binding data were treated as transition curves fitted to upper (m) and lower (b) endpoints using the equation:

$${\overline{Y}}_{\text{app}}=b+(m-b)·\overline{Y}$$ (8)

In order to determine accurate error estimates on the resolved parameters, we carried out Monte Carlo simulations using Scientist.³⁷ The experimentally determined parameter values (k₁, k₂, k_c1, k_c2, and k_c3) and the model shown in Table 1 were used to simulate individual-site binding isotherms (20 data points) for each of the seven promoter templates, covering the same range of protein concentrations as described earlier. Gaussian error was added to each data set equivalent to the local standard deviation of each experimental binding curve within the global fit. The simulated data sets were then globally analyzed to resolve a new set of k_i values. This procedure was repeated 100 times, and the resolved parameters from each iteration were binned as a histogram distribution. The parameter errors were estimated by integrating each distribution (KaleidaGraph v. 3.51, Synergy Software) to determine the area about the median, corresponding to the 68% confidence interval.

Determination of PR-A:MMTV stoichiometry using sedimentation equilibrium

Sedimentation was carried out in a Beckman XL-A analytical ultracentrifuge equipped with absorbance optics. A six-channel Epon centerpiece and an An-60 Ti rotor were used for all experiments. A 251-bp DNA fragment containing a mutated palindromic site and three unaltered half-site PREs (thus functionally equivalent to MMTV₁₋) was allowed to reach sedimentation equilibrium at an initial loading concentration of 20 nM. The fragment was also equilibrated in the presence of PR-A concentrations ranging from 0.02 to 0.275 µM. This fragment spanned 36 bp upstream of the mutated site 1 to 107 bp downstream of site 4 and, thus, did not contain the cryptic binding site discussed in the Results.

Sedimentation was carried out at 4 °C using the buffer described for the footprinting studies, less BSA and salmon sperm DNA. Rotor speeds were 8500, 10,500, and 12,500 rpm. Samples were monitored at 260 nm and judged to be at equilibrium by successive subtraction of scans. Since all protein concentrations were below detectability at 260 nm, the absorbance signal corresponded only to the composite average of all DNA species present in solution. Each data set was fit to a single-species model in order to resolve σ, the reduced molecular mass of the DNA population, using the equation:

$$Y_r=\delta +\alpha \text{exp}\left[\sigma \left(\frac{r^2-r_0^2}{2}\right)\right]$$ (9)

where Y_r is the absorbance at radius r, δ is the baseline offset, and α is the absorbance at the reference radius, r₀. σ, the reduced molecular mass, is defined as

$$\sigma =\frac{M_{\text{app}}(1-\overline{\mathrm{\upsilon }}\mathrm{\rho }){\mathrm{\omega }}^2}{\mathit{\text{RT}}}$$ (10)

where M_app is the weight-average molecular mass of a single apparent species, υ̅ is the partial specific volume,³⁸ ρ is the solvent density (as calculated on the basis of the salt composition and temperature³⁹), ω is the angular velocity, R is the gas constant, and T is the temperature in kelvin. The partial specific volume of each protein–DNA complex was assumed to be additive and was calculated using the approach of Howlett et al.⁴⁰

PR-A reaches its solubility limit at approximately 0.5 µM,¹⁵ which is below the concentration of receptor necessary to saturate the three half-sites. Thus, in order to estimate the stoichiometry under subsaturating conditions, the concentration-dependent change in the weight-average apparent molecular weight was compared to the predicted value as determined by the model in Table 1 and the experimentally determined binding energetics (Table 2). Since the promoter concentration of 20 nM does not correspond to a purely equilibrium binding regime (i.e., DNA concentration significantly less than PR-A dissociation constants), the free DNA and PR-A concentrations were determined at each receptor concentration by numerically solving the conservation of mass equations for total DNA and total PR-A concentrations, respectively (Scientist 3.0). The fraction of each PR-A:MMTV_wt species was then calculated over a wide range of PR-A concentrations using the resolved microscopic energetics presented in Table 2. Each PR-A:MMTV_wt species fraction was subsequently used to determine the weight-average molecular mass and the average partial specific volume at each receptor concentration. The predicted concentration-dependent σ_app curve was then generated using both the weight-average molecular weight and the average partial specific volume.

Abbreviations used

PR

progesterone receptor

PR-A

progesterone receptor A-isoform

PR-B

progesterone receptor B-isoform

PRE

progesterone response element

BUS

B-unique sequence

MMTV

mouse mammary tumor virus

GR

glucocorticoid receptor

SRC

steroid receptor coactivator

BSA

bovine serum albumin.