Abstract
3D-IPS/DFFT is an extension of the three dimensional Isotropic Periodic Sum (3D-IPS) for evaluation of electrostatic and Lennard-Jones interactions in heterogeneous systems; it utilizes a discrete fast Fourier transform (DFFT) for efficient calculation of the IPS potential with a large local region radius. The method is demonstrated to be highly accurate for simple bulk fluids, liquid/liquid and liquid/vapor interfaces, and lipid bilayers and monolayers. Values for rC (the cutoff distance for direct evaluation of pairs) and RC (the local region radius) equal to 10 Å and twice the longest edge of the periodic cell, respectively, provide excellent efficiency and accuracy. Dimyristoylphosphatidylcholine (DMPC) monolayers simulated with the CHARMM (Chemistry at HARvard Molecular Mechanics) C27r lipid parameter set and 3D-IPS/DFFT yield surface tensions approximately 8 dyn/cm higher than those simulated using Particle Mesh Ewald (PME), and with experiment. In contrast, surface tensions for DMPC bilayers are 16 dyn/cm/leaflet with both 3D-IPS/DFFT (rC = 10 and 12 Å) and PME (rC = 12 Å). This indicates that PME (rC = 12 Å) may be used for simulations of bilayers, but not monolayers, and that the large bilayer surface tension arising from C27r is incorrect.
Keywords: Surface tension, viscosity of TIP3P water, lipid force fields
1. Introduction
The evaluation of long-range forces is a critical factor in determining the quality of atomistic simulations. While electrostatics are accurately obtained by Particle Mesh Ewald (PME) summation for most periodic systems,1 until recently there was not an analogous treatment for long-range Lennard-Jones (LJ) interactions. This problem has been addressed by the Isotropic Periodic Sum (IPS) method of Wu and Brooks,2 which obtains short and long-range electrostatic and LJ interactions in periodic and non-periodic systems. The original implementation has two primary options: three dimensional (3D) IPS for isotropic systems and three dimensional (2D) IPS for interfaces. The latter is accurate, though too computationally demanding to apply to large systems such as lipid bilayers and monolayers. Consequently, a hybrid method, PME/IPS was proposed wherein electrostatics are evaluated with PME, and the LJ with 3D-IPS.3 Unfortunately, PME/IPS is inefficient (separate evaluations for two classes of forces are required) and is difficult to validate for large systems (i.e., long simulations with 2D-IPS or PME with very long cutoffs on the LJ interactions are required).
The newly developed 3D-IPS/DFFT4 remedies the difficulties found with 3D-IPS (inaccuracy for interfacial and other heterogeneous systems) and 2D-IPS (inefficiency). In essence, RC, the local region radius defining the “homogenous region”, is set to several edge lengths of the periodic cell, and the analytic 3D-IPS equations approximate the long-range interactions beyond this region. Figure 1 top illustrates a lipid monolayer and periodic images with RC equal to twice the longest edge length. The insight of Wu and Brooks is that even highly heterogeneous systems such as monolayers can be accurately treated as homogenous when particles from many periodic replicates are included. In principle this can be accomplished by simply increasing the cutoff rC for direct evaluation of pairs in the original 3D-IPS method from 10 Å to 100–200 Å. In practice it is not feasible. Instead, the 3D-IPS/DFFT method evaluates interactions within the homogeneous region in two steps. First, interactions within a 10–12 Å cutoff distance rC are calculated directly, like the “real-space” part in PME (Figure 2, bottom). The remaining 3D-IPS interactions within RC are then evaluated by a discrete fast Fourier transform on a grid (hence the name 3D-IPS/DFFT), and the direct interaction is subtracted to correct for overcounting. This is analogous to the splitting of real and k-space terms in PME that allows the Ewald equations to be solved in N ln N rather than N2 time, where N is the number of particles. The original 3D-IPS is recaptured when rC = RC. Wu and Brooks4 provide several examples, including an isotropic box of water, a water/vapor interface, and a protein in vacuum (a non-periodic system), to demonstrate that results with 3D-IPS/DFFT and PME are comparable when appropriate. 3D-IPS/DFFT is also applicable to systems with highly charged solutes, small simulation cells, and solvents of low dielectric permittivity, where Ewald summation can lead to artifacts.5,6
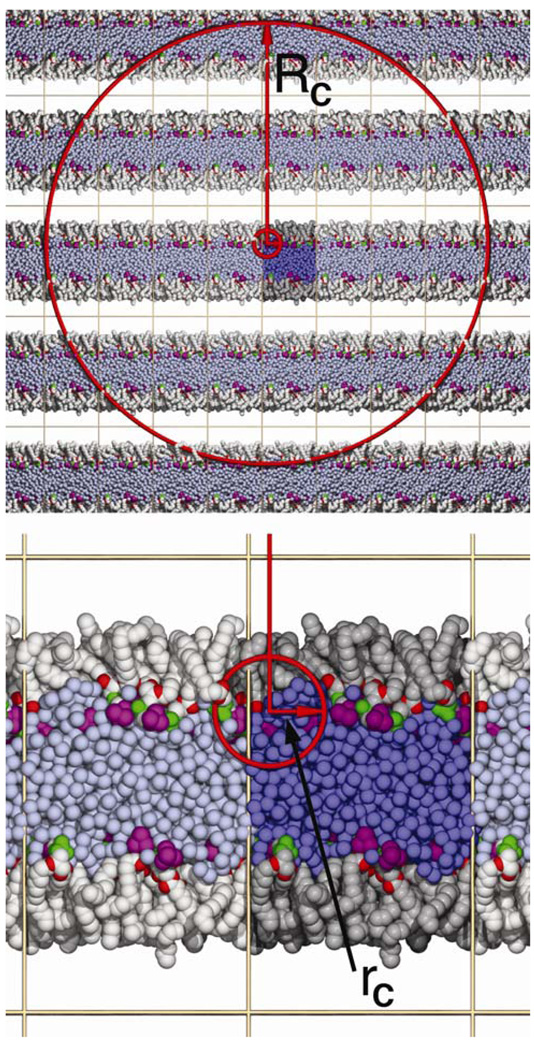
Figure 1.
The long (RC, equal to twice the longest edge length) and short (rC=10 Å) cutoffs of the 3D-IPS/DFFT method illustrated for a DMPC monolayer. Coloring is as follows: water, blue; hydrocarbon chains, grey; carbonyl oxygens, red; phosphate groups, green; quaternary amines, purple. The primary cell in the center is darker than the images, and the vapor phase between the chains is white. Top panel shows the substantial number of image atoms within RC (leading to homogeneity of the region) while bottom panel highlights the highly anisotropic distribution of atoms within rC(and why the longer cutoff is necessary).
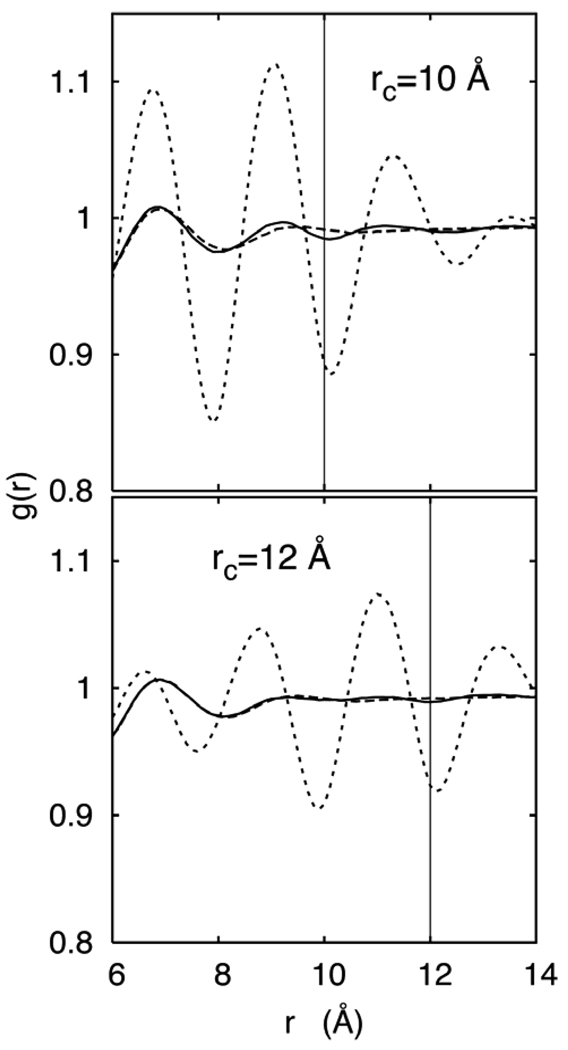
Figure 2.
Oxygen-oxygen radial distribution function, gOO(r), for 3D-IPS/DFFT (solid line), PME (long dashed line) and FSW (short dashed line) at rC = 10 and 12 Å from the 43 Å/edge box.
This paper focuses on validating 3D-IPS/DFFT for lipid bilayers and monolayers. Among other considerations, a consistent treatment of these two systems is essential for developing a potential energy function (or force field, FF) for cell membranes.7 This is because important experimental observables, such as pressure-area isotherms, are available for monolayers but not bilayers. For example, FF have been specifically tuned to yield a surface tension of zero for bilayers at the experimentally observed surface area per lipid.8 While this approach has theoretical justification,7,9 it is likely that more than one set of parameters could yield the same result. Consequently, it is reasonable to propose that such tuned parameters should also yield the experimental surface tension for a monolayer at the same area as a test of consistency.
Results presented here begin with neat water and alkanes, and three simple interfacial systems: water/vapor, octane/vapor, and water/octane. Densities, isothermal compressibilities, viscosities, self-diffusion constants, and surface tensions are calculated as a function of system size and cutoffs rC and RC, as appropriate. Performance of the force-switch cutoff is also evaluated. Bilayers and monolayers of dipalmitoylphosphatidylcholine (DPPC) and dimyristoylphosphatidylcholine (DMPC) are then considered. Homogeneity of these systems at RC equal to twice the cell height (as in Figure 1) is explicitly demonstrated, and surface tensions for different methods and parameter sets are evaluated. Taken together, the results presented here further validate the 3D-IPS/DFFT method, set appropriate cutoffs, explain differences in relative timings, and provide guidance as to when 3D-IPS/DFFT is essential to apply and when PME with 10–12 Å cutoff on the LJ terms is acceptable. As an application, inconsistencies in two different lipid parameter sets are demonstrated using simulations of bilayers and monolayers.
2. Methods
2.1. MD simulations
All simulations used CHARMM10 version c35, required for both the 3D-IPS/DFFT method and for a simplified means of obtaining data for computing viscosity. (The complete abbreviation 3D-IPS/DFFT is used throughout this manuscript because other extensions of IPS are under development.) The simulations were run on Linux clusters of both Intel and AMD machines, and used MPI parallel executables (Infiniband or shared memory transport). Extended system temperature and pressure methods11,12 with a 1 fs integration time step were used for simulations in all ensembles. Neat fluids were simulated in both the NPT and NVT ensembles (P, T, and V are pressure, temperature and volume, respectively), depending on the application (e.g., viscosity is evaluated by fluctuations in the pressure tensor, so constant volume is required). Liquid/vapor systems including lipid monolayers were simulated at NVT in order to ensure a stable non-condensed phase; liquid/liquid systems including bilayers were simulated at NPAT,13 where A is area. For NPT and NPAT systems the pressure piston mass equaled 500 amu; the mass of the temperature piston equaled 10000 kcal/mol/ps2 for the lipid monolayers and bilayers, and 5000 kcal/mol/ps2 for all other systems. For all viscosity calculations, the pressure tensor for each integration step of the simulations was stored for later evaluation using the Green-Kubo relation.14 The C27r parameters15 were used for all alkane and lipid simulations, with the exception of the DPPC simulations using C2716 with modified charges.17 Water and carbohydrate parameters are revised TIP3P18,19 and C35,20 respectively.
In addition to rC and RC, adjustable parameters for 3D-IPS/DFFT include the grid size ɛ for DFFT, and the update frequency for recalculation of the grid. For this study the current CHARMM default ɛ = min(rC / 4,3) was applied, yielding 2.5 and 3.0 Å for rC = 10 and 12 Å, respectively. Following the CHARMM default, grid updates were applied at each time step for all constant pressure simulations; grid updates are not required when simulating at constant volume. Fewer updates can be made by explicitly specifying a frequency or a volume change tolerance, though additional testing would be required. Grid spacing for PME was approximately 1 Å and κ = 0.33 Å−1. Initiation of the cutoff region for the force switch method21 was at 8 Å (i.e., the switching function was applied over 2 and 4 Å when rC =10 and 12 Å, respectively).
Water boxes were created by trimming a 60 Å cube to smaller cubes with the appropriate edge; the 60 Å cube was a 3×3×3 expansion of a briefly equilibrated (100 ps) 20 Å cube of TIP3P waters. Edge lengths were chosen to maintain the water density at 0.998 g/cm3, the experimental value at 293 K; the water simulations were all run at this temperature. For the 24 five ns NVT simulations used to compute viscosity and self-diffusion, the box sizes employed had approximately 25, 34, 43, and 54 Å edge lengths, with 526, 1040, 2665, and 5348 water molecules, respectively. Compressibility and density were evaluated from six 4.5 ns NPT simulations of the 34 Å water box.
Heptane and pentadecane starting coordinates, each with 64 molecules, were taken from previous work.15 As for water, the experimental density was used for the NVT simulations, six for each alkane. In order to achieve reasonable convergence for calculated viscosities, simulation times of 8.5 ns and 36.0 ns were required for heptane and pentadecane, respectively. Eight NPT simulations (4 methods, 2 cutoffs) of 8.5 ns were run for each of these two liquid alkanes to compute the density and compressibility. All of the alkane simulations were carried out at 312 K for comparison to liquid phase experimental data.
Both water/vapor and octane/vapor slabs were made by extending LZ, the unit dimension normal to the interface, of an equilibrated cube to 100 Å. For the octane based slab systems, a cube of 148 molecules with a 36 Å edge was first prepared by creating a library of conformations via Langevin dynamics of a single octane molecule in vacuum, then selecting conformations at random for a loosely packed (oversized) cubic lattice. The octane cube was then reduced in size via minimization to attain the experimental density, and then equilibrated for 2 ns of NPT dynamics. The water/octane slab system was made by adding a water box of matching size to the octane box and doubling the value of LZ. For all slab systems, the coordinates were placed to give planar interfaces parallel to and symmetric about the XY plane (Z=0). Slab systems were simulated for over 2 ns, with the final 2 ns used for evaluating the surface tension.
Starting coordinates for DPPC bilayers and monolayers were obtained from reference 22; those for DMPC bilayers are from reference 23. The DMPC monolayers were constructed from a DPPC monolayer at area/lipid of 64 Å2 by first removing 2 methylene groups from each chain. Surface areas of 48, 54, 60, 66, and 72 Å2/lipid were then generated by 1 ns simulations in the NPTLZT ensemble,13 where PT is the applied tangential pressure; i.e., the cell height remains constant at LZ while the surface area is expanded or contracted by PT. Trajectories were at least 20 ns for all lipid systems; the more condensed 48 and 54 Å2 area/lipid DMPC monolayer systems were run for 30 ns, and the DMPC bilayer and monolayer systems at 59.6 Å2 were run for 25 ns. These longer trajectories were required to obtain standard errors for the surface tension of 1 dyn/cm or less.
2.2. Data analysis
Instantaneous surface tensions for every integration step were averaged to blocks of 200 ps for the simple slab systems, and 1 ns for the more complex lipid bilayer and monolayer systems. Averages and standard errors were computed from these block averages; t-tests were performed on the block averages using Excel.
Densities and isothermal compressibilities were computed from time series of unit cell volumes. A Fortran program was used to compute the compressibility, using the exact average volume (from every integration step) and instantaneous volumes every 0.1 ps for fluctuations. Simulations were divided into 4 equal sized, independent time blocks to estimate the standard errors for density and compressibility.
Diffusion constants were computed from mean squared displacements using the Einstein relation.14 For water, the standard error estimates were obtained by dividing the simulations into 4 independent time blocks. For the alkanes, the molecules were divided into groups of 4 over the full length of the simulation, using two different schemes, and the averaged standard error estimate was used.
Autocorrelation functions of the 3 off-diagonal elements of the pressure tensor were computed, averaged, and integrated using CHARMM. The viscosity was computed by averaging over the plateau region of the integral; more viscous fluids required longer simulation and analysis intervals to achieve a stable plateau. Standard error estimates were again obtained by dividing the simulations into 4 independent time blocks.
3. Results and Discussion
3.1. One component isotropic systems
This subsection presents results of NVT and NPT simulations of neat TIP3P water (Table 1 and Table 3), and the alkanes heptane and pentadecane (Table 2 and Table 3). NVT simulations were generated with 3D-IPS/DFFT, PME (with no long range correction on LJ terms), and force switch (FSW) on both electrostatic and LJ. NPT simulations were carried out with 3D-IPS/DFFT, PME/IPS (3D-IPS/DFFT used for the LJ interactions), and with one of two distinct long range corrections (LRC) on the LJ terms: an analytic term derived from statistical mechanics relating the pressure and radial distribution function14 as implemented in CHARMM (denoted PME/LRC); the method of Lague et al.24 based on adding the “excess” pressure calculated with a 30 Å cutoff (PME/p-LRC). Diffusion constants (D) were corrected for system size effects of periodic boundary conditions using the formula of Yeh and Hummer,25 using the viscosity (η) calculated directly from the trajectory; corrections ranged from 4–22% depending on molecule, box size and method. No finite size corrections were applied to other properties discussed here.
TABLE 1.
Viscosities (η) and self-diffusion constants (D) of TIP3P water at 293 K for NVT simulations using 3D-IPS/DFFT, PME, and force-switch (FSW), two cutoffs rc, and four box sizes.
| Method | rc(Å) | η(cP) | D (10−5 cm2/s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Box edge length (Å) | Box edge length (Å) | ||||||||
| 25 | 34 | 43 | 54 | 25 | 34 | 43 | 54 | ||
| 3D-IPS/DFFT | 0.31 | 0.33 | 0.33 | 0.35 | 5.90 | 5.77 | 5.82 | 5.80 | |
| PME | 10 | 0.31 | 0.33 | 0.33 | 0.30 | 5.92 | 5.83 | 5.75 | 5.96 |
| FSW | 1.31 | 1.29 | 1.36 | 1.29 | 2.92 | 2.86 | 2.85 | 2.87 | |
| 3D-IPS/DFFT | 0.31 | 0.33 | 0.34 | 0.34 | 6.01 | 5.80 | 5.82 | 5.86 | |
| PME | 12 | 0.34 | 0.33 | 0.34 | 0.34 | 5.92 | 5.80 | 5.81 | 5.85 |
| FSW | 1.13 | 1.17 | 1.09 | 1.07 | 3.48 | 3.46 | 3.46 | 3.51 | |
| ave sea | 0.02 | 0.03 | |||||||
| experment | 1.0b | 2.02c | |||||||
TABLE 3.
Densities (ρ) and isothermal compressibilities (βT) of TIP3P water, heptane, and pentadecane from NPT simulations with 3D-IPS/DFFT, and PME with analytic (PME/LRC) and pressure-based (PME/p-LRC) long range corrections, and with LJ calculations evaluated with 3D-IPS/DFFT (PME/IPS) (alkanes only).
| Method | rc(Å) | ρ (g/cm3) | βT(10−10 m2/N) | ||||
|---|---|---|---|---|---|---|---|
| water | C7 | C15 | water | C7 | C15 | ||
| 3D-IPS/DFFT | 1.0199 | 0.6623 | 0.7549 | 4.85 | 18.7 | 10.7 | |
| PME/LRC | 10 | 1.0155 | 0.6611 | 0.7552 | 4.97 | 19.4 | 10.8 |
| PME/p-LRC | 1.0198 | 0.6607 | 0.7540 | 4.67 | 18.6 | 10.0 | |
| PME/IPS | 0.6623 | 0.7550 | 18.7 | 10.0 | |||
| 3D-IPS/DFFT | 1.0196 | 0.6638 | 0.7564 | 4.82 | 18.2 | 10.3 | |
| PME/LRC | 12 | 1.0148 | 0.6585 | 0.7520 | 5.06 | 20.6 | 10.9 |
| PME/p-LRC | 1.0196 | 0.6611 | 0.7546 | 4.78 | 17.8 | 10.3 | |
| PME/IPS | 0.6624 | 0.7551 | 18.1 | 10.6 | |||
| ave se | 0.00001 | 0.0004 | 0.0004 | 0.06 | 0.2 | 0.2 | |
| experimenta | 0.9982 | 0.668 | 0.755 | 4.58 | 15.8 | 9.2 | |
ref. 33
TABLE 2.
Viscosities and self-diffusion constants of heptane (C7) and pentadecane (C15) at 312 K for NVT simulations using 3D-IPS/DFFT, PME, and FSW at two cutoffs.
Table 1 lists the water viscosities and corrected diffusion constants for box sizes of 25, 34, 43 and 54 Å, and for rC = 10 and 12 Å. Results for 3D-IPS/DFFT and PME are within statistical error for all box sizes and both cutoffs, and the O-O radial distribution functions gOO (r) are nearly identical (Figure 2). In agreement with previous work,26 η for TIP3P water underestimates experiment by a factor of 3 when long range electrostatics are correctly included, and D correspondingly overestimates experiment. The origin of the low viscosity is the absence of the experimentally observed27 second and third maxima in gOO (r) at approximately 4.5 and 6.7 Å. In contrast, viscosities obtained from simulations with FSW overestimate experiment by approximately 30% for rC = 10 Å and 10% for rC = 12 Å. Figure 2 shows the spurious peaks in gOO (r) for FSW near the cutoffs. The 3- to 4-fold viscosity increase arises from this cutoff-induced long range structure, indicating that the approximate agreement with experiment of TIP3P with FSW is fortuitous.
NVT simulations of the two alkanes show the same trends noted for water. Viscosities and diffusion constants for 3D-IPS/DFFT and PME at both cutoffs are within statistical error. As for water, η is larger in simulations with FSW and D is smaller, although the differences are not as large. This is consistent with the lower charge density in alkanes. Agreement with experiment is also better, as might be expected. Alkanes are simpler than water and easier to parameterize, and recent FF development was carried out with PME and long range corrections.15
The results of NPT simulations are listed in Table 3. Densities from 3D-IPS/DFFT and PME/p-LRC and the two cutoffs are negligibly different (0.4% at most), although the differences are sometimes statistically significant because standard errors in density are small. Differences between 3D-IPS/DFFT and PME/LRC for these systems is slightly larger (as much as 0.8%), and likely arises from approximations in applying an LRC that only rigorously hold for monatomic fluids. All water densities overestimate experiment by approximately 2%. This is a well documented flaw in the TIP3P water model that is exacerbated when long range LJ interactions are included.24 Alkane densities agree nearly quantitatively with experiment, though it must be emphasized that a long-range correction on the LJ terms is required.15,24
Differences among the calculated isothermal compressibilities are mostly within statistical error, with the largest deviations arising from use of the analytic LRC. Agreement of simulation (averaging over the 3D-IPS/DFFT results) and experiment is very good to fair: 5.6% for water, 16.7% for heptane, and −14.1% for pentadecane; the agreement is substantially worse for alkanes when long-range LJ terms are ignored.15,24
3.2. Simple interfacial systems
This subsection focuses on the surface tension, γ, of three interfacial systems, water/vapor, octane/vapor, and water/octane, as evaluated with 3D-IPS/DFFT, PME, and PME/IPS. Previous studies have shown that interfacial systems are more sensitive to neglect of errors in long-range forces than isotropic ones,3,24 and the relative simplicity of the present set affords extensive testing.
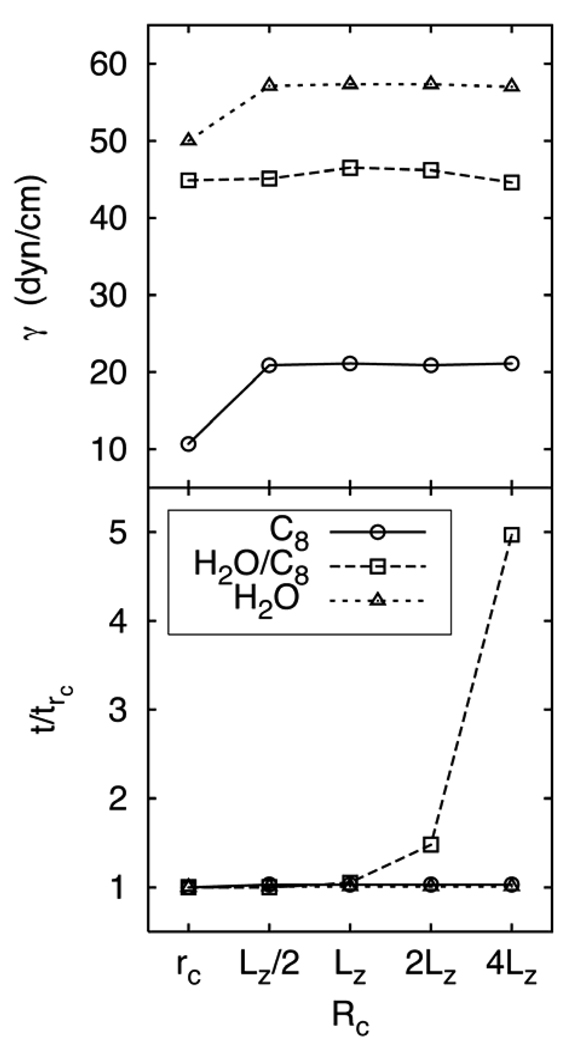
To begin, Figure 3 (top), plots γ for each system as a function of RC with rC = 10 Å. While the liquid/vapor systems show considerable deviation at RC = rC (the original 3D-IPS), all results are statistically equivalent from RC/LZ = 0.5 to 4.0. The lower panel of Figure 3 shows the impact on efficiency of increasing RC through the range from rC to 4LZ for the same simple slab systems. There is no difference in relative time for the fluid/vapor systems at these values of RC, while for water/octane it increased 50% for 2LZ (the current default in CHARMM), and five-fold for 4LZ. As discussed further in Section 3.4, the cost increase can be attributed to the cell height/width ratio and the use of constant pressure ensembles, which require frequent updates of the potential grid. To be conservative, the simulations described below were carried out with RC = 2LZ.
Figure 3.
Surface tensions of the octane/vapor (C8), and water/vapor (H2O), and water/octane (H2O/C8) interfaces as a function of RC relative to LZ, where LZ is the length of the cell normal to the interface (top). Time to completion relative to RC = rC; an increase means a slower (more costly) calculation (bottom).
Table 4 summarizes the results for different rC. Most germane to this study is that for each system the surface tensions calculated with 3D-IPS/DFFT with rC = 10, 12 and 14 Å show little variation and are within statistical error of those from PME with rC = 30 Å; with this cutoff on the LJ interactions, PME can arguably be considered a “gold standard”. At shorter cutoffs, surface tensions of the liquid vapor systems decrease for PME because the long-range LJ interactions are excluded. The effect is striking for octane/vapor (7.5 dyn/cm, a 35% drop when rC = 10 Å), and almost equal in magnitude (5.4 dyn/cm) though smaller in percentage (−9%) for water/vapor where electrostatic interactions dominate. Surface tensions for water/octane for 3D-IPS/DFFT and PME are equal at all listed cutoffs. Here hydrophobic interactions contribute substantially, and these are well captured with a short cutoff. Results for PME/IPS parallel those of 3D-IPS/DFFT. The excellent agreement with experiment for octane/vapor and water/octane and poor agreement with experiment for water/vapor for these parameter sets have been reported previously.3
TABLE 4.
Surface tensions (dyn/cm) for simple interfacial systems as simulated with 3D-IPS/DFFT, PME and PME/IPS.
| rC (Å) | |||||
|---|---|---|---|---|---|
| system | method | 10 | 12 | 14 | 30 |
| Water/vapor | 3D-IPS/DFFT | 57.4 | 56.2 | 56.6 | |
| PME | 52.0 | 53.2 | 55.7 | 57.4 | |
| PME/IPS | 56.9 | 58.1 | 57.0 | ||
| ave se | 0.5 | ||||
| expa | 72.9 | ||||
| Octane/vapor | 3D-IPS/DFFT | 21.0 | 21.2 | 20.8 | |
| PME | 13.6 | 16.0 | 18.8 | 21.1 | |
| PME/IPS | 21.1 | 22.2 | 21.8 | ||
| ave se | 0.5 | ||||
| expb | 21.6 | ||||
| Water/Octane | 3D-IPS/DFFT | 46.8 | 44.8 | 47.0 | |
| PME | 44.9 | 45.1 | 45.4 | 45.9 | |
| PME/IPS | 44.8 | 44.7 | 45.8 | ||
| ave se | 0.9 | ||||
| experimentb | 46.6 | ||||
3.3. DMPC monolayers and monolayers
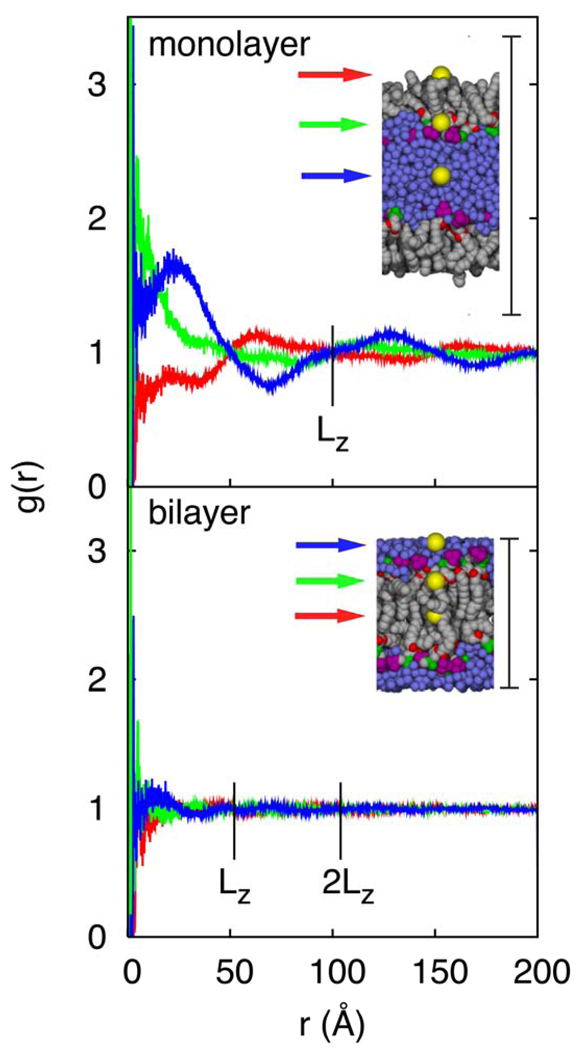
A central assumption of the IPS method is that the local region (a sphere of radius RC) is homogeneous. This implies that the radial distribution function g(r) for a particle should be close to 1.0 as r → RC. Figure 4 plots single particle g(r) for atoms at three representative positions (the center of the water layer, the water/lipid interface, and acyl chain termini) to all other heavy atoms in a DMPC monolayer (top) and bilayer (bottom). All six g(r) ≍ 1.0 for RC = 2LZ. Oscillations in g(r) at shorter distances are more pronounced for the monolayer and vary by atom and region type, as would be expected for a system with a vapor phase. Decay of g(r) to 1.0 is more rapid and the oscillations are less pronounced for the bilayer. Hence RC could plausibly be set to LZ for the bilayer for computational efficiency (Figure 3, and Section 3.4), though this should be validated; the monolayer, however, is better simulated with RC = 2LZ. It is also clear that both systems are exceedingly inhomogeneous on length scales of rC, which is why the original 3D-IPS method is not applicable.
Figure 4.
Radial distribution functions g(r) for a particle in the center of the water layer (blue line), at the lipid head group/water interface (green line), and the chain/vapor interface (red line), with all other heavy atoms for a DMPC monolayer (top) and bilayer (bottom). The yellow spheres mark the locations along the Z axis for the atom closest to the reference point; other atoms colored as in Figure 1. The vertical “I-bar” denotes the cell height RC = 100 Å for the monolayer and 52.3 Å for the bilayer; the widths of the insets are approximately 80% that of the complete systems. The single particle g(r) data were averaged over 50 frames spaced 500 ps apart.
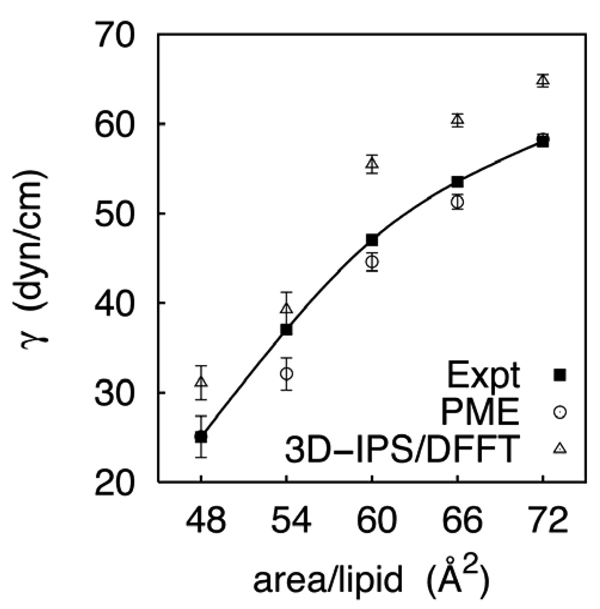
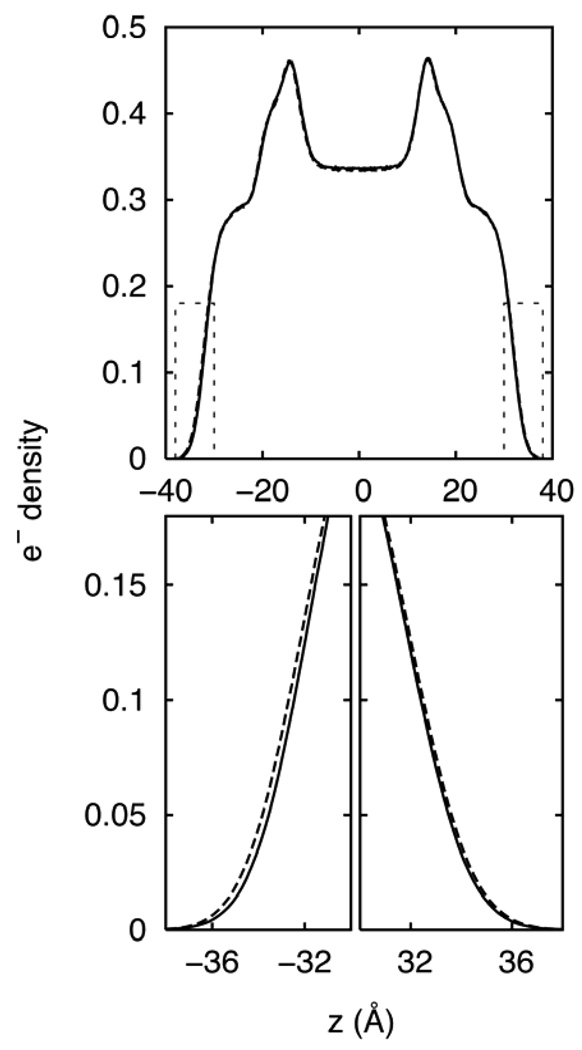
Columns 3 and 4 of Table 5 list surface tensions for DMPC for the assorted methods and rC = 10 and 12 Å. The most important and clear cut result is that γ for the monolayer for 3D-IPS/DFFT is substantially and statistically significantly higher than for PME. The difference is 10 dyn/cm for both cutoffs, and the trend holds for other surface areas of the DMPC isotherm (Figure 5), where the average difference is 8 dyn/cm. This parallels the results obtained for octane/vapor interfaces, where very long cutoffs on the LJ interactions are required. Figure 6 compares the density distributions for monolayers simulated with 3D-IPS/DFFT and PME. The water/head group interfaces (z = ± 10–20 Å) are nearly identical, as may be expected from the results for the water/octane. In contrast, the chain/vapor interface (detail in lower panel) is noticeably flatter for the 3D-IPS/DFFT system. This is consistent with the capillary wave model,28 where the surface tension is inversely proportional to the width of the interface. In other words, the inclusion of long range LJ interactions flattens the hydrocarbon/vapor interface and raises the surface tension. Consequently, the very good agreement of experimental29 monolayer surface tensions and those obtained from C27r simulated with PME arise from cancellation of errors.
TABLE 5.
Surface tensions of bilayers (dyn/cm/leaflet) and monolayers (dyn/cm) of DMPC (T=310 K, area/per lipid = 59.6 Å2) simulated with the force field C27r, and of DPPC (T=323 K, area/per lipid = 64 Å2) with a modified version8 of C27.
Figure 5.
Surface tension-surface area isotherm for a DMPC monolayer.
Figure 6.
Electron density distributions normal to the surface for a DMPC monolayer simulated with PME (dashed line) and 3D-IPS/DFFT (solid line) over entire range (top) and in detail at the alkane/air interface (bottom).
Based on t-tests with averages obtained from 2 and 5 ns blocks, the following additional conclusions may be drawn for the calculated DMPC surface tensions listed in Table 5 (differences are considered statistically significant when p < 0.05)
No difference between 3D-IPS/DFFT and PME/IPS for both the bilayer and monolayer. This provides further support that 3D-IPS/DFFT captures the long-range electrostatic interactions.
No difference between 3D-IPS/DFFT with rC = 10 and 12 Å, thereby allowing simulations at the shorter cutoff for cost savings.
Differences with 3D-IPS/DFFT and PME are significant for rC = 10 Å, but not for rC = 12 Å. This is because additional long-range interactions are included in the longer cutoff. It is possible that longer simulations would yield statistical significant differences, but the difference is substantially less for monolayers. This parallels the results for simple interfaces, where differences between 3D-IPS/DFFT and PME are much smaller for octane/water than for octane/vapor.
No difference between 3D-IPS/DFFT and PME/p-LRC for rC = 12 Å, but likely a difference for rC = 10 Å (p = 0.01 and 0.03 for 2 and 5 ns blocks, respectively). This again supports that notion that long range LJ forces are reasonably captured by a cutoff of 12 Å for bilayers.
The preceding results demonstrate conclusively that the C27r FF yields positive surface tensions for bilayers at their experimental surface areas even when long range electrostatic and Lennard-Jones are correctly taken into account; the average surface tension over statistically equivalent methods in Table 5 is 15.7 ± 1.1 dyn/cm/leaflet (the average excludes results for PME with rC = 10 Å). While a positive surface tension based on finite-size effects has been proposed,30 it is unlikely that the value is more than a few dyn/cm.7,31 The observation that surface tensions for DMPC monolayers are 8 dyn/cm too high (with 3D-IPS/DFFT) is further evidence that the C27r values for bilayer are incorrect. Consequently, a revision of the force field is appropriate.
3.4. Timing results
Table 6 compares the relative run times, using PME with a 10 Å cutoff as the reference time for most of the systems simulated. At the current stage of program optimization, there is a 10–20% cost increase for 3D-IPS/DFFT over PME for the cutoffs of 10 and 12 Å for the constant volume systems. The costs of 3D-IPS/DFFT with rC = 10 Å and PME with rC = 12 Å are comparable. For reference, PME with a 30 Å cutoff is 6–9 times slower than PME with rC = 10 Å for the systems simulated here, and is clearly impractical for routine simulations.
TABLE 6.
Run times relative to PME with a 10 Å pair cutoff for each simulation system; the time to completion for an equivalent time period from each method and cutoff was divided by the time for PME at 10 Å.
| Non-bond Method and Cutoff | |||||||
|---|---|---|---|---|---|---|---|
| 10 Å Cutoff | 12 Å Cutoff | ||||||
| System | Ensemble | 3D-IPS/DFFT | PME | PME/IPS | 3D-IPS/DFFT | PME | PME/IPS |
| water | NVT | 1.1 | 1.0 | 1.5 | 1.3 | ||
| water/vapor | 1.2 | 1.0 | 1.8 | 1.6 | 1.3 | 2.1 | |
| octane/vapor | 1.1 | 1.0 | 1.7 | 1.5 | 1.2 | 1.5 | |
| DMPC monolayer | 1.1 | 1.0 | 2.3 | 1.4 | 1.3 | 1.8 | |
| water | NPT | 1.3 | 1.0 | 1.7 | 1.3 | ||
| heptane | 1.3 | 1.0 | 4.1 | 1.6 | 1.2 | 4.5 | |
| pentadecane | 1.4 | 1.0 | 2.9 | 1.9 | 1.4 | 3.3 | |
| water/octane | NPAT | 1.6 | 1.0 | 6.2 | 1.8 | 1.4 | 6.7 |
| DMPC bilayer | 1.3 | 1.0 | 3.0 | 1.7 | 1.4 | 3.4 | |
The additional cost for 3D-IPS/DFFT is somewhat larger for constant pressure (NPT and NPAT) simulations. The primary reason for this is that the 3D-IPS/DFFT potential grid was recalculated at each integration step to account for volume changes (see Methods). The larger differences for the water/octane system for 3D-IPS/DFFT and PME arise from the larger anisotropy in the unit cell; i.e., the default 3D-IPS/DFFT RC value is twice the longest unit cell length, which leads to a larger spherical potential grid. For extreme cases, such as a lipid crystal structure with a unit cell of 8 ×5 ×60 Å, this choice of RC can make the 3D-IPS/DFFT method prohibitively expensive, and a reduction of RC is needed.
PME/IPS is highly inefficient compared to either PME or 3D-IPS/DFFT (a factor of 3 or more), as would be expected for a method that calculates the two different longrange interactions in two different ways. PME/IPS is useful for validation studies, but not as a production method.
3.5. Consistency Check for Lipid Parameter Modifications
This final subsection concerns a recent revision to the CHARMM lipid FF by Sonne et al..8 By adjusting charges in the head group region, they developed a modified parameter set that successfully yielded a surface area close to the experimental value for DPPC when simulating at constant pressure and temperature (NPT); this is the equivalent of simulating in the NPγT ensemble with an applied surface tension of zero. Following the logic of the preceding subsection, this set should also yield the correct surface tension for a DPPC monolayer. Table 5 lists the results for 3D-IPS/DFFT and PME simulations of DPPC bilayer (at NPAT) and a monolayer (NVT) at the surface area/lipid of 64 Å2. The bilayer surface tension is indeed close to zero, especially for 3D-IPS/DFFT. However, the monolayer surface tensions underestimate those of experiment by approximately 8 dyn/cm for 3D-IPS/DFFT and 18 dyn/cm for PME. This result implies that the surface tension lowering effected by the charge modification is at least partially fortuitous.
4. Conclusions
Based on comparisons for bulk liquids (water, heptane, and pentadecane) and for interfacial systems of water/vapor, octane/vapor, water/octane, and DMPC bilayers and monolayers, the 3D-IPS/DFFT method of Wu and Brooks is an accurate and efficient method for computing long range electrostatic and Lennard-Jones interactions for computer simulations. Specifically, 3D-IPS/DFFT yields equivalent results to PME with a long cutoff (30 Å) on the LJ terms.
A short range cutoff rC = 10 Å is as accurate as rC = 12 Å (Table 1–Table 4) when using 3D-IPS/DFFT, and is recommended on the basis of efficiency (Table 6). The appropriate long cutoff RC depends on the system (Figure 3 and Figure 4). Using the default value of twice the longest edge length does not increase the cost of the calculation substantially (Figure 3, bottom), and is important for lipid monolayers (Figure 4, top).
3D-IPS/DFFT, the hybrid PME/IPS, and the pressure-based LRC yield statistically equivalent results. However, PME/IPS is inefficient (separate calculations are required for electrostatic and Lennard-Jones interactions), and the pressure based LRC is not applicable to liquid/vapor systems such as monolayers. Given these considerations, 3D-IPS/DFFT is the method of choice among these three.
Decisions as to when 3D-IPS/DFFT instead of PME should be applied in simulations of periodic systems can be largely made by considering the importance of long range Lennard-Jones interactions for the system. These interactions must be included for accurate simulations of alkane/air interfaces (Table 4) and lipid monolayers (Table 5). In these cases simulating with PME with rC = 10 Å leads to underestimates of the surface tension of 8 dyn/cm. The underestimate of surface tension is somewhat less, 5 dyn/cm, and is proportionally smaller for the water/vapor interface because electrostatic interactions predominate (Table 4). Since simulating with PME and a very long cutoff (e.g., 30 Å) is not practical and long range correction (LRC) such as the analytic (denoted PME/LRC here) and pressure-based (PME/p-PRC) are not applicable, 3D-IPS/DFFT should be used to ensure accurate surface tensions. Long range LJ interactions are also important for neat alkanes, although PME/LRC and PME/p-PRC can be applied (Table 3). PME with a 12 Å cutoff yields accurate results for neat water (Table 1 and Table 3), water/octane (Table 4), and lipid bilayers (Table 5), with computational efficiency equal to that of 3D-IPS/DFFT with rC = 10 Å (Table 6). Consequently, PME at 12 Å is a reasonable alternative for these systems, and systems where 3D-IPS/DFFT presently cannot be used (e.g., those with rotational symmetry such as P21 boundary conditions32), or is inefficient (a highly anisotropic unit cell). The force switch truncation on the electrostatics, however, is not recommended.
Given the inapplicability of PME for monolayers, it is reasonable to use 3D-IPS/DFFT for bilayers in studies where the two systems are compared. This is critical in force field development, where the evaluation of surface tensions of monolayers and bilayers at the same area/lipid revealed errors in the CHARMM 27r parameter set not apparent from previous simulations with PME.
Acknowledgments
We thank Xiongwu Wu and Bernard Brooks for helpful discussions. This research was supported in part by the Intramural Research Program of the NIH, National Heart, Lung and Blood Institute. This study utilized the high-performance computational capabilities of the CIT Biowulf and NHLBI LoBoS clusters at the National Institutes of Health, Bethesda, MD.
References
- 1.Darden T, York D, Pedersen L. J. Chem. Phys. 1993;98:10089. [Google Scholar]
- 2.Wu XW, Brooks BR. J. Chem. Phys. 2005;122:044107. doi: 10.1063/1.1836733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Klauda JB, Wu XW, Pastor RW, Brooks BR. J. Phys. Chem. B. 2007;111:4393. doi: 10.1021/jp068767m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wu X, Brooks BR. J. Chem. Phys. 2008;129:154115. doi: 10.1063/1.2992601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hunenberger PH, McCammon JA. J. Chem. Phys. 1999;110:1856. [Google Scholar]
- 6.Weber W, Hunenberger PH, McCammon JA. J. Phys. Chem. B. 2000;104:3668. [Google Scholar]
- 7.Klauda JB, Venable RM, MacKerell AD, Pastor RW. Computational Modeling of Membrane Bilayers. Vol. 60. 2008. Considerations for lipid force field development; p. 1. [Google Scholar]
- 8.Sonne J, Jensen MO, Hansen FY, Hemmingsen L, Peters GH. Biophys. J. 2007;92:4157. doi: 10.1529/biophysj.106.087130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jahnig F. Biophys. J. 1996;71:1348. doi: 10.1016/S0006-3495(96)79336-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187. [Google Scholar]
- 11.Nosé S, Klein ML. J. Chem. Phys. 1983;78:6928. [Google Scholar]
- 12.Hoover WG. Phys. Rev. A. 1985;31:1695. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 13.Zhang YH, Feller SE, Brooks BR, Pastor RW. J. Chem. Phys. 1995;103:10252. [Google Scholar]
- 14.Allen MP, Tildesley DJ. Computer Simulations of Liquids. Oxford: Clarendon Press; 1987. [Google Scholar]
- 15.Klauda JB, Brooks BR, MacKerell AD, Jr, Venable RM, Pastor RW. J. Phys. Chem. B. 2005;109:5300. doi: 10.1021/jp0468096. [DOI] [PubMed] [Google Scholar]
- 16.Feller SE, MacKerell AD., Jr J. Phys. Chem. B. 2000;104:7510. [Google Scholar]
- 17.Sonne J, Hansen FY, Peters GH. J. Chem. Phys. 2005;122 doi: 10.1063/1.1862624. [DOI] [PubMed] [Google Scholar]
- 18.Durell SR, Brooks BR, Bennaim A. J. Phys. Chem. 1994;98:2198. [Google Scholar]
- 19.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 20.Guvench O, Greene SN, Kamath G, Brady JW, Venable R, Pastor RW, MacKerell AD., Jr J. Comput. Chem. 2008;29:2543. doi: 10.1002/jcc.21004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Steinbach PJ, Brooks BR. J. Comput. Chem. 1994;15:667. [Google Scholar]
- 22.Skibinsky A, Venable RM, Pastor RW. Biophys. J. 2005;89:4111. doi: 10.1529/biophysj.105.065953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klauda JB, Kucerka N, Brooks BR, Pastor RW, Nagle JF. Biophys. J. 2006;90:2796. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lagüe P, Pastor RW, Brooks BR. J. Phys. Chem. B. 2004;108:363. [Google Scholar]
- 25.Yeh IC, Hummer G. J. Phys. Chem. B. 2004;108:15873. [Google Scholar]
- 26.Feller SE, Pastor RW, Rojnuckarin A, Bogusz S, Brooks BR. J. Phys. Chem. 1996;100:17011. [Google Scholar]
- 27.Soper AK. Chemical Physics. 2000;258:121. [Google Scholar]
- 28.Rowlinson JS, Widom B. Molecular Theory of the Capillary. New York: Clarendon; 1982. [Google Scholar]
- 29.Sardone L, Pignataro B, Castelli F, Sarpietro MG, Nicolosi G, Marletta G. J. Colloid and Interface Sci. 2004;271:329. doi: 10.1016/j.jcis.2003.11.037. [DOI] [PubMed] [Google Scholar]
- 30.Feller SE, Pastor RW. Biophys. J. 1996;71:1350. doi: 10.1016/S0006-3495(96)79337-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marsh D. Biophys. J. 1997;73:865. doi: 10.1016/S0006-3495(97)78119-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dolan EA, Venable RM, Pastor RW, Brooks BR. Biophys. J. 2002;82:2317. doi: 10.1016/S0006-3495(02)75577-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lide DR. CRC Handbook. 81 ed. Boca Raton, FL: CRC Press; 2000. [Google Scholar]
- 34.Tofts PS, Lloyd D, Clark CA, Barker GJ, Parker GJM, McConville P, Baldock C, Pope JM. Magnetic Resonance in Medicine. 2000;43:368. doi: 10.1002/(sici)1522-2594(200003)43:3<368::aid-mrm8>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 35.Douglass DC, McCall DW. J. Phys. Chem. 1958;62:1102. [Google Scholar]
- 36.Small DM. Handbook of Lipid Research. Vol. 4. New York: Plenum Press; 1986. [Google Scholar]
- 37.Crane JM, Putz G, Hall SB. Biophys. J. 1999;77:3134. doi: 10.1016/S0006-3495(99)77143-2. [DOI] [PMC free article] [PubMed] [Google Scholar]