Finite element modeling of sound transmission with perforations of tympanic membrane

Abstract

A three-dimensional finite element (FE) model of human ear with structures of the external ear canal, middle ear, and cochlea has been developed recently. In this paper, the FE model was used to predict the effect of tympanic membrane (TM) perforations on sound transmission through the middle ear. Two perforations were made in the posterior-inferior quadrant and inferior site of the TM in the model with areas of 1.33 and 0.82 mm², respectively. These perforations were also created in human temporal bones with the same size and location. The vibrations of the TM (umbo) and stapes footplate were calculated from the model and measured from the temporal bones using laser Doppler vibrometers. The sound pressure in the middle ear cavity was derived from the model and measured from the bones. The results demonstrate that the TM perforations can be simulated in the FE model with geometrical visualization. The FE model provides reasonable predictions on effects of perforation size and location on middle ear transfer function. The middle ear structure-function relationship can be revealed with multi-field coupled FE analysis.

INTRODUCTION

The human middle ear includes the eardrum or tympanic membrane (TM) and three ossicles (malleus, incus, and stapes) that are suspended in an air-filled cavity by suspensory ligaments and muscles and connected by two joints (incudo-mallear and incudo-stapedial joints). Sound waves collected in the ear canal are passed to the middle ear through the vibration of the TM, which initiates acoustic-mechanical transmission in the ear. The output of the middle ear system is the movement of the stapes footplate, which sits in the oval window and transmits the ossicular vibration into cochlear fluid. Therefore, transfer function of the middle ear is commonly described as the relationship between vibrations of the TM and stapes footplate in response to sound stimuli in the ear canal (e.g., Zwislocki, 1962; Merchant et al., 1996; Aibara et al., 2001; Gan et al., 2004b).

Finite element (FE) method as a general numerical procedure has distinct advantages in modeling a complex biological system such as the ear. Since the first FE model of the cat TM was reported in 1978 (Funnell and Laszlo, 1978), FE modeling of static and dynamic behaviors of the middle ear has become a fast growing research area in the study of ear mechanics (e.g., Wada and Metoki, 1992; Koike and Wada, 2002; Sun et al., 2002; Kelly et al., 2003; Gan et al., 2004a; Gan and Wang, 2007). Using the technologies of three-dimensional (3D) reconstruction and multi-field FE coupled analysis, we have recently developed a comprehensive FE model of the human ear including the external ear canal, middle ear, and uncoiled cochlea with two straight fluid channels separated by the basilar membrane (BM) (Gan et al., 2007). The acoustic-structure-fluid coupled FE analysis or “three-chamber” multi-field FE modeling, including the air in the ear canal and middle ear cavity, the TM and middle ear ossicular structures, and the fluid in the cochlea, has been developed with the model. With the complete middle ear cavity connected to cochlea through the oval window and round window, modeling of middle ear transfer function in the ear with TM perforation becomes possible. In this study, we simulate TM perforations in the FE model to predict the perforation-induced change of middle ear function. This study evaluates a complex combination of two sound conduction routes: the mechanical route through the ossicular chain and the acoustic route through the air in the middle ear cavity.

Perforation of the TM is frequently caused by otitis media and Eustachian tube dysfunction, head trauma, and blast exposure. The reduction in energy transfer efficiency caused by TM perforation has been measured in human temporal bones and simulated in a simple circuit model by Voss et al. (2001a; 2001b; 2001c; 2007) with a series of publications. It has been tested in animals (Bigelow et al., 1996; Santa Maria et al., 2007) and clinical studies (Ahmad and Ramani, 1979; Mehta et al., 2006). However, the circuit model does not have structural geometry, and the parameters of the model are determined by fitting model results with experimental measurements in each individual temporal bone. In this paper, we will demonstrate that the FE model can be used to simulate various perforations with different sizes and different locations and to predict the effect of TM perforation on sound transmission from the ear canal to cochlea.

Perforations were created in the model as well as in human cadaver temporal bones. Two laser Doppler vibrometers were used to measure simultaneously the TM and stapes footplate movements in temporal bones. The FE model-derived results were compared with the measurements obtained from the bones. The study reported here is considered as a step toward the potential clinical applications of the FE model on prediction of structure alteration-induced hearing loss.

METHODS

3D finite element model

Brief description of the FE model

A 3D FE model of the human left ear with structures of the external ear canal, middle ear, and cochlea was developed recently by Gan et al. (2007). The model has complete geometry of the external ear canal and middle ear, including the TM, ossicles, suspensory ligaments and muscle tendons, and the middle ear cavity (Fig. 1). An uncoiled cochlear model was connected to the middle ear. The geometry of the cochlea was based on published dimensions of human cochlea in the literature. The scala vestibuli was connected to the stapes at the oval window and the scala tympani was contacted to the middle ear cavity air at the round window. These two chambers were separated by the BM and filled with an incompressible viscous fluid (perilymph).

Figure 1.

FE model of human left ear including the external ear canal, the middle ear [TM three ossicles (malleus, incus, and stapes), two joints and manubrium, ligaments and muscle tendons, tympanic annulus, stapedial annular ligament, and middle ear cavity], and the uncoiled cochlea in anterior-medial view. The middle ear cavity and cochlear chambers were assumed transparent. Here, C1, C2, C3, C4, C5, and C7 stand for the superior mallear ligament, lateral mallear ligament, posterior incus ligament, anterior mallear ligament, stapedial tendon, and tensor tympani tendon, respectively.

The ossicles, ligaments, and tendons were assumed as isotropic materials while the TM was assumed as orthotropic material. The mechanical properties of the TM, ossicles, joints, and manubrium in the model are listed in Table 1 of the paper of Gan et al. (2006). Poisson’s ratio was assumed to be 0.3 for all materials of the system. The Rayleigh damping parameters α and β for the middle ear system were assumed to be 0 s⁻¹ and 0.75×10⁻⁴ s, respectively. The human middle ear model was described as a linear acoustic-mechanical transmission system for sound energy within the normal hearing range.

The boundaries of the TM and middle ear ossicular chain include the tympanic annulus, middle ear suspensory ligaments or muscle tendons, stapedial annular ligament, and cochlea. Young’s moduli of suspensory ligaments∕tendons, tympanic annulus, and stapedial annular ligament were the same as that used in our previous analysis (Gan et al., 2007). Material properties used for cochlear structures, including the density and Young’s modulus of the oval and round windows, the inner and outer supports of the BM along the cochlear partition, and the stiffness of the BM, can be found from Gan et al. (2007). The fluid inside the scala vestibuli and scala tympani in cochlea was assumed as a viscous fluid with a density of 1000 kg∕m³ and a viscosity of 0.001 Ns∕m² or 1 cP. The damping coefficient β for the fluid was assumed as 1.0×10⁻⁴ s. Since the ear canal was open to the atmosphere in temporal bone experiment setup in this study, the boundary condition at the ear canal entrance of the FE model was set free. The Eustachian tube was modeled as being blocked similar to the experimental condition of the temporal bones.

TM perforations simulated in the FE model

Two perforations were made in the posterior-inferior quadrant and the inferior site of the TM in the model, as shown in Fig. 2A. The perforation size for Hole 1 were approximately 1.3 mm in diameter with a surface area of 1.33 mm² and for Hole 2 was 1.0 mm in diameter with an area of 0.82 mm². It is noted that the edge of the hole in the model was not smooth because of the element size. Similar holes were created in the temporal bones, in the same locations. The size of the hole created in the bone was approximately equal to the size of the hole in the model. In addition to Hole 1 and Hole 2, two other perforations were made in the model at the same location as Hole 1 (the posterior-inferior site). The size of Hole 3 [Fig. 2B] was approximately 1.65 mm in diameter with a surface area equal to the sum of Holes 1 and 2 (2.15 mm²). The area of Hole 4 [Fig. 3C] was approximately double that of Hole 3 at 4.34 mm² with an approximate diameter of 2.35 mm. The purpose for Hole 3 was an attempt to investigate the effect of multiple perforations (Holes 1 and 2) versus a single perforation (Hole 3) with the same perforation surface area. However, comparison of Holes 1 and 2 with Hole 3 may be also affected by different location. The design for Hole 4 was to study the effect of perforation size (from Hole 1 to Hole 3 and Hole 4) in the same location on middle ear function for sound transmission. It is noted that the size and shape of holes made in the model and temporal bones was approximately similar and the boundary or edge of the holes was not smooth, as shown in Fig. 2. These limitations were due to the element size of the TM model and the tool used for creating the holes in the temporal bones.

Figure 2.

Lateral view of the TM with perforations. The sizes of perforations are given in the text. (A) Two perforations: Hole 1—the perforation located in the posterior-inferior quadrant of the TM; Hole 2—the perforation located in the inferior part. (B) Single perforation Hole 3 in the posterior-inferior site. (C) Single perforation Hole 4 in the posterior-inferior site.

Figure 3.

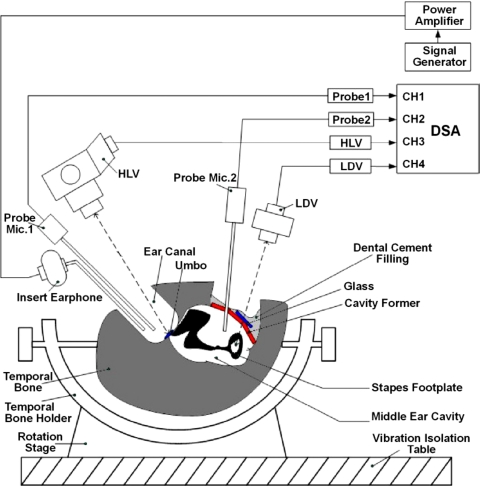
Schematic diagram of the experimental setup in human temporal bone with two laser vibrometers for measuring vibrations at the TM (umbo) and stapes footplate simultaneously. Two probe microphones were used for monitoring sound pressures in the ear canal and middle ear cavity.

Multi-field coupled FE analysis

In this study, the multi-field coupled analysis, including the air in the ear canal and middle ear cavity, the structures of the TM, middle ear ossicles and cochlea, and the fluid inside cochlea, was conducted on the FE model. The air in the ear canal and middle ear cavity was modeled as acoustic elements and governed by the simplified acoustic wave equation under the assumptions that the fluid (air) is compressible and inviscid with uniform mean density and pressure:

$$\frac{{\partial }^{2}P}{\partial t^2}-c^2{\nabla }^{2}P=0,$$ (1)

where P is acoustic pressure, c is speed of sound and $c=\sqrt{k∕{\rho }_o}$ in fluid medium, ρ_o is mean fluid density, k is bulk modulus of fluid, and t is time. The speed of sound and density of the air were assumed as 343 ms⁻¹ and 1.21 kgm⁻³, respectively.

The surface of acoustic elements (air) next to a fixed structure, such as the canal and middle ear cavity bony walls, was defined as “impedance surface” and assigned with a specified acoustic absorption coefficient μ (Gan et al., 2007). The surface of acoustic elements next to the movable structure, such as the TM (the lateral and medial surfaces of the TM and the surface around the holes on the TM), ossicles, and suspensory ligaments, was defined as a fluid-structural interface (FSI) where the acoustic pressure distribution was coupled into structural analysis as the force input in ANSYS (ANSYS Inc., Canonsburg, PA). The TM (both pars tensa and pars flaccida) had two FSIs on its lateral and medial sides, respectively. The round window membrane had two FSIs, one on its middle ear cavity side coupled with the air elements and one on the scala tympani side coupled with viscous fluid. On both sides of the BM (i.e., scala vestibuli and scala tympani), fluid that interfaced with solid structure nodes was kept distinct but coincident. These nodes were coupled together to form a no-slip condition for the fluid and to create the FSIs. The motion of fluid is described by the equation,

$$P=-k\nabla \cdot \mathit{u},$$ (2)

where u is displacement vector, k is bulk modulus of fluid and k=c²ρ. In this study, k was assumed as 220 GPa for perilymphatic fluid in the cochlea.

The harmonic analysis over the auditory frequency range of 100 Hz–10 kHz was conducted in the model using ANSYS v. 11. A sound pressure of 90 dB sound pressure level (SPL) (0.632 Pa or N∕m², rms value) was applied at the nodes of acoustic elements (Fluid 30) in the ear canal at 2 mm away from the TM at the umbo. This is the same situation as the experimental setup for human temporal bones in our laboratory. Our previous study on acoustic pressure distributions in the ear canal of the FE model (Gan et al., 2006) demonstrates that the pressure distributions reflect superposition of the incident and reflected sound waves from the TM and canal wall in the canal. The superposition is closely related to the frequency and location of the input sound source. The coupled FE analysis resulted in displacement movements of the TM (umbo) and stapes footplate as well as acoustic pressure inside the middle ear cavity.

Measurement of middle ear transfer function on human temporal bones

Five fresh-frozen, cadaveric temporal bones (two male and three female) obtained through the University of Oklahoma Health Sciences Center were included in this study. The donors’ average age was 73.8. The preparation of temporal bone specimen was the same as reported in our previous papers (Gan et al., 2004a, 2004b). The experimental setup for this study is schematically shown in Fig. 3. Briefly, after performing a simple mastoidectomy and extended facial recess approach on the bone, 90 dB SPL pure tone sound (P1) from a function generator (Model 193, Wavetek, San Diego, CA) was delivered to the TM by an insert earphone (Model ER-2, Etymotic Research, Elk Grove Village, IL) and monitored by two probe microphones (Model ER-7, Etymotic Research). The first probe tube was placed in the canal approximately 2 mm from the umbo. The second probe was placed between the round window and stapes for measuring the middle ear sound pressure (P2). The middle ear cavity was then covered by a glass sheet and sealed by filling dental cement (Reprosil, DDI Inc., Milford, DL). This glass sheet removed most of the mastoid cavity from the experimental volume.

Two laser vibrometers (Polytec, HLV-1000 and LDV-OFV 501) were used to measure vibrations of the TM and stapes simultaneously with one laser focused on the umbo and the other focused on the stapes footplate. The HLV laser beam was directed through the ear canal at the reflective tape on the umbo. Deviation of this laser beam varied 0° to 35° with respect to the direction of the stapes piston-like movement (i.e., the direction perpendicular to the plane of the footplate). In our experiments, the average angle was about 30°. The LDV laser was aimed on the reflective tape placed at the center of the stapes footplate. The deviation of the laser beam with respect to the piston-like direction of the stapes movement varied 30° to 55° and an average angle of 50° was used for this study. The deviation angles of laser beams were used as cosine correction factor to obtain the umbo and footplate displacements along the stapes piston-like direction.

Control experiments were performed first to measure the normal middle ear function with the intact TM. After control data were collected, two perforations were created [see Fig. 2A] using the cauterizer (Fine Science Tools, Inc., Foster, CA). It is noted that the edge of the hole made by cauterizer was not as smooth as that made by argon laser used by Voss et al. (2001a). The laser measurements of the umbo and footplate were conducted with Hole 1 first. The perforation Hole 2 was then made and Hole 1 was patched with cigarette paper (Voss et al., 2001a). To assure a patch on Hole 1 was effectively blocking the sound, the laser measurement on the umbo and stapes footplate was conducted before Hole 2 was made. The results showed that the difference between the intact TM and Hole 1 patched with the paper was within 1 dB. Finally, the paper was removed and the measurement was made with a combination of both Hole 1 and Hole 2.

RESULTS

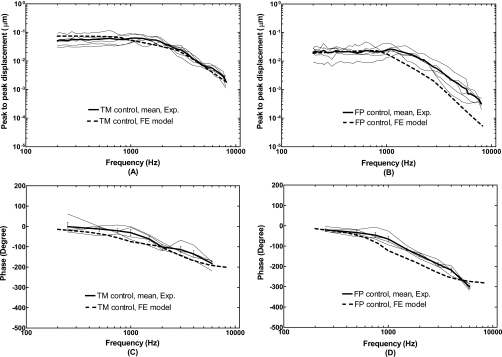
The FE model of a normal ear with the intact TM was first validated by comparison of the displacement curves of the TM (at the umbo) and stapes footplate derived from the model with that measured from human temporal bones. The magnitudes of the TM and footplate displacements were calculated from the model and projected to the stapes piston-like direction, the same direction as the data reported from temporal bones using laser vibrometers. Figure 4 shows the model-derived frequency response curves of the TM and footplate displacements (thick broken lines) in comparison with the umbo and stapes footplate displacement curves measured from five temporal bones with intact TMs when 90 dB SPL sound was applied in the ear canal. Panels (A) and (B) display the magnitudes of displacement data and panels (C) and (D) show the phase angles. The experimental data were consistent with these reported in our early papers (Gan et al., 2004a, 2004b).

Figure 4.

Comparison of the FE model-derived TM (at the umbo) displacement and stapes footplate displacement with the measurements from five human temporal bones with intact TM’s in magnitude and phase angle. The input sound pressure level was 90 dB at 2 mm from the umbo in the ear canal. The thick broken lines represent the model results. The thin solid lines represent the curves obtained from the individual temporal bones with the mean curves (thick solid lines). [(A) and (C)] TM displacement; [(B) and (D)] footplate displacement.

As can be seen in Fig. 4, the FE model-predicted TM (umbo) displacement curves fall well into the range of five temporal bone experimental curves across the frequencies of 200–8000 Hz. However, the model did not show the peak at 1000 Hz that was usually seen experimentally in most ears. There are some discrepancies between the model and experimental results on stapes footplate, as shown in Fig. 4B. The displacement magnitudes from modeling at high frequencies (f>1000 Hz) are below the experimental curves. The phase curves of the TM and footplate vibrations from modeling are slightly lower than the experimental results. The causes of these discrepancies could be due to the simplification of the real ear geometry and the accuracy of mechanical properties of ear tissues used for the model. However, in general, the simulations from the model show patterns that are similar to the temporal bone data.

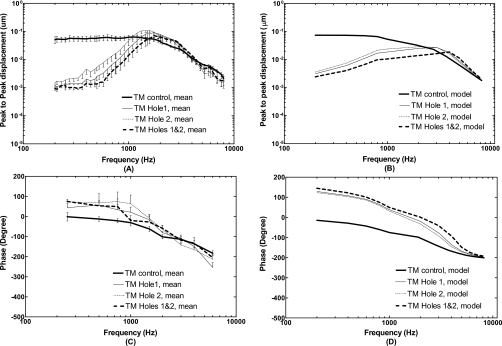
The effect of TM perforations [as shown in Fig. 2A] on sound transmission through the middle ear was investigated in temporal bones and FE model. Figures 567 illustrate the frequency response curves of the TM (umbo), stapes footplate, and middle ear pressure obtained from the temporal bones and the FE model, side-by-side for comparison. Panels (A) and (C) in Fig. 5 show the mean displacement curves with standard error bars of the magnitude and phase angle measured at the umbo from five bones under control, Hole 1, Hole 2, and combined Holes 1 and 2. The TM displacement curves predicted by the model are shown in panels (B) and (D). The experimental curves with perforations [Fig. 5A] show a maximum reduction of 30–33 dB of the TM displacement at 200 Hz. As frequency increased from 200 to 3000 Hz, the TM displacement increased rapidly and surpassed the control curves at 1–1.5 kHz. The curves flatten at the lowest frequencies (f<300 Hz) which was probably due to noise effect. The similar phenomenon was observed in the stapes footplate curves at the lowest frequencies [Fig. 6A].

Figure 5.

Mean displacements with standard errors (N=5) measured at the TM (umbo) and calculated from the FE model in control or intact TM (thick solid lines), perforations Hole 1 (thin solid lines), Hole 2 (thin dashed lines), and combined Holes 1 and 2 (thick broken lines). The input sound pressure level was 90 dB at 2 mm from the umbo in the ear canal. [(A) and (C)] Bone experiments; [(B) and (D)] FE model.

Figure 6.

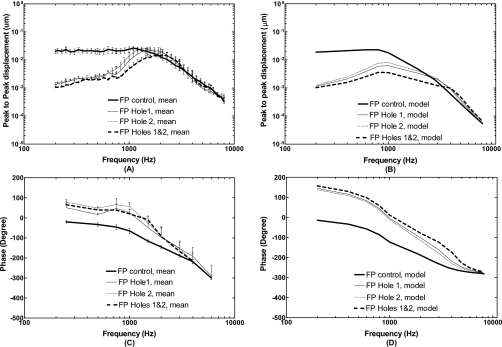
Mean displacements with standard errors (N=5) measured at the stapes footplate and calculated from the FE model in control or intact TM (thick solid lines), perforations Hole 1 (thin solid lines), Hole 2 (thin dashed lines), and combined Holes 1 and 2 (thick broken lines). The input sound pressure level was 90 dB at 2 mm from the umbo in the ear canal. [(A) and (C)] Bone experiments; [(B) and (D)] FE model.

Figure 7.

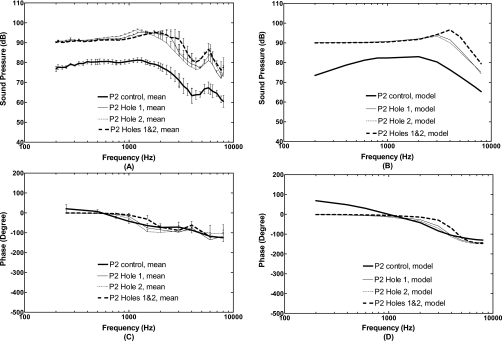
Mean sound pressure level in the middle ear cavity (P2) with standard errors measured from five temporal bones and calculated from the FE model in control or intact TM (thick solid lines), perforations Hole 1 (thin solid lines), Hole 2 (thin dashed lines), and combined Holes 1 and 2 (thick broken lines). The input sound pressure P1 was 90 dB at 2 mm from the umbo in the ear canal. [(A) and (C)] Bone experiments; [(B) and (D)] FE model.

The model results [Fig. 5B] show a maximum reduction of 28–31 dB of the TM displacement at 200 Hz caused by perforations and then the displacement increased slowly as frequency increased to 3 kHz. The model curves are much less steep than the experimental curves at frequency below 1 kHz. The reduced displacement values caused by perforations decreased to zero and then increased for the frequencies over 3 kHz. The TM displacement values at 3 kHz had the effect of downplaying the differences between experimental and model results. The experimental phase curves [Fig. 5C] at three perforation cases are higher than that of the control curve from 200 to 4000 Hz, which are also shown in the model phase curves. Figure 5 demonstrates that Hole 1 resulted in more reduction in the TM displacement than Hole 2, and combined Holes 1 and 2 resulted in more reduction in the TM movement than Hole 1 or Hole 2 only. This was observed from both the model and bone experiments, which demonstrated the effect of perforation size. It is noted that the difference of combined Holes 1 and 2 from a single hole, or the difference of Hole 1 from Hole 2, may be also affected by different locations. However, for small perforations (hole area less than 5% of the TM surface area), the effect of hole location on sound transmission through the middle ear may not be important as reported by Voss et al. (2001a) and Ahmad and Ramani (1979).

Figure 6 displays the frequency response curves of the stapes footplate displacement measured from the bones and derived from the FE model. Panels (A) and (C) of Fig. 6 show the mean magnitude and phase angle data of stapes footplate displacement with standard error bars from five bones for control, Hole 1, Hole 2, and combined Holes 1 and 2. The model-derived footplate displacement curves are displayed in panels (B) and (D). As can be seen in Fig. 6A, the footplate displacement had a maximum reduction of 23–25 dB at 200 Hz and 18–20 dB reduction at 500 Hz measured from temporal bones. The displacement increased as frequency increased to 1.5 kHz and surpassed the control curves at 1.5–3 kHz with a value less than 2 dB. Voss et al. (2001a) reported the reduction in the stapes velocity at frequencies below 1.5 kHz measured in temporal bones. The maximum reduction with a perforated TM at the hole size of 1.2 mm of diameter was reached at 200 Hz over the tested frequency range, and the reduction decreased as frequency increased to 1.5 kHz (Voss et al., 2001a). The results from temporal bones in this study are generally consistent with results of Voss et al. (2001a). However, there are some differences between this study and results of Voss et al. (2001a) at lowest frequencies. In the measurements of Voss et al., (2001a) the stapes displacement with holes continues to decrease as frequency decreases to 200 Hz, which is not seen here. The low frequency flattening of displacement curves observed in this study may be due to the noise level effect in our experiments.

The FE model shows a maximum of 25 dB reduction in footplate displacement for three perforations at 200 Hz and 20 dB reduction at 500 Hz in Fig. 6B. The displacement increased gradually and the reduction decreased to 7–13 dB at 1 kHz. Then, the footplate displacement with holes started to meet the control curve and surpassed the control at frequencies greater than 2.5 kHz with a value less than 2 dB. Both phase data from the model and experimental measurements with TM perforations increased compared with control curves.

In Fig. 7, the FE model-predicted frequency response curves of acoustic pressure P2 in the middle ear cavity (between the round window and stapes) were compared with the experimental data obtained in temporal bones. Panels (A) and (C) display the mean pressure curves (magnitude and phase) with standard errors measured from five temporal bones for control and three perforations. Panels (B) and (D) display pressure curves derived from the FE model with control and three perforations similar to the experiments in temporal bones. Sound pressure differences across the TM, P1-P2, measured from the temporal bones in control (with intact TM) were 15, 10, 15, and 25 dB at frequencies of 200 Hz, 1 kHz, 2 kHz, and 4 kHz, respectively. The model-derived pressure difference (P1-P2) at the corresponding frequencies of 200 Hz, 1 kHz, 2 kHz, and 4 kHz was 16, 8, 7, and 14 dB, respectively.

When the TM was perforated, the pressure difference across the TM vanished at f<1 kHz, which was observed from the measurements in temporal bones as well as the results calculated from the model. However, there are some discrepancies between the measurements and FE model at high frequencies (f>1 kHz). Experimental data [Fig. 7A] show that the P2 was greater than P1 at the frequency between 1 and 2 kHz for single hole (peak around 1.4 kHz) and between 1 and 2.5 kHz for two holes (peak around 2 kHz). Then, P2 decreased to less than P1 at the frequency greater than 2.5 kHz with some variations as frequency increases. For model results [Fig. 7B], P2 increased over P1 at the frequency between 1 and 3 kHz for single hole and between 1 and 5.5 kHz for two holes. Compared with experimental curves, peaks of the model curves were shifted to 3 kHz for single hole and 4 kHz for two holes. To explain the discrepancies of frequency behavior of P2 between the model and measurements after TM perforation needs further study on acoustic properties of the FE model.

DISCUSSION

FE model prediction of middle ear transfer function change by perforation

In this paper, the structural alterations of the ear (i.e., TM perforations) were visually created in our 3D model of human ear and the multi-field coupled FE analysis was conducted in the model. The TM and footplate displacements derived from the model were compared with the data measured from the temporal bones under normal and perforated conditions. The FE model predicted that the TM perforations affect the TM and stapes footplate displacements at low frequencies, which are consistent with the observations reported by Voss et al. (2001a, 2001b; 2007), Bigelow et al. (1996), and Ahmad and Ramani (1979). The value of displacement reduction was related to the perforation size, location, and multiplicity. The maximum reduction was reached at lowest frequency such as 200 Hz tested in this study. These results are consistent with our measurements in temporal bones and those reported by Voss et al.(2001a). The reduction in displacement decreased as the frequency increased and finally approximated zero. The high frequency end point for perforation effect was sensitive to the number of holes on the TM. For a single hole such as Hole 1 or Hole 2, the displacement curves of the TM and footplate were not shifted to a high frequency as predicted by the model and measured from temporal bones (Figs. 56). For multiple holes such as combined Hole 1 and Hole 2, the displacement curves were shifted toward the high frequency.

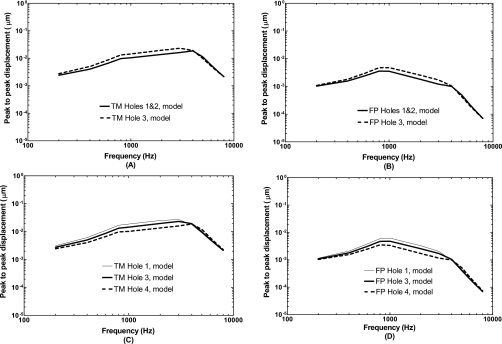
To further investigate the effects of perforation size and location on sound transmission through the middle ear, we created two additional perforation cases in the model which are displayed in Figs. 2B and 2C. Hole 3 in Fig. 2B has the size equal to the size of Hole 1 plus Hole 2 and is located in the posterior-inferior site, the same location as Hole 1. The TM and footplate displacement curves with two holes and with a single Hole 3 from the model are shown in Figs. 8A and 8B, respectively. As can be seen in each figure, the displacement curve obtained from the multiple holes was different from that of a single hole even though the perforation areas were equal. Multiple holes caused 1–3 dB more reduction in the TM or footplate displacement than that caused by a single hole at frequencies below 4 kHz. This effect is mainly due to multiplicity. We did increase the size of Hole 2 to the same as Hole 1 in the FE model and calculated the TM and footplate displacements. The results (not shown here) indicated that the effect of different location on TM or stapes footplate displacement curve was limited within 1 dB.

Figure 8.

Comparison of the effects of perforation size and location on TM (umbo) and footplate displacements. (A) TM displacements obtained from two holes (Hole 1 and Hole 2) and a single Hole 3 with the same perforation area. (B) Footplate displacements obtained from two holes (Hole 1 and Hole 2) and a single Hole 3. (C) TM displacement obtained from single hole with different sizes. (D) Footplate displacement obtained from single hole with different sizes.

Hole 4 in Fig. 2C has the size twice of Hole 3 and is also located in the posterior-inferior site, the same as Hole 3 and Hole 1. Comparison of the TM and footplate displacement curves obtained from three single perforations: Hole 1, Hole 3, and Hole 4 with the surface areas of 1.33, 2.15, and 4.34 mm², respectively, demonstrate the sole effect of perforation size on middle ear transfer function. The results are shown in Figs. 8C and 8D. As can be seen in these figures, the TM or footplate displacement decreased proportionally with the increase in hole size at frequencies below 4 kHz. The curve was not shifted to a high frequency when the hole size changed. These findings suggest that the perforation size plays an important role for reducing the TM and stapes movements or causing conductive hearing loss.

It is noted that the case of multiple perforations is worse than a single perforation even though the perforation size is same [Figs. 8A and 8B]. When there is more than one hole on the TM, the location of the hole also plays a role on changes of middle ear transfer function. The transmission of acoustic energy from the ear canal to the cochlea is affected by locations of the TM perforations as observed in multiple perforations. However, the mechanism of multiple perforations on sound wave transmission through the middle ear needs future study.

In summary, the perforation size and location are two main factors affecting perforation-induced reduction in middle ear transfer function or perforation-induced conductive hearing loss. These two factors interact with each other to influence the acoustic-mechanical transmission through the ear. For a better understanding of the effect of perforation on middle ear function, further studies such as different combinations of perforation size and location are needed. Moreover, it is noticed that the frequency response curves of the displacement magnitude and phase at the TM (umbo) and footplate with perforations from the model were not always similar to the experimental curves obtained in temporal bones (Figs. 56). Three speculated reasons could be counted for these discrepancies: first, the hole size and hole edge smoothness in FE model were not the same as those holes made in the temporal bones; second, the possible change of local material properties of the TM due to the process of creating the hole (e.g., cauterization) as well as the change of TM tension were not simulated in the model; third, the current model does not include the mastoid cavity even though the mastoid cavity was partially removed through facial recess surgical preparation. These factors may need further consideration in our model. However, the most critical factor affecting the model accuracy is the material properties of ear tissues which should be improved by including non-linear viscoelastic parameters in frequency domain in FE analysis.

FE model prediction of middle ear cavity pressure transfer function

Our previous study on sound pressure distribution in middle ear cavity (Gan et al., 2006) has demonstrated that there is no significant difference of acoustic pressure at different locations inside the cavity, particularly, at frequencies below 4000 Hz. In this study, we calculated the sound pressure P2 at a location between the round window and stapes in the model and monitored P2 at the same location in temporal bones. A constant sound pressure P1 of 90 dB SPL was applied at 2 mm from the umbo in the ear canal. The measurements are shown in Figs. 7A and 7C and the modeling results are in Figs. 7B and 7C . With the TM perforated, the pressure difference P1-P2 was zero at low frequencies for all perforation sizes. Voss et al. (2007) reported similar results for the perforation sizes they tested.

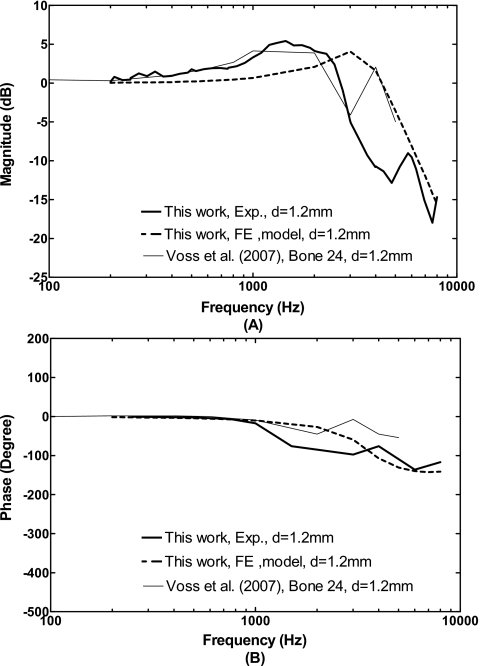
The ratio of middle ear cavity pressure P2 to the pressure at the ear canal P1 predicted by the model and measured in temporal bones from this study and from Voss et al. (2007) are shown in Fig. 9. The ratio P2∕P1 in decibels represents the middle ear cavity pressure transfer function. Figure 9A displays that the frequency response curves of the ratio P2∕P1 obtained from five bones (mean data) in this study are very close to the curve reported by Voss et al. (2007) on one bone at frequencies below 3 kHz with a 1.2 mm TM perforation. As frequency increased above 3 kHz, a peak at 4 kHz was observed by Voss et al. (2007), but not in this study. The modeling results show a peak at 3 kHz and the P2∕P1 ratio difference between the FE model and measurements in temporal bones were 2–3 dB at frequencies below 3 kHz. The discrepancies of the P2∕P1 ratio between the model and measurements at the frequencies of 3–6 kHz were mainly due to the peak of P2 curves. The P2 curve was shifted to a high frequency with a TM perforation shown in Fig. 7B. The phase of the ratio P2∕P1 obtained from the model and experimental measurements on temporal bones are in general consistent, as shown in Fig. 9B. However, there are some discrepancies at high frequencies (f=1.5–3 kHz) and an approximate 90° difference between the model and data of Voss et al. (2007) is observed.

Figure 9.

The ratio of middle ear cavity pressure P2 to pressure in the ear canal P1, or middle ear cavity pressure transfer function P2∕P1, measured from temporal bones and calculated from the FE model with perforations in comparison with the results reported by Voss et al. (2007). (A) Magnitude; (B) phase angle.

In summary, the TM is driven by pressure difference across the TM or the ratio P2∕P1. The change of P2∕P1 ratio in the case of a perforation is correlated to the TM and stapes footplate movements. This correlation is shown in the experimental measurements and FE modeling results in this study. The peaks of P2 pressure and P2∕P1 ratio of the measurements with Hole 1 in Figs. 79 around 1.5 kHz reflect the peaks of TM and footplate displacement measurement curves in Figs. 56. However, the peak of P2 or P2∕P1 ratio curve from the model with Hole 1 is at 3 kHz in Figs. 79, which represents that the resonance of the middle ear cavity in the model with hole is different from the real temporal bone experimental setup because of the cavity volume difference. Thus, discrepancies of the TM and footplate displacements curves at high frequencies between the model and measurements observed in Figs. 56 are probably due to the resonance difference between the model and temporal bone.

CONCLUSION

A 3D FE model of human ear including structures of the external ear canal, middle ear, and cochlea has been used to predict the effect of TM perforations on sound transmission through the middle ear. The displacement curves of the TM (at the umbo) and the stapes footplate as well as the sound pressure inside the middle ear cavity, or the middle ear cavity pressure transfer function, were derived from the model over the frequency range of 200–8000 Hz and compared with the data measured from temporal bones. These comparisons between the model results and measurements (Figs. 4567) are important to verify the validity of the model. We noticed that there were discrepancies of the TM, stapes footplate, and middle ear pressure P2 between the model and experimental measurements in temporal bones, particularly at higher frequencies. The dynamic behavior of the model for acoustic energy transmission through the middle ear needs to be improved over the auditory frequency range. However, this study indicates that the FE model of human ear equipped with multi-field coupled analysis capabilities can be used as a tool to investigate the relationship between middle ear structural changes and middle ear function alteration with geometric visualization.

The model predicts that the TM perforations mainly affect the middle ear transfer function at low frequencies, which is similar to the measurements from temporal bones observed in this study and reported in the literature. Using the model, we further investigated the effects of perforation size and location on TM and stapes footplate displacements. The results indicate that increase in perforation size reduces the TM and footplate movements and results in conductive hearing loss. Compared with a single perforation, the multiple perforations not only reduce the magnitude of the TM and footplate displacement but also move the displacement curve toward the high frequency. Therefore, the location of TM perforation may have some effect on hearing loss.

The effect of TM perforation on middle ear function for sound transmission has been thoroughly studied by Voss et al. (2001a, 2001b, 2001c) through a series of publications since 2001. They used a simple circuit model or lumped model to simulate different perforation-induced changes in stapes velocity and middle ear input impedance. The model results were compared with the measurements obtained from temporal bones (Voss et al., 2001c, 2007). Compared with the circuit model used by Voss et al. (2001, 2001c, 2007), the 3D FE model presented in this study is much more complicated because the structural geometry, mechanical properties, and boundary conditions of the ear are all involved in the model. The TM and stapes movements depend on all parameters of the model as well as the FE analysis method. Thus, it requires a great effort to improve the model by validating it with experimental measurements in temporal bones. The present study suggests that the FE model needs to be improved through our understanding of the middle ear mechanical system in both mechanical properties of middle ear components and dynamic behavior of the system.

We also realize that TM perforations may result in a complex combination of changes in sound transmission through two routes: the mechanical route through the ossicular chain and the acoustic route through the air in the middle ear cavity. The contributions of the mechanical route and acoustic route to the change of sound conduction from the ear canal to oval window, round window, and cochlea will be related to perforation size and location. Some of our future investigations will focus on identifying the mechanism and distribution of sound transmission through these two routes in the presence of TM perforations.