Abstract
The primary purpose of the present experiment was to test whether the binaural equal-loudness-ratio hypothesis (i.e., the loudness ratio between monaural and binaural tones presented at the same Sound Pressure Level, SPL, is independent of SPL) holds for hearing-impaired listeners with bilaterally symmetrical hearing losses. The outcome of this experiment provided a theoretical construct for modeling loudness-growth functions. A cross-modality matching task between string length and tones was used to measure three loudness functions for eight listeners: two monaural (left and right) and one binaural. A multiple linear regression was performed to test the significance of presentation mode (monaural vs binaural and left vs right), level, and their interaction. Results indicate that monaural loudness functions differ between the ears of two listeners. The interaction between presentation mode (binaural∕monaural) and level was significant for one listener. Although significant, these differences were quite small. Generally, the binaural equal-loudness-ratio hypothesis appears to hold for hearing-impaired listeners. These data also indicate that loudness-growth functions in two ears of an individual are more similar than loudness-growth functions in ears from different listeners. Finally, it is demonstrated that loudness-growth functions can be constructed for individual listeners from binaural level difference for equal-loudness data.
INTRODUCTION
A tone presented binaurally is louder than the same tone presented monaurally (Fletcher and Munson, 1933). Fletcher and Munson (1933) (see, also Fletcher, 1953) assumed that the binaural-to-monaural loudness ratio is independent of level. This assumption of a constant ratio between the binaural and monaural loudness-growth functions for the same sound is known as the binaural equal-loudness-ratio hypothesis (BELRH). The BELRH is supported by empirical data for normal listeners (Marozeau et al., 2006), but remains an untested assumption for listeners with hearing losses of primary cochlear origin. The first of four aims of the present experiment is to obtain a set of data that is comprehensive enough to permit testing of the BELRH for individual hearing-impaired (HI) listeners.
Testing the BELRH for HI listeners is important for two reasons. First, the BELRH was assumed to be true by Whilby et al. (2006) to model loudness-growth functions for HI listeners. This assumption needs to be tested. Second, current hearing-aid fitting procedures often assume that the binaural-to-monaural loudness ratio is about the same for all people with the same amount of hearing loss. This assumption may not be valid and could be partly responsible for the uncomfortable loudness experienced by hearing-aid users. A survey (Kochkin, 2005) of 1500 hearing-aid users indicates that only 60% of them reported being satisfied when asked about comfort with loud sounds.
Testing the BELRH for HI listeners presents a potential problem that is not encountered when testing normal-hearing listeners. For normal-hearing listeners, loudness functions for right and left ears usually grow at the same rate (Marks, 1978, 1980). Therefore, either ear can be used to obtain the monaural loudness-growth function for comparison with their binaural loudness-growth function. For HI listeners, it is unclear whether the loudness-growth functions are similar in both ears of the same listener, even if they have bilaterally symmetrical losses. Although most fitting procedures for binaural hearing aids assume the same loudness-growth functions in both ears of individual HI listeners with symmetrical hearing losses, it is possible that hearing losses could affect the two ears of an individual in different ways. Data clearly indicate that two ears from different HI listeners with the same amount of hearing loss can have different loudness functions (Dix et al., 1948; Knight and Margolis, 1984; Hellman and Meiselman, 1990; Brand and Hohmann, 2001; for a review see Marozeau and Florentine, 2007). In fact, HI listeners with similar audiograms can have different loudness-growth functions (Hellman, 1994; Florentine et al., 1997), as can normal-hearing listeners (Epstein and Florentine, 2005, 2006). Therefore, the second aim of the present experiment is to obtain a set of data from the right and left ears of individual listeners with symmetrical hearing losses to test the assumption that their monaural loudness-growth functions are similar. These data will be compared with binaural loudness-growth functions from the same listeners.
The third aim of the present experiment is to compare the binaural and monaural loudness-growth functions for individual HI listeners to those of normal-hearing listeners. There are two different measures used to study binaural loudness summation. One is the previously described binaural-to-monaural loudness ratio. The other is the binaural level difference for equal loudness (BLDEL), which was used by Whilby et al. (2006). When binaural and monaural loudness-growth functions are plotted together on a logarithmic scale, the binaural-to-monaural loudness ratio corresponds to the vertical distance and the BLDEL corresponds to the horizontal distance between the two functions. If the BELRH holds, the two functions are parallel and it would be possible to derive a loudness-growth function directly from the BLDEL data. This is possible because the slope of the loudness-growth function would be proportional to the inverse of the BLDEL.
The last of the four aims proposed for the present experiment is to compare the BLDEL of normal and HI listeners measured using an indirect method with the data of Whilby et al. (2006). This is an important cross-check of the method to derive loudness functions from BLDELs by Whilby et al. (2006) for HI listeners.
To accomplish all four aims of the present experiment as efficiently and effectively as possible, a reliable cross-modality matching procedure used by Epstein and Florentine (2005) and Marozeau et al. (2006) to measure loudness functions in normal-hearing listeners was used to test HI listeners in the present experiment.
METHOD
Stimuli
The stimuli were pure tones with equivalent rectangular durations of 200 ms, including 6.67-ms raised-cosine rises and falls. Frequencies were chosen individually for each listener around 1 or 2 kHz and can be found in Table 1. For each listener, the frequency of the tone was selected to have a threshold difference of less than 3 dB between the two ears. Although problems with threshold microstructure that could influence loudness judgments near threshold have been observed (Horst et al., 2003), none were observed in our listeners. Tones were presented monaurally (right and left ears) and binaurally at the same Sound Pressure Level (SPL) to both ears. Having the same threshold at the two ears prevented the potentially confounding issues of the differences in loudness at equal-SL (Sensation Level) vs equal-SPL. The level of the tone changed in 5-dB steps from the first multiple of 5-dB above threshold to 100 dB SPL, resulting in a total of approximately nine levels per listener. The upper limit of 100 dB SPL was chosen to be loud, but did not cause any tolerance issues for any of the listeners. The Institutional Review Board of Northeastern University protocol was strictly followed.
Table 1.
Summary of the individual data (gender, age); clinic measurements (thresholds at 0.25, 0.5, 1, 2, and 4 kHz in dB Hearing Level (HL) for both ears and presumed etiology); frequency in kHz selected for the experiment and threshold in dB SPL measured in the laboratory; individual results (exponent α and binaural-to-monaural ratio). Abbreviations for etiology are congenital or hereditary hearing loss (CHHL), presbycusis (Pres.), noise induced hearing loss (NIHL), and family history of hearing loss (FHHL).
| Listeners | Clinic threshold (dB HL) | Laboratory measurement | Expt. result | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gender | Age | Ear | 0.25k | 0.5k | 1k | 2k | 4k | 8k | Et. | Test frequency (kHz) | Threshold (dB SPL) | a | Ratio | |
| HI-1 | M | 65 | L | 55 | 60 | 65 | 65 | 75 | 70 | CHHL | 1.05k | 70 | 0.314 | 1.297 |
| R | 50 | 60 | 60 | 60 | 60 | 75 | 72 | |||||||
| HI-2 | M | 65 | L | 10 | 5 | 40 | 45 | 70 | 70 | Pres. | 1k | 65 | 0.201 | 1.15 |
| R | 10 | 15 | 40 | 45 | 75 | 85 | 64 | |||||||
| HI-3 | M | 76 | L | 20 | 30 | 40 | 45 | 75 | 85 | Pres. | 2k | 65 | 0.279 | 1.342 |
| R | 15 | 40 | 40 | 45 | 75 | nr | 67 | |||||||
| HI-4 | M | 60 | L | 55 | 60 | 65 | 65 | 70 | 90 | NIHL | 1k | 65 | 0.236 | 1.163 |
| R | 55 | 65 | 65 | 70 | 75 | 90 | 68 | |||||||
| HI-5 | F | 60 | L | 20 | 15 | 45 | 35 | 50 | 55 | Pres. | 0.95k | 45 | 0.25 | 1.533 |
| R | 15 | 15 | 40 | 60 | 45 | 60 | 47 | |||||||
| HI-6 | M | 61 | L | 5 | 10 | 30 | 55 | 95 | 95 | NIHL | 0.95k | 33 | 0.158 | 1.337 |
| R | 10 | 10 | 25 | 40 | 85 | 95 | 34 | |||||||
| HI-7 | M | 74 | L | 25 | 30 | 45 | 50 | 65 | 50 | Pres. FHHL | 1k | 53 | 0.19 | 1.141 |
| R | 25 | 30 | 40 | 45 | 50 | 50 | 55 | |||||||
| HI-8 | F | 73 | L | 45 | 40 | 45 | 45 | 75 | 75 | Pres. | 1k | 55 | 0.22 | 1.355 |
| R | 40 | 35 | 40 | 50 | 80 | 80 | ||||||||
Procedure
The experiment consisted of two parts: absolute threshold measurements and cross-modality matches. Except for the selection of the stimuli, the procedure was the same as that used by Marozeau et al. (2006) and is summarized below.
Absolute thresholds
Absolute thresholds were measured separately for each ear using a two-interval, two-alternative forced-choice paradigm with feedback. The listeners’ task was to indicate which 250-ms visually marked interval contained the signal by pressing a key on a small computer terminal. Each threshold measurement consisted of three interleaved tracks, each of which ended after five reversals. For each track, the level of the signal was initially set approximately 10 dB above the expected threshold of the listeners. The step size was 5 dB until the second reversal, after which it decreased to 2 dB. The threshold for each track was calculated as the average signal level of the last two reversals. The average of the three interleaved tracks was considered the absolute threshold. Absolute thresholds for right and left ears were then compared. If the difference was greater than 3 dB a different frequency was selected.
Cross-modality matching
For each listener, three modes of presentation were used: monaural (right and left ears) and binaural. As noted in Sec. 2A, approximately nine levels were tested for each presentation mode. This yielded about 27 stimuli for each listener.
Listeners judged the loudness of each stimulus using a string-length cross-modality matching procedure. This procedure was chosen because it has been shown to yield reliable individual data. (For further information, see Epstein and Florentine, 2005.) Listeners were asked to cut a piece of a string that was as long as the sound was loud from a virtually unbounded ball of very thin, but strong string (i.e., embroidery floss). After cutting each piece of string, the listener taped it into a notebook, turned the page, and pressed a button to indicate completion of the response. This response initiated presentation of the next stimulus after a 700-ms delay.
A total of six cross-modality matches were made for each monaural stimulus and a total of 12 matches were made for each binaural stimulus. The 216 matches per listener (6+6+12 matches×9 levels) were divided into four testing sessions administered in random order over two days, with two sessions per day separated by a 15-min break. Stimuli were presented binaurally (at the same SPL to each ear) and monaurally, always to the same ear within one session. The two test days were separated by less than two weeks, except for HI-7. The first part of HI-7’s data was collected in a pilot experiment performed two months before with slight variation of protocol in which tones were presented at the same SL, which is within 2 dB of equal SPL at the two ears and within the variability of the measurement for the other listeners. Each level was presented three times within a session.
At the start of each trial, a new tone level and one of the two modes (binaural or monaural) were randomly selected from all other stimuli that had not yet been presented three times and had a level within 30 dB of the level of the previous trial. The 30-dB level restriction was included to avoid surprising the listener with a sudden large level increase or decrease, which may cause the listener to miss attending to a stimulus. If no stimuli fulfilled these criteria, but some other stimuli still had been presented fewer than three times, a dummy trial was inserted. The dummy trial had the same mode and a level 30-dB above or below the preceding level, depending on the levels of the stimuli that remained to be presented. The dummy trials were not included in the final analysis.
Apparatus
A PC-compatible computer with a 24-bit sound card (Lynx Two-b) played the tone that was generated with MATLAB. The sampling rate was 48 kHz. The computer also recorded the listeners’ responses and executed the adaptive procedure. The output of the sound card was led to a headphone buffer (TDT HB6), which fed the earphones of the Sony MDR-V6 headset. For routine calibration performed before each session, the output of the headphone buffer was sent back to the sound card, such that the computer could sample the waveform and calculate its rms voltage.
Listeners
Eight naïve HI listeners with symmetrical sensorineural hearing losses of primarily cochlear origin participated in this experiment. Their hearing losses ranged from mild to severe. Table 1 shows gender, age, presumed etiology, and audiometric data. The audiometric data were obtained using a calibrated audiometer (ANSI, 2004) and a modified Hughson–Westlake procedure (Harrell, 2002, p. 73).
Data analysis
The geometric mean of string lengths for each stimulus was computed for each listener and level using all available data. The standard deviation was determined from the logarithms of the string lengths. The group mean and standard error were calculated across the individual listener’s geometric means for each presentation mode (monaural right, monaural left, or binaural) and level. The resulting data were transformed back into the string-length domain to show the probable range of each individual listener’s responses.
A correction factor was applied to each session in order to minimize any possible difference between the binaural data obtained across sessions caused by changes in the listeners’ internal judgment standard. First, the binaural data from the first session in which the monaural data were presented to the left ear were selected as a reference. A factor was obtained with the aid of a mean-square fit to minimize the differences between the logarithm of the binaural data of each subsequent session and the reference data. Each factor was then applied in the linear domain to the monaural data as well in order to not impact the binaural-to-monaural ratio. The factor applied was usually less than 0.2 (with a median of 0.1). To examine the effects of stimulus variability, a multiple linear regression was performed on the logarithms of the string lengths obtained for each level and mode using the statistics package R (www.r-project.org). Three models were tested:
| (1) |
| (2) |
| (3) |
where S is the string-length estimation, L is the level, and N is the Boolean factor condition. This factor will be set to zero for left monaural stimuli, and unity for right monaural stimuli, when analyzing the effect of ear (Sec 3B). It will be set to zero for monaural stimuli, and unity for binaural stimuli, when testing the BELRH (Sec. 3C). If the sum of squares of the error for model 2 is significantly lower than the sum of squares for model 1, then the effect of the presentation mode is significant. If the sum of squares of the error for model 3 is significantly lower than the sum of squares for model 2, then the effect of the interaction condition and level is significant. For all tests, p≤0.01 is considered significant.
RESULTS
Mean and variability
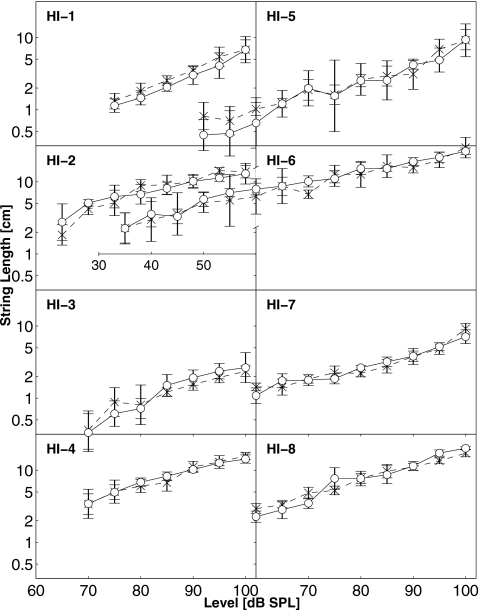
Figure 1 shows the two monaural loudness functions for each of the eight listeners. Figure 2 shows the binaural loudness functions and the average of the two monaural functions for each listener. String lengths ranged from 0.1 cm (the precision of the measurement) to 37.8 cm with an arithmetic mean of 4.2 cm [standard deviation (std) of the mean is 2.6 cm between subjects, and mean of the std is 1.33 within subjects] for the monaural left condition, 4.12 cm (std of 2.76 cm between subjects and 1.34 within subjects) for the monaural right condition, and 5.4 cm (std of 2.71 cm between subjects and 1.29 within subjects) for the binaural condition. The intra-subject variability differs among individual listeners. Whereas HI-4, HI-7, and HI-8 have relatively small variability, HI-3 and HI-5 have relatively large variability. However, the variability observed for the HI listeners is within the same range as the normal-hearing listeners measured by Marozeau et al. (2006).
Figure 1.
Individual monaural loudness functions for tones from all eight HI listeners. The geometric means of string lengths are plotted on a log scale as a function of level. Data are shown separately for left (x) and right (o) ears. The vertical bars show ±1 standard deviation of the log of the string lengths. Note that data for listeners HI-5 and HI-6 are continued into the left panel while maintaining the same relative scale.
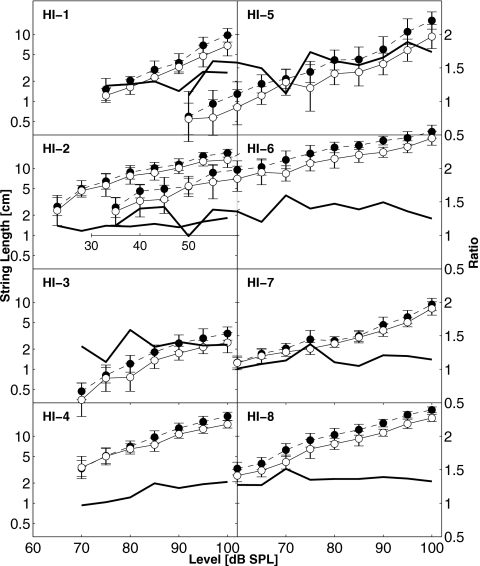
Figure 2.
Individual binaural (filled circles) and the averaged monaural (open circles) loudness functions for tones for eight HI listeners. The geometric means of string lengths (on the left ordinate) are plotted as in Fig. 1. The thick line shows the ratio of string lengths (on the right ordinate) for equal-SPL monaural and binaural tones.
It should be noted that a few listeners did not hear every presentation of the 5-dB-SL tone and did not cut any string. Because at least four estimations were available for each stimulus, statistical analyses were performed on the remaining data.
Monaural loudness functions
Figure 1 shows that monaural loudness functions for the two ears of an individual HI listener are more similar than monaural loudness functions for different HI listeners. A multiple linear regression was performed between the data for the left and right ears of individual listeners in order to test if the two ears were significantly different. The analysis indicates that the effect of level was always significant (p<0.001, as expected, for all eight listeners). The effect of ear presentation (left vs right) was significant (p=0.004, R2=2%) for only one listener out of eight, HI-1, indicating that the loudness function for his left ear was significantly higher than the one for his right ear. The interaction between ears and level was significant (p=0.002, R2=1%) only for listener HI-8, indicating that the slope of loudness function for his left ear was significantly shallower than the one for his right ear. For six of the eight listeners the ear and the interaction between ear and level were not significant (p>0.01). This provides support for the contention that the two monaural loudness functions are not essentially different. It is worth noting that if the two loudness functions of HI-1 were plotted in dB SL, the gap between the functions will decrease accordingly. The two functions show a difference of 3 dB. This is consistent with a threshold elevation in his right ear of 2 dB (a previous measurement in the clinic reported a 5-dB difference in threshold between his ears). When the statistical analysis was performed in SL, no significant effects of ear or interaction were found for this listener p>0.01.
Binaural vs monaural loudness function
Because the difference between the two monaural loudness functions for HI-1 and HI-8 was small enough, as shown by the R2, not to impact the rest of the analysis, the two monaural loudness functions were averaged and compared to the binaural function for each listener in Fig. 2. As expected, the binaural tones were perceived louder than the monaural tones. Statistical analysis supports this observation; the factor presentation mode (binaural vs monaural) was significant for all eight listeners (p<0.004). Despite the variability, the ratios between the monaural and binaural data appear relatively constant across level for most listeners. The interaction was significant only for HI-4 (p=0.002, R2=14%). As the analysis and Fig. 1 show, the two monaural loudness functions were similar; therefore, it appears that for this listener the binaural ratio increased with level. For the seven other listeners no significant interactions were found.
The binaural and monaural data for each listener were fitted with two parallel straight lines using the method of least-squares. Although the shape of the loudness functions differs somewhat from a straight line, this method was used as a rough approximation to derive the overall slope. The exponents of the power functions and the binaural-to-monaural ratio for each listener are summarized in Table 1. The exponent varies from 0.16 to 0.31, with an average of 0.23. The ratio varies from 1.14 to 1.53, with an average of 1.29. The average exponent is lower than the 0.3 of the power law (Stevens, 1955), and this ratio is lower than the doubling of loudness expected from perfect binaural loudness summation (Marks, 1978; Hellman, 1991). However, both are within the range of what has been found for normal-hearing listeners in literature (see Marozeau et al., 2006).
DISCUSSION
Testing the binaural equal-loudness-ratio hypothesis for hearing-impaired listeners
The first aim of the present experiment was to obtain a set of data to permit testing of the BELRH for HI listeners. Results of the present experiment support the BELRH, except for listener HI-4. The binaural loudness function for HI-4 is significantly steeper than his monaural loudness function. It is unclear why his binaural loudness summation is dependent on level. No apparent difference can be found in his audiological profile and the monaural loudness functions for both his ears were not significantly different.
Although the present experiment provides comprehensive data for eight individual HI listeners, the sample is not large enough to make precise inferences to all HI listeners. However, it seems reasonable to assume that the BELRH is supported for most HI listeners with bilaterally symmetrical-hearing losses, which is the most common type of hearing loss (http:∕∕www.nidcd.nih.gov∕funding∕programs∕ot∕inner_ear_summary.html).
Monaural loudness functions
The second aim of the present experiment was to obtain a set of data comprehensive enough to test the assumption that the right and left ears of an individual listener with symmetrical hearing losses have similar monaural loudness-growth functions. Although listeners HI-1 and HI-8 show significant differences between the ears, only listener HI-8 shows a loudness function with a shallower slope in the left ear than the right ear. (Recall that for listener HI-1 the loudness function for his left ear was significantly higher than the one for his right ear, but the slopes were not significantly different.) Although the difference in slope is small, it may be important because it illustrates the fact that there may be a difference in the loudness-growth functions between the two ears of the same listener even with the same threshold in both ears.
Loudness-growth functions in normal-hearing and impaired-hearing listeners
The third aim of the present experiment was to compare the binaural and monaural loudness-growth functions for individual HI listeners to those of normal-hearing listeners. Two types of loudness-growth functions have been described for listeners with sensorineural hearing losses of primary cochlear origin: the rapid growth type and softness imperception (for a review see Marozeau and Florentine, 2007). In the rapid growth type (same as the classical view of recruitment) the model is described as follows: (1) loudness at threshold is the same for normal-hearing and HI listeners, (2) loudness at and near threshold grows more rapidly than for normal-hearing,1 and (3) loudness is the same or approaches that of normal listeners at high levels. The second type of loudness growth is called softness imperception, because it refers to the inability of the listener to hear soft sounds. This model is described as follows: (1) Loudness at threshold is higher for HI listeners than normal-hearing listeners, (2) loudness growth at and near threshold is similar for normal-hearing and HI listeners, (3) the loudness of some HI listeners exhibits a reduction in the amount of gain (also known as loss of compression) at moderate levels, and (4) the loudness-growth function approaches that of normal-hearing listeners at higher levels.
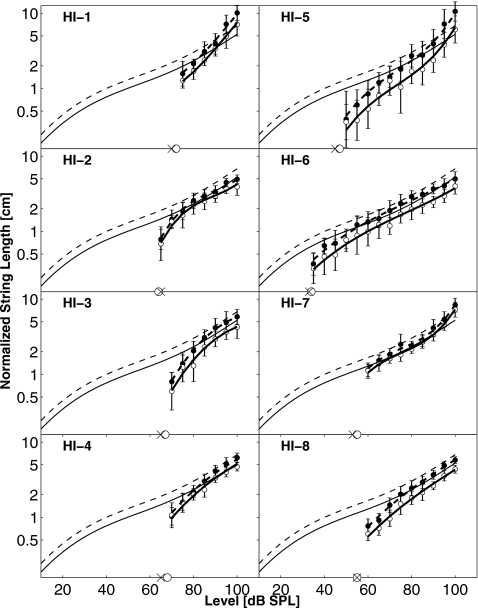
Data from individual HI listeners from the present experiment are compared in Fig. 3 to the average data from eight normal-hearing listeners obtained from Marozeau et al. (2006) using the same task as in the present study. In order to be able to compare the two sets of data across different individual scales, the present data were normalized using the same procedure as Whilby et al. (2006): The polynomial fit was set such that each individual average binaural loudness at 85 dB SPL matched the overall average binaural loudness of the average normal listeners at 80 dB SPL. Although this normalization was based on an assumption that is likely to be inaccurate in some cases, it cannot be too far off either because (1) listeners reported that the sounds were loud at these levels, and (2) loudness matching data in literature are more nearly equal at high levels for listeners with hearing losses of primarily cochlear origin.
Figure 3.
Individual normalized data (see text) replotted from Fig. 2 together with polynomial fits for the binaural (thick dashed lines) and the monaural (thick continuous lines) loudness functions. The averaged normal data for eight listeners from Marozeau et al., 2006 are also shown for the corresponding binaural (thin dashed line) and monaural (thin continuous line) loudness functions for 1-kHz tones. Absolute thresholds are shown for left (x) and right (o) ears on the abscissa.
Considerable individual differences can be observed in the rate of loudness growth with increasing level among the HI listeners. For example, HI-2 and HI-3 show behavior consistent with the rapid growth type, and HI-7 shows a behavior consistent with softness imperception. The loudness functions of HI-2 and HI-3 show rapid growth close to threshold and that quickly approaches normal. On the other hand, the loudness function of listener HI-7 is normal at all tested levels. The lowest level tested was 5 dB above threshold. This implies that for this individual listener either loudness increases at an improbable rate between threshold and 5 dB SL, or loudness at threshold is greater than normal at or very near threshold. The other HI listeners shown in Fig. 3 exhibit an intermediate behavior between these two extremes.
The present data are consistent with data in literature. Marozeau and Florentine (2007) reviewed five published experiments from different laboratories, obtained using different methods, to measure individual loudness functions for normal and HI listeners. They found that (1) individual differences are greater for HI listeners than for normal listeners, and (2) some HI listeners seem to show rapid growth, some softness imperception, and some a combination of both. Therefore, a sufficient number of individual functions for HI listeners exist in literature and they show clear individual differences. (N.B. loudness data should not be averaged across HI listeners because these important differences will be missed).
The binaural level difference for equal-loudness data
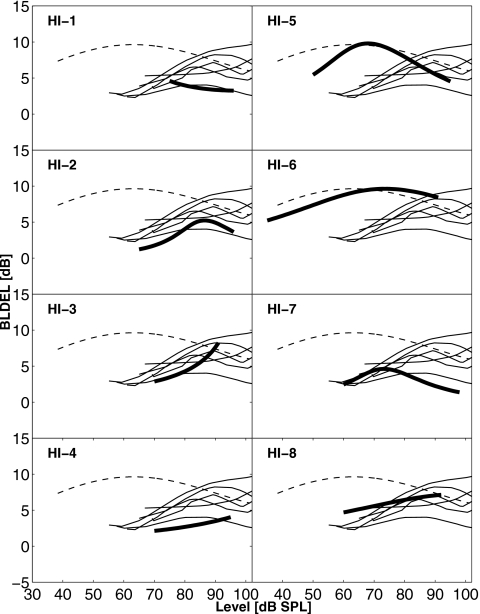
As explained in the Introduction, the fourth and final aim of the present experiment is to take the BLDEL data of normal and HI listeners (indirectly derived from the present loudness measurements) and compare them with the data of Whilby et al. (2006). The BLDELs were extracted by measuring the level difference of the fitted monaural and binaural functions for every listener. (For details of the fitting procedure and assumptions to derive loudness functions, see Whilby et al., 2006.) Figure 4 shows these data compared to those of Whilby et al. (2006) obtained using a loudness-matching procedure. As shown by Whilby et al. (2006), the BLDEL data vary with level and are non-monotonic. Values range from 1 dB for HI-2 at 65 dB SPL to 10 dB for HI-5 at 70 dB SPL. Six out of eight HI listeners show BLDEL data that vary within the range of the HI data shown by Whilby et al. (2006) and two listeners (HI-5 and HI-6) show BLDEL data that follow the normal range. It is noteworthy that the latter two listeners have the mildest hearing losses of all the listeners. Therefore, there appears to be a direct relationship between the BLDEL, the slope of the loudness-growth functions, and the binaural-to-monaural ratio. This provides support for the method proposed by Whilby et al. (2006).
Figure 4.
The BLDEL is plotted as a function of level. The polynomial fits to individual data from the present study (thick lines) are compared with the data of Whilby et al. (2006): individual data from eight HI listeners (thin lines) and averaged data from eight normal-hearing listeners (dashed lines). Each panel represents a polynomial fit for one listener from the present study compared with all the data from Whilby et al. (2006).
Validation of a method to derive loudness functions from loudness matches
The BELRH was studied because it was one of the assumptions of a method used to derive loudness functions from BLDEL data. This method is fully described in Whilby et al., 2006 and Marozeau et al., 2006. Instead of the classical power function, the logarithm of loudness was modeled with a third-order polynomial
| (4) |
| (5) |
where Fm and Fb are the monaural and binaural loudness functions, respectively, at the level L; am, bm, cm, dm, ab, bb, cb, and db are the free parameters of the polynomial fit. The BELRH assumes that the slopes of the two functions are parallel. Therefore, it implies that the first three coefficients of both functions are the same: am=ab, bm=bb, and cm=cb. It also implies that the difference of the last parameter is equal to the log of the binaural-to-monaural ratio, K:dm-db=log(K). The data of Whilby et al. (2006) indicate how the BLDEL for each individual listener will vary with level. For a fixed selected level of the monaural stimulus, Lm, the BLDEL estimates the level of the binaural stimulus, Lb, at which the loudnesses of the monaural and binaural stimuli were equal,
| (6) |
| (7) |
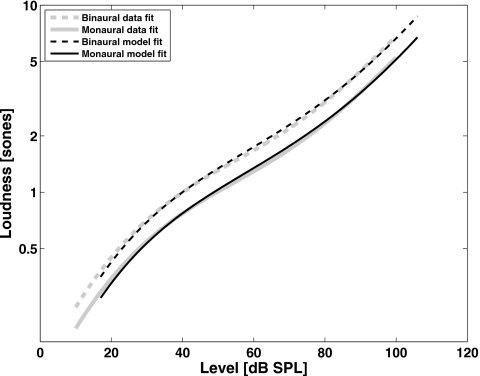
The BLDEL data from the study of Whilby et al. (2006) were fitted to extract the coefficients of the model. Then, by using a least-squares fit, the three free parameters (a, b, and c) were selected to minimize the error of the fit between the model and the BLDEL data. Marozeau et al. (2006) showed that the method was valid by comparing the averaged loudness function to the derived loudness function from the BLDEL data. The result indicates that the method accurately predicts the data from low-to-moderate levels. A review of literature on individual loudness functions (Marozeau and Florentine, 2007) shows that the slope as a function of level is not a symmetrical function. In other words, the slope changes more rapidly at low levels than high levels. Therefore, a third-order polynomial was required to fit the slope, and by extension a fourth order for the loudness function (i.e., the integral of the slope). Figure 5 shows the same data as in Fig. 4 of Marozeau et al. (2006), except that now the function has been fitted with a fourth-order polynomial, which fits the data better. The method to derive loudness functions from loudness matches now appears valid throughout the entire audible range of levels, not just low-to-moderate levels, at least for normal-hearing listeners.
Figure 5.
Modification of the method described in Marozeau et al., 2006. The thick gray lines represent the binaural (dashed line) and average monaural (continuous) loudness functions of eight normal-hearing listeners (Marozeau et al., 2006); the thin dark lines represent the binaural (dashed line) and monaural (continuous line) loudness-growth functions constructed for individual listeners from the binaural level difference data for equal loudness (Whilby et al., 2006). The function is constructed here with a fourth-order polynomial, instead of the third order used in Whilby et al., 2006.
CONCLUSION
The results of this study indicate that the BELRH holds for most HI listeners with symmetrical sensorineural hearing losses of primary cochlear origin. Furthermore, the results show that monaural loudness functions for right and left ears of an individual HI listener are quite similar. However, important individual differences are found among HI listeners. Some listeners have loudness functions that show rapid growth (also known as recruitment), some show softness imperception, and some an intermediate behavior. The BLDEL data extracted from the fitted monaural and binaural loudness functions are within the range found by Whilby et al. (2006). This last result—combined with the BELRH data—indicates that loudness-growth functions can be constructed for individual listeners from BLDEL data.
ACKNOWLEDGMENTS
The authors wish to thank Lauren Chase and Becky Daley, Au.D., for assistance in data acquisition. Professor Michael Epstein provided helpful comments. This research was supported by NIH-NIDCD Grant No. R01DC02241 and a fellowship for advanced researchers from the Swiss National Science Foundation.
A portion of this work was presented in a talk to the American Auditory Society. [Marozeau, J., and Florentine, M. (2008). AAS bulletin, 33, p. 29].
Footnotes
Moore (2004) modeled loudness-growth functions of HI listeners as follows: (1) HI and normal listeners have the same loudness at threshold, (2) both groups show the same loudness growth from 0- to 5-dB SL, and (3) HI listeners show a steeper slope after 5-dB SL.
References
- ANSI (2004). “American National Standard Specification for Audiometers,” ANSI S3.6–2004.
- Brand, T., and Hohmann, V. (2001). “Effect of hearing loss, centre frequency, and bandwidth on the shape of loudness functions in categorical loudness scaling,” Audiology 40, 92–103. 10.3109/00206090109073104 [DOI] [PubMed] [Google Scholar]
- Dix, M. R., Hallpike, C. S., and Hood, J. D. (1948). “Observations upon the loudness recruitment phenomenon, with especial reference to the differential diagnosis of disorders of the internal ear and VIII nerve,” Proc. R. Soc. Med. 41, 516–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein, M., and Florentine, M. (2005). “A test of the equal-loudness-ratio hypothesis using cross-modality matching functions,” J. Acoust. Soc. Am. 118, 907–913. 10.1121/1.1954547 [DOI] [PubMed] [Google Scholar]
- Epstein, M., and Florentine, M. (2006). “Loudness of brief tones measured by magnitude estimation and loudness matching,” J. Acoust. Soc. Am. 119, 1943–1945. 10.1121/1.2177592 [DOI] [PubMed] [Google Scholar]
- Fletcher, H. (1953). Speech and Hearing in Communication, 2nd ed., Bell Telephone Laboratories Series; (Van Nostrand, Princeton, NJ: ). [Google Scholar]
- Fletcher, H., and Munson, W. A. (1933). “Loudness, its definition, measurement and calculation,” J. Acoust. Soc. Am. 5, 82–108. 10.1121/1.1915637 [DOI] [Google Scholar]
- Florentine, M., Buus, S., and Hellman, R. P. (1997). “A model of loudness summation applied to high-frequency hearing loss,” in Modeling Sensorineural Hearing Loss, edited by Jesteadt W. (Erlbaum, New York: ), pp. 187–198. [Google Scholar]
- Harrell, R. W. (2002). “Puretone evaluation,” in Handbook of Clinical Audiology, 5th ed., edited by Katz J. (Lippincott Williams & Wilkins, Philadelphia, PA: ), pp. 71–87. [Google Scholar]
- Hellman, R. (1991). in Ratio Scaling of Psychological Magnitude, edited by Bolanowski S. J. and Gescheider G. A. (Erlbaum, Hillsdale, NJ: ), pp. 215–228. [Google Scholar]
- Hellman, R. P. (1994). “Relation between the growth of loudness and high-frequency excitation,” J. Acoust. Soc. Am. 96, 2655–2663. 10.1121/1.411445 [DOI] [PubMed] [Google Scholar]
- Hellman, R. P., and Meiselman, C. H. (1990). “Loudness relations for individuals and groups in normal and impaired hearing,” J. Acoust. Soc. Am. 88, 2596–2606. 10.1121/1.399979 [DOI] [PubMed] [Google Scholar]
- Horst, J. W., Wit, H. P., and Albers, F. W. J. (2003). “Quantification of audiogram fine-structure as a function of hearing threshold,” Hear. Res. 176, 105–112. 10.1016/S0378-5955(02)00749-9 [DOI] [PubMed] [Google Scholar]
- Knight, K. K., and Margolis, R. H. (1984). “Magnitude estimation of loudness. II: Loudness perception in presbycusic listeners,” J. Speech Hear. Res. 27, 28–32. [DOI] [PubMed] [Google Scholar]
- Kochkin, S. (2005). “Marketrak VII: Hearing loss population tops 31 million people,” Hear. Rev. 12, 16–29. [Google Scholar]
- Marks, L. E. (1978). “Binaural summation of the loudness of pure tones,” J. Acoust. Soc. Am. 64, 107–113. 10.1121/1.381976 [DOI] [PubMed] [Google Scholar]
- Marks, L. E. (1980). “Binaural summation of loudness: noise and two-tone complexes,” Percept. Psychophys. 27, 489–498. [DOI] [PubMed] [Google Scholar]
- Marozeau, J., Epstein, M., Florentine, M., and Daley, B. (2006). “A test of the binaural equal-loudness-ratio hypothesis for tones,” J. Acoust. Soc. Am. 120, 3870–3877. 10.1121/1.2363935 [DOI] [PubMed] [Google Scholar]
- Marozeau, J., and Florentine, M. (2007). “Loudness growth in individual listeners with hearing losses: A review,” J. Acoust. Soc. Am. 122, EL81–EL87. 10.1121/1.2761924 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. (2004). “Testing the concept of softness imperception: Loudness near threshold for hearing-impaired ears,” J. Acoust. Soc. Am. 115, 3103–3111. 10.1121/1.1738839 [DOI] [PubMed] [Google Scholar]
- Stevens, S. S. (1955). “The measurement of loudness,” J. Acoust. Soc. Am. 27, 815–829. 10.1121/1.1908048 [DOI] [Google Scholar]
- Whilby, S., Florentine, M., Wagner, E., and Marozeau, J. (2006). “Monaural and binaural loudness of 5- and 200-ms tones in normal and impaired hearing,” J. Acoust. Soc. Am. 119, 3931–3939. 10.1121/1.2193813 [DOI] [PubMed] [Google Scholar]