A framework for describing the effects of attention on visual responses

Abstract

Much has been learned over the past 25 years about how attention influences neuronal responses to stimuli in the visual cortex of monkeys and humans. The most recent studies have used parametric manipulations of stimulus attributes such as orientation, direction of motion, and contrast to elucidate the form of the attentional mechanism. The results of these studies do not always agree. However, some of this inconsistency may be caused which attentional effects are considered, such as contrast gain, response gain, or a baseline shift in firing rate with attention. Here, seven studies of spatial and feature-based attention, ranging from monkey electrophysiological studies in V4 and MT to fMRI studies in human visual cortex, are reevaluated in the context of a single parametric model that incorporates a variety of ways in which attention can influence neuronal responses. This reanalysis shows that most, though not all, of these results can be explained by a similar combination of attentional mechanisms.

INTRODUCTION

The first reports of spatial and feature-based attention in monkeys tended to focus on a restricted set of stimulus parameters, (e.g. (Moran & Desimone, 1985, Treue & Maunsell, 1996). These are landmark studies because they were the first to show that responses in visual areas that are relatively early in the visual processing stream can be influenced by factors other than the physical properties of the stimulus. However, due to their restricted set of stimulus and attentional parameters, these studies do not provide much insight into the exact nature of how attention affects the neuronal representation of a stimulus.

More recently, these investigators and others have extended these early results by measuring the effects of attention on electrophysiological responses across a range of stimulus and attentional parameters, such as stimulus contrast, or the physical or attended direction of motion (Martinez-Trujillo & Treue, 2004, McAdams & Maunsell, 1999, Reynolds, Pasternak & Desimone, 2000, Williford & Maunsell, 2006). A related set of parametric studies have also measured effects of attention on the population-based fMRI response in humans (Buracas & Boynton, 2007, Li, Lu, Tjan, Dosher & Chu, 2008, Murray, 2008). These studies are important because they help constrain the possible mechanisms of attention, such as whether attention acts as a gain change on the effective contrast of a stimulus, a multiplicative gain change on the response to the stimulus, or as an additive increase in response across all contrasts.

Some of these studies include a quantitative assessment of the measured attentional effects. However, not all studies allow for the same set of possible influences of attention. Also, due to the nature of different measurement techniques, the electrophysiological results are typically fit to the responses of individual neurons, while fMRI results are necessarily fit to a response that reflects a population average. This has lead to the perception that there is a great deal of disagreement in the results across laboratories and measurement techniques.

To address this issue, the results from four electrophysiological and three fMRI studies of attention are fit by a simple quantitative model that is capable of describing a wide variety of effects of spatial and feature-based attentional attention. This analysis shows that the results across these studies are actually in reasonable agreement when viewed within the context of a simple computational model that simultaneously considers the potential effects of both spatial and feature-based attention.

The model

Defining stimuli

We assume that stimuli are composed of multiple individual components (see Boynton, 2005). A stimulus consisting of two fields of dots would be considered as containing two components, as would two oriented lines. Each stimulus component is defined by two parameters; a feature dimension and contrast. A specific component of a stimulus will be represented by a feature value x_i, and contrast, c_i. For example, a 100% contrast plaid stimulus can be defined as the sum of two components with feature values x₁ = 0 and x₂ = 90 and contrasts c₁ = 0.5 and c₂ = 0.5. For simplicity, components are considered to be either inside or outside the RF.

Response to a stimulus

The stimulus-driven response of a neuron is shown in equation 1. We assume that every neuron has a sensitivity or tuning function F(x) ranging between 0 and 1 that is described as a Gaussian with standard deviation ω with and a peak at some specific feature value (such as upward motion or vertical orientation). The output of this tuning function is scaled by the contrast of the stimulus, which can be thought of as a linear filtering of the stimulus.

The output of this linear filter stage is normalized by a divisive contrast normalization process. The total excitatory response in the numerator is the sum of squared linear responses to each stimulus component. The inhibitory response in the denominator is the sum of squared contrasts within the neuron to each stimulus component plus a semisaturation term. The summed squared contrast in the denominator corresponds to the total contrast energy of the stimulus and represents the summed response from a population of neurons with peak sensitivities ranging across the spectrum of feature space (Heeger, 1993).

Note that the denominator is not feature-selective and only depends on the amount of contrast in the stimulus. This normalized response is then multiplied by a gain factor, γ, which represents the maximum response. A baseline firing rate, δ, is then added.

$$H(x,c)=\gamma \frac{{\displaystyle \sum _i}{\left(c_{i}F(x_i)\right)}^2}{{\displaystyle \sum _i}{c_i}^2+{\sigma }^2}+\delta$$ 1)

Where

$$F(x_i)=e^{-{(x_i-x_p)}^2)/w^2}$$ 2)

and x_p is the neuron’s preferred feature value.

This well-established normalization process predicts a variety of stimulus-dependent responses in the macaque and cat visual cortex (Carandini, Heeger & Movshon, 1997, Heeger, 1993, Heeger, Simoncelli & Movshon, 1996), including how increasing stimulus contrast increases neuronal responses without altering the selectivity of a neuron for a given feature, such as orientation or spatial frequency (Albrecht & Hamilton, 1982, Dean, 1981, Sclar & Freeman, 1982, Tolhurst, 1973).

This model also predicts a sigmoidal contrast-response function that is suppressed divisively when non-preferred stimuli are added to the RF. For example, the model makes the simple prediction that when two high contrast stimuli are placed in the RF of the neuron, the response to the pair is roughly the average of the response to the two individual components alone. This is because for high contrasts, the effect of the semisaturation constant σ becomes negligible. This prediction was demonstrated by Reynolds et al (Reynolds, Chelazzi & Desimone, 1999) in area V4. In their experiment 1, individual or pairs of oriented bars were placed in the RFs of V4 neurons while the monkey attended outside the RF. One stimulus was defined as the Probe, the other as the Reference. Reynolds et al calculated the regression line through a scatter plot of responses across neurons where the x-axis was defined as the difference in the response to Reference and the Probe, and the y-axis was the difference in the response to both Reference and Probe presented together and the response to the Probe in isolation. The regression line had a slope of 0.55, which is close to the slope of 0.5 as predicted by the model.

Three possible influences of spatial attention

Contrast gain

Two recent electrophysiological studies of attention suggest that attention directed inside the RF of a neuron shifts the contrast-response function leftward when plotted on a log contrast axis in V4 (Reynolds et al., 2000) and MT (Martinez-Trujillo & Treue, 2002). This can be incorporated in our model either by multiplying the contrast of all components within the receptive field by a constant, or equivalently, by dividing the semisaturation parameter, σ, by the same constant. Dividing the parameter σ by a constant s>1 increases the effective contrast of the stimulus by the same factor, shifting the contrast-response function leftward on a log-contrast axis. This is often referred to as ‘contrast gain’. One significant implication of contrast gain, as implemented by the present model, is that spatial attention simply increases the effective contrast of all stimulus components in the RF, regardless of which component is attended.

Baseline shift

While the presence of contrast gain with spatial attention is reasonably well established in the literature, there is physiological and fMRI evidence suggesting that spatial attention may also increase the baseline response of neurons in the absence of visual stimulation (Bisley, Zaksas, Droll & Pasternak, 2004, Chelazzi, Miller, Duncan & Desimone, 1993, Ferrera, Rudolph & Maunsell, 1994, Kastner, Pinsk, De Weerd, Desimone & Ungerleider, 1999, Luck, Chelazzi, Hillyard & Desimone, 1997, Ress, Backus & Heeger, 2000); for review see (Pasternak & Greenlee, 2005). This effect of attention on the baseline response can be incorporated by adding a positive value d to the baseline response δ when spatial attention is directed inside the RF of the neuron.

Multiplicative gain

A third option is a multiplicative gain change with spatial attention, sometimes called ‘response gain’ (Williford & Maunsell, 2006). Response gain is a multiplicative scaling of the response (prior to any baseline shift) to any stimulus inside the RF when attention is directed inside the RF. This can be modeled by multiplying the gain factor γ by a constant g>1 when attention is directed inside the RF.

To incorporate all three effects of spatial attention, the response to a stimulus when attention is directed inside the RF is:

$$H(x,c)=(\gamma g)\frac{{\displaystyle \sum _i}{\left(c_{i}F(x_i)\right)}^2}{{\displaystyle \sum _i}{c_i}^2+{(\sigma /s)}^2}+(\delta +d)$$ 3)

where s>1 represents contrast gain, d>0 represents an additive shift and g>1 represents multiplicative gain.

Single unit vs. population averages

It should be noted that although the model describes firing rates for single neurons, in the following sections the model was fit only to population averages. This was to allow a direct comparison between the electrophysiological results and the fMRI results which presumably reflect something related to a population average (Heeger, Huk, Geisler & Albrecht, 2000, Rees, Friston & Koch, 2000).

The way effects of attention on individual neurons is seen in the population average can be complex. This is because the model is nonlinear, so the best-fitting parameter values to the averaged responses are not necessarily the same as the average of best-fitting parameter values to the individual neuronal responses.

A useful way to illustrate the effects of attention on population responses is with a simulation. Parameters describing contrast response functions for 100 simulated macaque V1 neurons were generated by sampling from population distributions that matched the means, medians and standard deviations of parameters that described the responses of 71 neurons reported by Geisler and Albrecht (Geisler & Albrecht, 1997). Simulated contrast response functions (contrasts of 2.5, 5, 10, 20, 40 and 80%) were then generated from these sampled parameters, and the resulting values were taken as contrast response functions for unattended stimuli. The responses to attended stimuli were then estimated by varying each of the three spatial attention parameters, s, d and g for each simulated neuron. Means and standard errors for these 100 simulated neurons were calculated to generate a simulated population contrast-response functions for unattended and attended stimuli.

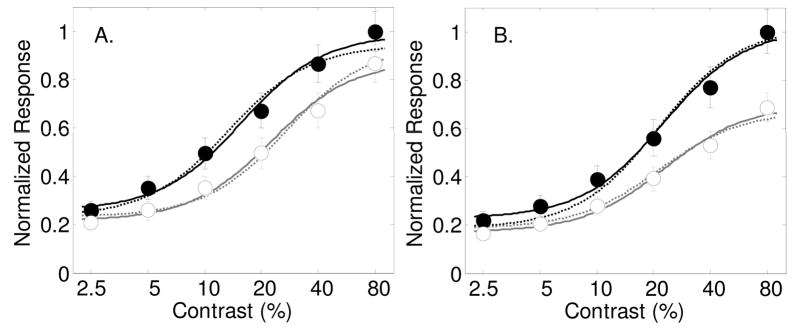
Figure 1a shows the simulated population average after incorporating a contrast gain parameter s=2 with attention on each individual neuron. Dark symbols and lines represent average responses to attended stimuli, open symbols and gray lines are for unattended stimuli. Contrast gain is apparent in the population average (by a leftward shift of the contrast response function). The dashed lines are fits of the data with a with four free parameters: three stimulus driven parameters σ, δ and γ and the contrast gain spatial attention parameter, s. The solid curves through the data are best fits of the model while allowing the three stimulus-driven parameters and all three spatial attention parameters s, d and g to vary. Allowing the contrast gain parameter to vary alone captures the majority of the effect of attention. A nested model F-test shows that adding the two parameters d and g does not significantly improve the fit (F(2,6) = 1.19 p=0.3665), as can be observed in the figure by the similarity between the predictions of the model with the single attention factor s, and the model with all three factors. With all three spatial attention parameters allowed to vary, the best fitting parameters for the contrast gain parameter, s, was 1.44, which is lower than the value of 2 used to simulate the individual neurons. The best-fitting baseline shift parameter was d=0.04, and the best fitting multiplicative gain factor was g=1.10 (All best-fitting parameter values are shown in Table 1). This analysis shows that although the estimated contrast gain parameter for the population is smaller than that for the individual neurons, the overall effect on the population average was dominated by the same contrast gain mechanism that was incorporated in the individual neurons. It should be noted also that the population average shows a small baseline shift with attention that was not present in the individual neurons.

Figure 1.

Results from a simulation showing how the effects of attention on individual neurons affect the averaged population response. Contrast response functions with and without attention in 100 simulated neurons were generated by sampling from parameter distributions as published by Geisler and Albrecht (1997). Filled symbols and dark lines represent the response to the attended stimulus, and open symbols with gray lines for the unattended stimulus. Panel A: Average response across 100 simulated neurons where spatial attention for each neuron was implemented by a contrast gain parameter s=2.0. Dashed lines are best fits of the model allowing for a contrast gain with attention. Solid lines are best fits allowing for all three spatial attention parameters to vary (s, d and g). Panel B: Similar analysis for spatial attention as a multiplicative gain factor g=1.5. Dashed curves are best fits to the population average allowing the parameter g to vary. Solid lines are fits with all three spatial attention parameters allowed to vary.

Table 1.

Best fitting parameter values. As described in the text above. Numbers in bold font represent parameters that were allowed to vary to fit a given experiment. Other parameters were held constant.

		Stimulus-dependent parameters				Attentional parameters
publication	Figure	γ	σ	δ	ω	s	d	g	w	Gmax	Gmin
Simulation	1a	0.66	22.7	0.22	90	1.44	0.04	1.10	1	1	1
	1b	0.52	22.7	0.17	90	1.01	0.07	1.50	1	1	1
(Reynolds et al., 2000).	2a	0.54	13.4	0.30	90	1.97	0.03	1.00	1	1	1
	2b	0.51	14.4	0.42	90	0.96	0.03	1.10	1	1	1
(Williford & Maunsell, 2006)	3a	0.63	11.1	0.09	90	1.00	0.05	1.03	1	1	1
	3b	0.35	12.1	0.10	90	1.18	0.05	0.99	1	1	1
(Buracas & Boynton, 2007)	4a	0.50	23.3	0.37	90	0.88	0.16	1.01	1	1	1
	4b	0.31	22.4	0.48	90	1.00	0.21	1.12	1	1	1
(Li et al., 2008)	5a	0.42	11.1	0.48	90	4.42	0.07	0.77	1	1	1
	5b	0.52	8.2	0.24	90	2.83	0.25	0.81	1	1	1
Murray et al. (2008)	6a	0.37	0.01	0.44	90	0.85	0.12	0.97	1	1	1
	6b	0.37	0.03	0.43	90	0.94	0.15	1.00	1	1	1
(Martinez-Trujillo & Treue, 2004)	7	0.71	67.3	0.26	78.5	1	0.01	1	0.967	1.30	0.76
(McAdams & Maunsell, 1999)	8	1	1.11	0.36	36.2	1	0.00	1	1.03	1.23	1.10

Figure 1b shows the simulation when spatial attention is incorporated as a multiplicative gain factor g =1.5 on the same simulated neurons. Again, solid symbols and dark lines indicate responses to attended stimuli, open symbols and gray lines are for unattended stimuli. Dashed lines are for the fit when only allowing for the multiplicative gain factor with attention, g, and solid lines are with all three spatial attention parameters allowed to vary. A nested model F-test shows that adding the two parameters d and s does not significantly improve the fit (F(2,6) = 3.12 p=0.1180), although a deviation can be seen at low contrasts between the two models. The model’s best fitting multiplicative gain factor for the population average was also g= 1.5. Mathematically, it is easy to show that the multiplicative gain factor for the population should be similar to the gain factor for the individual neurons. The other best-fitting spatial attention parameters were s = 1.01, d = 0.06 (see Table 1 for all best-fitting parameter values). The population average shows little evidence of contrast gain, but it does show a small baseline change with attention.

Adding a baseline shift with attention on the individual neurons has a predictable effect on the population response. Since the baseline effect is added after the nonlinear contrast-response function, the baseline shift parameter d for the individual neurons will result in the same shift in the averaged response across neurons.

This analysis shows that the dominant effect on the population average was the effect imposed on the individual neurons. This is at least true for these simulated V1 neurons based on the parameters published by Geisler and Albrecht (1997). Of course, parameters that describe neuronal responses in other visual areas will have different distributions of values, which could lead to misleading conclusions when looking at the population average. Also, the choices for the size of the attentional effect (e.g. s=2 and g=1.5) are somewhat arbitrary, and are also likely to vary across individual neurons.

Predicting electrophysiological studies of spatial attention

The effect of spatial attention on contrast response functions for two electrophysiological studies (Reynolds et al., 2000, Williford & Maunsell, 2006) will be discussed next in the context of the model.

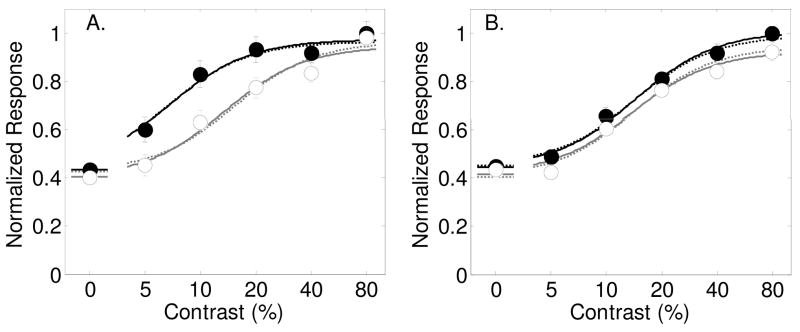
Figure 2a shows the results from Reynolds et al, 2000 (figure 5a in their paper) in which contrast-response functions were measured in macaque area V4 for sinusoidal grating stimuli. The monkey was trained to detect an oriented target grating that was either presented in the RF, or on the opposite side of the visual field. The data from this experiment, and all of the experiments described here, are normalized by the maximum response in the original figure to allow for comparison of parameter values across studies.

Figure 2.

Results from Reynolds et al., (2000, figures 5a and 5b) with best-fitting model predictions. Filled symbols and dark lines represent the response to the attended stimulus, and open symbols with gray lines for the unattended stimulus. Best fitting parameters are shown in Table 1. Panel A: Average response across the 39 neurons that showed a significant effect of spatial attention. Dashed lines are best fits of the model allowing only for a contrast gain change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary. Panel B: Average response across the 45 neurons that did not show, individually, a significant effect of spatial attention. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary.

Figure 5.

Results from (Li et al., 2008) (figure 3b) showing contrast response functions as measured with fMRI in humans wit hbest-fitting model predictions (smooth curves). Filled symbols and lines represent the response to the attended stimulus vs. an unattended blank field, and open symbols with gray lines for the estimated response to the unattended stimulus vs. an unattended blank field. Best fitting parameters are shown in Table 1. Panel A: fMRI responses from area V1. Dashed lines are best fits of the model allowing only for a contrast gain change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary. Panel B: Area V2. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary.

Results in figure 2a show the response to attended (black symbols) and unattended (empty symbols) stimuli across 6 contrasts (including 0%), averaged across the 39 neurons that showed a significant effect of attention.

The model fitting procedure for this experiment was similar for those for the remaining experiments. First, the results were fit by the model allowing only the three stimulus-dependent model parameters σ, γ and δ to vary. Fits were obtained using a multidimensional unconstrained nonlinear minimization algorithm (Mathworks, Natick, MA) that found the parameters that minimized the sum of squared errors, normalized by each data point’s standard error of the mean.

In this case, the ‘no attention model’ accounted for 89% of the variance in the data. Best fitting parameters from the ‘no attention model’ were used as starting parameters for subsequent fits in which each of the three spatial attention parameters, d, s and g were allowed to vary. A nested model F-test was applied to determine if the decrease in sums of squared error was justified by each additional free parameter.

The results of these F-tests are shown in table 2. Allowing for contrast gain alone accounts for 97.7% of the variance. Adding this parameter significantly improves the fit (F(1,8) = 19.90, p<.01, see the first row in Table 2 which shows the results of the nested-model F-test for adding the parameter s to the ‘No Attention model’). Adding a baseline shift with attention accounts for 94.7% of variance and is also a significant improvement (F(1,8) = 6.51, p<.05). Allowing for contrast gain accounts for 93.45% of the variance, which is not a significant improvement (F(1,8) = 4.12, p>0.05). Contrast gain is therefore the best description for the effects of spatial attention on the neurons recorded by Reynolds et al. (2000) that showed significant effects of attention. The dashed lines in Figure 2a show this best-fitting model.

Table 2.

Model fits and the results of nested model F-tests for the analysis of the V4 neurons showing significant attentional effects from Reynolds et al. (2000). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 2. Reynolds et al, 2000figure 5a (Figure 2a in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	2.2666	88.89	F(1,8) = 19.90 p=0.0021	F(1,8) = 6.51 p=0.0341	F(1,8) = 4.12 p=0.0767
S	0.6499	97.74		F(1,7) = 1.91 p=0.2094	F(1,7) = 0.19 p=0.6788
D	1.2493	94.67	F(1,7) = 10.13 p=0.0154		F(1,7) = 0.68 p=0.4363
G	1.4955	93.45	F(1,7) = 9.54 p=0.0176	F(1,7) = 2.20 p=0.1820
s,d	0.5106	97.96			F(1,6) = 0.00 p=0.9716
s,g	0.633	97.85		F(1,6) = 1.44 p=0.2752
d,g	1.1384	94.94	F(1,6) = 7.38 p=0.0348
s,d,g	0.5104	97.96

For comparison, the model was fit to the data allowing for all three spatial attention parameters to vary (s, d and g). The best-fitting 3-attention parameter model is shown as solid lines in Figure 2a. Table 2 shows nested model F-test results for adding each additional free parameter to the model. Allowing additional parameters to the model did not significantly improve the fit. This can be seen by the similarity between the dashed and solild curves in Figure 2a. The best-fitting contrast gain parameter was s = 1.93, which means that spatial attention effectively doubled the contrast of the attended stimulus. The best-fitting baseline shift was d = 0.03 and the best fitting multiplicative gain parameter was g =1.0. (All best fitting parameter values for this experiment, and all experiments described here, are provided in Table 1). This analysis supports the conclusion by Reynolds et al. that contrast gain is a good description of the attentional effect for these neurons. Interestingly, although contrast gain should have no effect with no stimulus present, the authors report that attention did significantly increase the response to an attended stimulus at 0% contrast (p <.05).

Figure 2b shows the averaged response across the remaining neurons (n=45) that did not show a significant effect of attention individually (their figure 5b). Allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping the attention parameters fixed accounts for 96.7% of the variance in the data. Adding just an attentional baseline shift had the greatest influence on the quality of the fit, increasing the percentage of variance accounted for to 98.7%. Allowing for contrast gain alone accounts for 98.0% of the variance, and allowing for multiplicative gain accounts for 98.5% of the variance. Nested model F-tests (see Table 3) show that both baseline shift and multiplicative gain provide similar and significant improvements in the fit (p<.05), while contrast gain did not. This analysis shows that attentional effects for these neurons are best explained by either a baseline shift or by a multiplicative gain factor. Best-fitting parameter values for the model with all three attentional parameters are shown in Table 1. The best-fitting contrast gain parameter was close to unity with s = 1.03, while the best-fitting baseline shift was d = 0.07 and the multiplicative gain factor was g = 1.5.

Table 3.

Model fits and the results of nested model F-tests for the analysis of the V4 neurons that did not show significant attentional effects from Reynolds et al. (2000). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 3. Reynolds et al, 2000figure 5b (Figure 2b in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	1.3481	96.74	F(1,8) = 4.25 p=0.0731	F(1,8) =9.71 p=0.0143	F(1,8) = 9.59 p=0.0147
S	0.6131	98.58		F(1,7) = 3.19 p=0.1171	F(1,7) = 0.07 p=0.7995
D	0.6089	98.66	F(1,7) = 0.05 p=0.8259		F(1,7) = 1.56 p=0.2518
G	0.6131	98.58	F(1,7) = 0.07 p=0.7995	F(1,7) = 1.62 p=0.2438
s,d	0.6044	98.66			F(1,6) = 1.37 p=0.2857
s,g	0.6071	98.63		F(1,6) = 1.41 p=0.2806
d,g	0.4979	98.84	F(1,6) = 0.07 p=0.7948
s,d,g	0.4919	98.82

The dashed lines in Figure 2b show the best fits of the model allowing for a baseline shift alone, and the solid lines are for allowing all three spatial attention parameters to vary. The curves are similar, indicating that a baseline shift sufficiently explains the attentional effect (but a multiplicative gain is essentially just as good).

In another careful study of spatial attention, Williford and Maunsell (2006) measured firing rates of 131 macaque V4 neurons while monkeys detected an orientation change in Gabor stimuli at a cued location either inside or outside the RF (within the same visual field). A full range of contrasts were used, yielding contrast-response functions for both attended and unattended stimuli.

Williford and Maunsell (2006) fit two models of multiplicative gain (with and without subtracting baseline responses) and a model of contrast gain to data from each individual neuron. These models did not include a simple change in baseline with attention. Across the cell population, each of the three models accounted for about the same amount of variance in the data.

Figure 3 shows their results averaged across all neurons for the preferred orientation (Figure 3a, their figure 6b) and the orthogonal orientation (Figure 3b, their figure 6c). For stimuli at the preferred orientation (Figure 3a), allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping attention parameters fixed accounted for 97.2% of the variance in the data. Allowing contrast gain increased the percentage to 98%, a baseline shift to 98.4% and multiplicative gain to 98.1%. The nested-model F-test (Table 4) shows that none of the spatial attention parameters alone significantly improves the fit, but the baseline shift just misses statistical significance at the 0.05 criterion (F(1,7) = 5.58, p=.0503). Dashed lines in Figure 4A show best fits of the model allowing for this baseline shift with attention and solid lines again show the best fit for all three spatial attention parameters allowed to vary. The solid lines are nearly identical to the dashed lines, indicating that the baseline shift describes the vast majority of the attentional effect. The best-fitting contrast gain parameter was unity with s = 1.00, the best-fitting baseline shift was d = 0.04 normalized units, and the best-fitting multiplicative gain parameter was near unity with g=1.03.

Figure 3.

Results from Williford and Maunsell (2006, figures 6b and c) with best-fitting model predictions (smooth curves) allowing for both a contrast gain and a baseline shift with spatial attention. Filled symbols and lines represent the normalized response to the attended stimulus, open symbols and gray lines for the unattended stimulus. Best fitting parameters are shown in Table 1. Panel A: Average response across the 131 neurons for stimuli at the preferred orientation. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary. Panel B: Average response across the same 131 neurons for stimuli at the null orientation. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary.

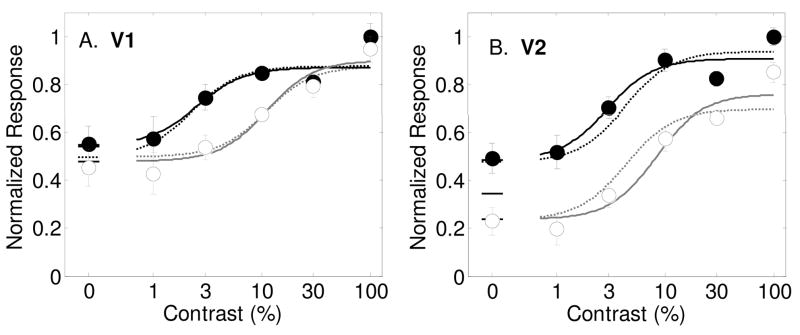
Figure 6.

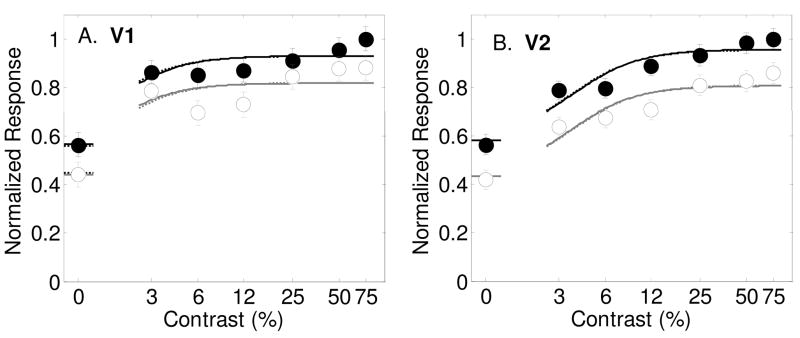
Results from Murray et al. (2008) showing contrast response functions as measured with fMRI in humans in area V1 (Panel A) and V2 (Panel B) with best-fitting model predictions (smooth curves). Filled symbols and dark lines represent the response to the attended stimulus vs. an unattended blank field, and open symbols with gray lines for the estimated response to the unattended stimulus vs. an unattended blank field. Best fitting parameters are shown in Table 1. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary.

Table 4.

Model fits and the results of nested model F-tests for the analysis of the V4 neurons showing significant attentional effects from Wiliford & Maunsell (2006). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 4. Wiliford & Maunsell, 2006figure 6b (Figure 3a in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	0.0036	97.17	F(1,7) = 2.59 p=0.1515	F(1,7) = 5.58 p=0.0503	F(1,7) = 3.26 p=0.1137
S	0.0026	97.94		F(1,6) = 1.87 p=0.2208	F(1,6) = 0.86 p=0.3899
D	0.0020	98.43	F(1,6) = 0.00 p=0.9982		F(1,6) = 0.06 p=0.8090
G	0.0025	98.07	F(1,6) = 0.41 p=0.5466	F(1,6) = 1.43 p=0.2771
s,d	0.0020	98.43			F(1,5) = 0.05 p=0.8263
s,g	0.0023	98.19		F(1,5) = 0.80 p=0.4129
d,g	0.0020	98.44	F(1,5) = 0.00 p=0.9872
s,d,g	0.0020	98.44

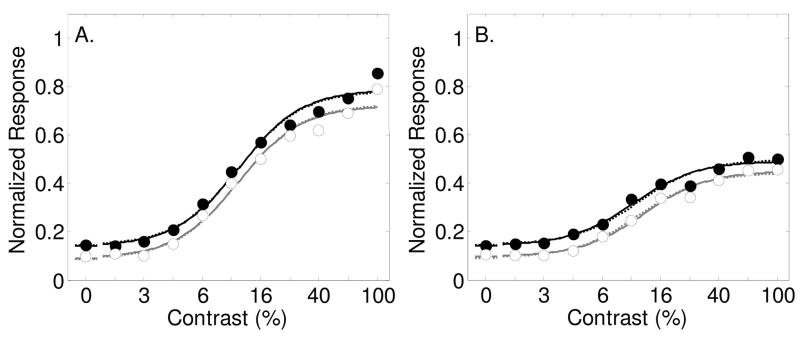
Figure 4.

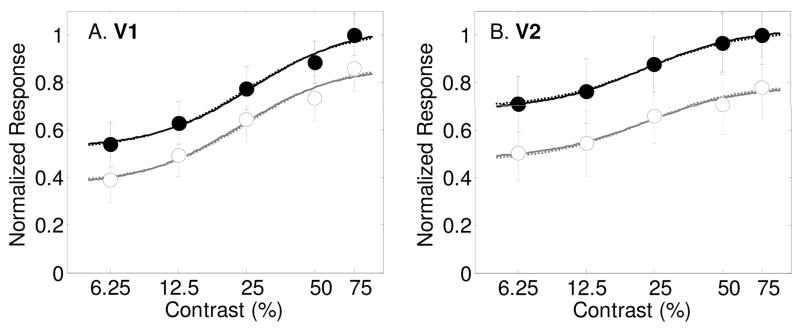
Results from Buracas and Boynton (2007) showing contrast response functions as measured with fMRI in humans in area V1 (Panel A) and V2 (Panel B) with best-fitting model predictions (smooth curves). Filled symbols and dark lines represent the response to the attended stimulus vs. an unattended blank field, and open symbols with gray lines for the estimated response to the unattended stimulus vs. an unattended blank field. Best fitting parameters are shown in Table 1. Dashed lines are best fits of the model allowing only for a baseline change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and g) to vary.

A similar result was found for the orthogonal orientation (Figure 3b). Allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping attention parameters fixed accounts for 94.5% of the variance in the data. Allowing for a baseline shift was most effective at improving the fit (see table 5; F(1,7) = 15.68, p<.01) while contrast gain also significantly improved the fit, but less than the baseline shift (F(1,7) = 8.07, p=<.05). Allowing for a multiplicative gain did not significantly improve the fit at the .05 criterion level (F(1,7) = 4.7,1 p=0.0666). Dashed lines in figure 3b shows the best fits allowing for a baseline shift and solid lines are for all three spatial attention parameters varying. Best-fitting spatial attention parameters (see Table 1) are s = 1.18, d = 0.05, and g = 0.99. It can be seen that the baseline shift accounts for the vast majority of the attentional effect in the averaged responses for stimuli orthogonal to the preferred orientation.

Table 5.

Model fits and the results of nested model F-tests for the analysis of the V4 neurons that did not show significant attentional effects from Wiliford & Maunsell (2006). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 5. Wiliford & Maunsell, 2006figure 6c (Figure 3b in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	0.0022	94.54	F(1,7) = 8.07 p=0.0250	F(1,7) = 15.68 p=0.0055	F(1,7) = 4.71 p=0.0666
S	0.0010	97.46		F(1,6) = 3.62 p =0.1058	F(1,6) =0.69 p =0.4365
D	0.0007	98.31	F(1,6) = 0.39 p =0.5543		F(1,6) = 0.01 p =0.9410
G	0.0013	96.73	F(1,6) = 2.62 p =0.1569	F(1,6) = 5.63 p =0.0553
s,d	0.0006	98.42			F(1,5) = 0.01 p =0.9114
s,g	0.0009	97.73		F(1,5) = 2.20 p =0.1977
d,g	0.0007	98.32	F(1,5) = 0.34 p =0.5873
s,d,g	0.0006	98.42

It is evident from this analysis of the results from Williford and Maunsell (2006) that the main effect of spatial attention on the population response is a baseline shift that increases the response to a stimulus by an equal amount across all contrasts. Interestingly, the baseline shift is roughly the same for both preferred and orthogonal stimuli, indicating that spatial attention may increase all neurons with RFs at the attended location by the same amount (around 1 spike/second).

Effects of spatial attention on fMRI responses

Over the past several years, a variety of functional MRI studies have shown that spatial attention increases fMRI responses in all retinotopically organized visual areas, including primary visual cortex, (V1) (Gandhi, Heeger & Boynton, 1999, Martinez, Anllo-Vento, Sereno, Frank, Buxton, Dubowitz, Wong, Hinrichs, Heinze & Hillyard, 1999, Somers, Dale, Seiffert & Tootell, 1999) in a retinotopic fashion (Brefczynski & DeYoe, 1999), even without the presence of a stimulus (Kastner et al., 1999, Ress et al., 2000). These fMRI responses presumably reflect some sort of spatial and temporal averaging of an underlying neuronal response (Boynton, Engel, Glover & Heeger, 1996). The spatial averaging blurs responses across sub-millimeter structures within visual areas, such as direction-selective columns. FMRI responses therefore presumably reflect a combined response across a population of neurons selective to a variety of stimulus features, such as direction of motion and orientation.

A recent study measured fMRI responses for attended and unattended grating stimuli across a range of contrasts (Buracas & Boynton, 2007). A blocked-design was used in which subjects alternated between attending to gratings on the left and the right side of the visual field. Attention was monitored by measuring performance on either a speed or a contrast discrimination task (results did not depend on the task). In one condition, the unattended hemifield was blank so the fMRI response in the region of interest was the difference in response between an attended stimulus and unattended blank field. In the second condition, a grating was always presented in both sides, so the response in the region of interest was the difference in response to attended and unattended stimuli. The response to an unattended stimulus could thereby be calculated as the difference between the first and second condition.

Figures 4a and b show the results of this experiment from areas V1 and V2 respectively, averaged across four subjects. For area V1, a baseline shift with attention was by far the most effective mechanism, significantly improving the percentage of variance accounted for from 82.6% to 98.1% (Table 6, F(1,6) = 49.6, p<.001), although the other two attention parameters alone also significantly improved the fit. The dashed lines in figure 4a show the best-fitting model allowing for a baseline shift alone. The solid lines are for the model allowing for all three spatial attention parameters to vary. Adding additional attention parameters to the baseline shift model did not improve the fit significantly, as can be seen by the similarity of the dashed and solid lines. The best-fitting baseline shift parameter was d = 0.16 (see Table 1). The best-fitting contrast gain parameter was s = 0.88, which indicates a slight rightward shift in the contrast response function with spatial attention. The best fitting multiplicative gain factor was near unity (g = 1.01);

Table 6.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V1 from Buracas & Boynton (2006). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 6. Buracas & Boynton, Area V1(Figure 4a in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	0.6806	82.66	F(1,6) = 18.91 =0.0048	F(1,6) = 49.57 p=0.0004	F(1,6) = 10.99 p=0.0161
s	0.1639	95.68		F(1,5) = 6.38 p=0.0527	F(1,5) = 0.40 p=0.5568
d	0.0735	98.14	F(1,5) = 0.10 p=0.7608		F(1,5) = 0.00 p=0.9512
g	0.2404	93.75	F(1,5) = 2.91 p=0.1486	F(1,5) = 11.37 p=0.0198
s,d	0.0720	98.17			F(1,4) = 0.01 p=0.9274
s,g	0.1519	96.03		F(1,4) = 4.46 p=0.1023
d,g	0.0734	98.14	F(1,4) = 0.09 p=0.7804
s,d,g	0.0718	98.18

An analysis of the results in area V2 shows a similar result. Allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping the attention parameters fixed accounts for only 47% of the variance in the data (see Table 7). Adding a baseline shift with attention significantly increases the percentage to 99.3% (F(1,6) = 471.6, p<.0001). Allowing all three spatial attention parameters to vary increases the percentage only slightly (and not significantly) to 99.5%. The dashed lines in Figure 4b show the model prediction allowing for a baseline shift alone, while the solid lines are for all three spatial attention variables varying. Best-fitting parameter values (see Table 1) are s = 1.00, d = 0.21 and g = 1.12. Just as for area V1, it is clear that a baseline shift describes the entire effect of attention on these fMRI responses. Similar results, showing a large baseline shift with spatial attention with little evidence of contrast or multiplicative gain were found in areas V3 and MT+ (data not shown).

Table 7.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V2 from Buracas & Boynton (2006). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 7. Buracas & Boynton, Area V2 (Figure 4b in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	0.8343	47.03	F(1,6) = 51.93 p=0.0004	F(1,6) = 471.6 p<0.0001	F(1,6) = 27.08 p=0.0020
s	0.0864	94.86		F(1,5) = 36.25 p=0.0018	F(1,5) = 1.45 p=0.2830
d	0.0105	99.33	F(1,5) = 0.00 p=0.9603		F(1,5) =1.53 p=0.2704
g	0.1513	90.46	F(1,5) = 6.29 p=0.0540	F(1,5) = 89.37 p=0.0002
s,d	0.0105	99.33			F(1,4) = 1.22 p=0.3305
s,g	0.067	95.87		F(1,4) = 29.44 p=0.0056
d,g	0.008	99.47	F(1,4) = 0.00 p=0.9931
s,d,g	0.008	99.47

A more recent publication also reports fMRI responses to attended and unattended stimuli across contrasts in human visual cortex (Li et al., 2008). In this study, subjects either performed an orientation judgment on an annular grating stimulus, or attended away from the annulus by performing a letter judgment task at fixation, so the attended feature (and task difficulty) differed when the stimulus was attended vs. unattended.

Their results are replotted in figures 5a and 5b (from their figure 4) for visual areas V1 and V2 respectively. Unlike the results from Buracas and Boynton (2007), Li et al.’s results show evidence of contrast gain with spatial attention in area V1. Allowing for contrast gain significantly improved the percent of variance accounted for by the model from 77.7% to 91.2% (Table 8, F(1,8) = 18.74, p<.005). A baseline shift alone also significantly improved the fit (F(1,8) = 7.25, p<.05), but by a smaller amount (to 87.9%). The contrast gain parameter could not significantly explain the attentional effects (F(1,8) = 2.96, p=.12). The dashed lines are the best-fitting model allowing for a contrast gain parameter alone. The solid lines are for all three spatial attention parameters varying. There is a slight deviation between the curves at lower contrasts, but adding these additional parameters did not significantly improve the fit. Best-fitting parameter values (Table 1) are s = 4.42, d = 0.07 and g = 0.77.

Table 8.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V1 from Li et al. (2008). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 8. Li et al., Area V1 (Figure 5a in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	3.5099	77.65	F(1,8) = 18.74 p=0.0025	F(1,8) = 7.25 p=0.0274	F(1,8) = 2.96 p=0.1237
s	1.0502	91.18		F(1,7) = 0.00 p=0.9476	F(1,7) = 0.27 p=0.6205
d	1.8416	87.89	F(1,7) = 5.28 p=0.0551		F(1,7) = 1.38 p=0.2784
g	2.562	80.96	F(1,7) = 10.73 p=0.0136	F(1,7) = 4.66 p=0.0678
s,d	1.0496	91.03			F(1,6) = 0.59 p=0.4701
s,g	1.0115	91.14		F(1,6) = 0.36 p=0.5730
d,g	1.5382	87.2	F(1,6) = 3.66 p=0.1041
s,d,g	0.955	92.72

For area V2, allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping the attention parameters fixed accounts for 65% of the variance in the data. Unlike the results from V1, a baseline shift with attention had the greatest influence on the fit, increasing the percentage significantly to 93.1% (Table 9, F(1,8) = 20.6, p<.005). The other two parameters also significantly improved the fit (contrast gain; 87%, F(1,8) = 17.54, p<.005, multiplicative gain; 78.3, F(1,8) = 7.06, p<.05). Dashed curves in Figure 5b show the best-fitting model allowing for baseline shift with attention, and solid curves are for all three spatial attention parameters varying. There is a clear deviation between the curves, indicating that allowing for these additional parameters alters the predictions of the best-fitting model. However, statistically, these additional parameters do not significantly improve the quality of the fit.

Table 9.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V2 from Li et al. (2008). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 9. Li et al., Area V2 (Figure 5b in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	10.2511	65.27	F(1,8) =17.54 p=0.0030	F(1,8) = 20.60 p=0.0019	F(1,8) = 7.06 p=0.0289
s	3.2108	87		F(1,7) = 3.66 p=0.0974	F(1,7) = 0.38 p=0.5574
d	2.8676	93.07	F(1,7) = 2.52 p=0.1565		F(1,7) = 1.20 p=0.3094
g	5.4443	78.3	F(1,7) = 5.51 p=0.0512	F(1,7) = 8.57 p=0.0221
s,d	2.1086	94.93			F(1,6) = 0.47 p=0.5167
s,g	3.0457	88.43		F(1,6) = 3.35 p=0.1169
d,g	2.4477	93.97	F(1,6) =1.52 p=0.2643
s,d,g	1.9541	95.88

An even more recent study also reported the effects of spatial attention on human fMRI responses in early retinotopically organized visual areas (Murray, 2008). An advantage of the experimental design used by Murray (2008) is that it allowed for a measurement at zero contrast. This is an important measurement because an attentional effect at zero contrast can only be explained by a baseline shift, and not by contrast gain or multiplicative gain. Murray concluded that the effects of spatial attention at zero contrast are very similar to the effects at all other contrasts and concludes that spatial attention effects are therefore independent on the strength of the stimulus. In the paper, the results of this experiment were analyzed in a manner similar to those described here where a model of contrast gain, multiplicative gain and a baseline shift were each fit to the data. A baseline shift with attention was found to best describe the results in areas V1, V2 and V3.

The results from this experiment in are shown in figure 6 along with fits of the model to the data. Figure 6a shows the results from area V1, averaged across four subjects. Filled symbols and dark lines indicate responses to attended stimuli, and open symbols and gray lines are for unattended stimuli. For area V1, a baseline shift with attention was the most effective mechanism, significantly improving the percentage of variance accounted for from 73.2% to 87.1% (Table 10, F(1,10)=10.98, p=0.0078). The multiplicative gain parameter improved the fit significantly also, but not as much as the baseline shift (84.6%, F(1,10) = 7.63, p=0.0201). The contrast gain parameter alone failed to improve the fit over the no-attention model (77.7%, F(1,10) = 2.01, p=0.1868). The dashed lines in figure 6a show the best-fitting model allowing for a baseline shift alone. The solid lines are predictions of the model allowing for all three spatial attention parameters to vary. Including the two additional attention parameters to the baseline shift model did not improve the fit significantly, as can be seen by the similarity of the dashed and solid lines. The best-fitting baseline shift parameter was d = 0.12 (see Table 1). The best-fitting contrast gain parameter was s = .85, which, like the results from Buracas and Boynton (2007) indicates a slight rightward shift in the contrast response function with spatial attention. The best fitting multiplicative gain factor was near unity (g = 0.97);

Table 10.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V1 from Murray (2008). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 10. Murray et al., Area V1(Figure 6a in text)
Model	SSE	Pct Var	Add parameter
			S	d	g
No attention	2.3075	73.21	F(1,10) = 2.01 p=0.1868	F(1,10)=10.98 p=0.0078	F(1,10) = 7.63 p=0.0201
s	1.9215	77.72		F(1,9) = 6.43 p=0.0320	F(1,9) = 4.23 p=0.0699
d	1.1000	87.05	F(1,9) = 0.17 p=1.0000		F(1,9) = 0.01 p=0.9179
g	1.309	84.61	F(1,9) = 0.01 p=0.9145	F(1,9) = 1.72 p=0.2217
s,d	1.1209	86.97			F(1,8) = 0.19 p=0.6729
s,g	1.3073	84.64		F(1,8) = 1.55 p=0.2478
d,g	1.0987	87.07	F(1,8) = 0.03 p=0.8680
s,d,g	1.0946	87.11

An analysis of the results in area V2 are very similar to the results from Buracas and Boynton (2007). Allowing the three stimulus-dependent model parameters σ, γ and δ to vary while keeping the attention parameters fixed accounts for 71.7% of the variance in the data (see Table 11). Adding a baseline shift with attention significantly increased the percentage to 93.2% (F(1,10)=31.46, p=0.0002). Allowing all three spatial attention parameters to vary had essentially no further improvement on the quality of fit. The dashed lines in Figure 6b show the model prediction allowing for a baseline shift alone, while the solid lines are for all three spatial attention variables varying. Best-fitting parameter values (see Table 1) are s = 0.94, d = 0.15 and g = 1.00. Just as for area V1, it is clear that a baseline shift describes the entire effect of attention on these fMRI responses.

Table 11.

Model fits and the results of nested model F-tests for the analysis of the fMRI responses in area V2 from Murray (2008). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 11. Murray et al., Area V2 (Figure 6b in text)
Model	SSE	Pct Var	Add parameter
			s	d	g
No attention	4.1362	71.71	F(1,10) =9.54 p=0.0115	F(1,10)= 31.46 p=0.0002	F(1,10)= 15.95 p=0.0025
s	2.1172	85.49		F(1,9) = 10.12 p=0.0112	F(1,9) = 4.64 p=0.0596
d	0.9978	93.24	F(1,9) = 0.01 p=0.9131		F(1,9) = 0.00 p=0.9722
g	1.594	89.15	F(1,9) = 1.27 p=0.2888	F(1,9) = 5.38 p=0.0455
s,d	0.9964	93.24			F(1,8) = 0.00 p=0.9969
s,g	1.3967	90.59		F(1,8) = 3.21 p=0.1107
d,g	0.9976	93.24	F(1,8) = 0.01 p=0.9226
s,d,g	0.9964	93.24

Feature-based attention

Feature based attention has been clearly demonstrated in macaque area MT in a pair of studies that show how responses to unattended stimuli are dependent on whether or not they shared a feature with an attended stimulus presented outside the RF. In the first study, MT responses to an unattended field of dots that moved in the neurons’ preferred direction were larger when attention was directed outside the RF to a remote field of dots moving in the same direction, compared to when the attended dots were moving in the opposite direction (Treue & Martinez Trujillo, 1999), even though the unattended stimulus inside the RF did not change.

The second study was a quantitative manipulation of this remote effect of feature-based attention (Martinez-Trujillo & Treue, 2004) in which responses were measured in area MT to moving fields of dots spanning the entire range of directions. Two attentional conditions were used. In both conditions, the monkey attended outside the RF. In the first condition the monkey responded to a luminance change of a small color square at fixation. This condition measured the effect of changing the direction of motion inside the RF while keeping spatial and feature-based attention constant. In the second condition, attention was directed to a stimulus outside the RF that moved in the same direction as the stimulus inside the RF. This measured the effects of feature-based attention, when both the attended feature and the stimulus had the same direction of motion.

Our model incorporates these authors’ concept of feature-similarity gain as a multiplicative gain factor, G, on the response, H from equation 1. Given a stimulus with features, x_i, and contrasts, c_i, attention to the feature y results in the response modeled in equation 4.

$$R(x,y,c)=G(y)H(x,c)$$ 4)

The feature-based multiplicative gain factors depend on the attended feature y; when the attended feature is near the preferred value, the gain factor is greater than 1, when the attended feature is sufficiently different from the neuron’s preferred value, the gain factor is similar to or less than 1. G(y) is assumed to be a Gaussian with the same width and peak location as the sensitivity function F, but is scaled to range between a maximum of Gmax > 1 and a minimum of Gmin <=1. Specifically:

$$G(y)=(G_{max}-G_{min})e^{-{(y-x_p)}^2/w^2}+G_{min}$$ 5)

Where x_p is the neuron’s preferred feature value.

Importantly, with this description of feature-based attention the attended feature, y does not need to be present in the stimulus within the neuron’s RF. Instead, the attended feature can be part of a stimulus that is attended outside the RF of the neuron. That is, G(y) is a purely feature-based effect, and is independent of spatial attention.

Figure 7 shows the results from Martinez-Trujillo & Treue (2004), showing the averaged response across 135 MT neurons (their figure 4a), with filled symbols and black lines for the ‘attend same’ condition and open symbols and gray lines representing the ‘attend fixation’ condition. Responses were normalized by the authors along the direction axis so that the preferred direction was always 0 degrees. The ‘attend fixation’ condition shows the expected direction-selective tuning of an MT neuron. The ‘attend same’ condition shows a similar shaped function, but with a greater overall amplitude of modulation. When the attention was in the preferred direction, responses were greater than the ‘attend fixation’ condition, implying an expansive gain factor. However, when attention was in the anti-preferred direction, responses were weaker than the ‘attend fixation’ condition, showing a suppressive gain change with feature-based attention.

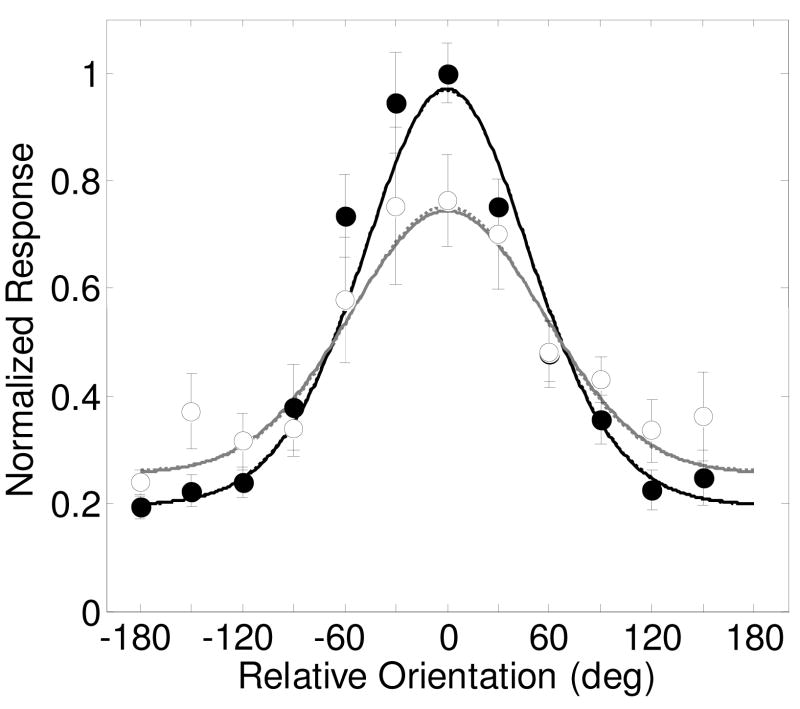
Figure 7.

Results from Martinez-Trujillo and Treue (2004, figure 4a) of the average response to 135 MT neurons and model predictions for the ‘attend same’ (filled symbols, black lines) and ‘attend fixation’ (open symbols, gray lines) conditions. The model assumes a 100% contrast stimulus. The parameter σ was fixed at 15% because the contrast of the stimulus was constant. Spatial attention parameters s, d and g’ were not allowed to vary as spatial attention was kept constant in this experiment. Best fitting parameters are shown in Table 1. Dashed lines are best fits of the model allowing only for the feature attention gain parameters Gmax and Gmin to vary. Solid lines are for allowing all three spatial attention parameters (Gmax, Gmin, d and w) to vary.

The model was fit to the data with three sets of attention parameters: a baseline parameter d, the pair of feature-based attention gain parameters Gmax and Gmin, and a parameter w is a scale factor that allows the width of the tuning to vary between the ‘attend same’ and ‘attend fixation’ conditions. Fits of the model to the data shows that Gmax and Gmin are the only parameters that provide an improvement in the fit (Table 10, from 89% to 93.8%, F(2,19) = 7.23, p<.005). Adding the additional parameters provided no additional improvement in the fit.

The dashed lines show the best-fitting model with Gmax and Gmin allowed to vary. The solid lines are for all attentional parameters varying. The curves overlap nearly completely, showing how the additional attention parameters d and w do not help to describe the effects of feature-based attention on these averaged neuronal responses. Best fitting attention parameter values are Gmax = 1.3, Gmin = 0.76, d = −0.01 and w = 0.97.

The effects of attention on tuning width

The analysis of the results from Martinez-Trujillo & Treue (2004) shows that the tuning width of direction selectivity of neurons in area MT is not affected by feature-based attention. Instead, fits of the model show that feature-based attention acts to enhance or suppress the stimulus-driven responses with a gain factor that has the same tuning width as the stimulus-driven response.

The invariance of tuning width with attention was more directly investigated for orientation selectivity in area V4 (McAdams & Maunsell, 1999). In this study, responses in macaque area V4 were measured while monkeys attended either to an oriented Gabor stimulus inside the RF (ranging across orientations), or to a colored Gaussian patch outside the RF. Responses to attended and unattended stimuli were closely fit by the authors with a single Gaussian function that varied only by scaling amplitude and adding a vertical offset.

One caveat about this experimental design is that both feature-based attention and spatial attention were manipulated due to the difference between the tasks and stimuli inside and outside the RF. The model here could predict these results either as a manipulation of feature-based attention or by spatial attention. For feature-based attention, Gmax and Gmin would be allowed to vary, keeping the spatial attention parameters constant. For spatial attention, Gmax and Gmin would be set to 1, while allowing the parameters s and d to vary. An equivalent model for spatial attention would to be to allow for a multiplicative gain change through the parameter g instead of a contrast gain factor. This is because for a fixed contrast, it is not possible to distinguish between contrast and response gain models of attention (Reynolds & Chelazzi, 2004).

It turns out that for this particular experiment, feature-based attention and spatial attention parameters make identical predictions because both sets of parameters impose a shift and scaling of the tuning function with attention. In either case, the invariance of tuning width with attention can be tested by allowing the tuning width scale factor w to vary with attention.

Without loss of generality, the feature-based attention version of the model was fit to the results. Figure 8 shows the average of responses across the 262 V4 neurons reported by McAdams and Maunsell (1999, their figure 7). The results from each of the individual neurons were adjusted by the authors before averaging so their peak responses were at zero orientation. Solid symbols are responses to attended stimuli and open symbols are for unattended stimuli.

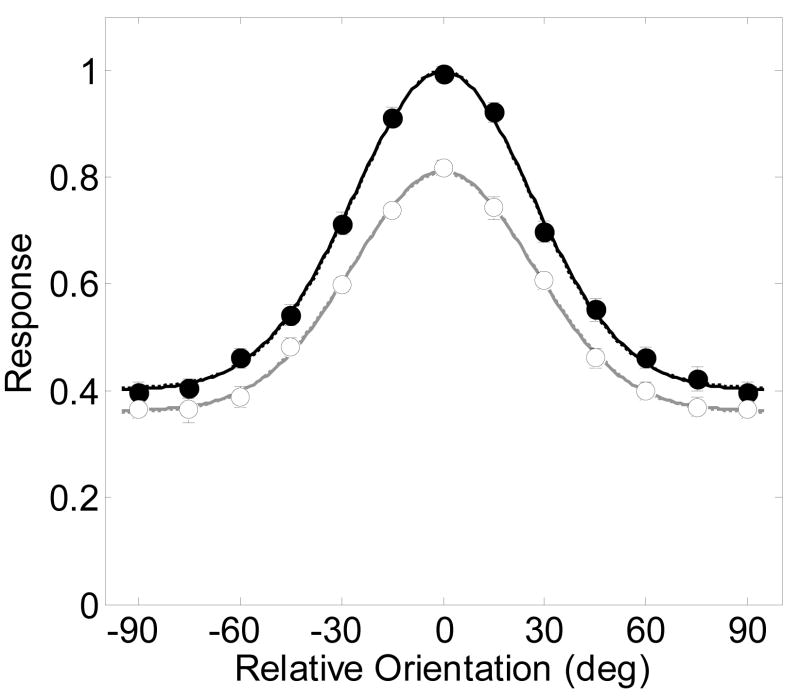
Figure 8.

Results reproduced from McAdams and Maunsell (1999, figures 7a and b) of the average response from 262 V4 neurons with best-fitting model predictions (smooth curves) allowing for both a contrast gain and a baseline shift with spatial attention. Filled symbols and lines represent the response to the attended stimulus, and open circles and gray lines for the unattended stimulus. The model assumes a 100% contrast stimulus. Best fitting parameters are shown in Table 1. Dashed lines are best fits of the model allowing only for a contrast gain change with spatial attention. Solid lines are for allowing all three spatial attention parameters (s, d and w) to vary.

Three specific effects of attention on the population response were quantified through fits of the model to the data. The relevant feature-based attention parameters were Gmin and Gmax. For a less constrained model, a version allowing a baseline change (d) and the parameter that allows the width of the tuning to vary with spatial attention (w) was also fit to the data.

The two parameters Gmax and Gmin that allow for a feature-based gain of attention increased the percent of variance accounted for from 92.5% to a remarkable 99.83% (Table 11, F(2,21) = 583.51 p<0.00001). Once these parameter were allowed to vary, adding a baseline parameter d failed to significantly improve the fit (99.83%, F(1,20) = 0.33 p=0.5746). This was due to redundancy in the effects of the baseline shift and the feature-based gain parameters for this particular implementation of the model. Allowing the tuning width parameter, w, to vary also failed to further improve the fit (99.84%, F(1,20) = 1.37 p=0.2548).

Dashed lines show the model fits with only the feature-based attention gain parameter allowed to vary, and solid lines are for all attention parameters varying (gMax, gMin, d and w). The curves overlap completely, showing how the feature-based attention parameters are sufficient for explaining the results.

A later study by McAdams and Maunsell supports the notion that the gain changes seen in the results showin in Figure 7 are at least in part due to a feature-based manipulation. In a second study, monkeys were trained to attend to an oriented Gabor stimulus that was identical to the stimulus in the RF (McAdams & Maunsell, 2000). This experiment was therefore a pure manipulation of spatial attention. They found that the difference in V4 responses between attending inside and outside the RF was greater for the Gabor outside the RF than for the colored Gaussian outside the RF (their original study). This is analogous to the feature-based attention measured by (Martinez-Trujillo & Treue, 2004) in area MT at the neuron’s preferred direction of motion (Figure 7).

Effects of feature-based attention on fMRI responses

The feature similarity gain model predicts that a neuron’s response to an unattended stimulus is modulated by the feature that is attended, even if attention is directed outside that neuron’s receptive field. Attention to a given feature will enhance the response of neurons tuned to the attended feature, and reduce the response of neurons tuned away from the attended feature. The population-based fMRI response is therefore unlikely to show modulation with feature-based attention, unless a particular subpopulation of feature-selective neurons is emphasized or selected in some way.

Saenz et al. (2002) biased the population based fMRI response toward neurons that respond to a particular feature (direction of motion) by placing a single field of moving dots in the unattended side of the visual field while subjects performed a speed discrimination task on one of two fields of overlapping dots on the attended side. When the unattended stimulus was moving in the same direction as the attended field the fMRI response to the unattended stimulus increased in areas V1, V2, V3, V3A and MT+, as compared to when attention was directed to motion in the opposite direction.

More recently it has been shown that feature-based attention can produce predictable changes in the pattern of responses across voxels. Pattern classification methods that analyze patterns of responses across voxels have demonstrated that it is indeed possible to predict which orientation (Kamitani & Tong, 2005) or direction a subject is either viewing or attending (Kamitani & Tong, 2006; Serences & Boynton, 2007). Successful pattern classification for motion occurs in all early human visual areas including V1, V2, V3V, V4 and MT+. Thus feature-based attention leads to increases and decreases in individual neuronal responses which have a measurable influence on the pattern of fMRI responses across voxels. It has also recently been shown, as predicted by our model and the results of Saenz et al. (2002) that the pattern of fMRI responses to an unattended stimulus is also affected in a systematic manner as a function of feature-based attention (Serences & Boynton, 2007).

One interesting prediction of the implementation of the feature-similarity gain model here is that baseline firing rates, when no stimulus is present, should be affected by feature-based attention. This is because the gain factor G is multiplied after the additive baseline parameter δ As a result, feature-based attention should affect the responses of neurons at all locations even in the absence of a stimulus. This prediction is supported by the recent finding that pattern classification methods can reliably predict the attended direction of motion from fMRI responses in an unattended hemifield that contains no stimulus (Serences & Boynton, 2007). Indeed, classification accuracy with no stimulus present was nearly the same as accuracy when either an attended or unattended stimulus was present. Further support for the effects of feature-based attention on baseline responses come from a recent behavioral study showing that the motion aftereffect can be elicited in an unattended visual hemifield, even when no stimulus is present, via adaptation caused by attending to a moving stimulus in the opposite hemifield (Boynton, Ciaramitaro & Arman, 2006).

DISCUSSION

The model described here can accurately predict a wide variety of experimental results on how spatial and feature-based attention influence responses in visually-driven neurons. The model has four stimulus-dependent parameters (σ, γ, δ and ω), and six attentional parameters (s, g, d, w, Gmax and Gmin). Each of these studies manipulated only certain stimulus and attentional properties, so that each of the fits to the data required only three stimulus-dependent parameters and up to three attentional parameters.

Spatial Attention

Placing these experiments in the common context of a single model allows for a direct comparison of how attention affects averaged neuronal responses in the visual cortex of humans and monkeys. For the effects of spatial attention on monkey V4 neurons across stimulus contrast, different subpopulations of neurons appear to require different parameter values. This can be seen in the results from Reynolds et al. (2000) (Figure 1) where the neurons that were most affected by attention primarily required a contrast gain parameter (Figure 1a), but the neurons that were not significantly affected by attention (Figure 1b) required only a baseline gain parameter. Assuming a maximum spike rate of 40 spikes/second, these baseline shifts correspond to about 1.5 spikes/second. It is not known why the individual neurons for figure 1b did not show significant attentional effects, but it is clear that their overall responses were about half of that of the neurons that do show an attentional effect. One possible explanation for this difference in overall response level is that the stimuli for the neurons in figure 1b were less optimally matched to the tuning properties of the neuron.

The parameters from the fits to the results from Reynolds et al. (2000) can be directly compared to the best-fitting parameters Williford and Maunsell (Williford & Maunsell, 2006). It can be seen visually from the results in Figure 2a that the effects of attention in the study by Williford and Maunsell (2006) are most clearly described by a baseline shift. Interestingly, for the non-preferred stimulus (figure 2b), a similar baseline shift was found even though, as expected, the overall responses were much weaker than for the preferred stimulus. Assuming from their data a maximum firing rate of 45 spikes/second, the best-fitting baseline shift parameters translate to an increase of about 2–3 spikes/second with spatial attention.

A hypothesis that can be generated from the combined analysis of these two studies is that all neurons show both a contrast gain and a baseline shift with spatial attention. The contrast gain effect will be most prominent for stimuli that strongly drive the neuron, but the baseline shift will occur for any neuron with its RF at the attended location. When the stimulus in the RF is not optimal for the neuron, then the effects of spatial attention will be dominated by the baseline component.

This could explain why the effects of spatial attention on the fMRI response across stimulus contrast as measured by Buracas and Boynton (2007) and by Murray et al. (2008) are dominated by a baseline shift. It is well-known that the properties of a visual scene are coded sparsely across neurons in the visual system (Olshausen & Field, 2004). This means that any given stimulus will only excite a small proportion of visual neurons, especially if the stimulus is a simple grating stimulus like those used in the experiments discussed here. If the fMRI signal reflects an aggregate response across the entire population of neurons, and spatial attention has an effect on the baseline response of every neuron in a given fMRI voxel, then it is easy to see how the fMRI response could be dominated by this small, but ubiquitous increase in baseline firing rates in individual neurons, compared to a contrast gain change in a small subset of neurons excited by the stimulus.

One fMRI study described here (Li et al., 2008) did not show a strong baseline shift with spatial attention in V1 (but a baseline shift was best at describing the effects in V2). While this result may be consistent with some of the electrophysiology results in monkey area V4, (Reynolds et al., 2000), it is not in agreement with the other two fMRI studies in area V1 described here (Buracas & Boynton, 2007; Murray, 2008). Li et al. found little or no effect of spatial attention at zero contrast, which is surprising because it does not agree with three published fMRI studies showing strong effects of attention in the absence of visual stimulation (Kastner et al., 1999; Ress et al., 2000, Murray, 2008).

One possible explanation for the discrepancy between Lit et al. (2008) and Buracas and Boynton (2007) is that the contrast-response functions measured by Li et al. (2008) show greater response saturation than those in the study by Buracas and Boynton (2007). The nearly constant slope in the results by Buracas and Boynton (2007) makes it difficult to distinguish between a contrast gain model and a baseline shift. Li et al. (2008) also measured responses across a broader range of contrasts. Their contrast response functions show more variability in slope, which perhaps allowed for better discrimination between the two attentional mechanisms. However, the results shown here from Murray et al. (2008) do show response saturation and variability in slope, yet are also dominated by a baseline shift with spatial attention.

Feature-Based Attention

For feature-based attention, the model incorporates the feature similarity gain hypothesis which predicts that feature-based attention acts as a multiplicative gain (after the baseline firing rate is added). Feature-based attention can either enhance or suppress the firing rate of the neuron, depending on the relationship between the attended feature and the preferred feature of the neuron. The model adequately describes the results from the parametric study by Martinez-Trujillo and Treue (2004) by letting the effects of feature based attention range from an excitatory multiplicative gain factor of 1.3 to an inhibitory gain factor of 0.76.

As described above, the study by McAdams and Maunsell (1999) (our figure 5) showing the effects of attention on the orientation tuning of V4 neurons manipulated both spatial and feature-based attention. For this experiment, parameters allowing for feature-based attention and spatial attention make equal predictions. We know that there is an effect of feature-based attention because a subsequent study (McAdams & Maunsell, 2000) showed that the effects of attention were smaller when only spatial attention was manipulated. When their results, shown in figure 8, are considered to be associated with feature-based attention, they can be closely fit with a multiplicative feature-based gain change with attention. The actual results are likely to be a combination of the two types of attention, but since this study was conducted with stimuli of a fixed contrast, there is not enough information in the results to be able to separately measure the effects of spatial and feature-based attention.

Baseline Effects

Perhaps the most surprising finding across the analyses described here is the strong role of baseline firing rates in both spatial and feature-based attention. For both the electrophysiological and the fMRI studies of spatial attention, a baseline shift with attention was often sufficient to describe the results. Model fits presented here suggest that the estimated increase in baseline firing rates with spatial attention is only a few spikes per second. This modest increase is unlikely to have a significant influence on the signal-to-noise of the firing properties of a responsive neuron. However, for the majority of neurons that do not respond to a given stimulus, this increase is relatively large; an increase of 2 spikes/second with attention corresponds to a 20% increase for a typical baseline firing rate of 10 spikes/second.

Nevertheless, the baseline shifts for fMRI responses with spatial attention still appear remarkably large, especially in light of a recent electrophysiology study in humans that showed little influence by attention on local field potentials in V1 (Yoshor, Ghose, Bosking, Sun & Maunsell, 2007). The relationship between the BOLD signal and the underlying neurophysiological response is still not well understood, and it is likely that the fMRI response is more complicated than a simple linear transform of spiking activity. Simultaneous recordings of electrophysiological and fMRI responses in monkeys suggest that coherent gamma-band activity correlates particularly well with the BOLD signal (Logothetis, 2002, Shmuel & Leopold, 2008). It has been shown that attention increases gamma band synchronization between LFPs and spike trains (Fries, Reynolds, Rorie & Desimone, 2001). Thus, it could be that the large effects of spatial attention on fMRI responses in V1 are not directly due to increases in spiking activity, but instead to increased gamma band activity.

One can only speculate about the functional significance of a baseline shift with attention. Increasing the baseline firing rate of neurons that are not tuned to the behaviorally relevant stimulus could have either beneficial or detrimental effects on performance, depending on the pooling rule used in the decision process. For an ideal observer pooling across all neurons, performance in a discrimination or detection task depends on the ratio of the mean and the standard deviation of the firing rate (Geisler & Albrecht, 1997). An increase in the baseline firing rate with attention would only be beneficial to an ideal observer if the standard deviation increases more slowly than the mean. This is generally true for stimulus-driven responses in individual neurons (where the variance of the firing rate is roughly proportional to the mean) (Geisler & Albrecht, 1997). However, less is known about the influence of attention on the variability of neuronal responses.

Physiological Mechanisms of Attention

The purpose of this exercise is to compare a wide range of experiments with the same model to determine the similarities and differences across results. The model is purely a descriptive model and makes no claims for how the attentional effects could be implemented physiologically. There some modeling efforts do employ physiologically-based mechanisms to describe attentional effects. For example, (Carandini & Heeger, 1994) show that the process of contrast gain could be implement through a process of shunting inhibition (but see (Holt & Koch, 1997). In another example, (Buia & Tiesinga, 2008) implicated different classes of interneurons for different types of attention and propose that feature-based attention is mediated by a projection of top-down interneurons to the feed-forward interneurons, while spatial attention may be the result of modulation of feed forward inputs alone. In another modeling effort, Ardid, Wang & Compte (2007) show how a network model of spiking neurons can mimic the feature similarity gain model of feature-based attention. Often these physiologically oriented models are designed to fit results from a specific published experiment. It is hoped that the analysis presented here will provide a description of typical attention effects found across the literature in order to restrict the set of effects needed to be explained through more physiologically-based models.

Table 12.

Model fits and the results of nested model F-tests for the analysis of the MT neurons from Martinez-Trujillo & Treue (2004). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 12. Martinez-Trujillo & Treue 2004figure 4a (Figure 6 in text)
Model	SSE	Pct Var	Add parameters
			Gmax,Gmin	d	w
No attention	1.4746	88.95	F(2,19) = 7.23 p=0.0046	F(1,20) = 0.00 p=1.0000	F(1,20) = 0.53 p=0.4748
Gmax,Gmin	0.8373	93.79		F(1,18) = 0.00 p=1.0000	F(1,18) = 0.04 p=0.8406
d	1.4746	88.95	F(2,18) = 6.85 p=0.0061		F(1,19) = 0.50 p=0.4863
w	1.4365	88.52	F(2,18) = 6.48 p=0.0076	F(1,19) = 0.00 p=1.0000
Gmax,Gmin,d	0.8373	93.79			F(1,17) = 0.04 p=0.8452
Gmax,Gmin,w	0.8354	93.7		F(1,17) = 0.00 p=1.0000
d,w	1.4365	88.52	F(2,17) = 6.12 p=0.0100
Gmax,Gmin,d,w	0.8354	93.7

Table 13.

Model fits and the results of nested model F-tests for the analysis of the V4 neurons from Madams & Maunsell (1999). The combination of attention parameters allowed to vary are shown in the first column, along with the sums of squared errors and percentage of variance accounted for. Additional columns show nested model F-tests for fits when parameters are added to each model.

Table 13. McAdams & Maunsell, 1999figure 7a (Figure 7 in text)
Model	SSE	Pct Var	Add parameter
			gMax,gMin	d	w
No attention	11.4679	92.49	F(2,21)=583.51 p<0.00001	F(1,22)=71.46 p<0.00001	F(1,22)=17.82 p=0.0004
Gmax,Gmin	0.2027	99.83		F(1,20) = 0.33 p=0.5746	F(1,20) = 1.37 p=0.2548
d	2.6995	97.96	F(2,20)=125.34 p<0.00001		F(1,21) = 0.19 p=0.6712
w	6.3355	96.31	F(2,20)=324.01 p<0.00001	F(1,21)=28.72 p<0.00001
Gmax,Gmin,d	0.1995	99.83			F(1,19) = 0.98 p=0.3354
Gmax,Gmin,w	0.1897	99.84		F(1,19) = 0.00 p=1.0000
d,w	2.6758	97.93	F(2,19)=124.50 p<0.00001
Gmax,Gmin,d,w	0.1897	99.84