Evaluation and Comparison of Simple Multiple Model, Richer Data Multiple Model and Sequential Interacting Multiple Model (IMM) Bayesian Analyses of Gentamicin and Vancomycin Data Collected from Patients Undergoing Cardiothoracic Surgery

Abstract

This study compared the abilities of three Bayesian algorithms: simple multiple model (SMM) using a single creatinine measurement; richer data multiple model (RMM) using all creatinine measurements; and the sequential interacting multiple model (IMM), to describe gentamicin and vancomycin concentration data from patients within a cardiothoracic surgery unit who had variable renal function. All algorithms start with multiple sets of discrete parameter support points obtained from nonparametric population modeling. The SMM and RMM Bayesian algorithms then estimate their Bayesian posterior probabilities by conventionally assuming that the estimated parameter distributions are fixed and unchanging throughout the period of data analysis. In contrast, the IMM sequential Bayesian algorithm permits parameter estimates to jump from one population model support point to another, as new data are analysed, if the probability of a different support point fitting the more recent data is more likely. Several initial IMM jump probability settings were examined: 0.0001%; 0.1%; 3%; 10%; and a probability range of 0.0001% to 50%. The data sets comprised 550 gentamicin concentration measurements from 135 patients and 555 vancomycin concentration measurements from 139 patients. The SMM algorithm performed poorly with both antibiotics. Improved precision was obtained with the RMM algorithm. However, the IMM algorithm fitted the data with the highest precision. A 3% jump probability gave the best estimates. In contrast, the IMM 0.0001% to 50% range setting performed poorly, especially for vancomycin. In summary, the IMM algorithm described and tracked drug concentration data well in these clinically unstable patients. Further investigation of this new approach in routine clinical care and optimal dosage design is warranted

INTRODUCTION

In complex and/or clinically unstable patients, such as those undergoing cardiothoracic surgery, there are well-recognised difficulties in maintaining appropriate drug dosage regimens. Vancomycin and gentamicin are commonly used to treat infections in this patient group and therapy may be complicated by post-operative fluctuations in renal function in association with the trauma of surgery^1–2, pre-existing kidney disease or the administration of potentially nephrotoxic drugs.

Although the management of unstable patients is a well-recognised problem in clinical practice, there have been few attempts to characterise changes in drug handling. An early study by Jelliffe et al³ found that a maximum aposteriori probability (MAP) Bayesian algorithm described gentamicin data reasonably well in a small group of patients with unstable renal function. That study used a method to estimate creatinine clearance based on either stable or changing serum creatinine pairs.⁴ In contrast, Böttger et al⁵, who used the Abbott Pharmacokinetic Systems Bayesian package, found it difficult to describe tobramycin data from patients who had rapid changes in clearance. Wählby et al⁶ examined the issue of changing clinical covariates using a population approach and, using the same methodology, Staatz et al⁷ found that including both a baseline and change from baseline effect of creatinine clearance improved the fit of gentamicin but not of vancomycin data from patients undergoing cardiothoracic surgery.

A program that is potentially useful for describing time-varying conditions in individual patients is the sequential interacting multiple model Bayesian method employed in the MM-USCPACK pharmacokinetic program developed by Jelliffe et al.^8,9 This program has been designed to handle data not only when clinical covariates that describe changes in function, such as creatinine clearance, are available but also when they are absent.

The aim of the present study was to evaluate and compare the abilities of simple multiple model (SMM), richer data multiple model (RMM) and the sequential interacting multiple model (IMM) Bayesian approaches within the MM-USCPACK pharmacokinetic program to track the behaviour of gentamicin and vancomycin concentrations in patients who were being treated within a cardiothoracic surgery unit.

MATERIALS AND METHODS

Patients

Approval for the study was given by the West Ethics Committee of the North Division of the National Health Service, Greater Glasgow. The patient dataset had been de-identified and collated for a previous population pharmacokinetic study.⁷ Data had been collected retrospectively and prospectively from the therapeutic drug monitoring (TDM) files of patients treated within the Cardiothoracic Surgery Unit at the Western Infirmary, Glasgow, between January 1998 and August 2004. All data within the TDM files had been recorded prospectively by ward-based clinical pharmacists and comprised a handwritten record of drug dosage amounts (mg), drug administration times, drug concentration measurements (mg/L), sampling times, patient age (years), weight (kg), height (m), serum creatinine concentration measurements (µmol/L) and estimated creatinine clearance (ml/min)¹⁰. The dates, times and values of any additional creatinine measurements had been obtained retrospectively from computer files. A preliminary screen of the available data forms had been conducted and data collected during renal replacement therapy, such as haemofiltration, were not considered for inclusion in the data set, along with concentration data for which dosage and/or sampling times were not clear. All data from the original data set⁷ were included in the present analysis.

Drug Analysis

Gentamicin and vancomycin concentrations were determined using fluorescence polarisation immunoassay (TDx™, Abbott Laboratories). The limits of quantification for gentamicin and vancomycin were 0.1 mg/L and 1.0 mg/L respectively and assay coefficient of variations were 4.4% at 8.3 mg/L, 7% at 4.3 mg/L and 11% at 0.9 mg/L for gentamicin and 4.2 % at 53 mg/L, 10.9% at 29 mg/L and 4.2% at 11 mg/L for vancomycin. The overall (assay plus environmental noise) error polynomials used in this study were SD (mg/L) = 0.09114 + 0.043524C + 0.004596C² for gentamicin, and SD (mg/L) = 0.059421 + 0.012291C + 0.000713C² for vancomycin, where SD is the standard deviation and C is the measured drug concentration.

Data Analysis

Individual data files were created for each patient within the MM-USCPACK Pharmacokinetic Program (University of Southern California, Laboratory of Applied Pharmacokinetics, Version 0.42, 2005). Each set of gentamicin and vancomycin concentration measurements was analysed using the following basic algorithms: SMM Bayesian analysis using a single (the first) creatinine concentration measurement to describe renal function and obtain the population estimates of drug clearance and RMM Bayesian analysis using all creatinine concentration measurements. In addition, the IMM Bayesian algorithm, which considers all creatinine concentration measurements and allows the pharmacokinetic parameters to jump or change either when a new dose is given or a new measured serum concentration is drawn, was used. The IMM procedure was used with jump probabilities set at 0.0001%, 0.1%, 3% and 10% and also with a jump probability range of 0.0001 – 50%. This final IMM setting allows the program to select an individual probability within that range for each patient. These IMM settings represent the probabilities that the population parameter estimates might possibly change as each dose is given or each new data point becomes available, if such a change appears more likely in fitting the data. The choice of jump probability settings for the IMM option was entirely empirical. The IMM default value is 0.0001%, with a suggested range of 0.1–3%, which was extended to 10% for comparison. The jump range was intended to cover probability settings from very small (0.0001%) to extremely large (50%).

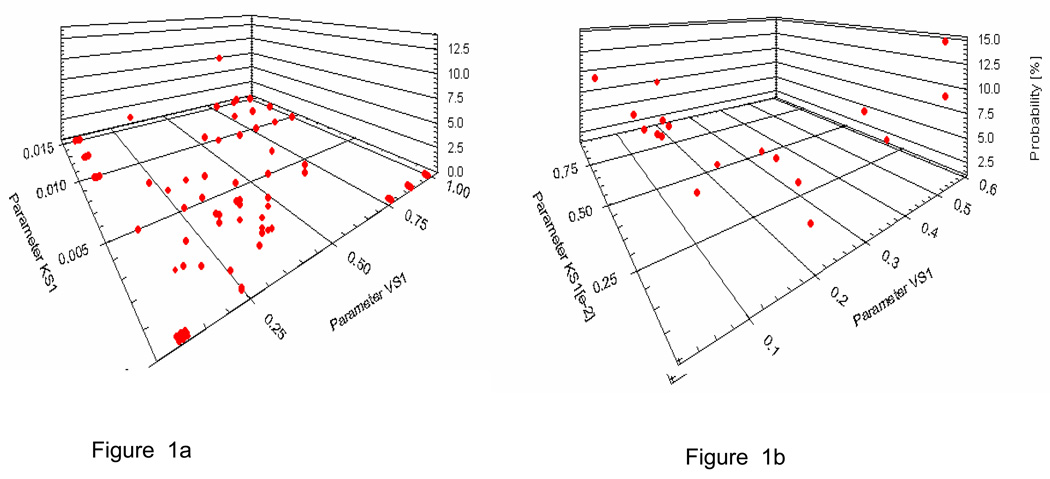
The gentamicin population model used in the MM-USCPACK programs was based on a nonparametric population analysis conducted in 634 general medical and intensive care unit patients from seven hospitals in France (Maire P, unpublished report). The final model contained 76 support points for the joint pharmacokinetic parameter distributions. In contrast to parametric population modelling approaches, which assume a continuous distribution (e.g. normal or lognormal), nonparametric (NP) approaches produce a collection of separate discrete points (support points).^11–13 Each support point consists of a single estimated value for each parameter in the model, plus an estimate of the probability of that collection of points given the population data and the error model employed. No assumptions are made about the connections between the points. Figure 1a shows a 3D view of the parameters Vslope (L/kg) and Kslope (hr⁻¹ per unit of creatinine clearance) for gentamicin and Figure 1b shows a similar figure for vancomycin. A preliminary analysis using data from 20 patients was conducted to compare four versions of the gentamicin population model which had different numbers of support points. Although there were no significant differences between models, the one that gave the best precision and accuracy was chosen for future analyses.

Figure 1.

a 3D plot of the discrete distributions of parameters VS1 (apparent central volume of distribution, L/kg) and KS1 (increment of elimination rate constant per unit of creatinine clearance) for (a) gentamicin and (b) vancomycin.

The vancomycin population model used in the MM-USCPACK programs was based on 28 subjects, and contained 18 support points. It was developed from patients who were allergic to penicillin, and who either needed dental work and had a prosthetic heart valve, or who were ill with endocarditis.¹⁴

Following each analysis in the current study, estimated gentamicin and vancomycin concentrations were recorded for each patient and compared with measured concentrations. The abilities of each algorithm to track each patient’s data were compared by examining bias and precision of the prediction errors (PEs) and percentage prediction errors (%PEs) in the concentration measurements. PEs and %PEs were calculated using the following quations:

$$\text{PE}=\text{measured concentration}-\text{predicted concentration}$$

$$\%\text{PE}=100\times [(\text{measured concentration}-\text{predicted concentration})/\text{predicted concentration}]$$

Correlations among concentrations measured in the same individual were accounted for by also examining patient averaged PEs and %PEs.

Bias was tested by comparing the mean PEs, %PEs and patient averaged PEs and %PEs with zero using an unpaired Student’s t-test with statistical significance set at p<0.05 . The 95% confidence intervals of the differences were also examined. Precision was determined by examining the magnitude of the root mean squared error or, if the data were not normally distributed, the median absolute (unsigned) error.¹⁵ Relative precision was examined by analysis of variance (ANOVA) of squared prediction errors with individual comparisons performed using Tukey’s method. If data were not normally distributed, a non-parametric Kruskal Wallis ANOVA was performed on the unsigned PEs, and individual comparisons were made using a Wilcoxon Signed Rank test of the differences in unsigned PE between models. Statistical significance was set at p<0.05 with correction for multiple comparisons, i.e. p<0.002 for each comparison, and all analyses were performed using Minitab® version 12.21 (Minitab Inc, 1998).

RESULTS

Patients

Data from 135 patients were included in the gentamicin analysis and from 139 patients in the vancomycin analysis. A summary of the clinical characteristics of the study patients is presented in Table 1. In brief, 71% were male; the median age was about 65 years; 42 patients received both gentamicin and vancomycin. Most of the patients had received antibiotics for post-operative sepsis, typically a combination of gentamicin and either a penicillin or vancomycin. Approximately 79% of patients had undergone cardiac surgery; 5% had had thoracic surgery; 2% had a wound infection and 1% had native valve endocarditis. The reason for admission was not available for 15% of gentamicin and 14% of vancomycin patients.

Table 1.

Summary of demographic and clinical characteristics of the patient group

Factor	Gentamicin patients	Vancomycin patients
	Number / Median (range)	Number / Median (range)
Number of patients	135	139
Female/male	39/96	41/98
Age (years)	64 (29–83)	67 (17–92)
Weight (kg)	72 (39–138)	75 (44–112)
Ideal body weight (kg)	67 (30–91)	63 (36–90)
Serum creatinine concentration (µmol/L)*	110 (60–527)	100 (60–527)
Creatinine clearance (ml/min)*	60 (9–171)	61 (12–173)

^*Key: creatinine concentration measurements < 60 µmol/L were fixed to 60 µmol/L

Eight patients in each group had creatinine concentration measurements below 60 µmol/L. To avoid generating non-physiological estimates of creatinine clearance, these were rounded up to 60 µmol/L, as described previously.^16,17 The resulting estimates of creatinine clearance in the patients receiving gentamicin and vancomycin ranged from 9 – 171 ml/min and 12 – 173 ml/min respectively (Table 1). In the gentamicin group, serum creatinine concentration changed by more than 20% in 58% of patients of whom 33% (n = 26) had an increase, 27% (n = 21) had a decrease and 40% (n = 31) had both an increase and decrease. Within the vancomycin group, 42% of patients had a creatinine concentration change of more than 20% of which 67% (n = 39) had an increase, 12% (n = 7) a decrease and 21% (n = 12) had both an increase and a decrease.

Both antibiotics were administered intravenously. Gentamicin doses of 60 – 300 mg were given over 2 to 30 minutes and vancomycin doses of 120 to 2000 mg were given over 0.2 to 4.4 hours. The dataset contained 550 gentamicin concentration measurements (range 1 to 20 per patient, median 1) and 555 vancomycin concentration measurements (range 1 to 19 per patient, median 3). Gentamicin sampling times ranged from 0.5 to 95.5 hours after the end of the most recent infusion (median 14 hours) and vancomycin sampling times ranged from 2.7 to 135 hours after the end of the most recent infusion (median 16 hours).

Data analysis

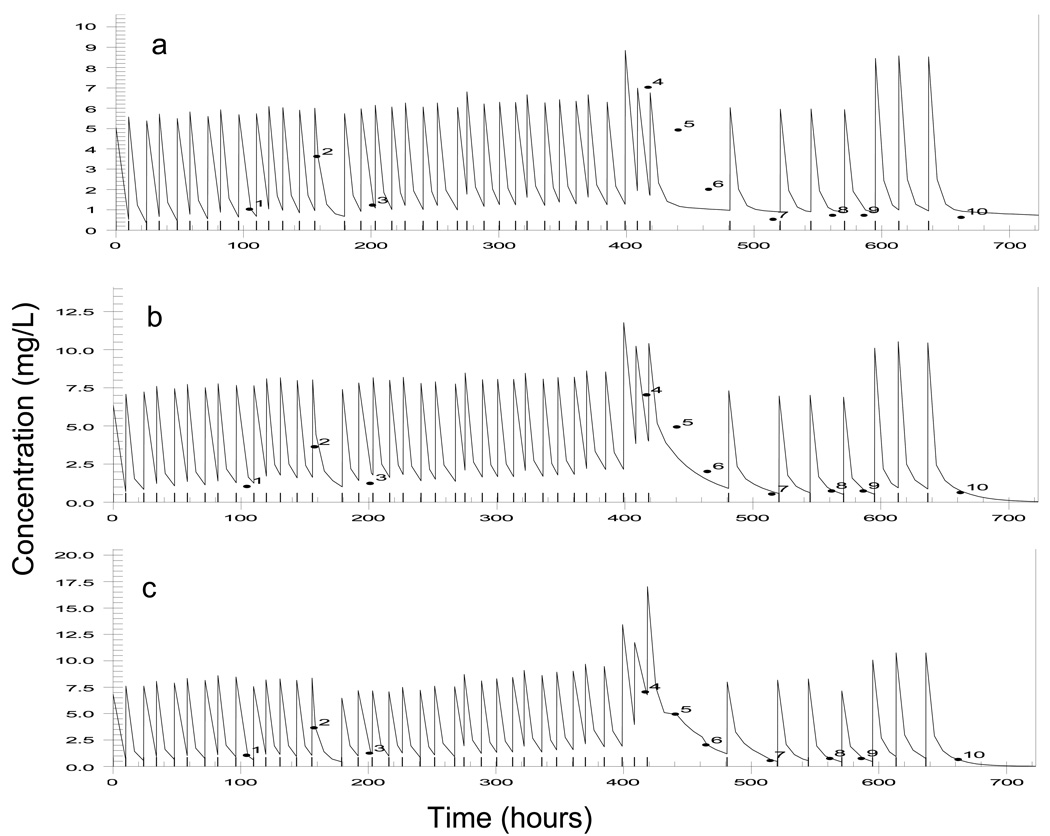
Figure 2 a–c show the measured versus predicted gentamicin concentration-time profiles when the data were analysed using the SMM, RMM and IMM (3%) settings for one patient who was particularly unstable (his creatinine concentration changed by 106% during therapy). The SMM approach provided a poor fit to the data and the IMM fit provided the closest estimation of the measured concentrations. Jump changes in the parameter values and their profiles over time were required to achieve this (Figure 1c). Figure 2a (gentamicin) and Figure 2b (vancomycin) show all measured concentrations plotted against the predictions obtained from the various algorithms and settings. Results for the IMM 0.1% setting are not shown as they were similar to those obtained for the IMM 0.0001% setting. The SMM setting produced the poorest predictions for both gentamicin and vancomycin and the IMM algorithm consistently provided the best description of the data. There was a clear improvement in the distribution of estimations around the line of identity as the jump probability increased from 0.0001% to 3%. However, when the probability was allowed to range from 0.0001% to 50% for each patient, estimates became more diverse for both gentamicin and vancomycin, and a clear bias was seen with the vancomycin estimations. The reason for this bias was not clear.

Figure 2.

Plot of measured versus predicted gentamicin concentrations from a patient with unstable renal function, using (a) simple multiple model Bayesian analysis, (b) richer data multiple model Bayesian analysis and (c) sequential interacting multiple model Bayesian analysis with a 3% probability of a change in parameter values

Table 2 shows the mean (95% CI) PEs and %PEs. Mean PEs (and %PEs) for gentamicin ranged from 0.03 mg/L (2.3%) for the IMM 3% probability setting to 0.28 mg/L (24%) for SMM, and for vancomycin from −0.26 mg/L (−1.8%) for the IMM 3% probability setting to −2.32 mg/L (−13%) for the IMM 0.0001–50% probability range setting. For gentamicin, the SMM setting produced the greatest bias whereas the 0.0001–50% IMM probability range setting was the most biased for vancomycin. For gentamicin, all methods apart from the IMM 10% probability setting and the 0.0001–50% probability range underpredicted the concentration measurements, whereas for vancomycin the IMM 3% and 10% probability settings and the 0.0001–50% probability range underpredicted the measurements.

Table 2.

Mean (95% confidence interval) prediction errors and % prediction errors using data from all patients

	Gentamicin dataset (n = 550)		Vancomycin dataset (n = 555)
Setting	PE mg/L	%PE	PE mg/L	%PE
SMM	0.28 (0.22, 0.34*)	23.9 (17.6, 30.2*)	1.01 (0.67, 1.34*)	15.0 (11.4, 18.6*)
RMM	0.16 (0.12, 0.21*)	12.6 (8.8, 16.3*)	0.26 (0.02, 0.50*)	5.4 (3.3, 7.4*)
IMM probability 0.0001%	0.09 (0.06, 0.12*)	5.1 (3.4, 6.8*)	0.44 (0.32, 0.55*)	4.0 (3.0, 5.0*)
IMM probability 0.1%	0.09 (0.06, 0.11*)	4.9 (3.3, 6.4*)	0.27 (0.18, 0.36*)	2.4 (1.6, 3.1*)
IMM probability 3%	0.03 (0.01, 0.05*)	2.3 (0.9, 3.6*)	−0.26 (−0.33, −0.19*)	−1.8 (−2.3, −1.2*)
IMM probability 10%	−0.07 (−0.08, −0.05*)	−2.4 (−3.6, −1.3*)	−1.33 (−1.43, −1.22*)	−8.9 (−9.3, −8.1*)
IMM probability range 0.0001–50%#	−0.06 (−0.09, −0.03*)	−0.19 (−2.0, 1.6)	−2.32 (−2.55, −2.09*)	−12.9 (−14.1, −11.7*)

Key: PE prediction error, SMM simple multiple model Bayesian analysis, RMM richer data multiple model Bayesian analysis, IMM interacting multiple model Bayesian analysis

^*significantly biased (p<0.05)

^#gentamicin n = 523, vancomycin n = 530

Footnote: For both drugs the IMM 3% setting gave the least bias. Clinically significant bias (above the limit of quantification) was observed with SMM for both gentamicin and vancomycin, RMM for gentamicin and both IMM10% and 0.0001–50% for vancomycin.

When the PE and %PE data within each patient were averaged and then analysed for bias, the results were similar to those obtained for the mean PE and %PE (data not shown). For gentamicin, the poorest results were obtained with the SMM analysis and for vancomycin the IMM 0.0001–50% probability range setting performed the worst. For both drugs, the bias of the four IMM settings was minimal.

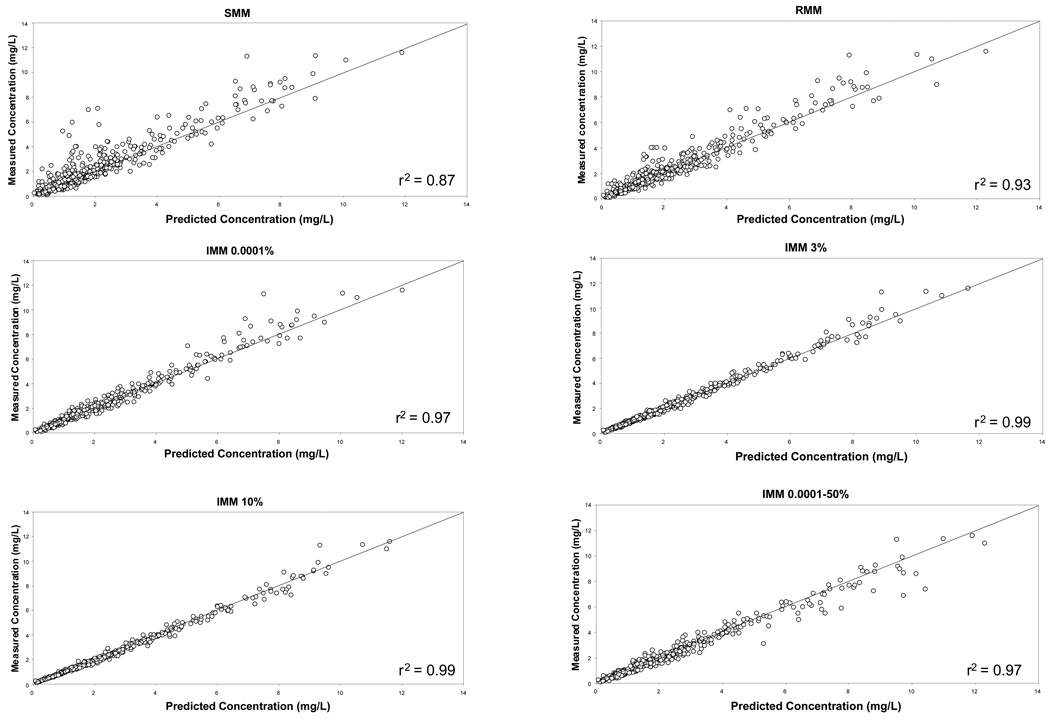
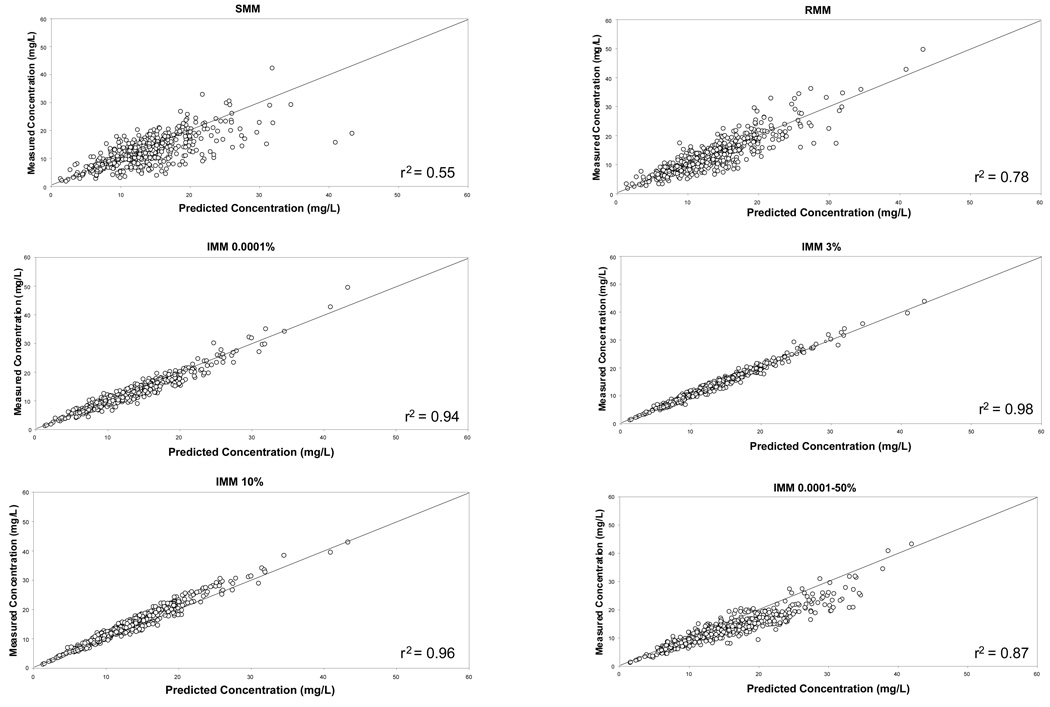
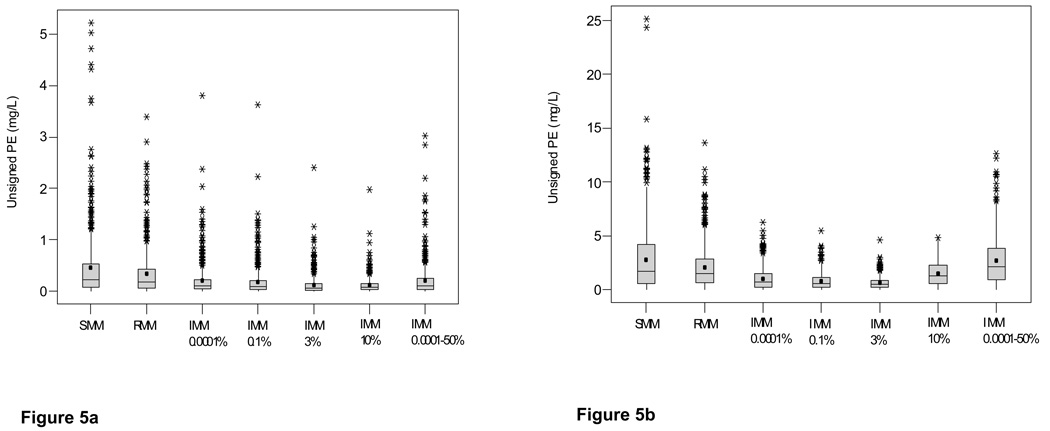
The distributions of the unsigned prediction errors, a measure of precision, are presented in Figure 3a (gentamicin) and Figure 3b (vancomycin). These plots show that the IMM 3% probability setting gave the most precise estimates (lowest prediction error), and that the SMM algorithm was the least precise. The 0.0001–50% probability range was the least precise IMM setting. Similar results were obtained when % PEs and patient averaged data were examined (data not shown). Since the data were highly skewed, a non-parametric analysis was conducted and significant differences among the settings were identified. For the gentamicin data, the SMM setting was the least precise and was significantly inferior to all other methods. In contrast, with the vancomycin data the IMM jump probability 0.0001–50% range was significantly inferior to all other settings except SMM, for which a non-significant trend was identified. For gentamicin, the IMM 3% probability setting was significantly better than all other settings except IMM 10% whereas for vancomycin the IMM 3% probability setting was the best.

Figure 3.

Plot of measured versus predicted concentrations following SMM, RMM and IMM Bayesian analysis of gentamicin concentration data collected from cardiothoracic surgery patients.

Key: SMM simple multiple model Bayesian analysis, RMM richer data multiple model, IMM interacting multiple model with fixed probabilities of 0.0001%, 3% and 10% and a range of 0.0001–50%

– is the line of identity

Footnote The IMM 3% and 10% settings provided the best description of gentamicin concentrations; the SMM setting was the worst.

In summary, the IMM initial probability settings (regardless of which value was chosen) were more precise and less biased than SMM and RMM for both gentamicin and vancomycin. SMM was significantly worse than all other settings for gentamicin and all except the IMM 0.0001–50% probability range setting for vancomycin. When the various IMM settings were compared to each other, the IMM 3% probability setting gave the best results in tracking the behaviour of the drug in these patients.

DISCUSSION

This study compared different multiple model Bayesian algorithms when applied to gentamicin and vancomycin concentration data from patients who were being treated in a cardiothoracic surgery unit. Overall, the IMM approach provided the best fit of the data.

Until recently, the problem of describing data in patients with rapidly changing clinical characteristics has received limited attention. It was first addressed in a population setting by Taright et al¹⁸ and subsequently by Wählby et al⁶, who used the population package NONMEM¹⁹ to examine four sets of data containing changing covariates. They evaluated two extended models: one in which the standard population covariate model was split into a baseline and change from baseline effect; and another which allowed interindividual variability in the covariate effect to vary between individuals. Both approaches improved the fit of all of the data sets they examined. More recently, Staatz et al⁷ applied the same approach to the gentamicin and vancomycin data that were analysed in the present study. An improvement in the fit of the data was identified for gentamicin, although not for vancomycin, when a baseline and change from baseline creatinine clearance model was applied.

The performance of maximum aposteriori probability (MAP) Bayesian methods when analysing individual data from patients with changing renal function has also been examined. Jelliffe et al³ found that a MAP Bayesian method coped equally well with data from 10 patients with stable or unstable renal function but reported a relatively high mean PE of −0.33 mg/L for patients with unstable renal function. In their analysis of data from 19 critically ill patients, Böttger et al⁵ identified unusually large PEs for patients who had rapid changes in clearance, indicating that their data analysis technique was unable to handle such data.

The SMM and RMM algorithms that were used in the present study contain a collection of discrete support points provided by a nonparametric population model.²⁰ The ability of these various population model support points to predict each individual patient’s measured antibiotic concentrations is examined with the multiple model Bayesian analysis. Support points that provide good predictions have their posterior probabilities increased according to Bayes’ theorem, while those that provide poor predictions have their posterior probabilities decreased. The SMM approach only included the first creatinine concentration measurement and, therefore, assumed that parameter values were unchanging throughout the whole course of therapy. Since a decline in renal function occurred more commonly than an improvement, it was not surprising that this approach tended to underestimate drug concentrations. The RMM algorithm allows covariate-linked parameters to change over time according to the changing clinical covariates, but assumes that all parameter values and distributions are fixed and unchanging throughout each period of data analysis. Consequently, if the analysis is done in a sequential Bayesian manner as each new data point is added, the same final Bayesian posterior parameter estimates would be obtained as if all the data had been analysed together. The RMM algorithm performed better than the SMM approach for both drugs, although an increase in % bias was observed for gentamicin. However, the precision of some predictions, especially in those patients whose renal function was particularly variable, was still poor.

Both the population and RMM approaches depend on measurements being available of a parameter covariate which changes in parallel with alterations in drug handling. In clinical practice, however, creatinine concentration measurements are not always accessible when changes in renal function occur. Furthermore, changes in creatinine concentration can lag behind changes in drug clearance, as previously described by Kirkpatrick et al.²¹ Such a lag may have contributed to the bias observed with these algorithms. In many patients receiving aminoglycosides apparent volume of distribution can change. For example, it may increase with increasing clinical severity and decrease again with recovery. No covariate is currently available to track such changes.

As demonstrated in the present study, the IMM algorithm offers advantages when there is a lack of covariate information to help describe changes in pharmacokinetic parameters. The IMM algorithm allows parameter estimates to ‘jump’ to different population model support points during the period of data analysis, after each sequential aposteriori update in the sequential Bayesian IMM parameter update, if this is more likely. To date, the IMM method has been compared to a MAP Bayesian approach and to an RMM approach using a simulated data set where all patient parameter values were exactly known, and with clinical data from only one patient⁹. In that study, the IMM approach tracked the simulated changing patient with slightly less than half the total error than that of the MAP and the multiple model Bayesian approaches. The present study thus represents the first time that the performance of the IMM program has been evaluated in a clinical setting using data from a large group of unstable patients.

As clearly illustrated in Figure 2, the IMM algorithm described the concentration data with greater precision than the simpler methods. Although a statistically significant bias was observed, this was probably related to the large number of samples, which led to very tight confidence intervals for the mean PE. Clinically significant bias (above the limit of quantification used by the laboratory for reporting results) was only observed with the SMM setting (both antibiotics), RMM for gentamicin and the IMM settings 10% and 0.0001–50% for vancomycin. One of the aims of the present analysis was to investigate how different IMM jump probability settings influenced the results. Although it might have been anticipated that the higher the jump probability, the better the fit of the data, improvements in fit only occurred with probability settings up to 3%, but there was no additional improvement at 10% for gentamicin, and the results were worse for vancomycin. Furthermore, when the program was allowed to select the probability from a range, the results were inferior to those obtained with fixed probabilities, especially for vancomycin, where there was a consistent underprediction of concentrations and very poor precision. It also took longer to run each analysis, particularly for the most unstable patients. This problem of fitting noisy data and then not predicting the model behaviour well is reminiscent of the problem of “overfitting’ data with a model that is too complex, and which has more parameters that there are observations.

The properties of the population model can have a significant influence on the results of a Bayesian analysis. The ability of the IMM program to track changing parameters (or ‘jumps’) during the period of data analysis depends on there being a support point available within the population model to describe what is happening to that particular patient. The 40 original support points within the gentamicin population model in the MM-USCPACK program were extended to include 36 additional values, to account for unusual parameter values which may occasionally occur in some patients. To reduce the possibility of tracking noisy data errors rather than real changes in pharmacokinetic parameter values, the extra extended range support points were given a much lower probability of 6 × 10⁻⁶, to make them less likely to be chosen.⁹ It is possible that allowing more jump flexibility led to more chances of hitting one of these outlying points and may have contributed to the deterioration in fit when the probability was allowed to vary up to 50% and even with the 10% probability setting, in the case of vancomycin. The relatively small number of support points in the vancomycin population model (18) may have contributed to the poor fits and bias that were identified in this study. Recharacterisation of the vancomycin population model with a large patient data set is currently underway.

A potential problem with the IMM program is that increasing the jump probability setting might produce a disproportionate emphasis on spurious results caused by dosage or sampling errors and lead to poor pharmacokinetic parameter estimation and inappropriate dosage recommendations. It might also be a good way simply to chase spurious noise in the patient’s data, especially when the dosage history is short, and there is no clinical indication that the patient’s clinical status may be changing. In that case, the RMM Bayesian option may well be adequate. However, if the RMM Bayesian analysis does not describe the data well, and especially if the dosage history is rather long and the patient is clinically unstable, then the results suggest that the IMM option with an initial jump probability of 3% may be the most useful value to use.

Conclusions

This study has highlighted some practical problems inherent in the interpretation of drug concentration measurements from clinically unstable patients, and in the pragmatic management of their dosage regimens. The IMM program tracked drug behaviour better than the RMM and SMM options in terms of both bias and precision. The best results were obtained with a 3% probability of a change in parameter values during the period of data analysis. Further work will be helpful to explore the clinical application of this new approach with respect to dosage regimen design for different patients with clinical instability and unpredictable variability in drug handling.

Figure 4.

Plot of measured versus predicted concentrations following SMM, RMM and IMM Bayesian analysis of vancomycin concentration data collected from cardiothoracic surgery patients.

Key: SMM simple multiple model Bayesian analysis, RMM richer data multiple model, IMM interacting multiple model with fixed probabilities of 0.0001%, 3% and 10% and a range of 0.0001–50%

– is the line of identity

Footnote The IMM 3% and 10% settings gave the best description of vancomycin concentrations; the SMM and IMM 0.0001–50% jump probability range settings were the worst.

Figure 5.

Box and whisker plots of unsigned prediction errors arising from SMM, RMM and IMM Bayesian analysis of (a) gentamicin and (b) vancomycin data collected from cardiothoracic surgery patients

Key: SMM simple multiple model Bayesian analysis, RMM richer data multiple model, IMM interacting multiple model with fixed probabilities of 0.0001%, 3% and 10% and a range of 0.0001–50%; means are indicated by solid circles

Footnote: The IMM 3% probability setting gave the most precise and the SMM setting the least precise estimates of both gentamicin and vancomycin concentrations. The 0.0001–50% probability range was the least precise IMM setting for both antibiotics.