Abstract
Background Context
Rat models with altered loading are used to study disc degeneration and mechano-transduction. Given the prominent role of mechanics in disc function and degeneration, it is critical to measure mechanical behavior in order to evaluate changes following model interventions. Axial compression mechanics of the rat disc are representative of the human disc when normalized by geometry, and differences between the lumbar and caudal disc have been quantified in axial compression. No study has quantified rat disc torsional mechanics.
Purpose
Compare the torsional mechanical behavior of rat lumbar and caudal discs, determine the contribution of combined axial load on torsional mechanics, and compare the torsional properties of rat discs to human lumbar discs.
Study Design
Cadaveric biomechanical study.
Methods
Cyclic torsion without compressive load followed by cyclic torsion with a fixed compressive load was applied to rat lumbar and caudal disc levels.
Results
The apparent torsional modulus was higher in the lumbar region than in the caudal region,: 0.081±0.026 (MPa/°, Mean±SD) for lumbar axially loaded; 0.066±0.028 caudal axially loaded; 0.091±0.033 for lumbar in pure torsion; and 0.056±0.035 for caudal in pure torsion. These values were similar to human disc properties reported in the literature ranging from 0.024 to 0.21 MPa/°.
Conclusions
Use of the caudal disc as a model may be appropriate if the mechanical focus is within the linear region of the loading regime. These results provide support for use of this animal model in basic science studies with respect to torsional mechanics.
Introduction
Animal models are widely used to investigate the pathogenesis of disc degeneration, its progression, and potential treatment approaches [1]. The rat model is often selected because it is economical, easy to handle, and molecular probes are available. Additionally, the rat intervertebral disc has similarities to the human with regards to composition, structure, biomechanics, and loss of notochordal cells [2-5]. Further, the rat disc can be injected with a 32G needle without causing degenerative changes [6,7], providing a model to study interventions. While degeneration is multi-factorial disorder, altered mechanical loading plays a key role [8,9]. Thus rat models with altered loading are used to study both degeneration, interventions, and disc mechano-transduction e.g.,[6,7,10-13]. Given the prominent role of mechanics in disc function and disc degeneration, it is critical to measure disc mechanical behavior in order to quantify changes following model interventions. However, the model selected should be evaluated for the similarity to human disc mechanics. Axial compression mechanics of the rat disc have been previously reported and shown to be representative of the human disc when normalized by geometry [2]. Differences between the mouse and rat lumbar and caudal disc have been measured in axial compression and shown to be different with respect to neutral zone and viscoelastic creep behavior but more similar in the linear region [3,14]. To the best of our knowledge, no study has quantified rat disc torsional mechanics.
The objective of this study was to compare the torsional mechanical behavior of rat lumbar and caudal discs, determine the contribution of combined axial load on torsional mechanics, and compare the torsional properties of rat discs to human lumbar discs. We hypothesized, based on previous findings for axial compression, that the lumbar disc will be stiffer than the caudal disc. We further hypothesized that combined torsion and axial compressive axial load will be stiffer in torsion than in the absence of compressive load.
Materials and Methods
Sample Preparation
Adult male Sprague-Dawley rats (age 7-9 months, weight 542±49 g) were acquired and euthanized. Eleven rats were utilized for mechanical testing and three were utilized to determine disc geometry. The lumbar spine and tail was dissected from each animal. For mechanical testing, surrounding musculature and soft tissues were removed and bone-disc-bone motion segments were prepared for L1 to L6 lumbar levels and C8 to C12 caudal levels. In order to isolate the torsional properties of the disc, the facet joints were removed from the lumbar levels.
Disc Geometry
Geometric parameters are required to normalize torsional mechanics for comparison across levels and to the human disc [2]. Because mechanical testing can alter these geometric measurements and the nucleus pulposus could only be measured following axial sectioning, geometry of each level was determined from a separate set of strain, age, and gender-matched rats that were acquired from the same vendor (n=3). MicroCT images were obtained at a resolution of 4.2 microns (eXplore Locus SP, GE Healthcare, Waukesha, WI). A custom MATLAB routine was used to map the height profile of the entire disc space and calculate disc height [7]. Next, transverse plane geometry was determined by sectioning the disc in the mid-transverse plane, acquiring a digital image of the disc cross-section processed by a custom MATLAB histomorphometry program [5]. Parameters measured included lateral width of the disc (WL) and nucleus pulposus (NL) and antero-posterior width of the disc (WAP) and nucleus pulposus (NAP). The disc cross-sectional area was calculated as A = (π/4)WLWAP [2]. Assuming the disc is a hollow ellipse, the polar moment of inertia (JP) was calculated as [2].
Mechanical Testing
A custom instrument was designed and built to test rodent motion segment samples under combined torsion and axial loading. Angle-controlled torsion was applied in using a stepper motor (AM15E0045, Faulhaber, Clearwater FL). Torque was measured using a torque load cell (T5100, Futek, Irvine CA). Axial loading was applied manually using a displacement stage and was measured using an axial load cell (Model 31, Sensotec, Columbus, OH). When the axial load of interest was achieved, the displacement was fixed in place using a set screw.
The testing protocol was comprised of cyclic torsion without compressive load followed by cyclic torsion with a fixed compressive load. Torsion loading consisted of ten cycles of preconditioning at constant rate of 2°/sec over ±10° followed by two cycles at a slower constant rate of 0.1°/sec to achieve high-resolution data acquisition. Following cyclic torsion with no axial load, a compressive load of 9.8 N (corresponding to 0.8 MPa, calculated as load/area) was applied to lumbar levels and 4.3 N (corresponding to 0.3 MPa) was applied to caudal levels. A lower stress was chosen to prevent excessive compressive creep as observed previously in caudal discs [14]; preliminary data in rat and other species demonstrate that the amount of axial load had little effect on the torsion stiffness, once a lower limit has been exceeded. The compressive load was held for 15 min. to allow for creep deformation. Next, the cyclic torsion protocol was repeated with combined axial load. The sample was kept hydrated with PBS throughout testing.
Data Analysis
To obtain torsional stiffness values in the neutral zone region (KNZ) and in the linear region (K) a trilinear curvefit was applied to the torque-angle response of the final cycle as previously described (Figure 1) [14,15]. The stiffness results were normalized by geometry to calculate the apparent torsional modulus in the neutral zone (GNZ) and linear region (G) as G = Kh/J (MPa/°), where K is the torsional stiffness described above, h the disc height, and J is the polar moment of inertia. The torque range (TR) was calculated as the total range of torque applied over the span of ±10° angular displacement (Figure 1). The maximum shear stress (τ) was calculated from the torque range as [16], where disc and nucleus pulposus widths are as defined above. Hysteresis area, representing energy dissipation, was quantified as the area between the loading and unloading response of the shear stress vs. angular displacement response.
Figure 1.
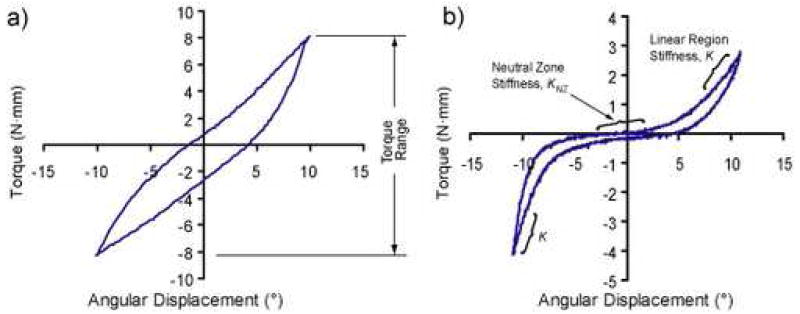
Characteristic nonlinear torque-angular displacement: a) lumbar b) caudal. The area within the curve represents the hysteresis area, a measure of viscoelastic dissipation. Note that both curves are nonlinear and that the lumbar region has a smaller and stiffer neutral zone. The parameters quantified in this study are shown on (a): torque range, and (b): stiffness values.
Statistical Analysis
Statistical analyses were conducted in Statview (SAS Institute, Cary, NC) to determine the effect on torsion mechanics of axial load (no load versus combined axial compression) and anatomical location (lumbar versus caudal). A two-factor ANOVA was performed together with a Bonferroni/Dunn post-hoc test. Significance levels were set at p < 0.05.
Results
The torque-angular displacement response for the lumbar (Figure 1A) and caudal (Figure 1B) discs was qualitatively different, although both regions were nonlinear and viscoelastic. Geometric parameters to normalize each lumbar and caudal level structural property to its apparent material property for comparison across regions and to human discs are shown in Table 1. The apparent torsional modulus in the neutral zone (GNZ) was significantly different with anatomical location and axial loading case (Figure 2A). With no axial load, the lumbar disc GNZ was 2.7X higher than the caudal, and with axial load the lumbar disc was 3.6X higher than the caudal. Within the lumbar spine GNZ was 48% larger with an axial load, and within the caudal spine GNZ was not significantly different with an axial load. The apparent torsional modulus in the linear region (G) was affected by anatomical region, to a lesser magnitude than in the neutral zone, but not by the application of axial loading (Figure 2B). With no axial load, the lumbar disc G was 62% higher than the caudal, and with axial load the lumbar disc G was 23% higher than the caudal. The maximum shear stress (τ) was affected by location and axial load (Figure 2C). With no axial load the lumbar shear stress was 2.6X higher than the caudal, and with axial load the lumbar shear stress was 64% higher than caudal. The lumbar region maximum shear stress was not affected by axial load, while the caudal region maximum shear stress was 66% higher with axial loading than with no load. Finally, the hysteresis area (HA), which represents the energy by volume dissipated, was affected by both location and axial load (Figure 2D). With no axial load the lumbar HA was 3.2X higher than the caudal HA, and with axial load the lumbar HA was 2.6X higher than caudal. Within the caudal region, the HA was 3.3X higher with applied axial compression than with no load, while in the lumbar region the HA was 1.9X higher with applied axial compression than with no load.
Table 1.
Mean (standard deviation) of lumbar and caudal disc geometry by level.
| Level | Height (mm) | WAP (mm) | WL (mm) | NAP (mm) | NL (mm) | Area (mm2) | JP (mm4) |
|---|---|---|---|---|---|---|---|
| L1-L2 | 0.76 (0.01) | 2.78 (0.24) | 4.19 (0.17) | 0.83 (0.24) | 1.74 (0.22) | 8.1 (1.0) | 14.3 (2.0) |
| L2-L3 | 0.72 (0.05) | 3.20 (0.26) | 4.62 (0.35) | 0.80 (0.40) | 1.94 (0.79) | 10.4 (2.5) | 23.0 (7.5) |
| L3-L4 | 0.76 (0.05) | 3.14 (0.47) | 4.36 (0.19) | 0.98 (0.11) | 1.80 (0.14) | 9.7 (1.8) | 19.2 (3.9) |
| L4-L5 | 0.77 (0.03) | 3.72 (0.35) | 4.96 (0.05) | 1.06 (0.18) | 1.51 (0.08) | 13.3 (1.7) | 34.8 (5.2) |
| L5-L6 | 0.99 (0.12) | 4.05 (0.04) | 4.85 (0.22) | 1.09 (0.19) | 1.55 (0.06) | 14.6 (0.6) | 38.6 (4.4) |
| Lumbar Avg | 0.80 (0.11) | 3.38 (0.51) | 4.60 (0.33) | 0.95 (0.13) | 1.71 (0.18) | 11.2 (2.7) | 26.0 (10.4) |
| C9-C10 | 0.94 (0.01) | 4.33 (0.16) | 4.35 (0.15) | 1.16 (0.10) | 1.42 (0.07) | 13.3 (0.7) | 34.5 (2.5) |
| C10-C11 | 0.96 (0.01) | 4.11 (0.59) | 4.33 (0.08) | 1.41 (0.28) | 1.63 (0.19) | 12.1 (1.6) | 31.2 (8.4) |
| C11-C12 | 1.03 (0.10) | 4.37 (0.10) | 4.34 (0.27) | 1.54 (0.17) | 1.48 (0.39) | 12.8 (1.4) | 34.9 (5.4) |
| Caudal Avg | 0.98 (0.05) | 4.27 (0.14) | 4.34 (0.01) | 1.37 (0.19) | 1.51 (0.11) | 12.7 (0.6) | 33.5 (2.0) |
Figure 2.
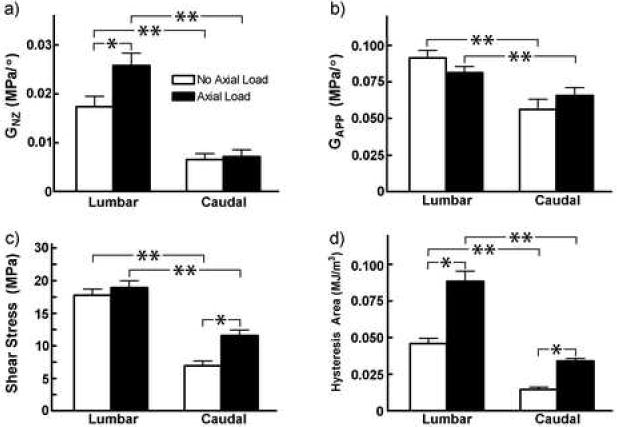
Mean (standard deviation) of torsional properties in the lumbar and caudal regions with and without axial load. a) Neutral zone apparent shear modulus (MPa), b) Apparent shear modulus in linear region (MPa), c) Maximum shear stress (MPa), and d) hysteresis area (MJ/m3). One asterisk represents significant difference vs. no axial load case, and two asterisks denote significant difference vs. lumbar (p<0.05).
The linear region apparent shear modulus can be compared to data reported in the literature in order to compare the rat lumbar and caudal mechanics to the human disc. The rat lumbar G is 0.08 MPa/° and the rat caudal G is 0.06 MPa/°. While these are significantly different from each other, they are within 23% and are more similar than the other torsional properties reported. These G compare quite well to the range of moduli previously published for healthy and degenerate human discs, obtained both under pure torsion and biaxial torsion-compression experiments. As normalized by Elliott and Sarver [2], Abumi et al. [17] and McGlashen et al. [18] measure a lower G~0.025; Beckstein et al. [19] and Kleinstueck et al.(degenerate discs, grade 2.9; range 1-4) [20] measure very similar G~0.09 MPa. Specifically, Haughton et al. [21], show G correlated to identifiable stages of disc quality in humans: healthy discs G=0.21 MPa/° and discs with tears G~0.06 MPa/°, similar to the results published by Farfan et al. [22] (Figure 3).
Figure 3.
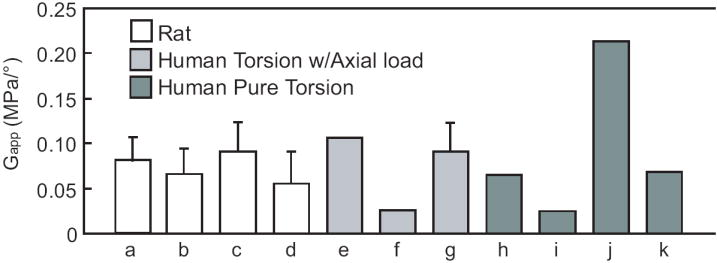
Comparison of apparent shear modulus (G) for rat (present study, a) lumbar, axially loaded, b) caudal, axially loaded, c) lumbar, pure torsion, d) caudal, pure torsion) and human. Cases e) to g) are from axially loaded human motion segments: e) Kleinstueck et al. [20], f) Abumi et al. [17], and g) Beckstein et al. [19]. Cases h) to l) correspond to human motion segments tested in pure torsion: h) Farfan et al. [22], i) McGlashen et al. [18]. Data from j) healthy discs and k) discs with annular tears are from Haughton et al. [21]. In cases that do not show error bars the source reports only an average value. Human apparent modulus was calculated as either tangent or secant modulus as described in Elliott and Sarver [2]
Discussion
This study quantified torsion-compression behavior in the lumbar and caudal intervertebral discs of adult male rats. The rat disc linear-region shear modulus was within the range of previously reported human values (Figure 3), thus providing support for use of this animal model in basic science studies. Human in vivo torsion studies have measured the degrees of axial rotation at each level to be 1.5-2.5° under a 50° torso passive rotation, have demonstrated complex coupled motion, and in some cases have shown an increased segmental motion with degeneration and low back pain [23-25]. These human in vivo rotations have two implications: 1) torsional mechanics have clinical relevance; 2) the neutral zone measurements made in this study are particularly relevant, as they are within the range observed in vivo. Unfortunately, experimental data for the human torsional neutral zone was not available for comparison to the rat disc values and this will be the subject of future study.
The clinical role of torsion in intervertebral disc function and degeneration is not fully understood and is somewhat controversial. Some assert that torsion loading is not likely to play a major role in disc failure, as the facet joint resists much of the torque loading and is the first structure to yield at the limit of torsion [26]. The torsional limit at which the facet yields is 2.9°, ranging from 1.2° in nondegenerate discs to 6.7° in severely degenerate discs [26]. The isolated disc can be rotated to large angles of ~10° without damage. Therefore, the facets prevent the disc from undergoing large stresses and strains under physiologic loading [26]. In contrast, however, fatigue loading to torsional angles well below the acute failure described above and within the physiological range leads to damage to the facet joints and disc [27]. Combined loading may also be important as low levels of torque added to cyclic flexion-extension fatigue loading accelerates injury and failure in the disc and vertebrae [28]. There is ample evidence for associations between compromised torsional stiffness and disc degeneration [21,22,29], facet cartilage osteoarthritis [29], nucleotomy [30], annulus fibrosus radial tears [31], circumferential tears [32], and rim lesions [31-33]. Together, these studies provide evidence for an important clinical role of disc torsion and thus support the need to consider torsion mechanics in animal models of disc degeneration.
A limitation in this study includes intentionally removing the facets to isolate the disc, as is widely done in disc torsion studies e.g., [17-22,33-35]. Facet joints contribute to the lumbar spine torsional stiffness [18,26,34,36]; in the linear region the disc contributes ~35% of the torque resistance, while the facets contribute ~65%, [22,26]. The facet joints do not contribute much within the neutral zone [17], likely due to the gap and lack of contact near the neutral position. Since the neutral zone is an important physiological region, this supports the focus on isolated discs here.
Rodent discs are widely used as a model of the human disc, although some concerns have arisen regarding the suitability of the caudal levels due to the different mechanical loading. The lumbar torsional mechanics were larger than the caudal for all four parameters evaluated (Figure 2). These differences were most dramatic for the neutral zone modulus and hysteresis area, on the order of a factor of 2-4 times higher; while the linear region modulus was within approximately 25% between lumbar and caudal. This is consistent with axial compression comparisons of mouse lumbar and caudal discs, where the largest effects were also observed in the neutral zone and in the viscoelastic creep [14]. Similarly the axial compression properties of the bovine tail have an elongated neutral zone [3]. Taken together, these studies suggest that use of the caudal disc as a model is appropriate if the mechanical focus is within the linear region of the compressive or torsion loading regime; however, caution should be applied when considering the low-load neutral zone region or the viscoelastic behaviors. Given the accessibility of the tail to apply controlled mechanical loading, the advantages of the caudal disc may outweigh the limitations as a model for basic disc research, depending on the questions being addressed.
In conclusion, this study compared the torsional mechanical behavior of rat lumbar and caudal discs, determined the contribution of combined axial load on torsional mechanics, and compared the torsional properties of rat discs to human lumbar discs. In general, the lumbar region torsional property was higher than in the caudal region. Use of the caudal disc as a model may be appropriate if the mechanical focus is within the linear region of the loading regime; however, caution should be applied when considering the low-load neutral zone region or the viscoelastic behaviors. The torsional properties were higher when an axial load was applied, likely due to pressurization from the nucleus pulposus placing the annulus fibers into tension. The normalized shear moduli measured in the rat discs were similar to the human disc properties and within the range of previously reported values, thus providing support for use of this animal model in basic science studies where torsion is relevant.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Dawn M Elliott, University of Pennsylvania Philadelphia, PA.
Alejandro A Espinoza Orías, Rush University.
Neil R Malhotra, University of Pennsylvania.
References
- 1.Lotz JC. Animal models of intervertebral disc degeneration: lessons learned. Spine. 2004;29:2742–50. doi: 10.1097/01.brs.0000146498.04628.f9. [DOI] [PubMed] [Google Scholar]
- 2.Elliott DM, Sarver JJ. Young investigator award winner: validation of the mouse and rat disc as mechanical models of the human lumbar disc. Spine. 2004;29:713–22. doi: 10.1097/01.brs.0000116982.19331.ea. [DOI] [PubMed] [Google Scholar]
- 3.Beckstein J, Sen S, Schaer T, et al. Comparison of animal discs used in disc research to human lumbar disc: axial compression mechanics and glycosaminoglycan content. Spine. doi: 10.1097/BRS.0b013e318166e001. in press. [DOI] [PubMed] [Google Scholar]
- 4.Hunter CJ, Matyas JR, Duncan NA. Cytomorphology of notochordal and chondrocytic cells from the nucleus pulposus: a species comparison. J Anat. 2004;205:357–62. doi: 10.1111/j.0021-8782.2004.00352.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.O’Connell GD, Vresilovic EJ, Elliott DM. Comparison of animals used in disc research to human lumbar disc geometry. Spine. 2007;32:328–33. doi: 10.1097/01.brs.0000253961.40910.c1. [DOI] [PubMed] [Google Scholar]
- 6.Elliott DM, Yerramalli CS, Beckstein JC, et al. The effect of relative needle diameter in puncture and sham injection animal models of degeneration. Spine. doi: 10.1097/BRS.0b013e318166e0a2. in press. [DOI] [PubMed] [Google Scholar]
- 7.Boxberger JI, Auerbach JD, Sen S, et al. An in vivo model of reduced nucleus pulposus glycosaminoglycan content in the rat lumbar intervertebral disc. Spine. doi: 10.1097/BRS.0b013e31816054f8. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stokes IA, Iatridis JC. Mechanical conditions that accelerate intervertebral disc degeneration: overload versus immobilization. Spine. 2004;29:2724–32. doi: 10.1097/01.brs.0000146049.52152.da. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Buckwalter JA, Boden SD, Eyre DR, et al. Intervertebral disk aging, degeneration, and herniation. In: Buckwalter JA, Einhorn TA, Simon SR, editors. Orthopaedic Basic Science. 2. American Acaemy of Orthopaedic Surgeons; 2000. pp. 557–66. [Google Scholar]
- 10.MacLean JJ, Lee CR, Alini M, et al. The effects of short-term load duration on anabolic and catabolic gene expression in the rat tail intervertebral disc. J Orthop Res. 2005;23:1120–7. doi: 10.1016/j.orthres.2005.01.020. [DOI] [PubMed] [Google Scholar]
- 11.Crevensten G, Walsh AJ, Ananthakrishnan D, et al. Intervertebral disc cell therapy for regeneration: mesenchymal stem cell implantation in rat intervertebral discs. Ann Biomed Eng. 2004;32:430–4. doi: 10.1023/b:abme.0000017545.84833.7c. [DOI] [PubMed] [Google Scholar]
- 12.Ching CT, Chow DH, Yao FY, et al. The effect of cyclic compression on the mechanical properties of the inter-vertebral disc: An in vivo study in a rat tail model. Clin Biomech (Bristol, Avon) 2003;18:182–9. doi: 10.1016/s0268-0033(02)00188-2. [DOI] [PubMed] [Google Scholar]
- 13.Iatridis JC, Mente PL, Stokes IA, et al. Compression-induced changes in intervertebral disc properties in a rat tail model. Spine. 1999;24:996–1002. doi: 10.1097/00007632-199905150-00013. [DOI] [PubMed] [Google Scholar]
- 14.Sarver JJ, Elliott DM. Mechanical differences between lumbar and tail discs in the mouse. J Orthop Res. 2005;23:150–5. doi: 10.1016/j.orthres.2004.04.010. [DOI] [PubMed] [Google Scholar]
- 15.Boxberger JI, Sen S, Yerramalli CS, et al. Nucleus pulposus glycosaminoglycan content is correlated with axial mechanics in rat lumbar motion segments. J Orthop Res. 2006;24:1906–15. doi: 10.1002/jor.20221. [DOI] [PubMed] [Google Scholar]
- 16.Roark R. Formulas for stress and strain. 4. New York: McGraw-Hill; 1965. [Google Scholar]
- 17.Abumi K, Panjabi MM, Kramer KM, et al. Biomechanical evaluation of lumbar spinal stability after graded facetectomies. Spine. 1990;15:1142–7. doi: 10.1097/00007632-199011010-00011. [DOI] [PubMed] [Google Scholar]
- 18.McGlashen KM, Miller JA, Schultz AB, et al. Load displacement behavior of the human lumbo-sacral joint. J Orthop Res. 1987;5:488–96. doi: 10.1002/jor.1100050404. [DOI] [PubMed] [Google Scholar]
- 19.Beckstein J, Espinoza A, Cloyd JM, et al. Axial and torsion disc mechanics for several animals compared to the human disc. Transactions of the Orthopaedic Research Society. 2007;1141 [Google Scholar]
- 20.Kleinstueck FS, Diederich CJ, Nau WH, et al. Acute biomechanical and histological effects of intradiscal electrothermal therapy on human lumbar discs. Spine. 2001;26:2198–207. doi: 10.1097/00007632-200110150-00009. [DOI] [PubMed] [Google Scholar]
- 21.Haughton VM, Lim TM, An HS. Intervertebral disk appearance correlated with stiffness of lumbar spinal motion segments. AJNR Am J Neuroradiol. 1999;20:1161–65. [PMC free article] [PubMed] [Google Scholar]
- 22.Farfan HF, Cossette JW, Robertson GH, et al. The effects of torsion on the lumbar intervertebral joints: the role of torsion in the production of disc degeneration. J Bone Joint Surg Am. 1970;52:468–97. [PubMed] [Google Scholar]
- 23.Haughton VM, Rogers B, Meyerand ME, et al. Measuring the axial rotation of lumbar vertebrae in vivo with MR imaging. AJNR Am J Neuroradiol. 2002;23:1110–6. [PMC free article] [PubMed] [Google Scholar]
- 24.Ochia RS, Inoue N, Takatori R, et al. In vivo measurements of lumbar segmental motion during axial rotation in asymptomatic and chronic low back pain male subjects. Spine. 2007;32:1394–9. doi: 10.1097/BRS.0b013e318060122b. [DOI] [PubMed] [Google Scholar]
- 25.Blankenbaker DG, Haughton VM, Rogers BP, et al. Axial rotation of the lumbar spinal motion segments correlated with concordant pain on discography: a preliminary study. AJR Am J Roentgenol. 2006;186:795–9. doi: 10.2214/AJR.04.1629. [DOI] [PubMed] [Google Scholar]
- 26.Adams MA, Hutton WC. The relevance of torsion to the mechanical derangement of the lumbar spine. Spine. 1981;6:241–8. doi: 10.1097/00007632-198105000-00006. [DOI] [PubMed] [Google Scholar]
- 27.Liu YK, Goel VK, Dejong A, et al. Torsional fatigue of the lumbar intervertebral joints. Spine. 1985;10:894–900. doi: 10.1097/00007632-198512000-00006. [DOI] [PubMed] [Google Scholar]
- 28.Drake JD, Aultman CD, McGill SM, et al. The influence of static axial torque in combined loading on intervertebral joint failure mechanics using a porcine model. Clin Biomech (Bristol, Avon) 2005;20:1038–45. doi: 10.1016/j.clinbiomech.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 29.Fujiwara A, Lim TH, An HS, et al. The effect of disc degeneration and facet joint osteoarthritis on the segmental flexibility of the lumbar spine. Spine. 2000;25:3036–44. doi: 10.1097/00007632-200012010-00011. [DOI] [PubMed] [Google Scholar]
- 30.Wilke HJ, Kavanagh S, Neller S, et al. Effect of a prosthetic disc nucleus on the mobility and disc height of the L4-5 intervertebral disc postnucleotomy. J Neurosurg. 2001;95:208–14. doi: 10.3171/spi.2001.95.2.0208. [DOI] [PubMed] [Google Scholar]
- 31.Haughton VM, Schmidt TA, Keele K, et al. Flexibility of lumbar spinal motion segments correlated to type of tears in the annulus fibrosus. J Neurosurg. 2000;92:81–6. doi: 10.3171/spi.2000.92.1.0081. [DOI] [PubMed] [Google Scholar]
- 32.Thompson RE, Pearcy MJ, Downing KJ, et al. Disc lesions and the mechanics of the intervertebral joint complex. Spine. 2000;25:3026–35. doi: 10.1097/00007632-200012010-00010. [DOI] [PubMed] [Google Scholar]
- 33.Thompson RE, Pearcy MJ, Barker TM. The mechanical effects of intervertebral disc lesions. Clin Biomech (Bristol, Avon) 2004;19:448–55. doi: 10.1016/j.clinbiomech.2004.01.012. [DOI] [PubMed] [Google Scholar]
- 34.Gardner-Morse MG, Stokes IA. Structural behavior of human lumbar spinal motion segments. J Biomech. 2004;37:205–12. doi: 10.1016/j.jbiomech.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 35.van Deursen DL, Snijders CJ, Kingma I, et al. In vitro torsion-induced stress distribution changes in porcine intervertebral discs. Spine. 2001;26:2582–6. doi: 10.1097/00007632-200112010-00011. [DOI] [PubMed] [Google Scholar]
- 36.Zimmerman MC, Vuono-Hawkins M, Parsons JR, et al. The mechanical properties of the canine lumbar disc and motion segment. Spine. 1992;17:213–20. doi: 10.1097/00007632-199202000-00016. [DOI] [PubMed] [Google Scholar]


