Estimating the Probability of de novo HD cases from Transmissions of Expanded Penetrant CAG Alleles in the Huntington Disease Gene from Male Carriers of High Normal Alleles (27–35 CAG)

Abstract

Huntington disease (HD) is a dominantly transmitted neurodegenerative disorder that arises from expansion of a CAG trinucleotide repeat on chromosome 4p16.3. CAG repeat allele lengths are defined as fully penetrant at ≥ 40, reduced penetrance at 36–39, high normal at 27–35, and normal at ≤ 26. Fathers, but not mothers, with high normal alleles are at risk of transmitting potentially penetrant HD alleles (≥ 36) to offspring. We estimated the conditional probability of an offspring inheriting an expanded penetrant allele given a father with a high normal allele by applying probability definitions and rules to estimates of HD incidence, paternal birth rate, frequency of de novo HD, and frequency of high normal alleles in the general population. The estimated probability that a male high normal allele carrier will have an offspring with an expanded penetrant allele ranges from 1/6241 to 1/951. These estimates may be useful in genetic counseling for male high normal allele carriers.

INTRODUCTION

Huntington disease (HD) is an autosomal dominant neurodegenerative disorder that arises from expansion of a CAG trinucleotide repeat on chromosome 4p16.3. CAG repeat alleles are defined as fully penetrant for repeats ≥ 40, reduced penetrance for repeats between 36–39, high normal for repeats between 27–35 and normal for repeats ≤ 26. We define the repeat range of 27–35 to be high normal because while a couple of studies have put forth suggestive cases of HD within this range there has never been a rigorously confirmed case of HD, hence the term ‘normal’, but there have been recorded transmissions of generational expansions into the penetrant range, hence the term ‘high’ [Andrich et al., 2008; Semaka et al., 2008; Kenney et al., 2007; Reynolds 2008]. Fathers, but not mothers, with high normal alleles, sometimes referred to as “intermediate alleles” or “mutable normal alleles”, are at risk of transmitting an HD allele with reduced or full penetrance (≥ 36) to offspring [Potter et al., 2004; Semaka et al., 2006]. Thus, the father is at risk of having an offspring who eventually develops HD even though the father himself will not develop the disease.

While several studies suggest that male carriers of high normal alleles have a low probability of transmitting an expanded HD allele in the penetrant range, few studies have attempted to estimate this probability [Duyao et al., 1993; Goldberg et al., 1995; Kremer et al., 1995; Maat-Kievit et al., 2001; Potter et al., 2004; Semaka et al., 2006]. Those studies that have attempted to estimate de novo transmission did not have large enough samples to detect expansion events or used currently outdated definitions of the high normal allele range [Brocklebank et al., 2008; Kokmen et al., 1994; Kremer et al., 1994; Semaka et al., 2006]. In this paper, we estimate the probability of a father who carries a high normal allele transmitting an expanded penetrant HD allele to his offspring using the current American College of Medical Genetics defined ranges of CAG repeat length for HD alleles [Potter et al., 2004]. We find that the probability of high normal allele male carriers transmitting an expanded penetrant HD allele has an approximate lower estimate of 1/6241 and an approximate upper estimate of 1/951. These probability estimates may aid genetic counselors in interpreting the risks associated with high normal allele test results and aid high normal allele carriers with family planning.

METHODS

Model/Assumptions

The probability of a maternal transmission of an expanded penetrant allele from a high normal allele is considered to be extremely small. Although it has not been proven impossible, there is as yet no recorded maternal transmission of a high normal allele expanded to a penetrant allele [Goldberg et al., 1993; Kremer et al., 1995; Semaka et al., 2006]. Thus, we will assume that the probability that a parent with a high normal HD allele has an offspring who develops HD is equivalent to the probability that a father with a high normal allele has an offspring who develops HD.

The following mathematical formulas to determine the probability of fathers transmitting an expanded penetrant HD allele can be invoked using the assumptions that (1) all de novo cases of HD arise from generational expansion of high normal alleles, (2) de novo mutations only arise from paternal transmission, and (3) possession of a high normal allele does not affect a father’s birth rate. Note that the following estimates always refer to a male high normal allele carrier who is having an offspring rather than the more general class of male high normal allele carriers.

$$\begin{array}{c}P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{male with a high normal allele has an offspring}})\\ \stackrel{I}{\iff }\frac{P(\mathit{\text{offspring is a de novo HD case}}\cap \mathit{\text{male with a high normal allele has an offspring}})}{P(\mathit{\text{male with a high normal allele has an offspring}})}\\ \stackrel{\mathit{\text{II}}}{\iff }\frac{P(\mathit{\text{offspring is a de novo HD case}})}{P(\mathit{\text{male with a high normal allele has an offspring}})}\\ \stackrel{\mathit{\text{III}}}{\iff }\frac{P(\mathit{\text{offspring is a de novo HD case}}\cap \mathit{\text{offspring develops HD}})}{P(\mathit{\text{male with a high normal allele has an offspring}})}\\ \stackrel{\mathit{\text{IV}}}{\iff }\frac{P(\mathit{\text{offspring develops HD}})·P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{offspring develops HD}})}{P(\mathit{\text{male with a high normal allele has an offspring}})}\\ \stackrel{V}{\iff }\frac{P(\mathit{\text{offspring develops HD}})·P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{offspring develops HD}})}{P(\mathit{\text{male has an offspring}})·P(\mathit{\text{male has a high normal allele}})}\\ \mathit{\text{KEY}}:"A|B"\mathit{\text{means}}"A\mathit{\text{given}}B";"A\cap B"\mathit{\text{means}}"A\mathit{\text{and}}B"\end{array}$$

1. Definition of conditional probability.

2. All de novo HD cases arise from men with high normal alleles. (Assumptions 1 & 2)

3. All de novo HD cases have HD.

4. Definition of conditional probability.

5. The probability that a male has a high normal allele is independent from the probability that a male has an offspring. (Assumption 3)

Thus, equation (1) defines the probability of a man with a high normal allele having an offspring who develops HD as a function of four estimable probabilities.

$$\begin{array}{c}P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{male with a high normal allele has an offspring}})\\ =\frac{P(\mathit{\text{offspring develops HD}})·P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{offspring develops HD}})}{P(\mathit{\text{male has an offspring}})·P(\mathit{\text{male has a high normal allele}})}\hfill \end{array}$$ (1)

For each of the four probabilities in equation (1), we attempted to choose estimates that would increase the final upper probability estimate. To be concise, we will here forth refer to choices of probability estimates that increase the final upper probability estimate as conservative. By choosing conservative estimates, our upper estimate of the probability that a man with a high normal allele will have an offspring who becomes a de novo HD case may be inflated and the actual estimate may be lower.

A detailed description of the mathematical properties behind each step of equation (1) is available in the supplementary material.

Probability that an Offspring Develops HD

In 2001, Almqvist et al. estimated the HD incidence rate for 1996–1999 in British Columbia to be 6.90 per million people per year [Almqvist et al., 2001]. We used this incidence rate in our calculations as it is the most current estimate of an HD incidence rate in North America. Prior HD incidence rates in North America were estimated before the repeat expansion mutation was identified and consequently also before the availability of genetic testing [Kokmen et al., 1994; Semaka et al., 2006]. Thus, the numbers of HD cases and consequently the incidence rate were both likely underestimated for the previous incidence rate estimates.

Almqvist et al. calculated the HD incidence rate by counting the number of newly diagnosed HD cases in British Columbia between the years of 1996–1999 and dividing by the population of British Columbia. Including the entire population of ages in the incidence rate calculation instead of that population within the ages most at risk to develop HD inflates the denominator and likely underestimates the probability that an offspring develops HD. Using the New England Huntington Disease Research Center Without Walls cohort (described later) we found that 90% of HD cases have an onset age of HD symptoms between 20–64 years. To avoid inflating the denominator and consequently underestimating the probability, we further standardized the incidence rate to the population of people within the age range of 20–64 years. We used this standardized incidence rate for our upper probability estimate and the original incidence rate calculated by Almqvist et al. for our lower probability estimate.

Probability that the Offspring is a de novo Case Given the Offspring has HD

The proportion of de novo cases in the HD population and the distribution of onset age for HD cases were both estimated using an HD sample gathered through the New England Huntington Disease Center Without Walls. The HD sample includes participants recruited from 1980 through the present. Participation in the study was voluntary and most participants were recruited through referral by neurologists who suspected HD or by family members aware that HD existed within their families. All participants signed a consent form approved by the Boston University IRB. Once consent was obtained, every effort was made to collect all available information on family members in both prior and succeeding generations. When the repeat expansion was identified in 1993, de novo cases were identified in the sample, which consisted at the time of mostly large families [Myers et al., 1993]. The resulting data set includes 461 families with HD and 11,950 family members with and without HD. In order to generalize to the North American population, we further limited the sample to North American families (N = 437).

In the early 2000s, a subsample of this dataset was used for a linkage study to identify genetic modifiers on the onset age of HD [Li et al., 2006]. The sample used to estimate the distribution of onset ages for HD cases uses the entire sample of the linkage study families as well as all other HD diagnosed individuals for whom blood samples were collected producing a total of 2074 cases. For more information on the ascertainment of HD cases and controls see the methods sections by Cupples et al.[1991] and Gagnon et al. [2003].

A subject was designated to be a de novo HD case by the following criteria: (1) the subject met diagnostic criteria for HD on a neurological evaluation or by autopsy, (2) neither parent had HD, HD symptoms, or any other neurologic disease and both parents lived to an advanced age, (3) no other ancestor in prior generations was known to have HD, HD symptoms or a similar disorder. When the second criterion could not be verified or at least one of the subject’s parents died young and the subject met all other criteria then the subject was designated to have uncertain family history of HD.

Inherited HD cases may be more easily ascertained from the population than de novo HD cases as the diagnosis of HD in a family may lead to the identification of additional HD cases in that family. This sampling bias may underestimate the frequency of de novo HD cases in a sample of HD cases and would subsequently underestimate the overall probability that a man with a high normal allele has an offspring who develops HD. To offset the sampling bias we calculated the number of de novo families instead of the number of de novo individuals. This estimate may also be slightly biased as it may overcorrect for the possible sampling bias and provide a higher and more conservative probability estimate.

Using this sample of HD families (N = 437), we calculated the proportion of confirmed de novo cases for the lower probability estimate as well as a more liberal estimate that includes confirmed de novo HD cases and possible de novo HD cases, defined as subjects with HD but with uncertain family history for the upper probability estimate. Further, we compared our estimates to those found by Almqvist et al. for the British Columbia population between the years of 1996–1999 (N = 141) [Almqvist et al., 2001].

Probability that a Male has an Offspring

An estimate of the probability that a male has an offspring was calculated by dividing the number of registered births in the United States by the population of males in the United States of child bearing age [Capt et al., 1940; Martin et al., 2006]. Since 90% of HD cases have ages of onset between 20–64 years, the majority of the births for the corresponding incidence rate occurred at least 20 years earlier. Thus, we calculated the paternal birth rate using data from 1940, 1950, 1960, and 1970. We also limited the calculation to men aged 15–64 in order to focus on the population of men from which most births would actually arise. Including men out of the normal reproductive range would under represent the probability that a male has an offspring and would thus dramatically over-estimate the final probability.

Probability that a Male has a High Normal Allele

The prevalence of the high normal allele in the general population was estimated using a sample of primarily Parkinson disease (PD) cases Study participants were recruited by the GenePD study, an international multi-site study of the genetics of PD, using a proband recruitment strategy. Participants were diagnosed for PD using the United Kingdom Brain Bank criteria for PD affection. The sample consists of sibling pairs, families, and individuals. All participants signed a consent form approved by the BU IRB. For more information on the ascertainment of PD cases and controls see the methods section by Maher et al. [2002].

All PD cases ascertained through October 2003 (N = 713) were genotyped for their HD CAG repeat lengths. In order to be consistent with the generalization to the North American population, non-North-American subjects (from sites in Germany, Australia, UK, Italy, New Zealand, and Denmark) were omitted from the sample used to calculate the frequency of the high normal allele. North American subjects were gathered from more than twenty sites across the United States and two sites in Canada. It is worth noting that the difference between the frequency of high normal alleles in the non-North-American sample (N = 75) and the North-American sample (N = 638) was not statistically significant using a two-sample test of proportions (p = 0.6483).

SOLAR was used to calculate the maximum-likelihood estimate for the frequency of high normal alleles, accounting for family structure [Almasy and Blangero 1998]. Sex specific estimates were also calculated; the estimated frequency for North American men was slightly lower than for the full sample of North American men and women (0.0234 and 0.0267 respectively). Limiting the sample to North American men substantially reduces the sample size from 638 subjects to 343 subjects but the sample directly corresponds to our desired population. While using both men and women from North America to estimate the frequency of high normal allele does not correspond directly to our desired population, including women provides a greater sample size and thus a more stable estimate. Consequently, we used the frequency estimate from the sample of North American men for the upper probability estimate and the frequency estimate from the sample of North Americans including men and women for the lower probability estimate.

To generalize the frequency of high normal alleles in the PD sample to the general population we assume that the length of the HD allele is not associated with the etiology of Parkinson’s disease. Our past studies support this assumption; McNicoll et al., looked for an association between the HD allele and the onset of Parkinson disease and found no statistically significant association [McNicoll et al., 2008].

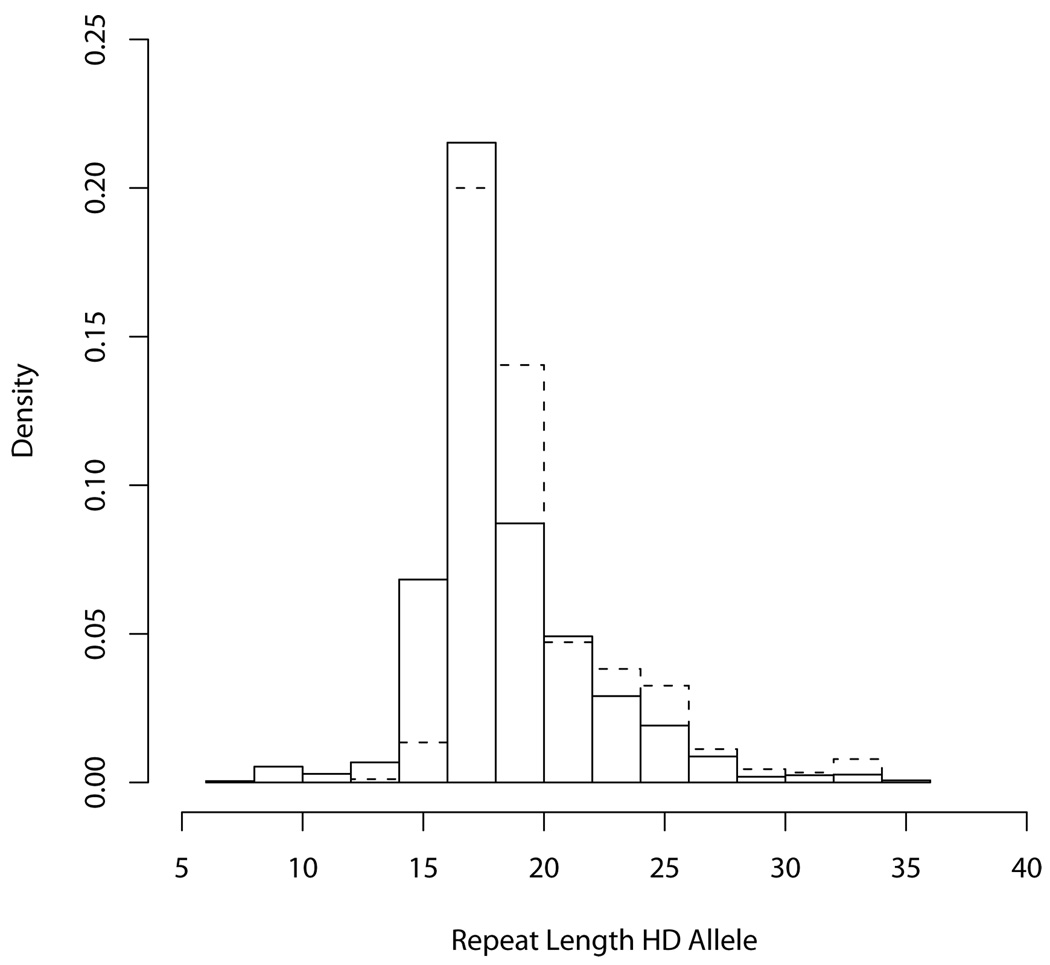
The distribution of HD allele lengths in the PD sample is very similar to the distribution of the non-penetrant length HD alleles in the HD sample that we used for the age of onset distributions, as seen in the histograms displayed in Figure 1. Note that the homozygote HD cases were removed from the HD sample before constructing the histogram in Figure 1. The similarity of the histograms further supports the assumption that the length of the HD allele is not associated with the etiology of PD.

Fig. 1. Histograms of HD Alleles.

HD non-penetrant length alleles in HD sample (solid line), HD alleles in PD sample (dashed line)

We tested whether the frequency of high normal alleles differed between the alleles in the PD sample and the non-penetrant length alleles in the HD sample. Because both samples consist of families and thus correlated observations, we compared the frequencies of high normal alleles using a naïve two-sample test of proportions assuming independence of individuals, and a more complex comparison taking into account correlation due to relatedness within families. In both comparisons, the proportion of high normal alleles is slightly higher in the HD sample than in the PD sample, but the difference is not significant (p=0.58 and p=0.41, respectively). We chose to use the slightly smaller estimate based on the PD sample. Since this estimate is used in the denominator of our risk formula, this choice is conservative in that it increases the final risk estimate.

In 1994, Kremer et al. typed 300 controls to produce a distribution of HD alleles in the unaffected population. He compared the unaffected distribution to the distribution formed from the non-penetrant length HD alleles of 995 symptomatic HD cases with expanded penetrant repeats [Kremer et al., 1994]. The range, mean, and median of each distribution are shown in Table I and are very similar to those found in our samples. The similarity of the measures in Kremer’s samples as well as our own provide further evidence that the PD sample is a good estimate for the prevalence of the high normal allele in the general population.

TABLE I.

Comparison of Distribution Measures in Our Samples and in Kremer et al.,’s Samples

		# of Alleles	Range	Mean	Median
Kremer et al (1994)	Both Alleles for Control Subjects	600	10–39	18.4	18
	Non-penetrant length Allele for HD Subjects	995	10–37	19.1	19
Our Estimates	Both Alleles for PD Sample	1276	14–34	20.0	19
	Non-penetrant length Allele for HD Subjects	2065	6–35	18.7	18

Variance Estimates

Bootstrapping was used to estimate the variance for the probability that an offspring is a de novo case given that the offspring has HD. Using the sampling distribution, two variance estimates for the natural log of the proportion were calculated: (1) for families classified as de novo and (2) for families classified as de novo or uncertain family history.

Standard error estimates were provided by SOLAR for the maximum likelihood estimate of the frequency of high normal alleles. The variance was then calculated and a first-order Taylor series expansion was used to calculate the variance of the natural log of the frequency of high normal alleles in the sample of North American men and the sample of North American men and women. A mathematical equation outlining the Taylor Series expansion is included in the supplementary material.

As previously mentioned, the probability that an offspring develops HD is estimated from an incidence rate of HD in the British Columbia population between 1996 and 1999. Since Almqvist et al. counted the number of newly diagnosed HD cases in the British Columbia population each year during the period 1996–1999, the incidence rate is taken as a population measure and thus has no variance. The probability that a male has an offspring was calculated using National Vital Statistics Reports and the US Census. This quantity is also considered a population measure that has no variance.

Using equation (2), variance estimates and then confidence intervals were calculated for the lower and upper probability estimates for the probability that an offspring is a de novo HD case given a male with a high normal allele has an offspring.

$$\begin{array}{c}\mathit{\text{Var}}[P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{male with a high normal allele has an offspring}})]\hfill \\ =\mathit{\text{Var}}\left[\frac{P(\mathit{\text{offspring develops HD}})·P(\mathit{\text{offspring is a de novo HD case}}|\mathit{\text{offspring develops HD}})}{P(\mathit{\text{male has an offspring}})·P(\mathit{\text{male has a high normal allele}})}\right]\hfill \\ \hfill =\mathit{\text{Var}}\left[\frac{A·B}{C·D}\right]={\left(\frac{A}{C}\right)}^2·\mathit{\text{Var}}\left[\frac{B}{D}\right]\approx {\left(\frac{A}{C}\right)}^2·\text{exp}\left\{\mathit{\text{Var}}\left[\text{ln}\right(\frac{B}{D}\left)\right]\right\}\hfill \\ \hfill ={\left(\frac{A}{C}\right)}^2·\text{exp}\{\mathit{\text{Var}}[\text{ln}(B)]-\mathit{\text{Var}}[\text{ln}(D)]\}\hfill \end{array}$$ [2]

      Where A = P(offspring develops HD)
            B = P(offspring is a de novo HD case | offspring develops HD)
            C = P(male has an offspring)
            D = P(male has a high normal allele)

Genotyping

The CAG repeat length was determined for each PD case and for each HD case at the Center for Human Genetic Research at the Massachusetts General Hospital. All genotyping was performed by the ABI 3730 DNA Analyzer (Applied Biosystems, Foster City, CA, http://www.appliedbiosystems.com). CAG repeat sizes were determined by polymerase chain reaction, using a previously reported primer pair that flanks the HD CAG repeat [Warner et al 1993].

RESULTS

The highest and lowest reasonable values for each of the four probabilities were estimated to generate the upper and lower estimates of the final probability.

Probability that an offspring develops HD

The incidence rate from Almqvist et al. is 0.0000069 when not standardized and 0.0000113 when standardized to the 20–64 age range.

Probability that the Offspring is a de novo Case given the Offspring has HD

In our sample, 22 of 437 families had confirmed de novo HD cases producing a proportion of 0.0503. A more liberal estimate that includes families with uncertain family history of HD produces a proportion of 0.1236 from 54 out of 437 families. For the British Columbia population between the years of 1996–1999 Almqvist et al., found the proportion of de novo HD cases to be 0.078 and the proportion of HD cases with no family history of HD, HD symptoms, or any other neurological disorder to be 0.135. These estimates are similar to the proportions found in our sample. We use our estimates for further calculations as our sample size was larger (437 families vs. 141 individuals). The proportions 0.0503 and 0.1236 were used in the lower and upper probability estimate calculations respectively.

Probability that a Male has an offspring

The birth rates for males aged 15–64 are 0.0568 in 1940, 0.0750 in 1950, 0.0810 in 1960, and 0.0613 in 1970. We used the birthrates from 1960 and 1940 for further calculations as each contained the highest and lowest birthrates respectively.

Probability that a Male has a High Normal Allele

The SOLAR maximum likelihood estimates for the frequency of high normal alleles are 0.0267 for North American subjects and 0.0234 for North American males. These values were used in the lower and upper probability estimates respectively.

Probability Estimates

The calculations using equation (1) and the values displayed in Table II produce an upper estimate of 1/951 and a lower estimate of 1/6241. This suggests that the highest probability that a male with a high normal repeat has an offspring who develops HD is 1 out of 951.

TABLE II.

Probability Estimates

	Low (Variance)		High (Variance)
P(offspring develops HD)	age range: ALL	0.00000690	age range: 20–64	0.0000113
P(offspring is a de novo HD case| offspring has HD)	# de novo Families	0.0503 (0.0001)	# de novo or uncertain family history Families	0.1236 (0.0002)
P(male has a offspring)	1960	0.08100	1940	0.05685
P (male with a high normal allele)	North Americans	0.0267 (0.0260)	North American Males	0.0234 (0.0228)
Estimate (Variance)	0.000160.(0791·10−9 )		0.001052 (3.8660·10−8 )
95% CI	(0*, 0.000325)		(0.000667, 0.001437)
Prop of Births (95% CI)	1/6241 (0*, 1/3078)		1/951 (1/1500, 1/696)

^*We truncated the confidence interval at a lower bound of zero since a negative proportion is not possible.

DISCUSSION

It should be noted that the CAG repeat cutoffs used for the terms fully penetrant, reduced penetrant, high normal, and normal are defined by observed cases rather than biological boundaries. Many studies have shown that age of onset of HD is inversely associated with CAG repeat length [Duyao et al., 1993]. Thus, as the average human lifespan increases the cutoffs used for high normal may change. A similar method to the one outlined in this paper could then be used to calculate the probability estimate for the new range.

De novo HD cases may also arise from parents with low penetrant alleles who never developed the disease. Thus, the first assumption used to produce equation (1) may be violated since some de novo cases in our sample may have arisen from the transmission of reduced penetrance alleles or may actually be a consequence of unrecognized non-paternity. However, these possible violations would lead to an increase in our final probability and thus our probability estimates are conservative.

Using the estimates and equation (1), we calculate the probability that a male with a high normal allele transmits an expanded penetrant HD allele to his offspring to be between 1/6241 and 1/951. The large width of the interval arises from the wide range and variation of the estimates used to calculate the probability. The lower and upper estimates indicate that the event may be as low as 1/6241 or as high as 1/951.

In order to find an estimate with a smaller error, a study could gather a large sample of men with high normal alleles who have children and calculate the proportion of these men who have children who develop HD. This strategy is straight-forward but is unfortunately very costly and resource prohibitive. As previously discussed, the proportion of males who have a high normal allele is less than 3%. Using our maximum probability estimate of 1/951 we see that over 30,000 men would need to be gathered to find one man with a high normal allele who has transmitted an expanded penetrant allele to his offspring.

The upper probability estimate that a male with a high normal allele transmits an expanded penetrant HD allele to his offspring should be used with care. Studies have shown that factors not considered here, such as family history, age, HD haplotype background, and high normal allele length affect the probability of mutations and these factors should be considered in genetic counseling [Chong et al., 1997; Goldberg et al., 1993; Semaka et al., 2006; Wheeler et 2007]. Specifically, the haplotypes of new mutation chromosomes often match the major HD haplotype that accounts for approximately 40% of HD cases, which suggests that high normal alleles of this haplotype may be more prone to expansion [Myers et al., 1993].

Even with our effort to provide a conservative estimate, our estimate for the maximum probability suggests that expansion events are rare. We believe that our upper probability estimate of 1/951 provides a baseline to assist genetic counselors and high normal allele carriers with family planning.