Anomalously large anisotropic magnetoresistance in a perovskite manganite

Abstract

The signature of correlated electron materials (CEMs) is the coupling between spin, charge, orbital and lattice resulting in exotic functionality. This complexity is directly responsible for their tunability. We demonstrate here that the broken symmetry, through cubic to orthorhombic distortion in the lattice structure in a prototype manganite single crystal, La_0.69Ca_0.31MnO₃, leads to an anisotropic magneto-elastic response to an external field, and consequently to remarkable magneto-transport behavior. An anomalous anisotropic magnetoresistance (AMR) effect occurs close to the metal-insulator transition (MIT) in the system, showing a direct correlation with the anisotropic field-tuned MIT in the system and can be understood by means of a simple phenomenological model. A small crystalline anisotropy stimulates a “colossal” AMR near the MIT phase boundary of the system, thus revealing the intimate interplay between magneto- and electronic-crystalline couplings.

The striking transport properties of many CEMs, such as unconventional superconductivity and “colossal” magnetoresistance (CMR), are believed to be manifested by a coexistence of a variety of complex interactions that couple simultaneously active degrees of freedom (1). Consequently, such complex couplings lead to multifunctionalities displayed by these materials. The hallmark of these materials is the multitude of competing ground states that can be tuned or manipulated by doping, structural manipulations, strain induction, or the application of external stimulus, such as pressure, electric or magnetic fields. In doped manganites Ln_1-xA_xMnO₃ where Ln and A are rare- and alkaline-earth cations, respectively, ferromagnetic (FM) metallic, paramagnetic (PM) insulating and antiferromagnetic (AF) charge/orbital ordered states are among these competing ground states (2). External fields influence the subtle balance of the interactions and induce phase transitions between different ground states (3–5). Examples include the CMR and giant anisotropic magnetoresistance (AMR) effects in which the transport has “colossal” response to an external field, thus offering intriguing opportunities for new technological applications with advanced correlated electron devices (6).

Magnetoresistance (MR) is a property of materials in which the resistivity depends on the strength of applied magnetic field. Anisotropic magnetoresistance (7), on the other hand, is when the resistivity also depends on the field orientation with respect to either the electrical current or the crystal axes. Whereas the dependence of resistivity on the field direction relative to the electrical current, known as ordinary MR or Lorentzian MR, is expected due to the Lorentz force acting on the conduction electrons; the dependence of resistivity on the field orientation with respect to the crystal axes is much more unusual. However, this kind of AMR provides detailed information about the underlying physics such as spin-orbital and magneto-elastic couplings in a material and it also enables wide range of technological applications. The most prominent technological application of giant MR is in the data storage industry. Yet, the advantage of AMR over conventional MR is that AMR can be applied for sensor of field direction and dimensional imaging.

AMR effects are small in most of FM metals and alloys (8), typically with a magnitude of few percent. Recently, it was discovered that giant and unusual AMR effects with a magnitude of >30% exist in several perovskite manganite thin films (9–14). Particularly, the observed AMR exhibits strong and nonmonotonic temperature (T) (11–14) and field (H) dependence (9, 14). This kind of behavior differs dramatically from what has been observed in conventional 3d transition metals or alloys, suggesting a different mechanism beyond conventional theories of AMR. For example, the AMR amplitude in La_0.7Ca_0.3MnO₃ films (10, 11, 13) and in the strained Pr_0.67Sr_0.33MnO₃ films (12) shows a giant enhancement near the Curie temperature or metal-insulator transition (MIT) temperature (T_MI), whereas conventional AMR in 3d transition metals or alloys depends monotonically on temperature. Furthermore, the sign of the AMR can be tuned from negative to positive by inducing lattice strain to the films through the lattice mismatch between the films and substrate, indicating a strong influence of lattice distortion (12). Most studies of the AMR have focused on thin films. Many extrinsic effects, including the substrate-induced strain and the large demagnetization field due to the large apical ratio in film geometry, have impeded thorough investigations of the inherent nature of AMR in this class of CEMs. In particular, it is unclear whether the observed giant AMR effect is truly intrinsic due to magneto-elastic or spin-orbital couplings. If indeed this is the case, then how does one understand the unusual temperature and field dependence of observed AMR? Why does the AMR always have its maximum value near T_MI? Here, we have taken a different approach by systematically investigating the single crystals of La_1-xCa_xMnO₃ (x ∼ 0.31). Our results on magneto transport clearly show that the observed anomalous AMR has an intimate relationship with the crystalline anisotropy in the system. We provide a phenomenological model to explain the observed phenomena, which should be also applicable to other CEMs with strong magneto-elastic coupling.

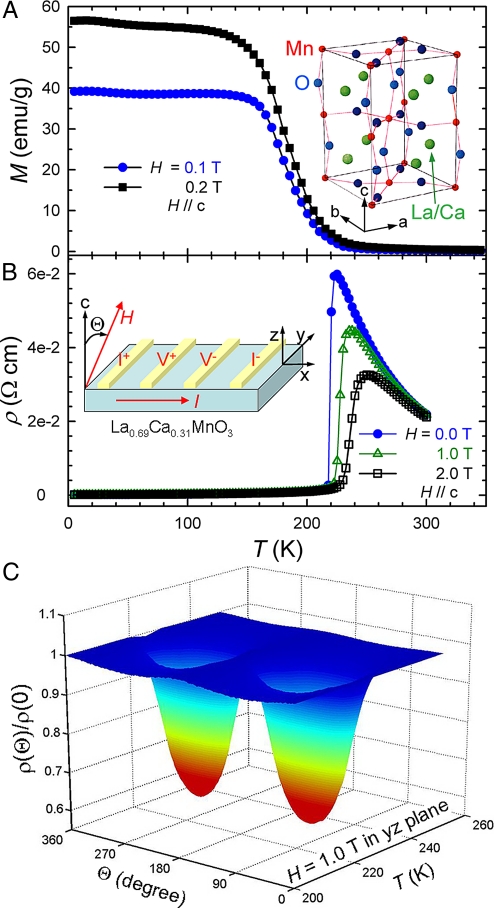
La_1-xCa_xMnO₃ (x ∼ 0.31) single crystals are orthorhombic, deviating from the cubic perovskite structure via two dissimilar Jahn-Teller (J–T) distortions—in-plane (i.e., in ab-plane) rotation and out-of-plane (c-axis) tilt of the MnO₆ octahedron (15, 16). A MIT coincides with a FM-to-PM transition at T_MI ≅ 220 K, characterized by the T-dependence of magnetization M(T) and the resistivity ρ(T) shown in Fig. 1 A and B, respectively. The measured ρ(T) vs. H curve demonstrates a typical negative magnetoresistance behavior. However, the observed MR shows a strong dependence on the field orientation, leading to a remarkable AMR effect.

Fig. 1.

Magnetic and magneto-transport properties of La_0.69Ca_0.31MnO₃. (A) T-dependence of the magnetization with an Inset showing the unit cell structure as well as the crystalline axes. (B) T-dependence of the resistivity measured from a slab of a single crystal under different fields. The Inset shows a schematic arrangement of the measurements from the crystal with a slab sample size: 3.8 × 0.85 × 0.15 mm³. The sample c-axis is normal to the slab plane. (C) Angle- and T-dependences of the normalized resistivity, ρ(Θ)/ρ(Θ) = 0°, measured under a magnetic field rotating about the x-direction (i.e., the current (I) direction).

We used a single crystal of a slab shape (shown in the Inset of Fig. 1B) where the c-axis is perpendicular to the slab plane (xy plane). Fig. 1C shows ρ(T,Θ) under a H = 1.0 T field rotating in the yz plane with angle Θ between the field and c-axis, which demonstrates a strong T-dependence of the AMR effect with the peak value achieved very close to T_MI. The AMR amplitude is defined as R_ρ ≡ (1 − ρ_⊥/ρ_//) × 100%, where ρ_{// ≡} ρ(Θ = 0) and ρ_{⊥ ≡} ρ(Θ = 90°) are the resistivities for a given field being parallel and perpendicular to the c-axis of the crystal, respectively. For H = 1.0 T, a peak value of R_ρ ∼ 40% is observed near T_MI. In this case, the measurement contains no contribution of the conventional Lorentzian MR because the field rotates in the plane perpendicular to the current direction. This anomalous T-dependent AMR must be related to the magneto-crystalline anisotropy and closely associated with the coupled MIT and FM-to-PM transition in the crystal.

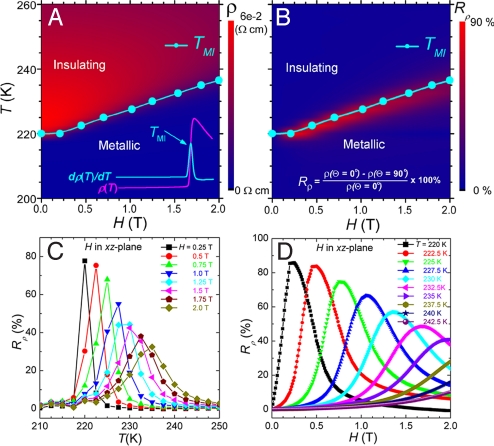
We systematically investigated the temperature- and field-dependence of AMR and their correlation with the field-dependent MIT. The results are shown in Fig. 2. T_MI increases almost linearly with field (see Fig. 2A). A key discovery here is that the measured R_ρ peak follows almost exactly the field-dependence of T_MI, as shown in Fig. 2B. Large AMR emerges only near T_MI (Fig. 2C), whereas no prominent AMR appears in either the pure FM-metallic state at T ≤ T_MI or the pure PM-insulating state at T ≥ T_MI. Likewise, the nonmonotonic field-dependence of R_ρ at a given T close to T_MI is evident in Fig. 2D, such that R_ρ(H and T) exhibits very similar line shapes for varying field or temperature.

Fig. 2.

Correlation between MIT and AMR of La_0.69Ca_0.31MnO₃. (A) T- and H- (along c-axis) dependence of the resistivity (ρ) and T_MI defined as the peak temperature in dρ/dT − T curve (see the Inset). (B) A contour plot and line plots of (C) the T- and (D) H-dependence of the measured R_ρ from the slab single crystal as the field was applied in the xz plane (thus including Lorentzian MR). The solid lines through the data points are guides to the eye.

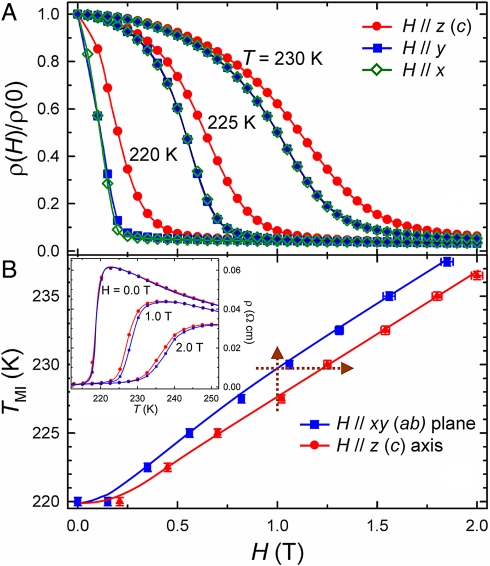
Fig. 3 presents the measured field-dependence of both the normalized resistivity and T_MI for the field along three different sample orientations. The measured ρ(H) has similar values for the H//x and H//y directions but quite different values for the H//z direction (see Fig. 3A). A small difference in ρ(H) between the H//x and H//y directions can mainly be attributed to the Lorentzian MR, whereas the large difference between the H//z and H//x(y) directions gives rise to the observed giant AMR. Also shown in the Inset of Fig. 3B, a small but clear shift of ρ(T) is evident by orienting H//z- from H//x(y)-direction, thus indicating an anisotropic field-dependent MIT. As presented in Fig. 3B, the T_MI(H) curve for the H//z direction deviates from that for the H//x(y) direction. The crystalline c-axis (i.e., the z direction), which is perpendicular to the sample plane, is the hard axis for the field-dependent MIT. We conclude that the observed large AMR simply reflects the uniaxial magneto-crystalline anisotropy in the system.

Fig. 3.

Field-orientation dependence of magnetoresistance and MIT in La_0.69Ca_0.31MnO₃. (A) Field strength and orientation dependence of resistivity normalized to its zero-field value at the temperatures near T_MI and (B) T_MI measured from the slab single crystal (see the Inset of Fig. 1B). The Inset presents the T-dependence of resistivity on warming under different values of magnetic field along z(c)-axis (solid circle) and in xy(ab)-plane. The solid lines are guides to the eye. The dashed arrows indicate the horizontal and vertical cuts for a fixed temperature and field, respectively.

The correlation between AMR and MIT displayed in Fig. 2 and Fig. 3, especially the gap of the two T_MI(H) curves shown in Fig. 3B, provide a crucial key for understanding the anisotropic magneto-transport properties. The difference in T_MI due to field orientations (H//c- or H⊥c-axis) leads to the observed unusual AMR effect. At a given field strength (vertical cut and between the two T_MI curves in Fig. 3B), the sample becomes insulating when H//c-axis while remaining metallic when H⊥c-axis—creating the R_ρ peak as shown in Fig. 2C. On the other hand, at a given T (horizontal cut in Fig. 3B), the sample becomes metallic as H⊥c-axis but remains insulating as H//c-axis, thus resulting in the R_ρ peak as shown in Fig. 2D. When the system is far away from the gap region of the two T_MI(H) curves, only conventional AMR with small amplitude should exist. Furthermore, increasing the field gradually reduces the R_ρ (see Fig. 2D). Thus, one can anticipate that the AMR effect as well as the anisotropy of field-dependent MIT (the gap in Fig. 3B) should vanish under a sufficiently strong field.

Jahn-Teller distortions (17) and double-exchange (DE) interactions (18, 19), which are intimately coupled in this class of doped oxides, play vital roles in both the transport and the magnetic properties. Simply speaking, Jahn–Teller (J-T) distortions tend to promote insulating phase to the system whereas DE interaction endorses FM metallic state, although the strength of DE interaction depends on the degrees of J-T distortions thus making a close coupling between them. Bending the Mn-O-Mn bond by enhancing J-T distortion reduces DE interaction so as bandwidth. The subtle competition between them causes the MIT in these doped manganites. However, external field tends to disturb such a competition by facilitating the metallic state, evident by appearing negative CMR near the T_MI and tuning the MIT (16, 20–22). Owning to the strong correlation character in these materials, lattice also has its response to applied magnetic field by alter J-T distortions, depending on the detailed lattice structure and applied field orientation. One possible lattice response is a suppression of J-T distortions by straightening the Mn-O-Mn bond thus causes negative CMR by enhancing DE interactions. Indeed, the giant AMR observed in La_1-xCa_xMnO₃ reflects exactly the different lattice response to the external field, depending on the field direction.

If, in a cubic peroviskite structure, lattice should have identical response to external field in all high-symmetry crystalline directions, thus no AMR is generated by magneto-elastic coupling. However, in orthorhombic La_1-xCa_xMnO₃, the structure has lower symmetry by bearing two distinct J-T distortions from a cubic perovskite. The lattice has larger response when the field is perpendicular to c-axis than parallel to c-axis, thus creating distinct effects on the transport properties including MIT through different couplings with the DE interaction. This different response exactly makes c-axis as the hard axis for the field-dependent MIT, having a small but crucial anisotropy as clearly shown in the two field-dependent T_MI curves (see Fig. 3B). Consequently, the system exhibits a giant AMR effect near the MIT region that is stimulated by the distinct lattice response to external field because of the asymmetric J-T distortions.

Based upon the above scenario for the nature of intrinsic AMR, we are able to qualitatively explain the dissimilar magnitude of AMR effects observed in different manganite systems (9–14). Because the AMR effect depends on the dissimilar response of J-T lattice distortions to external field, a system with stronger J-T distortions should have greater AMR effect. This mechanism explains that, in a similar doping level of x ∼ 0.3, La_1-xSr_xMnO₃ (14) has a smaller AMR effect than Pr_1-xSr_xMnO₃ (12) and La_1-xCa_xMnO₃ (9–11, 13) simply because of fewer J-T distortions.

Because the intrinsic AMR discussed above is closely related to crystalline orientation, twinning in a single crystal could dramatically affect the characterization of AMR properties. Imagine that a single crystal is randomly and completely twinned, then, the intrinsic AMR related to crystalline anisotropy would be averaged out. In such a case, a possible AMR would only be the result of the demagnetization field effects because of the geometric shape of the slab sample. However, we believe that this is not the case. First, demagnetization field effects cannot generate such large amplitude of AMR. More importantly, any demagnetization effect cannot result in the unusual field- and temperature-dependence of AMR as observed in the system.

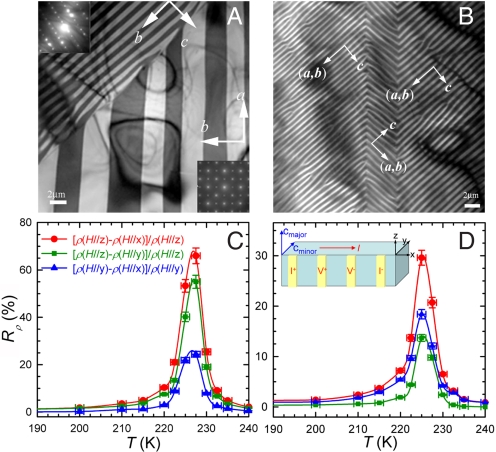
To further explore the issue arising from the twinning and demagnetization field effect, we have investigated the possible twinning domain structure in the system. Fig. 4 A and B presents two Lorentzian TEM images with selected-area electron diffraction patterns of the corresponding domain areas. The images reveal magnetic domain structure, thus reflecting crystalline twinning domain structure (23). Two distinct twinning cases are revealed. The twinning between the a- and b-axis, or in-plane twinning, is found via a 45° (or 135°) rotation of each other (Fig. 4A); whereas the twinning between the a- (or b-) and c-axis, or out-of-plane twinning, is found through a 90° rotation of each other (Fig. 4B). It is expected that in-plane twinning is more common than out-of-plane twinning in orthorhombic crystals. Both the small MR difference between the H//x and H//y directions (Fig. 3A) and relatively small R_ρ as the field rotates in the xy plane (Fig. 4C) indicate that the twinning existing in the slab sample is mainly the in-plane type.

Fig. 4.

Crystal twinning behavior of La_0.69Ca_0.31MnO₃. Lorentzian TEM images with the selected-area electron diffraction patterns of corresponding areas at T = 80 K with different crystalline orientations. (A) The 45° crystal twinning between a- and b-axis. (B) The 90° crystal twinning in the c-axis. The T dependence of the anisotropic R_ρ at H = 1.0 T measured from (C) the slab and (D) a square-rod La_0.69Ca_0.31MnO₃ single crystal. The Inset shows a schematic arrangement of the measurements from the square-rod sample size: 7.0 × 0.85 × 0.85 mm³. The c-axis is in the plane perpendicular to the current direction.

To corroborate this uniaxial anisotropy scenario, we have repeated the AMR measurements on a square-rod sample that, because of the increased size of the sample in the z direction, is anticipated to display more out-of-plane twinning and smaller demagnetization field than the slab sample. The results are shown in Fig. 4D. Compared with the results obtained from the slab sample, the R_ρ values, as the field rotates in the xz (red curve) and yz plane (green curve), are substantially suppressed in the square-rod sample. Furthermore, the order in the magnitude of R_ρ curves (green and blue) between the field rotating in the yz and xy planes is also switched. These results are exactly as expected because of the substantial out-of-plane twinning existing in the square-rod sample—portions of the crystal domain have their hard-axis (c-axis) oriented in the y direction (or x direction). Such a mixture of hard-axis orientation should suppress the intrinsic uniaxial anisotropy. Because there is a component of hard axis in the y direction, the R_ρ in the xy plane is enhanced, whereas that in the yz plane is reduced, resulting in the order switch of R_ρ curves.

The observed results can be quantitatively explained by a phenomenological model with a uniaxial AMR caused by the crystalline anisotropy. We start with the description of the model and then explain the data from both slab and square-rod samples. Assuming the resistivities for a given field parallel and perpendicular to the c-axis of the crystal are ρ_// and ρ_⊥, respectively, a uniaxial resistivity ellipsoid (a prolate if ρ_// ≥ ρ_⊥) can be constructed through the equation

as is shown in Fig. 5A, where the short-to-long axial ratio representing the uniaxial resistivity ratio is α ≡ ρ_⊥/ρ_//. The normalized resistivity ρ(Θ)/ρ_// can be expressed as

AMR is completely determined by the ratio α. If the anisotropy is relatively weak, i.e., α ≈ 1, the normalized resistivity can be approximately expressed as

that is described as a symmetric sinusoidal function of the angle Θ.

Fig. 5.

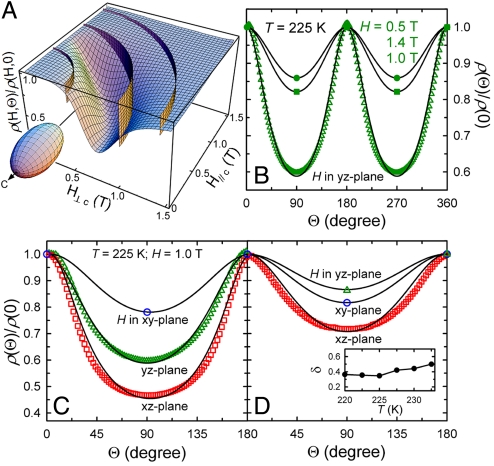
Phenomenological uniaxial anisotropy model for the AMR of La_0.69Ca_0.31MnO₃. (A) Calculated normalized resistivity at a given temperature as a function of magnetic field strength and orientation with respect to the crystal c-axis (Θ), based upon the uniaxial anisotropic model (see the Inset for the uniaxial resistivity ellipsoid). (B) Calculated (solid lines) Θ-dependence of normalized resistivity for three values of fields (corresponding to the three sheets in A) rotating in the yz plane, compared with the experimental results (symbols) measured from the slab sample at T = 225 K. (C and D) Calculated angle dependence of normalized resistivity for a field of H = 1.0 T rotating in three perpendicular planes (from y to x, z to y, and z to x direction), compared with the experimental results (symbols) measured at T = 225 K from the slab (see Fig. 1) and square-rod (see Fig. 4.) sample, respectively.

In conventional materials, uniaxial AMR is relatively small (R_ρ < 10%), weakly dependent on field and temperature, and can be described well with Eq. 3. However, as shown in Fig. 2 C and D, the R_ρ in La_1-xCa_xMnO₃ shows very strong T- and H-dependence, i.e., α = α(T,H). Furthermore, as shown in Fig. 5B, the ρ(Θ)/ρ (0) curve deviates greatly from the symmetric sinusoidal function depicted by Eq. 3. Thus, we used Eq. 2 to reproduce the measured data. For T close to T_MI, a normalized ρ(H,Θ)/ρ(H,Θ = 0) or ρ(H_// ,H_⊥)/ρ(H,Θ = 0) is calculated and shown in Fig. 5A as a curved 3D MR sheet, where H_// = HcosΘ and H_⊥ = HsinΘ, respectively. The only fitting parameter here is α(H) at a given T.* For a given H, the cross section between the MR sheet and a particular vertical H sheet reveals a normalized ρ(Θ)/ρ(0). Fig. 5B presents the calculated and measured ρ(Θ)/ρ(0) from the slab sample for the three H values at T = 225 K and as H rotates in the yz plane. We obtain α = 0.598 for H = 1.0 T and T = 225 K.

As shown in Fig. 5B and Fig. 1C, the line shape of ρ(Θ)/ρ(0) clearly shows a peak-to-valley asymmetry with a larger valley width, in contrast with the symmetric line shape given by Eq. 3. The excellent agreement between theoretical and experimental results in Fig. 5B along with an evidently large asymmetric line shape provides the justification for Eq. 2. It is noteworthy that films of Pr_2/3Sr_1/3MnO₃ with large AMR also exhibit similar asymmetry ρ(Θ)/ρ(0) shape (12).

The phenomenological model can reproduce all of the experimental AMR data for field rotation in different sample planes for both slab and square-rod samples. Fig. 5C shows both theoretical and experimental results with excellent agreement for the slab sample. For the square-rod sample (see Fig. 4D), the measured R_ρ is much smaller than that of the slab sample, mainly because of the substantial c-axis mixture in the yz plane (see Inset in Fig. 4D). Therefore, we propose a two-component model (see Methods). Each component satisfies Eq. 2 and has the same α value as the slab sample. The only additional parameter introduced here is the twinning portion parameter (δ): the amount of the minor c-axis component (δ ≤ 0.5). This single parameter δ is fitted with the ρ(Θ)/ρ(0) data from the square-rod sample, and the results are shown in Fig. 5D. The agreement between the theoretical results and experimental data are very impressive, considering that we neglect other contributions such as the Lorentzian MR. As shown in the Inset of Fig. 5D, a quite reasonable value of δ ∼ 0.40 is obtained, and it remains reasonably constant at different temperatures, further confirming the validity of the model.

Methods

Experimental.

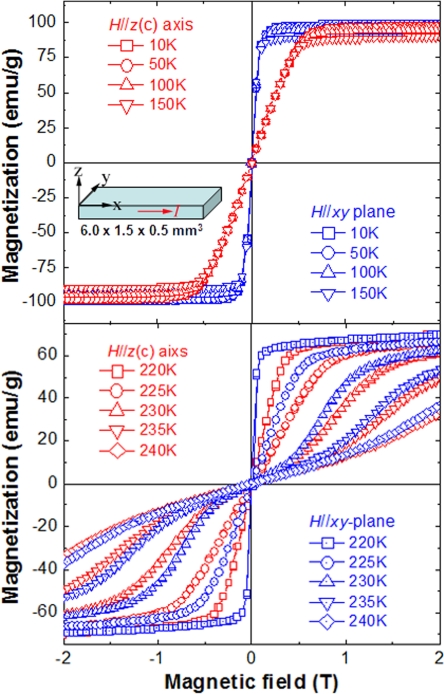
La_0.69Ca_0.31MnO₃ single crystals were grown using the traveling solvent optical floating zone technique. Samples of both the slab and square-rod shapes for the measurements were cut from the same single-crystal rod such that the x direction was almost along the crystal rod growing direction. There is a slightly offset in the doping concentration such that the measure T_MI ∼ 220 K is lower than the published value of T_MI ∼ 250 K. The crystal orientation of the samples was carefully examined by X-ray diffraction. The T-dependence of the magnetization was measured by a superconducting quantum interference device magnetometer (SQUID, Quantum Design). The MR measurements were carried out using a Physical Property Measuring System (PPMS, Quantum Design) equipped with a motorized sample rotator. The standard four-probe method was used for the resistivity measurements. The angular dependence of the resistivity ρ(Θ) was measured at a fixed magnetic field and temperature by varying the sample orientation relative to the field. To avoid Joule heating effects, a measuring electrical current was used below 100 μA in all of the electrical measurements. To ensure that the observed AMR is not just simply caused by a magnetization anisotropy, we have measured the magnetization as a function of magnetic field for the two distinct field directions, H//z(c)- and H⊥z(c)-axis, respectively. The result is shown in Fig. 6 for the measured magnetization curves at different temperatures. The magnetization anisotropy with hard magnetic axis in c-axis direction exists in the low field case; the saturation field is only ∼0.5 T in the FM phase. Therefore, the existence of magnetization anisotropy does not affect our argument for the cause of the observed anomalous AMR.

Fig. 6.

The magnetization of La_0.69Ca_0.31MnO₃ as a function of magnetic field for the two distinct field directions measured at different temperature, H//z(c)- and H⊥z(c)-axis, respectively.

The magnetic domain structures were imaged by means of Lorentzian transmission electron microscopy (TEM) (Hitachi HF-3000L) equipped with a cold-field emission gun and operated at an acceleration voltage of 300 kV. The microscope was equipped with a custom-made objective lens, making the magnetic field almost zero at the sample position. Electron-transparent thin samples were sliced from the same crystal for the AMR measurements and prepared by mechanical polishing and subsequent argon-ion thinning with an acceleration voltage of 4 kV at room temperature. In Lorentzian TEM observations, we used the Foucault mode (Fig. 4 A and B). In this mode, the incident beam is split by Lorentzian forces with different directions at the diffraction plane. In the case of the 180° magnetic domains, antiparallel magnetic domains produce two spots at the diffraction plane. When only one of the spots is selected by the objective aperture to form an in-focused image, the image with white/black band-shape areas is observed in the in-focused plane. These white/black areas correspond to antiparallel magnetic domains, and domain walls are imaged as a boundary between the white and black areas.

Two-Component Model.

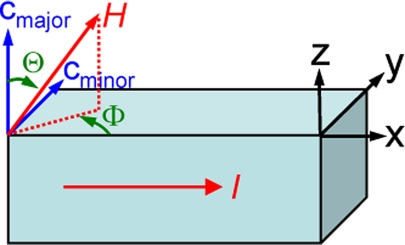
To include the effect of twinning existing in the square-rod sample, we realized that the sample has a mixture of twinning domains with their c-axis perpendicular to each other (see Fig. 7) and, as a result, is no longer uniaxial. We considered a simple two-component scenario—one has the c-axis along the y direction with a twinning portion δ (minor component), whereas the other is along the z direction with a twinning portion (1 − δ) (major component), and each component has the same prolate ellipsoid dependency as we used for the slab sample. The resistivity-field relation for the minor component, with its c-axis in the y direction, is then given by a prolate in the y direction:

When mixed with the major component (Equation (1)), while preserving the ellipsoid shape, we got the superposition of two perpendicular prolate ellipsoids:

where

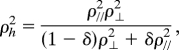and

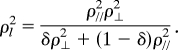ρ_h and ρ_l are the resistivities as the H field is along the major and minor component's c-axis, respectively, whereas ρ_⊥ is the resistivity when the H field is perpendicular to both the major and minor c-axis (or yz plane). This two-component model can account for the loss of uniaxial property in the square-rod sample. In addition, we can obtain the parameter δ, the portion of the minor component, by fitting the results from AMR measurements to the proposed two-component model. The result is shown in the Inset of Fig. 5D. The value found is ∼0.4 for the temperature range around the maximum AMR signals, which shows that this two-component model can adequately account for the experimental results of the square-rod sample.

Fig. 7.

Schematic view of the relative orientation relation between magnetic field (H), measured current (I), and crystal axis of square-rod sample existing two c-axis components due to twinning domains.