Abstract
The explicit polarization (X-Pol) potential is an electronic-structure-based polarization force field, designed for molecular dynamics simulations and modeling of biopolymers. In this approach, molecular polarization and charge transfer effects are explicitly treated by a combined quantum mechanical and molecular mechanical (QM/MM) scheme, and the wave function of the entire system is variationally optimized by a double self-consistent field (DSCF) method. In the present article, we introduce a QM buffer zone for a smooth transition from a QM region to an MM region. Instead of using the Mulliken charge approximation for all QM/MM interactions, the Coulombic interactions between the adjacent fragments are determined directly by electronic structure theory. The present method is designed to accelerate the speed of convergence of the total energy and charge density of the system.
1. Introduction
The inclusion of many-body polarization and charge delocalization effects in molecular dynamics1 simulations has received considerable attention in the last two decades. Polarization effects result from the redistribution of electron density within a molecule, and this is best modeled by quantum-mechanical (QM) electronic structure theory. However, it is still expensive to use explicit QM methods for the entire system in molecular dynamics simulations of large systems such as a solvated protein. Consequently, approximations, often severe ones, are usually introduced, such as using molecular mechanics or analytic force fields to describe large parts of the system rather than performing explicit quantum mechanical electronic structure calculations for the entire system. Recently we proposed an electronic-structure-based polarizable potential, called the explicit polarization (X-Pol) method, to be used as a quantum mechanical force field for large molecules or condensed-phase molecular systems.2–6
The X-Pol potential is generated by a double self-consistent field (DSCF) method in which a system is divided into QM fragments whose intrafragment interactions are treated using electronic structure theory,2–6 while interactions between fragments are treated using the same terms as in a combined quantum mechanical and molecular mechanical (QM/MM) approach.7–10 Polarization effects are naturally included in the X-Pol potential by optimizing the wave function of each fragment in the presence of the instantaneous electric field from the rest of the system. The external field can be conveniently represented by partial atomic charges located on the nuclear sites,2–6 which are calculated by Mulliken population analysis11 of the wave functions of all the other fragments. Due to the mutual dependence of the fragment wave functions, the wave function of the entire system is optimized self-consistently. The DSCF is accomplished by successively performing QM/MM calculations to achieve self-consistency in the wave function for each fragment in the presence of the electric field of the other fragments, and the process is iterated for the entire system until the total electronic energy or electron density converges to a given tolerance.2–6 The first version of the X-Pol potential, which was designed for use in Monte Carlo simulations, adopted this method and yielded Mulliken charges that agreed within 0.02 a.u. with those obtained by performing full QM calculations.2–5 A similar calculation following this procedure was reported for the calculation of liquid water,12 and an iterative optimization of a substrate-protein complex has recently appeared.13 In another subsequent calculation called fragment molecular orbital (FMO),14,15 a similar approach was adopted by iteratively optimizing the individual inner fragmental wave functions.
In the first version of the X-Pol potential, in which the “inner” SCF for each fragment and the “outer” SCF for the entire system are converged sequentially, the total electronic energy is not variational. The energy deviation from the variationally minimized energy is very small, and it has a negligible effect on geometry optimization2 and Monte Carlo sampling,3,4 but the lack of variational character means that analytical gradients would have to be computed by solving the coupled-perturbed Hartree-Fock equations, and that is too time consuming for efficient molecular dynamics simulations. Recently, we developed a method for variational optimization of the total molecular wave function by including additional terms in the Fock matrix;6 this yields efficient and stable analytical gradients. The present and future work on the X-Pol potential is based on the variational DSCF algorithm.6
For a molecular system without covalent bonds between the fragments, a QM fragment can be defined as the combination of one or more molecules, e.g., a QM fragment can be defined as one or more water molecules in a system of liquid water.2,3,12 In contrast, the partition of a protein or other polymer into fragments must include a protocol for treating boundary atoms connecting adjacent QM fragments.16–21 In the X-Pol potential, a protein is divided into peptide units at each Cα carbon.5 (Of course, one can use larger fragments in which a certain number of adjacent peptide units are combined to form a QM fragment.) The connection between neighboring fragments is treated by using the generalized hybrid orbital (GHO)16 method, extended to treating two active orbitals and two auxiliary orbitals on each boundary atom.5 The effective potential due to auxiliary orbitals is described by using a 2×2 density matrix which is derived directly from the optimized density matrix corresponding to the auxiliary orbitals that are treated as active ones in the adjacent fragment.5,6 Consequently, the GHO atom provides a smooth transition at the QM/MM boundary. Nevertheless, QM/MM interactions from “MM atoms” that are directly bonded to the “QM fragment” are still present, particularly between the active orbitals and auxiliary orbitals on the same boundary atom and the MM atoms bonded to it. Although the SCF calculation converges rapidly in traditional QM/MM calculations where there is only one QM fragment in the entire system, there is an increased cost in achieving the overall DSCF convergence in the X-Pol potential where all residues are treated quantum mechanically and are connected by the GHO boundary atoms. In this paper, we present a way to improve the QM/MM convergence by introducing a buffer zone such that the interactions between bonded QM fragments are calculated using Coulomb repulsion integrals instead of Mulliken charges.
The approach of adding a buffer zone is a special case of multi-layer or multi-scale modeling,22,23 and similar approaches have been described in other applications and different contexts.24–29 The present method is an example of this strategy, with the added refinement that active and buffer regions are rotated throughout the system until full self-consistency is obtained. As as one strives for treating the active site of an enzyme with greater accuracy, there is potential interest in treating the active site by a high-level quantum mechanical model, buffered by a less expensive QM theory before a transition into a pure MM representation.
In section 2, we review the theoretical background. In section 3 we present the analytical gradient equation for the case where a buffer region is present. In section 4, we examine the validity and effectiveness of including an intermediate layer in the X-Pol potential and we test this approach for small model compounds and a polypeptide. Section 5 contains concluding remarks.
2. Theoretical Background
We highlight the key principles of the X-Pol potential; refs 2–6 contain additional theoretical details. In X-Pol potential, a protein is partitioned into N fragments;5 for convenience of discussion, let N be the number of residues of the protein. Each residue is treated quantum mechanically, whereas it interacts with all other residues through the same kind of interaction terms as in a QM/MM treatment, where the other residues are treated analogously to “MM” fragments. Thus, each residue is treated both as a QM fragment and as an MM fragment. The interaction of QM fragment m and MM fragment n is:
| (1) |
where μ and ν are atomic basis functions on fragment m, Pμν is the density matrix element, and Iμν is the element in the QM/MM one-electron matrix I for interaction with the Mulliken charges of fragment n.5 The last term LB represents the interaction between the nuclear charge of atom B in fragment m and Mulliken charges of all atoms in fragment n. Similarly, if fragment n is taken as the QM fragment and fragment m is taken as the MM fragment, the interaction energy between the fragments becomes
| (2) |
where λ and σ are basis functions on fragment n, and A is an atom in fragment n. In the X-Pol potential, the interaction energy between two fragments is defined as2,3,5
| (3) |
In the variational derivation6 of the DSCF method it was shown that the contribution of an MM fragment n to the Fock matrix of QM fragment m using the Mulliken charge approximation for fragment n is
| (4) |
where the superscript 0 indicates that the matrix element is calculated by setting the MM charges on atom A to +e, and where μ ∈ m(B) means that μ is in the same molecule m as atom B, Sμν is an element of the overlap matrix, and the matrix D(μν) is given by with the definition of the latter quantities by
| (5) |
where δpq and δpμ are Kronecker deltas.
The original DSCF method in the X-Pol potential enables the overall charge density and total energy to converge reasonably fast,2–6 typically requiring about 20 outer SCF iterations for a protein; however, the number of iterations can be further reduced by introducing a secondary buffer zone for each fragment. For example, in the protein case, in addition to the “central” fragment (peptide unit—see below) m, we also include the peptide units prior to and after fragment m in each explicit QM treatment. In turn, fragment m becomes a buffer fragment for residues m−1 and m+1, respectively. This, of course, increases the number of QM integral evaluations for each residue, but the computational cost is reduced by decreasing the number of overall SCF steps to about 10. Note that in the QM SCF optimization of the wave function for fragment m, the electron densities of the buffer residues are kept frozen. When the DSCF process has converged, the chemical potentials of all fragments are equalized.
In general, the interaction between two QM fragments m and nb, where nb is a buffer fragment, is calculated using electronic structure theory with the approximation of “neglect of di-fragment differential overlap” (NDFDO),28 that is, the differential overlap between orbitals belonging to different fragments is neglected. The interaction energy is given by
| (6) |
where is a matrix element of the one-electron nuclear-attraction matrix Hnb that includes attraction between the charge density on fragment m and the nuclei of fragment nb, and is a matrix element of the two-electron repulsion matrix Jnb between electrons on fragments m and those on fragment nb, which is defined as
| (7) |
The last term in eq 6, Enucl, is the interaction energy between nuclei in fragment m and nuclei in fragment nb (Enucl also includes interactions of core electrons in valence-only treatments like AM1). In short, the contribution of fragment nb to the Fock matrix of fragment m is given by
| (8) |
Equation 8 is the same as the Fock matrix in Hartree-Fock theory except that the contribution from electron exchange is neglected due to the NDFDO approximation. This corresponds to approximating the system wave function as the Hartree product of wave functions of individual fragments.2–6
By adding the contributions from interactions with the QM buffer zone and the MM environment, the Fock matrix of fragment m can be written as5,6
| (9) |
where n denotes the set of fragments whose interaction with fragment m is calculated by using the QM/MM method with the Mulliken charge approximation for MM atoms (eq 4), and nb denotes the set of neighbor fragments whose interaction with fragment m is calculated by the QM/QM buffer zone treatment (eq 6). The prime over the first summation in eq 9 indicates that the number of buffer fragment is different in various situations: 0 in case where the fragment m has no covalent connection to other fragments (e.g., a solvent molecule), 1 for a terminal residue in a polypeptide chain, and 2 for all internal residues. Note that the one-electron matrix H without a superscript includes the kinetic energy of electrons in fragment m and the attraction from the nuclei in fragment m. J without a superscript includes the Coulomb repulsion of electrons on fragments m and is defined as
| (10) |
while K includes the exchange of electrons within fragment m
| (11) |
For a protein, the system is divided into peptide units (fragments) at the Cα carbon atoms such that each fragment has two boundary atoms except the C- and N- termini which have only one boundary atom. Let NB be the total number of valence atomic basis functions of the boundary atom, which is 4 for a carbon atom in a minimal basis representation. In the GHO treatment of fragment m,5 each boundary atom is represented by NB / 2 hybrid orbitals, derived from a linear combination of the original atomic orbital basis functions,16,17 and its nuclear charge (core charge) is assigned to be +2 a.u. The remaining half of the boundary atom, which belongs to a buffer zone fragment, is represented in exactly the same way, but the orbitals are not optimized in the SCF optimization of the wave function of fragment m. Therefore, each boundary atom is partitioned into two pseudo atoms, half of which are included in the explicit QM SCF optimization and the other half of which remain in the MM region.5 With this definition of the QM fragments, the discussion of a protein system is simplified to that of a molecular system containing pseudo atoms. Since the fragment division is at the boundary atom, there are no covalent bonds between fragments, thereby the system can be treated as a collection of separate fragments with the exception that nuclear charges of two pseudo-atoms belonging to the same boundary atom do not interact since they have identical coordinates. This is an important feature of the GHO boundary in the X-Pol potential.5
For convenience of discussion, we rewrite the Fock matrix in eq 9 as follows
| (12) |
where
| (13a) |
| (13b) |
| (13c) |
Starting from an initial guess for the electron density and charges on the buffer and MM atoms (for some choices of the first QM fragment), we present an algorithm to variationally optimize molecular orbitals for each QM fragment by the double SCF method (the “double” refers to the fact that the final orbitals are self-consistent not just within each fragment but between fragments) with fragment/buffer interactions treated by the NDFDO approximation. A pseudo-code is shown in Scheme 3 to illustrate the algorithm described below.
For a given QM fragment, m, along with fragments directly bonded to it treated as buffer, we first construct F1 in the fragment’s AO basis including all atomic basis functions on the two boundary atoms (each of which has +2 nuclear charge and two electrons for a carbon atom). F2 is then constructed in this atomic basis by calculating the nuclear attractions and Coulomb repulsions (eq 7). I0 is calculated together with the QM/MM attraction matrix I. This is followed by computing F3 by adding the QM core-unit charge interaction to L0 and by putting the elements in the appropriate positions in the matrix. The Fock matrix F for fragment m is assembled according to eq 12. Finally, the Fock matrix in the hybrid basis is obtained by transforming F into the hybrid basis representation.
We diagonalize the Fock matrix F and calculate the electron density matrix. Then, the density matrix is transformed into the atomic basis and the Mulliken charges are updated using the density matrix in the AO basis for use in QM calculations of other fragments.
Next, we move to the next fragment, m+1, and repeat steps (a) and (b).
After looping over all fragments, we calculate the total electronic energy associated with each fragment and check for convergence using the total energy or electron density.
If the energy and electron density are not yet converged, we repeat above steps.
Scheme 3.
An illustrative pseudo-code for the double self-consistent-field method used in the X-Pol potential.
In deciding whether SCF convergence has been attained, we utilized the criterion that the change in the largest electron density matrix element is less than 10−10 a.u. With this density convergence, the energy change is found to be less than 10−7 kcal/mol. Note that the present convergence criterion converges the energy to a very tight level to ensure conservation of energy during MD simulations. If one is only interested in energy minimization, it is not necessary to use such a tight convergence criterion.
In the present implementation of the X-POL potential, we also make use of the NDDO approximation30 for the QM method so that no basis set orthogonalization is needed.31,32 Furthermore, instead of moving to the next fragment after each diagonalization of the Fock matrix as outlined above, we can fully converge the wave function of an individual fragment by SCF optimization before we move to next fragment and fully optimize its wave function.3–5 Both algorithms give the same result at convergence.
3. Analytical first derivative of energy
The total electronic energy of the system is given in the AO basis by the following equation
| (14) |
with
| (15) |
| (16) |
| (17) |
The summation indices in eqs 15–17 have been defined in conjunction with eq 9. Consequently,
| (18) |
where X A is a Cartesian coordinate of atom A. The derivative of EQM can be explicitly written as follows
| (19) |
where the superscript AO denotes AO basis. The first term, which is the Hartree-Fock contribution, is calculated in the usual fashion in the AO basis. The second term, which comes from the derivative of the density matrix due to basis transformation,17 can be expressed as
| (20) |
where the superscript H denotes the density matrix in hybrid basis set, and where † denotes a transpose. The matrix T transforms the AO basis into a hybrid basis set. The derivative of EQM/QM is similarly calculated except that the exchange term is absent due to the NDFDO approximation. Similarly, the gradient of the last energy component EQM/MM is composed of the Hartree-Fock contribution and a correction term due to the derivative of density matrix as in eq 20.
4. Results and discussion
We have implemented the variational X-Pol potential with a buffer zone around each QM fragment into the CHARMM33 package, replacing the previous iterative DSCF approach.5 Austin Model 1 (AM1)34 is chosen as the QM method in the present work, and charges obtained by Mulliken population analysis are used to approximate the electrostatic potential for QM/MM interactions. The validity and implementation of the variational X-Pol potential are tested for a water dimer, for the propane, 2-methylpropane, 2,2-dimethylpropane, and 1,3,5-trifluorohexane molecules, and for a pentapeptide.
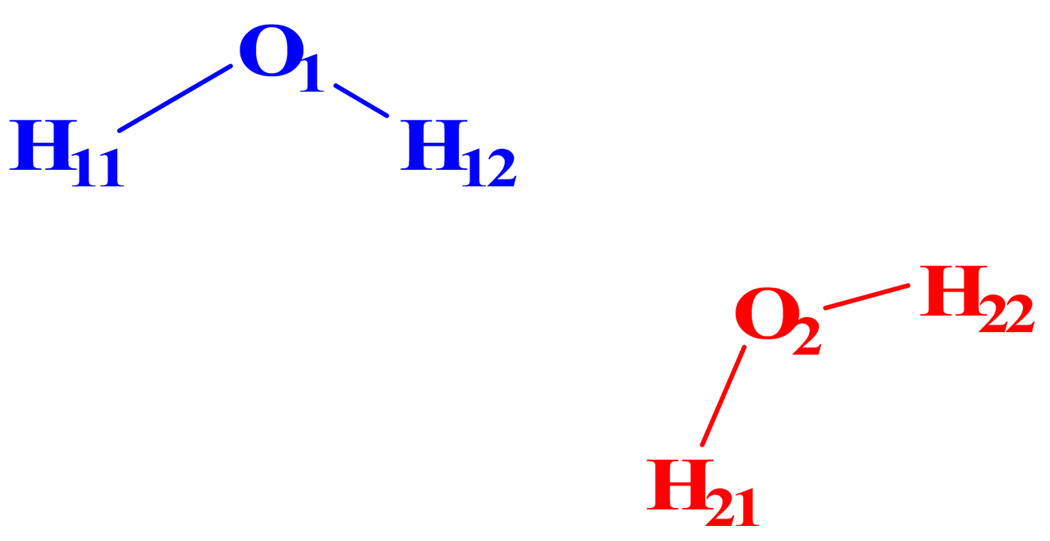
Table 1 lists the Mulliken population charges for a water dimer calculated by AM1, by the X-Pol potential without a secondary QM buffer zone, and by the X-Pol potential with a QM buffer zone. The same molecular geometry optimized at the AM1 level was used in all three calculations. In addition, we have fully optimized the water dimmer geometry using the X-Pol potential. In X-Pol calculations, each water molecule is defined as a QM fragment. All four calculations give similar Mulliken charges with the largest absolute deviation from full AM1 calculations being about 0.01 a.u. We conclude that both approximations are reasonable for fragments between which there is no covalent bond.
TABLE 1.
Mulliken population charges for water dimer from X-Pola
| atom | AM1 | Mulliken//AM1 | NDFDO//AM1 | Mulliken//X-Pol |
|---|---|---|---|---|
| O1 | −0.411 | −0.408 | −0.410 | −0.404 |
| H11 | 0.211 | 0.210 | 0.210 | 0.216 |
| H12 | 0.198 | 0.198 | 0.200 | 0.187 |
| O2 | −0.402 | −0.404 | −0.400 | −0.403 |
| H21 | 0.202 | 0.202 | 0.200 | 0.201 |
| H22 | 0.202 | 0.202 | 0.200 | 0.201 |
AM1 denotes the full AM1 calculation for water dimer; Mulliken denotes the result obtained using the Mulliken charge approximation for the MM fragment; NDFDO denotes the result obtained by the buffer zone method of the present article; //AM1 means at the AM1 geometry and //X-Pol means at the X-Pol geometry.
One goal is to use the X-Pol potential to carry out molecular dynamics simulations of solvated proteins in which amino acid residues are covalently bonded. Therefore, the next test is to examine the charge polarization between fragments that are covalently connected. In particular, we consider four model compounds, namely propane, 2-methylpropane (isobutane), 2,2-dimethylpropane (neopentane), and 1,3,5-trifluorohexane. We note that in a first glance it may seems to be irrelevant to use hydrocarbons as model compounds to test the X-Pol model for study of proteins. In fact, the key issue in charge polarization between fragments is the balance of electronegativity of the boundary pseudo-atoms and hydrocarbon compounds provide ideal models for this purpose because for symmetric compounds there is zero charge transfer. Thus, if the X-Pol model is demonstrated to maintain charge balance in hydrocarbons, the treatment of the boundary carbon atoms is balanced with the original AM1 model in electronegativity, and in principle, the boundary method is transferable just as in standard semiempirical theory. This has been the strategy adopted in the development of the original generalized hybrid orbital method.16,17
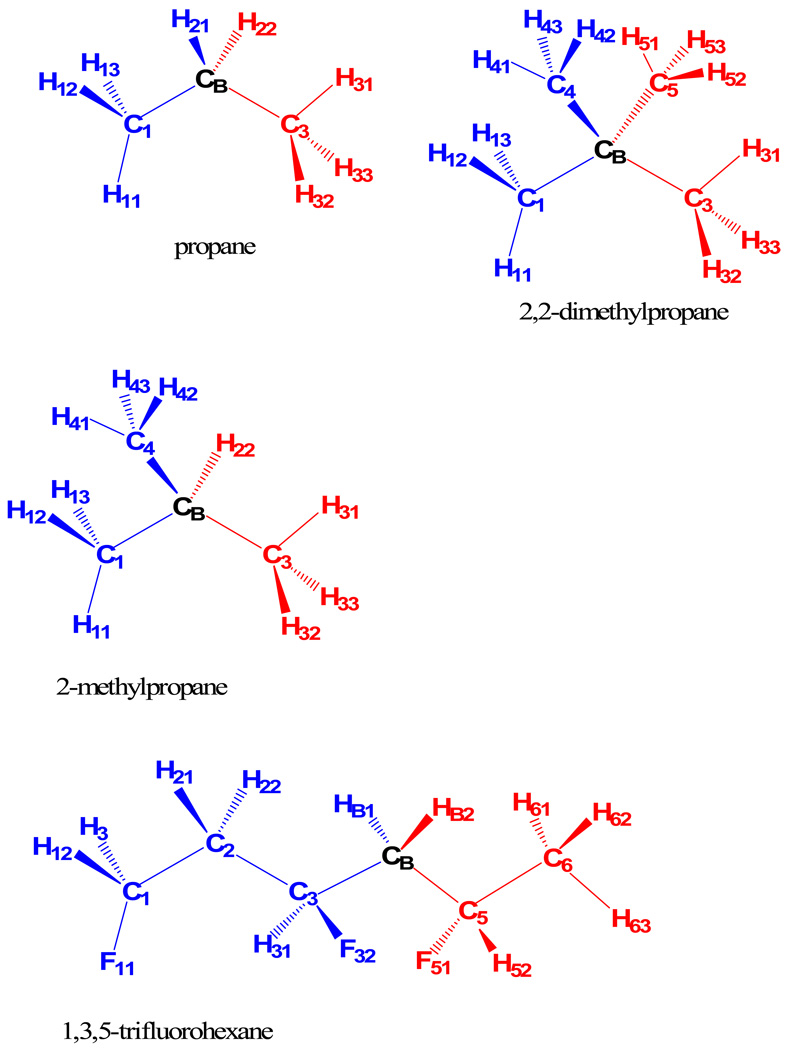
In each case, we partition the molecule into two fragments that are connected through a boundary atom. The definitions of the QM fragments are shown in scheme 2; the boundary atoms CB between the fragments are treated as two pseudo atoms in the X-Pol method. The electronic interactions between two fragments are determined by making use of the NDFDO approximation. Since the Fock matrix in the varational X-Pol potential with a QM buffer zone is different from that in the treatment without a QM buffer zone, it is possible that the parameters for the GHO atom need to be re-optimized. We found that all GHO parameters for the carbon boundary atom can be taken to be the same as those of the original AM1 set except the U ss and U pp, which are scaled by a factor of 0.99, just as in the X-Pol potential without a QM buffer zone; see Table 2.
Scheme 2.
Atom numbering of the three alkanes and 1,3,5-trifluorohexane, each of which is separated into two quantum mechanical fragments across a boundary atom CB.
TABLE 2.
Modified parameters for the carbon boundary atom in the present and previous X-Pol potentials along with the original AM1 values. All values are given in eV.
| Parameters | AM1 | X-Pol |
|---|---|---|
| Uss | −52.028658 | −51.508371 |
| Upp | −39.614239 | −39.218097 |
The geometry of each model compound is optimized using the adopted basis Newton-Raphson (ABNR) optimizer in CHARMM.33 Listed in Table 3 are optimized bond lengths and bond angles for the three alkanes. Overall, the X-Pol potential produces both bond lengths and bond angles that are in good agreement with full AM1 calculations. The absolute errors in bond lengths not involving a boundary atom are in the range of 0.001 to 0.003 Å. The largest error, 0.008 Å, comes from a bond distance involving a boundary atom. Interestingly, as the size of the alkane increases, the errors in optimized bond lengths become smaller, as shown in isobutane and neopentane (Table 3). Only bond angles involving heavy atoms are listed in Table 3. The largest error in such a bond angle, 1.3 degree, occurs in propane; the errors for isobutane and neopentane are smaller than 1 degree.
TABLE 3.
Optimized bond lengths (Å) and bond angles (degrees) using the X-Pol potential (including buffer zone) and the full AM1 method.
| Propane | 2-methylpropane | 2,2-dimethylpropane | ||||
|---|---|---|---|---|---|---|
| coordinatea | AM1 | X-Pol | AM1 | X-Pol | AM1 | X-Pol |
| CB-C1 | 1.516 | 1.519 | 1.523 | 1.522 | 1.527 | 1.526 |
| CB-C3 | 1.516 | 1.518 | 1.523 | 1.522 | 1.527 | 1.526 |
| CB-C4(H) | 1.118 | 1.110 | 1.523 | 1.522 | 1.527 | 1.526 |
| CB-C5(H) | 1.118 | 1.110 | 1.121 | 1.115 | 1.527 | 1.526 |
| H11-C1 | 1.114 | 1.116 | 1.114 | 1.114 | 1.114 | 1.115 |
| H12-C1 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 |
| H13-C1 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 |
| H31-C3 | 1.114 | 1.116 | 1.114 | 1.115 | 1.114 | 1.114 |
| H32-C3 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 | 1.115 |
| H33-C3 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 | 1.114 |
| H41-C2 | 1.114 | 1.115 | 1.114 | 1.114 | ||
| H42-C4 | 1.114 | 1.114 | 1.114 | 1.115 | ||
| H43-C4 | 1.114 | 1.114 | 1.114 | 1.114 | ||
| H51-C5 | 1.114 | 1.115 | ||||
| H52-C5 | 1.114 | 1.114 | ||||
| H53-C5 | 1.114 | 1.114 | ||||
| C1- CB-C3 | 111.9 | 110.6 | 110.8 | 111.2 | 109.5 | 110.0 |
| C1- CB-C4 | 111.0 | 110.2 | 109.5 | 109.4 | ||
| C1- CB-C5 | 109.5 | 109.2 | ||||
| C3- CB-C4 | 110.8 | 110.0 | 109.5 | 109.2 | ||
| C3- CB-C5 | 109.5 | 109.0 | ||||
| C4- CB-C5 | 109.5 | 110.0 | ||||
x-y denotes a bond length, and x-y-z denotes a bond angle
The Mulliken population charges for optimized geometries of the three alkanes are listed in Table 4. The charges from variational X-Pol calculations with the NDFDO approximation are in reasonable agreement with full AM1 calculations, although the parameters for GHO atoms are not optimized.5,16 If the GHO parameters were optimized to reproduce properties dependent on electronegativity, the agreement could be further improved.
TABLE 4.
Mulliken population charges obtained using the X-Pol potential (including buffer zone) and the full AM1 method.
| Propane | 2-methylpropane | 2,2-dimethylpropane | ||||
|---|---|---|---|---|---|---|
| atom | AM1 | X-Pol | AM1 | X-Pol | AM1 | X-Pol |
| CB | −0.160 | −0.161 | −0.111 | −0.121 | −0.060 | −0.081 |
| C1 | −0.210 | −0.235 | −0.206 | −0.228 | −0.202 | −0.218 |
| (0.004) | (0.002) | (0.010) | (0.010) | (0.015) | (0.020) | |
| H11 | 0.071 | 0.074 | 0.072 | 0.074 | 0.072 | 0.074 |
| H12 | 0.071 | 0.081 | 0.072 | 0.082 | 0.072 | 0.082 |
| H13 | 0.071 | 0.082 | 0.072 | 0.083 | 0.072 | 0.082 |
| C3 | −0.210 | −0.234 | −0.206 | −0.228 | −0.202 | −0.218 |
| (0.004) | (0.004) | (0.010) | (0.010) | (0.015) | (0.020) | |
| H31 | 0.071 | 0.074 | 0.072 | 0.082 | 0.072 | 0.082 |
| H32 | 0.071 | 0.081 | 0.072 | 0.074 | 0.072 | 0.074 |
| H33 | 0.071 | 0.082 | 0.072 | 0.083 | 0.072 | 0.082 |
| C4 (H) | 0.076 | 0.076 | −0.206 | −0.223 | −0.202 | −0.218 |
| (0.010) | (0.014) | (0.015) | (0.020) | |||
| H41 | 0.072 | 0.082 | 0.072 | 0.082 | ||
| H42 | 0.072 | 0.074 | 0.072 | 0.074 | ||
| H43 | 0.072 | 0.082 | 0.072 | 0.082 | ||
| C5 (H) | 0.076 | 0.079 | 0.081 | 0.086 | −0.202 | −0.218 |
| (0.015) | (0.020) | |||||
| H51 | 0.072 | 0.074 | ||||
| H52 | 0.072 | 0.082 | ||||
| H53 | 0.072 | 0.082 | ||||
The total charges on the methyl groups are listed in parentheses in Table 4. As we observed in calculations with the previous iterative X-Pol potential,5 charge transfer between neighboring fragments can take place at the GHO boundary atom. The X-Pol potential yields 0.002 and 0.004 a.u. of net charge for the two methyl groups in propane, in good agreement with a net charge of 0.004 a.u. from full AM1 calculations. (Note: 1 atomic unit (a.u.) of charge, sometimes denoted e, is the charge on a proton.) The slight imbalance of the charges on the two methyl groups results from the definition of hybrid orbitals in GHO method. Charge transfer in isobutane is also well reproduced with the largest deviation being 0.004 e. For neopentane, the four methyl groups are identical, and the deviation f the amount of charge transfer from a full AM1 calculation is only 0.005 e.
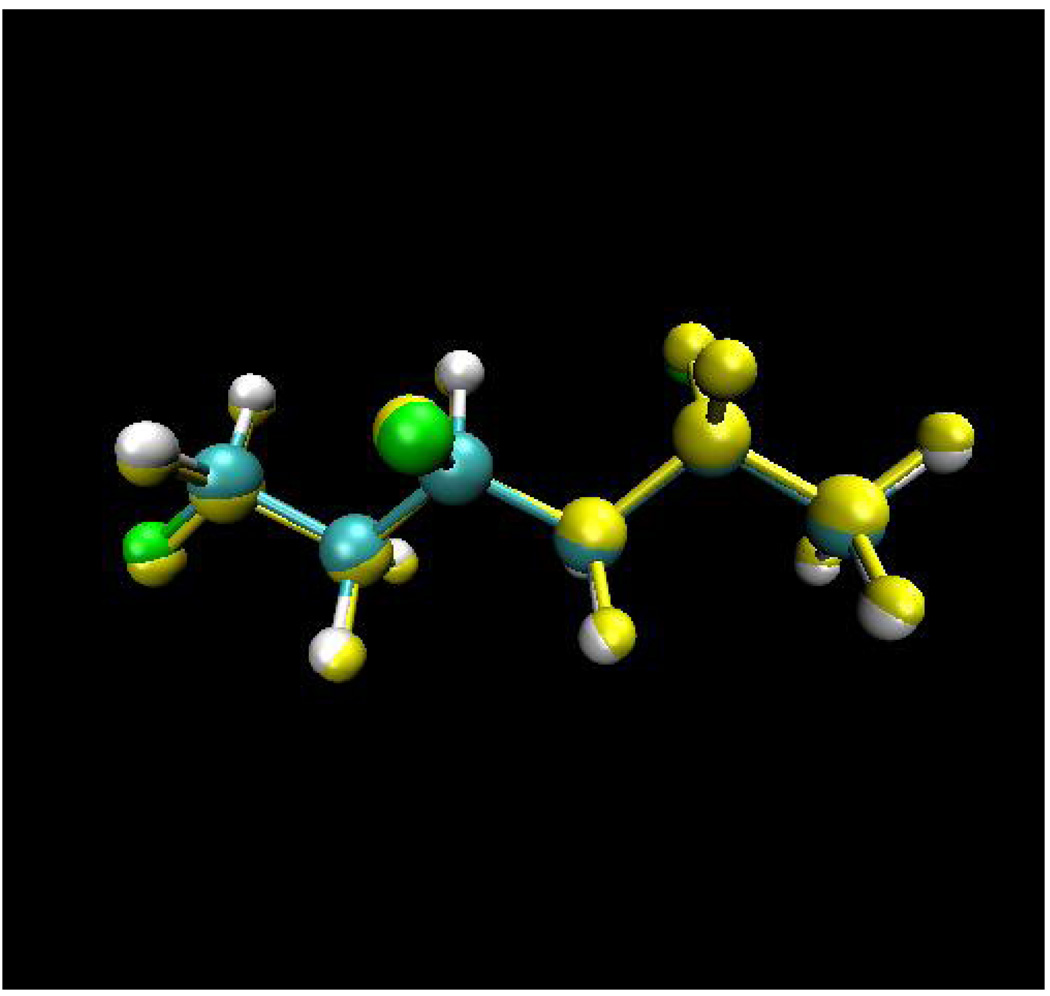
Next, the X-Pol potential is tested for 1,3,5-trifluorohexane, which serves as a model compound with strongly electronegative substituents. Optimized bond lengths and bond angles are listed in Table 5, along with the results from full AM1 calculations. The optimized structures from the X-Pol potential and from AM1 calculations are superimposed in Figure 1 to illustrate the similarity. Both bond lengths and bond angles are in good accord with full AM1 calculations. The largest unsigned error for bond length is 0.01 Å, and the largest error for bond angles is about 1 degree. Mulliken population charges for each atom and each group of atoms are listed in Table 6 and compared with full AM1 calculations. In particular, the Mulliken charge for the boundary atom is in reasonable agreement with the AM1 result, differing by only 0.008 a.u. The largest absolute error is 0.018 a.u., which occurs on a hydrogen atom bonded to the C3 carbon. The absolute largest error for any of the net group charges is about 0.01 a.u. Interestingly, the total charge of the CH2 group at the boundary is 0 as compared to −0.003 a.u. predicted by AM1. Thus, the electronegativity of the boundary atom is well balanced, even for a molecule with highly polar groups.
TABLE 5.
Optimized bond lengths (Å) and bond angles (degrees) using the X-Pol potential (including buffer zone) and the full AM1 method for 1,3,5-trifluorohexane.
| Bond | Angle | ||||
|---|---|---|---|---|---|
| AM1 | X-Pol | AM1 | X-Pol | ||
| CB-C3 | 1.544 | 1.533 | |||
| CB-C5 | 1.543 | 1.533 | |||
| CB-HB1 | 1.108 | 1.119 | |||
| CB-HB2 | 1.108 | 1.119 | |||
| C1-C2 | 1.527 | 1.526 | |||
| C2-C3 | 1.529 | 1.531 | |||
| C5-C6 | 1.524 | 1.525 | C3- CB-C5 | 109.5 | 109.1 |
| F11-C1 | 1.381 | 1.381 | |||
| H12-C1 | 1.126 | 1.126 | |||
| H13-C1 | 1.125 | 1.125 | |||
| H21-C2 | 1.120 | 1.120 | |||
| H22-C2 | 1.119 | 1.119 | C2- C3- CB | 111.4 | 110.5 |
| H31-C3 | 1.129 | 1.131 | C2- C3- CB | 111.1 | 111.3 |
| F32-C3 | 1.388 | 1.389 | F32-C3- CB | 110.8 | 111.1 |
| F51-C5 | 1.388 | 1.389 | |||
| H52-C5 | 1.129 | 1.131 | |||
| H61-C6 | 1.116 | 1.116 | CB - C5-C6 | 109.9 | 109.5 |
| H62-C6 | 1.115 | 1.115 | CB - C5-F51 | 111.0 | 111.2 |
| H63-C6 | 1.544 | 1.533 | F51-C5-C6 | 110.6 | 110.6 |
Figure 1.
Superposition of the optimized structures using the AM1 and the X-Pol potential for 1,3,5-triflourohexane. AM1 structure is in yellow.
TABLE 6.
Mulliken population charges obtained using the X-Pol potential (including buffer zone) and the full AM1 method for 1,3,5-trifluorohexane.
| atom | Atomic Charges | Group Charges | ||
|---|---|---|---|---|
| AM1 | X-Pol | AM1 | X-Pol | |
| CB | −0.219 | −0.211 | ||
| HB1 | 0.108 | 0.105 | ||
| HB2 | 0.108 | 0.105 | −0.003 | −0.000 |
| C1 | 0.009 | 0.009 | ||
| F11 | −0.173 | −0.173 | ||
| H12 | 0.095 | 0.095 | ||
| H13 | 0.083 | 0.083 | 0.014 | 0.013 |
| C2 | −0.226 | −0.217 | ||
| H21 | 0.109 | 0.109 | ||
| H22 | 0.106 | 0.108 | −0.011 | −0.001 |
| C3 | 0.105 | 0.110 | ||
| H31 | 0.059 | 0.041 | ||
| F32 | −0.173 | −0.171 | −0.009 | −0.020 |
| C5 | 0.056 | 0.039 | ||
| F51 | −0.175 | −0.173 | ||
| H52 | 0.102 | 0.107 | −0.017 | −0.027 |
| C6 | −0.243 | −0.234 | ||
| H61 | 0.088 | 0.088 | ||
| H62 | 0.093 | 0.092 | ||
| H63 | 0.088 | 0.089 | 0.026 | 0.035 |
Finally, the validity of the X-Pol potential is tested for two conformations of a pentapeptide with the amino acid sequence Ala-Gly-Leu-Phe-Ser, in which the terminal carboxyl group has been capped by ‒NHCH3 and the terminal amino group is capped by ‒C(O)CH3; this results in a total of 6 peptide bonds in the system. The present X-Pol model incorporating buffer residues reduces the total SCF cycles to about 10 iterations, starting with converged densities obtained in the previous minimization step or molecular dynamics step in simulations. Without the buffer zone, the outer DSCF iteration typically requires about 20 steps, sometimes 30. The total number of iterations in the buffered X-Pol method does not seem to increase as the size of the system increases, e.g., during molecular dynamics simulations of a fully solvated protein consisting nearly 15,000 atoms. For a pentapeptide calculation, 500 steps of minimization were performed using the ABNR method33 both with full AM1 and with the X-Pol potential. A calculation using full AM1 takes 40.9 min of CPU time on an IBM Power4 (1.3 GHz) processor, whereas the time for the same 500 minimization steps employing the present X-Pol potential is only 3.8 min.
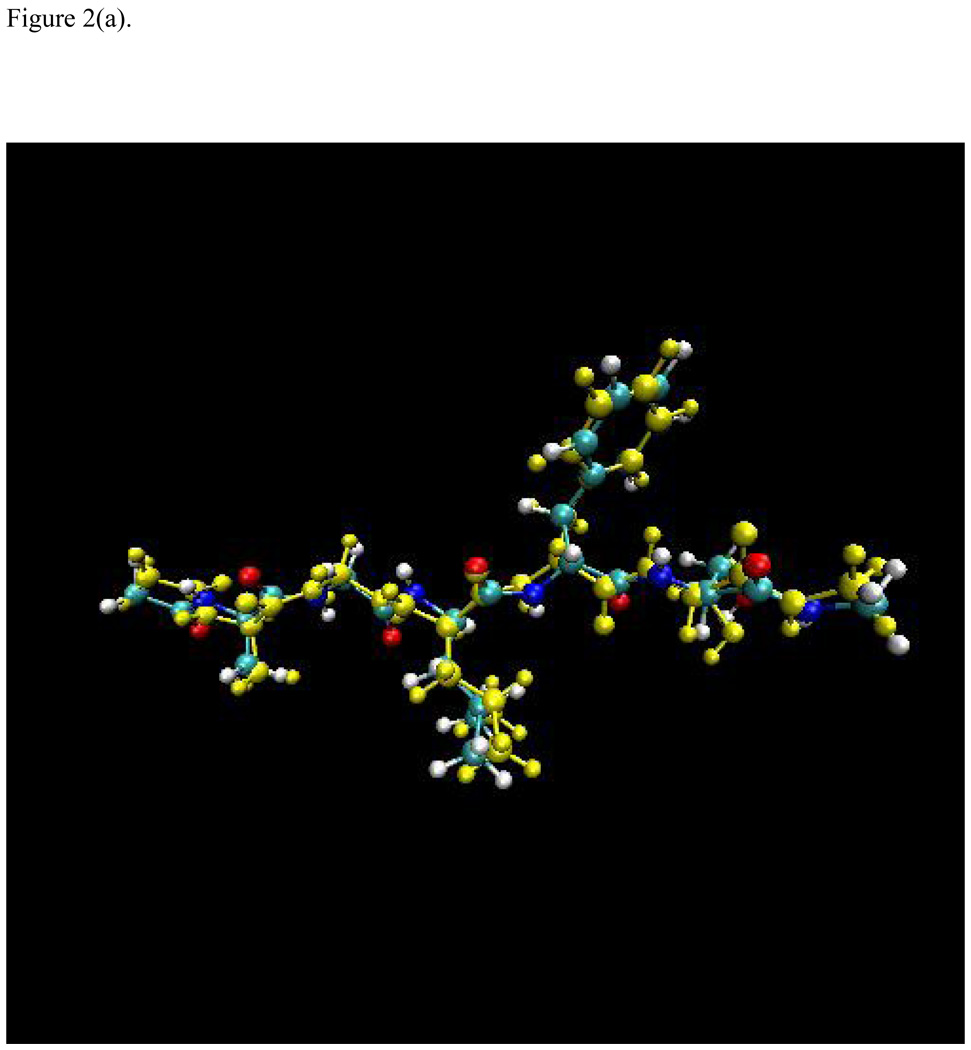
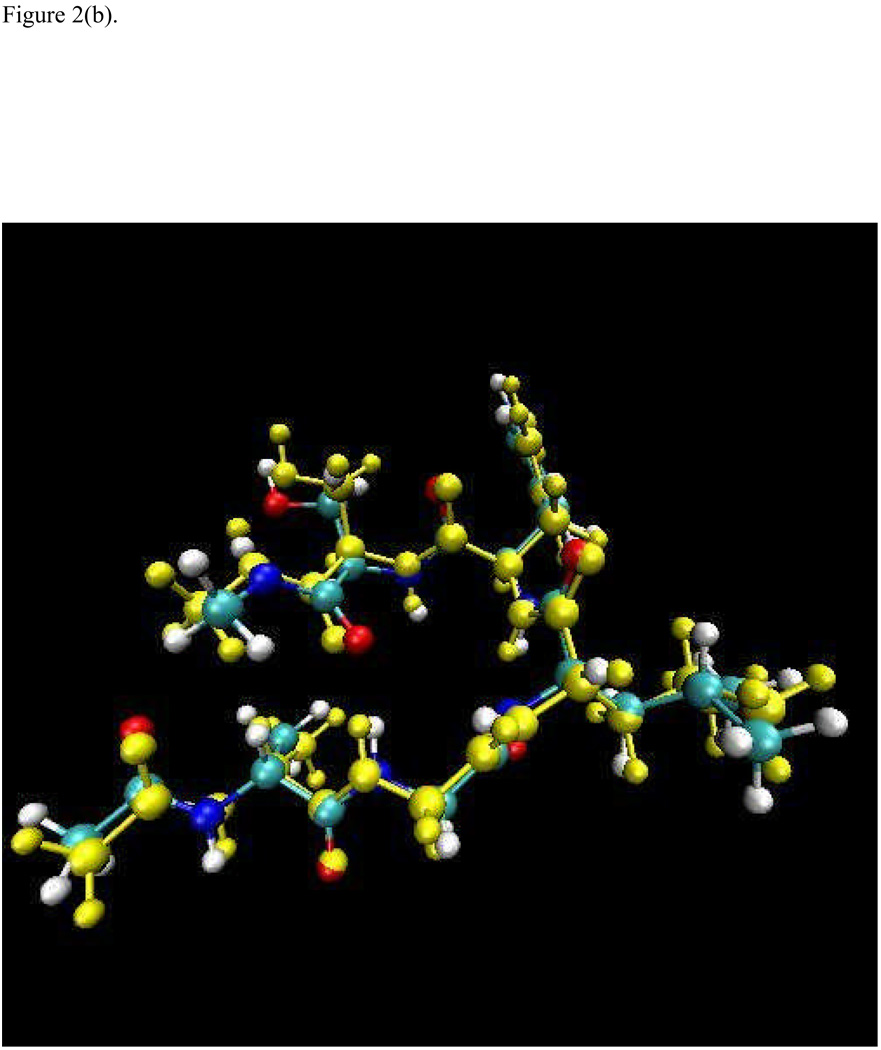
The optimized structures for an extended (linear) conformation and a β-turn configuration using the full AM1 and the X-Pol potential are superimposed and displayed in Figure 2. Overall, the optimized structures from these two methods agree well with small deviations in the sidechain positions. The β-turn configuration is −75.6 kcal/mol more stable than the linear conformation from full AM1 optimizations, which is in essentially exact agreement with the relative energies computed by the X-Pol potential (the difference in relative energy between AM1 and X-Pol is less than 0.01 kcal/mol). Thus, the X-Pol potential can provide an adequate description of the electronic structure and energy in comparison with the full quantum model for this test case. It would be interesting to apply the X-Pol potential to a solvated protein system to examine the capability of the method for full protein dynamics.
Figure 2.
Superposition of the optimized structures using the AM1 (in yellow) and the X-Pol potential (a) for a beta-turn conformation, and (b) for an extended linear configuration of the sequence Ala-Gly-Leu-Phe-Ser. The C-terminus is capped with the peptide unit ‒C(O)NH(CH3); and the N-terminus is capped with ‒NHC(O)CH3.
5. Concluding remarks
The variational X-Pol potential is improved by introducing a buffer zone at the QM/MM interface such that the interactions between MM fragments in the buffer zone with QM fragments are treated using explicit two-electron Coulomb integrals while electron exchange between fragments is neglected because of neglect of di-fragment differential overlap (NDFDO). The QM/MM buffer zone provides a smooth transition from the fully quantum mechanical treatment of intrafragment interactions to the QM/MM treatment of interfragment interactions. The explicit calculation of the two-electron integrals for interactions of bonded fragments reduces one the main sources of error in the DSCF method and makes the parametrization of the X-Pol potential more transferable.
Mulliken charges calculated for a water dimer show that the NDFDO approximation is a reasonable approximation. Even when the buffer zone is present, the wave function of the system is variationally optimized so that the gradient of the electronic energy is obtained analytically; this significantly reduces the computational costs based on coupled-perturbed Hartree-Fock method in the force evaluation needed for molecular dynamics simulations. Although the introduction of the buffer zone means that there are more two-electron integrals to be evaluated, the computational algorithm with buffer zones is actually simpler then the previous2–5 DSCF methods, resulting in less computational effort in matrix transformation. This is because the present DSCF method with buffer zones does not require special treatment of the boundary atoms5 in the QM subsystem except the use of a hybrid basis set representation. Furthermore, the boundary atom is effectively split into two pseudo-atoms, which are treated identically as different atoms without nucleus-nucleus repulsion.
The DSCF method with QM/MM buffer zones is tested for small model compounds, namely propane, 2-methylpropane, 2,2-dimethylpropane, and 1,3,5-trifluorohexane. With the current parameters for GHO atoms, the largest error for the bond lengths connecting to the boundary atom and for bond angles involving only heavy atoms are about 0.01 Å and 1.3 degrees, respectively. Mulliken charges obtained from the DSCF method with buffer zones are in excellent agreement with full AM1 calculations. Furthermore, the method captures the charge transfer effects for the model compounds with the largest deviation in partial atomic charge (excluding boundary atoms) being 0.005 a.u. for alkanes (2,2-dimethylpropane) and 0.01 a.u. for 1,3,5-trifluorohexane. Minimization test for a pentapeptide shows that the X-Pol potential is much faster than full AM1 calculations while the resulting geometries are very similar in both methods. The computed relative energies between an extended linear conformation and a β-turn structure are in exact agreement for this test case. These results are very encouraging for the prospects of using the DSCF method with buffer zones to create a transferable X-Pol force field that includes polarization effects in a natural way.
Supplementary Material
Tables of Cartesian coordinates optimized using the AM1 method and the X-Pol potential for all compounds described in this paper (9 pages). This material is available free of charge via the Internet at http://pubs.acs.org.
Scheme 1.
Atom numbers assigned to the water dimer with each of the monomers treated as a quantum mechanical fragment
Acknowledgments
This work was supported in part by the National Institutes of Health under grant number GM46736, the Office of Naval Research under grant no. N00012-05-01-0538, and the National Science Foundation under grant no. CHE07-04974.
References
- 1.Allen MP, Tildesley DJ. Computer Simulations of Liquids. London: Oxford University Press; 1987. [Google Scholar]
- 2.Gao J. J. Phys. Chem. B. 1997;101:657. [Google Scholar]
- 3.Gao J. J. Chem. Phys. 1998;109:2346. [Google Scholar]
- 4.Wierzchowski SJ, Kofke DA, Gao J. J. Chem. Phys. 2003;119:7365. [Google Scholar]
- 5.Xie W, Gao J. J. Chem. Theory Comput. 2007;3:1890. doi: 10.1021/ct700167b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xie W, Song L, Truhlar D, Gao J. J. Chem. Phys. 2008;128:234108. doi: 10.1063/1.2936122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Warshel A, Levitt M. J. Mol. Biol. 1976;103:227. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 8.Field MJ, Bash PA, Karplus M. J. Comput. Chem. 1990;11:700. [Google Scholar]
- 9.Gao J, Xia X. Science. 1992;258:631. doi: 10.1126/science.1411573. [DOI] [PubMed] [Google Scholar]
- 10.Gao J. Rev. Comput. Chem. 1995;7:119. [Google Scholar]
- 11.Mulliken RS. J. Chem. Phys. 1955;23:1833. [Google Scholar]
- 12.Field MJ. Mol. Phys. 1997;91:835. [Google Scholar]
- 13.Gascon JA, Leung SSF, Batista ER, Batista VS. J. Chem. Theory Comput. 2006;2:175. doi: 10.1021/ct050218h. [DOI] [PubMed] [Google Scholar]
- 14.Kitaura K, Ikeo E, Asada T, Nakano T, Uebayasi M. Chem. Phys. Lett. 1999;313:701. [Google Scholar]
- 15.Kitaura K, Sugiki S, Nakano T, Komeiji Y, Uebayasi M. Chem. Phys. Lett. 2001;336:163. [Google Scholar]
- 16.Gao J, Amara P, Alhambra C, Field MJ. J. Phys. Chem. A. 1998;102:4714. [Google Scholar]
- 17.Amara P, Field MJ, Alhambra C, Gao J. Theor. Chem. Acc. 2000;104:336. [Google Scholar]
- 18.Reuter N, Dejaegere A, Maigret B, Karplus M. J. Phys. Chem. A. 2000;104:1720. [Google Scholar]
- 19.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodoscek M, Brooks BR. J. Chem. Phys. 2002;117:10534. [Google Scholar]
- 20.Amara P, Field MJ. Theor. Chem. Acc. 2003;109:43. [Google Scholar]
- 21.Lin H, Truhlar DG. J. Phys. Chem. A. 2005;109:3991. doi: 10.1021/jp0446332. [DOI] [PubMed] [Google Scholar]
- 22.Bulatov VV, Diaz de la Rubia T, Phillips R, Kaxiras E, Ghoniem N, editors. Multiscale Modeling of Materials; MRS Symposium Proceedings Volume 538; Warrendale, PA. Materials Research Society; 1999. [Google Scholar]
- 23.Brandt A, Bernholc J, Binder K, editors. NATO Sciences Series III Computer and Systems Sciences 177. Amsterdam: IOS Press; 2001. Multiscale Computational Methods in Chemistry and Physics. [Google Scholar]
- 24.Kairys V, Jensen JHJ. J. Phys. Chem. A. 2000;104:6656. [Google Scholar]
- 25.Minikis RM, Kairys V, Jensen JH. J. Phys. Chem. A. 2001;105:3829. [Google Scholar]
- 26.Li H, Hains AW, Everts JE, Robertson AD, Jensen JH. J. Phys. Chem. B. 2002;106:3486. [Google Scholar]
- 27.Frerre N, Assfeld X, Rivail J-L. J. Comput. Chem. 2002;23:610. doi: 10.1002/jcc.10058. [DOI] [PubMed] [Google Scholar]
- 28.De Vivo M, Ensing B, Dal Peraro M, Gomez GA, Christianson DW, Klein ML. J. Am. Chem. Soc. 2007;129:387. doi: 10.1021/ja066150c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hu H, Lu Z, Yang W. J. Chem. Theory and Comput. 2007;3:390. doi: 10.1021/ct600240y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pople JA, Santry DP, Segal GA. J. Chem. Phys. 1965;43:S129. [Google Scholar]
- 31.Pu J, Gao J, Truhlar DG. J. Phys. Chem. A. 2004;108:632. [Google Scholar]
- 32.Pu J, Gao J, Truhlar DG. ChemPhysChem. 2005;6:1853. doi: 10.1002/cphc.200400602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Brooks BR, Bruccoleni RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187. [Google Scholar]
- 34.Dewar MJS, Zoebisch EG, Healy EF, Stewart JJP. J. Am. Chem. Soc. 1985;107:3902. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Tables of Cartesian coordinates optimized using the AM1 method and the X-Pol potential for all compounds described in this paper (9 pages). This material is available free of charge via the Internet at http://pubs.acs.org.