Abstract
Recent evidence suggests substantial response-time costs associated with lag-2 repetitions of tasks within explicitly controlled task sequences (Koch, Philipp, & Gade, 2006, Schneider, 2007), a result that has been interpreted as inhibition of no-longer relevant tasks. Experiments 1–3 confirm much larger lag-2 costs under serial-control than under externally cued conditions, but also show (a) that these costs occur only when sequences contain at least two distinct chunks and (b) that direct lag-2 repetitions are not a necessary condition for their occurrence. This pattern suggests the hypothesis that rather than task-set inhibition, the large lag-2 costs observed in complex sequences, reflect interference resulting from links between positions within a sequential plan and the individual tasks controlled by this plan. The remaining experiments successfully test this hypothesis (Exp. 4), rule out chaining accounts as a potential alternative explanation (Exp. 5), and demonstrate that interference results from information stored in long-term memory rather than working memory (Exp. 6). Implications of these results for an integration of models of serial-order control and serial memory are discussed.
In sequentially organized activities, such as playing the piano (e.g., Shaffer, 1981), producing complex rhythms (e.g., Krampe, Mayr, & Kliegl, 2005), or performing a ordered series of tasks (e.g., Logan, 2004; Schneider & Logan, 2006), a limited set of basic elements needs to be organized into an adequate action sequence. Theoretically, such behavior is often thought to be controlled through a recursive hierarchy of sequential representations (e.g., Lien & Ruthruff, 2004; Luria & Meiran, 2003, Miller, Galanter, & Pribram, 1960; Povel & Collard, 1982; Restle & Burnside, 1972; Rosenbaum, Kenny, & Derr, 1983), where chunks or subplans specify the order of a small set of elements (e.g., 2–4), which in turn can be organized by a higher-level plan that specifies the order of these chunks. This conceptualization can account for key aspects of how people actually produce behavioral sequences, in particular the fact that between-chunk transitions take much longer than within-chunk transitions. While models of this kind are successful in explaining on-line performance during sequential production, they are relatively silent regarding the nature of the representations that are used to specify serial order within a given chunk or subplan. This question, how exactly order is represented, is dealt with extensively in the context of research on serial memory (e.g., Anderson & Matessa, 1997; Botvinick & Plaut, 2006; Estes, 1972; Henson, 1998a; Lewandowsky & Murdock, 1989).
The immediate goal of this paper is to use what we can learn from models of serial recall to arrive at a more complete explanation of an interesting set of phenomena that have recently been reported in research on serial-task control (Koch, Philipp, & Gade, 2006; Schneider, 2007). The more general goal is to achieve closer contact between two research traditions, that some notable exceptions not withstanding (Schneider & Logan, 2006, 2007), have largely ignored each other: work on sequential control of action and work on serial-memory performance. In the remainder of the introduction, I will first describe the empirical starting-point of the current work, the so-called lag-2 repetition cost, and I will explain why it is a phenomenon that warrants the further investigation.
Task Selection and Inhibition
Recently, there has been strong interest in the question how people select, change, or maintain higher-order representations, often referred to as task sets, that constrain more basic perceptual and response-selection processes, such as responding either to the color or to the shape of a stimulus. The primary empirical tool used to examine task-set selection processes is the task-switching paradigm, where people are brought into situations that require flexible selection of different task sets on the basis of external cues or simple sequences (for reviews see, Logan, 2003; Monsell, 2003).
One important empirical phenomenon that has emerged from this research is the so-called backward-inhibition effect, or to use a theoretically more neutral term, the lag-2 repetition cost: When a task-set needs to be selected that had been recently abandoned for an alternate task set (i.e., a ABA sequence of tasks), then a return to the original task takes reliably longer than a return to a less-recently used task (i.e., a CBA sequence of tasks; Mayr & Keele, 2000; for a review, see Mayr, 2007). The dominant interpretation of this effect is that as we move from one task or rule to the next, some aspect of processing the formerly relevant rule is suppressed, making the reuse of this rule more difficult for some time thereafter. Consistent with this interpretation, the lag-2 repetition cost is increased in situations in which larger between-task competition is to be expected (e.g., Gade & Koch, 2005; Mayr & Keele, 2000).
Typically, lag-2 repetition costs have been obtained using cued task-switching paradigms where task selection is prompted through external signals that are randomly chosen for each trial. In these situations lag-2 costs are about 20–50 ms. Recently, however Schneider (2007), following up on earlier work by Koch et al. (2006), examined lag-2 costs in the context of a serial-order control situations. He instructed subjects to cycle through a block of trials using one of two different sequence “grammars” 1) ABA-CBC or 2) BAC-BCA, with the chunking structure between the first three and the second three elements explicitly induced. Across the two types of sequences, lag-2 repetitions occur either on position 3 of each chunk (i.e., a within-chunk repetition) or on position 2 of each chunk (i.e., a between-chunk repetition). Lag-2 repetitions were computed here by comparing the lag-2 repetitions from one sequence type with the RTs on the same position for the other sequence type. The main result featured in this paper was that the lag-2 repetition effect depended on the sequential structure: Within-chunk lag-2 repetition costs were about 100 ms shorter than the 200 ms costs for between-chunk lag-2 repetitions. Following Koch et al., Schneider interpreted this pattern as a mixture of two different processes. The first is a basic inhibitory process that is directed towards the no-longer relevant task set and that is observable for between-chunk lag-2 repetitions. The second is the proactive activation of task sets through the activation of a chunk, which facilitates selection/use of tasks that are repeated within the same chunk. Thus by this account, lag-2 repetitions that span chunk boundaries should allow a relatively pure assessment of basic task-set inhibition. Lag-2 repetitions within chunk boundaries, however involve two counteracting processes: inhibition and chunk-driven activation.
At first sight, the inhibition-plus-activation account provides s a plausible interpretation to the rather striking modulation of the backward inhibition cost through sequential organization. However, this ignores a second aspect of the Schneider’s results. Whereas the backward-inhibition cost obtained in cued task-switching situations is usually in the 20–50 ms range, Schneider (2007) reports an up to 10 times larger cost of 200–300 ms for between-chunk repetitions. This very large cost casts doubts on the interpretation that the between-chunk repetition cost reflects task-set inhibition in a pure manner that is counteracted by a within-chunk benefit. At the very least, one is left with a new puzzle: Why is “pure” task-set inhibition in the context of serial-order control by an order of magnitude more potent than when tasks are cued exogenously?
One might suggest perhaps, that due to higher top-down control demands in endogenous sequencing situations, inhibition of previous elements may become more important. However, such an interpretation would take for granted that the lag-2 repetition cost reflects the same basic process, namely inhibition, under cue-based and under sequence-based selection. This is the assumption that needs to be examined before entertaining further theoretical speculation. Therefore, the experiments reported in this paper come in two parts. Experiments 1–3 will first replicate and extend the basic result reported by Schneider (2007) and then examine the boundary conditions under which large lag-2 repetition costs arise. The results of these experiments will leave little doubt that the idea of genuine task-set inhibition as the sole cause of these costs needs to be abandoned. Then, in the remaining Experiments 4–6, I will develop the general idea that these costs provide a window into the serial-order representations used to control task sequences and can be used to better characterize the relevant processes and representations.
Experiment 1
The goal of this experiment is twofold. First, the informal observation that sequence-based lag-2 costs are much larger than cue-based lag-2 costs needs to be confirmed using an explicit within-experiment contrast. Second, I wanted to replicate the basic finding of large lag-2 costs and the modulation of these costs through the sequence structure by Schneider (2007), however extending it to all three within-chunk positions. Recall, that the difference in lag-2 costs had been interpreted by Schneider (2007) as a modulation of inhibition through sequential structure (i.e., inhibition across versus within chunk boundaries). However, at this point we do not know how the lag-2 cost behaves across all three possible within-chunk positions. Thus, aside from the sequence types ABC-ACB and ABA-CBC, I also used the sequence ABC-BAC here, where the lag-2 repetition occurs on chunk position 1. Note, that these three sequences constitute all possible abstract sequence grammars that can be constructed for a sequence length of 6 with two chunks of three elements and with the constraint of no immediate repetitions. The three grammars differ from each other only in terms of phase shifts relative to the chunk boundaries.
Here, and throughout this paper the spatial rules task introduced by Mayr (2002, Mayr & Bryck, 2005) was used. Specifically, subjects were asked to apply one of three possible spatial translations to a stimulus location (a dot in one of four corners of a square) in order to determine the correct response (a key press on one of four keys arranged as a 2×2 matrix). For example, the “vertical” rule implied that response locations were determined by mirroring the dot location on a virtual horizontal line through the middle of the square. Each of the three rules (“horizontal”, “vertical”, and “diagonal”) specified a unique set of translations between the stimulus and the response location. These tasks were chosen because they are relatively simple, yet require the use of abstract rules (Mayr & Bryck, 2005).
The sequence blocks were closely modeled after the task-span procedure used by Schneider and Logan (2006) and Schneider (2007). At the beginning of each block, participants received a cue that specified the entire sequence of six tasks. After memorizing this sequence, participants applied it to consecutive stimuli, cycling through the sequence until the end of the block without additional task cues. Different from Schneider (2007) and Koch et al. (2006), who had used very short response-stimulus intervals (RSI), the response-stimulus interval used here was 1000 ms.
In the cueing blocks, the task cue was presented during the response-stimulus interval for a short interval (300 ms), after which it disappeared. Thus, except for this short cue presentation, the stimulus-response situation was identical for the cue-based and the sequence-based blocks.
Methods
Participants
Twenty students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
Stimulus presentation occurred on a 17-inch Macintosh Monitor. The stimulus display contained a frame in form of a square with side lengths of 8 cm (9.1°). On each trial, a circle with a diameter of 1 cm appeared in one of the four corners of the frame (see Figure 1). Responses were entered using four keys on the standard Macintosh keyboard with the same spatial arrangement as the four circle locations (“1”, “2”, “4”, and “5”) on the numerical keypad. Participants were instructed to rest the index finger of their preferred hand in the middle between the four keys and to move the finger to the correct key. After pressing the key, participants were instructed to bring back the index finger to the center position. Correct keys were co-specified by the circle location and the currently relevant rule. For the “horizontal” rule, a horizontal shift of the circle position led to the response location; for the “diagonal” rule, the diagonal translation of the circle position led to the response location (e.g., upper left corner to lower right corner).
Figure 1.
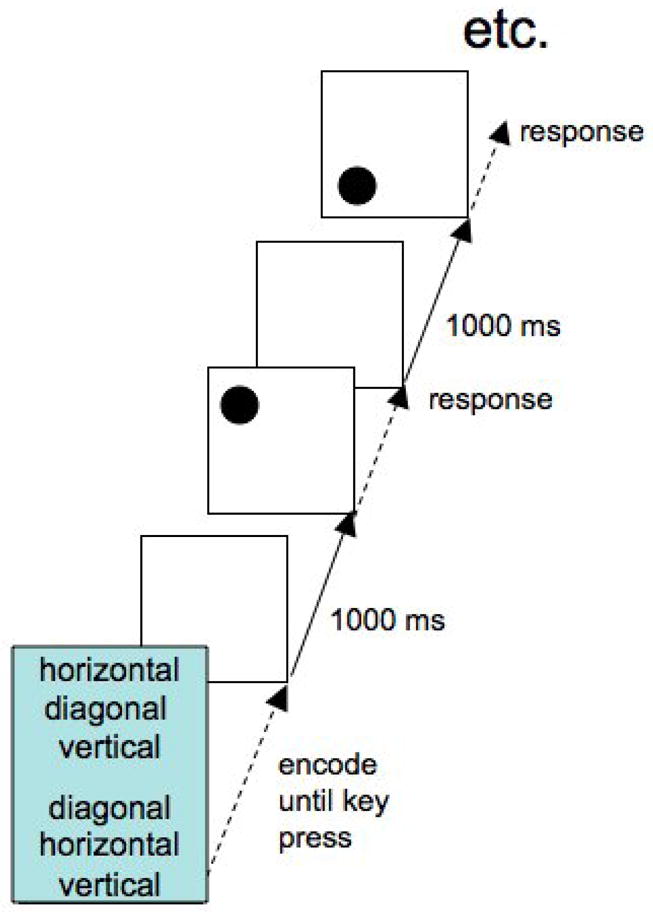
Sequence of events in the task-span procedure.
During sequencing blocks, the rule to be applied to the stimulus in a given trial was specified through that trial’s position in the task sequence. Sequences could have three different grammars: 1=ABC-BAC, 2=ABC-ACB, or 3=ABA-CBC. In total, there were 24 different specific sequences that can be implemented with these three abstract sequences. Each individual subjects was presented a random subset of 12 of these sequences, one for each of 12 sequence blocks. Blocks were 42 trials long so that each 6-element sequence was repeated 7 times within block. Prior to each block, the relevant six-rule sequence of task labels was presented on the screen above the empty stimulus frame. To facilitate organization of the sequence into two chunks of three trials each, the two chunks were presented with a spatial separation (see Figure 1). With a press of the space bar, subjects could initiate the actual block. At this point the sequence cue disappeared and after 1000 ms the first stimulus appeared and was presented until the correct response was entered; all following stimuli were presented in the same manner, with a constant response-stimulus interval (RSI) of 1000 ms. Participants moved through the memorized sequence element by element, starting over after the sixth element. In case of an error, the stimulus remained on the screen and the sequence of six task labels reappeared with the currently relevant task label presented in highlighted. This allowed subjects to realign themselves with the sequence. The sequence information disappeared and the block resumed after subjects entered the correct response.
During the cued blocks, rules were selected completely randomly with the constraint of no repetitions. This implies that lag-2 repetitions occurred here with a probability of p=.5 in contrast to the p=.33 in the sequence condition. I decided against matching of probabilities in the random blocks to those in the sequenced blocks because this would have required deviations from randomness in the cued blocks and thus potential expectancy violations for lag-2 repetitions. In contrast, given the explicit sequences in sequenced blocks, participants always knew when these would occur, thus the lower frequency of lag-2 repetitions should not violate expectancies. Nevertheless, to ensure that the unequal frequency of lag-2 repetitions across conditions did not bias results, I did conduct a follow-up experiment with matched lag-2 repetition frequencies (see Footnote 1).
As task cues, verbal task labels were presented centered in the stimulus frame 200 ms after the previous response for 300 ms. Then, the cue was replaced by the empty frame for 500 ms, followed by the stimulus. There were twelve 42-trial blocks of cued task selection. The order of sequenced and cued blocks was determined randomly. Prior to actual testing, subjects went through a practice phase of 108 trials during which six 36-trial blocks with different, randomly selected sequences were presented.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all response times (RTs) longer than 4000 ms (i.e., eliminating 0.6% of all trials). We also eliminated the first 6 trials of each block.
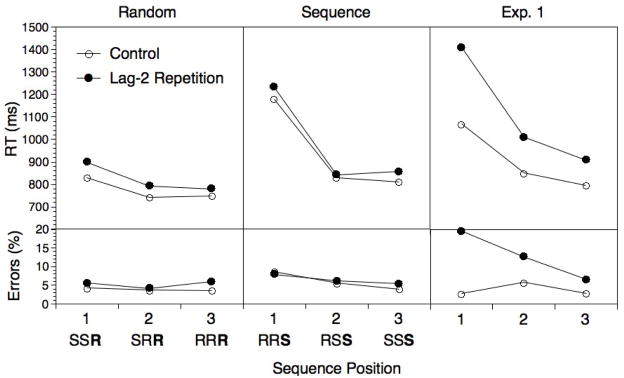
Figure 2 presents RTs and error rates across the six sequence positions and for the cueing condition, separately for lag-2 repetition and control trials. These data were analyzed using a-priori, orthogonal contrasts over a combined, 7-level sequence-position and cued factor (sequence vs. cued, 1st subsequence vs. 2nd subsequence, position 1 vs. positions 2 and 3 and position 2 vs. position 3 within subsequence) and the lag-2 repetition versus control factor. As evident, RTs were generally longer in the sequencing than in the cueing condition, F(1,19)=102.6, p<.001, MSE=28897.8, 1st position RTs were longer than RTs for the remaining two positions, F(1,19)=96.3, p<.001, MSE=66414.9, and 2nd postion RTs were longer than 3rd position RTs, F(1,19)=8.7, p<.01, MSE=26904.8. In addition, the 1st position slowing was longer for the first than for the second chunk, F(1,19)=13.4, p<.01, MSE=19000.5, consistent with a representation of the 6-element sequences in terms of two hierarchical levels (i.e., the level of chunks and the level of within-chunk elements; see also Schneider & Logan, 2006).
Figure 2.
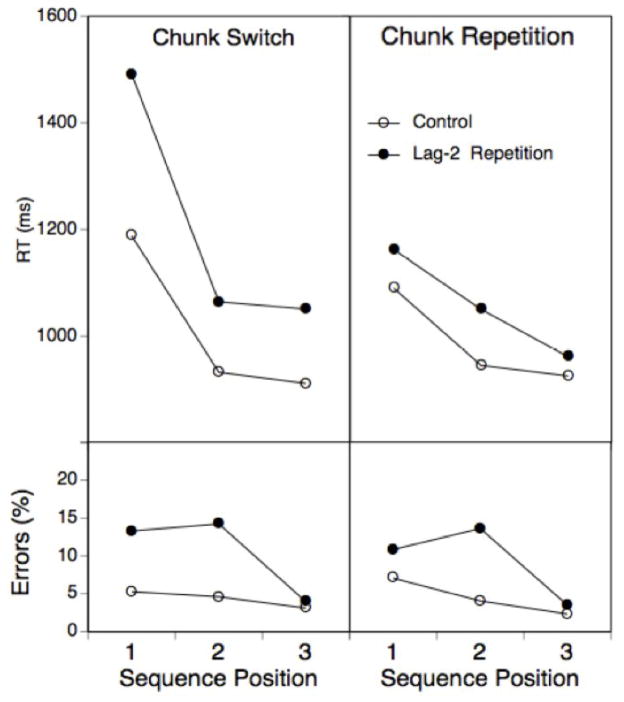
Experiment 1: Mean RTs and error percentages for each sequence position and the cued task selection condition and as a function of lag-2 repetitions versus changes.
More importantly, there was a highly reliable lag-2 repetition effect, F(1,19)=40.9 p<.001, MSE=55817.1, which however was much larger for the sequence than for the cue-based condition, F(1,19)=30.3, p<.001, MSE=8420.9. The lag-2 repetition effect in the cued condition was with 33 ms highly reliable, t(19)=5.1, p<.001, and in the range of lag-2 costs typically obtained in this type of paradigm (e.g., Mayr, 2002). However, with 205 ms, the overall lag-2 cost in the sequencing condition was about six times longer than that.1 In addition, the lag-2 cost was modulated by sequence position. In particular, it was much longer for position 1 than for the remaining two positions, F(1,19)=14.5, p<.001, MSE=40669.9, whereas the numerical difference between position 2 and 3 was not reliable, F(1,19)=.5. Note, that the difference in lag-2 costs between positions 2 and 3 was found by Koch et al. and Schneider and had been interpreted in terms of a between-versus-within-chunk repetition contrast. Certainly it is not possible to rule out that with greater power such a difference might be obtained within our paradigm; in fact, we did find a reliable difference between positions 2 and 3 in later experiments. However, the overall pattern that arises when taking into consideration all three within-chunk positions suggests that lag-2 costs may be the longer, the earlier the repetition occurs within the chunk rather than qualitatively different for within-versus-between chunk repetitions.
It is useful to look at the sequence-position effects also for the three different sequence grammars (Figure 3). As apparent, there was a very selective increase of RTs for each lag-2 repetition while the across sequence RT differences were small for all other positions. This is important because it indicates that there were no overall difficulty differences between the sequence types.
Figure 3.
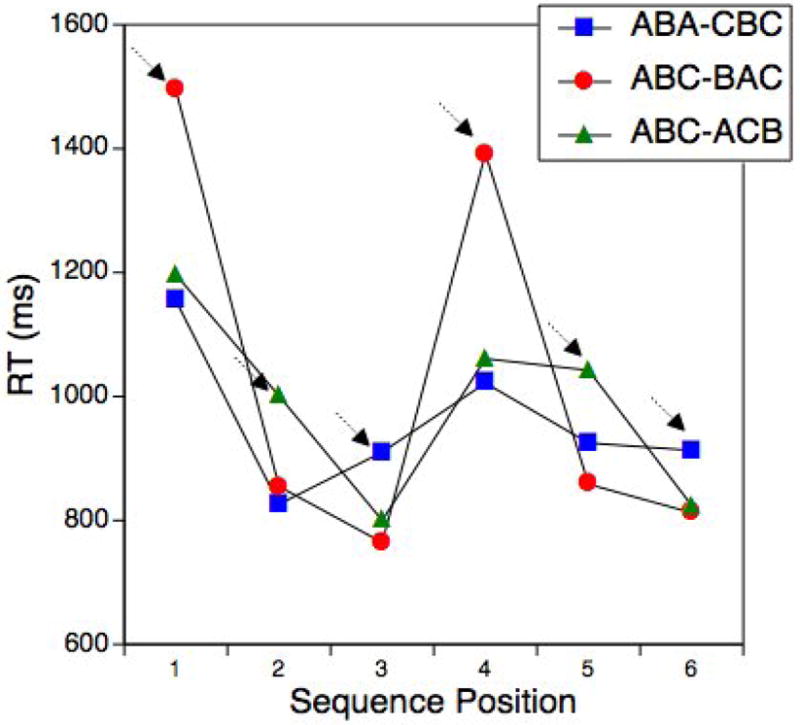
Experiment 1: Mean RTs for the regular-sequence trials as a function of sequence grammar and position.
In terms of lag-2 repetition effects, the error pattern presented in Figure 2 was consistent with the RT pattern and therefore no separate analyses will be reported. Error rates for lag-2 repetitions were in part rather high (around 20% for a four-choice task), in particular for positions 1 and 2. It is possible that these high error rates indicate that a proportion of subjects did not adequately memorize the sequences. However, when looking at participants with a below-median error rate, their pattern of RT results was in all aspects identical to that of the full group. Another aspect that deserves mentioning is that while there was a general, within-chunk position effect on RTs (i.e., subjects got faster with each sequence position, even for control trials), there was no comparable effect for errors.
Experiment 2
This preceding experiment confirmed that at least in the serial-order control situation used here, lag-2 repetition costs were in fact much than when tasks were cued on a trial-by-trial basis. This raises the theoretically important question to what degree the lag-2 costs during sequential control reflect the same inhibitory process that seems to be present during random cueing—only much stronger, or to what degree some qualitatively different process comes into play. As a first step towards addressing this question it is important to better delineate the boundary conditions for obtaining the large sequence-based costs. Experiment 1 compared sequential and cue-based control in a global manner, thus providing no information about what exactly it is about a sequentially controlled transition of tasks that produces the large costs. Logically, at least three different constellations of necessary conditions for large costs are possible: (1) large costs arise when the “disengage” transition in the critical ABA sequence (i.e., from A to B) is under sequential control, (2) large costs may arise when the “reengage” transition is under sequential control (i.e., from B back to A), or (3) it may be necessary that both transitions are under serial-order control. Theoretically, the first possibility, namely that large costs arise specifically when sequential control is used to switch away from a task is most consistent with the inhibition view.
To examine these three possibilities, the next experiment used hybrid sequences that alternated between a fixed, 3-element sequential plan and three randomly selected tasks. For example, at the beginning of a block, participants might receive the sequential cue: vertical-horizontal-vertical—random-random-random (the different elements will be referred to as S1, S2, S3, and R1, R2, and R3). In this case, participants would use the sequential plan for the first three stimuli in sequence, then use tasks signaled through visually presented task cues for the next three, then return to the sequential plan and so forth. This design allows examining (1) disengage transitions that are under sequential control, but where the return transition is under cue control (i.e., S2-S3-R1, in the above example: horizontal to vertical when the next randomly cued task is horizontal), (2) at re-engage transitions that are under sequential control, but where the disengage transition is under cue control (i.e., R3-S1-S2, in the above example: vertical-to-horizontal when the previous randomly cued task was horizontal) and (3) at situations where both the disengage and the reengage transition are under sequential control (i.e., S1-S2-S3 in the above example).
Methods
Participants
Thirty-four students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
All aspects were identical to Experiment, except for the following changes. Prior to each block of 42 trials, participants had to memorize hybrid sequences consisting of three regular elements and three random elements. Regular subsequences consisted of the same 3-element subsequences used to construct the 6-element sequences in Experiment 1. For example, participant might receive a cue such as “horizontal – vertical – horizontal – random – random – random”. Random sequence portions were selected from the same set of 3-element subsequences, with the only constraint that at the transition points between random and regular subsequences, no rule repetitions could occur. Thus, in this experiment, lag-2 repetitions across both random and sequenced blocks were matched.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all response times (RTs) longer than 4000 ms (i.e., eliminating about 0.5% of all trials). We also eliminated the first 6 trials of each block.
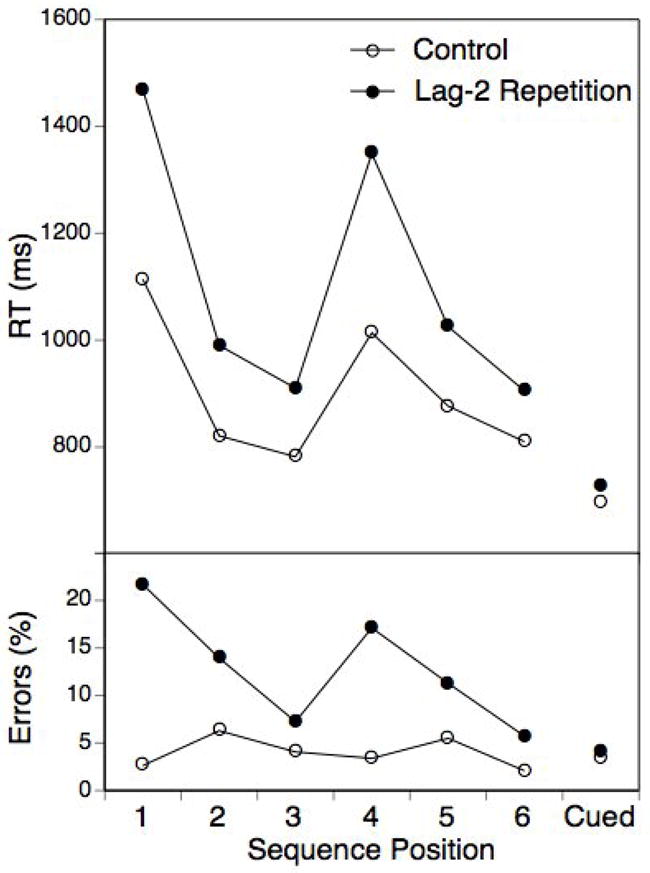
Figure 4 shows RTs and error scores separately for random and regular sequence portions as a function of sequence positions. For better comparison, also the corresponding results from Experiment 1, collapsed across the two chunks, are presented. As apparent, lag-2 costs were present for most positions, however were generally much smaller than for Experiment 1. Specifically, there was little evidence that disengage transitions from one sequenced element to the next produced particularly large lag-2 costs, no matter whether the repetition itself was cued (i.e., random position 1) or sequenced (i.e., sequence position 3). Individual t-tests confirmed reliable lag-2 costs for all three random positions, all ts(33)>2.62, p<.05. For sequence position 1, the cost was reliable, t(33)=2.39, p<.05, it was clearly not reliable for position 2, t(33)=.72, p>.4, but it was reliable again for position 3, t(33)=2.41, p<.05. There is no immediate interpretation of the absent cost for position 2, however it is possible that there is something special about a transition from a random to a sequenced element that makes inhibition unnecessary. The pattern of RT results was not qualified by the pattern of error results, however as evident from Figure 4, lag-2 error costs for both random and sequenced positions were much smaller than for Experiment 1.
Figure 4.
Experiment 2: Mean RTs and errors for the sequenced and cued trials of the hybrid sequences and as a function of lag-2 repetitions versus changes. The letters beneath the X-axis indicate if the current and preceding tasks were randomly cued (C) or sequenced (S). As a comparison also the data for Experiment 1 are shown, collapsed across the first and the second chunk.
Experiment 3
The preceding experiment used regular 3-element sequences and this led to much smaller lag-2 costs than in Experiment 1, where 6-element sequences (consisting of two 3-element chunks) had been used. This result is not consistent with the idea that sequential control situations per se lead to very large inhibition effects. So what exactly is it about such situations that produces large lag-2 costs?
If one wanted to save task-set inhibition as the explanation of large lag-2 costs, one might speculate that inhibition is particularly critical when the same sequential element is used across two different chunks. Maybe inhibition occurs not only on the level of rules or tasks, but also on the level of more abstract sequential elements. Given that such abstract sequential elements would not be involved during randomly cued sequences, this might also explain why lag-2 costs are relatively small for lag-2 repetitions between a sequenced and a randomly cued element (see Experiment 2).
An alternative possibility is that the large lag-2 costs have nothing to do with inhibition. Rather, costs might reflect the demands of coordinating identical sequential elements across a limited set of positional cues. We will expand on this idea in the introduction to Experiment 4. At this point it is sufficient to understand that in the sequences used this far, the repeated elements inevitably occurred at different sequence positions across chunks (e.g., in ABC-BAC the lag-2 repeated B occurs at position 1, which in the other chunk is associated with element A). Thus, lag-2 repetitions may be points where positional interference from competing task-position conjunctions needs to be resolved (e.g., B at position 1 needs to compete against B at position 2 and/or A at position 1). Note, that a key consequence of this account is that lag-2 repetitions per se are not actually critical for large costs. Thus, if this account has any merit, it should be possible to construct situations where interference from competing task-position conjunctions needs to resolved in the absence of lag-2 repetitions.
In this experiment I attempted to create a situation in which interference across sequence positions might arise even when there are no lag-2 repetitions. I used the same 6-element sequences from Experiment 1, but instead of cycling through them in an uninterrupted manner, the two chunks were separated by a varying number (2–4) of intermittent trials. These intermittent trials were always cued, but in order to keep the task at a manageable level of difficulty, a simple “compatible” rule was used (i.e., subjects had to respond in a compatible manner with the stimulus location). Thus, a series if trials might take the form ABC-cc-BAC-cccc-ABC-ccc-BAC-cccc etc (where c stands for the cued, compatible trial). Obviously, for the first two elements of each chunk, the lag-2 repetitions are “broken apart” through the intermittent trials. Thus, if inhibition of the lag-2 task drives the costs then they should be eliminated for these two elements. In contrast, the between-chunk interference structure should not be affected much by the intermittent elements and therefore the previously observed pattern of costs should remerge here.
Methods
Participants
Because in this experiment a fewer number of critical trials could be assessed, a larger sample of thirty-eight students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
All aspects were identical to Experiment 2, except for the following changes. Prior to each block, participants had to memorize sequences consisting of six regular elements. In addition, subjects were informed that after each 3-element sequence two to four compatible tasks would be interspersed, signaled by a cue. The first full sequence was presented in an intact manner, then 2–4 cued trials with the compatible rule were interspersed after each chunk. Participants went through a total of 18 blocks of 60 trials each.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all RTs longer than 4000 ms (i.e., eliminating 0.5% of all trials). We also eliminated the first 15 trials of each block.
Figure 5 shows RTs and error rates for the regular sequence as a function of within-chunk position and whether or not a trial would be a lag-2 repetition if sequences were cycled through continuously. Recall, that the first two elements of each chunk were never contained actual lag-2 repetitions. What is referred to here as lag-2 repetitions is relative to the use of the alternate chunk, ignoring the intermittent compatible trials.
Figure 5.
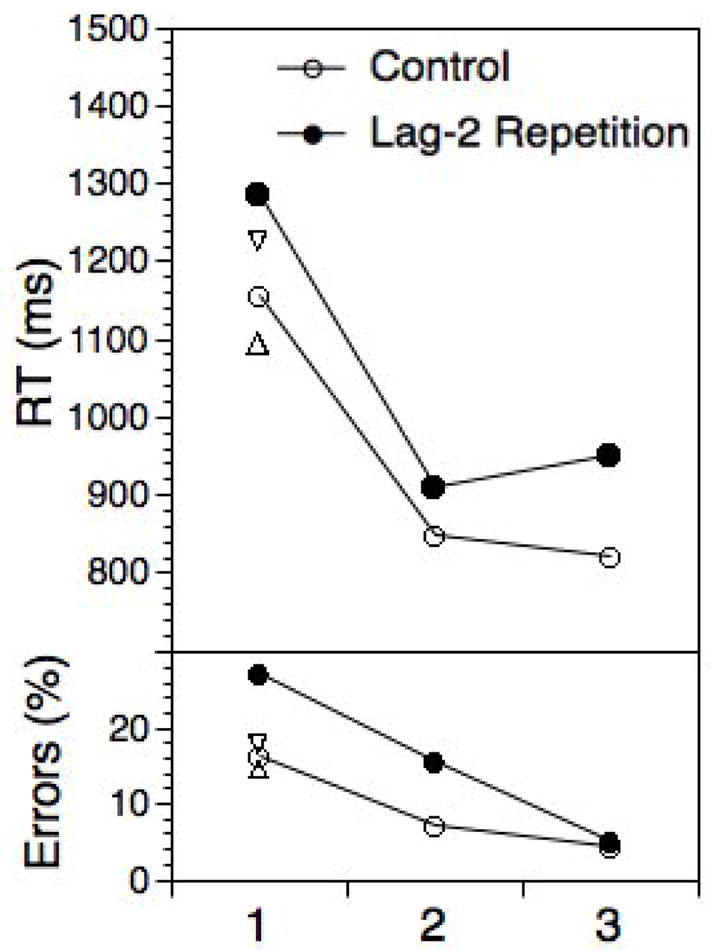
Experiment 3: Mean RTs and error rates for the sequenced trials as a function of lag-2 repetitions versus changes. Note, that lag-2 repetitions for positions 1 and 2 are not actual repetitions, but relative to the previous sequenced positions (i.e., spanning 2–6 cued trials). Triangles for position 1 indicate mean RTs and errors for the ABA-CBC (inverted) and the ABC-ACB (upright) sequences (discussed in section “Self-Inhibition?”).
As apparent, substantial RT costs emerged for all chunk positions and for errors for positions 1 and 2. The RT lag-2 cost main effect was reliable, F(1,37)=27.56, p<.001, MSE=23372.01, there was also a reliable effect for the first position against the remaining positions, F(1,37)=85.74, p<.001, MSE=67730.03, but no reliable interaction between these two factors, F(1,37)<1.0. In an analysis focusing only on the first two positions within a sequence (which did not include actual lag-2 repetitions), again, both the lag-2 cost F(1,37)=10.35, p<.01, MSE=33131.07, and the position effect, F(1,37)=93.54, p<.001, MSE=476650.83, were highly reliable, but again without a reliable interaction, F(1,37)=1.53, p>.2, MSE=30756.05. Regarding errors, the overall pattern was very similar to that of RTs, with the exception that due to the lack of a lag-2 repetition effect for position 3, the interaction between position (position 1 versus 2 and 3) and lag-2 repetitions was highly reliable. For the analysis including only positions 1 and 2, the interaction between the lag-2 repetition contrast and positions 1 versus 2 again failed the reliability criterion, p>.15.
From these analyses, it is clear that the lag-2 repetition cost does not depend on actual lag-2 repetitions.2 However, there also seem to be some differences to the pattern obtained in Experiment 1. First, the RT cost for positions 1 and 2 was somewhat smaller than that obtained for the continuously cycling sequences in Experiment 1. This might suggest that the costs observed in Experiment 1 and by Schneider (2007) consist of two components: actual lag-2 repetition costs and costs that are due to positional interference. Only the latter would be present in positions 1 and 2 of the current experiment. Note, that this would explain why in position 3, where both effects might be present, costs were at least numerically higher than in position 2.
Maybe even more striking is the fact that the position modulation of the lag-2 costs that figured so prominently in Experiment 1 seemed to be absent, or at least strongly reduced for the critical positions 1 and 2 in the present experiment. This leaves some ambiguity regarding the question whether the position modulation of the costs is associated with the actual lag-2 repetitions (and thus related to inhibition) or to the non-repetition component (and thus related to interference). Here I ask the reader to withhold judgment for now. After developing the complete positional-interference account in the next sections, it will become apparent that the position modulation is in fact present in these data, but occluded by an opposing effect (see section “Self-inhibition?”).
Representation of Serial Order and the Lag-2 Repetition Effect After the results of Experiment 3, inhibition can safely be ruled out as the sole, critical factor behind the large lag-2 costs. Thus, it is now time to take a serious look at possible alternative interpretations of this phenomenon. Participants in the present experiments had to memorize an organized sequence of tasks and apply this sequence repeatedly throughout a block of trials. This bears strong similarities to the demands of traditional, short-term serial memory tasks. Typically in serial memory tasks, subjects are presented a list of items (e.g., consonants) and are asked to reproduce them in order. The main dependent variable is accuracy, which is analyzed as a function of aspects such as such as serial position, list length, presentation rate, encoding-retrieval delays, within-list repetitions of items, or chunking structure. There is no need to review all of the benchmarks results here (e.g., Botvinick & Plaut, 2006; Marshuetz, 2005). However, there is one aspect, namely the manipulation of chunking structure that is of particular interest in the current context. Specifically, when a to-be-memorized sequence of items is organized in term of several chunks, usually a characteristic error pattern emerges where subjects insert an element from a different chunk, while preserving its within-chunk position. For example, if the consonant sequence is “tvr-gdk-sln”, a subject might reproduce it as “tvr-glk-sdn”, thus exchanging position 2 of chunks 2 and 3. Such between-chunk transpositions have been cited as one of the strongest empirical arguments in favor of so-called positional models and against associative chaining models of sequential representation (e.g., Henson, 1998a).
Traditional associative chaining models assume that sequences are represented in terms of associative links between adjacent elements of a sequence. Obviously, such models have a hard time explaining between-chunk transposition errors. From an associative chaining perspective there is nothing that would explain why the letter “l” might follow the letter “g” in the above example (e.g., Henson, 1998a).
In contrast, positional-coding models assume that there is a sequence-extraneous representation that codes for serial order by allowing associations between sequence elements and some kind of “position code”. In its simplest form, such a position code can be thought of as a number of “slots” labeled 1, 2, 3, etc., into each of which an incoming sequential elements is placed. More realistic are models that assume one or more continuous, temporal gradients (e.g., Marshuetz, 2005). The value of a gradient at the time a particular element is presented serves as a kind of time stamp for that particular element. For example, the start-end model proposed by Henson (1998a) proposes two gradients of activation, one with a maximum at the beginning of a sequence, the other with the anticipated end. Each of these provides contextual information that can cue sequential positions.
How would a generic positional model deal with the type of sequences used in the present experiments? Take the sequence ABC-ACB. I will refer to the six positions of such a sequence with the letters X and Y for the two chunks and indices 1–3 for the positions within a chunk. The starting assumption is that each of the two chunks is handled by the same set of positional code. For simplicity sake, I assume an explicit code such as “1”, “2”, and “3”. Across the two chunks, the first elements (X1 and Y1) are identical so that in each case element A is associated with cue “1”. However, both B and C (X2 and Y2) are used in conjunction with cue “2” so that here competition would have to be resolved if common sequential position codes are actually used to code serial order across different chunks. In principle, competition could arise in two different ways: First, the use of a particular position cue (e.g., “2”) might lead to activation not only of the currently relevant task (e.g., B for the first chunk), but also of the currently irrelevant task (e.g., C from the second chunk). Second, selection of a particular task (e.g., B) can activate not only the currently relevant position code (e.g., “2”), but also the currently irrelevant position code (e,g., “3”). The demands of resolving such conflict could account for the lag-2 RT cost at locations X2 and Y2 of the sequence ABC-ACB.
If we now move to the next element X3 or Y3, in principle the same type of competition should arise, again implying both elements B and C, and the shared position code “3”. However, resolution of this type of competition might come for free while dealing with the preceding sequence element. After all, the potential for conflict while selecting element C into position “3” would come from the same element that has just been selected as the previous element (i.e., B). Many theoretical models of sequencing assume a self-inhibition process that prevents perseveration of a once-selected element (Burgess & Hitch, 1999; MacKay, 1987; Page & Norris, 1998, Lewandowsky & Farrell, 2000). Self-inhibition would leave element C as the only element with ties to the position code “3” and therefore enable relatively easy selection of that element.
The identical logic applies to sequences of the type ABC-BAC and possibly with some qualifications also for sequences of the type ABA-CBC. In the former, the point where conflict from interfering position-task associations needs to be resolved is at positions X1/Y1 and self-inhibition counteracts interference at X2/Y2, and for the latter the corresponding points are X3/Y3 and X1/Y1 respectively. Admittedly, for sequences of the ABA-CBC type the situation is more ambiguous, as here part of the potential interference comes from within the same chunk (i.e., the fact that tasks used with positions X3/Y3 are also used for positions X1/Y1). This issue will not be completely resolved in the context of this paper, however I will provide some additional relevant information on this in the General Discussion (see section “Sources of Positional interference”).
Self-Inhibition?
According to the positional interference conception, in the sequences used this far, lag-2 repetitions simply happened to be those points in the sequence where conflict between shared position/element codes needs to be resolved. However an additional mechanism, self-inhibition, is required to explain why positional interference only strikes at certain locations in the sequence, but not at others. A reasonable question at this point is whether there is any other reason to postulate this mechanism than the fact that it is necessary to explain the pattern of data.
In fact, the previous Experiment 3 provides an originally unanticipated test case for the self-inhibition idea. Recall, that self-inhibition is supposed to eliminate interference in those cases where the potentially interfering task code had been used on the previous trial. Thus, in a sequence like ABA-CBC there should be no interference for position Y1 (or X1) because the potentially interfering task code was used for the preceding positions X3 (or Y3) and then presumably inhibited. However, this is only true for intact sequences. In Experiment 3, where randomly selected task elements preceded each chunk, no self-inhibition could be in place for the initial chunk positions. In other words, if self-inhibition actually protects from positional interference, we should expect to see costs for the initial positions of chunks from the ABA-CBC types of sequence, if preceded by randomly selected elements. I compared RTs for these trial types with first-position trials from the ABC-ACB types of sequence, where no positional interference is expected at within-chunk positions 1. The relevant data are presented in Figure 5 as inverted (ABA-CBC) and upright (ABC-ACB) triangles. A highly significant RT cost of 133 ms, t(37)=3.54, p<.01, and a significant error cost of 3.3%, t(37)=2.68, p<.05, emerged. Note, that no comparable cost can be found for the corresponding positions in the intact sequences used in Experiment 1 (see Figure 3).
This result has also consequences for the failure of finding a clear positional modulation of the interference cost in Experiment 3. Within-chunk positions 1 of the ABA-CBC sequences had served together with the corresponding positions from ABC-ACB sequences as control trials for ABC-BAC sequences, which in Experiment 1 had produced very large position-1, lag-2 cost effects. However, we now know that ABA-CBC sequences are actually not appropriate no-interference controls for position 1, as they themselves contain substantial interference effects. When we exclude these as control trials, the RT costs were 193 ms for within-chunk position 1, compared to 60 ms for position 2, F(1, 19)=4.52, p<.05, MSE=37170.60; corresponding error costs were 12.4% and 8.3%, F(1, 19)=4.0, p<.052, MSE=37.70.
These results show that self-inhibition can explain a highly specific pattern of performance costs and thus lend additional credibility to the self-inhibition hypothesis. They also they allow us to clarify the role of within-chunk position in modulating lag-2 costs. Re-analyses of the position effect that take self-inhibition into account revealed a clear modulation of costs at positions 1 and 2 (where no lag-2 repetitions could occur). In other words, the modulation pattern is a characteristic of positional inference and is not tied to actual lag-2 repetitions.
Sticky Plans: Experiment 4
This experiment was designed to provide a more direct test of the positional interference account and to independently assess the effects of costs due to positional interference and costs due to actual lag-2 repetitions, presumably due to inhibition. Two situations were compared. The first used the standard set of sequences from Experiment 1, organized as two chunks of three elements (referred to as 2-chunks-of-3 structure). The second used these same sequences, but now organized as three chunks of two sequences (referred to as 3-chunks-of-2 structure).
Table 1 spells out for each element in each of the three basic sequence grammars the theoretically critical events. There are three event types that are relevant here: lag-2 repetitions, interference events, and self-inhibition events; the fourth type, labeled “chaining”, will become relevant in the context of Experiment 5. The lag-2 repetition category is self-explanatory. To the degree to which traditional, inhibitory lag-2 costs are present in this paradigm we should expect costs at these points. Interference events are those where different elements are used across positions. By the interference account, these are events where we should expect particularly large costs. For the 2-chunks-of-3 structures, this is very straightforward, with two tasks and two positions that overlap (e.g., for the sequence ABC-BAC tasks A and B and positions 1 and 2). As already discussed, in this type of sequence, lag-2 repetitions and points of positional interference coincide and thus cannot be dissociated.
Table 1.
Theoretically Critical Sequence Events for the 3-Chunks-of-2 and the 2-Chunks-of-3 Sequence
| Sequence | Sequential Organization | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 Chunks of 3 | 3 Chunks of 2 | |||||||
| Lag-2 | PI | SI | IC | Lag-2 | PI | SI | IC | |
| A | + | + | + | + | ||||
| B | + | + | + | |||||
| C | + | + | ||||||
| B | + | + | + | + | ||||
| A | + | + | + | |||||
| C | + | + | ||||||
| A | + | + | ||||||
| B | + | + | + | + | ||||
| C | + | + | + | |||||
| A | + | + | ||||||
| C | + | + | + | + | ||||
| B | + | + | + | |||||
| A | + | + | + | |||||
| B | + | + | ||||||
| A | + | + | + | + | ||||
| C | + | + | + | |||||
| B | + | + | ||||||
| C | + | + | + | + | ||||
Note. Lag-2=lag-2 repetitions, PI=positional interference, SI=self-inhibition, IC=integrative chaining. For Lag-2, PI, and IC the table shows positions where these accounts predict costs. For SI the table shows positions where self-inhibition would counteract interference from the prime competitor.
This confound is clearly not present for the 3-chunks-of-2 structure where Table 1 shows that lag-2 repetitions and points of positional interference do not overlap. Thus, this sequential structure should allow dissociating the two potential sources of costs. Yet, it also needs to be acknowledged that there is a bit of an ambiguity with these types of sequences, which has to do with the earlier mentioned fact that there are two possible ways in which overlapping task and position codes can produce interference. First, if the same task is associated with more than one within-chunk position code, selecting the task into one position can lead to inadvertent activation of the incorrect position code. In each of the 3-chunks-2 sequences, there are two points where this interference could come into play (e.g., in the sequence AB-CB-AC for the two occurrences of task C) whereas no such conflict can arise for the remaining elements. The second possible source of interference arises from the fact that within-chunk position codes are shared across more than one task code. In principle, this is the case for each of the two position codes used in the 3-chunks-of-2 sequences. However, for each position there is one task that is used twice (e.g., in AB-CB-AC task A for position 1 and task B for position 2) and one task only used (e.g., in AB-CB-AC task C for positions 1 and 2). Thus, while for this potential type of interference, the 3-chunks-of-2 sequences do not present a straightforward all-or-none contrast, they do allow pitting sequence positions with more (task A and task B positions in the above example) versus less interference (task C positions in the above example) against each other.
Whether or not interference is actually expressed should depend on the third event category: self-inhibition. Self-inhibition is relevant when the task that could potentially interfere on the present trial had been used on the previous trial and is therefore not available to produce conflict. Going through the table it becomes apparent that situations where lag-2 repetitions and interference events are not counteracted by self-inhibition coincide for the 2-chunks-of-3 structure. Thus, the contribution of lag-2 repetitions and interference cannot be distinguished here. However, for the 3-chunks-of-2 structure the lag-2 repetition and the interference events occur at different positions. Thus, here we can determine to what degree large costs are associated with lag-2 repetitions, position interference events, or both.
Inspection of Table 1 also makes clear that across the different sequences and sequence structures, the potential influences are not distributed in terms of orthogonal factors.3 In such a situation, the standard ANOVA approach is not the best suited analytic strategy. Therefore, I will also analyze these data using a linear-regression based, model testing approach, which allows dealing with the non-orthogonality in the design and provides a concise description of the data.
Methods
Participants
Forty students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
The experiment was similar to Experiment 1, except for the following changes. Subjects were randomly assigned to two different conditions (n=20 each), differing in the structural format of presenting the sequences during the initial encoding phase, namely either in terms of two chunks of three tasks, or in terms of three chunks of two tasks. To ensure organization of the sequences according to instructions, during the sequence-cue phase, each chunk was presented sequentially and subjects had to press the space bar to exchange one chunk with the next. We used a total of 18 blocks and in each block sequences were cycled through 12 times.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all response times (RTs) longer than 5000 ms (i.e., eliminating 0.5% of all trials). We also eliminated the first 6 trials of each block.
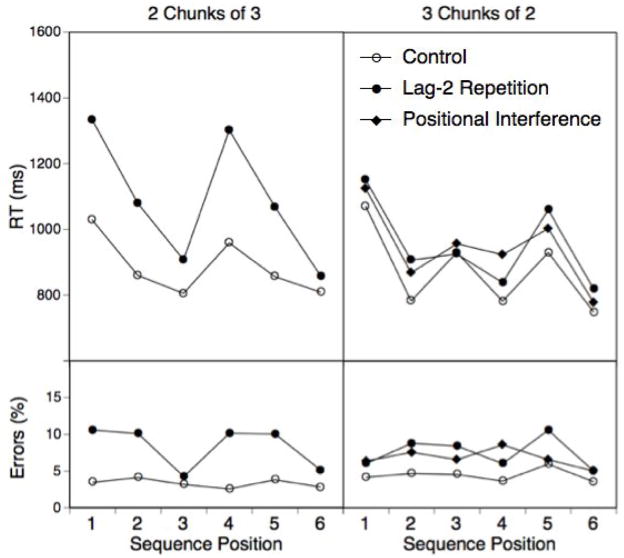
Figure 6 shows the pattern of RT and error results as a function of sequence structure, position, and critical event types. As apparent, the RT effects in the 2-chunks-of-3 structure are qualitatively very similar to those in Experiment 1. In fact, when analyzing these data using the same analytic strategy as in Experiment 1 (using a-priori, orthogonal contrasts that test 1st subsequence vs. 2nd subsequence, position 1 vs. positions 2 and 3 and position 2 vs. position 3 within subsequence as well as the lag-2 repetition versus control factor) the same pattern of significant effects emerged. The only exception was that in this experiment, the lag-2 repetition cost decreased significantly, not only between the first chunk position and the remaining positions (all ps<.01), but also between positions 2 and 3, F(1, 19)=6.63, MSE=29657.9, p<.05.
Figure 6.
Experiment 4: Mean RTs and error rates as a function of chunking patterns, position, and lag-2 repetitions versus changes.
The RT profile in the 3-chunks-of-2 structure looks very different. In part, this simply reflects the fact that subjects did actually use the induced structure, resulting in a saw-tooth pattern with RT peaks on trials 1, 3, and 5. Consistent with these observations, the first position of each chunk was reliably slower than the second position, F(1, 19)=41.72, MSE=77908.33, p<.01, and consistent with the assumption of a two-level hierarchical plan, this position effect was particularly large for the first chunk, F(1, 19)=10.39, MSE=23569.26, p<.01. More importantly, RTs for lag-2 repetitions were longer than for control trials, F(1, 19)=25.72, MSE=13538.39.26, p<.01, but they were also highly reliably longer for interference trials than for control trials, F(1, 19)=24.21, MSE=11541.16, p<.01. These two effects were modulated somewhat by sequence position. However, only for the lag-2 repetition effect was there a reliable interaction with the contrast between the second and the third chunk, F(1, 19)=6.05, MSE=9904.87, p<.05. It is noteworthy, that there was no indication of a general decline of either the interference costs or the lag-2 repetition costs as a function of within-chunk position, as found in the 2-chunks-of-3 sequence. None of the error effects shown in the lower panel of Figure 6 contradicted the pattern of RT effects.
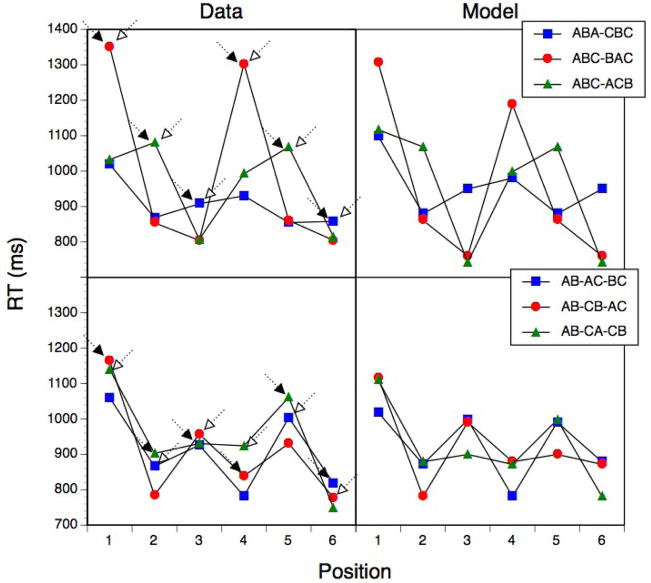
As stated in the introduction to this experiment, an orthogonal variation of the various aspects that might theoretically influence RTs is impossible and given the structure differences across sequences there is also no straightforward way of combining both sequential structures within one ANOVA. I therefore used a second type of analysis that subjected the group-level mean RTs from all three types of primary sequences (shown in Figure 7) and for both sequence structures (total: N=36) to a regression analysis with theoretically important effects as predictors.
Figure 7.
Experiment 4: Empirical RTs and model RTs as a function of chunking patterns, sequence grammars, and position. Filled arrows indicate lag-2 repetition trials and unfilled arrows indicate trials where positional interference should be large.
In order to capture essential aspects about the sequential structure, I used one predictor for the within-chunk position (1–3), as well as an additional predictor that was set to 1 for the first position in the sequence and to 0 otherwise. This, parameter captured the fact that RTs for the initial sequence position reflect the demands of assessing the plan level and the chunk, whereas RTs for the first position of a chunk only reflect the demands of accessing the chunk level. In addition, I used a parameter that was set to 0 for the 3-chunks-of-2 sequence and to 1 for the 2-chunks-of-3 sequence, and that was supposed to capture remaining differences between the two sequence structures. A baseline model that used these three parameters to predict the 36 data points achieved a modest R2 of .61.
In a second step, the theoretically critical parameters were entered one by one (see Table 1). Not surprisingly, the lag-2 repetition parameter explained highly significant, additional 17.3% of the variance, F(1,31)=24.5, p<.01. The interference parameter reflects the prediction that RTs should be increased when the present task or position is associated with other task/positions. It also produced a reliable increase in variance of 4.4%, F(1,30)=7.7, p<.05. Finally, the self-inhibition parameter reflects the prediction that interference costs from other tasks associated with the current chunk position (i.e., positional interference costs) are counteracted when the potentially interfering task had been used on the preceding trial and is therefore still suppressed. This predictor produced another significant, 4.9% increase in variance explained. The complete, 6-paramter model had an R2 of .87. All individual coefficients were highly reliable (all ps<.01). In the model, the lag-2 repetition effect was estimated as 98 ms, the interference effect as 90 ms, and the self-inhibition effect as 109 ms. As can be seen from the predictions shown in Figure 7, the fit is very good for the 2-chunks-of-3 grammar. For the 3-chunks-of-2 grammar, the model captures essential qualitative aspects. Except for one instance (position 3), the RTs for trials affected by either lag-2 repetitions or interference are longer than the trials affected by neither.
The combination of the reliable interference and self-inhibition effect, both independent of the lag-2 repetition effect, is the most important result in this analysis. It is consistent with the idea that positional interference combined with self-inhibition is at least partly responsible for the characteristic pattern of very large lag-2 repetition costs obtained by Schneider (2007), and reported in the present article. However, these results also indicate that there are actual lag-2 costs that also contribute to this effect. In fact, the estimated size of these lag-2 costs (i.e., 98 ms) were surprisingly large, in particular considering the reliable, but much smaller, “pure” lag-2 costs observed in Experiments 2. The actual lag-2 costs obtained in the 3-chunks-of-2 sequences (where it was not confounded by interference costs) was with 79 ms somewhat smaller, but still quite substantial, an issue I will return to in the General Discussion.
The model captures important aspects of the data, but is not perfect. In particular, there is no mechanism for the modulation of the interference cost in the 2-chunks-of-3 sequence. Again, this is an aspect I will return to in the General Discussion.
Experiment 5: Position Codes versus Integrative Chaining
In the context of the preceding experiment, I had proposed that the lag-2 costs observed in the 2-chunks-of-3 sequence are due to interference from associations between chunk positions and tasks used at other parts of the sequence. I had argued that this phenomenon is analogous to the type of inter-chunk transposition errors often found in serial-memory experiments using structured sequences. In fact, the occurrence of this type of errors has been one of the main empirical arguments in favor of plan-based sequencing models. According to such models, sequence positions are represented via associations between sequential elements and position codes that are extraneous to the actual elements.
Recently, however Botvinick and Plaut (2006) have posed an important theoretical challenge to this type of models. They argued that many, if not all typical serial-memory effects can be explained by a new variant of a so-called chaining model. In traditional chaining models, sequence position is coded intrinsically, namely through associations between adjacent elements. There is overwhelming evidence, that this simple account is incorrect (e.g., Baddeley 1968; Farrell & Lewandowsky, 2003). For example, the position translation errors across chunks cannot be explained via traditional chaining models, simply because positions are not part of the representation. Botvinick and Plaut, however suggested that a recurrent neural network implementation of the chaining model would fare much more successfully. In a recurrent network, the output of each sequential step is fed back into a hidden layer that also feeds back onto itself. This way, the network maintains a continuously updated memory of its recent past and it can use this memory to determine the next step. Importantly, given that the hidden layer integrates information in a non-linear manner, it retains information not in terms of discrete sequential elements (such as the traditional chaining model), but as integrated conjunctions of the various sources of information. Therefore, we refer to this type of account here as “integrative chaining”.
While the Botvinick and Plaut paper’s central focus is not on sequence structure effects, in their General Discussion they suggest how their model might account for transposition errors. Specifically, they show that their model reproduces such errors across identical positions of different chunks within the same sequence if the internal representations of these elements are more confusable between chunks than across elements within the same chunk. In addition, they argue that what could make same-position elements across chunks particularly confusable is the fact that subjects use some kind of “coarse indication of their position” (p. 227), for example by using articulatory stress patterns (e.g., Reeves, Schmauder, & Morris, 2000).
It is probably fair to say that such coarse position coding is not too different from the kind of extraneous codes suggested by proponents of the positional-coding camp (e.g., Henson, 1998a). However, what is different is the fact that such additional codes do not simply serve as cues to which sequential elements are attached, but that they enter along with other pieces of information (e.g., the actual sequential elements) into the internal representation that then is used to determine the next sequential element.
Why is this relevant in the current context? Close inspection of the types of sequences that give rise to the large lag-2 repetition costs reveals that this type of integrative chaining might actually be responsible for the costs we have observed. Take the sequence ABC-ACB. In a recursive network model, elements X1 and Y1 should be represented in a highly confusable manner because they share both the same task (A) and the same position. Of course, this should not matter for selection of these elements themselves because they are identical. However if, as the recurrent model assumes, selection of the next sequence event is based on the integrated representation of recent sequence events then we should expect selection difficulties at events that follow high-similarity portions of the sequence (for a similar logic, see Keele & Summers, 1976 and Kahana & Jacobs, 2000). In fact, this is exactly where we find the large lag-2 costs in this type of sequence. The same is also true for the other two variants of this sequence. In each case, lag-2 repetition points follow the position with identical task-position combination across the two chunks, which implies that costs arise at the position that follows the point of greatest representational ambiguity (from the perspective of a chaining model). In contrast, if the sequential representation is actually handled through extraneous position cues then this type of representational ambiguity should be irrelevant. Thus, there are two models of sequential representation that both predict interference in the sequences studied, but by very different mechanisms.
It is possible to conduct an initial comparison of these two models in the context of the preceding experiment. In the 2-chunks-of-3 sequences, the recursive chaining model, the positional-coding account, and the inhibition account (i.e., lag-2 repetitions) all make identical predictions. However, in the 3-chunks-of-2 sequences they can be dissociated. Table 1 shows the positions that follow positions with identical task-position combinations across two of the three chunks. According to the chaining model, these positions should produce particularly large costs. Again, we ran the regression analyses using in a first step sequence type, first position of the sequence, within-chunk position as predictors, and lag-2 repetitions, resulting in an R2 of .78. When the “chaining” predictor was included in the next step, the amount of variance explained increased by .075, F(1, 30)=15.47, p<.01, which is only slightly less than the .093, F(2, 29)=10.85, p<.01, we achieve when adding the two parameters necessary for the positional interference account (interference and self-inhibition). When adding the chaining predictor fist, the additional amount of variance explained (R2=.022) by the two positional-interference parameters barely misses the significance criterion, F(2, 28)=2.5, p=.1. However, the chaining parameter is clearly not significant, when added last, R2=.003, F(1, 28)<.7. Also, in the full model, the interference parameter ends up significant, p=.04, and the inhibition parameter almost, p=.08, whereas the chaining parameter is not, p=.4.
The statistical power of this regression analysis on the level of mean RTs is not very high. However, we can also directly compare those sequence positions in the 3-chunks-of-2 sequence where the two models make divergent predictions. For example, in the sequence AB-AC-BC, the recursive model predicts costs at positions 1, 2, 4, and 5, whereas the interference account only predicts costs at positions 2 and 5. The relevant contrast for the divergent positions (i.e., in the above case 2 and 5 versus 1 and 4) is actually identical to the contrast between control and interference events shown in Figure 6 and is highly reliable. This is a difference that the integrative chaining model cannot explain, but that is clearly predicted by the position-based interference account.
Nevertheless, the integrative chaining model would provide a very parsimonious account of the large costs in the 2-chunks-of-3 sequences compared to the two-parameter account required for the positional-interference model. Also, Experiment 4 was not really designed to compare these two accounts. For example, in the critical 3-chunks-of-2 sequence the integrative chaining model predicted costs at four out of six positions and this may have provoked subjects to enact strategies to counteract chaining-based interference.
In this experiment, I tried to come up with a more direct test of the integrative chaining account. According to this account costs should arise in a sequence like ABC-ACB at positions X2 and Y2 because they follow the high-ambiguity positions X1 and Y1. Conversely, costs should disappear if the ambiguity at positions X1 and Y1 is eliminated. A straightforward way of eliminating ambiguity is by using non-identical elements at these positions. To achieve this, while at the same time leaving the rest of the sequence as intact as possible, I replaced one of the two high-ambiguity positions by a forth type of task D. A resulting sequence such as DBC-ACB has no representational ambiguity at positions X1 and Y1 and therefore, by the integrative chaining account, there is no reason to expect a cost at positions X2 and Y2. In contrast, this change to the sequence does not affect the predictions of the positional coding account.
Methods
Participants
Twenty students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
The experiment was similar to Experiment 1, except for the following changes. As an additional response rule the compatible rule was used, where the subjects had to respond to the key that was spatially compatible with the stimulus location. This is the one remaining rule that does not overlap in terms of individual S-R links with any of the other three rules. Taking the three possible 2-chunks-of-3 sequence structures, the compatible rule was inserted in the first chunk, at the high-ambiguity points (i.e., with same rules and positions). Thus, sequence ABA-CBC becomes ADA-CBC, sequence ABC-ACB becomes DBC-ACB, and sequence ABC-BAC becomes ABD-BAC. We used a total of 18 blocks and in each block sequences were cycled through 10 times.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all response times (RTs) longer than 5000 ms (i.e., eliminating 0.5% of all trials). We also eliminated the first 6 trials of each block.
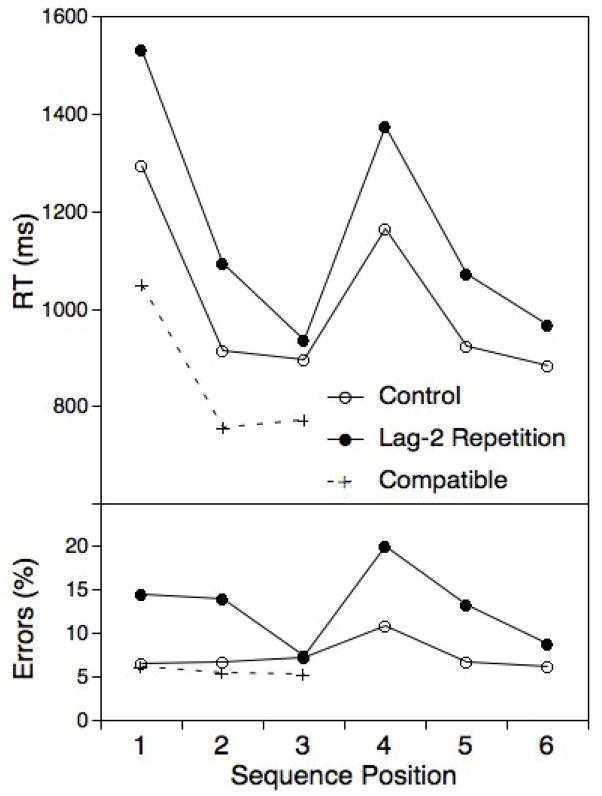
Figure 8 shows the pattern of RT and error results as a function of sequence position, and critical event types. The compatible-rule trials are shown separately because this rule has a different status than the remaining rules: It is not balanced in its occurrence across all sequence positions and it is easier than the other, all non-compatible rules. Therefore, trials with this rule were not included in any of the following analyses. As apparent, the qualitative pattern of RT effects is very similar to the one in the remaining experiments using this sequence structure. In fact, lag-2 repetition costs were highly reliable, F(1,19)=25.39, MSE=52768.29, p<.001. This result is clearly inconsistent with the integrative-chaining account, but is it compatible with the positional interference account.
Figure 8.
Experiment 5: Mean RTs and error rate as a function of sequence position and lag-2 repetitions versus changes. The unique task element was used for sequence positions 1 to 3. The dashed line shows RTs for trials with the unique task and which were always lag-2 changes.
The numerical pattern of costs across chunk positions is also consistent with the preceding experiments, however the interactions between the lag-2 repetition and the two different chunk contrasts (position 1 vs. 2 and 3, position 2 vs. 3) failed the reliability criterion, F(1,19)=2.27, MSE=73115.04, p=.15 and F(1,19)=2.39, MSE=42854.86, p=.14.
One reason why this experiment may have been less sensitive to position effects than the preceding experiments is that inclusion of the compatible rule increased general selection difficultly for the remaining rules. It is generally more difficult to select non-dominant rules if dominant rules are potentially relevant within the same context (e.g., Allport & Wylie, 2000). In fact, Figure 8 shows that RTs for the non-lag-2 repetition conditions were about 100 ms longer than in the comparable experiments (e.g., Figures 2 and 6). Moreover, this increase was particularly strong on the first sequence position. It is possible that this difficulty effect is underadditive with the modulation of the lag-2 cost and as a result makes this effect harder to detect. This minor divergence from the previous results non-withstanding, the large lag-2 costs observed here are inconsistent with the integrative-chaining model.
Experiment 6: Carry-Over in Working Memory versus Long-Term Memory Interference
So far, the results clearly indicate positional interference as the main culprit behind the large lag-2 costs. However, one question that still needs to be addressed is where exactly this interference comes from. Specifically, performance costs could either be the consequence of incompatible control representations “colliding” in working memory or from interfering information in long-term memory (LTM).
In previous work on hierarchical control, the idea of control representations colliding in working memory often seemed to be the default perspective (e.g., Kleinsorge & Heuer, 1999; Rosenbaum, Weber, Hazelett, & von Hindorff, 1986). In fact, it is interesting to note that the pattern we observed here bears some interesting similarities to the so-called parameter-remapping effect reported by Rosenbaum et al. (1986) in the context of phoneme or keypress sequences. For example, these authors reported that participants had a relatively hard time producing repeated, odd-numbered chunks of phoneme sequences with alternating stress levels (e.g., AbC-aBc-AbC etc.) compared to even-numbered sequences (e.g., AbCd-AbCd-AbCd etc.). Obviously, while even-numbered sequences allow the same mapping between stress level and letters across repeated cycles, the odd-numbered sequences require constant switching of mappings. From these and similar observations, Rosenbaum et al. concluded that production of the phoneme sequences involves the parameterization of a motor program maintained in working memory, which includes setting up the rule for assigning stress levels. Between consecutive cycles, the motor program is preserved and will be changed only for those parameters that actually need changing. Difficulties with the odd-numbered phoneme chunks arise because they require substantial re-parameterization after each cycle. Similarly, the lag-2 costs observed in the current series of experiments might arise because of the need to constantly remap position-task combinations.
A second possibility is that interference occurs not via representations maintained in working memory, but rather because selection events leave traces in long-term memory. Specifically, in line with instance-based models of episodic memory (e.g., Hintzman, 1986; Logan, 1988) one might assume that using a particular task with a particular sequential position leaves a trace of that association in LTM. When at a different position of that sequence the same task needs to be used, the desired task representation in LTM may be less findable, because of its associations with a different position code.
Recall that in Experiment 3 regular sequences had alternated with a series of intermittent trials. That experiment had revealed the same basic pattern of costs as in uninterrupted sequences, a pattern that seems more consistent with LTM-based interference than with interference that takes place in working memory. However, such an interpretation would rest on the assumption that serial-control representations in working memory do not survive cued task-selection events. While certainly plausible, we know too little about the constraints on serial-order representations to draw such a conclusion.
Fortunately, there should be another, relatively straightforward way of distinguishing between these two ways in which interference might occur, namely by using sequences that contain immediate repetitions of chunks. For example, instead of the 6-element sequence ABC-ACB one can use the 12-element sequence ABC-ABC-ACB-ACB. If interference occurs in working memory, it should be eliminated for direct repetitions of chunks—even in the presence of other, potentially interfering chunks. After all, the serial-order representation for a specific chunk can be simply maintained in case of a repetition. In contrast, from an LTM perspective, direct repetitions of chunks should not protect from interference. It is possible that interference is reduced, simply because the most recently used memory traces are consistent with the currently relevant ones. However, the fact that there are other possible positions/element combinations in the same context should produce memory traces that can lead to interference.
Methods
Participants
Eighteen students of the University of Oregon participated in a single-session experiment in exchange for course credit or $7.
Stimuli, Tasks, and Procedure
The experiment was similar to Experiment 1, except for the following changes. Instead of 6-element sequences 12-element sequences were used here. This sequences were constructed analogous to the 2-chunks-of-3 sequences used in Experiments 1, 3, and 4, however each chunk was repeated once. We used a total of 18 blocks and in each block sequences were cycled through five times.
Results and Discussion
Error trials and the two trials following an error were eliminated, as well as all response times (RTs) longer than 5000 ms (i.e., eliminating 0.5% of all trials).
Figure 9 shows the pattern of RT and error results as a function of chunk repetition versus switch, chunk position, and lag-2 repetition/interference. Note, that lag-2 repetitions are actual repetitions only for the switch chunk. Because we have fewer observations here for each one of the 12 sequence positions than in the preceding experiments, results were averaged across corresponding positions of the first the second half of the overall sequence. For the chunk-repetition condition, results showed the usual pattern of costs that are particularly large for position 1. For the chunk-switch condition, costs were reduced and relatively independent of position, but still clearly present (M=79 ms). The ANOVA reveals as theoretically interesting effects, a general lag-2 repetition cost, F(1,17)=30.89, MSE=34897.30, p<.001, a switch by lag-2 repetition interaction, F(1,17)=7.99, MSE=26072.79, p<.05, and a triple interaction that also includes the contrast between within-chunk positions 1 versus 2 and 3, F(1,17)=5.99, MSE=17916.86, p<.05. When analyzing only repeat chunks, the lag-2 cost remained highly reliable, F(1,17)=12.99, MSE=13036.47, p<.01, but there was no interaction with the position contrasts, both Fs<1.1. Most importantly, costs were clearly present even for repeat chunk positions 1 and 2. Obviously, because of the chunk repetition, these did not involve actual lag-2 repetitions of tasks, and therefore cannot be explained in terms of task-set inhibition.
Figure 9.
Experiment 6: Mean RTs and error rate as a function of chunk repetition versus switch, sequence position, and lag-2 repetitions versus changes. Note, that lag-2 repetitions were defined relative to the alternative chunk, even for chunk-repeat trials.
The pattern of error costs differed somewhat from the pattern of RTs, as here, the switch factor did not seem to have much of an effect. There was a general lag-2 repetition cost, F(1,17)=37.71, MSE=46.73, p<.001. This effect was not modulated significantly through the switch factor, F(1,17)=2.07, MSE=21.88, p>.15, but it was modulated through the contrast between position 2 and 3, F(1,17)=30.10, MSE=29.90, p<.001. As apparent in Figure 9, error costs were substantial for positions 1 and 2, were eliminated for position 3.
In general, both the RT and the error effects were consistent in showing substantial costs even for chunk repetitions. This strongly favors the LTM interference account over a working-memory carry-over account. An additional interesting aspect is that the modulation of costs through within-chunk position was completely eliminated for the chunk-repeat condition. I will return to this result in the General Discussion.
General Discussion
Both common wisdom and prominent memory theories suggest: Repetition facilitates performance. Thus, when this general rule is violated and repeated events elicit performance costs, special scrutiny is in order as such counterintuitive results can be particularly informative about underlying mechanisms. In this paper, I have taken a close look at the so-called lag-2 repetition cost that had been documented in situations when people need to select tasks on the basis of complex task sequences (Koch et al., 2006; Schneider, 2007).
Experiment 1 not only replicated previous results of very large lag-2 repetition costs within a 6-element sequence consisting of 2 chunks of 3 elements (Schneider, 2007), but also demonstrated that these costs were in fact much larger than lag-2 repetition costs observed when tasks are exogenously cued (e.g., Mayr & Keele, 2000). This experiment, along with Experiments 3, 4, 5, and 6 also showed that the lag-2 costs were largest for within-chunk position 1, with perhaps some additional reduction of costs for the contrast between positions 2 and 3. Experiment 2 demonstrated that the large-sized costs are not due to sequencing demands per se. Rather, as demonstrated in Experiment 3, a necessary and sufficient condition for the emergence of the large-cost pattern is the requirement to use two different chunks within the same context––even when the two different chunks are separated by random events, thus eliminating direct lag-2 repetitions. This latter result provides the tipping point between an inhibition interpretation of the large-cost pattern and the positional-interference account of these costs, which is developed in the remaining experiments. Specifically, Experiment 4 allowed us to distinguish between actual lag-2 repetitions costs, which presumably reflect inhibition, and costs due to positional interference. Experiment 5 demonstrated that the pattern of costs is consistent with a positional coding account of how sequences are represented, rather than with a chaining account and Experiment 6 demonstrated the positional interference originated from LTM traces, rather than from carry-over effects within working memory.
In the remainder of the General Discussion, I first deal with the implications of these results for the notion of task-set inhibition and then I will address what we have learned about sequential control and some of the new questions raised.
Lag-2 Costs and Inhibition
The starting point of this research was the observation that the sequential lag-2 costs reported by Schneider (2007) were by orders of magnitudes larger than what had been reported previously (e.g., Mayr, 2007) and that they were modulated by sequential structure. In fact, the present results show that neither the very large costs, nor the modulation through sequential structure, can be attributed to inhibition. The strongest evidence in this regard comes from Experiments 3, which revealed that the costs and the sequential modulation were present even in the absence of actual lag-2 repetitions.
Schneider (2007), based on earlier results by Koch et al. (2006), had explained the fact that within-chunk repetition costs were reduced in terms of a two-factor account: Pure inhibition, expressed in between-chunk lag-2 repetition costs, and counteracting activation, which is added for within-chunk repetitions. This account is certainly plausible when looking only at repetition costs in the context of these two studies. However, there are two problems with it. First, so far all the available evidence suggests that lag-2 repetition costs are remarkably insensitive to the opportunity for preparation, as operationalized through the variation of the cue-stimulus interval in the cued task-switching situations (see Mayr, 2007). Thus, it is at least not immediately obvious why the fact that a task is preplanned within a chunk should affect the lag-2 cost. Second, and more important in the current context, the activation-plus-inhibition account provides no explanation for the large size of the repetition cost, in particular for between-chunk repetitions in Schneider (2007) and the current experiments.
The account developed here also assumes that two factors need to come together to produce the pattern of costs observed in serial-order control situations. However, instead of counteracting negative and positive effects there are two different types of negative effects. The first is task-set inhibition that arises in actual lag-2 repetition situations. The second is positional interference, which arises when the same position and task codes need to be recombined in different ways in different parts of a sequence. Moreover, all the evidence from the current experiments suggests that the positional modulation of costs affects the interference component, and not the inhibitory component. In other words, there is no need to find an explanation for why inhibition is so large in serial-order control conditions, or why inhibition may be modulated by sequential structure––these aspects of the costs are simply not related to inhibition. This also means that the current results do not really tell us very much new about actual task-set inhibition as typically studied in task-cuing experiments (e.g., Mayr, 2007; Schuch & Koch, 2003).
The fact that according to these results, a substantial portion of sequence-based lag-2 repetition cost is much better explained by a retrieval/interference explanation than by an inhibition explanation might raise questions whether such a retrieval/interference interpretation could be generalized to the entire range of lag-2 repetition costs (e.g., MacLeod, 2007). However, both in the standard cueing paradigm and in those situations in which actual lag-2 costs were obtained in the current experiments (e.g., Experiment 2 and Experiment 4) it is not obvious what the source of interference would be. Moreover, Mayr (2002) has found reliable lag-2 costs even in situations in which all possible sources of interference were eliminated (by using “complete” lag-2 repetitions for which not only the task, but also all stimulus and response aspects repeated). Thus, rather than undermining the interpretation of standard lag-2 costs, the present results serve as a reminder of the fact that empirical effects are rarely process-pure and that for supposedly “inhibitory” effects it is particularly important to test against non-inhibitory explanations.
The current results may contain no major news regarding the actual task-set inhibition, but they do provide some hints that inhibition-related lag-2 repetition costs might actually increase in the context of serial-order control demands. In Experiment 4, where actual lag-2 costs and interference costs could be assessed independently, the former was in the 70 to 100 ms range, which is at least twice as large as what we found with cued task selection or shorter, 3-element sequences in Experiment 2. Clearly, this is a result that needs to be followed up on and the present experiments suggest ways in which actual lag-2 costs can be assessed without contamination by non-inhibitory influences. Theoretically, it is possible that complex sequencing situations produce demands for inhibitory control that are not present when task selection is based on cues or very simple sequences (as used in Experiment 2). For example, it is possible that self-inhibition, which was proposed to counteract positional interference when the interfering element was selected on the preceding trial (see Experiment 4 and also Lewandowsky & Farrell, 2007), becomes manifest as lag-2 costs beyond immediate repetitions.
How is Task Order Represented?
Instead of telling us something about task-set inhibition, the sequential lag-2 repetition cost proved indicative of the type of representations used to control an ordered sequence of tasks. The key insight is that the pattern of RT costs resembled in important ways the pattern of error costs observed in serial-memory tasks. In particular, when people try to remember a chunked sequence of elements, they tend to transpose elements across chunks while retaining their within-chunk position. This type of error pattern has served as an empirical argument in favor of models that propose positional serial-order codes. Such codes are thought to be extraneous to the actual sequential elements, but serve as cues that specify, via associative links, an element’s within-chunk position. The very fact that between-chunk transposition errors occur suggests that the same cues need to be reused across different chunks. Thus, selection conflict can arise when cue-element associations from alternate chunks interfere with currently relevant cue-element combination. As it turns out, in the types of sequences used by Koch et al. (2006) and Schneider (2007), this type of positional interference coincides with the points of lag-2 repetitions.
However, before concluding that the interference observed in the current experiments is actually due to positional codes it was important to address an important, recent challenge to this type of explanation. Botvinick and Plaut (2006) have argued that a recurrent network models that uses no positional codes could explain many of the standard serial-memory results, including—with some additional assumptions––transposition errors. The sequential representation in this model consists of a hidden layer that keeps an integrated record of both its own prior states and the previous network output. The integrated memory of previous sequence events is used to predict the next sequential element. This model proposes a new variant of the so-called chaining model where sequential representations are based on associations between adjacent elements. Different from its predecessor models, however, the association is not between elements per se, but between a highly integrated representation of past network states and the next element. Theoretically, the integrative chaining model provides a parsimonious explanation of many sequencing results without requiring assumptions about explicit codes of sequential position.
A prediction that we can derive from this model is that positional interference should be particularly large for those sequential elements for which the representation of the preceding sequence positions provides little disambiguating information. Interestingly, the points at which we had seen large interference costs followed events with elements overlapping both in position and identity (for example, the high-cost elements X2 and Y2 in ABC-ACB followed the overlapping elements X1 and Y1). However, when we eliminated the ambiguity by using distinct elements at the critical positions (e.g., DBC-ACB instead of ABC-ACB; Experiment 5) the costs remained. This is remarkable, given that from the perspective of the chaining model, introduction of an additional, unique element should have made selection of the following elements (i.e., X2and Y2 in the above examples) particularly easy relative to all other elements, each of which are preceded by non-unique elements.
Botvinick and Plaut (2006) had not explicitly applied their model to sequential control situations with continuously recycling sequences, as I have examined here. It is very well possible that such situations put a particularly strong emphasis on the establishment of extraneous position codes. In contrast, the recurrent network model might fare well when the sequencing demands are less explicit. Interestingly, research on implicit sequence learning has revealed that ambiguity of sequences, defined as whether or not there are unique associations between adjacent elements, has strong effects on learning (e.g., Cohen, Ivry, & Keele, 1990; Keele, Ivry, Mayr, Hazeltine, & Heuer, 2003). Thus, it would be useful to directly contrast explicit and implicit sequencing requirements to see whether they lead to different types of interference patterns diagnostic of either positional or integrated chaining representations.
Another potentially critical aspect is the time between successive sequential elements. In all of the present experiments, there was a 1000 ms pause between adjacent sequential elements. Keele and Summers (1976) report evidence suggesting that position codes might dominate serial control when there is sufficient time between adjacent elements, but that when this time is short, a chaining-based representation takes over.
Serial-Order Representation and Self Inhibition
For the positional interference model to explain the full pattern of costs, an additional step is necessary. As is, the model would predict costs also at points where there are no costs in the empirical pattern. For example, in the sequence ABC-BAC positional interference should occur not only for elements X1 and Y1, but also for elements X2 and Y2. However, in these cases, the prime candidate for interference, namely the element associated with the same position for the alternate chunk, has just been selected for the preceding element. I have proposed that in such cases, self-inhibition of the just-executed task prevents this task from interfering with ongoing selection. There are theoretical and empirical reasons for assuming some kind of self-inhibition process in the context of serial control (e.g., Arbuthnott, 1996; Burgess & Hitch, 1999; Lewandowsky & Li, 1994; MacKay, 1988; Page & Norris, 1998). In particular, in many neural network models, such a process is critical to prevent the system from getting stuck within the current sequential element.
While the assumption of such a self-inhibitory process is consistent with the literature and seems to work well in the current context, a number of open issues remain. For example, one peculiarity of the regular sequences used in the present experiments is that they never contained repetitions, different for example from the kind of task sequences used by Logan (2004). This allowed us to safely ignore the question what would happen to self-inhibition in the presence of repeated elements. It is very well possible that a no-repetition environment strengthens the tendency to avoid repetitions (for related results with the backward-inhibition effect, see Philip & Koch, 2006). Thus, it would be important to explore in future work whether the presence of repetitions might reduce potential self-inhibition effects.
Interestingly, in theory there may also be a representational solution to the problem of how to implement repetitions in the face of inhibition between successive elements. Specifically, Lashley (1951) and Shaffer (1976) have pointed out the relatively high frequency of doubling errors during sequence production (e.g., “bokk” instead of “book”). Such errors suggest that representation of repetitions requires that a specific content element becomes associated with a “repetition code”. Doubling errors result when this code gets incorrectly associated with an inappropriate content element (e.g., Rumelhart & Norman, 1982). With this type of representation, element repetitions are unitized into a single “repeat element”, thus, avoiding the need for inhibition between the individual, repeated elements. Consequently, large task-repetition benefits could coexist with self-inhibition in other parts of a complex task sequence.
Sources of Positional interference
What exactly is the source of positional interference that seems to be behind the large lag-2 costs reported here and in Scheider (2007)? One theoretical possibility is that, consistent with traditional models of hierarchical motor control, performance costs arise when control structures carried over from most recent action events need to be changed to program current actions (e.g. Rosenbaum et al., 1986; see also Kleinsorge, Heuer, & Schmidtke, 1999). For example, in the critical situations studied here, particular position-task combination may be carried over from the preceding chunk in working memory. The costs may reflect the process of “breaking up” these associations in order to use each of the individual elements in a new combination.
The results from Experiment 6 showed that positional interference could be observed even when the same chunk had to be produced twice in a row. This finding is clearly inconsistent with the working-memory account of interference. It suggests that serial-order representations are not simply carried over in working memory, but rather need to be rebuilt from long-term memory during chunk transitions (and possibly even within chunks). At these points of “reconstruction”, memory traces in long-term memory have an opportunity to interfere with ongoing selection. Of course, such interference will be modulated by changes in general context and/or recency. Therefore, interference should be maximal for memory traces used within the current sequence (rather than from all other sequences used during the experimental session) and it should be largest for the most recent traces (thus the reduced costs for chunk repetitions versus chunk switches).
There is an interesting analog to the conclusions about the LTM origin of positional interference that comes from research on interference during traditional task-switching situations. There too, a standard assumption has been that costs of switching arise from the collision between current control demands and control representations carried over in working memory from the immediately preceding trial (e.g., Gilbert & Shallice, 2002). However, results by Waszak, Hommel, and Allport (2003) showed that switch costs can be modulated by interference from stimuli many trials back. Moreover, Bryck and Mayr (2008) recently showed that what has been interpreted as a signature of the carryover of control representations from one trial to the next, the so-called switch-cost asymmetry (e.g., Gilbert & Shallice, 2002), can occur even when tasks repeat, as long as the inter-trial delay is sufficiently long to enforce re-retrieval attempts. Thus, I suggest that a general conclusion from these related literatures is that task-set interference and interference of serial-control representations alike results from long-term memory traces of previous selection events.
Another interesting question is what exactly the source of positional interference is. As remarked in the introduction to Experiment 4, in principle there are two possibilities: 1) the currently relevant position is associated with more than one task (e.g., during selection of Y2 for ABC-BAC, task A might interfere) and 2) the currently relevant task is associated with more than one position (e.g., during selection of Y2 for ABC-BAC, the code for position 1 might interfere). Basically, this comes down to the question of whether subjects are confused about what the current task is or in which position of the sequence they are. Traditionally, in serial-memory research inter-chunk transposition errors have been interpreted in terms of the former type of interference (e.g., see Kahana & Jacobs, 1994). However, I know of no explicit tests of whether the reverse type of interference might exist as well. The present results too, do not allow a clear answer as both types of interference could be a factor in all of the constellations we have tested. Again, further experiments with a larger variation of sequences would be necessary to address this issue.
A related question is associated with the modulation of the lag-2 cost as a function of within-chunk position. Previous results had suggested a modulation in the form of less repetition costs within than across chunk boundaries (Koch et al., 2006; Schneider, 2007). The present results suggest a somewhat different pattern. First, across experiments there is a clear reduction of costs from position 1 to position 2 (which both cross chunk boundaries). Second, in line with Schneider (2007), there seemed to be some suggestion of a cost reduction from position 2 to 3, but that was much less consistent across experiments. To get more clarity on this issue, I analyzed lag-2 costs for 2-chunks-of-3 sequences across all relevant experiments (Experiments 1, 4, 5, and the switch chunks in Experiment 6, N=78). Experiment 3 was not included because positions 1 and 2 could not contain actual lag-2 repetitions whereas position 3 could. Costs went from 311 ms for position 1 to 172 ms for position 2 to 95 ms for position 3. In individual comparisons with experiment as additional between-subject factor, the reduction from position 1 to 2 was highly reliable, F(1,77)=17.8, p<.01, but also the smaller reduction from position 2 to 3 met the reliability criterion, F(1,77)=5.86, p<.05. In terms of effect sizes, for errors the reverse pattern emerged with a small reduction of costs from positions 1 to 2, 10.1% to 7.9%, F(1,77)=7.77, p=.056, and a larger drop from position 2 to 3, 7.9% to 1.9%, F(1,77)=31.24, p<.01. Thus all in all, the overall pattern seems to be characterized by a reduction in costs as a function of within-chunk position for the 2-chunks-of-3 sequences. But, what exactly is the source of this modulation?
Important hints come from those instances in which the modulation did either not occur, or was weakened. Specifically, no apparent modulation was present in the 3-chunks-of-2 sequences (Experiment 4), it was weakened in sequences where one element was unique for one of the two chunks (e.g., DBC-BAC; Experiment 5), and it was again absent for repeated chunks (Experiment 6). Arguably, in each of these cases, the context reduced ambiguity about the currently relevant chunk. In the 3-chunks-of-2 constellations, each of the three chunks is differentiated from each other chunk by at least one element. In sequences with unique elements (e.g., DBC-BAC) the unique elements helped to reduce between-chunk ambiguity. Finally, repeated chunks could profit from the fact that the chunk identity has already been established during the chunk switch.
In contrast, consider the sequence ABC-BAC. Here, neither chunk contained a unique element and the question “Which chunk is it?” needs to be resolved at the very first position. For the sequence ABC-ACB, again, there are no unique distinguishing elements, however there is more time to establish chunk identity as the first element is the same for both chunks. Assuming that an established chunk context is critical for resolving positional ambiguity it would follow that costs should be larger for the ABC-BAC type of sequence than for the ABC-ACB type. What I suggest here is very similar to Rosenbaum, Hindorff, and Munro’s (1987) model of finger sequencing, which assumes that some resolution of ambiguities can be occur in parallel with execution of non-ambiguous sequence elements.
According to this analysis sequences of the ABA-CBC might constitute a special case. They do require establishment of the correct chunk identity for the first chunk position, however ambiguity should be relatively low as the two chunks have distinct repeated elements. Further, it is interesting to note that in the above cross-experiment analysis, the RT lag-2 cost was with around 100 ms very close to the “pure inhibition” component estimated from Experiment 4 and that in terms of error costs there seemed to be a substantial drop between positions 2 and 3. This general pattern suggests that for the sequences used here, positional interference occurs when it crosses chunk boundaries, namely for positions 1 and 2, but not when position-task associations need re-assembling within a chunk. Rather, lag-2 repetition in the ABA-CBC cases may reflect mainly actual inhibition. Obviously, at this point this is a suggestion that needs to be followed up with further research.
Implications for Models of Serial Memory
Empirical results from the serial-memory literature have informed the investigation of the lag-2 repetition cost presented here. At the same time, the results revealed in the course of this investigation have potential implications for open questions in the area of serial memory. One particularly important question has already been discussed above: Is serial-order information coded apart from the actual sequence, through positional codes (e.g., Henson, 1998) or is it coded implicitly, via an integrated representation of past sequential elements that cue subsequent elements (e.g., Botvinick & Plaut, 2006). The contrast between sequences used in Experiments 1 and 4 on the one hand and the sequences used in Experiment 5, allows positional coding and integrated chaining models to go head to head. The current results are clearly more consistent with interference due to positional cues than with interference due to preceding sequence elements. While it may be premature to generalize these findings to more typical serial-memory situations, it should be relatively straightforward to resolve this theoretical issue by adapting sequence manipulations similar to the ones used here.
Interestingly, one could argue that potentially relevant findings already exist, namely from research on the so-called Ranschburg effect. The Ranschburg effect denotes an important empirical phenomenon observed in the context of standard serial-memory research, namely the fact that people are more likely to produce errors when recalling a repeated element within a list, as long as repetitions are separated by at least one intervening element (e.g., Crowder, 1968; Henson, 1998b; Ranschburg, 1902; Wickelgren, 1965). The Ranschburg effect has been explained in terms of response inhibition (e.g., Jahnke, 1969; Henson, 1998b) or guessing strategies (e.g., Greene, 1991). However, neither of these explanations is completely satisfactory (e.g., Kahana & Jacobs, 2000).
More importantly, Kahana and Jacobs (2000) noted that both chaining models and positional-coding models have difficulties explaining the Ranschburg effect. The chaining model has difficulties with this effect for similar reasons as it has difficulties with explaining the lag-2 costs in Experiment 5. According to this model, costs should appear after repeated elements. For example, in a sequence such as KRT-RFS, the chaining model assumes that the repeated element R becomes associated with both T and F and therefore predicts costs for these elements, but not for the repeated element itself. According to Kahana and Jacobs, also the standard positional coding model cannot explain this phenomenon. According to this type of model, a sequence such as KRTRFS is represented by associating each sequential element with position codes p1 to p6. Kahana and Jacobs claim that there is little reason to assume that p4 suffers as a cue for element R only because there is also an association between p2 and R. Note, however, that this comes back to the question whether interferences arises from shared positions across tasks or shared tasks across positions. As discussed in the section Sources of Positional Interference, the verdict is still out which of these two are actually relevant.
What is striking in this context is that the Ranschburg effect and the lag-2 repetition cost show similar sequence structure influences. In particular, Henson (1998b) demonstrated that large repetition costs were obtained for chunked sequences such as KRT-RFS or KRT-SFR, but there were basically no costs for a sequence such as KRT-SRF. Costs for the first two types of sequences along with an elimination of costs for the latter type of sequence is predicted by the chunk-based positional coding account. For example, for the sequence KRT-RFS, costs for the repeated element R arise because it is associated with position code p2 and with code p1. In contrast, costs should be eliminated for a sequence such as KRT-SRF because element R is associated with p2 in both chunks. Thus, the present results provide an interesting new explanation for the Ranschburg effect, based on the hypothesis that interference arises when different element-position conjunctions are used across chunks.
Implications for Models of Sequential Control
A final question we need to deal with here is what the current results have to say about hierarchical, sequential control. The observant reader may have noticed an aspect in the results that is somewhat peculiar, at least when viewed from the perspective of serial motor control models. Such models have usually dealt with situations where subjects had to produce a sequence of simple motor responses. A standard finding from this literature is a strong effect of sequential structure on inter-response times with large latencies for the first element of a chunk or sequence.4 Further, these chunk-initiation times usually increase with chunk complexity or length (e.g., Sternberg, Monsell, Knoll, & Wright, 1978). The standard interpretation of this pattern is that important aspects of the upcoming chunk are retrieved into a motor plan that then allows a fluent execution of individual movements (e.g., Keele & Summers, 1976). In the present experiments, we also see strong effects of chunking structure, suggesting that subjects pre-program the upcoming chunk. However, we also see large lag-2 costs beyond the first chunk position, which supposedly reflect positional interference that arises during retrieval of the next sequential element. The question then is: Why, if the sequential program for the chunk is retrieved at the beginning of the chunk, would it be necessary to retrieve the individual elements again within each chunk?
Likely, the answer to this question has to do with the specific limitations associated with maintaining an action plan. One interesting hypothesis is that maintaining a sequential plan and selecting an abstract response rule involve the same capacity-limited system. For example, Rushworth, Walton, Kennerley, and Bannerman (2004) argued based on neural imaging and transmagnetic stimulation evidence that sequencing and selection of response sets involve overlapping neural areas. If selection of a stimulus-response rule interferes with maintenance of a sequential plan then the plan will have to be re-constructed from LTM for each individual element, at this point opening the door for interference from competing task-position bindings. In future work it will be important to systematically explore the continuum between simple motor responses to the selection and execution of abstract response rules, in order to determine what aspect is responsible for the pattern of costs observed here.4 Many real-world sequential plans involve not just a succession of simple motor acts, but a succession of complex actions, each requiring the specification of free parameters. Thus, it is important to determine in what way exactly sequential control demands change as the type of sequenced activity becomes more complex.
Conclusion
When people transition through certain structured sequences of tasks, they show large RT costs when returning to a task that was relevant two trials earlier, a result that in the past has been interpreted as an indication of inhibition targeted at a no-longer relevant task. Instead, I showed that while inhibition plays some role, such costs arise mainly when unique bindings between tasks and chunk positions need to be established against the interference from competing combinations involving the same set of tasks and positions. These positional-interference costs provide an important point of contact between models of serial memory and the literature on sequential control of action. So far, analyses of these costs reveal that the representation underlying sequential task control is based on position codes (rather than on variants of chaining) and that positional interference arises from long-term memory rather than from working memory. Further detailed analyses in the context of the task-sequencing paradigm (see also Schneider & Logan, 2006) should reveal additional insights about the representations involved in the serial control of action, while also providing a new test bed for models of serial memory.
Acknowledgments
I thank Lara Barnes, Rebekah Naphack, and Miranda Rieter for help with data collection, as well as Bernhard Hommel, Iring Koch, and Darryl Schneider for constructive comments. This work was supported by National Institute of Aging Grant R01 AG19296-01A1.
Footnotes
There are two possible threats to the validity of the central conclusions from Experiment 1. First, in the cued blocks, there was a higher proportion of lag-2 repetitions (p=.5) than in the sequenced blocks (p=.33) which in principle could have affected the relative size of lag-2 costs across these two conditions. Second, Druey and Huebner (2007) recently reported that lag-2 repetitions were larger when cues and stimuli overlapped rather than when as in Experiment 1, cues disappeared prior to stimulus presentation (but for a failure to replicate this pattern, see Grange & Houghton, in press). Each of these two factors might have biased the difference between lag-2 costs for cued and sequenced conditions in Experiment 1 in the direction of larger costs for the sequenced condition. I conducted a follow-up experiment (N=20) that was identical to Experiment 1 except that in the cueing condition the probability of lag-2 repetitions was constrained to p=.33 and that cue-stimulus overlap was manipulated in a blockwise manner (i.e., cues were either presented in the same way as in Experiment 1 or cues remained on the screen until the response was entered). Cued lag-2 repetitions costs were with 37 ms, t(19)=3.43, p<.01, in the no-overlap and 35 ms, t(19)=3.00, p<.01, in the overlap condition very similar to the costs obtained in Experiment 1 and cue-stimulus overlap had no reliable effect. As in Experiment 1, the lag-2 costs for the sequenced condition (160 ms) were substantially larger for the cued condition (37 ms), F(1,19)= 60.64, p<.01. Lag-2 costs across the six sequence positions were 230 ms, 126 ms, 136 ms, 290 ms, 66 ms, and 37 ms. This replicates the general pattern found in Experiment 1 although in general lag-2 costs were a bit lower in this experiment and in particular the lag-2 costs for positions 5 and 6 were unusually small (compared to both Experiment 1 and other comparable experiments reported here). One possible reason for this minor deviation is that subjects were somewhat faster in this experiment than in Experiment 1 (mean RT in sequenced control conditions 789 ms versus 903 ms).
One could question at this point whether the intermittent compatible trials were really sufficient to wipe out potential inhibitory aftereffects. However that the final Experiment 6 provides additional, even more definitive evidence that costs do not depend on actual repetitions.
The lag-2 repetitions parameter correlates .0 with the positional interference parameter, and −.32 with the self-inhibition factor. The interference and the inhibition parameter correlate with .45.
In unpublished work I have confirmed that with the same sequences as used here, but with individual key-press responses as sequential elements, a cost for the first position within a chunk that increased the closer the lag-2 repetition was to the beginning of the chunk (i.e., ABC-BAC > ABC-ACB > ABA-CBC). These preliminary results suggest that the demands of dealing with positional interference migrate towards the point at which a chunk is planned, when response sequences are used instead of task sequences (see also Rosenbaum et al., 1987).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arbuthnott KD. To repeat or not to repeat: Repetition facilitation and inhibition in sequential retrieval. Journal of Experimental Psychology: General. 1996;125:261–283. [Google Scholar]
- Allport A, Wylie G. Task-switching, stimulus-response bindings, and negative priming. In: Monsell S, Driver JS, editors. Attention and performance XVIII: Control of cognitive processes. Cambridge, MA: MIT Press; 2000. pp. 35–70. [Google Scholar]
- Altmann EM. Cue-independent task-specific representations in task switching: Evidence from backward inhibition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:892–899. doi: 10.1037/0278-7393.33.5.892. [DOI] [PubMed] [Google Scholar]
- Anderson JR, Matessa M. A production system theory of serial memory. Psychological Review. 1997;104:728–748. [Google Scholar]
- Baddeley AD. How does acoustic similarity influence short-term memory? Quarterly Journal of Experimental Psychology. 1968;20:249 –264. doi: 10.1080/14640746808400159. [DOI] [PubMed] [Google Scholar]
- Botvinick M, Plaut DC. Short-term memory for serial order: A recurrent neural network model. Psychological Review. 2006;113:201–233. doi: 10.1037/0033-295X.113.2.201. [DOI] [PubMed] [Google Scholar]
- Bryck RL, Mayr U. Task-selection cost symmetry without task switching. Psychonomic Bulletin and Review. 2008;15:128–134. doi: 10.3758/pbr.15.1.128. [DOI] [PubMed] [Google Scholar]
- Burgess N, Hitch GJ. Memory for serial order: A network model of the phonological loop and its timing. Psychological Review. 1999;106:551–581. [Google Scholar]
- Cohen A, Ivry RI, Keele SW. Attention and structure in sequence learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1990;16:17–30. [Google Scholar]
- Crowder RG. Journal of Verbal Learning and Verbal Behavior. Vol. 7. Erlbaum; 1968. Intraserial repetition effects in immediate memory; pp. 446–451. [Google Scholar]
- Ericsson KA, Kintsch W. Long-term working memory. Psychological Review. 1995;102:211–245. doi: 10.1037/0033-295x.102.2.211. [DOI] [PubMed] [Google Scholar]
- Estes WK. On types of item coding and sources of recall in short-term memory. In: Hockley WE, Lewandowsky S, editors. Relating theory and data: Essays on human memory in honor of Bennet B. Murdock. Hillsdale, NJ: Erlbaum; 1991. pp. 155–173. [Google Scholar]
- Farrell S, Lewandowsky S. Dissimilar items benefit from phonological similarity in serial recall. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:838 – 849. doi: 10.1037/0278-7393.29.5.838. [DOI] [PubMed] [Google Scholar]
- Gade M, Koch I. Linking inhibition to activation in the control of task sequences. Psychonomic Bulletin and Review. 2005;12:530–534. doi: 10.3758/bf03193800. [DOI] [PubMed] [Google Scholar]
- Gilbert SJ, Shallice T. Task switching: A PDP model. Cognitive Psychology. 2002;44:297–337. doi: 10.1006/cogp.2001.0770. [DOI] [PubMed] [Google Scholar]
- Greene RL. The Ranschburg effect: The role of guessing strategies. Memory & Cognition. 1991;19:313–317. doi: 10.3758/bf03211155. [DOI] [PubMed] [Google Scholar]
- Henson RNA. Short-term memory for serial order: The start-end model. Cognitive Psychology. 1998a;36:73–137. doi: 10.1006/cogp.1998.0685. [DOI] [PubMed] [Google Scholar]
- Henson R. Item repetition in short-term memory: Ranschburg repeated. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998b;24:1162–1181. doi: 10.1037//0278-7393.24.5.1162. [DOI] [PubMed] [Google Scholar]
- Jahnke JC. The Ranschburg effect. Psychological Review. 1969b;76:592–605. [Google Scholar]
- Hintzman D. “Schema abstraction” in a multiple-trace memory model. Psychological Review. 1986;93:411– 428. [Google Scholar]
- Kahana MJ, Jacobs J. Interresponse times in serial recall: Effects of intraserial repetition. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2000;26:1188–1197. doi: 10.1037//0278-7393.26.5.1188. [DOI] [PubMed] [Google Scholar]
- Keele SW, Summers JJ. The structure of motor programs. In: Stelmach GE, editor. Motor control: Issues and trends. New York: Academic Press; 1976. pp. 109–142. [Google Scholar]
- Keele S, Ivry R, Mayr U, Hazeltine E, Heuer H. The cognitive and neural architecture of sequence representation. Psychological Review. 2003;110:316–339. doi: 10.1037/0033-295x.110.2.316. [DOI] [PubMed] [Google Scholar]
- Lewandowsky S, Li S-C. Memory for serial order revisited. Psychological Review. 1994;101:539–543. [Google Scholar]
- Kleinsorge T, Heuer H. Hierarchical switching in a multi-dimensional task space. Psychological Research. 1999;62:300–312. [Google Scholar]
- Koch I, Philipp AM, Gade M. Chunking in task sequences modulates task inhibition. Psychological Science. 2006;17:346–350. doi: 10.1111/j.1467-9280.2006.01709.x. [DOI] [PubMed] [Google Scholar]
- Lashley KS. The problem of serial order in behavior. In: Jeffress LA, editor. Cerebral mechanisms in behavior. New York: Wiley; 1951. pp. 112–136. [Google Scholar]
- Lewandowsky S, Farrell S. A redintegration account of word-length, lexicality, and articulatory suppression effects in short-term serial memory. Psychological Research. 2000;63:163–173. doi: 10.1007/pl00008175. [DOI] [PubMed] [Google Scholar]
- Lewandowsky S, Li SC. Memory for serial order revisited. Psychological Review. 1994;101:539–543. [Google Scholar]
- Lewandowsky S, Murdock BB. Memory for serial order. Psychological Review. 1989;96:25–57. [Google Scholar]
- Lien MC, Ruthruff E. Task switching in a hierarchical task structure: Evidence for the fragility of the task repetition benefit. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:697–713. doi: 10.1037/0278-7393.30.3.697. [DOI] [PubMed] [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Logan GD. Executive control of thought and action: In search of the wild homunculus. Current Directions in Psychological Science. 2003;12:45–48. [Google Scholar]
- Logan GD. Working memory, task switching, and executive control in the task span procedure. Journal of Experimental Psychology: General. 2004;133:218–236. doi: 10.1037/0096-3445.133.2.218. [DOI] [PubMed] [Google Scholar]
- MacKay DG. The organization of perception and action. New York: Springer.; 1988. [Google Scholar]
- MacLeod CM. The concept of inhibition in cognition. In: Gorfein DS, MacLeod CN, editors. Inhibition in Cognition. Washington: APA; 2007. pp. 3–24. [Google Scholar]
- Marshuetz C. Order information in working memory: An integrative review of evidence from brain and behavior. Psychological Bulletin. 2005;131:323–339. doi: 10.1037/0033-2909.131.3.323. [DOI] [PubMed] [Google Scholar]
- Mayr U. Inhibition of action rules. Psychonomic Bulletin and Review. 2002;9:93–99. doi: 10.3758/bf03196261. [DOI] [PubMed] [Google Scholar]
- Mayr U. Towards principles of executive control: How mental sets are selected. In: Kluwe RH, Lüer G, Rösler F, editors. Principles of learning and memory. Vol. 1. Basel: Birkhäuser; 2003. pp. 223–241. [Google Scholar]
- Mayr U. Inhibition of task sets. In: Gorfein D, MacLeod C, editors. The place of inhibition in cognition. Washington, DC: APA Books; 2007. [Google Scholar]
- Mayr U, Bell T. On how to be unpredictable: Evidence from the voluntary task- switching paradigm. Psychological Science. 2006;17:774–780. doi: 10.1111/j.1467-9280.2006.01781.x. [DOI] [PubMed] [Google Scholar]
- Mayr U, Bryck RL. Sticky rules: Integration between abstract rules and specific actions. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31:337–350. doi: 10.1037/0278-7393.31.2.337. [DOI] [PubMed] [Google Scholar]
- Mayr U, Keele SW. Changing internal constraints on action: The role of backward inhibition. Journal of Experimental Psychology: General. 2000;129:4–26. doi: 10.1037//0096-3445.129.1.4. [DOI] [PubMed] [Google Scholar]
- Miller GA, Galanter E, Pribram KH. Plans and the structure of behavior. New York: Holt, Rinehart, & Winston; 1960. [Google Scholar]
- Monsell S. Task switching. Trends in Cognitive Sciences. 2003;7:134–140. doi: 10.1016/s1364-6613(03)00028-7. [DOI] [PubMed] [Google Scholar]
- Page M, Norris D. The primacy model: A new model of immediate serial recall. Psychological Review. 1998;105:761–781. doi: 10.1037/0033-295x.105.4.761-781. [DOI] [PubMed] [Google Scholar]
- Philipp AM, Koch I. Task inhibition and task repetition in task switching. European Journal of Cognitive Psychology. 2006;18:624–639. [Google Scholar]
- Povel DJ, Collard R. Structural factors in patterned finger tapping. Acta Psychologica. 1982;52:107–123. doi: 10.1016/0001-6918(82)90029-4. [DOI] [PubMed] [Google Scholar]
- Reeves C, Schmauder AR, Morris RK. Stress grouping improves performance on an immediate serial list recall task. Journal of Experimental Psychology. 2000;26:1638 –1654. doi: 10.1037//0278-7393.26.6.1638. [DOI] [PubMed] [Google Scholar]
- Ranschburg P. Über Hemmung gleichzeitiger Reizwirkungen. Zeitschrift fiir Psychologie und Physiologie der Sinnesorgane [On inhibition of simultaneous stimulus effects] 1902;30:39–86. [Google Scholar]
- Restle F, Burnside BL. Tracking of serial patterns. Journal of Experimental Psychology. 1972;95:299–307. doi: 10.1037/h0033619. [DOI] [PubMed] [Google Scholar]
- Rosenbaum DA, Hindorf V, Munro EM. Scheduling and programming of rapid finger sequences: Tests and elaborations of the hierarchical editor model. Journal of Experimental Psychology: Human Perception and Performance. 1987;13:93–103. doi: 10.1037//0096-1523.13.2.193. [DOI] [PubMed] [Google Scholar]
- Rosenbaum DA, Inhoff AW, Gordon AM. Choosing between movement sequences: A hierarchical editor model. Journal of Experimental Psychology: General. 1984;113:372–393. [Google Scholar]
- Rosenbaum DA, Kenny SB, Derr MA. Hierarchical control of rapid movement sequences. Journal of Experimental Psychology: Human Perception and Performance. 1983;9:86–102. doi: 10.1037//0096-1523.9.1.86. [DOI] [PubMed] [Google Scholar]
- Rosenbaum DA, Weber RJ, Hazelett WM, Hindorff V. The parameter remapping effect in human performance: Evidence from tongue twisters and finger fumblers. Journal of Memory and Language. 1986;25:710–725. [Google Scholar]
- Rubinstein J, Meyer ED, Evans JE. Executive control of cognitive processes in task switching. Journal of Experimental Psychology: Human Perception and Performance. 2001;27:763–797. doi: 10.1037//0096-1523.27.4.763. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, Norman DA. Simulating a skilled typist: A study of skilled cognitive-motor performance. Cognitive Science. 1982;6:1–36. [Google Scholar]
- Rushworth MFS, Walton ME, Kennerley SW, Bannerman DM. Action sets and decisions in the medial frontal cortex. Trends in Cognitive Sciences. 2004;8:410–417. doi: 10.1016/j.tics.2004.07.009. [DOI] [PubMed] [Google Scholar]
- Shaffer LH. Intention and performance. Psychological Review. 1976;83:375–393. [Google Scholar]
- Shaffer LH. Performances of Chopin, Bach, and Bartok: Studies in motor programming. Cognitive Psychology. 1981;13:326–376. [Google Scholar]
- Schneider DW. Task-set inhibition in chunked task sequences. Psychonomic Bulletin & Review. 2007;14:970–976. doi: 10.3758/bf03194130. [DOI] [PubMed] [Google Scholar]
- Schneider DW, Logan GD. Hierarchical control of cognitive processes: Switching tasks in sequences. Journal of Experimental Psychology: General. 2006;135:623–640. doi: 10.1037/0096-3445.135.4.623. [DOI] [PubMed] [Google Scholar]
- Schuch S, Koch I. The role of response selection for inhibition of task sets in task shifting. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:92–105. doi: 10.1037//0096-1523.29.1.92. [DOI] [PubMed] [Google Scholar]
- Sternberg S, Monsell S, Knoll RL, Wright CE. The latency and duration of rapid movement sequences: Comparisons of speech and typewriting. In: Stelmach GE, editor. Information processing in motor control and learning. New York: Academic Press; 1978. pp. 117–152. [Google Scholar]
- Waszak F, Hommel B, Allport A. Task-switching and long-term priming: Role of episodic stimulus-task bindings in task-shift costs. Cognitive Psychology. 2003;46:361–413. doi: 10.1016/s0010-0285(02)00520-0. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA. Short-term memory for repeated and non-repeated items. Quarterly Journal of Experimental Psychology. 1965;17:14–25. doi: 10.1080/17470216508416404. [DOI] [PubMed] [Google Scholar]