Cellular Morphogenesis In Silico

Abstract

We describe a model that simulates spherical cells of different types that can migrate and interact either attractively or repulsively. We find that both expected morphologies and previously unreported patterns spontaneously self-assemble. Among the newly discovered patterns are a segmented state of alternating discs, and a “shish-kebab” state, in which one cell type forms a ring around a second type. We show that these unique states result from cellular attraction that increases with distance (e.g., as membranes stretch viscoelastically), and would not be seen in traditional, e.g., molecular, potentials that diminish with distance. Most of the states found computationally have been observed in vitro, and it remains to be established what role these self-assembled states may play in in vivo morphogenesis.

Introduction

The formal study of biological pattern formation dates at least to Turing (1), who proposed that a competition between reaction and diffusion of chemical agents leads to a variety of spatially and temporally varying patterns. Turing's proposition has been explored in numerous applications (2,3) including in patterns of importance for development (4–8), camouflage (9), mate choice (10,11), and evolutionary diversity (12).

In Turing's approach to biological morphogenesis, chemical patterns are established through a reaction-diffusion mechanism of chemotropic or chemotrophic agents, and cells are considered to be mere passive constituents that are laid down in response to chemical prepatterns. Malcolm Steinberg proposed an alternative approach (13), the “differential adhesion hypothesis”, which postulates that biomechanics between cells plays an active role in biological pattern formation (14). In this scenario, adhesion or cohesion relations and consequent migration between cells lead to morphogenesis—e.g., in an aggregate of two types of cells, those cells that adhere more strongly would tend to migrate to the interior of developing biological structures, and cells that adhere less strongly would migrate to the exterior (Fig. 1 g). The differential adhesion hypothesis has been confirmed using a variety of cell types (15–18), and its role during developmental morphogenesis has been extensively studied in numerous animal models, beginning perhaps with the work of Edelman (19).

Figure 1.

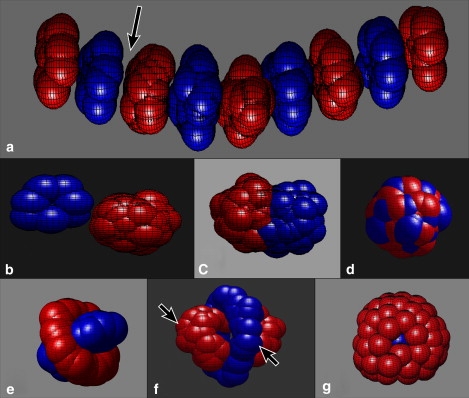
Examples of self-assembled cellular morphologies produced by the in silico model. (a) Alternating segmented discotic state, which appears when like cells repel (i.e., blue cells repel blue cells and red cells repel red cells) and unlike cells attract (i.e., when red cells attract blue cells). Note that, surprisingly, compact clusters of like cells form despite their mutual repulsion, and unlike cells can become separated (arrow) despite their attraction (see text). (b) Homoclusters are produced when like cells attract and unlike cells repel. (c) Hemiclusters are seen when like and unlike cells attract, with like attraction stronger than unlike. (d) Heteroclusters of mixed cell types appear when like and unlike strengths between cells are equally attractive. (e and f) Shish-kebab states can appear when like cells repel more strongly than unlike cells attract. (g) Traditional enveloped states appear when one species (blue) attracts more strongly than another (red). Arrows in f identify examples of cells in contact with like neighbors but separated from unlike cells. Parameter choices needed to produce states (a–f) are defined in Fig. 4.

In recent years, evidence has emerged showing that morphogenesis is regulated by active cellular repulsion as well as attraction (20) (i.e., during the development of zebrafish rhombomeres (21), in Drosophila embryogenesis (22), in vertebrate hindbrain segmentation (23), and in retinal mapping (24,25)). At least two mechanisms for cellular repulsion are documented in the literature. First, incorporation of sialic acid in cell surface receptors generates repulsion through electrostatic interactions between nearby acid pairs (26), and second, Eph receptors and their corresponding membrane-bound ligands are known to modulate both attraction and repulsion during development (23,27). These constitute two subclasses of receptors from the tyrosine kinase family, EphA and EphB, that specifically interact with GPI-membrane linked EphrinA and transmembrane EphrinB ligands (28). Hence the receptor and ligand interaction, Eph-Ephrin, requires cell-cell proximity to initiate and modulate repulsion (29,30), analogously to cellular attraction that occurs through stable cadherin links or integrin-fibronectin focal points.

To our knowledge, no theoretical analysis or inventory of morphologies that form due to direct cellular attractive and repulsive interactions has appeared previously in the literature. We present an in silico study intended to fill this void by investigating what structures self-assemble when two types of cells are allowed to interact attractively or repulsively. As we will show, it is straightforward to simulate cellular self-assembly using established computational techniques, and we find that both obvious and unexpected morphologies of cells emerge spontaneously. In Fig. 1, we show several computationally reproducible examples of both commonplace (Fig. 1, b, c, d, and g) and unusual (Fig. 1, a, e, and f) cellular morphologies from simulations that we describe.

Algorithmically, our approach resembles dissipative particle-dynamics simulations, in which spherical particles interact or migrate according to prescribed rules. Cells differ from inert particles in a number of ways, for example effects of reproduction and differentiation have been discussed previously (31), and other cell-specific dynamical features have also been discussed in the literature (32–36). For a review of these approaches, as well as a modeling approach that includes nonspherical cell geometries, see Palsson (37). In this study, we model only spherical cells to facilitate rapid exploration of parameter space, and we define idealized forces between interacting cells. We do not include intracellular behaviors associated with cytoskeletal anisotropies, nor do we consider history-dependent forces, transport of surface-binding proteins, or nonspherical cell shapes. Thus our results are not applicable to cells with complex shapes (e.g., neurons or glia), or to cells whose dynamics are strongly influenced by interior structures (e.g., platelets or myocytes). Our results may be germane to nearly spherical cells that move slowly compared with timescales of making and breaking of bonds (e.g., cells early in development or undifferentiated neoplastic cells). Despite these limitations, a variety of nontrivial morphologies form spontaneously, several of which do not seem to have been reported or analyzed previously.

The model that we use is described in the Appendix (see also Shinbrot (31) and Caicedo-Carvajal and Shinbrot (38)), and contains both mechanical responses to compression and prescribed attractive or repulsive behaviors produced by membrane-bound proteins such as cadherins, integrins, and Eph receptors and ephrin ligands. To simulate cellular responses to compression, we prescribe that cells compress according to a “Voigt” model, like damped springs (39,40), producing an outwardly directed normal force as sketched in Fig. 2 a. Cells can attract one another in one of two ways: they can cohere through membrane-bound molecules (e.g., cadherins), or they can exert forces intermediated by the extracellular matrix (ECM) (via integrin binding) (18,32,42,43).

Figure 2.

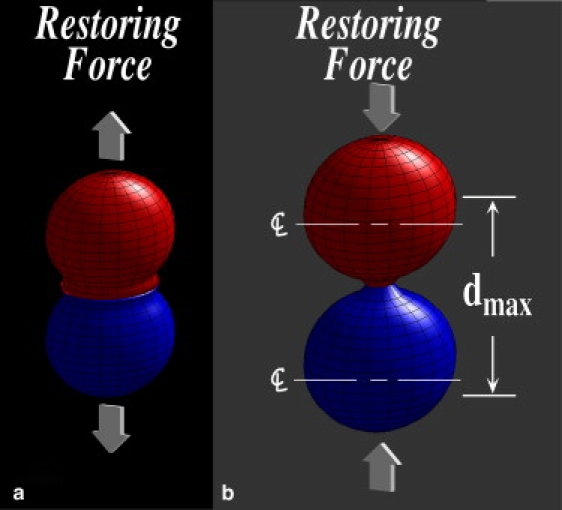
Schematics of interactions between cells. (a) Caricature of two cells being compressed together, illustrating the outward restoring force described in text. (b) Caricature of cells responding to being pulled apart by exerting an attractive restoring force. As suggested by the scale indication to the right, cells within a maximum separation between cell centers, d_max interact; cells further apart than this distance move freely.

As sketched in Fig. 2 b, we model cell-cell attraction by allowing cells that are within a distance, d_max, of one another to attract, again as damped springs. This attraction is intended to model membrane tension of two cells connected to one another either directly or through the ECM (44–46). A cell that is pulled further than d_max is assumed to break free and to feel no further force from its neighbor (47,48); likewise once cells begin to compress one another, their attraction vanishes. Beyond these prescribed interactions between cells, we include randomized cellular motion and viscous damping due to a surrounding fluid or ECM in standard ways: randomized motion is simulated as an integrated random walk (49), and viscosity is included by reducing the velocity of every cell by a fixed fraction each computational time step. Finally, in view of the existence of distinct attractive and repulsive cellular cues (23,26,50,51), we permit cells to either attract or repel one another, and for this purpose we consider two cell types that can interact either homotypically (between like cells) or heterotypically (between unlike cells) with different attractive or repulsive strengths.

We show results using repulsion modeled using either a Voigt relation, which increases in strength with distance, or a κ/r² repulsive force, which decreases with distance. The Voigt form has the merit that both attractive and repulsive interactions use the same units for interaction strengths, differing only in sign. That is, the interaction force goes as k × (r − d), where r is the separation between the cell centers, d is the cell diameter, and k is a constant that is positive for repulsive interactions and negative for attractive ones. The κ/r² form, on the other hand, is more biomechanically reasonable in that one expects repulsive forces to diminish with separation. In this case, however, k and κ have different units; dimensionally, κ = k × L³, where L is a characteristic length. In our simulations, L is of order of the diameter of a cell, D, which we set to unity so that the interaction strengths κ and k will have comparable units.

We note that Young's moduli for cells in living tissue range from hundreds to millions of kilopascals (53) depending on tissue type and environment; hence a dimensional simulation applicable across relevant scales would be problematic. Consequently, our simulations are strain based rather than stress based: that is, we provide dimensionless computations from which the fractional deformation of a cell defines its elastic response. To convert our results to dimensional units—i.e., to estimate stress based data—one would need to multiply the strain by the Young's modulus for the cells of interest. As examples, strains in our simulations are of order 10%, so that corresponding stresses would be of order 10 Pa for brain tissue and 1 kPa for muscle, and corresponding forces on a single cell (for cell surface area of order 10⁻⁶ cm²) would range from 10⁻⁴ dyne (1 nN) to 10⁻² dyne (100 nN).

The formulation that we use is surely not definitive, and one can include any number of possible complications, however to lowest order, our approach of using a Voigt model for attraction and either Voigt or an inverse r² repulsive model seems to span the range of plausible inter-cell interactions mediated by membrane-bound factors (54). In the following section, we detail transitions in cellular morphology that occur as homo- and heterotypic strengths are altered, as in the case of in vitro experiments in which cadherin or integrin expression levels are varied (17) (also described in Fig. 6).

Figure 6.

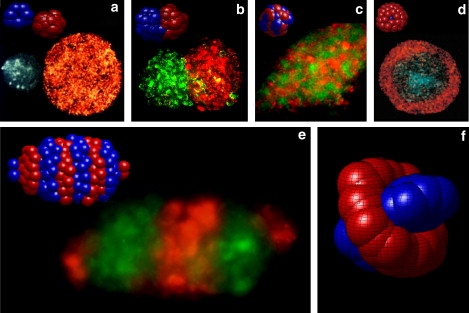
Comparison in vitro (a–e) and in silico (upper insets a–e) cell patterns. (a) Homoclusters: green cells are embryonic chick limb bud mesenchyme; orange cells are embryonic chick neural retina. (b) Originally noncohesive L cells transfected with B-cadherin (green) and R-cadherin (red) (reprinted with permission from Duguay et al. (17)). (c) Mixed cluster: green cells are invasive prostate cancer cells; red cells are carcinoma-associated fibroblasts. (d) Orange cells are embryonic neural retina, and blue cells are embryonic chick liver cells (reprinted with permission from Foty et al. (16)). (e) Alternating segments: green cells are MIN6 mouse insulinoma cells; red cells are mouse α-TC glucagonoma cells. Experimental details described in Foty et al. (16). (f) To our knowledge, simulated shish-kebab state has not yet been reported experimentally.

Phase diagrams

We present phase diagrams obtained using a damped spring model for the attractive interaction, and either of the two forms of repulsive interactions described above. In both cases, we allow cells to interact up to a maximum distance between their centers of d_max = 3 cell diameters. This is not an unphysiological distance, as cells deform considerably during development (33), and interactions between cells over larger distances than this are seen in both vertebrates (56) and more primitive life forms (57). The simulations use reflective boundary conditions, and simulated cells are identical in size but are of two types: half of type “A” and half of type “B”. By defining two types, we can explore the effects of homotypic (A-A or B-B) versus heterotypic (A-B) interactions on cellular self-assembly.

In the simulations described first, we consider the Voigt repulsive model, using 250 spherical cells in a computational domain 20 computational units on a side, where each cell has a 1 unit diameter. We find that the patterns described appear at approximately the same parameter values for various randomized initial conditions, however they assemble most reproducibly and rapidly if cells begin in close proximity to one another: more sparse initial arrangements result in long transients during which cells seem to wander aimlessly until they happen on compatible neighbors. To avoid this nomadic situation, we initially place all cells with zero velocities at random locations within a planar square 5 units on a side.

Simulations also have been carried out using up to 1000 cells, however as we will describe, many of the morphologies seen are essentially spherical in shape, and spherical structures are unstable at high cell numbers. That is, larger aggregates tend to break apart into smaller clusters. This is simply a consequence of finite surface tension, and is the identical effect to that which produces water droplets of limited size. To avoid long transient calculations as these “droplets” form, we carry out most of our calculations using only 250 cells, however, we have confirmed in separate simulations that nonspherical structures (especially discotic states described below) persist at larger cell numbers.

In Fig. 3, we display the morphologies seen for simulations using a Voigt form for both attractive (negative on the axes shown in Fig. 3) and repulsive (positive axis values) interactions. Simulations are carried out at increments of 0.01 in interaction strength. Simulations are run for at least 100 computational time steps before halting—more time steps are used when the morphology is uncertain. Morphologies are determined when they remain unchanged for >20 time steps; if a pattern continues to evolve, the simulation is not halted until its state remains unchanged. All simulations are repeated at least once with different random initial cell locations, more times if the morphological outcome is unclear and near phase boundaries (to refine boundary locations).

Figure 3.

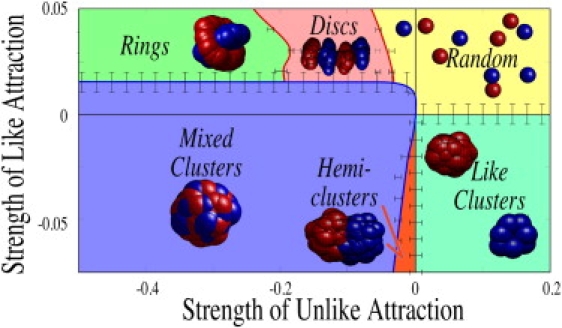
Phase diagram for Hookean attraction and repulsion. Positive strengths indicate repulsion; negative strengths indicate attraction (details in Appendix). All simulations use equal numbers of two cell types (red and blue). Error bars indicate maximum deviation of interface, i.e., at opposite ends of the error bar, different morphologies are distinguishable; within the scale bars, simulations produce variable results depending on initial conditions.

As we have mentioned, the simulation permits interactions at a distance, through the ECM, which influences cell motion both passively (i.e., through viscous effects (39)) and actively (e.g., through contractile forces exerted by the cytoskeleton via integrins on the cell membrane (3), or through repulsive sialic-acid or ephrin mediated interactions).

Numerous different morphologies emerge in these simulations; to aid in visualization, we provide movies of the formation of many of these structures in the Supporting Material (Movie S1, Movie S2, Movie S3, Movie S4). In the first quadrant (Fig. 3, yellow), all particles repel one another, and only random arrangements of separated particles are seen. In the second quadrant (Fig. 3, light green shading), like particles attract whereas unlike particles repel, and so as one would expect, separated clusters of like particles form. In the third quadrant (Fig. 3, blue and orange), both like and unlike cells attract, and clusters of both particle types appear. When the like attraction is stronger than the unlike (Fig. 3, orange), hemiclusters of nearly equal numbers of each cell type form. These and other clusters seem to grow through “coarsening” in our simulations (59), as smaller clusters coalesce into larger ones.

In the fourth quadrant, two unexpected morphologies emerge. First, a ring-like state self-assembles spontaneously (Fig. 3, upper left green region), in which one or another species encircles the second species in a shish-kebab formation. These structures appear where like cells repel weakly and unlike cells attract more strongly. At weak unlike attraction strengths, the inner species appears to form a ring-like shape as shown in Fig. 1 f; at stronger unlike attraction, the inner ring collapses into a nearly cylindrical inner post, as shown in Fig. 1 e. When equal numbers of cells are present in each cluster, this shish-kebab morphology rapidly self-assembles with 10–50 cells. When, on the other hand, a larger number of one or another species arrives by chance in the vicinity of a cluster, an enveloped pattern (Fig. 1 g) appears instead, with the majority species on the outside. A second new morphology is also shown in the fourth quadrant of Fig. 3: a state of alternating red and blue discs appears when like repulsion is of the same magnitude as unlike attraction (Fig. 3, puce). The emergence of this pattern is surprising, because like particles aggregate together into discs despite the fact that they repel one another. We discuss the mechanism for the formation of these discs in the penultimate section of this study.

Finally, we remark that a marginally stable state of inelastic clusters can also be observed on the red line of Fig. 3, where like interactions vanish and the unlike interactions are repulsive. In principle, no patterns should form here because no forces are attractive. On the other hand, collisions between cells are strongly dissipative, and our simulations have reflective boundaries, so cells cannot escape the computational domain. Consequently, clusters of cells form, held together only by inertia: similar structures are well documented in other computational contexts (60). These clusters are in one sense inconsequential in that they are very weakly held together; nevertheless it is conceivable that during development or under rapidly dividing and migrating conditions (61,62), cells may form transient states such as these, and for completeness we include snapshots of these structures in the Supporting Material.

As described previously, in addition to the Voigt repulsive model summarized in Fig. 3, we also consider interactions represented by an inverse r² repulsive force. Thus we reproduce the simulations described already, but when either homotypic or heterotypic force is repulsive, we evaluate the distance, r, between cell centers, and define the repulsive force to be κ/r², where κ is the magnitude of the repulsive strength plotted on the positive domains in Fig. 4. Attractive interactions are of the same form as in Fig. 3. We find that patterning regimes extend over a larger range in parameter values, so in Fig. 4, we plot homotypic and heterotypic strengths over larger values than before, and correspondingly the resolution over which we evaluate transitions between morphologies (Fig. 4, error bars) is enlarged.

Figure 4.

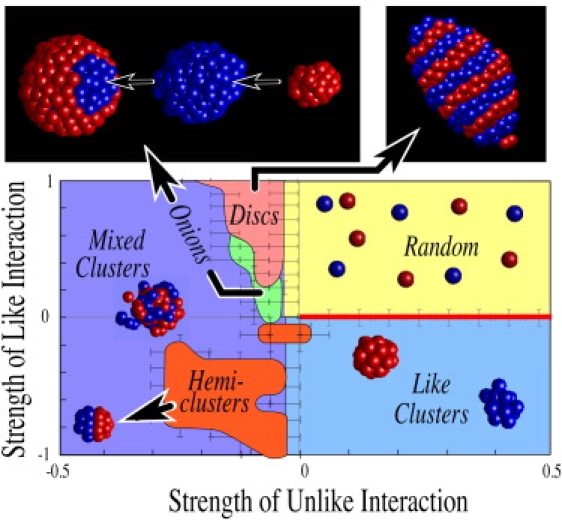
Phase diagram for Hookean attraction and inverse r² repulsion. Simulations carried out as in Fig. 3 and as described in the Appendix. Enlarged view at top left shows “onions”, which have the appearance of rounded rings of Fig. 3, but contain additional layers as shown in expanded views to right. The discotic state is likewise more compact and rounded than in Fig. 3, as shown at top right. The isolated small island near the origin contains large hemiclusters.

The phase spaces for Voigt and inverse r² models are qualitatively similar, with the exception that the ring (Fig. 1, e and f) and discotic (Fig. 1 a) states are more rounded and compact in the latter case. This suggests that the patterns shown are robust and do not depend strongly on details of interaction models. The ring state using 1/r² repulsion contains additional layers, displayed in exploded view in the upper left panel of Fig. 4, and to distinguish this state from the ring state shown in Fig. 3, we rename this “onion” state by virtue of its additional layers and lack of identifiable rings.

Mechanisms

The ring (or onion) and disc patterns are unexpected insofar as the a priori expectation for cells that repel homotypically and attract heterotypically is that they would form heterodimer chains (63) so that mutually repelling elements are separated from one another. On the contrary, in the disc state, like cells become compressed close to one another, whereas spaces (Fig. 1 a, arrows) even sometimes intervene between unlike cells. Likewise in the ring state, there are cells that only contact like neighbors and nowhere contact unlike cells (Fig. 1 f, arrows). To our knowledge, although it is not unique for heterodimer chains to form compact structures (64), the self-assembled disc and ring structures described in this study have not been studied previously, and these counterintuitive morphologies can be explained through direct analysis of the forces exerted on the relevant cells. As we will show, these morphologies would not form for molecules, which attract by electrostatic, van der Waals, or other forces that diminish with distance, but do form for cells that, crucially, can attract with forces that increase with distance (39).

This effect can be analyzed most clearly in the disc configuration as sketched in Fig. 5 a, using the case where both attraction and repulsion are Hookean. The configuration shown to the left of the isolated red cell was obtained from an actual simulation with negative unlike and positive like forces and d_max = 3 diameters. In the morphology shown, the lone red cell to the right feels a weak repulsion (Fig. 5, red arrow) from the other nearby red cells, but is constrained by stronger attraction forces (Fig. 5, blue arrows) from the blue clusters. These attractive forces are stronger because they act at a greater distance than the repulsive force. We will calculate the magnitudes of the forces shortly; for the time being, we note that the lone red cell shown is stable to perturbations in the vertical direction: if the red cell moves up, say, toward the upper blue cluster, the force attracting it to these blue cells will weaken, whereas the force attracting it to the more distant, lower, blue neighbors will strengthen. Thus the red cell is stabilized against vertical transverse fluctuations by the same forces that draw it inward toward the red cluster.

Figure 5.

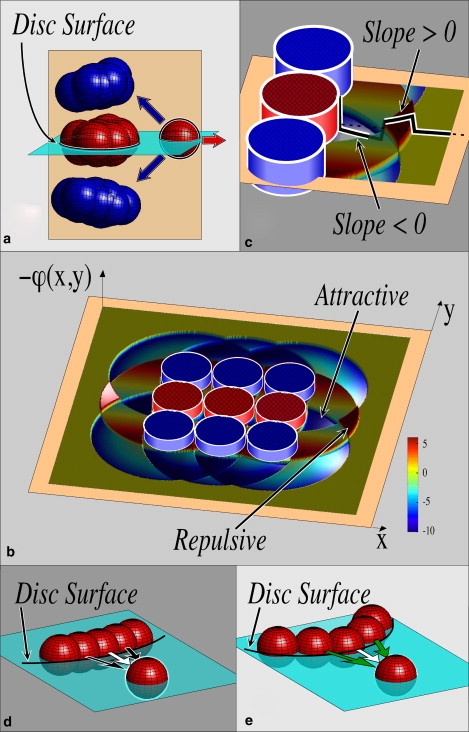
Forces on an isolated red cell nearby a segmented assembly for the case where both attractive and repulsive forces are spring-like. (a) Red arrow indicates repulsive, like, force; blue arrows indicate attractive, unlike, forces. These latter forces can overcome homotypic repulsion and additionally stabilize the isolated cell against vertical fluctuations. (b) Plot of the potential energy nearby a 2D striped array in the vertical (tan) plane of a. The hatched red and blue cylinders indicate locations of fixed cells in the striped array. The blue well indicated is attractive to an isolated red cell, whereas the red barrier shown is repulsive to it. (c) Enlarged view of well and barrier including a plot (black) of the potential along the y = 0 line of symmetry. In b and c, the negative of the potential is plotted for simplicity of interpretation: this causes negative slopes to be leftward and positive slopes to be rightward. (d) Small curvature discotic surface (cyan in a) tends to repel the isolated like cell more strongly than (e) higher curvature surface. At higher curvature, weaker repulsion is produced because some neighboring cells are further than d_max away from the isolated cell (green arrows indicate forces released from cells further than d_max away).

Because the forces between all cells are prescribed perfectly, it is elementary to evaluate the net force between an individual cell and any defined morphology. The simplest way of displaying this information is shown in Fig. 5 b, where we plot on the z axis the potential—ϕ(x,y), produced by a 2D striped arrangement of cells. This arrangement can be used to describe (in 2D where plotting is straightforward) the force, F = −∇ϕ, acting on a point-like cell. The red and blue cylinders represent boundaries of cells in the orange plane shown in Fig. 5 a, and we plot the force acting on a red cell as a function of position. A red cell will feel an attractive net force if its nearest boundary lies in the blue well identified with the “Attractive” marker. This is not completely self-evident because the force is obtained from the gradient of the potential, so in Fig. 5 c we display an enlarged view of the potential well, including a plot (black curve) of the potential along the symmetry line in the figures. The slope of this line is negative, so the force on a red cell is oriented leftward, i.e., toward the other red cells. Contrariwise, a red cell nearby a blue disc would feel a net repulsive force caused by the surrounding red discs.

We note that for a wandering red cell to reach the potential well adjacent to the other red cells, the cell must either cross or bypass the repulsive barrier indicated by the “Repulsive” marker in Fig. 5 b. This seems to be an example of the so-called “freezing by heating” mechanism (66) in that the self-assembled pattern will only form if the cells migrate sufficiently energetically to overcome the repulsive barrier. We also note that for these structures to form, the attractive forces must increase with distance—as agrees with measurements for membrane-bound ligands—but the repulsive forces need not increase with distance. We have used a model in which both attraction and repulsion increase with distance for pedagogical simplicity, but the argument summarized in Fig. 5 merely requires that there be some repulsive potential that is overcome by attractions that increase with distance. Further studies will be needed to establish whether the conditions prescribed by this model agree with developmental or evolutionary conditions of practical importance.

A final remark concerns the three-dimensional nature of the patterns that we have described. By the same token that neighboring blue cells stabilize the red interrogating cell in Fig. 5 a against vertical fluctuations, other red cells can destabilize an interrogating cell if they are within d_max of it. As a consequence, if the curvature of the central red disc in the horizontal surface identified in Fig. 5 a is too small (compared with 1/d_max), then red neighbors of the nearest red cell in the disc will tend to be repelled from the disc. That is, referring to Fig. 5 d, a lone cell (red in the figure) near a low curvature discotic surface is repelled by multiple like cells on the surface (black arrows), and so will not settle onto the disc. By contrast, as shown in Fig. 5 e, a lone cell near a higher curvature surface is repelled by fewer like cells (indicated in the figure by green arrows that are presumed to be associated with cells more than d_max away from the isolated cell). Large discs with low curvature, compared with 1/d_max, tend to repel new cells, whereas smaller discs with higher curvature tend to attract newcomers. This implies that the radius of discs must be on the order of d_max, which is indeed what we see in our simulations: discotic assemblies of apparently arbitrary axial length can form, but the diameters of individual discs never grow beyond a few cells across. We speculate that this could in principle constitute a mechanism for the biological control of boundary shapes and sizes during development (67).

In summary, the mechanism by which the discotic state forms seems to be that heterotypic attraction overcomes the effects of homotypic repulsion, stabilizing structures against both radial and vertical perturbations. Apparently, this leads to the formation of small curvature structures; similarly we have mentioned that simple surface tension considerations imply that small clusters tend to be stabilized in other regions of parameter space. It remains to be seen what role these smaller scale self-assembled structures play in the construction of larger scale tissue and organ systems: at this stage, we can only conclude that the structures shown in Fig. 1 appear to be the stable building blocks that can be formed from simple attractive and repulsive interactions between individual cells.

Conclusion

We have shown through direct simulation that interactions between cells in a simplified computational model can generate several distinct self-assembled morphologies. In Fig. 6, we show comparisons between these simulated morphologies (upper insets) and similar states (main panels) found through in vitro experiments in which different cell types exhibiting different cadherin or integrin expression levels are mixed in cocultures using established techniques (16). In Fig. 6, a–d, we show respectively: separated homoclusters, joined hemiclusters, a mixed cluster, and an enveloped cluster. These structures have been reported previously, for example, in Foty and Steinberg (68). Our simulations have also revealed two additional structures. First, as shown in Fig. 6 e, we find that an alternating segmented morphology, which we have referred to as “discs”, appear robust and reproducible in simulations. Such structures abound in studies of both vertebrate and invertebrate development; we will have more to say about this shortly. We are unaware of in vitro cell culture experiments that have produced such structures i.e., repeating discs of a characteristic size, however a search of our laboratory's record, involving numerous experiments using a variety of cell types, showed several examples of alternating segments. In the main panel of Fig. 6 e, we show such an example of a potential discotic state seen in a coculture of immortalized mouse insulinoma and glucagonoma cell suspensions. It seems likely that other such examples may be forthcoming now that they have been theoretically predicted. On the other hand, we have not been able to identify from existing in vitro experiments a second structure that appears robustly in our simulations, the shish-kebab, or ring, structure, shown in Fig. 6 f; nor have multilayered onion states been reported to our knowledge. These latter structures are predicted to occur at weak homotypic attraction and strong heterotypic repulsion, and it may be that these conditions are seldom encountered. On the other hand, if these structures can be found, or reproduced through careful experimentation, it will represent a strong confirmation of our in silico approach.

In closing, the philosophy of this study has been that morphogenesis is regulated both by passive responses of cells to genetically prescribed chemical gradients and by active interactions between cells as mediated by membrane proteins such as adhesion molecules. The discotic state is a case in point: examples are seen in numerous segmented structures (e.g., in rhombomeres) and arguably in annelid segments and even in the Drosophila syncytium. Careful experimental investigations indicate that alternating segmentation in rhombomeres may be influenced strongly by active cellular interactions (21–23,69). However, it is well documented in Drosophila that alternating segmentation appears under tightly regulated genetic control (70,71), and where in any event segmentation appears before cell boundaries have even formed. Thus examples of both mechanical and chemical patterning paradigms are found readily.

This suggests several open questions. First, it remains to be seen how these two patterning influences interact. Our simulations show that mechanical interactions alone can spontaneously generate a few specific building blocks. This being the case, it is difficult to hold the view that evolution could have proceeded without, at some point, sampling these building blocks. This leaves it unclear which structures may be produced by chemical prepatterns and genetically established despite the tendency of cells to self-assemble into these building blocks, and which structures may have been constructed as evolution capitalized on this tendency.

Second, our simulations are considerably simplified, neglecting important effects including shape changes due to cytoskeletal forcing, feedback between external stresses and internal cellular functions, and even precise conservation of cellular volumes as agglomerates are compressed. Certainly many of these shortcomings can be improved through embellishments to the spherical cell model that we have presented (see Palsson (37)), and it would be important to establish whether the structures predicted in our simplified simulations are reproduced in more detailed and complicated models.

Third, the simulations described in this study only used two components, whereas complex organ systems contain many more cell types, and even the earliest developmental processes progress from a three-part layer of endoderm, mesoderm, and ectoderm cells. Thus it is desirable to investigate what self-assembled morphologies appear using more cell types.

Finally, our simulations have exclusively been under steady conditions, whereas in vitro development exhibits extensive temporal control over protein expression affecting everything from small-scale growth and migration to larger scale entire organ size and shape. Evidently considerable in silico work remains ahead to understand how structures emerge, grow, and change during normal, as well as future engineered development.

Appendix

We describe the simulation used in this study. We first summarize the mechanical interactions between simulated cells, and we then define the boundary and initial conditions and the integration approach used.

The mechanical system

The flow chart for the approach is shown in Fig. 7. As summarized in the text, we use a Voigt model, in which a cell of unit mass displaced from an equilibrium position (typically defined to be when cells are first placed in contact) from its j neighbors by a distance Δx_j, feels a restoring force,

$$F_{\text{i}}=-\sum k\times \Delta x_{\text{j}}-{\eta }_{\text{cytoplasm}}\times v_{\text{i}},$$ (A1)

where k is a Hooke constant, and v_i is the velocity of the ith cell. η_cytoplasm is a viscosity representing the cytoplasmic resistance to strain. Including viscoelasticity into the model allows cells to have time dependent stress-strain relations and energy dissipation as the cellular interactions mature over time due to viscous damping.

Figure 7.

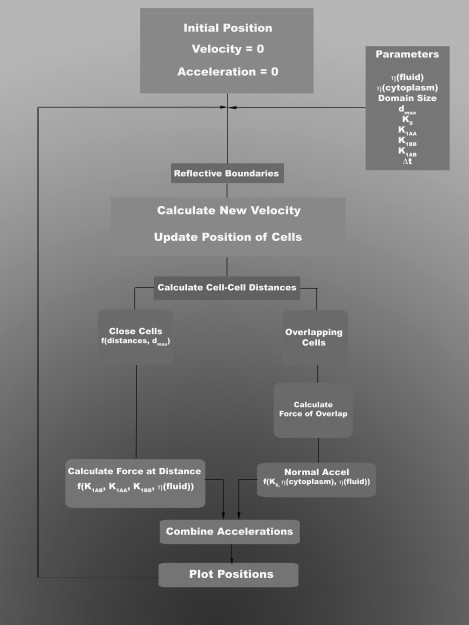
Flow chart for simulation used. Beginning with cells randomly distributed with zero velocity and acceleration, cells move and interact under the influence of parameters defining viscosities (h_fluid and h_cytoplasm), interaction strengths (k_1AA, k_1BB, k_1AB, and k₀), and computational features such as the size of the computational domain and time step (Δt). Cells that are close to one another (i.e., within d_max) are attracted or repelled with prescribed heterotypic (k_1AA, k_1BB) or heterotypic (k_1AB) interaction strengths, and cells that overlap are repelled hydrostatically with a different strength (k₀).

The signs of forces are chosen so that the restoring force is negative (attractive) when the cells are pulled apart, and positive (repulsive) when cells are compressed together. Because negative forces represent attractive interactions mediated by cadherins (for short ranges) or integrin-ECM interactions (for longer ranges), whereas positive forces represent hydrostatic responses of cells to being compressed, there is no reason for the Hooke constant to be the same for each alternative, and indeed in the simulation they take on different values. Explicitly, when cell surfaces overlap, they repel with one constant, k₀, intended to represent their response to compression; when they are separated up to a distance, d_max, they attract or repel with a different constant intended to represent forces due to cadherins and integrins as described in the body of this study; and beyond d_max, cells are assumed to break free from one another. The simulation can include any number of cell types, but in this simulation we consider only two cell types, denoted A or B, so that cadherin or integrin mediated forces is defined by a homotypic interaction strength, k_1AA or k_1BB between like A-A cells or B-B cells respectively, or by a heterotypic strength, k_1AB, between unlike cells.

Computational details

Cells have initial positions (x_i, y_i, z_i), taken initially to be random within a computational domain of fixed volume, “domain size”. Reflective boundary conditions are used to contain cells within the computational domain, and to allow cells to rearrange, domain size is scaled with the number of cells used (typically 250, although we have confirmed that similar patterns obtain using particle numbers up to 1000). The simulations are highly damped to represent the low Reynolds' number environment surrounding cells, so even if by chance two cells are initially placed nearly on top of one another, the cells move slowly apart to accommodate the large initial compressive forces without numerical artifacts. All cells wander stochastically as described elsewhere (31,38), to avoid persistent metastable states.

We simulate the velocity of the cells using Euler integration. Because the cellular environment is highly dissipative, there is no need for a time-reversible integration method; nevertheless we have carried out separate comparison simulations using Verlet integration, which revealed no noticeable differences in outcomes. Explicitly, the force obtained in Eq. A1 is used to update the velocity and position of the ith cell according to:

$${\overrightarrow{v}}_{\text{i}}(t+\Delta t)\to {\overrightarrow{v}}_{\text{i}}\left(t\right)+\frac{1-{\eta }_{\text{fluid}}}{m}{\overrightarrow{F}}_{\text{i}}\left(t\right)\Delta t+{\overrightarrow{r}}_{\text{i}}\left(t\right),$$ (A2)

$${\overrightarrow{x}}_{\text{i}}(t+\Delta t)\to {\overrightarrow{x}}_{\text{i}}\left(t\right)+{\overrightarrow{v}}_{\text{i}}\left(t\right)\Delta t+{\overrightarrow{F}}_{\text{i}}\left(t\right)\frac{\Delta t}{2m},$$ (A3)

where the cell mass, m, is taken to be unity, η_fluid = 0.5 produces exponential damping to represent the viscosity of the interstitial fluid or matrix, ${\overrightarrow{r}}_{\text{i}}\left(t\right)$ is a random vector producing migration and is distributed uniformly up to a maximum radius of 0.01, and the time step Δt = 0.5 (smaller time steps were investigated, and produced no noticeable difference in the final states shown).

Supporting Material

Four movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01024-8.