Perturbations to trophic interactions and the stability of complex food webs

Abstract

The pattern of predator–prey interactions is thought to be a key determinant of ecosystem processes and stability. Complex ecological networks are characterized by distributions of interaction strengths that are highly skewed, with many weak and few strong interactors present. Theory suggests that this pattern promotes stability as weak interactors dampen the destabilizing potential of strong interactors. Here, we present an experimental test of this hypothesis and provide empirical evidence that the loss of weak interactors can destabilize communities in nature. We ranked 10 marine consumer species by the strength of their trophic interactions. We removed the strongest and weakest of these interactors from experimental food webs containing >100 species. Extinction of strong interactors produced a dramatic trophic cascade and reduced the temporal stability of key ecosystem process rates, community diversity and resistance to changes in community composition. Loss of weak interactors also proved damaging for our experimental ecosystems, leading to reductions in the temporal and spatial stability of ecosystem process rates, community diversity, and resistance. These results highlight the importance of conserving species to maintain the stabilizing pattern of trophic interactions in nature, even if they are perceived to have weak effects in the system.

For decades, scientists have argued over the natural phenomena that allow complex communities to persist in nature (1–3). Randomly assembled communities become less stable with increasing complexity (2, 4), but natural communities are finely structured (5, 6), displaying properties that promote stability despite complexity (7). Experiments (8–10) and theory based on empirical data (11, 12) have shown that real food webs are characterized by few strong interactions embedded in a majority of weak links. It is thought that this nonrandom arrangement of interaction strengths promotes community-level stability by generating negative covariances, which suppress the destabilizing effect of strong consumer-resource interactions (3). Theoretical studies provide overwhelming support for the idea that the pattern of strong and weak predator–prey interaction strengths confers stability to food webs (11–14); however, these predictions have never been tested experimentally in natural systems.

One difficulty in testing the importance of interaction strength patterns for the stability of real food webs is the disparity between empirical and theoretical estimates of stability. Theoretical studies often assume that a system is stable only if it is governed by stable equilibrium dynamics (2, 7, 12, 15). Consequently, stability is often measured as the system's ability to defy change, i.e., resilience or resistance (3). In contrast, laboratory and field experiments rarely possess a well-defined equilibrium, so it is difficult to measure resilience or resistance (16). Given the highly variable nature of population dynamics, empirical studies often rely on measures of variability as indicators of system stability (17–21). The 2 approaches are not necessarily contradictory (22), but the challenge for explorations of stability in real ecosystems is to bridge the gap between theory and experiment.

To investigate how a change in the pattern of species interactions might disrupt food-web stability, we first empirically quantified the strength of per capita interactions individually for a set of 10 marine consumer species (see Materials and Methods). These consumers included both vertebrates and invertebrates and are characteristic of the shallow subtidal food web found along the temperate east Atlantic seaboard (23). We ranked these species based on their average per capita effects, measured in isolation, classifying them as either strong or weak interactors (Fig. 1). In a second experiment, by using large subtidal cages that included all 10 consumers (and hence a range of interspecific interactions and multiple predator effects), we allowed natural food webs to develop over a 6-month period (with in excess of 100 species of benthic invertebrates). Based on the classification of species as either strong or weak interactors, we then removed the 2 and 3 strongest and weakest interactors from the mesocosms by using a fully factorial experimental design (see Materials and Methods). We examined the consequences for the structural and functional components of our experimental ecosystems and their stability in time and space. We measured ecosystem process rates (primary and secondary production) and community-level properties (community diversity and stability). We chose to quantify temporal and spatial variability as measures of dynamic stability, and resistance as a measure of the system's ability to defy change. This approach facilitates a comparison of our results with both empirical and theoretical definitions of stability (3).

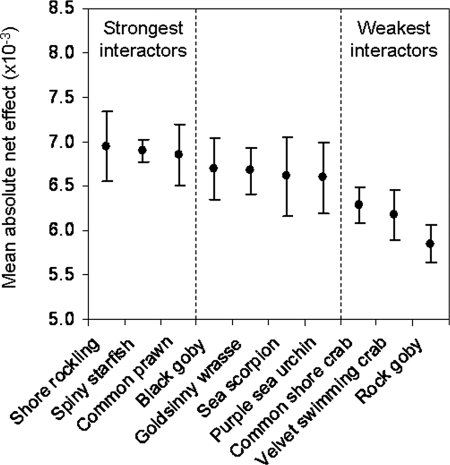
Fig. 1.

Categorisation of 10 marine consumers as strong or weak interactors. The mean absolute net effect (± SEM) of the 10 manipulated species on the rest of the mesocosm communities was measured by using the dynamic index (10). We chose the 3 strongest and 3 weakest interactors for manipulation in the final phase of the experiment.

Results

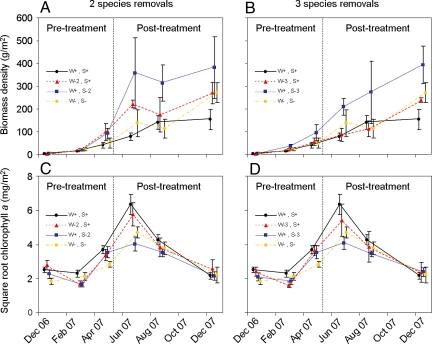
There were no significant effects on primary or secondary production during the community-assembly phase of the experiment, i.e., pretreatment. This suggests that the ecosystem process rates of the mesocosm communities were sufficiently similar before the interaction strength manipulations were applied. The removal of strong interactors produced a dramatic trophic cascade (Fig. 2). Secondary production increased after the interaction strength manipulations were applied, i.e., posttreatment, in the absence of 2 (F_1,9 = 5.119, P = 0.050) and 3 (F_1,9 = 6.802, P = 0.028) strong interactors. As a consequence of the community-level increase in the biomass density of benthic invertebrates, primary production declined posttreatment in the absence of 2 (F_1,9 = 5.214, P = 0.048) and 3 (F_1,9 = 6.902, P = 0.027) strong interactors. The removal of weak interactors had no significant effects on primary or secondary production.

Fig. 2.

Ecosystem process rates in the experiment. Levels of secondary production (A and B) and primary production (C and D) in the experimental mesocosms (± SEM) at each of 6 different sampling sessions. Three of these sessions occurred before the interaction strength manipulation (pretreatment) and 3 after (posttreatment). In the key, W⁺S⁺ = an intact community; W⁻²S⁺ = 2 weakest interactors removed; W⁻³S⁺ = 3 weakest interactors removed; W⁺S⁻² = 2 strongest interactors removed; W⁺S⁻³ = 3 strongest interactors removed; and W⁻S⁻ = all strong and weak interactors removed. Data were transformed for statistical analyses, but original values are shown here for clarity.

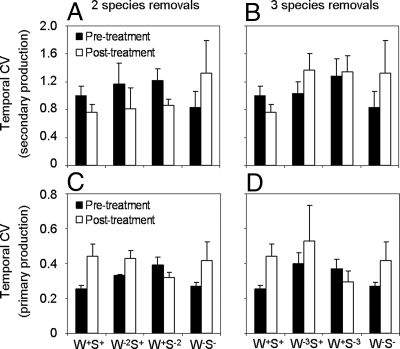
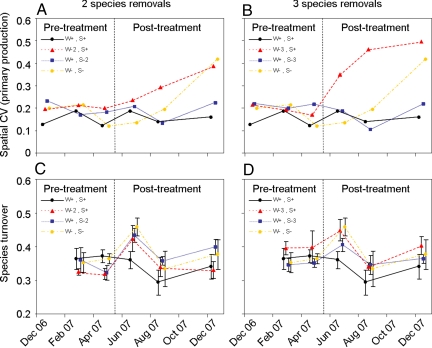
We found significant effects of the interaction strength manipulations on the stability of the mesocosm communities (Figs. 3 and 4 A and B). First, we examined the coefficient of variation (CV) for the different ecosystem process rates within each replicate mesocosm over time as a measure of temporal stability (17, 20). Note that high variability equates with instability. For the 3 species removals, we found that if only strong or weak interactors were present in the community, the temporal variability of secondary production increased (strong × weak: F_1,21 = 5.555, P = 0.028; Fig. 3 A and B). The temporal variability of primary production was significantly lower after 2 (F_1,21 = 9.811, P = 0.005) and 3 (F_1,21 = 10.045, P = 0.004) strong interactors were removed (Fig. 3 C and D). We also investigated spatial stability (CV across replicates within each sampling period) as a measure of consistency in the ecosystem processes of the replicate communities (18, 19, 21). Here, the removal of 2 (F_1,16 = 5.123, P = 0.038) and 3 (F_1,16 = 11.090, P = 0.004) weak interactors increased the spatial variability of primary production (Fig. 4 A and B), i.e., there was greater spatial heterogeneity between the communities. This effect was most pronounced in the 3 species removals (weak × treatment: F_1,16 = 9.420, P = 0.007). Furthermore, when we considered spatial variability in the 3 species removals, we found that the presence of the weak interactors significantly reduced the destabilizing effect of the strong interactors (strong × weak: F_1,16 = 6.326, P = 0.023).

Fig. 3.

Temporal stability effects in the experiment. These effects were measured as the coefficient of temporal variation (temporal CV; ± SEM) of secondary production (A and B) and primary production (C and D). Black bars indicate that stability effects precede the interaction strength manipulation (pretreatment); white bars indicate that stability effects occur after the manipulation (posttreatment). W⁺S⁺ = an intact community; W⁻²S⁺ = 2 weakest interactors removed; W⁻³S⁺ = 3 weakest interactors removed; W⁺S⁻² = 2 strongest interactors removed; W⁺S⁻³ = 3 strongest interactors removed; and W⁻S⁻ = all strong and weak interactors removed. Data were transformed for statistical analyses, but original values are shown here for clarity.

Fig. 4.

Spatial stability and resistance of the mesocosm communities. (A and B) Spatial stability effects in the experiment, measured as the coefficient of spatial variation (spatial CV) of primary production. Each data point represents a single measure calculated across the replicates within each treatment. Therefore, no y axis error bars are included in the plot. (C and D) Resistance of the experimental mesocosm communities to invasions and extinctions, measured as the species turnover (beta diversity) between consecutive sampling sessions. The first sampling session took place in December 2006, so there is no comparison for species turnover in this month. In the key, W⁺S⁺ = an intact community; W⁻²S⁺ = 2 weakest interactors removed; W⁻³S⁺ = 3 weakest interactors removed; W⁺S⁻² = 2 strongest interactors removed; W⁺S⁻³ = 3 strongest interactors removed; and W⁻S⁻ = all strong and weak interactors removed.

Lastly, we examined the effect of the interaction strength manipulations on the diversity of the mesocosm communities. First, we used the Shannon–Wiener index as a measure of richness and evenness in the community. We found no significant diversity effects during the community assembly phase. We found inconsistent effects posttreatment, with the removal of 2 weak interactors (F_1,9 = 9.417, P = 0.013) and 3 strong interactors (F_1,9 = 7.166, P = 0.025) reducing the diversity of our experimental ecosystems. We also measured Whittaker's index of beta diversity, β_w, to examine compositional changes in the communities within a given treatment through time. Here, β_w = (s/α)−1, where s is the total number of species in a replicate community over 2 consecutive sampling sessions and α is the average species richness of the 2 samples. A high turnover of species in the community equates with low resistance to species invasions or extinctions, and hence β_w is used here as a measure of resistance (3, 24). We found no significant species turnover effects during the community assembly phase. Again, we found inconsistent effects posttreatment, with the loss of 2 strong interactors (F_1,9 = 5.199, P = 0.049) and 3 weak interactors (F_1,9 = 5.381, P = 0.046) leading to increased species turnover in the mesocosm communities (Fig. 4 C and D).

Discussion

Natural ecosystems are a complex tangle of interactions, with 95% of species typically no more than 3 links apart (25). This natural complexity persists against the odds (2, 15) because it is governed by fundamental laws and principles that confer stability. One of the most widely accepted of these principles is the pattern of species interactions (3, 6, 8, 9, 11, 12). There is a tendency to consider biodiversity loss in terms of taxonomic identities or functional roles, yet every species can also be considered as a node in a complex web of interactions. Each node contributes to the overall balance of interactions, whether it is a strong or weak interactor. Given the highly interconnected nature of food webs (25) (Fig. S1), any loss of biodiversity could contribute to a ripple effect, changing the pattern of interaction strengths and thus threatening to unbalance the stability conferred by this pattern (3, 6).

Here, for the first time in an experimental study, we have explicitly manipulated species based on the strength of their interactions in nature. We have shown that the removal of strong interactors can produce dramatic trophic cascades. The loss of just 2 or 3 strongly interacting predators led to a massive increase in secondary production, which subsequently caused a reduction in the energy available to the food web through the primary productivity of our experimental ecosystems (Fig. 2). Here, secondary production increased as benthic invertebrates were released from heavy predation pressure, due to removal of the strong interactors. Because many of the benthic invertebrates are grazers, this led to a knock-on effect on primary productivity. That is, an increased density of grazers, and hence grazing pressure, led to a reduction in primary productivity. It should be noted that this effect is largely driven by a suppression of primary productivity in the absence of strong interactors during the summer months. These effects suggest that strong interactors are analogous to keystone species, which typically have effects disproportionately large relative to their abundance (26–28). Fluctuations in population biomass are commonplace, and compensatory reactions among species can maintain aggregate biomass (22). The changes in primary and secondary production shown here are community-level responses however, suggesting that the insurance effect (29) of community diversity is not sufficient to overwhelm the impacts of strong interactors. Trophic cascades like this can alter energy flow, community composition, and habitat provision, and lead to secondary extinctions (26, 30, 31).

Although the loss of weak interactors from our experimental food webs did not lead to cascading effects, their importance in an ecosystem-level context should not be underestimated. Weak interactors appear to play a vital stabilizing role in the delivery of key ecosystem process rates by reducing the variability associated with both primary and secondary production (Fig. 3 A and B and Fig. 4 A and B). Crucially, when strong interactors were present in the community without a sufficient number of weakly interacting species around them, the temporal variability of secondary production and the spatial variability of primary production increased. The lowest levels of variability in these ecosystem process rates could be found when the normal pattern of strong and weak interactors was restored. It is clear from these results that when strong interactors lack a sufficient buffer of weakly interacting species to dampen their destabilizing potential (11), they can disrupt patterns of species interactions, undermining ecosystem functionality and the structures that allow complex communities in nature to persist (17, 20, 24, 32).

There is also a suggestion that weak interactors may be destabilizing in the absence of strong interactors. In our mesocosm communities, there was high temporal variability of secondary production when weak interactors were present in the community without the 3 strongest interactors (Fig. 3B). This implies that strong interactors are also important for stability. Indeed, the highest levels of stability were consistently seen in the intact communities, which contained both strong and weak interactors. As we have seen above, some strong interactors are necessary to maintain the productivity of the system or else cascading effects occur (Fig. 2). Many weak interactors are also required to reduce the destabilizing effect of the strong interactors, most likely through predator interference, e.g., weak interactors may limit predation by strong interactors, through behavioral (i.e., trait-mediated) interactions and competition for resources (33, 34).

It must be noted that the measure of stability discussed above, i.e., variability, is not directly comparable with many of the theoretical studies that suggest a stabilizing pattern of few strong and many weak interactions (e.g., 7, 11, 12). In theoretical studies, stability is typically defined as the return time of a system to equilibrium, or the degree to which a variable changes, after a perturbation. Consequently, we also investigated Shannon diversity and species turnover as measures of the degree to which our experimental communities were perturbed from equilibrium. We see that any disruption to the normal pattern of strong and weak interactors has the potential to upset the community dynamics. Loss of either strong or weak interactors led to a reduction in Shannon diversity, as well as increased species turnover within the experimental communities. High turnover can be attributed to an increased number of species invasions and/or secondary extinctions as a result of the interaction strength manipulations. Consequently, these results suggest that loss of either strong or weak interactors reduced the resistance of the community to changes in species composition. This outcome highlights the need to preserve the natural pattern of predator–prey interactions to maintain the ability of natural ecosystems to resist change (3, 14).

Our experimental design led to the gradual development of communities during a 6-month pretreatment phase. All mesocosms in this phase contained the full complement of manipulated consumer species and, therefore, the communities that developed were quite similar. Subtle differences exist between the mesocosms in this pretreatment phase, which may be due to mortality of some manipulated species between sampling sessions or small differences in the body size of the individuals added to the mesocosms. These pretreatment differences are unlikely to carry over to the interaction strength-manipulation phase. For example, the communities with the lowest temporal variability pretreatment have the highest temporal variability posttreatment (Fig. 3 A–D). Additionally, we found no significant differences between the treatments in the community-assembly phase of the experiment. This suggests that any observed pretreatment differences are minimal and do not influence posttreatment results.

Lastly, the effects on temporal variability of primary production in this experiment initially appear counterintuitive to our arguments above. Here, temporal variability of primary production was high in the intact community (Fig. 3 C and D). This effect was driven by the seasonality of primary production however, with the normal seasonal cycle of primary production (high in summer; low in winter), leading to high temporal variability. The removal of strong interactors led to a significant reduction in temporal variability by diminishing the summer high in primary productivity. Consequently, our measure of ecosystem similarity—spatial variability of primary production—quantified stability effects that were not obscured by the seasonality of primary production.

Through these experimental manipulations, we have shown that strong interactors are analogous to keystone species, driving productivity in our ecosystems through cascading effects (27, 28). We have also shown that extinction of either strong or weak interactors can have detrimental effects on diversity and stability, as the stabilizing natural pattern of trophic interactions breaks down (11, 14). The strong and weak interactors that were removed in this experiment all represent well-connected consumers (see Fig. S1 and Table S1). It would be interesting to investigate whether effects are consistent for the removal of poorly connected species (specialists) and basal species. On the basis of our experimental results, we contend that any loss of biodiversity has the potential to upset the delicate balance of interactions in natural food webs, whether the species lost are strong or weak interactors. Our results emphasize the need to conserve biodiversity, and thus the pattern of species interactions, as a means of maintaining ecosystem structure and functioning and the stable provision of ecosystem services.

Materials and Methods

Experimental Design.

The experiments were carried out in an array of subtidal mesocosms at Lough Hyne in southwest Ireland. The mesocosms were placed on stony substrate, in shallow water, on the south shoreline of the Lough. The mesocosms were secured to the benthos by spreading clean, stony substrate across the bottom of each cage. Lough Hyne is a highly sheltered sea lough, and the weight of substrate in the cages was sufficient to keep them in place for the duration of the experiments. Consequently, the study site was not cleared or disturbed in any other way. Each mesocosm used in the experiments consisted of a large subtidal cage, cylindrical in shape, 0.5 m tall, with a diameter of 0.76 m and a 5-mm mesh size (benthic surface area = 0.45 m²). The mesh size of the mesocosms was sufficiently small to contain the manipulated species, while allowing small benthic invertebrates from lower trophic levels to recruit naturally into the cages (see Fig. S1 and Table S1 for details of the food web). The study consisted of 2 experiments: (i) single-species impacts, where the aim was to identify the strongest and weakest interactors from our 10 chosen consumers; and (ii) interaction strength manipulation, wherein we removed the strongest and weakest interactors from intact communities. The design of these 2 experiments is now discussed in greater detail.

Experiment 1: Single-Species Impacts.

Thirty-three mesocosms were used in this experiment. To identify strong and weak interactors, we added single consumers to empty benthic cages and quantified the net per capita impact of our manipulated species on the rest of the mesocosm community that recruited into those cages. We used a randomized block design, with 3 blocks of 11 treatments placed in the shallow subtidal at depths of 1 m, 2 m, and 3 m at low spring tide. Within each block, we had 10 monocultures of our manipulated species (1 individual per cage) and 1 empty cage (for comparison in the absence of the manipulated species). The position of these treatments within the block was randomly assigned. The experiment ran from 8/17/06 to 9/26/06 (40 days). The net impacts of these predators were quantified by using the dynamic index (10)

where X_i^+j and X_i^−j are the density of species i in the presence and absence of manipulated species j, X_j is the density of the manipulated species, and t is the duration of the experiment in days. The manipulated species had positive as well as negative effects on benthic invertebrates. They also had effects on species that they do not feed on directly. This implies that the 40-day duration of the experiment was sufficient for indirect effects to take place, and so a_ij represents the net (direct plus indirect) effect of the manipulated species. Because the interactions for each manipulated species are a mixture of positive and negative values (which tend to cancel each other out), we obtained the absolute value of each net effect to better represent the magnitude of a species' impact on the community. Thus, we calculated the mean absolute net effect for each of our 10 manipulated species (Fig. 1).

Experiment 2: Interaction Strength Manipulation.

Twenty-four mesocosms were used in this experiment, which was divided into 2 phases. (i) Community assembly: In this phase of the experiment, each mesocosm contained 1 individual of all 10 manipulated species, i.e., the starting point of all 24 mesocosms was the same, and any mortalities among these predators were replaced as they were observed. Small benthic invertebrates were free to recruit naturally into the cages, and so similar communities were allowed to develop over a 6-month period (comparable with the food web in Fig. S1). We arranged the cages into 4 blocks of 6 cages in the shallow subtidal, parallel to the shore, with 2 blocks each at depths of 1 m and 2 m at low spring tide. The community assembly period ran for 195 days from 10/5/06 to 4/18/07. (ii) Manipulation: We removed species based on the strength of their interactions (Fig. 1) and examined the effects on ecosystem structure, functioning, and stability. The 6 treatments that we used were: (i) the 10 species community (W⁺S⁺), i.e., an intact community; (ii) the 2 weakest interactors were removed (W⁻²S⁺); (iii) the 3 weakest interactors were removed (W⁻³S⁺); (iv) the 2 strongest interactors were removed (W⁺S⁻²); (v) the 3 strongest interactors were removed (W⁺S⁻³); and (vi) all strong and weak interactors were removed (W⁻S⁻), i.e., only intermediate interactors present. These 6 treatments were randomly assigned within each of the 4 blocks. The experiment ran for a further 230 days from 4/18/07 to 12/4/07.

Measures of Ecosystem Process Rates.

All sampling substrates used to estimate primary and secondary production were attached to the inside of the cages at the outset of the experiment and removed without replacement at each sampling session, i.e., the sampling substrates represent independent measurements of primary and secondary production but nonindependence among sampling times. Therefore, they constitute a repeated measures design (35). Primary productivity was measured by quantifying the square root of chlorophyll a (mg/m²) on glass slides by using the spectrophotometric method (36). The square root of chlorophyll a has been shown to be a good approximation for primary productivity (37). The slides mostly consisted of small green and red algae, although small fucoids occasionally settled as well. We assessed secondary production in the mesocosms by using (i) settlement panels (100 × 100 mm PVC squares) to quantify sessile species (sponges, bryozoans, calcareous polychaetes, etc.) and (ii) nylon pot scourers (approximate radius, 40 mm; approximate height, 20 mm) to quantify mobile species (amphipods, isopods, gastropods, polychaetes, etc.). We calculated the density of every species identified on these substrates. We also measured the length of every individual identified (n = 228,163) and estimated its corresponding body mass by using length–weight relationships defined for all species (Table S2). We used the square root of chlorophyll a as a surrogate for primary production and biomass density (body mass × density) as a surrogate for secondary production. All of the manipulated species in the cages, as well as the benthic invertebrate community, had access to the sampling substrates, and so could contribute to our measurements of primary and secondary production.

Statistical Analysis.

We used a general linear model (GLM) to analyze the data, with primary and secondary production, Shannon diversity, and Whittaker's beta diversity as response variables. This analysis corresponded to a fully factorial 2-way ANOVA for repeated measures, including the main effects and interaction terms for the presence/absence of strong interactors and presence/absence of weak interactors, with the addition of a single main effect term for block. We split the analysis to examine responses pre- and posttreatment, i.e., during the community-assembly phase (pretreatment) and after the interaction strength manipulations were initiated (posttreatment). There were 3 repeated measurements pretreatment (Dec 2006, Feb 2007, and Apr 2007) and 3 repeated measurements posttreatment (Jun 2007, Aug 2007, and Dec 2007). It was not possible to analyze temporal and spatial CV by using the repeated-measures design. This analyzation was impossible because a comparison across the seasons is implicit in the temporal CV analysis, and there is only 1 measurement per season in the spatial CV analysis. Consequently, we used a 3-way ANOVA with temporal and spatial CV as response variables and presence/absence of strong interactors, presence/absence of weak interactors and treatment as factors (with the addition of block as a single main effect term in the temporal CV analysis). We applied a log₁₀ transformation to the secondary production data and a square root transformation to the temporal CV data to meet the assumptions of normality and homogeneity of variance. To analyze the data in a balanced statistical design, we grouped the treatments according to number of species removed, i.e., we carried out 1 GLM on W⁺S⁺, W⁻²S⁺, W⁺S⁻² and W⁻S⁻ and 1 GLM on W⁺S⁺, W⁻³S⁺, W⁺S⁻³ and W⁻S⁻. This approach permitted us to investigate whether effects were consistent for both 2 and 3 strong or weak interactors removed. Note that block was a significant main effect for the 2 and 3 species removals in the analysis of secondary production and temporal CV of primary production. However, we are accounting for block in all of the models.