Bifurcation and Chaos in a Model of Cardiac Early Afterdepolarizations

Abstract

Excitable cells can exhibit complex patterns of oscillations, such as spiking and bursting. In cardiac cells, pathological voltage oscillations, called early afterdepolarizations (EADs), have been widely observed under disease conditions, yet their dynamical mechanisms remain unknown. Here, we show that EADs are caused by Hopf and homoclinic bifurcations. During period pacing, chaos always occurs at the transition from no EAD to EADs as the stimulation frequency decreases, providing a novel explanation for the irregular EAD behavior frequently observed in experiments.

Complex oscillatory behaviors, such as spiking and bursting dynamics in pancreatic β-cells [1], neurons [1–5], and optical lasers [6], are common phenomena in excitable systems. These complex dynamics are generally described by systems with fast and slow time scales, where the full system behavior can be described by slow dynamics evolving the fast subsystem through a series of bifurcations [1,2]. Cardiac myocytes can exhibit pathological excitations called early afterdepolarizations (EADs), which are voltage oscillations during the repolarizing phase of the action potential (AP). They have been implicated as a cause of lethal cardiac arrhythmias [7–9] and have been widely investigated in experiments [8,10–12] and also in simulations [13–16]. It is commonly agreed that EADs occur when inward (depolarizing) currents are increased and/or outward (repolarizing) currents are decreased. But many such changes do not produce EADs, and the general underlying dynamical mechanism still remains unknown. In single myocytes, EADs typically occur irregularly [10–12], which is generally attributed to random fluctuations of the underlying ion channels [13]. In a recent study [16], we presented evidence from isolated myocyte experiments and computational simulations that irregular EAD behavior is not random, but rather dynamical chaos, and gives rise to novel tissue scale dynamics.

EADs have typically been studied in computational simulations using highly detailed AP models making dynamical analysis difficult [13–16]. In this study, we show that EADs can occur in a simple AP model and the Poincare-Andronov-Hopf (“Hopf”) and homoclinic bifurcations are responsible for the genesis of EADs. We also show that due to the homoclinic bifurcation, EAD chaos can be readily induced during periodic pacing, providing a mechanistic explanation for the irregular EAD dynamics widely observed in cardiac experiments [10–12].

Dynamical origin of EADs

There are typically three time scales in a normal cardiac AP. The sodium (Na) current activates very rapidly, causing the fast upstroke of the AP, and then rapidly inactivates. The L-type calcium (Ca) current activates and inactivates more slowly than the Na current, playing a key role in maintaining the long AP plateau. Time-dependent potassium (K) currents activate even more slowly and eventually overcome the inward currents, repolarizing the cell back to the resting potential. EADs have typically been studied using highly detailed AP models [13–16] which include both detailed membrane currents and intracellular Ca cycling dynamics. Although intracellular Ca cycling has been shown to regulate EAD behavior through its effects on Ca-sensitive currents [17], a simple AP model that includes a fast Na current, an intermediate time-scale Ca current, and a slow K current, is sufficient to produce EADs. Here, we choose the Luo and Rudy (LR1) model [18] to uncover the nonlinear dynamics responsible for the formation of EADs and to explore their dynamics during periodic stimulation. The differential equation for membrane voltage V is

$$C_m\mathit{\text{dV}}/\mathit{\text{dt}}=-\left[I_{\text{Na}}+I_{\text{si}}+I_K+I_0\left(V\right)\right]+I_{\text{sti}},$$ (1)

where C_m = 1 µF/cm²; I_Na is the Na current; I_si = Ḡ_sidf(V − E_si) is the Ca current with gating variables d and f; I_K = Ḡ_Kxx₁(V − E_K) is the time-dependent K current with gating variable x, and x₁ is a voltage-dependent function. The gating variables satisfy the following type of equation: dy/dt = [y_∞(V) − y]/τ_y(V), where y_∞(V) is the steady state and τ_y(V) the relaxation time constant of channel gating, with y standing for the gating variables, such as d, f, and x, etc. I₀(V) represents all the other voltage-dependent currents. The detailed formulation of the LR1 model is available in the original paper [18]. We set E_si = 80 mV and E_K = −77 mV. To study the effects of the time constants for the gating variables d, f, and x on the AP dynamics, we change these time constants by multiplying them by a scalar factor, i.e., τ_d(V) → ατ_d(V), τ_f(V) → βτ_f(V), and τ_x(V) → γτ_x(V). We refer to this modified LR1 model as the whole system. I_sti in Eq. (1) is a stimulus pulse of 2 ms duration and 30 µA=cm² amplitude. We solve the differential equations with a fourth-order Runge-Kutta method and a time step of 0.01 ms.

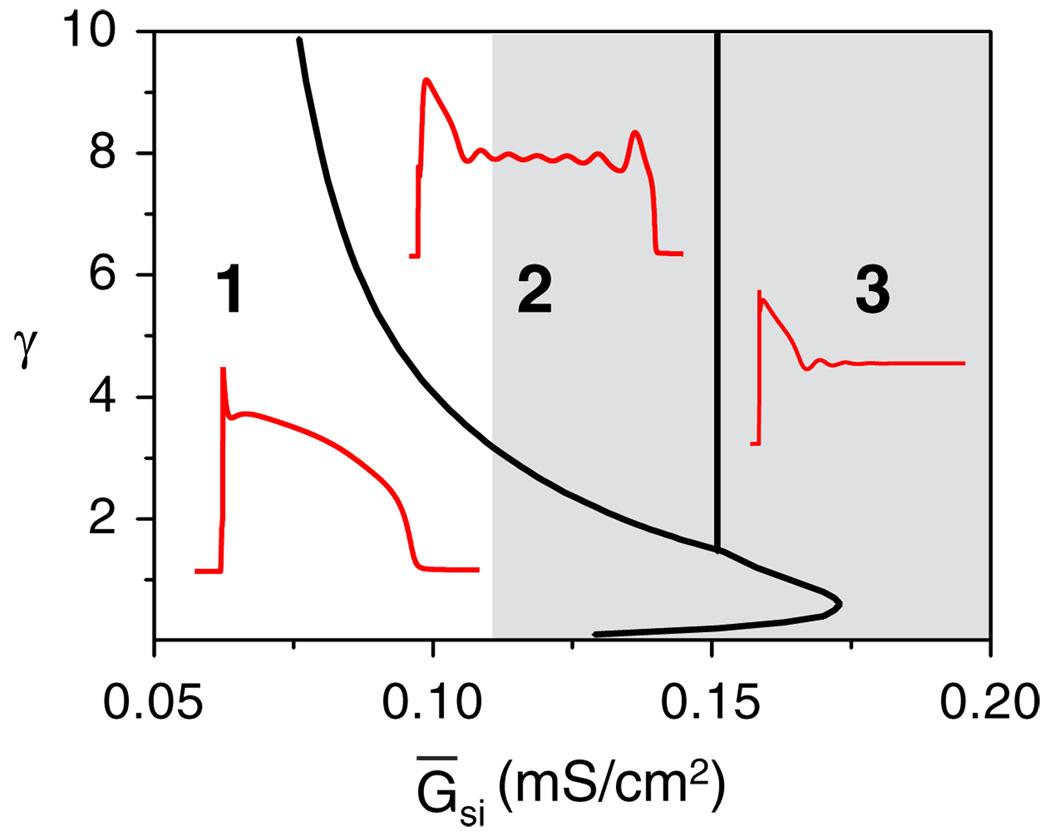
There are three types of AP morphologies found in the LR1 model (Fig. 1): normal APs, APs with EADs, and nonrepolarizing APs (bistable regime), obtained by altering Ḡ _si (in unit of mS/cm²) and the time constant τ_x (by changing γ), with other parameters unchanged. The whole system has only one fixed point (the resting potential) when Ḡ_si is small (white region in Fig. 1) and three fixed points when it is larger (gray region in Fig. 1). The non-repolarizing AP behavior does not occur until Ḡ_si > 0:155, which is maintained by the Ca window current. EADs occur when the time constant of the K current, γ, is greater than a certain value. The Ḡ_si range that produces EAD behavior increases with γ.

FIG. 1.

(color online). Phase diagram of different AP behaviors obtained by changing γ and Ḡ_si. The system has one fixed point in the white area but three in the gray area.

To investigate the underlying dynamics that produces EADs, we first remove I_Na from Eq. (1). I_Na has little effect on EADs in the LR1 model, since it is activated mostly during the upstroke phase of the AP and largely vanishes during the plateau and the repolarizing phases. We then follow a standard method for analyzing a fast-slow system [1]: we analyze the bifurcations in the three-variable system of (V, d, and f), which we call the fast subsystem, by setting x as a parameter, since x varies much more slowly than d and f.

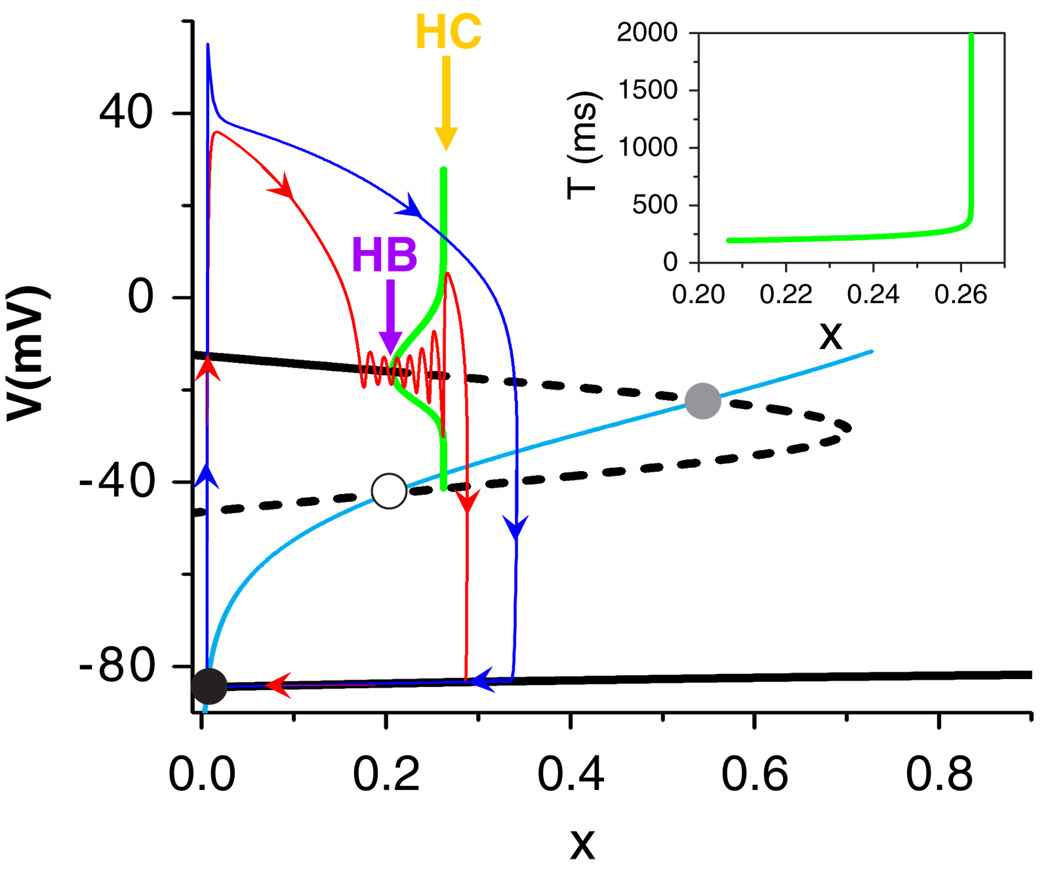
The bifurcation structure of this subsystem can then be analyzed, which is a bistable system (Fig. 2). There are three fixed points when x is small (black lines), but only one when x is large (e.g., 0:7<x<1:0 in Fig. 2). The intersections of the fixed points of the subsystem with x_∞(V) are the fixed points of the whole system (circles). Linear stability analysis of the subsystem shows that the lower branch of fixed points is always stable (the resting potential) and the middle branch is always unstable (saddle points). The upper branch can be either stable, or become unstable via a Hopf bifurcation (purple arrow) leading to limit cycle oscillations which terminate at a homoclinic bifurcation point (yellow arrow).

FIG. 2.

(color online). Black lines: the steady states of the 5 three-variable subsystem versus x (solid: stable; dashed: unstable). Cyan line: x_∞(V). Circles: fixed points of the whole system. Green lines: the maximum and minimum amplitudes of oscillation in the subsystem and the corresponding period T (inset), computed via numerical continuation package auto (E. Doedel et al., http://indy.cs.concordia.ca/auto/). Red line (γ = 10): V versus x from an AP with EADs in the whole system. Red arrows indicate the time course. Blue line (γ = 4): Same as red but with no EAD. Purple arrow marks the Hopf bifurcation (HB) point, yellow arrow the homoclinic (HC) bifurcation point. Ḡ_si = 0:15, α = 0:1, β = 1:1.

To show how the subsystem dynamics affect the behavior of the whole system, we superimpose on the bifurcation diagram two representative APs from the whole system, corresponding to two different values of γ (Fig. 2). For the AP with EADs (red line), the voltage first increases quickly from −80 to 40 mV with almost no change in x. After reaching its peak, the voltage decreases towards the upper branch of the steady state of the subsystem as x increases. After reaching the steady state of the subsystem, the voltage starts to oscillate around the steady state (stable focus) with dampening amplitude. The amplitude of the oscillations begins to grow after the Hopf bifurcation point (purple arrow), and the period extends to infinity (Fig. 2 inset) as x approaches the homoclinic bifurcation point (yellow arrow). Thus, when the system oscillates beyond the homoclinic bifurcation point, it repolarizes back to the resting potential. For the AP without EADs (blue line), x grows much faster (smaller γ), and the whole system is away from the attracting basin of the subsystem. Therefore, it repolarizes to the resting potential without oscillations.

Besides the dependence on γ, the occurrence of EADs also depends on Ḡ_si and the stability of the fixed point on the upper branch (grey circle in Fig. 2). When Ḡ_si is small (white region in Fig. 1), the whole system has only one fixed point, which is the resting potential. When the entire upper branch of steady states of the subsystem is stable, the APs are normal for any γ. If Hopf and homoclinic bifurcations occur on the upper branch, then EADs occur for large γ (white area in region 2 of Fig. 1). When Ḡ_si is larger, the whole system has three fixed points (gray region in Fig. 1). The stability of the upper fixed point (gray circle in Fig. 2) determines whether or not the system repolarizes. If it is unstable (as in Fig. 2), then the AP can always repolarize; whether EADs occur or not depends on γ. If this fixed point is stable, then the system is bistable. A stimulated AP cannot repolarize back to the resting potential (region 3 in Fig. 1).

While the common wisdom that EADs occur when inward currents overwhelm outward currents in magnitude is true, this is a necessary, but not a sufficient, condition. The sufficient condition involves the time constants and kinetics of the Ca current (I_si), which we can study using an analytical approach. We evaluate the eigenvalue properties of the three-variable subsystem, assuming that the time constants τ_d and τ_f are fixed. The differential equations then become dV/dt = F(V, d, f); dd/dt = [d_∞(V) − d]/τ_d, and df/dt = [f_∞(V) − f]/τ_f, where F(V, d, f) = −[I_si + I_K + I₀(V)]/C_m, d_∞(V) is a sigmoid function increasing with V, and f_∞(V) is a sigmoid function decreasing with V. The Jacobian for the steady state of this system is

$$J=\left(\begin{array}{lll}\hfill a\hfill & \hfill b\hfill & \hfill c\hfill \\ \hfill s_d/{\tau }_d\hfill & \hfill -1/{\tau }_d\hfill & \hfill 0\hfill \\ \hfill -s_f/{\tau }_f\hfill & \hfill 0\hfill & \hfill -1/{\tau }_f\hfill \end{array}\right),$$ (2)

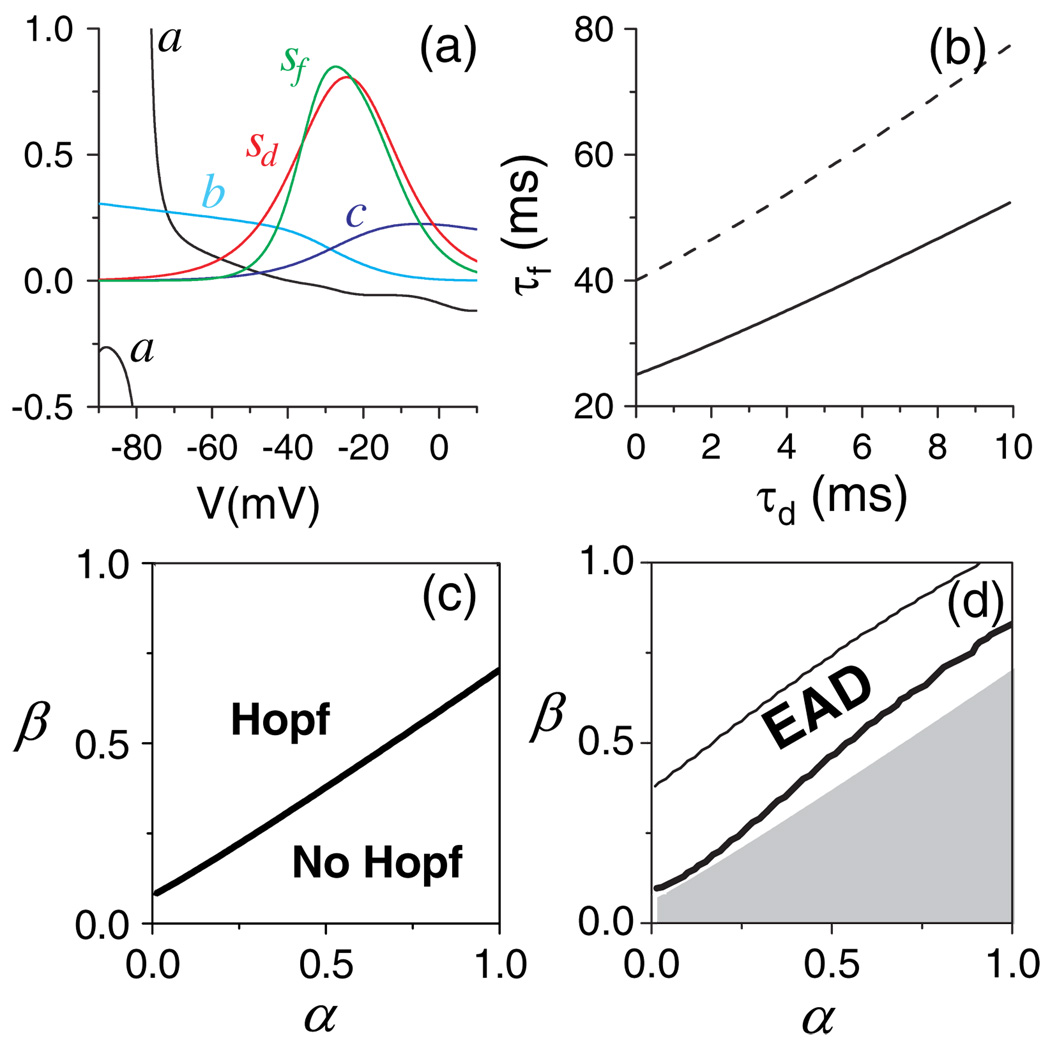
where a = ∂F/∂V, b = ∂F/∂d, c = ∂F/∂f, s_d = ∂d_∞/∂V, and s_f = −∂ f_∞/∂V:b > 0, and c > 0 for V < E_si, and s_d > 0 and s_f > 0 for any V. These quantities from the original LR1 model are shown in Fig. 3(a).

FIG. 3.

(color online). (a) a, b, c, s_d, and s_f versus V for the original parameters in the LR1 model. (b) The Hopf bifurcation point in (τ_d, τ_f) space predicted by Eq. (4). a= −0:05, b = c = 0:1. Solid line: s_d = s_f = 0:9; Dashed line: s_d = s_f = 0:75. (c) The border in the (α, β) space below which no Hopf bifurcation occurs in the upper branch of the steady state of the subsystem. Ḡ_si = 0:1. (d) The EAD region in the (α, β) space of the whole system for Ḡ_si = 0:1. The gray region is a replot of the “No Hopf” region in (c).

At a Hopf bifurcation point, two of the three eigenvalues are λ_1,2 =±iω, and the following conditions can be derived from the characteristic equation of the Jacobian,

$${\omega }^2=\frac{1}{{\tau }_d{\tau }_f}-\frac{a}{{\tau }_d}-\frac{a}{{\tau }_f}-\frac{s_{d}b}{{\tau }_d}+\frac{s_{f}c}{{\tau }_f}>0$$ (3)

and

$$\begin{array}{c}h=\frac{1}{{\tau }_f}\left(\frac{1}{{\tau }_f}-a\right)\left(\frac{1}{{\tau }_d}-a+s_{f}c\right)\hfill \\ \hfill +\frac{1}{{\tau }_d}\left(\frac{1}{{\tau }_d}-a\right)\left(\frac{1}{{\tau }_f}-a-s_{d}b\right)=0.\end{array}$$ (4)

Oscillations occur when h<0. At the Hopf bifurcation point, the third eigenvalue λ₃ is negative so that λ₁λ₂λ₃ = det(J) < 0, where det(J) is the determinant of J. Using det(J) = (a − s_fc + s_db)/τ_dτ_f, one has s_db − s_fc < −a. According to Fig. 3(a), this relation can be satisfied when V >−30 mV at which a<0 and s_db − s_fc <0. For a given set of τ_d, τ_f, and a, Eq. (4) has the form of A − s_dB + s_fC = 0, indicating that s_d and s_f satisfy a linear relation at the Hopf bifurcation point. The τ_f-threshold for Hopf bifurcation versus τ_d calculated from Eq. (3) and Eq. (4) is almost a straight line [Fig. 3(b)]. This is confirmed by results calculated directly from the subsystem [Fig. 3(c)], where the Hopf bifurcation occurs on the upper branch of the steady state only above a certain ratio β/α. Therefore, the activation and inactivation time constants and kinetics of the slow inward Ca current need to be matched properly for the Hopf bifurcation to occur.

To study whether the Hopf bifurcation is necessary for EADs, a search of the (α, β)-parameter space of the whole system reveals that EADs occur in the intermediate range of β/α, whereas APs without EADs occur when this ratio is either low or high [Fig. 3(d)]. The upper border (thin line) moves to higher β/α ratios as γ increases, but the lower border [thick line in Fig. 3(d)] does not vary as γ changes. This lower border is always in the (α, β)-region for which Hopf bifurcation occurs in the subsystem, indicating that the Hopf bifurcation is necessary for EAD occurrence.

Bifurcation to chaos

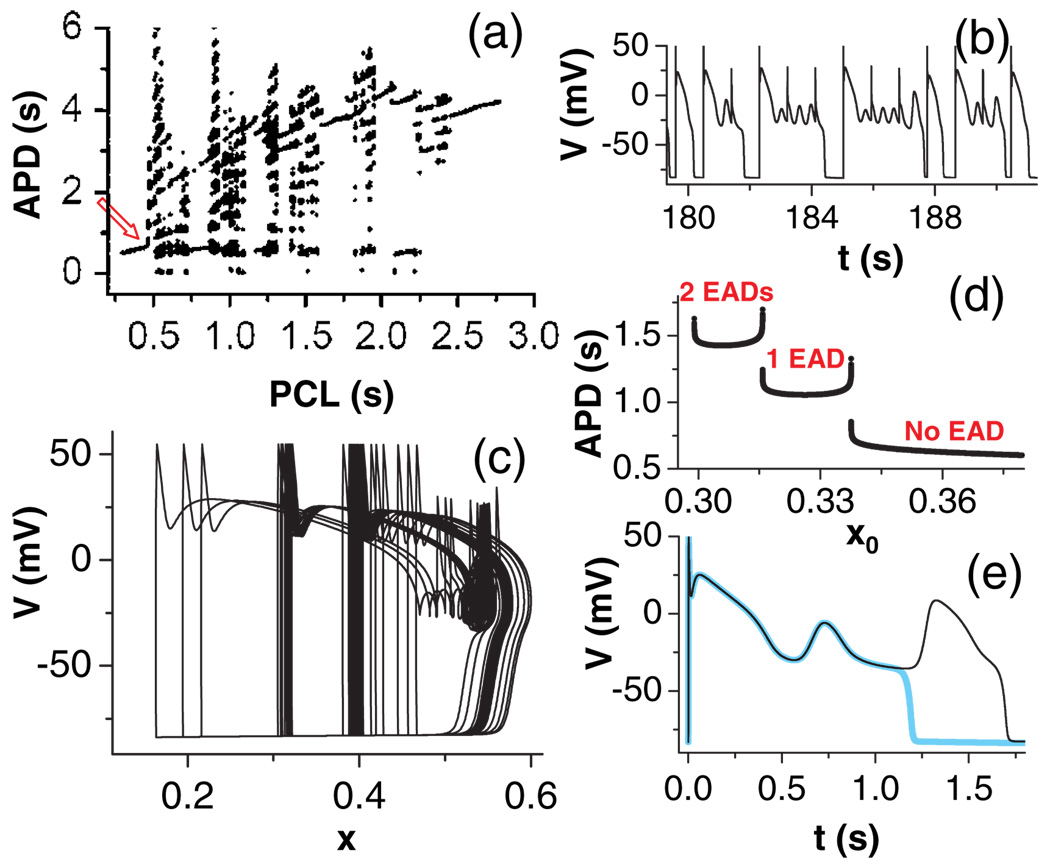
EADs observed in experiments are typically irregular [10–12], which has been attributed to purely random fluctuations in the underlying ion channels [13]. However, the presence of the homoclinic bifurcation suggests an alternative explanation: dynamical chaos. Indeed, chaotic EAD behaviors can always be observed in our system when driven periodically within a certain range of pacing cycle lengths (PCLs), once the parameters are properly set for the system to exhibit EADs. A bifurcation diagram, plotting AP durations (APDs) versus PCL, shows that at both slow and fast pacing, the system is periodic, while chaos occurs at intermediate PCLs [Fig. 4(a)]. A sample voltage trace at PCL = 0:907 s, in the chaotic regime, shows irregular EAD behavior [Fig. 4(b)]. Note that the bifurcation to chaos is directly from period 1 at both the short and long PCL regimes. The mechanism of this type of bifurcation was first shown by Wang [19] and subsequently analyzed by Shilnikov et al. [3,4] in their neuronal bursting and spiking models. Since the transition from period 1 to chaos in the short PCL regime [arrow in Fig. 4(a)] is also the transition from APs with no EAD to APs with EADs, we can always observe chaos in our system under periodic pacing, as long as EADs occur.

FIG. 4.

(color online). (a) APD vs PCL from the whole system with γ = 2:5. APD is defined as the duration of V >−72 mV. (b) A voltage trace from a chaotic regime for PCL = 0:907 s. Sharp spikes are the results of stimulation. The calculated Lyapunov exponent of this trajectory is 0:38 s⁻¹. (c) V vs x from the same chaotic recording as in (b). (d) APD vs different initial x (x₀) while keeping the initial conditions of the other variables the same. (e) Voltage traces for two different x₀: 0.31581 (cyan) and 0.31580 (black), showing the all-or-none nature of EADs.

To further understand how periodic stimulation induces chaos in this system, we plot V against x [Fig. 4(c)] for the same chaotic recording as is shown in Fig. 4(b). Note that the periodic stimuli (sharp spikes in the trajectory) occur at very different initial x values for each stimulated AP. We also plot the APD against different initial x (x₀) while keeping the initial conditions of other variables unchanged [Fig. 4(d)], showing that the APD increases steeply and discontinuously at certain critical values of x₀. The discontinuity occurs at the transitions from no EAD to one EAD, or one EAD to two EADs, and so on [Fig. 4(d)], as also shown by the voltage traces with slightly different x₀ in Fig. 4(e). The x gate of the K channel recovers slowly so that it remains at high values during fast pacing. This keeps the K current large, so there are no EADs, and the system is periodic. For slow pacing, x fully recovers before the next stimulus, and so the APs (with multiple EADs) are identical for each paced beat. In the intermediate range of PCLs, one can always choose a proper PCL so that the steady state x at the time of stimulation is in the steep and discontinuous regime, which makes a small difference in x at the time of stimulation result in a large difference in the following APD and the number of EADs, generating chaos and other periodic states. Therefore, chaos and periodic windows can easily be seen once EADs are present.

Conclusions

While many studies have described ionic mechanisms causing EADs, such as failure of complete inactivation of I_Na [14] or suppression of K currents [8], this study presents a general dynamical mechanism, giving overall necessary and sufficient conditions. We show that the necessary dynamical condition for EAD to occur is that the upper steady state of the voltage/Ca current bistable subsystem loses stability via a Hopf bifurcation, leading to oscillations which are destroyed at a homoclinic bifurcation point. The time constants of activation and inactivation of the Ca current and of activation of the K current need to be properly matched to allow the oscillatory behavior to occur. Because of the homoclinic bifurcation, chaos always accompanies the appearance of EADs, providing a novel mechanistic explanation for the irregular EAD behavior frequently observed in experiments [10–12]. This is also the basis for a novel mechanism of arrhythmogenesis by EADs, as described in our previous studies [16,20]. In addition, our findings may be applicable to other excitable systems which exhibit spiking dynamics.