Hemodynamics in Normal Cerebral Arteries: Qualitative Comparison of 4D Phase-Contrast Magnetic Resonance and Image-Based Computational Fluid Dynamics

Abstract

Detailed knowledge of the hemodynamic conditions in normal cerebral arteries is important for a better understanding of the underlying mechanisms leading to the initiation and progression of cerebrovascular diseases. Information about the baseline values of hemodynamic variables such as wall shear stresses is necessary for comparison to pathological conditions such as in cerebral aneurysms or arterial stenoses. The purpose of this study was to compare the blood flow patterns in cerebral arteries of normal subjects determined by 4D phase-contrast magnetic resonance and image-based computational fluid dynamics techniques in order to assess their consistency and to highlight their differences. The goal was not to validate (or disprove) any of the two methodologies but rather to identify regions where disagreements are to be expected and to provide guidance when interpreting the data produced by each technique.

Introduction

Knowledge of the in vivo hemodynamics in cerebral arteries is important to better understand the underlying mechanisms of initiation and progression of cerebrovascular diseases. In particular, hemorrhagic strokes are most commonly caused by the rupture of a cerebral aneurysm [1]. Intracranial aneurysms are pathological dilatations of the cerebral arteries, commonly located at arterial bifurcations near the circle of Willis [2, 3]. The processes responsible for the initiation, growth and rupture of cerebral aneurysms are multi-factorial and involve the arterial hemodynamics, the vessel wall biomechanics and mechano-biology, and the peri-aneurysmal environment. However, it is widely accepted that hemodynamics plays a fundamental role by producing wall shear stress induced wall degradation and remodeling that lead to aneurysm progression [4]. Hemodynamic studies of cerebral aneurysms using patient-specific geometries have been carried out using in vitro [5, 6] and computational [7-10] models. These studies have characterized the complex intra-aneurysmal blood flow patterns. In order to compare these pathologic blood flow patterns to the normal hemodynamic conditions it is important to determine the normal flow conditions in cerebral arteries. Realistic image-based computational fluid dynamics (CFD) models of cerebral arteries of normal subjects have been constructed [11-14]. Recently, 4D phase-contrast magnetic resonance (PC-MR) imaging techniques have been used to study the hemodynamics of cerebral arteries of normal subjects [15, 16]. Each of these approaches has a number of strengths and limitations. The purpose of this study was to compare the blood flow patterns in cerebral arteries of normal subjects determined by 4D phase-contrast MR and image-based CFD techniques in order to assess their consistency and to highlight their differences. The goal was not to validate (or disprove) any of the two methodologies but rather to identify regions where disagreements are to be expected and to provide guidance when interpreting the data produced by each technique.

Methods

Magnetic Resonance Imaging

Time-resolved or four-dimensional (4D) phase-contrast magnetic resonance (PC-MR) images of the major cerebral arteries at the level of the Circle of Willis were acquired on three young normal subjects. These images were obtained on a 3.0 Tesla (Signa LX CNV, 12.0) scanner (GE Healthcare, Milwaukee, WI, USA) using an eight-channel head array coil (MRI Devices, Waukesha, WI, USA) and peripheral gating by a finger-pulse oxymeter. The scanning parameters were: Field of View (FOV) = 180 × 180 mm, 90% fractional phase FOV, acquisition matrix = 300 × 180 × 30, frequency encoding direction = anterior-posterior, TR/TE = 5.46 ms/2.12 ms, α = 15°, NEX = 1, and receiver bandwidth = ± 62.5 kHz. A flow velocity encoding (venc) = 100 cm/s was chosen along each of the three principal axes. The velocity encoding parameter is used to convert measured phase angles to velocity and is important because if the blood speed is larger than the venc, aliasing artifacts arise that prevent an accurate quantification of the velocity. The data were zero-filled to a reconstruction matrix of 512 × 512 × 60 resulting in an effective spatial resolution of (0.6 × 1.0 × 1.6) mm³ and an interpolated spatial resolution of (0.35 × 0.35 × 0.8) mm³. The data was reconstructed at 20 time points evenly spaced over the R-R interval (cardiac cycle). More details on the acquisition protocol and reconstruction procedures can be found in Bammer et al. [15]. In summary, the data consist of 20 volumes or cardiac phases (one at each time instant) of 512 × 512 × 60 voxels containing the three velocity components along the three principal axes.

Image-Based Computational Hemodynamics Modeling

Subject-specific computational models of the major cerebral arteries were constructed from the magnitude images of the 4D phase-contrast MR acquisition. For each patient, the volumetric magnitude images corresponding to each phase of the cardiac cycle were combined by taking the maximum intensity of each voxel during the entire cardiac cycle. These “time maximum intensity projection” (tMIP) images were then segmented with a seeded region growing algorithm and an iso-surface deformable model [17]. In one case (subject #1) due to variations in the gray level intensity of the MR images the posterior communicating arteries could not be segmented simultaneously with the rest of the vasculature. Therefore, these arteries were independently reconstructed with a tubular deformable model [18] and fused to the vascular model using an adaptive voxelization technique [19]. In the other two cases (subjects #2 and #3) the communicating arteries were not visible in the MR images and were not included in the models. The reconstructed vascular models were smoothed with a volume preserving algorithm [20] and arterial branches were interactively truncated perpendicularly to their axes. The vascular models were meshed with an advancing front method [21]. The resulting tetrahedral grids had a resolution of approximately 0.01 cm and contained between 4.7 and 10.3 million elements. Volume renderings of the magnitude images and the corresponding vascular models of the three normal subjects are shown in Figure 1.

Figure 1.

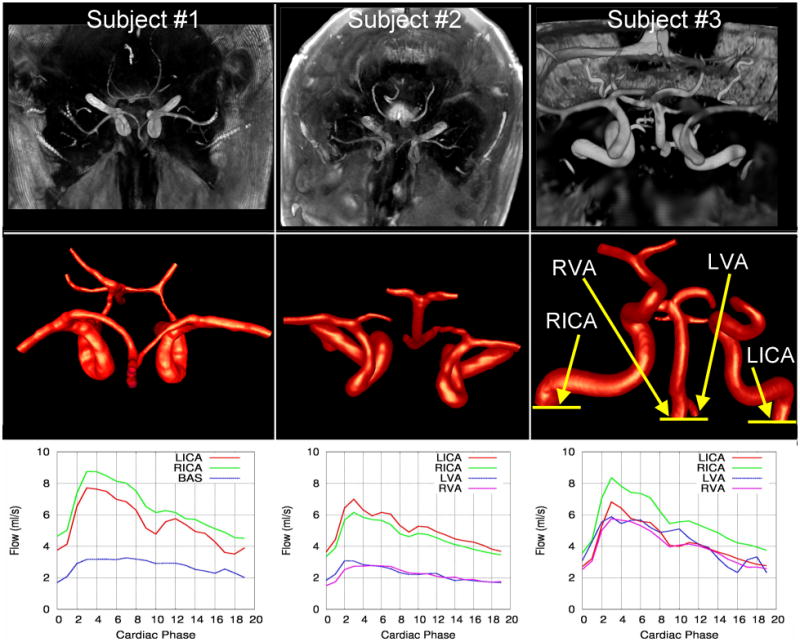
Magnitude PC-MR images (top row), corresponding vascular models (center row), and flow rate waveforms at the inflow vessels of three normal subjects. Subjects 1 and 2 are shown from a superior-inferior view and subject 3 from an anterior-posterior view.

Physiologic flow rate waveforms were obtained for all the inflow vessels of all models. Time dependent flow rates were measured by integrating the through-plane PC-MR velocity component over the artery lumen on a slice perpendicular to its axis. The vessel lumens were manually segmented on the corresponding magnitude images. The flow rate curves obtained for the left and right internal carotid arteries (LICA and RICA), the basilar artery (BA) and the left and right vertebral arteries (LVA and RVA) are shown in the bottom row of Figure 1 for each subject. The locations where the flow rates were obtained are indicated in the model of subject #3 (right panel of center row of Figure 1). Reported PC-MR flow rate measurements in intracranial arteries [22] indicate an error of approximately 5% for the larger vessels (about 6mm diameter) and about 10% for smaller ones (less than 2 mm diameter). The heart rates were 75 bpm, 72 bpm and 70 bpm for subjects 1,2, and 3, respectively. The corresponding Womersley number defined as $\alpha =a\sqrt{\omega /\nu }$ (a is the vessel radius, ω the angular frequency and ν the kinematic viscosity) ranged from 2.8 to 3.8 for the ICAs, from 1.58 to 2.66 for the VAs. The systolic or peak Reynolds numbers based on the vessel diameter ranged from 382 to 531 for the ICAs and from 97 to 379 for the VAs. The diastolic or minimum Reynolds numbers ranged from 200 to 277 for the ICAs and from 40 to 203 for the VAs.

Computational fluid dynamics simulations were carried out for each subject. The governing equations were the 3D unsteady Navier-Stokes equations for an incompressible Newtonian flow:

$$\nabla \cdot \text{v}=0$$ (1)

$${\text{v}}_{,t}+\text{v}\cdot \nabla \text{v}=-(1/\rho )\nabla p+\nu {\nabla }^{\text{2}}\text{v}$$ (2)

where v is the velocity, v_,t represents the derivative of the velocity v with respect to time t, p the pressure, ρ the density, and ν the kinematic viscosity. In the simulations, the density and viscosity were set to ρ = 1.0 g/cm³ and υ = 0.04 cm²/s, respectively. Pulsatile flow boundary conditions were prescribed at the inlets of the models using the Womersley velocity profile [23], which in cylindrical coordinates can be written as:

$$\text{v}(r,t)=\frac{2Q_{\text{0}}}{\pi a^{\text{2}}}\left[1-{(r/a)}^{\text{2}}\right]+\sum _{n=\text{1}}^N\frac{Q_n}{\pi a^{\text{2}}}\left[\frac{1-J_{\text{0}}({\beta }_{n}r/a)/J_{\text{0}}({\beta }_n)}{1-2J_{\text{1}}({\beta }_n)/{\beta }_n{J}_{\text{0}}({\beta }_n)}\right]\text{exp}(i\omega nt)$$ (3)

where a is the vessel radius, Q_n is the n^th Fourier components of the flow rate Q(t), ω is the angular frequency, ${\beta }_n=i^{\text{3}/\text{2}}a\sqrt{n\omega /\nu }$ and J₀ and J₁ are the Bessel functions of the first kind. Traction-free boundary conditions were prescribed at the model outlets. The vessel walls were assumed rigid and no-slip boundary conditions were prescribed at the walls. The numerical solutions of the governing equations were obtained using an in house incompressible flow solver [24]. This solver is based on a fully implicit fractional-step formulation that uses a lower-upper symmetric Gauss-Seidel (LUSGS) algorithm. An edge-based second order upwind finite element formulation is used to discretize the equations in space. At each iteration, the momentum equation is advanced using a generalized minimal residuals (GMRES) method and the pressure Poisson equation is solved using a preconditioned conjugate gradients algorithm (PCG). This formulation is unconditionally stable and thus allows arbitrary time-step sizes. For more details the reader is referred to [25]. The calculations were performed for three cardiac cycles using 100 time steps per cycle, and it was verified that the second and third cycles were identical. CFD results are thus presented for the second cycle. The CFD calculations took approximately 24 hs, running on 8 AMD 3.0GHz Opteron processors in shared memory mode using OpenMP.

Blood Flow Visualization

For comparison, the instantaneous PC-MR velocity fields were linearly interpolated to the unstructured grid used for the CFD simulations. For this purpose, the instantaneous 3D PC-MR velocity images were thought of as a Cartesian grid and the cell containing each unstructured grid point was identified and the velocity values linearly interpolated from the 8 cell nodes. The CFD and PC-MR velocity fields were then visualized using streamlines. The streamlines were obtained by advancing the equation of motion of massless particles:

$${\text{x}}_{,\tau }=\text{v}(\text{x},t)$$ (4)

where x is the position of each particle, v is the fluid velocity field at time t, and τ represents a pseudo time, and x_,τ is the derivative of the position with respect to the pseudo time. These equations were numerically solved using a fourth order Runge-Kutta scheme [26]. The velocity field was linearly interpolated to the particle positions using a fast neighbor to neighbor algorithm for interpolation on unstructured grids [27]. A set of instantaneous streamlines were computed for the PC-MR and CFD velocity fields at each instant during the cardiac cycle. The origin of the velocity streamlines were placed inside the desired artery (e.g. ICA) half way between the inflow and outflows and propagated both in the positive and negative velocity directions. The same initial positions were used to propagate streamlines in the PC-MR and CFD fields. The streamlines were color coded according to the local velocity magnitude. In addition, the local velocity magnitude or velocity profiles were visualized at a number of manually selected planes cutting the major cerebral arteries. The wall shear stress distribution was calculated from the velocity field as:

$$\tau =\mu \frac{\partial }{\partial n}(\text{v}-\text{v}\cdot n)$$ (5)

where n is the normal to the surface and (v − v · n) represents the tangential velocity component. The normal derivatives of Eq. (5) were numerically calculated using a second order approximation based on a parabolic recovery of boundary gradients algorithm [28], which is basically equivalent to placing three points in a layer of thickess 0.01 cm (the uniform mesh resolution used) close to the vessel wall. This mesh resolution should be sufficient to resolve the velocity gradients for the range of Reynolds numbers considered, at least for the major vessels.

Results

The flow patterns along the selected cerebral arteries at peak systole obtained from the PC-MR images and the corresponding CFD models are presented in Figure 2, Figure 3 and Figure 4 for subjects 1, 2 and 3, respectively. These visualizations show that qualitatively, the major flow structures, swirling flows, flow directions in communicating arteries, etc. observed in the PC-MR images and the CFD simulations coincide. However, there are a number of differences: a) the velocity magnitudes tend to be higher in the CFD models, b) secondary flows (rotational or non-axial velocity components) are weaker in the PC-MR images, making the flow pattern more parallel or laminar, c) flow recirculation regions observed in the CFD models near vessel bifurcations are not well captured by the PC-MR images, d) the flow fields derived from the PC-MR images are not divergence-free and some streamlines stop inside the vascular domain.

Figure 2.

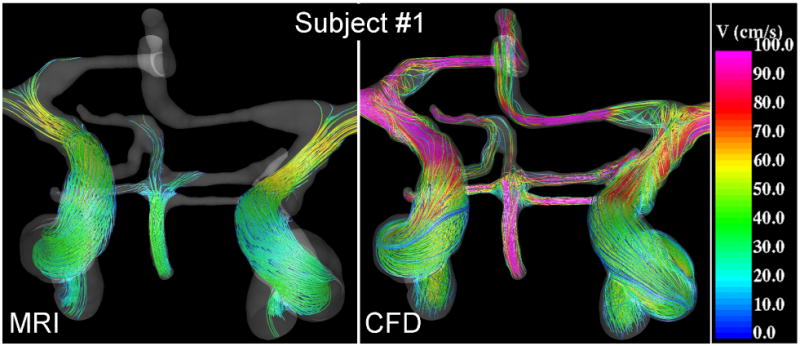
Visualizations of the blood flow patterns at peak systole in the major cerebral arteries of subject #1 obtained from the MRI (phase-contrast MR) data and CFD model.

Figure 3.

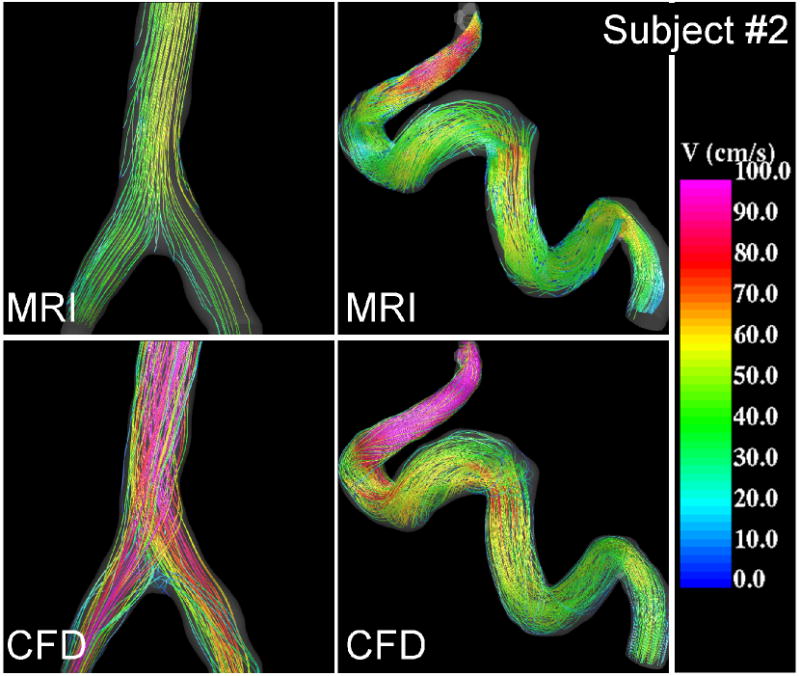
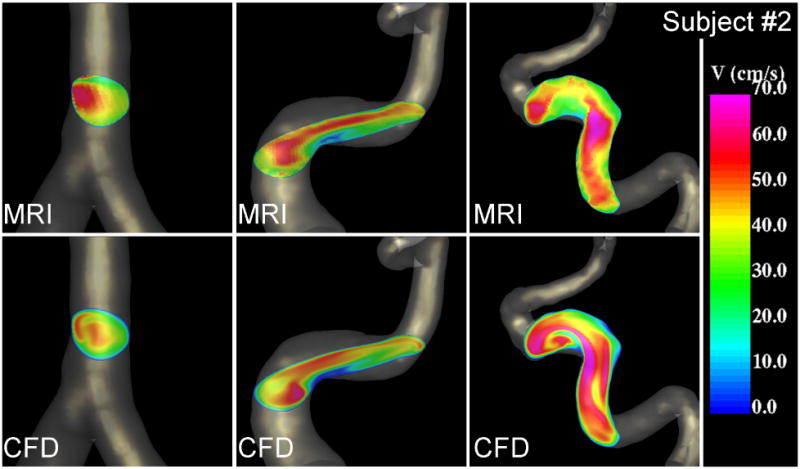
Visualizations of the blood flow patterns at peak systole near the V-V junction (left) and in the left internal carotid artery (right) of subject #2 obtained from the MRI (phase-contrast MR) data and CFD model.

Figure 4.

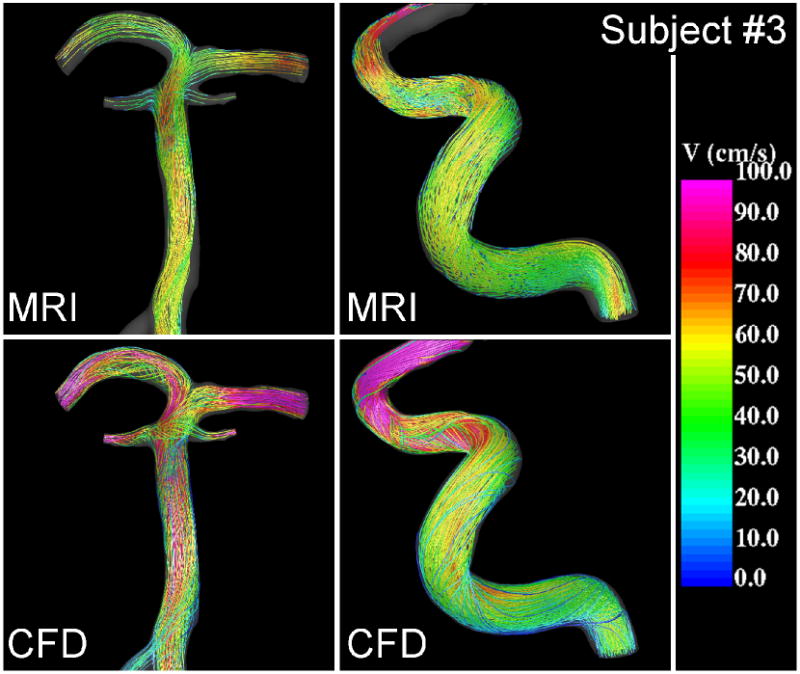
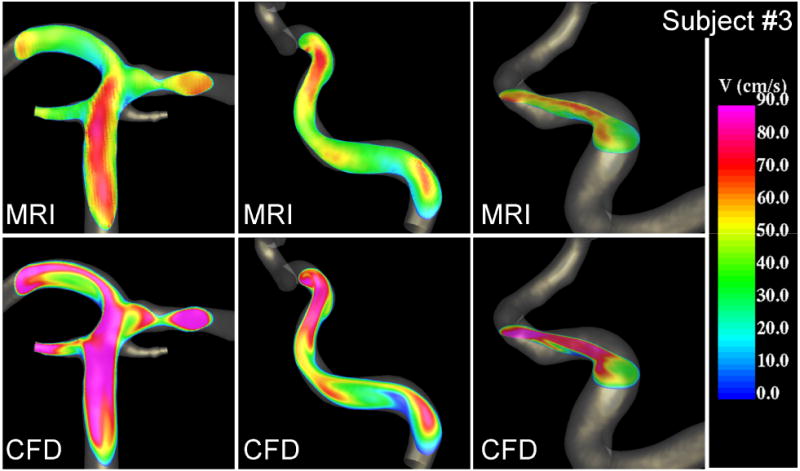
Visualizations of the blood flow patterns at peak systole in the basilar (left) and right internal carotid artery (right) of subject #3 obtained from the MRI (phase-contrast MR) data and CFD model.

Peak velocity profiles at selected cuts through cerebral arteries obtained from the PC-MR images and the CFD models of subjects 2 and 3 are presented in Figure 5 and Figure 6, respectively. These velocity profiles are non-trivial skewed profiles produced by the curving, branching and tapering arteries with non-uniform distributions of velocity magnitudes along the vessels. These visualizations show that qualitatively the complex PC-MR and CFD velocity profiles are remarkably similar. As noted before, the CFD models tend to exhibit larger velocity magnitudes than the corresponding PC-MR images, however the shape of the velocity profiles, regions of low and high blood flow speed, location of maximum velocities, etc. are in good agreement. The maximum systolic velocity at different locations along the cerebral arteries was determined for each patient from both the PC-MR data and the CFD results. It was found that along the ICA, the maximum CFD velocity ranged from roughly 40 to 60 cm/s in the cavernous segment near the inflow, 60 to 80 cm/s in the ophthalmic segment, and 80 to 100 cm/s in the paraclinoid segment near the carotid terminus. The corresponding ranges determined from the PC-MR data were: 40-50 cm/s in the cavernous segment, 50-70 cm/s in the ophthalmic segment, and 60-70 in the paraclinoid region. The CFD models yield a maximum velocity 5-10% higher than the PC-MR data in the cavernous segment, about 20% higher in the ophthalmic segment, and about 30% higher in the paraclinoid region. Similarly, differences of roughly 40% were observed in the basilar artery, and up to 50% in the middle cerebral arteries. This indicates that as the arteries become smaller, larger differences are observed between the CFD and PC-MR velocity quantifications.

Figure 5.

Velocity profiles at peak systole near the V-V junction (left), the right (center) and left (right) internal carotid arteries of subject #2 obtained from the MRI (phase-contrast MR) data and CFD model.

Figure 6.

Velocity profiles at peak systole in the basilar (left), the right (center) and left (right) internal carotid arteries of subject #3 obtained from the MRI (phase-contrast MR) data and CFD model.

The distributions of wall shear stress at peak systole obtained from the CFD models of each subject are presented in Figure 7. This data indicates that the values of WSS vary along the cerebral vessels. For instance, the peak WSS in the cavernous ICA segment upstream of the carotid siphon has a baseline value of approximately 20 dyne/cm², while this value reaches 50 dyne/cm² near the ophthalmic region, 100 dyne/cm² in the paraclinoid region and about 200 dyne/cm² in the middle cerebral and anterior cerebral arteries, and about 50 dyne/cm² in the basilar artery. However, substantial deviations from these baseline values are produced by the patient-specific vessel geometry. In particular, zones of increased and decreased WSS can be observed in regions of high arterial curvature and near bifurcations. The increase of the WSS magnitude observed along the vessels is a consequence of the tapering geometry of the cerebral arteries. Some similarities in the distribution of wall shear stress among the different subjects can be observed. However, the local values of WSS depend on the shape of the velocity profile (axial flow velocity) and secondary flows (rotational flow velocity), which in turn are determined by the subject-specific arterial geometry. For instance, subjects 2 and 3 have ICAs with larger curvature in the siphon region than subject 1, and therefore larger WSS values (it reaches approximately 200 dyne/cm² in the left ICA of subject 2 and about 230 dyne/cm² in the left ICA of subject 3, while it is about 100 dyne/cm² in the left ICA of subject 1). On the other hand, all subjects had smaller curvatures in the right ICA and closer values of maximum WSS, around 100 dyne/cm². Maximum WSS baseline values in the basilar artery varied from about 30 dyne/cm2 in subject 3 to 100 dyne/cm² in subject 2 and 150 dyne/cm² in subject 1. Again local variations around these values are observed depending on the curvature and shape of the arteries of each patient. For example, the BA of subject 1 has larger curvature which produces a region of increased peak WSS which reaches values over 200 dyne/cm². As mentioned before, as the arteries become smaller the differences between the CFD and PC-MR velocity fields become larger, with the actual velocity likely in between the PC-MR and CFD values. The accuracy of the WSS estimations strongly depends on the accuracy of the geometry of the vascular model. Thus, it is to expect larger deviations of the WSS values from the actual values in smaller arteries. The large values of WSS observed in arteries such as the MCAs and ACAs are most probably due to underestimations of their cross sectional areas obtained during the vascular model reconstruction from the PC-MR magnitude images.

Figure 7.

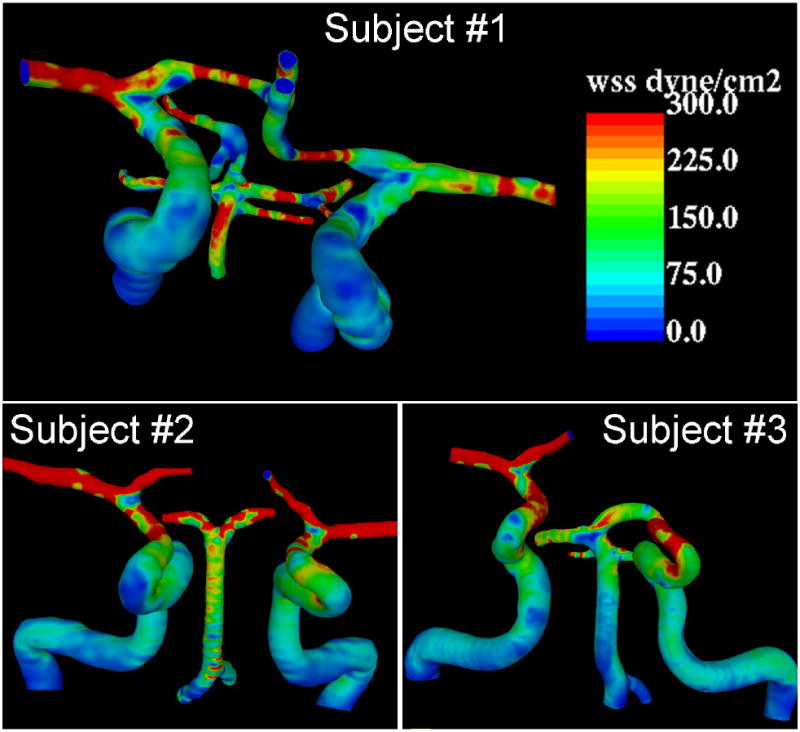
Wall shear stress distributions in three normal subjects determined from CFD models.

Discussion

Blood flow patterns in the major cerebral arteries at the level of the circle of Willis have been quantified from both PC-MR imaging and image-based CFD modeling. Both techniques yield consistent descriptions of the major flow characteristics in these vessels. However, a number of differences have been observed. These differences are caused by the limitations of each technique, which are discussed in what follows.

The main issue of PC-MR imaging is resolution, both spatial and temporal. The velocity measurements obtained at each voxel of a PC-MR image are the spatial average of the velocities inside each voxel. Furthermore, in most MR acquisitions, anisotropic voxels are used in order to cover the field of view with a small number of slice planes. In addition, the cardiac cycle is divided into a number of temporal intervals or phases and the instantaneous velocities are averaged over each of these intervals. The primary effect of the limited spatial and temporal image resolution is an underestimation of the local instantaneous velocity magnitude and a smoothing of the velocity pattern as a result of the averaging processes. Therefore, compared to the CFD models, the PC-MR velocity patterns exhibit smaller secondary flow velocities, i.e. less swirling more parallel flows, and less complex flows in regions of flow recirculation or disturbed flow near arterial bifurcations. These are important aspects of flow hemodynamics for some clinical applications such as aneurysms [8], and may limit the potential use of PC-MR in these cases. Anisotropic voxels with a 4:1 ratio of the z to xy sizes were used in the scans presented above. The effects of these anisotropic voxels can be seen in horizontal arterial segments (parallel to the xy plane). In these segments the PC-MR velocity pattern is parallel to the xy plane with almost no swirling (i.e. no secondary or rotational flow velocity). This is even more evident in smaller vessels which can have only two or three voxels across their lumen, and therefore the PC-MR velocity is almost the average velocity over the vessel cross-sectional area.

The effect of averaging the flow field over the volume of each voxel is illustrated in Figure 8. This figure shows the peak velocity magnitudes of the CFD model (left panel), the CFD velocities interpolated and averaged on the PC-MR voxel space (center panel) and the PC-MR velocity field interpolated to the CFD mesh for subject #1. It can be seen that averaging the CFD velocities over the MRI voxels reduces the velocity magnitudes and yields values closer to the PC-MR measurements.

Figure 8.

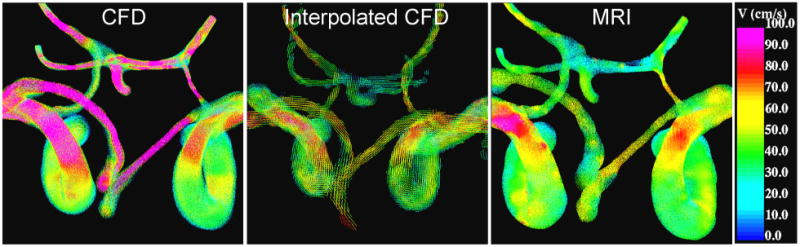
Velocity field at peak systole of subject 1. Left panel: CFD velocity, center panel: CFD velocity interpolated and averaged on MRI voxel space, right panel: PC-MR velocity interpolated to CFD mesh.

Another problem associated with limited image resolution is that some of the smaller vessels such as the ophthalmic artery or some of the communicating arteries may not be detected in the MR images. However, the spatial and temporal resolutions of the PC-MR images can be increased at the cost of scanning time. Despite these limitations, PC-MR images provide realistic quantifications of the volumetric blood flow rates along the major cerebral vessels [22] and visualizations of the main blood flow structures, and can play an important role for the assessment of hemodynamic disturbances in patients. In addition, estimations of the wall shear stress from the PC-MR velocity profiles can be obtained but typically require fitting a parabolic profile through the axial velocity profile [29] – which would likely yield a poor estimation of the local WSS in curved tortuous vessels – and/or accurate determination of the location of the vessel wall in order to calculate the velocity gradients.

The primary issue of image-based CFD modeling is an accurate representation of the arterial geometry. Blood flow patterns strongly depend on the geometry of the vessels. The accuracy of anatomical models constructed from MR images depends on the image resolution and the reconstruction algorithms. In particular, the construction of anatomical models from PC-MR magnitude images can lead to underestimations of the vessel caliber which in turn can result in overestimations of the blood flow velocity and wall shear stress magnitudes. This is especially important in smaller horizontal arteries that have been scanned with anisotropic voxels, and therefore could introduce significant errors in the reconstruction of the cross-sectional area. The use of higher resolution time of flight MR angiography images could lead to more accurate CFD models. On the other hand, numerical models provide a very detailed blood flow characterization including axial and rotational velocity components along arteries as well as complex recirculation regions near bifurcations. In addition, these models yield divergence-free velocity fields and a realistic estimation of the non-uniform wall shear stress distribution that are not based on the assumption of a parabolic velocity profile – which as shown earlier, the velocity profiles can be substantially different from simple parabolic shape. These estimations of wall shear stress combined with detailed hemodynamic patterns can play an important role to further our understanding of (and in some cases to predict) the development of various vascular abnormalities.

Conclusions

Phase-contrast magnetic resonance imaging and image-based computational fluid dynamics techniques yield qualitatively consistent representations of the in vivo hemodynamics in the major cerebral arteries. However, each technique has limitations that introduce differences between the corresponding blood flow velocity fields. It is important to understand these differences in order to better interpret the results obtained with each technique, and to be aware of the regions along the arteries where each technique is expected to over simplify the velocity patterns or yield under or over estimations of the velocity and wall shear stress magnitudes. In turn, this is important to better characterize the hemodynamics in normal subjects which is useful to compare to pathological conditions.