Improved Self-Calibrated Spiral Parallel Imaging Using JSENSE

Abstract

Spiral MRI has several advantages over Cartesian MRI such as faster acquisitions and reduced demand in gradient. In parallel imaging, spiral trajectories are especially of great interest due to their inherent self-calibration capabilities, which is especially useful for dynamic imaging applications such as fMRI and cardiac imaging. The existing self-calibration techniques use the central spiral data that are sampled densely in the accelerated acquisition for coil sensitivity estimation. However, the resulting sensitivities are not sufficiently accurate for SENSE reconstruction due to the data truncation. In this paper, JSENSE which has been successfully used in Cartesian trajectories is extended to spiral trajectory such that the coil sensitivities and the desired image are reconstructed jointly to improve accuracy through alternating optimization. The improved sensitivities lead to a more accurate SENSE reconstruction. The results from both phantom and in vivo data are shown to demonstrate the effectiveness of JSENSE for spiral trajectory.

1 INTRODUCTION

In many dynamic MRI applications, it is desirable to reduce imaging time to achieve high spatio-temporal resolution. A classical approach is to use fast-scan methods that traverse quickly through k-space. Among these methods, spiral trajectory is known to have several advantages over the Cartesian trajectory due to its reduced influence from T₂-decay and its robustness against bulk physiologic motion [1, 2]. When combined with the recent parallel MRI technique, which takes advantage of spatial sensitivity information inherent in an array of multiple receiver surface coils to reduce the number of gradient encoding steps, the imaging speed can be further enhanced. The parallel spiral imaging is especially useful in high-resolution fMRI, arterial spin labeling, diffusion imaging, and cardiac imaging [1, 3].

Over the past few years, a number of parallel magnetic resonance imaging (pMRI) techniques have been proposed in reconstructing a complete MR image from reduced k-space data in Cartesian trajectories, such as SMASH [4], SENSE [5], and GRAPPA [6]. Although many advances have been made in Cartesian reconstruction for parallel imaging, spiral reconstruction techniques still need further improvement. Most existing techniques for spiral parallel imaging still require a separate calibration scan with full field of view before or after the accelerated scans. In spiral SENSE, these scans are used to derive sensitivities [4, 5], and in spiral GRAPPA, they are used to estimate the fitting coefficients [3, 6]. This calibration scan can prolong the total imaging time, partially counteracting the benefits of reduced acquisition time associated with parallel MRI. Another practical problem with this technique is that misregistrations or inconsistencies between the calibration scan and the accelerated scan result in artifacts in the reconstructed images, which is a major concern in dynamic imaging applications. The self-calibrated technique [7] is known to be able to address the above problems in SENSE reconstruction. In spiral and radial SENSE, even with reduced number of interleaves, the central k-space is automatically sampled beyond Nyquist rate, and thus can be used for estimation of sensitivities without the need for additional encodings to acquire the self-calibration data as in Cartesian case. This inherent self-calibration capability makes the self-calibrated technique especially of interest for spiral and radial trajectories. However, as noted in [7], the data that satisfy the Nyquist rate only provide low spatial frequencies of coil sensitivity. In addition, the accuracy is not guaranteed in the regions where the image has low intensity. The resulting errors in sensitivity is propagated to the final reconstruction.

In this paper, we extend to spiral trajectories our earlier joint estimation technique [8] which has shown to be able to improve coil sensitivity accuracy for Cartesian trajectory. The method jointly estimates the coil sensitivities and reconstructs the desired image through alternating optimization so that the sensitivities are estimated from the full data recovered by SENSE instead of the center k-space data only, thereby increasing high frequency information without introducing aliasing artifacts. The method was tested on a number of scanned parallel imaging data sets, and the reconstruction results are shown to be superior to the conventional self-calibrated spiral SENSE.

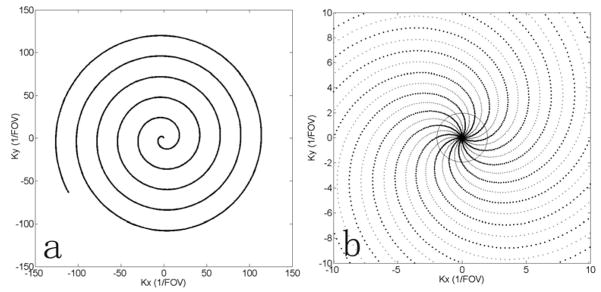
2 METHOD

In this study, we used an approximation of the desired constant-linear-velocity Archimedean spirals [9, 10]

$$k(t)=\alpha \theta (t)e^{i\theta (t)},$$ (1)

where $\theta (t)=2\pi \omega \sqrt{t}$. The real and imaginary parts of the complex function k(t) = k_x(t) + ik_y(t) give the trajectory in the x-y coordinate, the constant ω gives the number of rotations, and the constant α determines the rate of increase in the radial direction with respect to the rate of rotation. For multiple interleaves, a phase shift of 2π(n −1)/N_leaf is added for the n-th interleaf, where N_leaf is the total number of interleaves. The actual trajectory approaches this constant-linear-velocity spiral under the hardware constraints of the gradient system. Spiral trajectories with ω = 5, a = 3.8 (1/FOV) were used in this study. Figure 1(a) shows a single interleaf of a constant-linear-velocity spiral trajectory and (b) shows the central k-space trajectory with 24 interleaves. As seen in Figure 1(b), the center k-space is automatically sampled densely enough to satisfy the Nyquist sampling criterion even in the accelerated scan where some interleaves are skipped [7]. This so called self-calibrating property is desirable in parallel imaging where the central reduced data can be used for sensitivity estimation without the need for additional acquisition. To estimate the sensitivity functions, these truncated central k-space data are Fourier transformed to generate several low-resolution reference images for all channels, and the sensitivity functions are obtained by normalizing these reference images by their sum-of-squares reconstruction. The estimation can be mathematically expressed as

Fig 1.

The spiral trajectory used in this study, with a single interleaf shown in (a), and all 24 interleaves in (b). The dashed curves in (b) denote the interleaves to be skipped in an accelerated scan when R = 2. Inside the circle in (b), the Nyquist sampling rate is satisfied for the accelerated scan with R = 2.

$${\widehat{s}}_l(\overrightarrow{r})\approx \frac{[\rho (\overrightarrow{r})s_l(\overrightarrow{r})]\ast h(\overrightarrow{r})}{\sqrt{{\sum }_l{\mid [\rho (\overrightarrow{r})s_l(\overrightarrow{r})]\ast h(\overrightarrow{r})\mid }^2}}$$ (2)

where ŝ_l (r⃗) and s_l (r⃗) are the estimated and true sensitivities respectively, ρ(r⃗) is the image, and h(r⃗) is the point spread function of the k-space sampling trajectory inside the circle with a chosen radius. This estimation method implicitly assumes the sensitivity weighting and convolution with the point spread function are commute [11], which is not satisfied in general. For the spiral trajectories used in this study, the radius inside which the Nqyuist rate is satisfied for the reduced scan is given by [7]

$$k_0=\frac{N_{\text{red}\_\text{leaf}}}{2\pi \text{FOV}},$$ (3)

where N_{red_leaf} is the number of interleaves in the reduced scan and FOV denotes the field of view. This radius is shown as a circle in Fig. 1(b) for a reduction factor of 2. When the truncation radius is less than k₀, the corresponding point spread function has no aliasing artifacts, but is so wide that truncation effect is serious. As the radius of truncation circle increases, the point spread function becomes sharper, but the aliasing artifacts start to appear. This tradeoff between reduced truncation effect and reduced aliasing artifacts leads to inaccurate sensitivity functions, which becomes serious especially at locations where the object transverse magnetization has high spatial frequency components. Consequently, the self-calibrated SENSE reconstruction suffers from residual aliasing artifacts.

We extend the JSENSE method [8] to improve the self-calibrated spiral SENSE. Specifically, we treat both the sensitivities and the desired image as unknowns in the imaging equation

$$d_{l,m}=\sum _n{s}_l({\overrightarrow{r}}_n)\rho ({\overrightarrow{r}}_n)e^{-i2\pi {\overrightarrow{k}}_m·{\overrightarrow{r}}_n},$$ (4)

where k⃗_m is the m^th sampling location on a spiral trajectory in k-space, d_l,m is the corresponding k-space data point acquired at that location from the l^th channel, r→n is the n^th pixel location of an image on a Cartesian grid, and s_l(r⃗_n) and ρ(r⃗_n) are the corresponding sensitivity and image values at that pixel location, with both m and n in lexicographical order. To reduce the degree of freedom for the unknowns to be solved for, we use a polynomial parametric model instead of a pixel-based function for the coil sensitivities:

$$s_l(\overrightarrow{r})=\sum _{p=0}^N\sum _{q=0}^N{a}_{l,p,q}{(x-\overline{x})}^p{(y-\overline{y})}^q,$$ (5)

where (x, y) =r⃗ denotes the location of a pixel, (x̄, ȳ) denotes the image center location, and a_{l, p,q} is the coefficient of a polynomial, forming an unknown vector a. Several other models, such as wavelet and spline, are also appropriate for the smooth sensitivity functions. With the unknown a written in the SENSE equation explicitly, the JSENSE solves

$$\mathbf{E}(\mathbf{a})\mathbf{f}=\mathbf{d}$$ (6)

for a and f jointly, where f is the vector representation of the desired image ρ(r⃗_n) and vector d is the vector representation of the acquired k-space data, E(a) is the spiral SENSE encoding matrix

$$\mathbf{E}{(\mathbf{a})}_{\{l,m\},n}=\sum _{p,q}{a}_{l,p,q}{(x_n-\overline{x})}^p{(y_n-\overline{y})}^q{e}^{-i2\pi (k_{xm}·x_n+k_{ym}·y_n)},$$ (7)

with k_xm and k_ym denoting the x and y components of the k-space sampling location k⃗_mon a spiral trajectory. JSENSE employs an iterative alternating optimization, where the self-calibrated SENSE reconstruction is used as the initial value for the first iteration. The detailed description of the JSENSE method can be found in [8].

Both phantom and human experiments were performed on a GE 3T Excite whole-body scanner (Waukesha, WI). In the phantom experiment, a set of watermelon phantom data was acquired with an eight channel head coil and gradient echo sequence (TE=3.2ms, TR=2sec, FOV=24cm, matrix=256 × 256, slice thickness=5mm). The fully sampled data were acquired with 24 interleaves, and 2332 points in each interleaf. We simulate the downsampled data with a reduction factor of 2 by keeping every other interleaf. In the cardiac imaging experiment, 27 cardiac phases were acquired on a 3-T Excite MR system (GE Healthcare Technologies, Waukesha, WI, USA) using a four-channel cardiac coil and the cardiac gated spiral SPGR (125kHz, 30-degree flip angle, 36cm FOV, 8mm slice thickness, min TE) with breath-holding. Written informed consent was obtained from the subjects and the experiments were performed in compliance with regulations of the institutional review board. The full acquisition includes 20 interleaves per 256 × 256 image with 1024 points in each interleave. Spectral-spatial selective excitation was employed to suppress fat signal. Similar to the phantom experiment, 10 out of 20 interleaves were manually selected to simulate the reduced acquisition with R = 2. The proposed method is implemented in Matlab (MathWorks, Natick, MA).

3 RESULTS

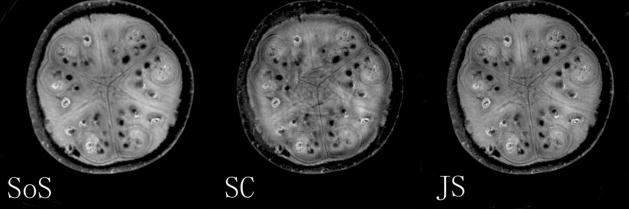
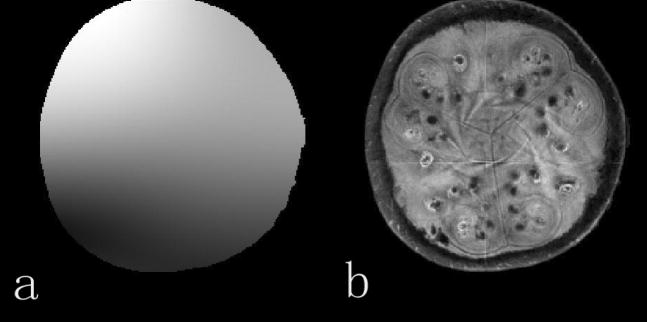
Figure 2 compares the sensitivity maps estimated from the 2x undersampled data within a circle of optimal radius 4/FOV using the conventional self-calibration (SC) and the JSENSE (JS) method, with the map estimated from the full data (SoS) as the reference for comparison. The order of the polynomial for coil sensitivities was chosen to be 12 (i.e, p + q ≤ 12). It is seen that the JSENSE method improves the estimation over the conventional self-calibration method.

Fig 2.

For the watermelon phantom, estimated sensitivity maps of the first channel based on full data (SoS), self-calibration (SC) with reduced data inside a circle of radius 4/FOV, and JSENSE (JS) with self-calibration as the initial estimate.

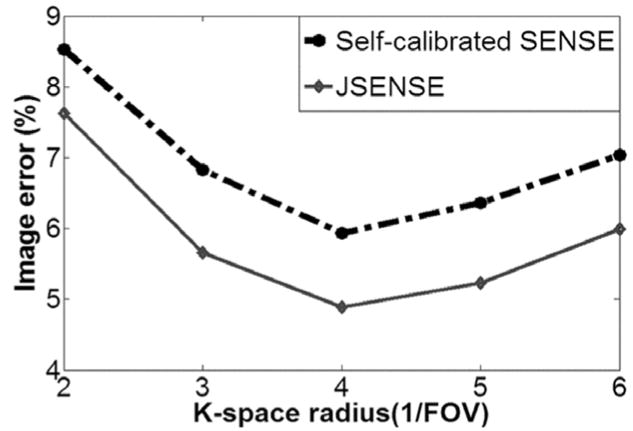
Figure 3 shows the corresponding final reconstructions obtained by the sum-of-squares (SoS) from full scan, self-calibrated SENSE using conjugate gradient, and JSENSE. In comparison, JSENSE significantly suppress the artifacts in the conventional self-calibrated SENSE reconstruction. With SoS as the gold standard, reconstructions were also compared quantitatively in terms of normalized mean-squared-error (NMSE) for various radii of truncation circle. The error curves plotted in Figure 4 demonstrates that JSENSE is superior to the conventional self-calibrated SENSE for any radius, and the optimal radius is the same for both methods, being 4/FOV.

Fig 3.

The reconstructed watermelon images using SoS from full data (SoS), self-calibrated spiral SENSE (SC), and JSENSE (JS) from 8-channel reduced data by a factor of 2.

Fig 4.

For the watermelon phantom, comparison of the NMSEs of JSENSE and self-calibrated SENSE using self-calibration data within different radius.

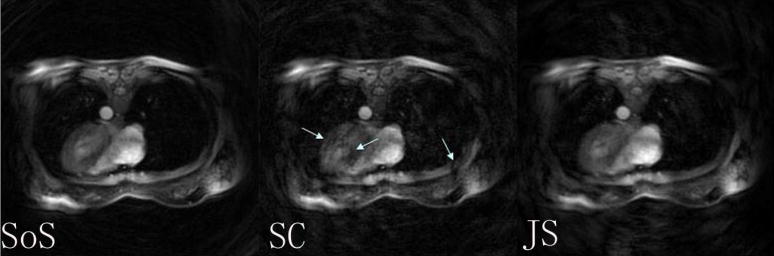
Figure 5 shows the cardiac reconstructions using SoS, self-calibrated SENSE, and JSENSE at a certain cardiac phase. The cardiac region is zoomed and a set of results are compared at several different cardiac phases in Figure 6. It is seen that the inaccurate sensitivities cause severe artifacts and noise enhancement in self-calibrated spiral SENSE, which are greatly reduced in JSENSE reconstruction.

Fig 5.

The reconstructed cardiac images using SoS from full data (SoS), self-calibrated (SC) spiral SENSE, and JSENSE (JS) from 4-channel reduced data by a factor of 2.

Fig 6.

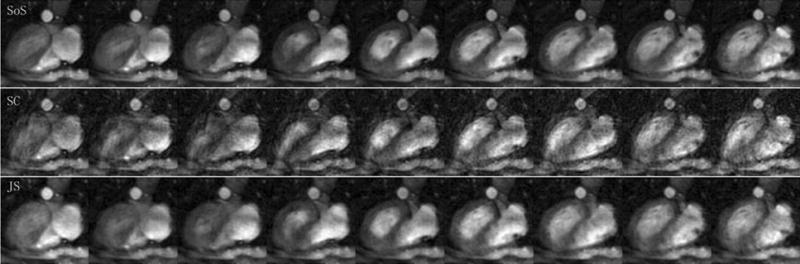
The zoomed images for the cardiac reconstructions at several different cardiac phases.

4 DISCUSSION

Similar to the self-calibrated spiral SENSE, the JSENSE method reconstructs the desired image using only the reduced spiral data without the need for additional full scans, thus shortening imaging time and avoiding the misregistration problem due to motion. On the other hand, the JSENSE method uses the self-calibration results as the initial value to further improve both the sensitivities and reconstruction using alternating minimization, thus producing superior results. All of our results have shown the case with a reduction factor of 2. When the reduction factor increases, although the JSENSE generates better reconstruction than self-calibrated SENSE, both reconstructions become to have obvious aliasing artifacts for the data we acquired.

The sensitivity maps from full data only provide a reference but may not give the ground truth. As shown in Figure 2, the sensitivity map in (JS) has similar shape as that in (SoS), but is lack of the object-dependent features in (SoS). These features can be artifacts caused by the pixel-wise division in the estimation procedure which amplifies error and noise at locations where the image has low intensity (e.g. the peel and seeds of the watermelon). JSENSE does not rely on pixel-wise division and thus avoids such object-dependent artifacts. However, similar to all model-based method, JSENSE depends on the accuracy of model. The polynomial model may not be universal even if it works well in our experiments.

As a non-convex nonlinear problem, JSENSE equation (6) is not guaranteed for a unique global optimal solution and the solution obtained by the alternating minimization may be one of the local optimal ones. Therefore, the JSENSE reconstruction depends on its initial value which is set to be the self-calibrated spiral SENSE in our implementation. This dependence can be seen by the error curve comparison in Figure 4. The trend of the JSENSE errors exactly matches that of the self calibrated SENSE errors. It suggests that the JSENSE result did not reach a global optimum because otherwise its errors should be independent of the radius which affects the initial value only. The results show that the optimal k-space radius (4/FOV) for estimating coil sensitivity is slightly larger than the Nyquist radius k₀ = 1.91/FOV in [2]. As justified in [7], the optimal radius should best balance the reduced aliasing artifacts and the improved spatial resolution for the sensitivities, and is thereby larger than the Nyquist radius.

JSENSE may improve the image signal-to-noise ratio (SNR). The SENSE matrix is usually ill-conditioned which deteriorates the reconstruction SNR by amplifying both the measurement noise and the sensitivity errors [12, 13]. JSENSE improves the sensitivity accuracy and thus improves the SNR of the reconstruction. This is demonstrated in the cardiac imaging results in Figure 5 and 6 where JSENSE looks much less noisy than the self-calibrated SENSE. Although it is interesting to calculate the SNR improvement analytically as done in [8] for Cartesian case, computation of g-factor maps is challenging for spiral. The NMSE serves an alternative for both artifacts and noise measurements.

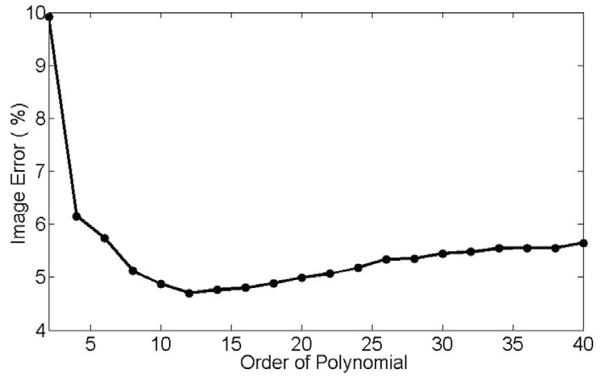
The order of the polynomial model is an important parameter in implementation of JSENSE. Higher order polynomials would include the artifacts and noise in the sensitivity model, thus counteracting the smoothing effects of the polynomial model. On the other hand, lower order ones would not be able to fully characterize the variation in the true sensitivity functions. Figure 7 shows the sensitivity map and the reconstructed image for the watermelon experiment when the polynomial order is 2. The result is seen to be worse than those in Figure 2 and 3 when the order is 12. Figure 8 summarizes the reconstruction errors as a function of the polynomial order. It is seen that the reconstruction is rather insensitive to the polynomial order in some range. In our experiments, the orders have been chosen empirically. The order used in this study should serve as a good choice for most 8-channel head coils.

Fig 7.

The sensitivity map (a) and the reconstructed image (b) when the polynomial order is 2.

Fig 8.

The reconstruction error curve as a function of the order of the polynomial. The reconstruction is shown to be rather insensitive to the order.

As noted in [8], JSENSE is computationally intensive due to the iterative procedure on top of the conventional SENSE. In our implementation, NUFFT [14] was used to speed up the conjugate gradient spiral SENSE reconstruction. In the spiral watermelon experiment, the running time for JSENSE is 110 seconds on an Intel Xeon-2.33GHz workstation, which is much longer than the 3.4 seconds for the conjugate gradient SENSE. The computational complexity of JSENSE is expected to reduce significantly when combined with the fast algorithms recently published for non-Cartesian SENSE [15–17] which will be investigated in our future work.

In summary, we have demonstrated the JSENSE method can be applied to spiral trajectories to improve the self-calibrated spiral SENSE using experimental results. The method should also be applicable to apply to radial and other trajectories that densely sample the center k-space. The improvement makes the self-calibrated JSENSE more appealing, especially in dynamic parallel imaging applications, due to its ability to accurately update the continuously-changing sensitivities.