Abstract
Recent advances in cryo-electron microscopy have led to an increasing number of high (3 to 5 Å) to medium (5 to 10 Å) resolution cryoEM density maps. These density maps contain valuable information about the protein structure but frequently require computational algorithms to aid their structural interpretation. It is these hybrid approaches between cryoEM and computational protein structure prediction algorithms that will shape protein structure elucidation from density maps.
Introduction
Cryo electron microscopy (cryoEM) can provide important structural information about proteins of unknown fold and relative arrangement of proteins of known folds within large macromolecular assemblies such as viruses [1–3]. Medium resolution (5–10 Å) cryoEM density maps reveal positions of α-helices [2], while near atomic resolution (3.8–4.5 Å) resolution maps can reveal β-sheets and large, aromatic side chains in space [3]. In addition, near atomic resolution cryoEM density maps can allow tracing of the protein backbone chain and provide restraints for computational atomic-detail refinement techniques [3,4]. Here we review computational methods that have been applied to interpret cryoEM density maps and seek to organize newly emerging methodologies with respect to the specific research tasks they address. In the context of cryoEM guided computational protein structure prediction, there are three main computational components: residue-based secondary structure prediction and identification of secondary structure elements, determination of the protein fold, and atomic-detail structure refinement.
Secondary structure prediction algorithms use machine learning techniques like artificial neural networks (ANNs) or hidden Markov models (HMMs) to predict secondary structure, usually as three-state probability (helix, strand, coil) for every residue in the primary sequence of the protein. State of the art techniques like jufo [5,6], psipred [7] and sam [8,9] have been demonstrated to achieve accuracies of up to 80%. Determination of secondary structure elements (SSEs: α-helices and β-strands) from the residue-based predictions is an important aspect in interpreting cryoEM density, however it receives only modest attention in the computational structure prediction field. In order to compensate for prediction inaccuracies from any one method, we have developed a consensus prediction protocol in which residue-based predictions are combined and averaged over a sequence window (Lindert et al., unpublished).
Protein fold or topology prediction algorithms determine the three dimensional arrangement of the amino acids from the sequence of the protein. Two major approaches have to be considered: comparative modeling of a template structure and de novo protein structure prediction in the absence of a template. Since 1994, a community-wide blindfold experiment CASP has been carried out bi-yearly to allow these algorithms to be tested on proteins whose structure was already solved but not yet published [10]. Over the course of the last experiments the program Rosetta has been identified as one of the most successful de novo protein structure prediction algorithms [11]. However, even if the correct topology is identified, the prediction will still be off by about 5 Å RMSD to the native structure. De novo computational structure prediction methods can be applied to soluble proteins smaller than about 180 amino acids in size with success rates of about 50% [11,12]. Successful comparative modeling programs include Rosetta [13,14] and Modeller [15–17] among others and achieve models of 2–5 Å RMSD depending on the similarity between template and target structure.
Atomic detail refinement techniques are used to add side-chain coordinates (e.g. using SQWRL [18]) and improve the medium resolution structures produced by comparative modeling or de novo prediction to less than 2 Å RMSD to native in favorable cases. These algorithms use higher-resolution energy functions and finer grained sampling techniques. For these algorithms to be successful, the starting structure has to be sufficiently close to the native conformation. Typically side-chain and backbone degrees of freedom need to be optimized in an iterative cycle of rapid side-chain repacking, larger scale backbone perturbations, and gradient minimization [19]. It has been demonstrated that in a few favorable cases computational algorithms can refine de novo models of small proteins (size 40–90 amino acids) to atomic detail (< 2 Å RMSD) [20]. Atomic-detail comparative models can be built for much larger proteins if a suitable template structure exists.
Figure 1 gives an overview of the most notable hybrid approaches between these computational protein structure prediction methods and cryoEM.
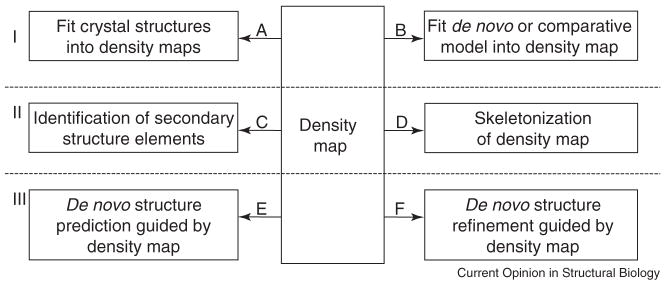
Figure 1.
Overview of current hybrid approaches between cryoEM and computational protein structure prediction algorithms. Computational algorithms that work on cryoEM density maps can be divided into three main classes: I) The first class of algorithms fits structures into cryoEM density maps. These may be A) high resolution experimental structures (X-ray crystallography, NMR) or B) computationally built models (de novo models from e.g. Rosetta or comparative models created with e.g. Modeller). II) Algorithms that analyze the density map itself. C) SSEHUNTER and HELIXTRACER both attempt to identify regions of the cryoEM density map that correspond to secondary structure elements. D) The skeletonization algorithm described in [42] builds skeletons of the density map and can be used to trace the backbone of high resolution density maps. III) The third class of software uses cryoEM density maps as experimental restraints in de novo protein structure E) prediction (EM-Fold) and F) refinement (ICM).
Fitting of crystal structures and computational models into cryoEM density maps
In the presence of a crystal structure or a complete model of the target protein a direct fit into cryoEM density maps is possible. The most frequently used fitting methods employ a six dimensional search (three translational and three rotational degrees of freedom) of the rigid-body model in the density map [21]. Use of a Fast Fourier Transformation (FFT) accelerated translational search is implemented in state-of-the-art algorithms such as Colores [22]. Recently (Wötzel et al., unpublished) reported a fitting method based on a geometric hashing algorithm that proved to be faster than traditional fitting methods. In addition even with shorter computational times, the hashing procedure identified more symmetry related positions and independent repeating units within an experimental cryoEM density map. Agreement of positioned model and density map is determined by a cross correlation coefficient [23]. Frequently flexible fitting algorithms are used to fit and adjust high resolution structures to optimally fit into EM density maps. Programs such as S-flexfit [24,25] are suited for medium resolution density maps, while algorithms using normal mode analysis (NMA) [26] are tailored towards low resolution density maps. Even though the structures themselves are perturbed during the fitting, the main focus of these algorithms is the optimal fit with the density map.
An example of using fold recognition in cryoEM is SPI-EM [27] that identifies the superfamily that a protein belongs to from its density map using CATH. Topf et al. demonstrated that comparative models may be ranked in terms of their accuracy by fitting them into a cryoEM density map [28]. The authors then went on to develop an iterative protocol that improves comparative models by optimizing their agreement with the cryoEM density maps [29]. These methods require the presence of a comparative model but have the advantage that no SSEs or even backbone trace have to be identified from the density map.
The authors in [30] compared Rosetta de novo predicted structures with the 8.5 Å resolution cryoEM density map of the herpes simplex type 1 capsid. They were able to rank the agreement of the model with the map by using a two-way distance measure. The model for the virus structural protein VP26 that agreed best with the density exhibited a new fold (see Figure 2, panels A, B and C). This approach eliminates the need for a comparative model, which in many cases is not readily available. One drawback is however that the density map is only used as a filter of de novo models and the density does not guide the folding step. Therefore this method relies on Rosetta to fold the protein correctly de novo which works in favourable cases for proteins with up to 180 amino acids [31].
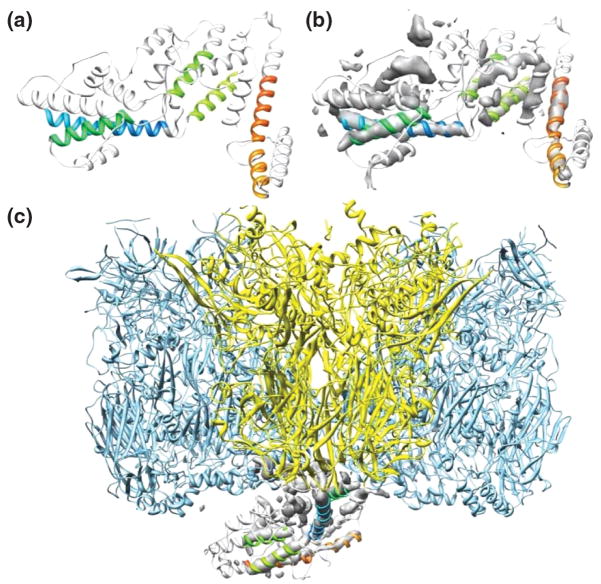
Figure 2.
Two different approaches of using cryoEM density maps in conjunction with computational algorithms. Panels A through C show how an computational model of VP26 is superimposed with the segmented experimental density [30]. Here the cryoEM density map is used as a filter for de novo protein models. D) Example from [41] of segmented cryoEM density (gray) and the skeleton that SSEhunter built for the density (red). E) In certain cases the skeleton can approximate the backbone trace of a protein. Panels (d) and (e) are reprinted from [41**], with permission from Elsevier.
Computational algorithms to identify secondary structure elements in medium resolution density maps
Density maps begin to reveal α-helices at about 10 Å resolution, β-sheets at about 5–7 Å resolution, and large side chains at about 3.0–4.5 Å resolution [3,32]. Several programs provide an alternative to manual identification of these SSEs. The HelixHunter program was initially developed in 2001 and uses segmentation and feature extraction to identify α-helix positions, orientations and lengths [33]. HelixHunter has been successfully applied to identify nine α-helices in the 6.8 Å resolution density map of rice dwarf virus outer capsid shell protein P8 [34,35]. In order to identify α-helices, EMatch [36,37] employs a method very similar to HelixHunter exploiting the fact that α-helices generally are observed as continuous, long, thin and highly dense cylindrical regions. A third available algorithm that focuses on the reliable identification of α-helices in medium resolution density maps is called HelixTracer and utilizes gradient analysis to recognize and classify volumes in density maps [38]. Dal Palu et al. noted significant improvements in recognition and precision over the HelixHunter software.
Tools such as SheetMiner [39] and SheetTracer [40] have been developed for detecting β-sheets in density maps. The desire to have a single tool capable of identifying both α-helical and β-sheet regions led to the development of the program SSEHunter [41]. This algorithm uses density skeletonization (see Figure 2, panels D and E), local geometry calculations and a template-based search to identify SSEs in medium resolution density maps.
Skeletonization algorithms help to trace the backbone in higher resolution cryoEM density maps
Density maps at medium resolution (5–10 Å) do not contain sufficient information to unambiguously trace the backbone of the protein from the map. On the other hand, high resolution density maps (<3 Å) can contain enough detail to trace the backbone, as is routinely done in X-ray crystallography. In the intermediate resolution range (4–7 Å) a density map may contain valuable information in the loop regions that can guide model building. The connections between identified SSEs may be clear in some areas of the density map and not evident in other areas. The skeletonization algorithm in SSEHunter [41] computes skeletons of volumetric data by alternation between a thinning and a skeleton pruning routine [42]. The authors in [43] used a combination of SSEHunter and this skeletonization algorithm to trace the backbone of a ~4 Å resolution density map of GroEL.
Using α-helix positions in the density map to build models of proteins promises best results
Membrane proteins are frequently only resolved to medium resolution. Based on the surface charge and evolutional variability of their lipid-exposed faces, Fleishman et al. developed an algorithm [44] that can correctly orient transmembrane helices within the density rod.
We have developed an approach called EM-Fold that uses a Monte Carlo sampling strategy to build and refine protein topologies into intermediate resolution cryoEM density maps (of soluble proteins) where α-helices are resolved as density rods (Lindert et al., unpublished). The first step is to identify density rods that are likely to be α-helices in a medium resolution density map (5–10 Å). Then a pool of predicted α-helices is used as input to a de novo folding algorithm. A novel feature of EM-Fold is that α-helices are only placed in positions where density rods were identified, thus constraining and guiding the de novo model building process. The density map is used as a restraint during the initial assembly stage and not just as a post-sampling filter as in other approaches. This decreases the conformational space that has to be sampled considerably and ensures that the final models agree with the density map. Missing loop regions are added and final models are refined using Rosetta. In a benchmark with 10 proteins of size 250 to 350 amino acids the algorithm identified the correct topology in 70% of the cases and showed that the limiting factor was incorrect secondary structure prediction. A partial model of human adenovirus protein IIIa was built by assembling predicted helices into the experimental density rods (see Figure 3).
Figure 3.
Computational de novo protein structure prediction with the cryoEM density map as a folding restraint. EM-Fold was used to build computational models into an experimental cryoEM density map of human adenovirus protein IIIa at ~6 Å resolution (Lindert et al., unpublished). A) A preliminary reduced model of protein IIIa where only helices that have been placed with at least 60% confidence are colored in rainbow. B) Same as in A, but shown in density. C) Side view of preliminary reduced model of protein IIIa (rainbow) in contact with penton base (yellow) and two peripentonal hexons (light blue).
High resolution refinement guided by EM density maps
High resolution refinement techniques can also be guided by EM density maps. This was impressively shown in [4], where the prediction of atomic-detail structures of helical proteins was aided by simulated EM maps (see Figure 4). The authors assume that a medium resolution density map of a transmembrane helical bundle is available and that helical segments are known (see Figure 4). By a three stage process that included 1) flexible fitting of helices into density rods, 2) optimization of side chains and 3) further refinement of lowest-scoring conformations, Kovacs et al were able to achieve RMSD values between 0.9 and 1.9 Å for their test cases GpA, KcsA and McsL.
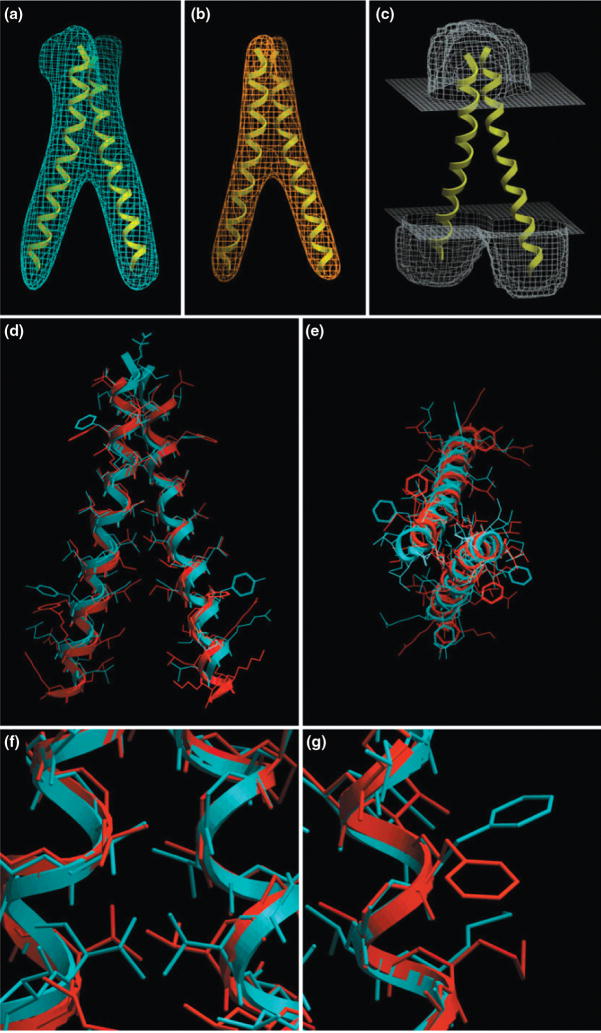
Figure 4.
High resolution de novo protein structure refinement guided by EM density maps. Benchmark of the high resolution refinement protocol in ICM [4]. A) A density map was simulated from the NMR structure of Glycophorin A (GpA). B) A tethering map was derived from the EM map and serves to restrain the α-helices. C) A solvent-accessibility map is also calculated. D) and E) Side and top views of the NMR structure (blue) and predicted structure (red). F) Closeup view showing the good agreement of the predicted and experimental structures in a helix packing region. G) Closeup view of a region that faces the lipid where packing constraints are not present and some of the side chain conformations are not recovered. This figure is reprinted from [4**], with permission from the Biophysical Society.
Other notable examples for high resolution refinement in EM density maps are real space refinement algorithms such as RSRef [45], Flex-EM [46] and MDFF [47]. These methods use molecular dynamics to refine the models and use the density map to guide this refinement.
Conclusion
Future improvements in both cryoEM and computational protein structure prediction methods are expected. Better microscopes, higher voltages, more coherent electron beams and possibly the development of phase plates to improve image contrast will enhance cryoEM structure determination. Methods for automated data collection will be employed more widely, allowing for a substantial increase in data collection capacity. Advanced image processing software in combination with computers that have larger RAM will allow researchers to process data for larger complexes and with a smaller pixel size, and this may help to improve resolution. Judging from the recent determination of near-atomic resolution structures by cryoEM [43,48–50], we expect that there will be a number of cryoEM structures determined in the < 5 Å range during the next few years. We also expect the number of medium resolution structures (5–10 Å) to grow considerably.
Equally, computational protein structure prediction will undoubtedly witness many improvements in the near future. One major external factor that will positively influence the field will be the elucidation of more (novel) folds by X-ray crystallography and NMR spectroscopy, leading to the availability of better and novel templates for comparative modeling and the development of more accurate knowledge based energy functions for de novo structure prediction. This will be particularly true for membrane proteins where only 50 distinct folds have been reported so far [51]. An increase in computing power will allow for increased sampling capacity.
Beyond these external developments there will also be advances in method development in all three fields of computational protein structure prediction discussed here. Secondary structure prediction algorithms will likely be extended to predict transmembrane regions and secondary structure simultaneously. Also consensus methods like the one presented in (Lindert et al., unpublished) will improve prediction accuracy and allow for reliable identification of SSEs. De novo structure prediction will be extended to larger protein folds by enhanced sampling approaches and both prediction and refinement techniques will greatly benefit from the incorporation of sparse experimental data such as cryoEM density maps.
Given the current developments, we can confidently predict that hybrid approaches utilizing both cryoEM and computational methods will continue to grow in their power and scope. We expect the biggest impact of hybrid methods in de novo protein structure prediction or refinement algorithms (class III in Figure 1), depending on the resolution of the cryoEM map.
Acknowledgments
Sources of funding for this work include: NSF (0742762 to J.M.) and NIH (R01-GM080403 to J.M. and R01-AI42929 to P.L.S.). We thank the ACCRE staff at Vanderbilt for computer support.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References and recommended reading
Papers of particular interest, published within the period of review, have been highlighted as:
• of special interest
•• of outstanding interest
- 1.Henderson R. Realizing the potential of electron cryo-microscopy. Q Rev Biophys. 2004;37:3–13. doi: 10.1017/s0033583504003920. [DOI] [PubMed] [Google Scholar]
- 2•.Saban SD, Silvestry M, Nemerow GR, Stewart PL. Visualization of alpha-helices in a 6-angstrom resolution cryoelectron microscopy structure of adenovirus allows refinement of capsid protein assignments. J Virol. 2006;80:12049–12059. doi: 10.1128/JVI.01652-06. This paper presents a 6.9 Å resolution cryoEM structure of human adenovirus. Docking of the crystal structures of the two major capsid proteins into the cryoEM density demonstrated that α-helices of 10 or more residues are resolved as rods. Revised assignments for the locations of minor capsid proteins are proposed on the basis of combining secondary structure information with analysis of the cryoEM density. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou ZH. Towards atomic resolution structural determination by single-particle cryo-electron microscopy. Curr Opin Struct Biol. 2008;18:218–228. doi: 10.1016/j.sbi.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4••.Kovacs JA, Yeager M, Abagyan R. Computational prediction of atomic structures of helical membrane proteins aided by EM maps. Biophys J. 2007 doi: 10.1529/biophysj.106.102137. This paper shows a benchmark of high-resolution de novo protein structure refinement in simulated density maps. RMSDs between 0.9 and 1.9 Å are achieved. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Meiler J, Muller M, Zeidler A, Schmaschke F. Generation and evaluation of dimension-reduced amino acid parameter representations by artificial neural networks. Journal of Molecular Modeling. 2001;7:360–369. [Google Scholar]
- 6.Meiler J, Baker D. Coupled prediction of protein secondary and tertiary structure. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:12105–12110. doi: 10.1073/pnas.1831973100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. Journal of Molecular Biology. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- 8.Karplus K, Sjolander K, Barrett C, Cline M, Haussler D, Hughey R, Holm L, Sander C. Predicting protein structure using hidden Markov models. Proteins-Structure Function and Genetics. 1997:134–139. doi: 10.1002/(sici)1097-0134(1997)1+<134::aid-prot18>3.3.co;2-q. [DOI] [PubMed] [Google Scholar]
- 9.Chandonia JM, Karplus M. New methods for accurate prediction of protein secondary structure. Proteins. 1999;35:293–306. [PubMed] [Google Scholar]
- 10.Moult J. Rigorous performance evaluation in protein structure modelling and implications for computational biology. Philos Trans R Soc Lond B Biol Sci. 2006;361:453–458. doi: 10.1098/rstb.2005.1810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Moult J. A decade of CASP: progress, bottlenecks and prognosis in protein structure prediction. Curr Opin Struct Biol. 2005;15:285–289. doi: 10.1016/j.sbi.2005.05.011. [DOI] [PubMed] [Google Scholar]
- 12.Kryshtafovych A, Venclovas C, Fidelis K, Moult J. Progress over the first decade of CASP experiments. Proteins. 2005;61 (Suppl 7):225–236. doi: 10.1002/prot.20740. [DOI] [PubMed] [Google Scholar]
- 13.Chivian D, Baker D. Homology modeling using parametric alignment ensemble generation with consensus and energy-based model selection. Nucleic Acids Res. 2006;34:e112. doi: 10.1093/nar/gkl480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Misura KM, Chivian D, Rohl CA, Kim DE, Baker D. Physically realistic homology models built with ROSETTA can be more accurate than their templates. Proc Natl Acad Sci U S A. 2006;103:5361–5366. doi: 10.1073/pnas.0509355103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eswar N, Webb B, Marti-Renom MA, Madhusudhan MS, Eramian D, Shen MY, Pieper U, Sali A. Comparative protein structure modeling using MODELLER. Curr Protoc Protein Sci. 2007;Chapter 2(Unit 2 9) doi: 10.1002/0471140864.ps0209s50. [DOI] [PubMed] [Google Scholar]
- 16.Marti-Renom MA, Stuart AC, Fiser A, Sanchez R, Melo F, Sali A. Comparative protein structure modeling of genes and genomes. Annu Rev Biophys Biomol Struct. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
- 17.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 18.Canutescu AA, Shelenkov AA, Dunbrack RL., Jr A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci. 2003;12:2001–2014. doi: 10.1110/ps.03154503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qian B, Raman S, Das R, Bradley P, McCoy AJ, Read RJ, Baker D. High-resolution structure prediction and the crystallographic phase problem. Nature. 2007;450:259–264. doi: 10.1038/nature06249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20••.Bradley P, Misura KM, Baker D. Toward high-resolution de novo structure prediction for small proteins. Science. 2005;309:1868–1871. doi: 10.1126/science.1113801. A benchmark of Rosetta high-resolution de novo protein structure refinement on 16 proteins is presented. Atomic resolution structures for five of the benchmark proteins are reported. [DOI] [PubMed] [Google Scholar]
- 21.Wriggers W, Milligan RA, McCammon JA. Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. J Struct Biol. 1999;125:185–195. doi: 10.1006/jsbi.1998.4080. [DOI] [PubMed] [Google Scholar]
- 22•.Wriggers W, Birmanns S. Using Situs for flexible and rigid-body fitting of multiresolution single-molecule data. J Struct Biol. 2001;133:193–202. doi: 10.1006/jsbi.2000.4350. This paper presents the Situs package for fitting high-resolution protein structures into low resolution density maps. The precision and reliability of the fitting was evaluated with simulated EM density maps. [DOI] [PubMed] [Google Scholar]
- 23.Roseman AM. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Crystallogr D Biol Crystallogr. 2000;56:1332–1340. doi: 10.1107/s0907444900010908. [DOI] [PubMed] [Google Scholar]
- 24.Velazquez-Muriel JA, Carazo JM. Flexible fitting in 3D-EM with incomplete data on superfamily variability. J Struct Biol. 2007;158:165–181. doi: 10.1016/j.jsb.2006.10.014. [DOI] [PubMed] [Google Scholar]
- 25.Velazquez-Muriel JA, Valle M, Santamaria-Pang A, Kakadiaris IA, Carazo JM. Flexible fitting in 3D-EM guided by the structural variability of protein superfamilies. Structure. 2006;14:1115–1126. doi: 10.1016/j.str.2006.05.013. [DOI] [PubMed] [Google Scholar]
- 26.Tama F, Miyashita O, Brooks CL., 3rd Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. J Struct Biol. 2004;147:315–326. doi: 10.1016/j.jsb.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 27.Velazquez-Muriel JA, Sorzano CO, Scheres SH, Carazo JM. SPI-EM: towards a tool for predicting CATH superfamilies in 3D-EM maps. J Mol Biol. 2005;345:759–771. doi: 10.1016/j.jmb.2004.11.005. [DOI] [PubMed] [Google Scholar]
- 28.Topf M, Baker ML, John B, Chiu W, Sali A. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J Struct Biol. 2005;149:191–203. doi: 10.1016/j.jsb.2004.11.004. [DOI] [PubMed] [Google Scholar]
- 29•.Topf M, Baker ML, Marti-Renom MA, Chiu W, Sali A. Refinement of protein structures by iterative comparative modeling and CryoEM density fitting. J Mol Biol. 2006;357:1655–1668. doi: 10.1016/j.jmb.2006.01.062. In this paper a novel iterative protocol that improves comparative models by maximizing their agreement with cryoEM density maps is presented. RMSD values of 5.3 to 6.0 Å are reported for models of the upper domain of the P8 capsid protein of rice dwarf virus. [DOI] [PubMed] [Google Scholar]
- 30•.Baker ML, Jiang W, Wedemeyer WJ, Rixon FJ, Baker D, Chiu W. Ab initio modeling of the herpesvirus VP26 core domain assessed by CryoEM density. PLoS Comput Biol. 2006;2:e146. doi: 10.1371/journal.pcbi.0020146. This paper combines de novo protein structure prediction with fitting models into cryoEM density maps. A model with a novel fold is presented for the core domain of the herpes virus structural protein VP26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bonneau R, Strauss CE, Rohl CA, Chivian D, Bradley P, Malmstrom L, Robertson T, Baker D. De novo prediction of three-dimensional structures for major protein families. J Mol Biol. 2002;322:65–78. doi: 10.1016/s0022-2836(02)00698-8. [DOI] [PubMed] [Google Scholar]
- 32.Jiang W, Ludtke SJ. Electron cryomicroscopy of single particles at subnanometer resolution. Curr Opin Struct Biol. 2005;15:571–577. doi: 10.1016/j.sbi.2005.08.004. [DOI] [PubMed] [Google Scholar]
- 33.Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. Journal of Molecular Biology. 2001;308:1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- 34.Nakagawa A, Miyazaki N, Taka J, Naitow H, Ogawa A, Fujimoto Z, Mizuno H, Higashi T, Watanabe Y, Omura T, et al. The atomic structure of rice dwarf virus reveals the self-assembly mechanism of component proteins. Structure. 2003;11:1227–1238. doi: 10.1016/j.str.2003.08.012. [DOI] [PubMed] [Google Scholar]
- 35.Zhou ZH, Baker ML, Jiang W, Dougherty M, Jakana J, Dong G, Lu G, Chiu W. Electron cryomicroscopy and bioinformatics suggest protein fold models for rice dwarf virus. Nat Struct Biol. 2001;8:868–873. doi: 10.1038/nsb1001-868. [DOI] [PubMed] [Google Scholar]
- 36.Dror O, Lasker K, Nussinov R, Wolfson H. EMatch: an efficient method for aligning atomic resolution subunits into intermediate-resolution cryo-EM maps of large macromolecular assemblies. Acta Crystallographica Section D-Biological Crystallography. 2007;63:42–49. doi: 10.1107/S0907444906041059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lasker K, Dror O, Shatsky M, Nussinov R, Wolfson HJ. EMatch: Discovery of high resolution structural homologues of protein domains in intermediate resolution cryo-EM maps. IEEE-ACM Transactions on Computational Biology and Bioinformatics. 2007;4:28–39. doi: 10.1109/TCBB.2007.1003. [DOI] [PubMed] [Google Scholar]
- 38.Dal Palu A, He J, Pontelli E, Lu Y. Identification of alpha-helices from low resolution protein density maps. Comput Syst Bioinformatics Conf; 2006. pp. 89–98. [PubMed] [Google Scholar]
- 39.Kong Y, Ma J. A structural-informatics approach for mining beta-sheets: locating sheets in intermediate-resolution density maps. J Mol Biol. 2003;332:399–413. doi: 10.1016/s0022-2836(03)00859-3. [DOI] [PubMed] [Google Scholar]
- 40.Kong Y, Zhang X, Baker TS, Ma J. A Structural-informatics approach for tracing beta-sheets: building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J Mol Biol. 2004;339:117–130. doi: 10.1016/j.jmb.2004.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41••.Baker ML, Ju T, Chiu W. Identification of secondary structure elements in intermediate-resolution density maps. Structure. 2007;15:7–19. doi: 10.1016/j.str.2006.11.008. This paper reports the novel algorithm SSEhunter that can simultaneously identify α-helices and β-sheets in intermediate-resolution density maps. Secondary structure topology is obtained by a skeletonization algorithm. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ju T, Baker ML, Chiu W. Computing a family of skeletons of volumetric models for shape description. Comput Aided Des. 2007;39:352–360. doi: 10.1016/j.cad.2007.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43•.Ludtke SJ, Baker ML, Chen DH, Song JL, Chuang DT, Chiu W. De novo backbone trace of GroEL from single particle electron cryomicroscopy. Structure. 2008;16:441–448. doi: 10.1016/j.str.2008.02.007. This paper reports a near atomic resolution (~4 Å) cryoEM structure of GroEL. It also serves as a good example of an application of the SSEhunter algorithm described in [41] [DOI] [PubMed] [Google Scholar]
- 44.Fleishman SJ, Harrington S, Friesner RA, Honig B, Ben-Tal N. An automatic method for predicting transmembrane protein structures using cryo-EM and evolutionary data. Biophys J. 2004;87:3448–3459. doi: 10.1529/biophysj.104.046417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Korostelev A, Bertram R, Chapman MS. Simulated-annealing real-space refinement as a tool in model building. Acta Crystallogr D Biol Crystallogr. 2002;58:761–767. doi: 10.1107/s0907444902003402. [DOI] [PubMed] [Google Scholar]
- 46.Topf M, Lasker K, Webb B, Wolfson H, Chiu W, Sali A. Protein structure fitting and refinement guided by cryo-EM density. Structure. 2008;16:295–307. doi: 10.1016/j.str.2007.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 2008;16:673–683. doi: 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48•.Zhang X, Settembre E, Xu C, Dormitzer PR, Bellamy R, Harrison SC, Grigorieff N. Near-atomic resolution using electron cryomicroscopy and single-particle reconstruction. Proc Natl Acad Sci U S A. 2008;105:1867–1872. doi: 10.1073/pnas.0711623105. In this paper a near atomic resolution cryoEM structure of the rotavirus inner capsid particle, or double-layer particle, is presented. The clarity of the cryoEM density is comparable to a 3.8 Å resolution X-ray crystallography density map. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49•.Jiang W, Baker ML, Jakana J, Weigele PR, King J, Chiu W. Backbone structure of the infectious epsilon 15 virus capsid revealed by electron cryomicroscopy. Nature. 2008;451:1130–U1112. doi: 10.1038/nature06665. This paper reports a near atomic resolution (4.5 Å) cryoEM structure of the capsid of the infectious epsilon15 particle. A complete backbone trace of the major capsid protein, gene product 7, was possible. [DOI] [PubMed] [Google Scholar]
- 50•.Yu X, Jin L, Zhou ZH. 3.88 A structure of cytoplasmic polyhedrosis virus by cryo-electron microscopy. Nature. 2008;453:415–419. doi: 10.1038/nature06893. This paper reports a near atomic resolution (3.88 Å) cryoEM structure of Cytoplasmic polyhedrosis virus that reveals grooves of α-helices, strand separation in β-sheets, and densities for loops and bulky sidechains and permits atomic model building. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tusnady GE, Dosztanyi Z, Simon I. Transmembrane proteins in the Protein Data Bank: identification and classification. Bioinformatics. 2004;20:2964–2972. doi: 10.1093/bioinformatics/bth340. [DOI] [PubMed] [Google Scholar]