Electrostatic Environment of Hemes in Proteins: pK_as of Hydroxyl Ligands

Abstract

The pK_as of ferric aquo–heme and aquo–heme electrochemical midpoints (E_ms) at pH 7 in sperm whale myoglobin, Aplysia myoblogin, hemoglobin I, heme oxygenase 1, horseradish peroxidase and cytochrome c oxidase were calculated with Multi-Conformation Continuum Electrostatics (MCCE). The pK_as span 3.3 pH units from 7.6 in heme oxygenase 1 to 10.9 in peroxidase, and the E_ms range from −250 mv in peroxidase to 125 mV in Aplysia myoglobin. Proteins with higher in situ ferric aquo–heme pK_as tend to have lower E_ms. Both changes arise from the protein stabilizing a positively charged heme. However, compared with values in solution, the protein shifts the aquo–heme E_ms more than the pK_as. Thus, the protein has a larger effective dielectric constant for the protonation reaction, showing that electron and proton transfers are coupled to different conformational changes that are captured in the MCCE analysis. The calculations reveal a breakdown in the classical continuum electrostatic analysis of pairwise interactions. Comparisons with DFT calculations show that Coulomb’s law overestimates the large unfavorable interactions between the ferric water–heme and positively charged groups facing the heme plane by as much as 60%. If interactions with Cu_B in cytochrome c oxidase and Arg 38 in horseradish peroxidase are not corrected, the pK_a calculations are in error by as much as 6 pH units. With DFT corrected interactions calculated pK_as and E_ms differ from measured values by less than 1 pH unit or 35 mV, respectively. The in situ aquo–heme pK_a is important for the function of cytochrome c oxidase since it helps to control the stoichiometry of proton uptake coupled to electron transfer

Heme cofactors are found in many proteins. Cytochromes having two axial ligands contributed by the protein are six-coordinate and function as redox intermediates in electron transfer chains. However, five-coordinate hemes with one His ligand and one open position are the most common heme motif (1). The open site can bind different molecules for transport or catalysis. Hemoglobins and myoglobins are O₂ transporters (2). Heme oxygenase is an essential protein in heme metabolism, using three O₂s and seven electrons to degrade heme to biliverdin (3). Peroxidases reduce toxic hydrogen peroxide to water and then carry out one electron oxidization of a wide range of substrates (4, 5). Cytochrome c oxidase is the terminal electron acceptor in the respiratory chain (6–9). Here Heme a3 forms a binuclear center with a copper complex (Cu_B) that reduces O₂ to water. The protein uses the released chemical energy to pump protons across the membrane. Other five-coordinate heme proteins carry out NO storage and transport (10), steroid synthesis (11, 12), and O₂, CO, and NO sensing (13, 14).

Hemes can carry out many biological functions because the protein, especially the active site residues, modulates the ligand binding specificity and resultant chemistry. The diversity of in situ heme functions highlights important interactions of proteins with their cofactors and substrates. Extensive studies have explored how ligand geometry (15–17) and the protein scaffolding (18) affect in situ heme properties (1). The range of redox free energy and pK_as of protein-bound hemes and their ligands show the importance of electrostatic interactions (19, 20). For example, six-coordinate bis-His–hemes have E_ms ranging from −410 to +360 mV with the redox differences being predominately due to the intraprotein electrostatic environment (1, 20–22). In these proteins the loss of solvation energy (15, 23, 24), interactions with the protein backbone and with other residues (15, 20–22, 25), and local conformation changes on ionization changes (20, 26) determine the thermodynamic equilibrium measured by pK_as and E_ms.

Theoretical studies have analyzed hemes in different systems using a number of techniques. The large span of E_ms in cytochromes has been subject to analysis by Protein Dipole Langevin Dipole (PDLD) (27, 28), continuum electrostatics (CE)¹ (20, 21, 29, 30), and other techniques (31–37). E_ms of the two hemes in quinol:fumarate reductase have been determined within 30 mV of experimental values using MCCE, allowing the low- and high-potential heme to be assigned to the distal and proximal positions in the structure (38). The heme propionic acid pK_as and their influence on the pH dependence of cytochrome E_ms have been considered by CE analysis (20, 38–40). The pK_as and E_ms of aquo–heme a3 and CuB in cytochrome c oxidase have been analyzed by CE (41–43) and density functional theory (DFT) (44). DFT and QM/MM calculations have been used to explain the unusual low-spin state of ferric aquo–heme (45–47) and to study the hydroxylation mechanism (48–51) of cytochrome P450.

In the work presented here, pK_as and E_ms of aquo–heme in myoglobins from sperm whale and Aplysia, hemoglobin I, heme oxygenase 1, and horseradish peroxidase are calculated with Multi-Conformation Continuum Electrostatics (MCCE) (20, 38). The calculated pK_a is compared with the pH of the acid–alkaline transition, which is attributed to the deprotonation of a water molecule as the sixth heme ligand (52). Calculations are also carried out on cytochrome c oxidase. Here the pK_a is compared with the pH dependence of the proton release on oxidation of heme a3 (53). Several of these proteins have positively charged groups in the active site. The interaction of the heme with these charges is compared in CE and DFT methods, showing that CE overestimates the interaction. With the appropriate corrections, MCCE calculations reproduce the experimental pK_as and E_ms, showing how the protein structures yield the observed in situ reaction energetics. The differences in the shifts of aquo–heme pK_as and E_ms in different binding sites show that electron and proton transfers can be coupled to different active site conformational changes. The aquo–heme E_m is not a factor in the function of myoglobin or hemoglobin, nor are the pK_as important for the reaction mechanism of most of the proteins studied here. However, the aquo–heme pK_a in cytochrome c oxidase appears to determine whether heme a3 binds a proton during the reduction of the binuclear center (43). Thus, this pK_a helps to control the electroneutrality of the oxidase reduction. The comparison of calculated and measured pK_as and E_ms in the smaller and simpler proteins provides a benchmark for the analysis of the more puzzling oxidase system.

METHODS

Structures of sperm whale myoglobin (1A6G, 1A6K, 1A6M, 1A6N, 1HJT, 1JP6, and 1JP9), Aplysia myoglobin (1MBA and 5MBA), monomeric clam hemoglobin I (1B0B, 1EBT, 1FLP, and 1MOH), rat heme oxygenase 1 (1DVE, 1IVE, 1IX4, 1ULX, and 1VGI), horseradish peroxidase (1ATJ, 1H55, 1H57, 1H58, 1H5A, 1H5C, 1H5D, 1H5E, 6ATJ, and 7ATJ), and Rhodobacter sphaeroides cytochrome c oxidase (1M56) were obtained from the Protein Data Bank (54). All crystal waters are deleted and protein cavities filled with continuum water. Multi-Conformation Continuum Electrostatics (MCCE) samples both residue ionization state and rotamer position as a function of pH and E_h (55–57). The cytochrome c oxidase calculations use the model generated for analysis of proton uptake coupled to anaerobic reduction in MCCE2.0 (43). In this larger protein a rotation angle of 120° is used to make side chain rotamers, reducing the number of conformers. All other calculations use MCCE 2.2, which adds local optimization of side chain positions, pruning to delete energetically indistinguishable conformers and corrections of the CE energy terms for the errors in the dielectric boundary due to extra surface conformations (see www.sci.ccny.cuny.edu/~mcce). Preselected side chain rotamers are generated in 60° increments around each rotatable bond for all amino acids. In each protein, a water or hydroxyl is added to the open heme coordinate position. The aquo–oxygen is placed on the heme iron with square bipyramidal geometry and a 1.95 Å Fe–O bond length. Hydrogens are added in a tetrahedral geometry with a 0.96 Å H–O bond length. Then additional hydroxyl and water conformations are generated in 30° increments around the Fe–O bond, creating 12 conformers for both water and hydroxyl.

Look-up tables are calculated for electrostatic and non-electrostatic conformer self and conformer–conformer pairwise interactions. The electrostatic pairwise interactions and reaction field energies are determined with a finite-difference technique to solve the Poisson–Boltzmann equation using the program DelPhi (58–60). Focusing (61) is used to ensure a final grid spacing of >2 grids/Å. The protein residues are given PARSE charges and radii (62). The protein has a dielectric constant, ε, of 4 while the surrounding water has an ε of 80 with a salt concentration of 150 mM. Cytochrome c oxidase is surrounded by a 32 Å slab with ε = 4 placed with IPECE to bury the fewest ionizable residues to simulate the membrane (63). The Lennard-Jones interactions are calculated with AMBER parameters (64), rescaled by 0.25 (65). A metal-centered charge set is used for hemes with a +2 or +3 charge on the ferrous and ferric Fe and −0.5 on each N atom of the porphyrin as used previously in cytochrome benchmark calculations (20, 21). The water–heme ligand uses TIP3 charges, and the hydroxyl charge, calculated with B3LYP (66) in Gaussian98 (67), has +0.2 on H and −1.2 on O. For the a-type heme in cytochrome c oxidase, a +0.3 charge is placed on the formyl group C and −0.3 on O.

MCCE calculates the shift in pK_a or E_m when a group is moved from aqueous solution to the protein. The solution pK_a (pK_a,sol) and E_m (E_m,sol) are obtained from measurements in water. pK_a,sol for amino acids are taken from studies of peptides (68, 69). The heme propionic acids are treated as described previously with a pK_a,sol of 4.9 (20). The five-coordinate hemes are assumed to bind a water or hydroxide as the sixth ligand. Heme and its His and water or hydroxide ligands are treated as a complex. A pK_a,sol of 9.6 for the hydroxyl in the ferric (70, 71) and 10.9 in the ferrous (71) His–aquo–heme has been measured in microperoxidase 8 (MP8) which has a heme c. The water p_Ka,sols are assumed to be the same for hemes a and c. The E_m,sol for the His–water heme is −120 mV, and −200 mV (72) for the His–hydroxyl heme. The value of −120 mV is slightly higher than the measured value of −140 mV (72, 73), giving an 80 mV shift from His–hydroxyl, consistent with the 1.3 pK_a shift between the pK_as of ferric and ferrous aquo–heme (70,71). With the same ligands, the E_m of heme a is 100 (1) to 160 (74, 75) mV more positive than that of heme c. An E_m,sol of − 20 mV for His–water heme a3 and −100 mV for His–hydroxyl heme a3 is used here. No explicit pairwise interactions of water or hydroxide ligands with the His ligand or heme to which they are bound are considered since these interactions are included in E_m,sol and pK_a,sol. The reaction field energies in both solution and the protein were calculated for the aquo–heme complexes. A systematic shift of −0.74 ΔpK unit (−1 kcal/mol) is added to the reference reaction field energy of ferric hydroxyl–heme in the solution (ΔG_RX-N,sol) and 0.5 ΔpK unit (0.67 kcal/mol) to that of ferrous water–heme. This raises all ferric heme pK_as by 0.74 pH unit and raises the aquo–heme E_ms by 30 mV. Systematic shifts are also applied to the ionized form of ionizable amino acids on the basis of pK_a benchmark studies (43, 56, 65).

Possible microstates with different ligand and side chain position and protonation states are subjected to Monte Carlo sampling. A microstate is made up of one conformer for each residue, cofactor, and water. The energy of microstate n (ΔGⁿ) is the sum of the electrostatic and nonelectrostatic energies (20):

$$\begin{array}{l}\mathrm{\Delta }{G}^n=\sum _{i=1}^M{\delta }_i\{[2.3m_i{k}_{\text{b}}T(\text{pH}-\text{p}{K}_{\text{sol},\text{i}})+\\ n_{i}F(E_{\text{h}}-E_{\text{m},\text{sol},i})]+(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn},i}+\mathrm{\Delta }{G}_{\text{pol},i})\}+\\ \sum _{i=1}^M{\delta }_i\sum _{j=i+1}^M{\delta }_j[\mathrm{\Delta }{G}_{ij}]\end{array}$$ (1)

where the summation is over the total M conformers of all residues in the protein; for each conformer i, δ_i) 1 if it is present in the current microstate n and 0 if it is not. Each residue has one conformer with δ_i) 1 and the rest δ_i) 0. In the double summation δ_i and δ_j are both 1 only when conformer i and j are from two different residues. k_bT is 0.59 kcal/mol (25.8 meV), and m_i is 1 for bases, −1 for acids, and 0 for polar groups and waters. n_i is the number of electrons gained or lost compared to the ground state conformer. For example, if an oxidized conformer is defined as the ground state, it has n_i = 0 and the reduced conformer has n_i = 1; F is the Faraday constant. pK_sol,i is the pK_a and E_m,sol,i the midpoint potential of the ith cofactor in solution. ΔΔG_rxn,i is the difference between the conformer reaction field energy in solution and in the protein (desolvation energy). ΔG_pol,i is the pairwise electrostatic and nonelectro-static interaction of the conformer with the backbone and with side chains that have no conformational degrees of freedom. The torsion energy for each conformer is added to ΔG_pol,i. ΔG_ij is the electrostatic and Lennard-Jones pairwise interaction between each pair of conformers in the microstate. The limits on the summation of the interconformer terms ensure that each interaction is counted once. Monte Carlo sampling establishes the Boltzmann distribution of the different conformers of each residue at 25 °C. Residue pK_as and E_ms are determined from the fraction group ionization in a series of Monte Carlo simulations at different pHs or E_hs (eq 1). Multiflip (76) between closely coupled residues is implemented (63). The SOFT function is not used (56). For pK_a calculations the heme is fixed in its oxidized state, and the probability of residue protonation, including that of the aquo–heme, is determined as a function of pH (56). For E_m calculations the pH is fixed at 7 and the E_h varied. All groups are allowed to sample different protonation states throughout the heme titration.

Analysis of the MCCE pK_as and E_ms

The E_m or pK_a changes on moving a group from solution to its position in the protein. Thus

$$\text{p}{K}_{\text{a}}=\text{p}{K}_{\text{a},\text{sol}}-m\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}$$ (2)

where pK_a is the group pK_a in the protein, m is −1 for an acid and +1 for a base, and

$$E_{\text{m}}=E_{\text{m},\text{sol}}-\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}/nF$$ (3)

where E_m is the heme in situ E_m and n is the number of electrons. The shift in energy of ionization (ΔΔG_protein) is due to different changes of the reaction reactant and product energies when the reaction is moved into the protein. This term can be broken down in MCCE into the sum:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{protein}}=(\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{rxn}}+\mathrm{\Delta }{G}_{\text{pol}})+\mathrm{\Delta }{G}_{\text{res}}$$ (4)

including the change in reaction field energy from solution (ΔΔG_rxn), the added interaction with the rigid backbone (ΔG_pol), and the side chains in their ionization and conformation states equilibrated at the given pH and E_h (ΔG_res) (20, 43, 77).

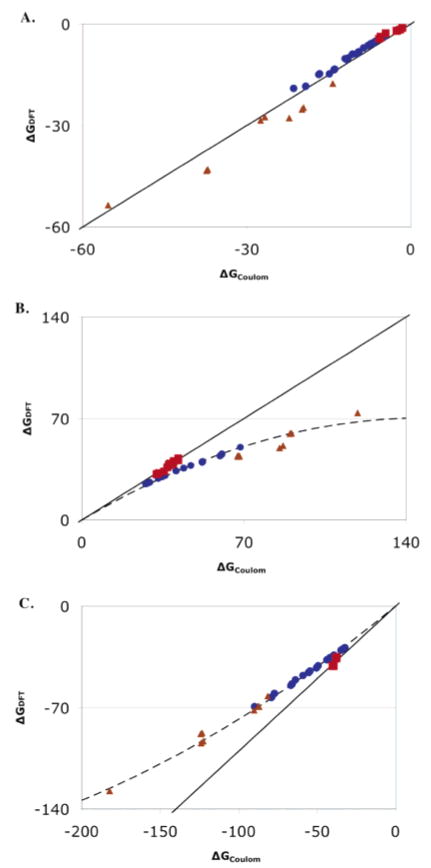
MCCE uses continuum electrostatics to calculate the interaction between the aquo–heme and charges and dipoles in the protein. Selected interactions with the ferric heme porphyrin together with its imidazole and water or hydroxyl ligand were also calculated using Gaussian 98 (67). The heme and imidazole are taken from the crystal structure of sperm whale myoglobin (1A6K), with water or hydroxyl added in GaussView (67). Each structure is then optimized using the B3LYP method (66) with the LANL2DZ basis set (78). Hydroxyl–hemes are expected to be low spin (53, 79) while water–hemes are generally high spin (53, 80). The water–heme is given a net charge +1 and spin 5/₂, while the hydroxyl–heme has a net charge 0 and spin 1/₂. The change in system energy is then calculated with an external charge of +1 or −1 placed next to the aquo–heme complex in positions shown in Figure 1. All atoms are fixed in the structure optimized before the charge is added.

Figure 1.

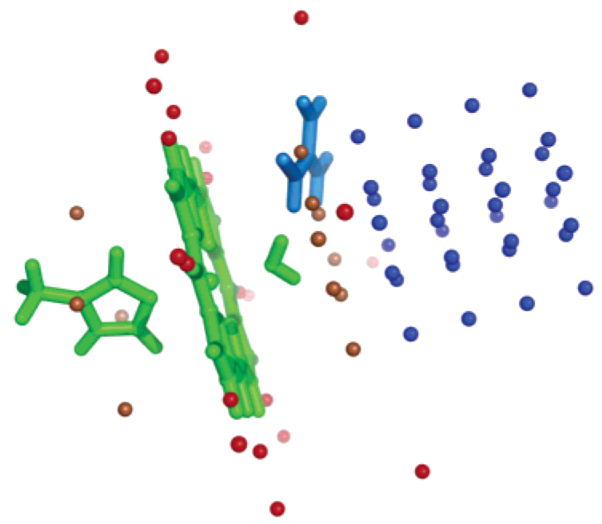
Position of external charges for comparison of CE and DFT interactions. Blue points are near the heme face; red points are in the plane of the heme and near the heme edge. Those within 4 Å of the heme plane are in brown. His–aquo–heme is in green. The position of Arg 38 in horseradish peroxidase is shown in blue.

Nine external charges are placed on a plane parallel to the porphyrin plane located 4, 6, 8, 10, or 12 Å from the heme (Figure 1). Points that overlap the water or imidazole ligand are removed. The interactions are also calculated with Coulomb’s law with the metal-centered charges used in the MCCE calculations with ε = 1. For the ferric hydroxyl–heme, Coulomb’s law reproduces the DFT interactions with an error of <10% and a slope of 0.94 with the exception of points within 4 Å of the heme plane (Figure 2). However, for the water–heme, the Coulomb’s law interactions with the points above the heme plane are significantly larger than those obtained with DFT. In contrast, for charges on the heme edge (Figure 1) the Coulomb’s law interactions reproduce the DFT interactions with <5% error and a slope of 1.0 for both water and hydroxyl ligated hemes (Figure 2). The source of the error in the CE calculation is not known. However, the large unfavorable interactions with water–heme are relaxed in the DFT calculations, while the smaller, favorable interactions with hydroxyl–heme are not. This suggests that there is significantly more polarization of the ferric water–heme by the external charge. In addition, the correction could be needed if there is significant charge at positions that are not well described by the atom-centered charges used here. Further studies are in progress to develop a water–heme charge distribution, perhaps including charges out of the heme plane, which can better reproduce the DFT interaction with Coulomb’s law. Preliminary calculations show that in general there is no systematic error in the CE calculations of the interactions of the standard amino acids with external charges.

Figure 2.

Comparison of interactions with a positive charge (blue ●) near the heme face, (red ■) in the plane of the heme and near the heme edge, and (brown ▲) within 4 Å of the heme plane as shown in Figure 1 calculated with DFT or CE Coulomb’s law with 3ε = 1. (A) Neutral, ferric (hydroxyl–heme). The ideal straight line through the origin with a slope of 1 is shown. (B) Cationic, ferric water–heme. The line through the points, y = 0.95x− (3.2 × 10⁻³)x², is the best fit to a binomial function for the points near the heme face (blue). (C) (Hydroxyl–heme) – (water–heme). The line through the points is y = 0.89x + (1.1 × 10⁻³)x².

The ferric water–heme interaction of a simple external charge at the position of Arg 38 in peroxidase or CuB in oxidase calculated with DFT is only 60% of that found with Coulomb’s law. The interaction with a charge at the position of Arg 99 in hemoglobin I is 65% as large. The influence of the charge distribution for the external group on the correction was examined by using a PARSE Arg charge distribution, rather than a single +1 charge. The DFT interaction is now 63% of that found with Coulomb’s law, very similar to that found with a unitary charge model. The influence of the charge distribution of CuB is more complex and cannot be described by a simple scaling factor. The details are discussed in ref 43.

Corrections are applied to interactions of the water–heme with Arg 99 in hemoglobin, Arg 38 in peroxidase, and CuB in oxidase. However, pairwise electrostatic interactions in MCCE are calculated with the Poisson–Boltzmann equation (PB), a CE analysis which takes into account the different dielectric constants of the protein and water (30, 81). The scaling factor derived for particular heme–residue geometry from the comparison of Coulomb’s law and DFT interactions in a vacuum (Figure 2) is used to scale the individual PB interactions in MCCE. Corrections used for CuB can be found in ref 43.

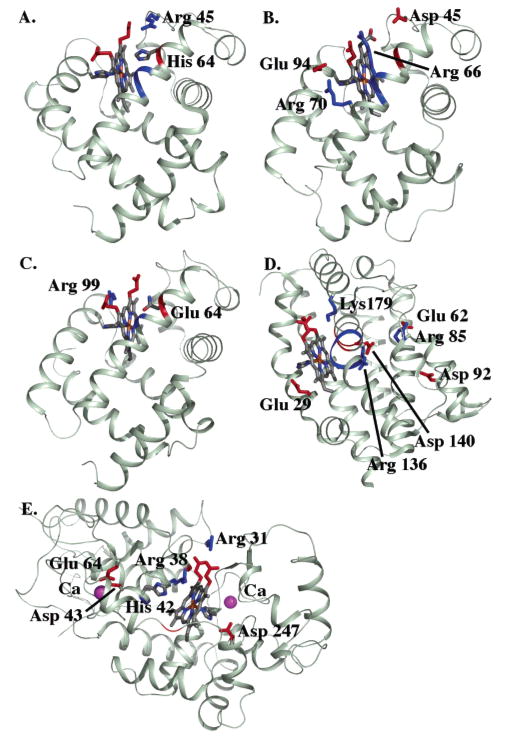
Interactions with residues that are on the heme plane or far away from the heme are shown to need no correction. Residues that have significant interactions with the aquo–heme which are not corrected because of their position include the following: all of the heme propionates; Arg 45 which is hydrogen bonded to a propionic acid in myoglobin; Lys 179 which is hydrogen bonded to a propionate in hemoglobin 1; Arg 136 and Asp 140 which form an ion pair on the porphyrin edge furthest from the propionates in hemoglobin 1 (Figure 4).

Figure 4.

Structures of (A) sperm whale myoglobin, (B) Aplysia myoglobin, (C) hemoglobin I, (D) heme oxygenase, and (E) horseradish peroxidase. Residues and backbone segments that interact with the cationic ferric aquo–heme by more than 0.5 ΔpK unit (0.68 kcal/mol) are shown.

RESULTS AND DISCUSSION

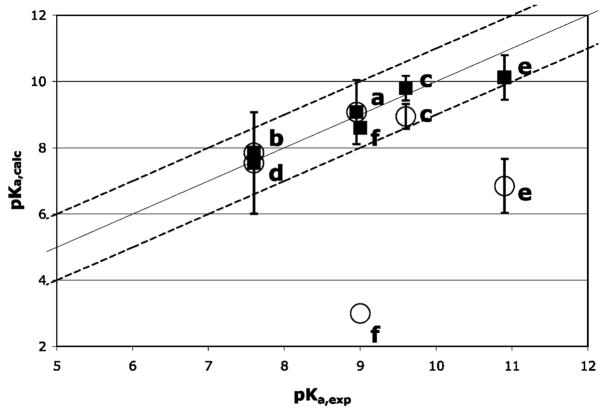
The ferric aquo–heme pK_as were calculated with MCCE in myoglobins from sperm whale and Aplysia, hemoglobin I, heme oxygenase 1, horseradish peroxidase, and cytochrome c oxidase and compared to measured values. These pK_as span 3.3 pH units from 7.6 in heme oxygenase 1 to 10.9 in the peroxidase. Two sets of calculations are presented. In the first set, standard Poisson–Boltzmann continuum electrostatics (CE) calculations are used for all pairwise interactions between the aquo–heme and the surrounding protein residues. In the second, an additional correction derived from DFT calculations is applied. Calculated pK_as are compared to the experimental values. Calculations of the heme E_ms are discussed below.

The pK_as calculated using the standard CE-based pairwise interactions in MCCE (20) do not provide consistent agreement with the experimental data (Figure 3). Calculated pK_as for the myoglobins and heme oxygenase are within 1 pH unit of the measured values. However, errors as large as 6 pH units are found in horseradish peroxidase and cytochrome c oxidase. In these proteins a nearby positive charge in the heme distal pocket lowers the calculated pK_a, while the myoglobins have no charges in similar positions. As described in the Methods section CE and DFT calculations provide very similar values for pairwise interactions between a charge and a neutral hydroxyl–heme, probably because the electronic polarization does not contribute much to this smaller, favorable interaction. For the cationic water–heme, both methods also yield similar results when the charge is on the heme edge. However, when the charge is above the heme plane near the iron, the interactions derived with a CE analysis are significantly larger than those obtained with DFT calculations. The closer the charge is to the heme plane, the larger the discrepancy (Figure 2). The large unfavorable interactions are relaxed when electronic polarization is considered in the DFT calculations. The DFT corrections are applied to the pairwise electrostatic interaction of the water–heme with Arg 99 in hemoglobin I, Arg 38 in horseradish peroxidase, and CuB in cytochrome c oxidase to recalculate the pK_as. Now calculated pK_as in the six proteins agree with the measured values within 1 pH unit. Analysis of the MCCE calculations can then show how interactions and conformational changes shift the pK_a,sol of 9.6 to different in situ values in these proteins.

Figure 3.

Comparison of calculated and experimental pK_as (■) with and (○) without the DFT correction for (a) sperm whale myoglobin, (b) Aplysia myoglobin, (c) hemoglobin I, (d) heme oxygenase, (e) horseradish peroxidase, and (f) cytochrome c oxidase. The ideal line of slope 1 passing through the origin and lines with differences between experimental and calculated of (1 pH unit (dashed lines) are shown. References for experimental values are in Table 1.

Sperm Whale Myoglobin

Sperm whale myoglobin has a folded six-helix core (Figure 4). The pK_a of the ferric aquo–heme is 8.95 (52), little different from the pK_a,sol of 9.6. MCCE calculations with seven different crystal structures give an average aquo–heme pK_a of 9.1 ( 1.0, in good agreement with experiment. This heme is close to the protein surface. However, pK_a ≈ pK_a,sol not because the heme does not interact with the protein but rather because a number of effects cancel (Table 1). The water–heme, with a net +1 charge, has 7 ΔpK units (9.52 kcal/mol) less solvation energy in the protein than it does in water, but the hydroxyl–heme, which has a large dipole moment, has a 5 ΔpK unit desolvation energy. Thus, the resultant desolvation penalty (ΔΔG_rxn) favors the water–heme complex raising the pK_a by about 2 pH units. The backbone amide dipoles tend to raise the electrostatic potential within all proteins, shifting residue pK_as (25, 82) and cytochrome E_ms (20). Here they favor the hydroxyl–heme, lowering the pK_a by 1 pH unit. The E helix, which contains His 64 in the distal pocket, is the largest contributor.

Table 1.

Experimental and Calculated pK_as and E_ms and Energy Terms Contributing to pK_a and E_m Shifts in the Protein

(a) pKa of Ferric Aquo–heme
	exp pKa	MCCE pKa	ΔΔGrxn (ΔpK unit)	ΔGpol (ΔpK unit)	ΔGres (ΔpK unit)
sperm whale myoglobin (7)a	8.95 (52)	9.1 ± 1.0	2.07 ± 0.29	0.91 ± 0.14	−2.45 ± 0.83
Aplysia myoglobin (2)	7.6 (52)	7.7 ± 1.0	1.70 ± 0.34	0.88 ± 0.23	−0.75 ± 0.49
hemoglobin I (4)	9.6 (83)	9.8 ± 0.3	1.30 ± 0.18	1.02 ± 0.09	−2.57 ± 0.24
heme oxygenase 1 (5)	7.6 (84, 85)	7.5 ± 1.5	0.16 ± 0.37	3.34 ± 0.69	−1.44 ± 1.10
horseradish peroxidase (10)	10.9 (52)	10.1 ± 0.7	1.58 ± 0.39	−0.61 ± 0.07	−1.49 ± 0.66
cyt c oxidase (1)	9.0 (53)	8.6	3.9	0.4	−3.3
(b) Em of Aquo–heme at pH 7
	exp Em (mV)	MCCE Em (mV)	ΔΔGrxn (ΔpK unit)	ΔGpol (ΔpK unit)	ΔGres (ΔpK unit)
sperm whale myoglobin (7)	50 (86)	25 ± 33	4.50 ± 0.56	0.98 ± 0.15	−2.97 ± 0.66
Aplysia myoglobin (2)	125 (86)	126 ± 64	4.25 ± 1.24	0.89 ± 0.11	−0.89 ± 0.24
hemoglobin I (4)	103 (87)	83 ± 15	4.33 ± 0.17	0.85 ± 0.12	−1.68 ± 0.09
heme oxygenase 1 (5)	NA	37 ± 13	2.47 ± 0.36	1.84 ± 0.44	−1.61 ± 0.30
horseradish peroxidase (10)	−250 (88, 89)	−215 ± 27	3.80 ± 0.51	−0.62 ± 0.06	−4.79 ± 0.49
cyt c oxidaseb (1)	NA	9	5.77	0.77	−5.70

^aThe value in parentheses is the number of PDB files analyzed. NA, not available. Negative free energy terms favor the cationic ferric water–heme raising the aquo–heme pK_a and favor the oxidized heme lowering the E_m. The ferric aquo–heme pK_a,_sol is 9.6 (70, 71). The b-type water–hemes have an E_m,sol of −120 mV, while the a-type heme in cytochrome c oxidase has an E_m,sol of −20 mV. Hydroxyl–hemes have E_m,sols 80 mV lower than the water–hemes (72, 73), consistent with the 1.3 pK_a unit shift between the pK_as of ferric and ferrous aquo–heme (70, 71).

^bThe pK_a and E_m of the aquo–heme a₃ is calculated with Cu_A oxidized and heme a and Cu_B reduced to mimic the experimental pK_a measurements in the CO photolyzed mixed-valence complex (53). 1 ΔpK unit ) 58 meV ) 1.36 kcal/mol. A systematic shift of −0.74 ΔpK unit (−1 kcal/mol) is added to the reference reaction field energy (ΔΔG_RXN,sol) of ferric hydroxyl–heme and 0.5 ΔpK unit (0.67 kcal/mol) to ferrous water–heme in deriving the in situ E_ms and pK_as using eqs 2–4.

There are 4 Arg, 14 Glu, 7 Asp, and 19 Lys in the protein and all of them are >95% ionized between pH 7 and pH 9. However, most of these charges have little effect on the aquo–heme pK_a because they are solvent exposed. Arg 45, which is hydrogen-bonded to the D-ring propionic acid, does shift the pK_a down by 0.6 pK unit (propionate A and D designated as assigned in the PDB structure files). The two heme propionic acids are both fully ionized and together shift the pK_a up by 2.3 units. As these are all near the heme edge, the CE interaction agrees with the DFT values (Figure 2). His 64 in the distal heme pocket near the aquo–ligand undergoes a conformational change with the change in the aquo–heme protonation state (Figure 4). The His is always neutral, but the δ proton tautomer stabilizes the positive water–heme by 3–4 ΔpK units, while the protonated ε tautomer stabilizes the hydroxyl–heme by 1.6–2.5 ΔpK units. In different PDB structures the His tautomer is restricted by the rigid backbone to different extents, yielding the dependence of the calculated pK_a on the starting structure. Arg 45 not only lowers the aquo–heme pK_a by direct electrostatic interaction but it also lowers the pK_a indirectly by favoring the εHis 64 conformer.

Aplysia Myoglobin

Myoglobin from the sea hare Aplysia limacine has a folded six-helix structure (Figure 4). It is calculated to have a ferric aquo–heme pK_a of 7.7, 2 pK units lower than that of sperm whale myoglobin, in agreement with the experimental value of 7.6 (52). The Aplysia and sperm whale proteins have the same protein folds and are 27% identical. The analogue of myoglobin His 64 is Val 64 in the Aplysia distal pocket, providing a bigger cavity, so the heme is slightly better solvated, shifting the pK_a up. However, the biggest difference between the two proteins is in ΔG_res. The loss of His 64 and protonation of the ring D propionic acid lowers the aquo–heme pK_a. The propionate pK_a is raised to 8.6 by the nearby Asp 45, while in myoglobin Arg 45 lowers the propionate pK_a to 4.6.

Hemoglobin I

Monomeric clam hemoglobin I also has a folded six-helix structure (Figure 4). The aquo–heme pK_a is calculated to be 9.8 and measured to be 9.6 (83), close to that of sperm whale myoglobin. The hemoglobin I and myoglobin have similar structures with 23% identity. A larger cavity in the heme distal pocket leads to a smaller desolvation energy. As His 64 does in myoglobin, Gln 64 changes conformation, keeping its oxygen pointing toward the water–heme and nitrogen pointing toward the hydroxyl–heme. Arg 99, on the proximal side of the heme, shifts the pK_a down by 1.5 pH units, while the two propionic acids, both of which are ionized, shift the pK_a up by 2.2 pH units.

Heme Oxygenase 1

Rat heme oxygenase 1 is a multihelical bundle with two three-helix motifs (Figure 4). The aquo–heme pK_a is calculated to be 7.5, in agreement with the experimental value of 7.6 (84, 85). In this protein heme is an exchangeable substrate and is significantly more exposed than in the other proteins considered here and so has a very small ΔΔG_rxn. The large positive potential from the backbone lowers the pK_a by 3.3 pH units. The distal pocket helix is kinked at Gly 143 and Gly 144 so the backbone amides of Ser 142, Gly 143, and Gly 144 all point toward the heme iron, stabilizing the hydroxyl–heme. Arg 136 and Asp 140 are in a salt bridge near the porphyrin edge. While each interacts with the aquo–heme by over 3 ΔpK units, their combined impact is small.

Horseradish Peroxidase

The multihelical peroxidase uses heme to reduce hydrogen peroxide to water. The aquo–heme pK_a is calculated to be 10.1, in reasonable agreement with the measured 10.9 (52). The aquo–heme has a similar reaction field energy loss as the globins. Unlike the globins, interactions with the backbone amides near the metal center are small and somewhat negative, raising the pK_a by 0.6 pH unit. Interactions with other residues raise the pK_a by 1.5 ΔpK units. His 42 and Asp 43 raise the pK_a by 6 pH units while Arg 38 shifts the pK_a down by 4.5 pH units (assuming a 60% DFT correction). His 42 sits in the distal pocket in a position similar to His 42 in myoglobin. However, this His is fixed in the δ tautomer by Arg 38, Glu 64, and Asn 70, stabilizing the protonated water–heme.

Cytochrome c Oxidase

Heme a3 in cytochrome c oxidase is deeply buried in the transmembrane 12-helix subunit I of the protein. In the mixed-valence state, with heme a and CuB reduced, the ferric aquo–heme pK_a has been measured to be 9 (53). Using the full CE interaction between CuB and the aquo–heme, the calculated pK_a is 3. The DFT correction reduces the interaction from 6.4 to 3.2 ΔpK units. Since the aquo–heme titration now occurs at higher pH, the protein net charge is more negative than when the titration is at pH 3. This raises the pK_a further to 8.6, in good agreement with experiment (43). The cytochrome c oxidase heme is more deeply buried than in the other proteins, losing more reaction field energy, which shifts the pK_a down. Within the membrane-embedded protein, pairwise electrostatic interactions with other residues are quite long range. However, the net interaction of the fully ionized propionic acids and the rest of the protein shifts the pK_a up by only 2 pH units.

E_m Calculations

The aquo–heme E_ms were calculated in each protein at pH 7. E_ms previously measured in four of the proteins range from −250 mV in peroxidase to 125 mV in Aplysia myoglobin (86) (Table 1b). MCCE calculations agree with the experimental values with errors of e35 mV. MCCE allows protonation of the aquo–heme to be coupled to heme reduction (20). The relevant E_m,sol for water–heme of −120 mV (72, 73) and for hydroxyl–heme of −200 mV (72) is included in the microstate energy (eq 1) so the pH dependence of the E_m is properly treated in the redox titration. This degree of freedom could be important for Aplysia myoglobin and heme oxygenase, which have pK_as near 7. However, since their ferric pK_as are above 7 and ferrous pK_as are higher, the aquo–heme ligand remains predominately water at pH 7.

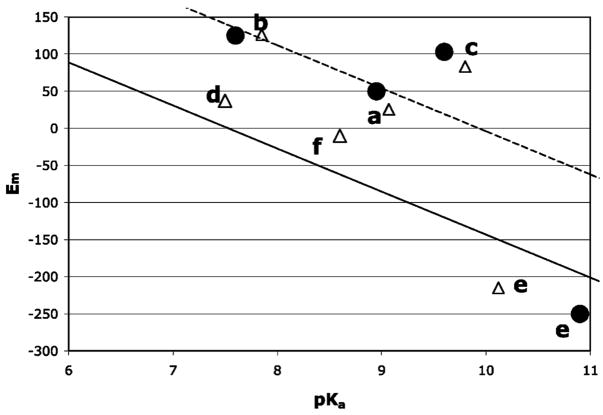
Electrostatic interactions that favor the ferric heme with its net charge of +1 over the neutral ferrous heme shift the E_m down. The same electrostatic interactions favor the cationic ferric water–heme over the neutral hydroxyl–heme, raising the pK_a. While a higher pK_a is correlated with a lower E_m, the connection is by no means exact (Figure 5). In most proteins, the ΔΔG_protein for the redox reaction is larger than for the protonation reaction so the E_m is shifted from E_m,sol by more than the pK_a is shifted from pK_a,sol (Figure 5, eqs 2 and 3). One difference is the desolvation energy is on average 2.4 ± 0.3 ΔpK units larger for the redox reaction than for the protonation reaction (Table 1). Because of its significant dipole the solvated neutral ferric hydroxyl–heme has a solvation energy that is not much smaller than the positively charged ferric water–heme. Thus, both reactant and product of the protonation reaction have similar ΔΔG_rxn. With the exception of cytochrome c oxidase, the desolvation penalty, which always favors the neutral species, shifts the pK_a down by at most 2 pH units. In contrast, when compared to the neutral, ferrous water–heme, the cationic, ferric water–heme has much larger interactions with water. The impact of the desolvation energy on the redox reaction when the heme is buried in the protein is thus much larger.

Figure 5.

E_m versus pK_a at pH 7 for (a) sperm whale myoglobin, (b) Aplysia myoglobin, (c) hemoglobin I, (d) heme oxygenase, (e) horseradish peroxidase, and (f) cytochrome c oxidase. (△) Calculated and (●) available experimental values. The solid line has the same ΔΔG_protein for the in situ E_m and pK_a (eqs 2 and 3). The dashed line of ΔΔG_protein is 2.4 ΔpK units larger for E_m than pK_a; 2.4ΔpK units is the average difference in the ΔΔG_rxn for the two types of reactions (Table 1).

Hemoglobin I has a pK_a which is only 0.2 pH unit higher than the pK_a,sol, while the E_m is 223 mV more positive than E_m,sol (ΔΔG_protein = 3.8 ΔpK units). The difference in desolvation energy for the two reactions contributes 3 ΔpK units. In addition, Gln 64 in the distal pocket changes conformation in the aquo–heme pK_a titration but does not in the E_m titration. The rigid Gln 64 raises the water–heme E_m by 1 ΔpK unit (58 meV) more than it shifts the ferric aquo–heme pK_a down. The reorientation of the Gln is part of the protein dielectric response that is captured by the explicit motions available in MCCE (30, 55). The Gln motion coupled to aquo–heme protonation thus diminishes the effective pairwise interaction.

In horseradish peroxidase, ΔΔG_protein shifts the E_m down more than it shifts the pK_a up. Besides the 2.2 ΔpK unit difference in the desolvation energy, ΔG_res favors heme reduction 3.3 ΔpK units more than water deprotonation. Although both ferrous water–heme and ferric hydroxyl–heme have a net charge of 0, they interact differently with nearby residues. The hydroxyl–heme has a large dipole with its negatively charged hydroxide pointing toward the distal pocket. Arg 38 in the distal pocket and Asp 247 on the opposite side form a dipole stabilizing the hydroxyl–heme. The difference in interactions with hydroxyl–heme and water–heme is relatively small, leading to a small ΔG_res, contributing to the pK_a shift. On the other hand, the neutral ferrous water–heme is not stabilized by the electrostatic dipole generated by these two amino acids while interactions of the ferric water–heme with nearby negative charges shift the E_m down.

As in horseradish peroxidase, the favorable interaction of CuB with the hydroxyl–heme in cytochrome c oxidase makes the contribution of ΔG_res to the in situ pK_a smaller than found for in situ E_m. Assuming the E_m,sol of heme a is 100 (1) to 160 (74, 75) mV more positive than that of heme c, the E_m of heme a3 is predicted to be 9 to 69 mV in cytochrome c oxidase when CuA is oxidized and heme A and CuB are reduced.

There are no experimental data available for the E_m in heme oxygenase 1. These calculations predict an E_m of 40 mV. A run of four backbone dipoles lowers the pK_a more than the E_m. All of the other proteins studied here have similar values of ΔG_pol for the redox and protonation reactions.

CONCLUSIONS

The pK_as of ferric aquo–heme at pH 7 in sperm whale myoglobin, Aplysia myoglobin, hemoglobin I, heme oxygenase 1, horseradish peroxidase, and cytochrome c oxidase were calculated with MCCE. The calculations reveal a breakdown in the classic continuum electrostatic analysis of pairwise interactions. Large errors in calculated pK_as were found in horseradish peroxidase and cytochrome c oxidase. DFT calculations suggest that CE calculations overestimate pairwise interactions between ferric water–heme and a positive charge above the heme plane. This could be due to significant out-of-plane charge density, which would be ignored in the atom-centered charges used in the CE analysis. Alternatively, these external charges could polarize ferric hydroxyl–heme significantly more than the amount accounted for by the ε = 4 used in the MCCE calculation. Using a correction that brings the DFT and CE interactions into agreement, the calculated pK_as in six proteins are within 1 pH unit of the experimental values. The calculated E_ms using the correction derived from DFT calculations are within 35 mV of the experimental values.

Proteins with higher ferric aquo–heme pK_as have lower E_ms since both arise from the protein stabilizing a positively charged heme. However, the proteins shift the free energy of the redox reaction (ΔΔG_protein) by an amount that would shift a pK_a by >6 pH units (375 mV), while the pK_as span only 3.3 pH units (eqs 2 and 3). The difference in ΔΔG_protein shows that there is a larger effective dielectric response for the protonation than the redox reactions. In sperm whale myoglobin and hemoglobin I protonation is coupled to conformational changes while the redox reaction is not. These conformation changes allow a residue in the distal pocket to stabilize both protonation states, reducing the energy difference between them. In contrast, when the group is rigid as it is for the redox reaction, the pairwise interactions are larger, shifting the E_m more. This difference in flexibility for the two reaction types found in MCCE is supported by the good match between calculation and experiment for both pK_as and E_ms.