Quantitative Microplate-Based Respirometry with Correction for Oxygen Diffusion

Abstract

Respirometry using modified cell culture microplates offers an increase in throughput and a decrease in biological material required for each assay. Plate based respirometers are susceptible to a range of diffusion phenomena; as O₂ is consumed by the specimen, atmospheric O₂ leaks into the measurement volume. Oxygen also dissolves in and diffuses passively through the polystyrene commonly used as a microplate material. Consequently the walls of such respirometer chambers are not just permeable to O₂ but also store substantial amounts of gas. O₂ flux between the walls and the measurement volume biases the measured oxygen consumption rate depending on the actual [O₂] gradient. We describe a compartment model-based correction algorithm to deconvolute the biological oxygen consumption rate from the measured [O₂]. We optimize the algorithm to work with the Seahorse XF24 extracellular flux analyzer. The correction algorithm is biologically validated using mouse cortical synaptosomes and liver mitochondria attached to XF24 V7 cell culture microplates, and by comparison to classical Clark electrode oxygraph measurements. The algorithm increases the useful range of oxygen consumption rates, the temporal resolution, and durations of measurements. The algorithm is presented in a general format and is therefore applicable to other respirometer systems.

Novel multiwell plate based respirometry assays (Seahorse extracellular flux analyzer,(1) Luxcel MitoXpress(2)) revive classical bioenergetics by enabling an increase in throughput and decrease in biological material required for each assay. Importantly, plate based assays broaden the gamut of biological specimens that can be measured, ranging from attached cell cultures(1) and tissue slices to plate-attached synaptosomes(3) or isolated mitochondria.(4)

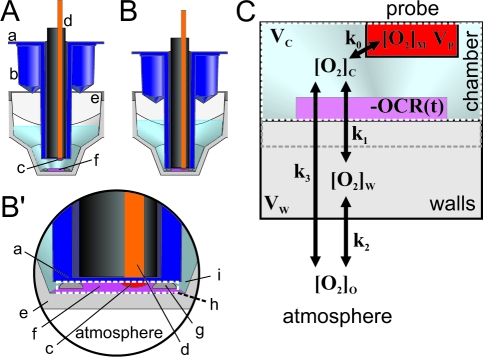
Classical Clark electrode oxygraphs are sealed, “closed” systems that do not allow ambient oxygen to access the measurement volume, so the decay of [O₂] within the chamber directly relates to the actual biological oxygen consumption. Conversely, plate based assays are open or “semiclosed” designs in which the chamber or measurement volume including the specimen and the sensor is exposed to ingress or leakage of oxygen from the atmosphere. For example, in the Seahorse XF24 extracellular flux analyzer a small, temporary chamber volume is created around the cells during the measurement by lowering a piston-like probe into the well to amplify the changes in [O₂] (Figure 1A and B). This measurement volume (Figure 1B’ h) is not completely isolated from the environment because the piston does not fully enclose the temporary microchamber and the polystyrene plate material is not impermeable to O₂.

Figure 1.

Seahorse XF24 V7 microplate chamber and the generalized compartment model for semiclosed chamber oxygraphs. (A and B) Well of the XF24 V7 microplate, with probe in up (A) and in measure (B and B’) positions. (a; blue) disposable cartridge consisting of the drug injection ports (b) and the O₂ probe (c; red; the pH and optional CO₂ sensors are not shown). (d) steel rod containing fiber optics for fluorescence data collection. (e; gray) one well of the flux plate with assay medium and the biological material (f; purple). (g) Bumps in the bottom of the well acting as spacers establishing the thickness (∼200 μm) of the entrapped volume denoted as “chamber” (h; dashed white outline). The entrapped volume is open from the sides, but slow diffusion rates limit O₂ exchange with fluid spaces (i) around the rim of the tip of the sensor piston (a). (C) Compartment model of open or semiclosed oxygraphs. Color coding corresponds to (A and B). See details in text.

As a result, these open or semiclosed designs experience a range of diffusion phenomena. As [O₂] depletes within the chamber, atmospheric O₂ leaks into the measurement volume, leading to an underestimation of the biological oxygen consumption rate. In addition, oxygen dissolves in commonly used multiwell plate materials such as polystyrene.^5,6 Consequently, the bottom and walls of such chambers are not just permeable to O₂ but also store substantial amounts of gas.

Here we describe a general, compartment model-based, correction algorithm to deconvolute the biological oxygen consumption rate from the measured [O₂] in open or semiclosed respirometer chambers. We optimize the algorithm for the Seahorse XF24 extracellular flux analyzer. The correction algorithm is biologically validated using mouse cortical synaptosomes and liver mitochondria centrifugally attached to XF24 V7 cell culture microplates. To facilitate general use, the correction algorithm is presented as an Excel spreadsheet (Supporting Information (SI)).

Experimental Section

Preparation of Synaptososmes

Synaptosomes were isolated from cerebral cortices of male CD1 mice aged 17−21 days by the method of Dunkley et al.(7) with slight modifications. A cortex was rapidly removed, rinsed with ice-cold SDE medium (320 mM sucrose, 1 mM EDTA, 0.25 mM dithiothreitol, pH 7.4), transferred to a prechilled Dounce glass homogenizer containing 2 mL SDE medium and homogenized gently by 12 up-and-down strokes. The homogenate was then centrifuged at 1000g for 10 min at 4 °C. The supernatant was layered on top of a discontinuous Percoll gradient (3 mL layers of 3, 10, and 23% v/v Percoll in SDE medium) in a 15 mL centrifuge tube, and centrifuged at 32 500g for 10 min at 4 °C in a JA-25.50 rotor in a Beckman Avanti J-26 XPI centrifuge (Beckman Coulter Inc., Fullerton, CA). Synaptosomes were isolated as the band between 10 and 23% Percoll, diluted into HBS medium (20 mM HEPES, 10 mM d-Glucose, 1.2 mM Na₂HPO₄, 1 mM MgCl₂, 5 mM NaHCO₃, 5 mM KCl, 140 mM NaCl, pH. 7.4) and centrifuged at 15 000g for 15 min at 4 °C to remove Percoll.

Respirometry of Plate-Attached Synaptosomes

Respirometry of synaptosomes was performed using an XF24 extracellular flux analyzer (Seahorse Bioscience, North Billerica, MA) as described by Choi et al.(3) The final synaptosome pellets were resuspended in HBS medium and synaptosomes (10 μg protein as determined by Bradford assay in unlysed synaptosomes, equivalent to ∼50 μg protein using biuret assay) were aliquoted into 20 wells of an XF24 V7 cell culture microplate coated overnight with polyethyleneimine (1:15 000 dilution of 50% w/v solution in H₂O). The plate was centrifuged at 3400g for 1 h at 4 °C in an A-4-62 rotor in an Eppendorf 5810R centrifuge (Eppendorf, Westbury, NY). The plated amount of protein was recovered without significant loss when the contents of the wells were lysed and assayed for protein after the respirometry assay. The HBS medium was replaced with 700 μL of “Seahorse medium” (3.5 mM KCl, 120 mM NaCl, 1.3 mM CaCl₂, 0.4 mM KH₂PO₄, 1.2 mM Na₂SO₄, 2 mM MgSO₄, 15 mM d-glucose, 10 mM Na-pyruvate, 10 mM TES, 4 mg/mL BSA, pH 7.4), at 37 °C. Plates were incubated at 37 °C for 25 min to allow temperature and O₂ equilibration and then loaded into the XF24, where samples were further incubated for 12 min before the baseline was recorded. Experiments consisted of 30 s mixing, 150 s wait, and 3 min measurement cycles, unless otherwise stated. All experiments were performed at 37 °C.

Preparation of Isolated Mitochondria

Mouse liver mitochondria were isolated according to Chappell and Hansford(8) with slight modification. Liver was removed from euthenized mice, rinsed with ice-cold STE medium (0.25 M sucrose, 2 mM EGTA, 5 mM Tris, pH 7.2), chopped into small pieces, then homogenized with a Dounce homogenizer, with 10 up-and-down strokes. Homogenates were centrifuged at 1000 g for 3 min to remove nuclei and cell debris. The supernatant was transferred to a new tube, and recentrifuged at 11 630g for 10 min. The pellet was rinsed with ice cold STE medium, transferred into a 1.5 mL microtube and resuspend with 0.5 mL STE medium. Protein concentration was determined with a Bradford assay.

Respirometry of Plate-Attached Mitochondria

Isolated mitochondria were seeded at 2.5 μg of protein (Bradford assay) per well in polyethyleneimine-coated XF24 V7 cell culture microplates, as described above for synaptosomes. After centrifugation, medium was replaced with prewarmed KHE medium (115 mM KCl, 10 mM KH₂PO₄, 3 mM HEPES, 1 mM EGTA, 2 mM MgCl₂, pH 7.2, 700 μL/well) plus carbonyl cyanide 4-(trifluoromethoxy) phenylhydrazone (FCCP; 0.5 μM), rotenone (2 μM) and cytochrome c (10 μM). Plates were immediately loaded into the XF24 instrument, where the respirometry assay was preceded by a ∼12 min preincubation. The experiment consisted of 30 s mixing, 30 s wait, and 3 min measurement cycles, repeated three times to record baseline respiration, followed by injection of succinate (10 mM) and a 30 s mixing, 30 s wait, and 30 min measurement cycle.

Clark Electrode Respirometry of Suspensions

The mitochondrial (or synaptosomal) suspension was split and incubated in parallel, in identical conditions as for the XF24 measurement, with the exception that mitochondria (synaptosomes) were in suspension and not plate-attached. Respirometry was performed with a Mitocell S200 micro respirometer (Strathkelvin Instruments Limited, Scotland) in a 100 μL experimental volume containing 0.5 mg/mL mitochondria or 0.25 mg/mL synaptosomes at 37 °C, continuously stirred. The Clark electrode chamber was closed and the assay was started simultaneously with the recording of the third baseline data point in the XF24. The respirometer was calibrated to 100% by KHE (or Seahorse) medium equilibrated with the atmosphere at 37 °C ([O₂] = 0.214 mM; this value was also used for the initial oxygen, [O₂]₀, for the Seahorse respirometry) and to 0 mM by Na-dithionite.

Preparation and Respirometry of Cortical Cultures

Primary cortical neurons were prepared from E18 rat hippocampi (BrainBits LLC, Springfield, IL). Cortices were dissociated with 2 mg/mL papain (Worthington, Lakewood, NJ) in Hibernate (BrainBits) for 30 min at 37 °C, and were dispersed manually by 5−10 strokes with a 1 mL pipet. Cells were plated onto poly-d-lysine-coated (0.2 mg/mL in H₂O; overnight) XF24 V7 cell culture microplates at a density of 6·10⁴ cells/well in Neurobasal medium (Invitrogen, Carlsbad, CA) containing 2% v/v B27 supplement, 0.5 mM GlutaMAX, 1% v/v dialyzed fetal bovine serum, and 100 IU/ml penicillin plus 100 μg/mL streptomycin. Respirometry was performed on days 11−13 in the XF24 in Seahorse medium lacking Na-pyruvate and BSA, in a paradigm similar to that described above for synaptosomes.

Imaging Attached Organelles

Mitochondria or synaptosomes attached to XF24 V7 cell culture microplates were incubated with Mitotracker Red (100 nM; Invitrogen, Carlsbad, CA) for 30 min, then medium was replaced with fresh Seahorse medium. The entire areas of representative wells were imaged by the “large image acquisition” tiling feature of the NIS Elements 3.0 image acquisition software (Nikon, Melville, NY) using a Nikon Eclipse Ti-PFS inverted fluorescence microscope, with 543/22 nm excitation and 617/73 nm emission wavelengths.

Calculation of [O₂] from the Fluorescence (Phosphorescence) Response of the Oxygen Probe

The deactivation or quenching of the fluorescence (phosphorescence) of a material by another molecule, in this case the quenching of the sensor probe (Figure 1A and B’ (c)) by O₂ molecules, is expressed by the Stern−Volmer relationship (eq 1),

where K_sv is the Stern−Volmer constant, F₀ is the maximal fluorescence intensity of the probe at zero [O₂], and F is the fluorescence intensity of the probe at the actual [O₂].

Fluorescence intensity is also influenced by the temperature of the sensor (or assay medium), the fluorescence intensity of the sensor being inversely proportional to temperature with a dependency of about −0.3%/°C (according to the manufacturer). During mixing, the contents of the open chamber (cycling between positions Figure 1A and B) are exposed to dry air, causing evaporative cooling of the medium, which in turn causes a change in sensor output. To track these changes, temperature control wells are employed, which contain medium but no respiring biological material.

The first aim is to normalize fluorescence intensities within a well, with the assumption that the intensities measured in the temperature control wells correspond to ambient [O₂] at all times. The XF24 assigns 10 000 fluorescence units (FU) to ambient [O₂] during its internal calibration procedure by setting the intensity of the light emitting diode (LED) used to excite the sensor. Therefore F₀ is directly linked to the K_sv value:

where [O₂]₀ is the ambient oxygen concentration. This has two consequences; if F₀ increases, K_sv also increases (since the [O₂]₀ − 10 000 FU relation is maintained by definition); and second, K_sv can be directly calculated from the F₀ fluorescence measured in oxygen-depleted wells, e.g., after addition of Na-dithionite. In our experiments F₀ was 44 000.

To perform a temperature or a generalized “gain” correction we assume (as a simplification) that both K_sv and F₀ are scaled by a k_T factor (eq 3) due to a changed temperature. The fluorescence measured in the temperature control well at ambient [O₂]₀ is F_T. The solution of eq 3 for k_T is eq 4. Substitution of eq 4 into the Stern−Volmer relationship using the scaled K_sv and F₀ yields eq 5.

In summary, eq 5 converts F fluorescence into [O₂] by assuming that K_sv and F₀ are scaled proportionally by the temperature change. The scaling factor is estimated from the change of F_T fluorescence in the temperature control wells that detect constant ambient [O₂]. In addition, other “gain” factors such as the slow degassing of improperly air-equilibrated samples can cause baseline drift, and such drift was also successfully corrected by the above method (not shown). Thus, this correction increases the robustness of the respirometry technique.

Calculation of Noncorrected Oxygen Consumption Rate (−d[O₂]_M/dt)

For visualizing temporal changes in oxygen consumption rate, time based differentiation of the measured [O₂] ([O₂]_M) time lapse data was performed. Temporal sequences of the [O₂] data points and the time points were filtered using a 7 point wide, second order polynomial, first order derivative Savitzky−Golay(9) kernel [0.107, 0.071, 0.036, 0, −0.036, −0.071, −0.107]. Filtered [O₂] values were multiplied by −1 and divided by the filtered time values.(10) Differentiation amplifies noise, therefore this method provides additional smoothing of the calculated differentiated signal, but results in the loss of the first three and last three data points of each measurement period.

Compartment Model for O₂ Storage and Diffusion

In semiclosed systems, the measured change of O₂ concentration (d[O₂]_M(t)/dt) underestimates the biological oxygen consumption (OCR(t)) because O₂ is replenished within the chamber by diffusion from the walls of the chamber and from the atmosphere. The aim of the correction algorithm is to deconvolute the biological oxygen consumption rate from the d[O₂]_M(t)/dt. Oxygen diffusion was modeled as the exchange of O₂ at each time point between the following compartments (Figure 1C): the chamber volume (“chamber”), the walls of the well, the probe, and the atmosphere. The model estimates oxygen diffusion from the atmosphere into the chamber and into the walls, O₂ storage in the walls, and deconvolutes the response time of the O₂ sensor (Figure 1C arrows).

Because the actual geometry of the chamber is complex (Figure 1B’), the aim of the compartment model is to simplify the geometry into a series of compartments, so that an algorithm can be applied using a set of diffusion rate or time constants that will accurately calculate OCR(t). A single storage compartment V_W (Figure 1C “walls”) is considered to be the sum of all physical entities which affect the [O₂] in the chamber volume by storing [O₂]. This includes the walls and the bottom of the chamber (Figure 1B’ (e)), the surface of the sensor (a), and also possible aqueous compartments that are outside the measured volume (i). In addition, while diffusion will establish concentration gradients, as a further simplification compartments are considered to have uniform [O₂]. The consequences of this simplification for the apparent chamber volume (V_C) will be considered below.

The probe readout is a time course of measured [O₂]: [O₂]_M(t). The probe exchanges O₂ with the chamber volume (V_C) with k₀ first-order rate constant (Figure 1C). The probe is assumed to have a negligible volume (V_P≪ V_C), therefore while the [O₂] in the chamber volume ([O₂]_C(t)) affects [O₂]_M(t) (eq 6), the amount of [O₂] diffusing into the probe is also negligible, so that [O₂]_M(t) does not affect [O₂]_C(t) (eq 7). The O₂ in the chamber exchanges with the walls ([O₂]_W(t)) with k₁ rate constant and is consumed by the specimen by OCR(t) (eq 7), the biological oxygen consumption (consumption is positive and is given as concentration change/time). The chamber and the atmosphere can exchange O₂ with a rate constant k₃ (eq 7). Finally, eq 8 describes the change of [O₂] in the walls: O₂ exchanges between the chamber and the walls with a rate constant k₁ and between the walls and the atmosphere with a rate constant k₂. V_C and V_W are “apparent volumes”, which take into account the different partitioning coefficients of O₂ in the medium and in the walls.

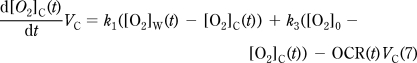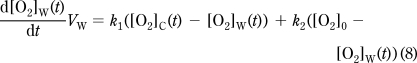Calculation of the Biological Oxygen Consumption Rate OCR(t) from [O₂]_M(t)

The k and V values from eq 8 are combined to yield apparent rate constants (eq 9); k_AC describes the rate of diffusion from the atmosphere into the chamber, k_AW from the atmosphere into the walls, k_W from the chamber into the walls, and k_C from the walls into the chamber. k_P is the response rate of the slow-response probe. Equations 10−12 correspond to eq 6−8 and are now devoid of volume terms. Equation 6 is a nondifferential equation for the unknown [O₂]_C(t), so [O₂]_C(t) can be expressed as shown by eq 10.

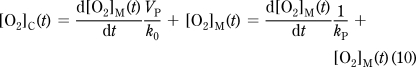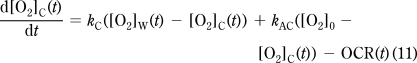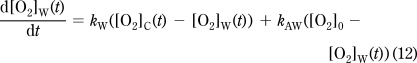Next we express [O₂]_W(t) by the solution of the differential equation eq 12 for the [O₂]_W(0) = [O₂]_C(0) = [O₂]_M(0) = [O₂]₀ initial condition (eq 13). In addition, [O₂]_C(t) was substituted with eq 10. Importantly, because of the integral, this solution requires the whole respirometry timecourse, starting from t = 0, with the assumption that at t = 0 the system is in equilibrium. This is typically valid, as the sample is preincubated for a long period with the chamber open.

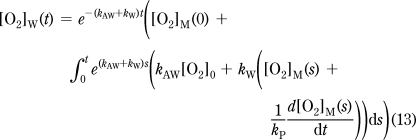Finally, OCR(t) is calculated by eq 14, which was derived from eq 11 after substituting eq 10, and requires values of [O₂]_W(t) calculated above by eq 13:

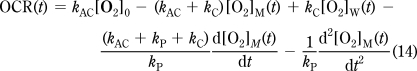OCR(t) has the units of concentration change over time. Thus the respiration of the biological sample per well is calculated by

Importantly, V_C is not necessarily the “geometric” volume of the aqueous compartment of the chamber. V_C was defined above as “apparent” chamber volume, i.e., the volume of that compartment that is in direct, “instantaneous” O₂ exchange with the respiring biological material and the sensor. Another important simplification was made above where the compartments are modeled as having homogeneous oxygen concentrations despite the expected presence of concentration gradients in the walls due to diffusion. The superficial layers of the chamber walls facing toward the medium are expected to be in rapid [O₂] exchange with the medium, whereas deeper layers behave more like a storage compartment, due to the slower diffusion of O₂ into the greater depth of wall material. Consequently, the layers of the wall that behave more like the chamber belong to the chamber compartment of the model (Figure 1C area bounded by the white plus gray dashed lines). The deeper layers of the wall which behave more like a storage compartment belong to the uniform storage compartment. Thus apparent chamber volume, V_C, expands into the wall, so V_C is larger than the geometric volume of the chamber. This effect is augmented by the large partitioning coefficient for O₂ into the polystyrene wall.

In summary, the compartment model correction is performed by calculation of eq 13 followed by eq 14. The calculation requires the experimental determination of five rate constants: k_P, k_AC, k_AW, k_W, and k_C. For more intuitive handling of rate constants their reciprocals, time constants, are used for the experimental work below (τ = k⁻¹). In some cases zero may be assigned to k, meaning that the given pathway is disabled. If absolute respiration per unit of biological material is to be calculated, the value of V_C is required, and is determined by external calibration. The derivation of the above equations and initial implementation of the correction algorithm was done in Mathematica 5.2 (Wolfram Research, Campaign, IL). An Excel implementation of the correction algorithm is provided in the SI.

Optimization of Rate Constants

The optimization of rate constants was based on constant biological respiration, that is justified by early studies of synaptosomal respiration,^11,12 and by our data (see below, Figure 2B). To assess the ability of the model to accurately reflect constant respiration, we performed regression analysis of OCR(t) calculated by the compartment model correction algorithm to a theoretical respiration model where the variance of the OCR(t) trace was calculated for the measurement period. The optimization of the rate/time constants was performed by seeking the minimum of the variance of the OCR(t) trace in each well using the NMinimize standard function of Mathematica 5.2 with the ’Differential Evolution” method.(13) Wells where the minimal variance was found at the boundary of the sought variable were rejected. The τ values shown are means of optimizations performed well-by-well (see Table 1).

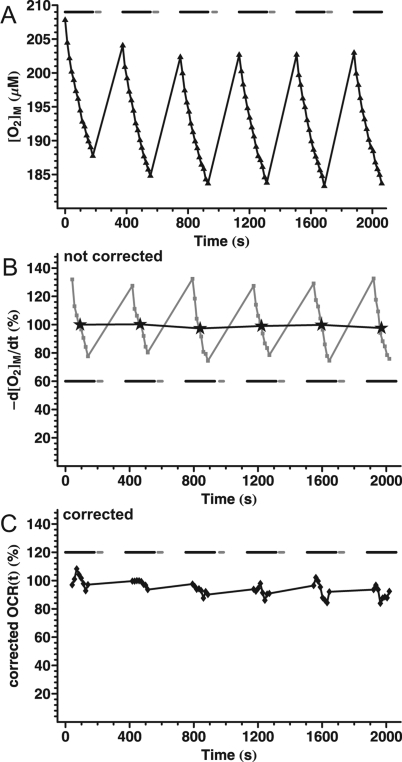
Figure 2.

Basal respiration of cortical synaptosomes in Seahorse medium containing glucose plus pyruvate. (A). Fluorescence values from a representative well in a XF24 V7 microplate were converted to [O₂] using eq 5 and F₀ = 44000 as determined in a separate experiment by addition of Na-dithionite. Data points correspond to the measured [O₂] ([O₂]_M) with a 13 s data acquisition interval within the measurement periods (3 min in length; black bars). Each measurement period was followed by mixing (30 s; gray bars) and a wait period. Data are from one well and represent >5 independent plates. (B) Noncorrected basal oxygen consumption rate of synaptosomes, as calculated by temporal differentiation of the [O₂]_M data from (A). Stars indicate mean oxygen consumption rate for each measurement period, normalized to the first data point. Gray squares show the temporally differentiated concentration data (noncorrected oxygen consumption rate trace). The first and last three data points were dropped in each measurement period due to the effect of kernel filtering with a width of seven points for differentiation. Note that the decay of the differentiated trace is simply the reflection of the decelerating decay of [O₂] in (A). (C) Corrected basal oxygen consumption rate of synaptosomes, as calculated by the compartment model correction using the time constants in Table 1.

Table 1. Time Constant Values Measured in Polystyrene (Standard) and Polyethylene (Alternative) XF24 V7 Microplates^a.

	polystyrene microplate		polyethylene microplate
τP	43 ± 2 s	42 ± 2 s	25 ± 2 s	23 ± 2 s
τAC	746 ± 18 s	N/A	1457 ± 58 s	N/A
τAW	N/A	1217 ± 34 s	N/A	1247 ± 67 s
τC	246 ± 8 s	184 ± 5 s	334 ± 16 s	294 ± 14 s
τW	296 ± 8 s	392 ± 12 s	246 ± 17 s	302 ± 11 s

^aN/A: not assigned, as k_AW or k_AC was set as 0. Data are shown as mean ± sem for n = three independent microplates. The time constants shown in bold were used for corrections of experimental data shown in this paper.

Results and Discussion

In a Semiclosed Respirometer Chamber the Apparent Oxygen Consumption Rate Decays with a Characteristic Curve

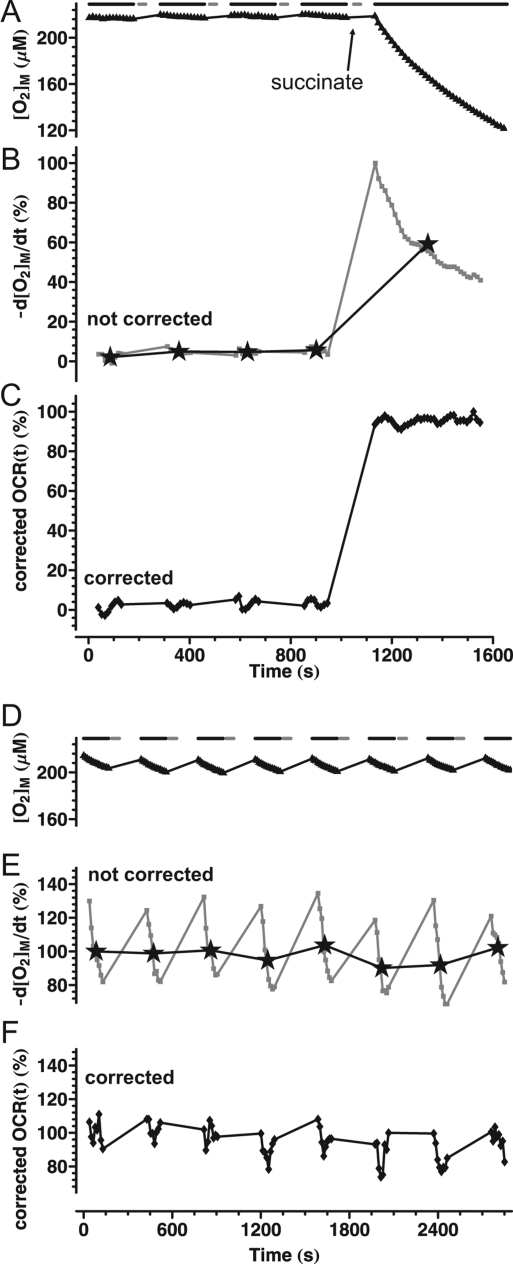
Respiration of plate-attached synaptosomes was measured with a Seahorse XF24 extracellular flux analyzer. Cortical synaptosomes respiring at their basal rate in medium containing glucose plus pyruvate exhibited steady respiration. This is supported by Figure 2A and B, where oxygen consumption rate determination was repeated over time by periodic entrapment of the chamber volume (black bars). Each measurement period was followed by withdrawal of the probe and reoxygenation of the medium by mixing (gray bars). The mean oxygen consumption rate calculated for each measurement period did not decay significantly over the repeated measurements (Figure 2B, stars), confirming that basal synaptosomal respiration is constant in time.^11,12

In contrast, when the oxygen consumption rate was visualized as −d[O₂]_M/dt within each measurement period with no correction algorithm applied (Figure 2B squares), the rate exhibited a curved decay, decreasing by almost 50% during the two minute measurement period. When the noncorrected oxygen consumption rate from wells with different absolute oxygen consumption rates was plotted normalized to the first time point, these decaying curves overlaid each other (not shown). Therefore the shape of the decay curve was independent of the magnitude of the respiration.

We hypothesized that the decay of the noncorrected oxygen consumption rate (Figure 2B squares) is caused by O₂ diffusion from the atmosphere and walls into the chamber. As the [O₂]_C decreases, this diffusion makes a greater and greater contribution, masking the O₂ consumption of the biological material, therefore the apparent oxygen consumption rate decreases. However, a simple concentration gradient dependent correction model (Figure 1C with k₃ only) did not describe the experimental findings sufficiently or accurately (data not shown).

The Experimental Data Suggests Effects of O₂ Storage and Leakage

When the measurement volume around synaptosomes respiring at their basal rate was entrapped for a longer period (30 min, Figure 3A) the decay of the rates slowed after the initial fast phase (Figure 3B), suggesting that at least two different processes account for the decay. Next, respiration was inhibited by injection of rotenone (20 nM) plus myxothiazol (2 μM), inhibitors of respiratory complexes I and III, respectively, which are known to completely inhibit respiration within seconds.(14) When the measurement volume was entrapped for the second time, immediately after a short, 20 s mixing period, [O₂]_M continued to decay for the next three minutes (Figure 3A and B (a)), even though respiration was expected to be completely inhibited. This 3 min decay was followed by a gradual increase of [O₂]_M (b) signifying leakage of atmospheric O₂ into the chamber (k₃ in Figure 1B).

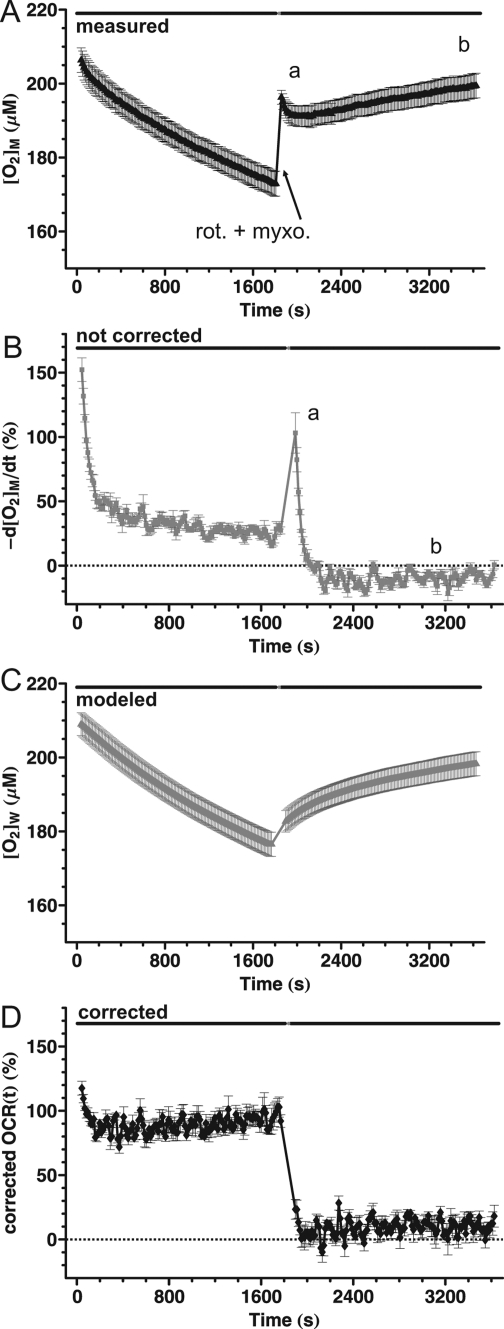
Figure 3.

The behavior of noncorrected oxygen consumption rate suggests effects of O₂ storage and diffusion. (A) Basal respiration of cortical synaptosomes in Seahorse medium containing glucose plus pyruvate was inhibited by addition of rotenone (20 nM) plus myxothiazol (2 μM) as indicated. Symbols represent [O₂]_M (determined as for Figure 2) with a 13 s data acquisition interval within 30 min measurement periods (black bars). The two measurement periods were separated by drug injection and mixing (20 s). Data are mean ± sem of n = 4 wells from a representative plate. Note (a) the decaying [O₂]_M after respiration was inhibited, which suggests that O₂ diffuses into a previously depleted storage compartment, and (b) the increasing [O₂]_M in the entrapped chamber volume when mitochondria do not respire, which suggests O₂ leakage from the atmosphere. (B) Noncorrected basal oxygen consumption rate of synaptosomes, calculated by temporal differentiation of the [O₂]_M data from (A). Note (a) initial high noncorrected oxygen consumption rate for minutes after respiratory inhibition; (b) negative noncorrected oxygen consumption rate. (C) [O₂] in the walls of the chamber ([O₂]_W) as calculated by eq 13 of the compartment model correction using the time constants obtained below. (D) Corrected basal oxygen consumption rate of synaptosomes, calculated by the compartment model correction using the time constants in Table 1.

To explain Figure 3 we hypothesized that O₂ is removed from the chamber into a storage compartment that had been depleted of O₂ during the first long measurement period, mimicking respiration (a). Therefore a wall storage mechanism (k₁) was added to the model. To illustrate this, the value of [O₂]_W, the oxygen concentration in the walls of the chamber calculated by the finalized model (eq 13), is plotted in Figure 3C. Figure 3D will be discussed below.

Experimental Design to Tune the Compartment Model

To amplify possible wall-storage effects using synaptosomes respiring at their basal rate, the following paradigm was designed. Two short (3 min) and two long (20 min) measurements were conducted shortly after each other, so the walls are exposed to low chamber [O₂] for a longer time (Figure 4A). At the beginning of the second long phase, the walls have a lower [O₂] than the chamber, so the direction of O₂ diffusion is expected to reverse. This flux results in overestimation of the respiration. The increased initial noncorrected oxygen consumption rate at the beginning of the second long measurement phase (Figure 4B (a)) supports this mechanism.

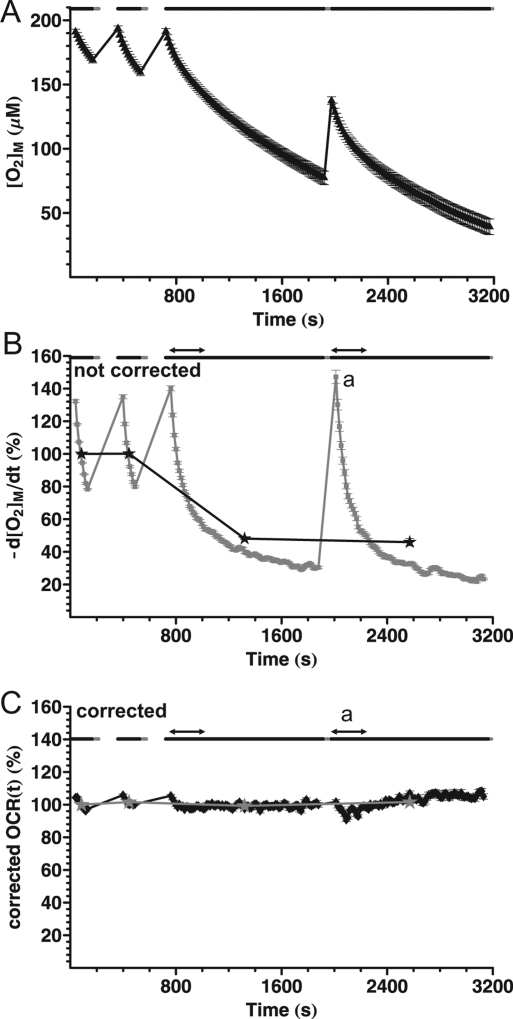
Figure 4.

Experimental design for amplified wall storage effects and optimization of time constants. (A) Basal respiration of cortical synaptosomes in Seahorse medium containing glucose plus pyruvate. [O₂] was determined as for Figure 2. Two 20 min measurements were taken following each other with only a short mixing period in between. Data are from a representative well from three independent experiments and 20 wells per experiment. (B) Noncorrected oxygen consumption rate corresponding to (A). Stars indicate mean oxygen consumption rate for each measurement period, normalized to the first data point. Note that while respiration is considered to be steady based on Figure 2B, the mean oxygen consumption rate in long measurement periods is underestimated. Gray diamonds show the temporally differentiated [O₂] trace. Note (a) the higher initial noncorrected oxygen consumption rate, which supports the ideas that the walls are O₂ depleted at this point, and O₂ diffusion from the chamber into the walls contributes to the measured rates. Arrows indicate the range of variance calculation for the time constant optimization. (C) Corrected OCR(t) calculated by the compartment model correction using the time constants in Table 1. Data are mean ± sem of n = 20 wells from a representative of three independent plates.

Figure 4B also illustrates a confounding consequence of the decaying noncorrected oxygen consumption rate; if the mean rates from different measurement period lengths are calculated (stars), an artifact is generated. The longer the measurement period, the more underestimated the calculated mean oxygen consumption rate will become, although the biological respiration is constant. In addition, the decaying characteristic of the noncorrected oxygen consumption rate values confounds its relation to the real value of the biological respiration.

Optimization of Time Constants for the Compartment Model-Based Correction of Oxygen Consumption Rate

The aim of the compartment model-based correction algorithm is to eliminate the artifactual decay of the oxygen consumption rate. The complete model requires five time constants (τ = k⁻¹; the more self-explanatory time constants are used below instead of rate constants), which are determined by numeric optimization performed on experimental data. The goal of the numeric optimization is to find time constants that yield a constant, nondecaying, corrected OCR(t) (Figures 2C, 3D, and 4C). The correction has to cope with two scenarios: when wall to chamber O₂ diffusion leads to an underestimate of respiration, and when chamber to wall O₂ diffusion overestimates respiration. Therefore the optimization is performed by taking both long measurement cycles of the paradigm illustrated in Figure 4 into account.

Since the compartment model was designed based on hypothetical considerations, all modeled O₂ exchange pathways do not necessarily play a significant role in a given chamber design (e.g., for the Seahorse XF24 V7 microplate). Therefore, another aim of the numerical optimization is to decide which time constants can be unambiguously determined (with a small error in multiple wells/plates), and which have no role (and could be set to 0). This approach can yield a simplified and more robust model.

To optimize the time constants, the variance of the corrected OCR(t) data points pooled from the first 24 time points of both long measurement periods (Figure 4B and C; arrows) was calculated. This variance is greater if the oxygen consumption rate trace decays, or if there is a biased estimation of the second, O₂-depleted long measurement period (Figure 4B and C; a)). In contrast, the variance is smaller if the OCR(t) trace is steady as is expected from the steady biological respiration. Performing the optimization on all five time constants by seeking the minimum of the variance yielded large errors in τ_AC (atmosphere to chamber) and τ_AW (atmosphere to walls) suggesting that these parameters are redundant (not shown). Therefore the model was simplified by assuming that either k_AW = 0 or k_AC = 0, and the optimization was performed on four parameters.

Table 1 provides the time constant values that were experimentally obtained as described above. The τ values were calculated for both polystyrene (standard) and alternative polyethylene microplates. The τ values that were obtained had relatively small well-to-well (not shown) and plate-to-plate (n = 3) variability (Table 1). τ_AC was significantly larger, and therefore O₂ redistribution between the atmosphere and the chamber was slower, in the less oxygen-permeable (polyethylene) microplates. When k_AC was set to 0 and τ_AW values were determined, they were similar between polystyrene and polyethylene plates. In contrast, in this case τ_C (describing the flux from the walls to the chamber) was larger in polyethelene, again indicating slower diffusion of O₂ into the chamber in the less permeable (polyethylene) microplate. Notably, a greater τ_P increases the noise in OCR(t), therefore minimization of the variance tends to underestimate the value of τ_P.

The above effects of the microplate material on the time constants confirm the presence of O₂ diffusion and storage phenomena in the plate material. Using time constant sets either with k_AC = 0 or with k_AW = 0 did not make a difference in the corrected OCR(t) (see SI; Excel version of the correction algorithm), so the k_AW = 0 constant set is used for all calculations in the XF24 instrument.

Biological Validation of the Correction Algorithm in the XF24 Instrument: Oxygen Consumption Rate Relative to the Baseline

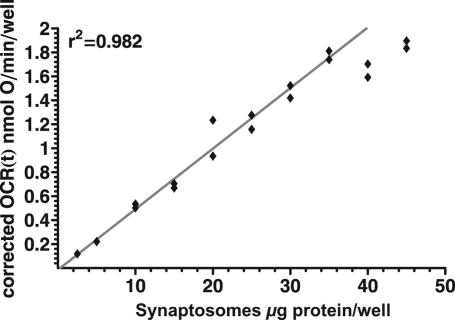
Corrected OCR(t) traces were calculated using the time constants obtained above (Table 1, bold) in all further experiments. Cortical synaptosomes were spun down into XF24 V7 microplates in amounts between 2.5 and 45 μg/well (Bradford assay). The corrected OCR(t) (Figure 5) exhibited a good linear relationship to the micrograms of plated synaptosomes up to a density of 35 μg/well (r² = 0.98).

Figure 5.

Linearity of corrected OCR(t). Between 2.5 and 45 μg synaptosome protein/well (Bradford assay) were spun down into XF24 V7 microplates, and basal respiration was measured in Seahorse medium containing glucose plus pyruvate. The corrected oxygen consumption rate was calculated by the compartment model correction using the optimized rate constants given in Table 1 for polystyrene plates. Absolute values of respiration are shown using the value of V_C = 22.7 μL obtained below. Linear regression was performed for the 2.5−35 μg/well concentration range. Data points correspond to individual wells in a single microplate representative of three experiments.

The correction algorithm canceled the decay of the raw oxygen consumption rate traces in synaptosomes respiring at basal rate (Figures 2C and 4C), in uncoupled mitochondria (Figure 6A−C), and in cultured cortical neurons respiring at their basal rate (Figure 6D−E).

Figure 6.

Noncorrected and corrected oxygen consumption rates recorded in plate-attached mitochondria and in cultured cortical neurons. (A−C) Mouse liver mitochondria were spun down into XF24 V7 microplates at 2.5 μg protein/well and preincubated with FCCP (0.5 μM), rotenone (2 μM) and cytochrome c (10 μM). Respiration was started by the addition of succinate (10 mM) as indicated. Data are from a representative well of three independent microplates. (D−F) Rat cortical cultures were plated into XF24 V7 microplates at 10⁵ cells/well and grown for 12 d. Basal respiration was measured in Seahorse medium containing 15 mM glucose. Data shown are from a representative well from >5 independent plates. (A and D) [O₂]_M as calculated by eq 5 and F₀ = 44 000. Data points correspond to the 13 s data acquisition intervals within the measurement periods (black bars). Each measurement period was followed by mixing (30 s; gray bars) and a wait period as indicated. (B and E) Gray squares indicate noncorrected oxygen consumption rate calculated as −d[O₂]_M/dt, stars mark the mean noncorrected oxygen consumption rate for each acquisition period. (C and F) Corrected OCR(t).

Cultured neurons typically had a smaller oxygen consumption rate than synaptosomal and mitochondrial samples (above), and this is reflected in the greater noise in Figure 6E. The corrected oxygen consumption rate is noise sensitive, mostly because of the second temporal derivative required for handling the slow-probe response (eq 14). For example; as τ_P increases, noise will become amplified, conversely, as τ_P is reduced, the noise injected by the algorithm will decrease. Importantly, this random noise decreases by averaging multiple wells, in contrast to the systematic error introduced by the decay of the noncorrected rates.

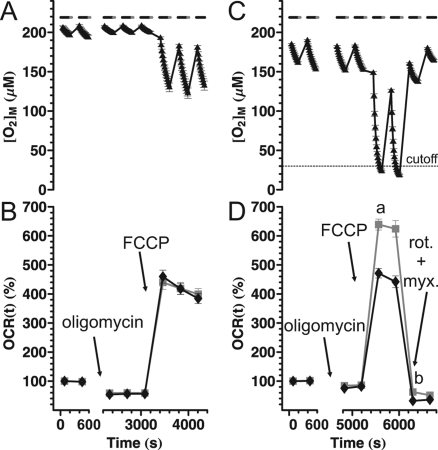
Next, a typical experiment assessing basic bioenergetic parameters was performed as a sequence of additions of oligomycin (2 μg/mL), and FCCP (4 μM/0.4% w/v BSA). First, the experiment was performed in “ideal” conditions, meaning that short and equal measurement periods were used (as shown in Figure 2), at a suitable synaptosomal loading (10 μg protein/well), not allowing O₂ to substantially deplete in the chamber (Figure 7A). In this case, wall O₂ storage-related effects are expected to be small. The corrected (black diamonds) and noncorrected mean oxygen consumption rate (gray squares) were essentially identical (Figure 7B).

Figure 7.

The compartment model correction avoids artifacts caused by O₂ depletion in the chamber and in the walls. Basal respiration of cortical synaptosomes in Seahorse medium containing glucose plus pyruvate was recorded, followed by addition of oligomycin (2 μg/mL), FCCP (4 μM in the presence of BSA) and in (C and D) rotenone (2 μM) plus myxothiazol (2 μM), as indicated. (A and B) The experiment was designed according to the manufacturer’s recommended ideal conditions, not allowing [O₂]_M to deplete by more than 50 mmHg. Data points show the mean ± sem of values from 11 wells from four independent plates. (C and D) Double density plating of synaptosomes resulted in oxygen depletion during uncoupled respiration. Data points show the mean ± sem of values pooled from 55 wells from three independent plates. (B and D) Gray squares, noncorrected oxygen consumption rate calculated as mean −d[O₂]_M/dt for each measurement cycle; black diamonds, mean corrected OCR(t) calculated using the rate constants given in Table 1 for polystyrene plates. Note that in ‘ideal conditions’ (B) noncorrected and corrected relative oxygen consumption rates overlap, but in (D) the noncorrected values substantially deviate from (A) or from the corrected OCR(t) (black diamonds). The noncorrected rates are overestimated because of (a) rejecting data points corresponding to very low [O₂] and (b) O₂ depletion in the walls.

The experiment was repeated using a greater amount of synaptosomes per well (20 μg protein), which caused substantial depletion of O₂ in the chamber volume and in the walls (Figure 7C and D). In this case, the experiments were finished by adding rotenone (1 μM) plus myxothiazol (1 μM) to completely inhibit mitochondrial respiration. In this “extreme” case, the noncorrected oxygen consumption rate is burdened by artifacts resulting in overestimation of rates. First, (Figure 7Da) when anoxia is reached during the measurement period and the mean noncorrected respiration is calculated from data points before the anoxic period, only the beginning of the decay curve contributes to the mean, therefore the rates are biased toward higher values. Second, (b) when the respiration is suddenly inhibited after the chamber walls became O₂ depleted, the diffusion of [O₂] from the replenished chamber volume into the walls contributes to the noncorrected oxygen consumption rate. In contrast, the corrected OCR(t) traces were similar to the ones recorded in ideal conditions (Figure 7A), which we expect to best reflect the actual biology.

Biological Validation of the Correction Algorithm: The Absolute Oxygen Consumption Rate

We have shown above that the corrected OCR(t) is proportional to the amount of biological material in the well (Figure 5), and is devoid of time-dependent factors (Figures 2C, 3D, 4C, 6C and F), indicating that the corrected OCR(t) correctly reflects the relative biological oxygen consumption throughout the entire measurement period. Next, we assessed how the absolute magnitude of corrected OCR(t) relates to the actual biological respiration.

To determine the oxygen consumption rate per unit of biological specimen (e.g., mg of synaptosomal protein per well), OCR(t)·V_C is calculated. Because V_C can be greater than the geometric volume (see ), this value is determined experimentally by direct comparison of the same biological material under the same conditions in a closed chamber and the “semiclosed” system. In addition, the experimentally determined V_C works as a factor to correct proportional deviations in OCR(t) that may arise from inaccuracies in the model.

To calculate V_C, the respiration of the same biological material was measured with the XF24 instrument using the compartment model correction algorithm, and simultaneously in nearly identical conditions in a Clark electrode oxygraph. To minimize possible biological differences between plate-attached and suspension specimens, isolated mouse liver mitochondria respiring uncoupled on succinate (10 mM) in the presence of rotenone (1 μM), cytochrome c (10 μM) and FCCP (0.5 μM/no BSA) were used. This paradigm supports a minimalistic metabolic pathway to drive oxygen consumption since respiration can be maintained regardless of mitochondrial membrane integrity. This effectively minimizes the difference between attached and suspended mitochondria. The respiration rates measured in the Clark electrode respirometer and in the XF24 were 441 ± 56 nmol O.min⁻¹.mg⁻¹ and 19.5 ± 2.2 nmol O.μL⁻¹·min⁻¹·mg⁻¹, respectively. This comparison yielded V_C = 22.7 ± 2.5 μL (n = 4), in stark contrast to the geometric volume of the V7 microplates, which is 7 μL (according to the manufacturer).

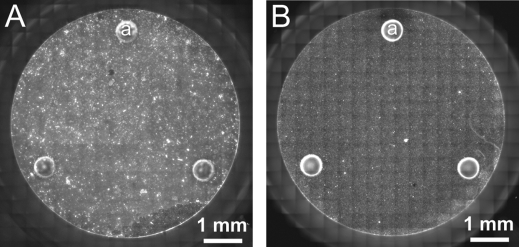
The O₂ sensor of the Seahorse flux cartridge measures [O₂] in a small spot close to the middle of the well (Figure 1B’). The size of the sensed area or volume is determined by the size of the probe (∼1 mm) and the lateral diffusion of O₂, thus it is significantly smaller than the bottom of the well. Therefore, one prerequisite of the calculation of oxygen consumption rate per mg protein is that the layer of mitochondria or synaptosomes (see below) is uniformly distributed on the well bottom. A uniform layer of respiring specimen is expected to produce laterally uniform changes of [O₂], therefore the oxygen consumption rate measured in units of concentration/time reflects the respiration of the total contents of the well enclosed in the V_C volume. Synaptosomes and mitochondria were stained with Mitotracker Red after the oxymetry was performed, and the bottoms of the wells were imaged with fluorescence microscopy. Figure 8 indicates that both synaptosomes and mitochondria formed fairly homogeneous layers, supporting the prerequisite for eq 15.

Figure 8.

Plate-attached synaptosomes and mitochondria distribute evenly on the bottom of the microplate wells. (A) Cortical synaptosomes plated at 10 μg protein/well or (B) isolated liver mitochondria plated at 2.5 μg protein/well were stained with Mitotracker Red, and the bottom of the well was imaged with fluorescence microscopy. (a) The round structures are the spacers (Figure 1A and B (g)) which set the height of the chamber.

Finally, the Clark electrode vs. XF24 comparison was repeated using cortical synaptosomes. Synaptosomes respiring on glucose plus pyruvate are bioenergetically more complicated than succinate-driven uncoupled mitochondria. Synaptosomal respiration relies on several factors that can affect oxygen consumption, including intact plasma and mitochondrial membranes, ATP turnover and signal transduction pathways. Therefore, they are more likely than isolated mitochondria to demonstrate respiration differences solely due to being adhered to the well bottom versus in suspension. The oxygen consumption rate values measured by the XF24 were converted into values per mg protein using the value of V_C = 22.7 μL determined above. Table 2 summarizes the comparison of synaptosomal respiration using the Clark electrode oxygraph and the XF24. While the basal respiration was faster as measured by the Clark electrode in suspension synaptosomes, the oligomycin-insensitive and uncoupled rates were similar between the two systems. This suggests a higher ATP turnover of free-floating synaptosomes in suspension compared to the compacted layer in the bottom of the XF24 V7 microplate (Figure 8A). At the end of the assay, succinate (10 mM) plus cytochrome c (10 μM) were added to the sample to enable respiration of contaminating mitochondria or broken mitochondrial membranes, which could not respire when glucose plus pyruvate were the substrates (because they lack the tricarboxylic acid cycle). The high succinate-driven respiration reflected the fact that synaptosomal preparations contain substantial amounts of free (broken) mitochondria.^7,15 The insignificant difference found between the oxygraph methods for the oligomycin-insensitive, uncoupled, and succinate-driven rates, where the possibility of biological differences between the suspension and spun-down synaptosomes is minimized, further validates the V_C value determined above.

Table 2. Synaptosomal Respiration Measured by Clark Electrode Oxygraph Compared to the XF24^a.

condition	XF24 noncorrected oxygen consumption rate (nmol O/mg protein)	XF24 corrected oxygen consumption rate (nmol O/mg protein)	Clark electrode oxygen consumption rate (nmol O/mg protein)
basal respiration (glucose)	6.25 ± 0.51	34.3 ± 1.5	54.6 ± 2.7b
oligomycin (2 μg/mL)	4.31 ± 0.23	23.9 ± 0.9	32.5 ± 4.0ns
FCCP (4 μΜ)	29.3 ± 2.4	157 ± 14	140.8 ± 7.6ns
succinate + cytochrome c	61.0 ± 3.1	318 ± 18	267.8 ± 9.3ns

^aOxygen consumption rate is given as mean ± sem per mg of unlysed synaptosomal protein determined by Bradford assay from n = 3 synaptosomal preparations. The non-corrected oxygen consumption rate is given as −d[O₂]_M/dt times V_C = 7 μl (geometric volume of entrapped medium in XF24 V7 microplates). Corrected oxygen consumption rate in the polystyrene XF24 V7 microplates was determined using the time constants in Table 1 and using V_C = 22.7 μl. ns, not significant.

^bp < 0.05 significance by paired t-test comparing corrected oxygen consumption rate and Clark electrode values.

Conclusions

Here we have described an algorithm to correct distortions of oxygen consumption rate measurements by O₂ diffusion and storage in open or “semiclosed” oxygraphs such as plate-based respirometers. We have optimized the algorithm working with the [O₂] data provided by the Seahorse XF24 extracellular flux analyzer. The optimization procedure revealed that the major cause of the distortion (decay) in the measured, noncorrected oxygen consumption rate is the combined effect of sensor response time and buffering of [O₂] by the walls of the chamber. Repletion of the O₂ from the atmosphere accounts for the slower component of the decay of the noncorrected oxygen consumption rate traces.

Advantages and Limitations

The corrected oxygen consumption rate values reflect the true biological respiration per unit of biological material plated into each well of the XF24 V7 microplate. The compensation for the decay of the oxygen consumption rate trace enables accurate measurement of respiration over any measurement time. This has two implications. First, slow rates can be more accurately measured over longer measurement periods, while fast rates may require a short measurement period to avoid anoxia. Using the correction algorithm short and long measurement cycles can be freely combined, whereas longer measurement periods introduce underestimation without using the correction algorithm. Second, in cases when anoxia is reached during a measurement period, the corrected oxygen consumption rate can be accurately calculated from the period before the onset of the anoxia. Without correction such truncation of the data (taking only early time points of a measurement cycle) results in overestimation of the oxygen consumption rate. Moreover, the correction algorithm prevents fouling the oxygen consumption rate value by O₂ depleted chamber walls, which typically happens when respiration is inhibited after fast, uncoupled respiration driving the chamber to low [O₂], leading to overestimation of low rates.

The algorithm amplifies noise because of the differentiation step required to compensate for the slow sensor response. The time constants depend on the plate (chamber) and sensor geometry and material, therefore the optimization procedure would have to be reperformed should any dimensions or materials of the chamber change. In contrast, the optimization does not depend on the actual biological material, so the time constant for a given plate/sensor can be universally used for all specimens.

The correction algorithm resolves changes of oxygen consumption rate within a measurement cycle, enabling a highly dynamic and “continuous” monitoring of oxygen consumption rate similar to a closed chamber Clark electrode measurement. Using continuous rate determination instead of linear fitting the whole measurement periods enables quantification of initial or maximal respiration in addition to the mean oxygen consumption rate measurements. This is important when rates are biologically decaying, as typically observed during fully uncoupled respiration in synaptosomes or cell cultures.

Further Implications

Due to oxygen diffusion from the atmosphere into the sample the continuous oxygen consumption rate measurement is extended well beyond the availability of O₂ in the entrapped volume. As the specimen depletes O₂ in the surrounding volume (V_C), the diffusion from the atmosphere increases, and a dynamic equilibrium is reached when the diffusion matches the oxygen consumption rate. Therefore, in samples with smaller oxygen consumption rate than the maximal diffusion capacity ≈k_AC[O₂]_OV_C = 0.78 nmol O.min⁻¹/well (for the polystyrene microplates), the measurement periods can have arbitrary lengths. When the chamber volume is entrapped for a longer period of time, the specimen will reach an equilibrium [O₂]_C, which is defined by the oxygen consumption rate and plate material. This phenomenon can be further exploited in experimental design for keeping cell cultures in predefined low [O₂] environments.

Notably, the diffusion phenomena demonstrated in XF24 V7 microplates is not a unique feature of respirometry measurements, but also regulate O₂ availability in regular tissue culture plates under normal cell culture conditions. Our results emphasize that local [O₂] in a respiring monolayer of any cell culture could be very different from the ambient [O₂]. Knowledge and/or awareness of the actual [O₂] that the cell monolayer is subjected to could be critical for properly interpreting or optimizing conditions for particular biological effects or cell-based assays, respectively. For example, assays either measuring or dependent on the HIF1α pathway would be significantly affected by the supply of O₂ at the cell monolayer interface.

In summary, the correction of the oxygen consumption rate with the compartment model for O₂ storage and diffusion described here greatly enhances the accuracy of plate based respirometry, and widens the operating conditions of these instruments. If applied properly, the useful range of [O₂] in the chamber and durations of measurements can be maximized.

This manuscript originally posted ASAP on June 25, 2009. A correction was made to equation 13, and this corrected manuscript posted ASAP June 29, 2009.

Supporting Information Available

Additional experimental details and references. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States