Summary
Regulatory networks controlling bacterial gene expression often evolve from common origins and share homologous proteins and similar network motifs. However, when functioning in different physiological contexts, these motifs may be re-arranged with different topologies that significantly affect network performance. Here we analyze two related signaling networks in the bacterium Bacillus subtilis in order to assess the consequences of their different topologies, with the aim of formulating design principles applicable to other systems. These two networks control the activities of the general stress response factor σB and the first sporulation-specific factor σF. Both networks have at their core a “partner-switching” mechanism, in which an anti-sigma factor forms alternate complexes either with the sigma factor, holding it inactive, or with an anti-anti-sigma factor, thereby freeing sigma. However, clear differences in network structure are apparent: the anti-sigma-factor for σF forms a long-lived, “dead-end” complex with its anti-anti-sigma factor and ADP, whereas the genes encoding σB and its network partners lie in a σB-controlled operon, resulting in positive and negative feedback loops. We constructed mathematical models of both networks and examined which features were critical for the performance of each design. The σF model predicts that the self-enhancing formation of the dead-end complex transforms the network into a largely irreversible hysteretic switch; the simulations reported here also demonstrate that hysteresis and slow turn off kinetics are the only two system properties associated with this complex formation. By contrast, the σB model predicts that the positive and negative feedback loops produce graded, reversible behavior with high regulatory capacity and fast response time. Our models demonstrate how alterations in network design result in different system properties that correlate with regulatory demands. These design principles agree with the known or suspected roles of similar networks in diverse bacteria.
Keywords: sigma factor, sporulation, design, stress, feedback, bistability
Introduction
The ability of cells to respond to environmental stimuli with differential gene expression is key to the diversity of life. One approach to understand the dynamic and functional properties of such responses involves studying the organization of the signaling networks that control them. Even though the underlying diversity of these networks is enormous, some common motifs are repeated in different contexts 1; 2; 3; 4; 5. In many cases this appears to reflect divergent evolution from a common origin, since these network motifs comprise modules assembled from homologous proteins.
Upon close examination, differences become evident even in apparently similar networks that function in different physiological contexts. These differences can be divided into parametric or structural categories. Parametric differences have to do with variability of biochemical parameters whereas structural differences have to do with variations in network organization, such as additional reactants, interactions or reactions. The structural variations are thought to reflect more significant evolutionary changes and therefore are more likely to correlate with specific physiological demands on the network. To reveal such correlations and the underlying design principles of the biochemical circuitry, we have used the method of mathematically controlled comparison 6; 7; 8; 9. This method facilitates the analysis of network performance by concentrating on structural differences; it introduces mathematical constraints to ensure that the observed differences in systemic behavior of alternative designs are a result of differences in network topology rather than accidental differences in the values of the kinetic parameters. Here we examine the key features in the designs for the partner-switching networks that regulate activity of the σB and σF sigma factors in the bacterium Bacillus subtilis. This partner switching mechanism is widely distributed among eubacteria and can be configured to accomplish different signaling tasks 10; 11; 12; 13; 14; 15. In B. subtilis it regulates two sigma factors, σB and σF, each of which controls a distinctive stress response.
σB controls a general stress regulon encoding more than 150 products that protect against diverse future challenges (reviewed in Refs. 11; 16). This general stress response is triggered by a broad array of energy and environmental stimuli, and loss of σB function leads to increased sensitivity to acid, cold, heat, ethanol, osmotic and oxidative stress 17. The response is readily reversible, providing the cell with a flexible, moderate answer to growth-limiting stresses. By contrast, σF is one of five specialized sigma factors that control the sporulation process, an essentially irreversible program marked by an asymmetric division that produces two cell types, a mother cell and a smaller forespore, each with a different developmental fate (reviewed in Refs. 18; 19). The sporulation process is induced by a combination of nutritional, cell density, and DNA replication signals, and it results in the production of a metabolically inert endospore that is highly resistant to damage by heat, desiccation, solvents, and UV light. Significantly, σF is key to this process, and its specific activation in the forespore compartment initiates a chain of events that leads to activation of subsequent sigma factors in both the mother cell and forespore 18; 19.
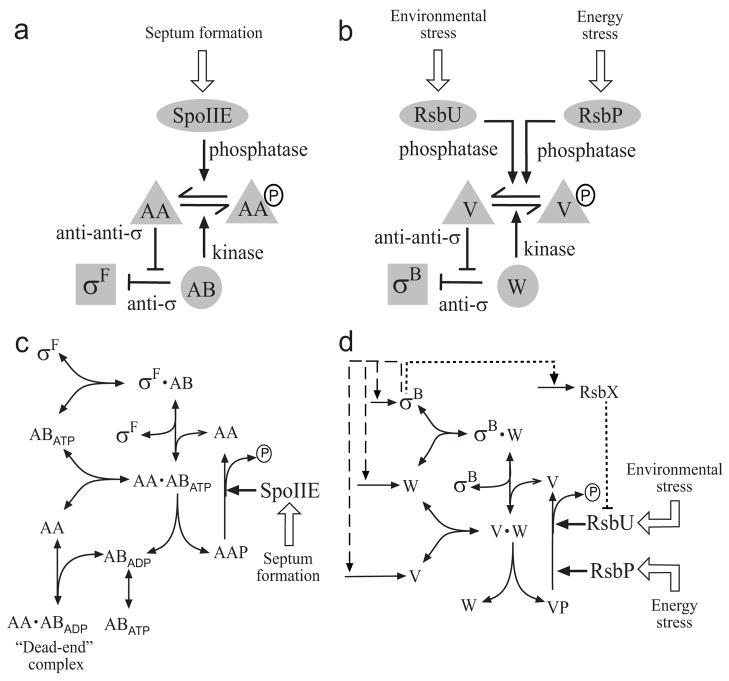
The activities of σF and σB are controlled by similar signaling networks that function via the partner-switching mechanism (for reviews see Refs. 11; 18; 19; 20). The essential feature of this mechanism is the control of protein-protein interactions by means of serine or threonine phosphorylation. The implementation of this mechanism in the σF and σB networks is shown in Fig. 1a and b. Free sigma factor is capable of associating with RNA-polymerase core (not depicted in Fig. 1) and activating transcription of the sigma-specific regulon. Prior to receiving the activation signal, an anti-sigma factor (either SpoIIAB or RsbW; henceforth abbreviated AB or W) binds to its respective sigma factor and prevents its association with RNA polymerase, turning the system OFF. Under these conditions, the anti-sigma factor also acts as a serine kinase that phosphorylates its cognate anti-anti-sigma factor (either SpoIIAA or RsbV; AA or V); the phosphorylated form of the anti-anti-sigma factor has low affinity for the anti-sigma factor and they quickly dissociate. This kinase activity of the anti-sigma factor (either AB or W) requires the presence of ATP in its catalytic site; during phosphorylation ATP is hydrolyzed to ADP, which must be exchanged for another ATP before the next round of phosphorylation. In the cartoon models shown in Fig. 1, specificity in signal reception is largely provided by an input phosphatase and is governed by the association of a particular N-terminal sensing domain with a C-terminal PP2C domain 11; 18; 19. This specific phosphatase (either SpoIIE or RsbP/U) activates the anti-anti-sigma factor by dephosphorylating it, thereby turning the system ON. The unphosphorylated anti-anti-sigma factor attacks the anti-sigma/sigma factor complex to induce sigma factor release. Thus, in both networks the level of sigma factor capable of binding to RNA polymerase is determined by the interplay between phosphorylation and dephosphorylation of the anti-anti-sigma factor.
Fig. 1.
Conceptual (a, b) and kinetic (c, d) models of the partner-switching networks regulating σF and σB. For simplicity, only one subunit of the anti-sigma factor dimer is shown, and binding of sigma to RNA polymerase core is omitted as it does not affect the partner-switching equilibrium (see Modeling Procedures). (a) Level of free σF is determined by the level of unphosphorylated SpoIIAA anti-anti-sigma (AA), where P indicates serine phosphate (see text). Activity of the SpoIIE phosphatase in the forespore increases upon formation of the asymmetric sporulation septum, turning the system ON. (b) Level of free σB is determined by the level of unphosphorylated RsbV anti-anti-sigma (V). Activity of either the RsbU environmental phosphatase or the RsbP energy phosphatase increases when a stress is perceived, turning the system ON. (c) Formation of a long-lived, dead-end complex in the σF network. The SpoIIAB anti-sigma factor (AB) with ATP in its catalytic site can phosphorylate and release the AA anti-anti-sigma factor, leaving AB associated with ADP in a non-catalytic complex. The binding of another AA molecule locks AB in this state. (d) Feedback loops in the σB network. Genes encoding σB, its anti-sigma RsbW (W) and anti-anti-sigma V lie in the σB-controlled sigB operon. The resulting feedback loops are shown by dashed lines. An additional feedback loop through the RsbX phosphatase, which acts indirectly via the environmental-stress branch of the network, is shown by the dotted line. Each of the nodes containing W and its complexes are assumed to be in equilibrium, with a mixed population of ATP, ADP and nucleotide-free forms, so no explicit nucleotide exchange is shown.
Although the networks controlling σF and σB share the core of the partner switching mechanism, genetic, biochemical and biophysical studies have identified several important differences that are not conveyed by the simple models shown in Fig. 1a and b. Some of these differences are parametric. For example, the equilibrium dissociation constants of ATP and ADP with the anti-sigma factor are in the micromolar range for AB whereas they are in the millimolar range for W 21; 22; 23; 24. This is thought to render the kinase activity of W sensitive to the ATP concentration within the cell, thereby providing an additional mechanism for sensing energy stress that complements the RsbP energy phosphatase. In addition to these parametric differences, significant structural differences exist between the networks, and these structural differences are our focus here:
Presence of a long-lived complex in the σF network (see Fig. 1c). After phosphorylation and release of the AA anti-anti-sigma factor, the AB anti-sigma factor has ADP in its catalytic site. Binding another molecule of AA then locks AB-ADP in a long-lived complex incapable of exchanging ADP for ATP, and therefore incapable of phosphorylating AA to free itself 21; 25; 26; 27; 28. Under these conditions, AA must dissociate in order to allow AB to exchange ATP for ADP, which permits the reaction cycle to resume. In our previous paper 29 we referred to this long-lived complex as a “dead-end” complex. Such a dead-end complex was originally identified by biochemical analysis of AA-AB, and was not found by similar analysis of the corresponding V-W regulators in the σB network 21; 22; 24; 25; 28; 30. These results argue that the complex of V, W and ADP is capable of rapid exchange of ATP for ADP without requiring the prior dissociation of V, and, therefore, is neither long-lived nor dead-end.
Feedback loops regulate the synthesis of core components of the σB network (see Fig 1d, dashed lines). Genes encoding σB and its partner-switching regulators V and W lie within a σB-controlled operon 31, thereby manifesting both positive and negative feedback loops that would operate under either energy or environmental stress. In contrast, the spoIIA operon encoding AA, AB and σF is transcribed in predivisional cells by a non-cognate sigma factor, σH19. Therefore, no such feedback loops exist at the time of asymmetric septum formation, when σF is initially activated in the forespore compartment. A later round of read-through transcription from the upstream dacF gene does extend into the spoIIA operon, and this later round is under σF (and subsequently σG) control 32; 33; 34; 35; 36. However, dacF transcription does not commence until 2.5 hours after the asymmetric septum is formed. Thus this potential autocatalytic feedback loop is not relevant for the commitment-to-sporulation switch we are considering here.
An additional negative feedback loop is present exclusively in the environmental-stress branch of the σB network (see Fig. 1d, dotted line). Here the activity of the environmental-stress phosphatase, RsbU, is indirectly down-regulated by the RsbX feedback phosphatase, a component of another partner-switching network (not shown) that modulates RsbU 37; 38; 39; 40; 41. The gene encoding RsbX also lies within the σB-controlled operon that encodes σB and its network partners V and W 31.
We and others have recently published mathematical models of the σF regulatory network 29; 42. The comparison of these two models is beyond the scope of this work and will be presented elsewhere. Nonetheless, while there are clear differences in the assumptions that underlie the two models, the essential conclusions of our work discussed here and in Ref. 29 are not significantly affected. Here we modify our previous σF model to describe the partner-switching mechanism of the σB network. To elucidate the impact of the three structural differences outlined above, we performed a series of mathematically controlled comparisons in which one or another key element of each model was altered and tested for its effect on network performance. The results of this analysis suggest that the differences in network organization correlate closely with their different physiological roles.
Results
By incorporating biochemical, biophysical and genetic data from the literature we constructed mathematical models of the σB and σF signaling networks. (For details of the modeling procedures and parameters assigned to the various reactions, please see the Modeling Procedures section.) Such modeling integrates all the relevant system components, imposes important thermodynamic constraints, and uses uniform criteria to characterize the steady state and dynamic performance of each network. Our goal was to elucidate the role and physiological consequence for each of the distinctive topological elements in the two networks. We therefore analyzed the performance of each network individually, using a series of mathematically controlled comparisons between a wild-type network and various hypothetical alternative designs in which one of the topological elements was altered.
Role of dead-end complex formation
An essential feature of the σF network is the formation of a long-lived, non-catalytic “dead-end” complex between the AB anti-sigma factor, its AA anti-anti-sigma factor, and ADP 21; 22; 25; 26; 27; 28. We have previously shown29 that this dead-end complex causes the σF network to behave as an essentially irreversible hysteretic switch. This system property was associated with the self-enhancing formation of the dead-end complex: higher concentrations of dephosphorylated AA lead to higher concentrations of the non-catalytic complex at the expense of the active, phosphorylating complex, leading to even higher concentrations of dephosphorylated AA and of the dead-end complex (see Ref. 29 for a discussion). Here we ask whether the dead-end complex shapes other network properties independently from its contribution to hysteresis. To this end we analyze mathematical models that either include or exclude the formation of the complex (see the Modeling Procedures section for details).
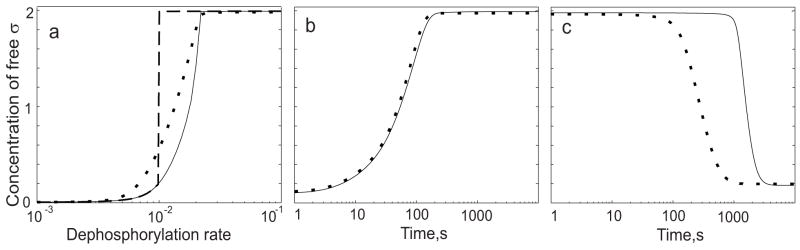
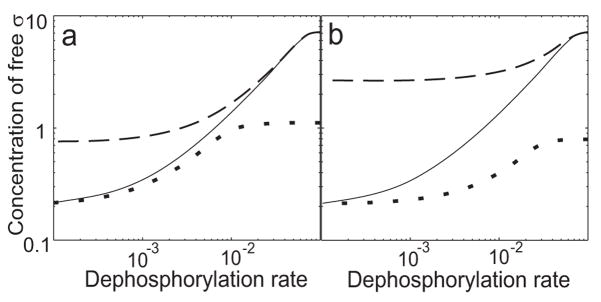
For comparison purposes we repeat part of our earlier analysis29 in Fig. 2a. In this panel, dashed and solid lines show the steady-state concentration of free sigma factor in the wild type network, expressed as a function of the rate of AA anti-anti-sigma dephosphorylation. This rate is a key determinant of σF activity in cells. That is, increased phosphatase activity (together with depletion of the AB anti-sigma in the forespore compartment) serves to convey the morphological signal of asymmetric septum formation to activate expression of σF-dependent genes 19; 20; 43. In this simulation, the concentration of AA anti-anti-sigma factor was chosen to exceed that of the AB anti-sigma factor (considered as a monomer) by 50% – the excess necessary for hysteretic bistability 29.
Fig. 2.
Comparison of σF networks with (dashed or solid lines) and without (dotted line) dead-end complex formation using parameter values that allow hysteresis ([AA]=1.5[AB]=9μM; [σF]=2μM) (a) Steady-state concentration of free sigma factor as a function of dephosphorylation rate. Under these conditions, when [AA] is in 50% excess to [AB], the network with the dead-end complex possesses two stable steady states, depending on system history. For comparison, only one steady state is possible for the network without the complex (see text). (b) Dynamic response of free sigma factor to a step increase in rate of dephosphorylation. (c) Dynamic response of free sigma factor to a step decrease in the rate of dephosphorylation. Note that the time axes in kinetic plots (b and c) are represented with a logarithmic scale.
As we showed previously 29, at intermediate dephosphorylation rates there are two stable, steady-state solutions for the concentrations of the network partners. The system can end up in either state depending upon the initial conditions. The solid line in Fig. 2a shows the steady-state solution corresponding to an initially OFF condition; this is the steady state for a low rate of dephosphorylation, with very little dead-end complex formed and most of the sigma factor in a complex with the AB anti-sigma factor. The dashed line in Fig. 2a shows the final steady-state solution corresponding to an initially ON condition; this is the steady state for a high rate of dephosphorylation, with most of the AA in the dead-end complex with the AB anti-sigma and most of the sigma factor free. The two stable steady states only exist for a range of dephosphorylation rates: at the boundaries of this range, the concentration of free sigma factor jumps from one branch of the solution to the other.
In our earlier modeling study this hysteretic behavior was shown to be associated with the self-enhancing formation of the dead-end complex coupled to the amount of dephosphorylated AA anti-anti-sigma factor 29. To further test this argument mathematically and to see if dead-end complex formation has other effects on steady-state response, we compared the response of an otherwise similar network that only lacks the possibility of forming the complex. This alternative network was chosen to be as close to the reference system as possible, i.e. to produce the same concentration of free sigma factor at high and low rates of dephosphorylation (see Modeling Procedures for details). As shown by the dotted line in Fig. 2a, the network lacking the dead-end complex has a graded (continuous) response with only one stable steady state, corresponding to the rate of dephosphorylation. This strong effect of the dead-end complex on the steady-state properties of the system is in accord with the results of our earlier study.
In addition to these bistable steady-state properties, our earlier study 29 also predicted that the dynamic behavior of the system strongly contributes to the largely irreversible nature of σF activation: its partner-switching network is much faster to turn ON then to turn OFF. Here we ask whether this network property relates to the existence of the dead-end complex by comparing the transient responses of σF networks with and without this complex. Fig. 2b shows the dynamic behavior of sigma factor activity (i.e., amount of free sigma factor) in response to a step increase in the rate of dephosphorylation for networks with (solid line) and without (dotted line) formation of the dead-end complex. The time to turn ON sigma activity is about the same for both networks, with the network lacking the dead-end complex being slightly faster. By contrast, Fig. 2c shows the dynamic behavior of sigma factor activity in response to a step decrease in the rate of dephosphorylation for networks with (solid line) and without (dotted line) the dead-end complex. Significantly, the time to turn OFF sigma activity is much longer for the network containing the dead-end complex. For the network with the dead-end complex, the OFF time scale is determined by the lifetime of the complex, whereas for the network lacking the complex, the time scale is determined exclusively by the phosphorylation rate of the system. On the basis of the comparisons shown in Figs 2, we conclude that the presence of the dead-end complex has a marked effect on both the steady-state and dynamic properties of the σF signaling network.
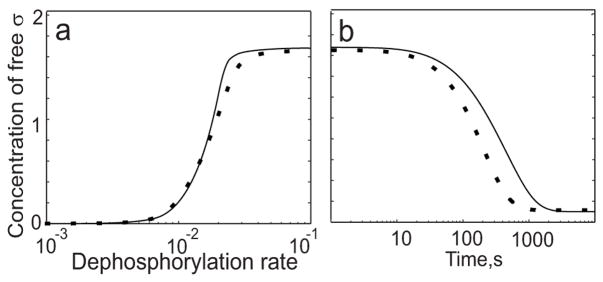
Does this strong influence of the dead-end complex require conditions that promote hysteresis? Our model predicts that a 50% or greater excess concentration of AA anti-anti-sigma factor over AB anti-sigma factor is needed for hysteretic behavior to be observed. However, no reliable in vivo concentration measurements exist for these important parameters (see Ref.29 for discussion). Therefore, it was important to investigate the properties of the σF network using parameter values that do not lead to hysteretic bistability in order to determine if there might be other roles for the dead-end complex. For these simulations the concentration of AA anti-anti-sigma factor was chosen to be equal to that of the AB anti-sigma factor (considered as a monomer); under these conditions hysteresis is absent 29. As expected from our previous study, with these parameter values the σF network displays a graded steady-state response lacking hysteresis (Fig. 3a, solid line). The network without the possibility of forming the dead-end complex produces a very similar response (Fig. 3a, dotted line). Thus the steady-state effect of the dead-end complex is dependent on parameter values. However, formation of the dead-end complex still slows the transient response when turning OFF σF activity even in a network lacking hysteresis (Fig. 3b). In response to an instant decrease of the dephosphorylation rate, the network lacking the dead-end complex (Fig. 3b, dotted line) turns OFF several-fold faster than the σF network with the dead-end complex (Fig. 3b, solid line). These effects of the dead-end complex on the dynamic properties of the network are therefore at least partly independent from hysteresis.
Fig. 3.
Comparison of σF networks with (solid line) and without (dotted line) dead-end complex formation using values that preclude hysteresis ([AA]=[AB]=6μM; [σF]=2μM). (a) Steady-state concentration of free sigma factor as a function of dephosphorylation rate. Under these conditions when [AA] is equal to [AB], the network with the dead-end complex possesses only one stable steady-state; the network without the complex performs similarly. (b) Dynamic response of free sigma factor to a step decrease in the rate of dephosphorylation (compare to Fig 2c).
Role of autocatalytic feedback involving σB
The genes encoding the stress-response factor σB and two of its network partners lie in a σB-controlled operon resulting in three feedback effects: (i) the activation of σB synthesis by the sigma factor itself is a positive feedback effect; (ii) the concomitant up-regulation of the W anti-sigma factor, which binds and inactivates σB, is a negative feedback effect; and (iii) the up-regulation of the V anti-anti-sigma factor releases σB from W, thereby creating another positive feedback effect. The overall sign of the feedback depends on the values of the parameters that characterize these three processes. Delumeau et al. 24 demonstrated that σB and its network partners are found in similar ratios both before and after stress, with a two- to three-fold excess of W and V monomers over σB. These ratios are required by the stoichiometry of the partner switching mechanism – W functions as a dimer that binds two molecules of V or one molecule of σB 24. We incorporated this observation into our model (see Modeling procedures). In Appendix A we also investigate the physiological consequences of a violation of this assumption, i.e. what will happen when one of the partner switching regulators is removed from σB control. To elucidate how these feedback mechanisms influence the systemic properties of the σB network, we performed mathematically controlled comparisons of the reference model with an alternative model lacking feedback effects, i.e. a system in which the synthesis of σB and its network partners are controlled by another, hypothetical sigma factor and are therefore independent of σB activity (see the Modeling Procedures section for details). For simplicity we show only the analysis of the V-W-σB autocatalytic feedback loops under energy stress conditions, i.e. when the special environmental feedback via RsbX is absent. Similar conclusions are obtained regarding the effect of V-W-σB feedback under environmental stress conditions (data not shown).
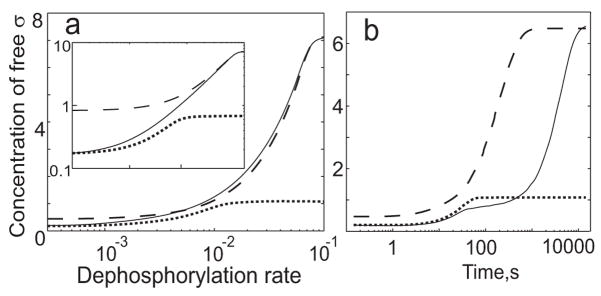
The results for the reference system (Fig. 4a, solid line) show the steady-state concentration of free sigma as a function of the V anti-anti-sigma dephosphorylation rate. For the alternative system lacking feedback, it apparently is not possible to match both the pre-stress and maximum-stress activities of sigma to those of the reference system. We therefore compared the reference system with two alternatives: one in which we match the pre-stress level of free sigma factor and the other in which we match the maximum-stress level. The results for the first alternative (Fig. 4a, dotted line) show that matching the pre-stress level of free sigma leads to a lower post-stress level, whereas the results for the second alternative (Fig. 4a, dashed line) show that matching the maximum-stress level of free sigma leads to a higher pre-stress level. Thus, in the absence of feedback effects, the network exhibits a trade-off between high levels of free sigma in the maximum-stress condition and low levels in the pre-stress condition, and the capacity for regulation (the ratio between the maximum and the minimum levels of free sigma factor) is less than that of the reference system. Note that depending on the choice of the alternative system and the value of dephosphorylation rate, the level of free σB for the alternative systems can be either above or below the level of free σB for the reference system (Fig. 4a). Thus, the overall influence of the feedback on the system output can be either positive or negative depending on the parameter values.
Fig. 4.
Comparison of σB networks with and without feedback resulting from σB-dependent transcription of the operon encoding σB and its network partners. These simulations were done under energy stress conditions to focus on the contribution of the V-W-σB feedback loop. (Fig. 5 separately addresses the contribution of the RsbX feedback loop in the environmental signaling branch.) The solid line corresponds to the reference (wild type) system with feedback present. The dashed line corresponds to an alternative system without feedback in which the rate of protein synthesis is set to match the level of free sigma at high dephosphorylation rates. The dotted line corresponds to an alternative system without feedback in which the rate of protein synthesis is set to match the level of free sigma at low dephosphorylation rates. (a) Steady-state concentration of free sigma as a function of the dephosphorylation rate. The insert shows the same curve plotted with log-log scales. (b) Dynamic response of free sigma following a step increase in the rate of dephosphorylation.
The intuitive reason for this trade-off is as follows. If no feedback is present, the total concentrations of sigma factor, anti-sigma factor and anti-anti-sigma factor proteins are fixed. Matching the maximum-stress level of sigma factor activity requires a high total concentration of network proteins whereas matching the pre-stress level requires a low total concentration. Under pre-stress conditions, even when all of the V is phosphorylated, a certain concentration of σB is free from the W anti-sigma. According to our simulations, an increasing fraction of σB escapes from W with an increasing total concentration of proteins. Thus at the high total concentrations needed to achieve maximum-stress levels of activity, the pre-stress activity of σB is disproportionately high (Fig. 4a, dashed line).
In addition to examining these steady-state effects, we also compared the dynamics of sigma factor release in the reference system with the same two alternative systems following a step increase in the rate of phosphorylation from the pre-stress level ( ) to the maximum-stress level ( ). The results (Fig. 4b) show that the alternative systems without feedback reach their steady state faster than the reference system with feedback. The dynamic response of the reference system occurs on two timescales. The initial response time is determined by the dephosphorylation rate, and the concentration of free sigma quickly reaches the total concentration of sigma factor in pre-stressed cells. In contrast, the second response time is determined by the rate of transcription/translation of σB operon products, and the concentration of free sigma eventually reaches the total concentration of sigma factor in maximum-stressed cells. The same trend is seen for the dynamics of sigma factor inactivation following a step decrease in the rate of dephosphorylation (results not shown). This is consistent with other studies showing that inducible catabolic systems with positive feedback are slower to respond than otherwise identical systems lacking such feedback 6; 44.
Thus, our comparisons indicate that the existence of the autocatalytic feedback loops with V, W and σB contribute to both the steady-state and dynamic properties of the network. The physiological consequences of these results are addressed in the Discussion section.
Role of negative feedback involving RsbX
The feedback mechanisms considered thus far operate on the σB network when activated by either energy or environmental stress. However, there is an additional feedback that operates exclusively in the environmental signaling branch of the network (Fig. 1d). Here the activity of the RsbU phosphatase (which dephosphorylates the V anti-anti-sigma in response to environmental stress) is modulated by another partner-switching mechanism involving the RsbX feedback phosphatase 37; 38; 39; 40; 41. The gene for RsbX also lies within the σB-controlled sigB operon, and increasing RsbX levels have a negative effect on RsbU activation. This has led to the proposal that RsbX serves to damp the environmental stress response and prevent continuous signaling during sustained stress 38; 39.
We investigated the role of this RsbX-dependent feedback mechanism by means of mathematically controlled comparisons. We compared the reference system that includes negative feedback via RsbX to an alternative system in which the RsbX concentration (or equivalently, the rate of its synthesis) is held constant independent of sigma factor concentration. The results were most dramatic when comparing the dynamics of σB activation following a step increase in the rate of V anti-anti-sigma dephosphorylation. Fig. 5 shows the dynamic response of the reference system (solid line) and that of two alternative systems. One alternative (dashed line) corresponds to the case in which RsbX concentration is held constant at the pre-stress level of the reference system; the other (dotted line) corresponds to the case in which RsbX concentration is kept constant at the maximum-stress level of the reference system. For the latter alternative there is a good match to the reference in both the pre- and maximum-stress levels of free sigma factor, but the dynamics of moving from one stress condition to the other are very different. In the absence of RsbX-dependent negative feedback, the time dependence of the increase in sigma factor concentration is monotonic. However, if the feedback is present as in the reference system, the concentration of sigma factor first overshoots the steady-state level found at maximum-stress, then gradually decreases to reach it. This time dependence results in a fast initial rate of sigma factor-dependent synthesis of stress proteins followed by a slower, steady-state synthesis (data not shown). We conclude that the RsbX negative feedback contributes to the ability of the network to mount a rapid response to a sudden environmental stress while retaining the ability to maintain the steady state response appropriate for the continued presence of such a stress. This is consistent with other studies showing that repressible biosynthetic systems with negative feedback are faster to respond than otherwise identical systems lacking such feedback 6; 44.
Fig. 5.
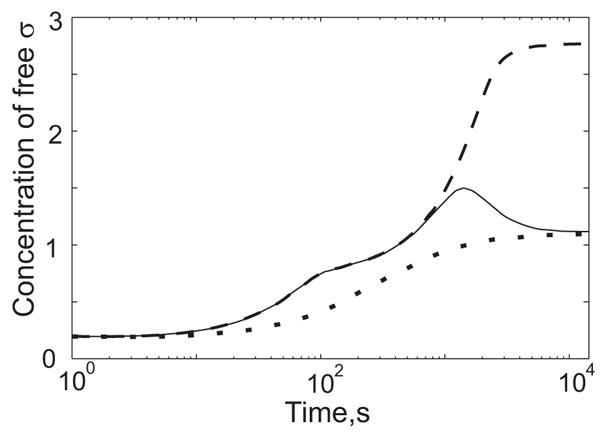
Comparison of σB networks with and without negative feedback involving RsbX. These simulations were done under environmental stress conditions. The dynamic behavior of the concentration of free sigma factor in the reference (wild type) system with negative feedback (solid line); in the alternative system without feedback and the RsbX concentration kept constant at the pre-stress level of the reference system (dashed line); and in the alternative system without feedback and the RsbX concentration kept constant at the maximum-stress level of the reference system (dotted line).
Discussion
Essential modeling results are consistent with the physiological role of each network
Results of the mathematically controlled comparisons indicate how differences in σF and σB network organization result in qualitative differences in both the steady-state and dynamic behavior of each network. Additionally, inspection of the steady-state and dynamic properties of the reference (wild-type) systems in Figures 2–5 does allow direct comparison of the two networks, using common criteria. However, by itself such a direct comparison cannot reveal the fundamental basis of any difference in performance, and therefore it is not very illuminating. In contrast, the mathematically controlled comparisons of reference and alternative networks as performed here associate these differences in performance with differences in network topology. We find these associated differences correlate well with the roles the networks play in the normal physiology of the organism.
Long-lived dead-end complex in the σF network
Our mathematical comparisons between σF networks with and without formation of the long-lived, non-catalytic AA-AB-ADP complex extend our previous analysis regarding the role of this complex in determining fundamental system properties: hysteresis and slow turn-OFF kinetics 29. The simulations reported here demonstrate that these are the only two properties associated with dead-end complex formation. As a consequence of hysteresis, different threshold signals are required to turn ON or turn OFF expression of σF-dependent genes, as we described previously. Moreover, the simulations shown in Fig. 2c indicate that even after reducing the dephosphorylation rate below the OFF threshold, the dynamics of turning off the system with the dead-end complex are much slower. In contrast, the network lacking the dead-end complex shows a graded response with faster OFF times. It should be noted that the slower turn-OFF of the σF network with the dead-end complex is observed even for parameter values that result in a graded steady-state response, i.e., hysteresis is absent (Fig. 3b). Therefore, of the two network properties associated with dead-end complex formation, hysteresis is more dependent on parameter values than is slower turn-OFF.
As we argued previously 29, these results make sense from a physiological point of view because the σF network controls a cell-fate decision. Once the asymmetric septum is formed, the decision to sporulate soon becomes irreversible 45 and the entire developmental program should be executed. Therefore, once σF activity is turned ON, it should be robustly protected from turning OFF due to fluctuations in kinetic parameters such as the rate of dephosphorylation. The slow temporal responsiveness of the system provides an additional level of protection by “filtering out” transient fluctuation in the values of kinetic parameters that might otherwise result in deactivation of σF. In contrast, σB activity is required to turn ON and OFF quickly in response to external conditions, and this readily reversible behavior correlates with the absence of a long-lived dead-end complex in the σB network.
Autocatalytic feedback in the σB network
The σB network possesses autocatalytic feedback loops resulting from σB-dependent control of the operon encoding V, W and σB. Our analysis shows that, depending on the choice of parameter values, the activity of σB for the system with autocatalytic feedback can be either above or below the σB activity for the system lacking this feedback. However, independent of these specific parameter values, the capacity for regulation (defined as the ratio between the maximum and the minimum levels of free sigma factor) is larger for the system with these feedback loops compared to the system lacking feedback. Therefore, we predict that autocatalytic feedback will reduce the trade-off that exists between a low, pre-stress level of σB activity and a high, maximum-stress level of activity (Fig. 4a). Physiologically, the σB network must accommodate energy and environmental stresses that are highly diverse in both a qualitative and quantitative sense. The data of Akbar et al. 46 suggest that peak σB activity varies linearly with increasing ethanol stress. Presumably, higher levels of stress require higher σB activity, and indeed, under high-stress conditions σB-directed gene expression can account for 25% of total cellular protein synthesis 47. On the other hand, inappropriate activation of σB, such as during exponential growth in unstressed cells, has a deleterious effect on growth and survival 48. It is therefore important for the σB network to have a high capacity for regulation.
We argue that high capacity for regulation, while essential for the σB network, is irrelevant for the initial function of σF network, which results in a digital ALL or NONE decision to activate σF in the forespore compartment and to keep it inactive in the mother cell. Additional physiological roles for σF later in forespore development may involve a subsequent increase of σF activity that autoregulation from the upstream dacF promoter could provide32; 33; 34; 35; 36. However, our simulations show that the initial role of σF in establishing differential gene expression between the two compartments and in making the commitment to sporulation does not need autocatalytic feedback. In accord with this hypothesis, mRNA transcribed from the σF-dependent dacF promoter does not appear until 2.5 hours after septum formation32; 34, well past the critical point at which the cell fate decision has been made 19; 45. Indeed, the role of this later, autoregulated transcription is presently unclear, because its interruption has no noticeable effect on sporulation 34.
As a further link between feedback and the physiological role of the σB network, the temporal adaptation of the network containing this feedback has two stages, fast and slow (Fig. 4b). Due to the presence of the slow stage, the response is not as rapid as for the alternative system lacking feedback. However, when the systems are matched so they have the same level of pre-stress activity, the system with feedback is initially slower but actually achieves a significantly higher level of free sigma within a few minutes of stress exposure. Having such a two-stage response might allow the cell to generate sufficient σB activity on the fast timescale (to prevent deleterious consequences from a stress) while avoiding inappropriate generation of a full-scale stress response by transient signals.
The autoregulatory feedback in our σB model is implemented as a combination of two positive loops (upregulation of σB and V expression) and one negative loop (upregulation of W expression), with the network partners synthesized in nearly constant stoichiometric ratios. We argue that these loops are not completely independent from one another, and an appropriate balance among the players is necessary for the mechanism to work properly. To address this point, we investigated the consequences of removing individual feedback loops, as described in Appendix A. We conclude that presence of both positive feedback loops is essential for high regulatory capacity, i.e. if the expression of V is removed from σB control, regulatory capacity is significantly reduced. On the other hand, the existence of negative feedback via W is essential for the graded response of the σB network. If expression of W is removed from σB control, the network behaves as an ALL-or-NONE bistable switch, which, after activation, becomes insensitive to the rate of dephosphorylation. Thus all three components of the autoregulatory feedback are essential for its physiological role.
RsbX feedback in the σB network
The environmental branch of the σB signaling network contains an additional negative feedback mechanism involving RsbX. The system with this feedback manifests a non-monotonic dynamic release of σB (Fig. 5). A physiological rationale for such a non-monotonic response appears to reflect two different demands on a stress-signaling network. When cells are first exposed to an environmental stress they must quickly synthesize the stress-response proteins that help them adapt to the new condition. However, when cells are subjected to prolonged environmental stress, they must continue to synthesize the stress-response proteins at a lower rate to replace those lost by damage and by dilution due to cell growth. It is clear that the network without the RsbX-dependent negative feedback could produce either (i) a rapid initial response coupled with too high a level of σB activity for prolonged stress (dashed line on Fig. 5), or (ii) a slower initial response coupled with an appropriate steady-state level of σB activity (dotted line). From this perspective, the systems with the RsbX-dependent negative feedback appear to have optimized both the rapid initial response and the appropriate prolonged response.
Therefore, the negative feedback mechanism involving RsbX is physiologically beneficial during a prolonged stress response controlled by the σB network. Why then does RsbX feedback operate only on the environmental branch of the σB network? We speculate that, in contrast to environmental stress, under energy stress it is more important to be efficient than fast, and overshooting is therefore not the best strategy.
Contrasting roles and mechanisms of feedback in the σB and σF networks
Positive feedback at the transcriptional level is often associated with bistable hysteretic behavior leading to the lock-ON of a developmental switch 49; 50; 51; 52 Indeed, as part of the B. subtilis sporulation process, positive feedback tuned to morphological events serves to enhance transcription of the genes encoding σG and σK, the final two sigma factors controlling forespore and mother cell gene expression 19. In contrast, the lock-ON of σF activity is achieved at the posttranslational level – the positive feedback is the result of the self-enhancing formation of the dead-end complex. Such a design guarantees an ALL or NONE steady-state response and fast dynamics to the turn-ON of σF activity on a biochemical time-scale. On the other hand, once turned ON, σF activity is protected from accidental turn-OFF by the long lifetime of the dead-end complex. While beneficial for the σF network, this design would be a disadvantage for the σB network. Activation of σB should be easily reversible and tunable to the magnitude of stress because excessive σB activity is deleterious for cell growth48. Apparently at odds with this requirement for reversibility, the positive feedback that results from autogeneous regulation of the operon encoding V, W and σB would at first seem to parallel the classic bistable hysteretic switch, with its all or none behavior49; 50; 51; 52. However, our simulations show that despite this autoregulation, the σB network displays continuous (graded) response over a wide range of input signals and does not manifest bistability (Fig 4a). Such performance is in accord with the physiological demand and is ensured by a critical aspect of network design: positive feedback in the σB network is partially counteracted by a negative one, namely the parallel up regulation of the synthesis of the W anti-sigma factor, which binds and inactivates σB. Indeed, elimination of this negative loop appears to convert the network into a bistable switch (Appendix A). What selective advantage might this elaborate feedback scheme confer? We have identified two physiologically beneficial effects of the autogenous regulation of sigB: increased capacity for regulation and a two-stage kinetic response. These effects apply equally to σB activation via the energy or environmental stress pathways. An additional negative feedback loop acting only in the environmental branch (via RsbX) gives rise to a non-monotonic dynamic response, which would elicit a burst-like synthesis of gene products needed to counteract the initial stress.
Autoregulatory feedback loops are conserved in homologous partner-switching networks that control a general stress response
Our modeling study suggests that the presence of autocatalytic feedback serves to increase the regulatory capacity of a partner-switching network. This increased capacity would be most useful in a network that must respond to diverse stresses of unpredictable magnitude, such as those that induce the general stress response. To ask whether this correlation between network architecture and physiological role could be extended to other Gram positive bacteria, we compared the structures of operons encoding σB or σF orthologs. In each case, autocatalytic feedback was inferred to be present in those operons implicated in a general stress response. The results of our survey are presented in Tables 1 and 2 and discussed in Appendix B. The main conclusions are briefly summarized below.
Table 1.
Autoregulation of sigB operons in other gram-positive bacteria
| Bacteria | SigB Function | Operon Structure | Autoregulation established |
|---|---|---|---|
| Bacillus licheniformis | General stress | pA RSTU pB? VWBX | By sequence analysis only68 |
| Listeria monocytogenes | General stress | pA RSTU pB VWBX | Ref.83 |
| Staphylococcus aureus | General stress | pA U pB VWB | Ref.84 |
| Bacillus cereus | General stress | pB VWB | Ref.73 |
| Bacillus anthracis | General stress | pB VWB | Ref.76 |
Table 2.
Autoregulation of several sigB-like factors in S. coelicolor
Despite considerable variations of sigB operon structure among the low-GC Gram-positive bacteria, the striking feature of the general stress operons is the conservation of an apparently irreducible core: rsbV (encoding the V anti-anti-sigma), rsbW (W anti-sigma), and sigB (σB), all linked in an autocatalytic, σB dependent transcription unit (Table 1). We therefore argue that unless there was selective pressure to maintain this network architecture, it would almost certainly be lost 53; 54. We conclude from this comparison of B. subtilis and its close relatives that networks associated with the general stress response must benefit from the presence of autocatalytic feedback.
Our prediction regarding a correlation between autocatalytic feedback and general stress is further extended by considering examples of partner-switching networks from Streptomyces coelicolor, a bacterium phylogenetically distant from B. subtilis. Even though differentiation and stress response networks in S. coelicolor are highly interrelated 55; 56, one may conclude that at least two sigma factors that participate not only in differentiation but also in a broader stress response are subject to complex autoregulation, with positive and negative feedback loops (Table 2 and Appendix B).
Can autoregulation of a partner-switching network be viewed as a signature of a general stress response function? The contrasting bacterial differentiation function controlled by partner switching primarily appears to be a cell fate decision that represents a digital ALL or NONE response. Thus, in this case there may be no physiological need for an increased regulatory capacity that would require autoregulation. As we have discussed, autoregulation does not impact the σF network at the time of asymmetric septum formation, when cell fate is decided. In the absence of experiment, it is not possible to rule out an immediate role for autoregulation in similar σF networks that operate in related bacteria. However, as a first approximation, the genes encoding the AA, AB and σF proteins in these bacteria all appear to be transcribed from a σH-like promoter directly upstream from the three-gene cluster, as they are in B. subtilis (see Appendix B).
Proposed Experimental Tests of σB Model Predictions
Our simulations are consistent with the published data on the B. subtilis σB network. However, no experiments have been done specifically to test the predicted roles of the feedback loops in shaping its in vivo performance. Our results indicate that elimination of the positive autocatalytic feedback via RsbV or σB – or elimination of the autocatalytic feedback loops altogether – will lead to a reduced regulatory capacity and an altered dynamic response. On the other hand, elimination of the negative feedback via RsbW is predicted to transform the network into a bistable ALL-or-NONE switch. In addition, our model predicts that loss of negative feedback via RsbX will eliminate the non-monotonic dynamic response of σB activity seen during prolonged exposure to environmental stress.
We suggest that these predictions can be tested using mutants corresponding to the hypothetical ones modeled in this study. To construct these mutants, one or another of the genes encoding the network partners could be removed from the sigB operon and placed elsewhere on the chromosome, under control of an inducible promoter to allow matching the removed regulator to its normal pre- or post-stress level. The responses of these mutants to energy or environmental stress could then be measured indirectly using well-characterized, σB-dependent lacZ fusions. These fusion results may not exactly replicate the simulations, which were based in part on an estimated rate of dilution and degradation of the V-W-σB partners. However, the relative differences in regulatory capacity and response should be clear. For the strain lacking the RsbW feedback it may be necessary to reconstitute the relevant part of the network in E. coli to avoid lethality of the ON bistable state. Such a reconstitution has been successfully accomplished for another purpose.57
Conclusions
Our aim was to use kinetic modeling to determine how topological variations affect network performance and correlate with physiological function. We constructed mathematical models and analyzed the partner-switching networks that control activity of two B. subtilis sigma factors: σF and σB. We demonstrated that despite clear conservation in the core mechanism of the networks, relatively small changes in network design significantly affect their transient and steady-state behavior. We suggest that these observed variations in performance correlate with the physiological role of each network. In the course of our modeling work we focused on qualitative differences in performance that are likely to hold over a wide range of parameter values. Therefore, we expect that the relationships between network design and physiological role that we describe here will hold for similar networks in other bacteria.
Modeling Procedures
We previously constructed a mathematical model for the partner-switching network that controls activation of σF 29. Here we modify that model to describe the partner-switching mechanism of the σB network. To elucidate the impact of the structural differences between the two networks, we performed a series of mathematically controlled comparisons for each of these models, in which one or another critical topological element was altered.
It should be noted that the multiplicity of binding partners for the anti-sigma factor dimer complicates both models. For example, the σF model contains 27 species and 53 reactions, primarily due to the requirement to include the effects of slow nucleotide exchange from the dead-end complex. In contrast, the σB model can be reduced to 10 species and 19 reactions if equilibrium in all nucleotide binding reactions is assumed. Despite this apparent complexity, many of the reactions can be characterized by the same kinetic parameters due to symmetry between the two dimer subunits and other simplifying assumptions. Nonetheless, an explicit presentation of the differential equations for both models would be overly cumbersome. We therefore chose to formulate a set of reactions and describe the corresponding kinetic mechanisms. This information can be transformed into differential equations using publicly available software 58. SBML files with complete model descriptions are included in Supplemental Materials, and the independent kinetic parameters we used for both networks are summarized in Table 3.
Table 3.
Parameter values used in our simulations
| Parameter | Value, σB network | Value, σF network |
|---|---|---|
| 0.2 μM−1s−1 | 0.3 μM−1s−1 | |
| 0.5 μM−1s−1 | ||
| 5· 10−3 s−1 | 10−3 s−1 | |
| 10−3 s−1 | ||
| k3 | 5· 10−3 s−1 | 9.2 10−3 s−1 |
| 0.3 μM−1s−1 | ||
| 10−3 s−1 | ||
| k5f | 1 s−1 | |
| k5b | 0.2 s−1 | |
| 0.2 μM−1s−1 | 0.1 μM−1s−1 | |
| 5 · 10−3s−1 | 10−3s−1 | |
| 0.1 μM−1s−1 | 0.25 μM−1s−1 | |
| K | 0.1 μM | 0.1 μM |
| Kinh | 0.5 μM | |
| k9 | 7 · 10−4 s−1 | |
| 4· 10−3μM/s | ||
| 1· 10−5 μM/s | ||
| Ks | 2 μM |
Model reactions and notation
The reactions and notations used are summarized below (note that non-consecutive numbering of equations was chosen to keep the notation consistent with our previous paper 29):
-
Dephosphorylation of phosphorylated anti-anti-sigma factor:
(F.1) -
Reversible binding of anti-anti-sigma factor to anti-sigma factor with ATP in the catalytic site:
(F.2) -
Phosphorylation of the anti-anti-sigma factor and its subsequent dissociation:
(F.3) -
Reversible binding of the anti-anti-sigma factor to an ADP bound form of the anti-sigma factor, producing a dead-end complex:
(F.4) -
Reversible nucleotide exchange in the catalytic site:
(F.5) In the reactions above AB stands for one of the four states (ABT, ABD, ABTAA, ABDAA) and only the state of the second subunit of the dimer is allowed to change.
-
Binding of σF to an anti-sigma factor dimer subunit in either the ABT or the ABD state (denoted by ABN):
(F.6) -
Reversible displacement of σF by anti-anti-sigma factor:
(F.8)
Here we develop a framework that is also capable of describing the partner-switching network of σB and that allows comparison of both networks. Several important distinctions between the σF and σB networks are summarized in the Introduction. These require modification of the reaction scheme to describe the σB network. First of all, in contrast to the σF network, the presence of ATP or ADP is not required for binding between anti-sigma factor W and its partners 21; 22; 24; 25. Moreover, nucleotide exchange is faster and does not require dissociation of the V anti-anti-sigma from W. Therefore, we chose not to explicitly treat the nucleotide-binding state of W, assuming that equilibrium between the nucleotide pools is rapidly reached and that the subscripts can be dropped. Delumeau et al. 24 presented evidence indicating a higher affinity for the binding of a second V to the V-W-W complex. Therefore, the binding of the first and second V are treated as separate reactions. In order to model feedback arising from σB controlling transcription of its own operon, protein synthesis and degradation are taken into account. The resulting reactions are presented below:
-
Dephosphorylation of phosphorylated anti-anti-sigma factor:
(B.1) -
Reversible binding of the first anti-anti-sigma factor to anti-sigma factor dimer:
(B.2a) -
Reversible binding of the second anti-anti-sigma factor to the anti-sigma factor dimer:
(B.2b) -
Phosphorylation of the anti-anti-sigma factor and its subsequent dissociation:
(B.3) -
Binding of σB to an anti-sigma factor dimer:
(B.6) -
Reversible displacement of σF by anti-anti-sigma factor:
(B.8) -
Protein degradation is assumed to be a first-order process combining “dilution” due to cell growth and specific or non-specific degradation by proteases.
(B.9) where Pr is any protein or protein complex in the σB network. Since little is known about the differences in the lifetimes of the proteins and protein complexes for the σB network, we assume them all to be the same.
-
We assume that the synthesis rates for σB and its network partners are such that the proteins achieve concentrations near their stoichiometric ratios in the network:
(B.10) where aa stands for the amino acid pool, which is assumed to be constant. In the same fashion, we model synthesis of the RsbX protein (denoted X), which is involved in down-regulating the rate of VP dephosphorylation by RsbU, as
(B.11)
We chose not to explicitly include the binding of sigma to core RNA polymerase in our models. The available evidence indicates that σF and σB bind their cognate anti-sigma factors with at least ten-fold greater avidity than they bind to core 24; 30; 59; 60. Moreover, there is very little free core RNA polymerase in the cell -- most of it occupied in transcribing DNA. Therefore, the core-binding reactions can be ignored.
Reaction kinetic mechanisms and kinetic parameters for the σB network
The kinetics of association and dissociation of protein complexes, reactions (B.2a), (B.2b) and (B.6), are modeled as reversible mass action reactions. The corresponding rates of association and dissociations are denoted as and respectively; here and below the subscript i stands for the equation number of the corresponding reaction. The equilibrium dissociation constant is denoted . Delumeau et al. 24 used Surface Plasmon Resonance (SPR) to obtain rate constants for association and dissociation of W (the anti-sigma factor of the σB system) and its network partners. The results are of the same order of magnitude as the corresponding parameters of the σF system: and . Note that the equilibrium dissociation constants obtained from these measurements are quite high, e.g. K6 ~ 100 (nM). This indicates that around 25% of the sigma factor would be free if sigma and anti-sigma factor were mixed in a stoichiometric ratio with typical cellular concentrations of 1 μM. However, the results of independent experiments (Figure 2 of Delumeau et al. 24) show that less than 10% of anti-sigma factor (and sigma factor) remains free under such conditions. This discrepancy may reflect the tendency of SPR to overestimate dissociation constants 61; 62. To account for this possibility we chose to decrease the measured rates of dissociation by 10-fold. These reduced values are consistent with the data presented in Figure 2 of Delumeau et al. 24. Note that a similar reduction of dissociation rate was performed in our modeling of the σF network 29. The results of Delumeau et al. 24 further indicate stronger binding of the second anti-anti-sigma factor to the anti-sigma factor dimer, i.e. binding cooperativity. In order to account for this effect we chose to further reduce the dissociation constant of the second anti-anti-sigma factor by a factor of 5.
Delumeau et al. 24 measured the kinetics of anti-anti-sigma factor phosphorylation and found it to be linear in time. The turnover rate was found to vary from 1.0×10−3 s−1 to1.0×10−2 s−1, depending on ATP and ADP concentrations. Since this rate is much faster than the rate of complex formation, we use it to estimate the rate constant k3.
-
The dephosphorylation of the anti-anti-sigma factor is an enzymatic reaction performed by either of the two input phosphatases. Therefore, increase in phosphatase activity represents the signal for activating the transcription of σB-dependent genes. We model the rate of this dephosphorylation with a Michaelis-Menten-like expression:
(1) For the σB network, the activity of the RsbU environmental-signaling phosphatase is regulated by another partner-switch involving RsbX together with other proteins and protein complexes 37; 38; 39; 40; 41. Since very little biochemical data are available for this second partner switch, we choose not to model it explicitly but rather phenomenologically by modifying Eq. (1). The influence of RsbX on the activity of the phosphatase will be treated empirically as non-competitive inhibition:
(2) Here [X] stands for the concentration of RsbX and Kinh is the effective inhibition constant, which is equal to the concentration of RsbX that results is a 50% reduction in phosphatase activity.
-
Similar to our consideration of the σF network 29, we can then treat the kinetics of the exchange reaction (B.8) as second-order mass action with rate constants and for the forward and backward reactions respectively. As was the case in our σF model 29, as long as no energy is consumed, the law of detailed balance provides a relationship among the equilibrium constants irrespective of the actual mechanism:
(3) The degradation/dilution reaction (B.9) is described by first-order kinetics with rate constant k9. We used data from β-galactosidase assays to estimate the decay rate for proteins. Experiments of Kim et al. 63 show a 50% decrease in β-galactosidase specific activity following a 15 to 30 min exposure to stress. This gives k9~ log(2)/1000 ≈ 7.0×10−4 s−1.
-
We approximate the complex multi-step process of protein synthesis by reactions (B.10) and (B.11) as first order processes in which the rate (flux) of synthesis depends on the concentration of free sigma factor as follows
(4) Here is the rate of synthesis in the complete absence of σB activity; this reflects “priming” transcription from a σA-dependent promoter that regulates the upstream half of the σB operon and extends into the rsbV-rsbW-sigB-rsbX cluster 64. is the maximum rate of synthesis at saturating concentrations of sigma factor and KS is the concentration of sigma factor at which half the maximum rate of synthesis is achieved. These parameters are estimated as follows. Delumeau et al. 24 showed that sigma factor concentration increased by 4μM during the first 30 minutes of exposure to stress. This allowed us to estimate the rate of protein synthesis as k10≈ k11~ 2·4μM/1800s≈ 4.0 ×10−3 μMs−1, where we assume that protein synthesis occurred at half its maximum rate in the experiments of Delumeau et al. 24. To estimate KS we assumed it to be about one-half of the total concentration of RNA polymerase core in B. subtilis cells, KS ~ 2 μM. (We used 5000 RNA polymerase molecules per cell as in E. coli, and a cell volume of 1.8·10−15 liter). This value is consistent with the results of Rollenhagen et al. 60. In contrast, there is no available data on the flux from the priming transcription . We choose the value 1.0×10−5 μMs−1 more than two orders of magnitude smaller than . The exact value of this priming flux does not affect the main conclusions of our analysis because under pre-stress conditions the major contribution to sigB (σB) expression comes from the second term in Eq. (4): even when all of the V is phosphorylated, a certain fraction of σB is free from the W anti-sigma. This free σB then sets the basal expression level for the rsbV-rsbW-sigB-rsbX cluster via the σB-dependent promoter preceding rsbV. This interpretation of the relative importance of priming vs. autocatalytic transcription is consistent with the data presented in Fig. 2 of Delumeau et al. 24 and in Fig. 6 of Wise and Price 64. This latter study showed that elimination of priming transcription did not impact activation of σB by energy stress. Although this value for priming transcription does not play a signifcant role in our reference system, it does affect the performance of the alternative networks considered in Appendix A.
The parameters used for numerical calculations are assembled in Table 3. For comparison we also included parameters for the σF network estimated in 29
Mathematically controlled comparison of alternative designs
In order to reveal how variations in network design affect the physiological performance of signaling we used a technique known as mathematically controlled comparison 6; 7; 8; 9. This technique introduces mathematical constraints to ensure that the differences observed in the systemic behavior of alternative designs are a result of the specific differences in the network organization rather than of accidental differences in the values of the kinetic parameters.
In addition to differences in the values of the kinetic parameters, there are three major structural differences between the networks controlling σB and σF. As described in the Introduction section, these differences correspond to structural elements present in one network but absent in the other:
In the σF network, formation of a long-lived, dead-end complex involving anti-sigma factor, its anti-anti-sigma factor, and ADP.
In the σB network, autocatalytic feedback involving σB regulation of the operon containing the genes for sigma factor, anti-sigma factor, and anti-anti-sigma factor.
In the σB network, a negative feedback involving σB regulation of the synthesis of RsbX protein, which indirectly inhibits dephosphorylation of the anti-anti-sigma factor during environmental stress.
To analyze the physiological consequence of these structural differences we performed three mathematical controlled comparisons. For each of the differences (i)–(iii) we chose the wild-type network as a reference system and compared it to an alternative design – a “mutant” network lacking this element. To ensure that any functional differences between the two can be attributed to differences in network organization and not to differences in parameter values, we compared the systems under conditions of internal and external equivalence. Internal equivalence requires that the values of the corresponding parameters in the reference and alternative systems are the same. External equivalence requires that the systemic performance of the reference and alternative systems are made to match as closely as possible by suitably adjusting the values of the unique parameters, which represent degrees of freedom in the alternative system. After having introduced these constraints, we compared the two designs in terms of steady-state and transient responses. Specifically, we computed the steady-state concentration of free sigma factor as a function of the rate of anti-anti-sigma factor dephosphorylation and the sigma factor dynamics following a sudden increase (or decrease) in . Below we summarize comparisons I–III corresponding to differences i–iii:
-
We chose as the reference system the σF model that is characterized by reactions (F.1)–(F.8) and used the parameter values estimated from biochemical data 29. As the alternative system we chose a system lacking formation of the long-lived complex, i.e. where anti-sigma factor has very little affinity for ADP, resulting in very rapid nucleotide exchange after phosphorylation. Formally, this system can be characterized by reactions (F.1), (F.2), (F.6), (F.8) and an effective phosphorylation reaction similar to (B.3):
(5) In this alternative system we essentially have only ATP bound in the catalytic site of AB. To emphasize the difference (i) we ignored protein synthesis and degradation. To ensure internal equivalence we assigned the same values for the corresponding kinetic parameters in the two systems, namely for those found in reactions (F.1), (F.2), (F.6), and (F.8). For external equivalence, first we required both systems to have the same (or similar) steady-state concentration of free sigma factor at very low and very high rates of anti-anti-sigma factor dephosphorylation . These conditions were satisfied if we chose the total concentration of the corresponding proteins in the two networks to be the same. Second, we required both systems to make the transition between low- and high-sigma levels at the same rate of anti-anti-sigma factor dephosphorylation: 50% of free σF in the alternative system is achieved at the geometric mean of the bistability region in the reference system. This second condition allowed us to determine the rate constant for the phosphorylation reaction (5) in the alternative system. For our simulations we had to decrease the catalytic rate of phosphorylation three-fold to have the alternative network without the dead-end complex activate at the same dephosphorylation signal as the wild-type network with the complex.
We chose as the reference system the σB model that is characterized by reactions (B.1)–(B.9) with the kinetics described by (1), (3) and (4). This model includes the feedback manifested by sigma-factor dependent transcription of the genes encoding sigma (σB), its anti-sigma (W), and its anti-anti-sigma (V). As the alternative system we chose the system lacking this feedback, which is characterized by reactions (B.1)–(B.10) with the kinetics described by (1) and (3) but with a constant rate of protein synthesis (i.e., independent of sigma-factor concentration as opposed to equation (4)). For internal equivalence, we assigned the same values for the corresponding kinetic parameters in the two systems, namely for reactions (B.1)–(B.9). For external equivalence, we required both systems to have the same steady-state concentration of free sigma either in the low-stress condition (slow dephosphorylation of anti-anti-sigma) or in the high-stress condition (fast dephosphorylation of anti-anti-sigma). Either of these conditions was sufficient to fix the rate of protein synthesis V10 in the alternative system. Each of these alternative systems was compared to the reference system, as shown in the Results section.
We chose as the reference system the full σB model that is characterized by reactions (B.1)–(B.11) with the protein synthesis rate given by Eq. (4) and with dephosphorylation rate given by Eq. (2). Under environmental stress, this model includes (i) specific feedback via RsbX-mediated inhibition of the RsbU environmental signaling phosphatase activity as well as (ii) general feedback via the sigma factor on the synthesis of sigma, anti-sigma, and anti-anti-sigma. As the alternative system we chose the system lacking feedback via RsbX, which is characterized by the reactions (B.1)–(B.10) but with a constant RsbX concentration. For internal equivalence, we assigned the same values for the corresponding kinetic parameters in the two systems, namely for those in reactions (B.1)–(B.10). For external equivalence, we required both systems to have the same steady-state concentration of free sigma either in the low-stress condition (slow dephosphorylation of anti-anti-sigma) or in the high-stress condition (fast dephosphorylation of anti-anti-sigma). Either of these conditions was sufficient to fix the concentration of RsbX in the alternative system. Each of these alternative systems was compared to the reference system, as shown in the Results section.
Software
Calculation of steady-state and dynamic responses was done using MATLAB© (MathWorks Inc, Natick, MA) and the Gepasi program 65; 66; 67. SBML files for the models are available for download from Supporting Information.
Supplementary Material
Acknowledgments
We thank Richard Losick for his helpful discussions and comments on the manuscript. This work was funded in part by grants from the US Public Health Service to MAS (RO1-GM30054) and CWP (RO1-GM42077).
Appendix A: Interplay of autocatalytic feedback loops
In response to both energy and environmental stress, expression of the last four genes in the sigB operon (rsbV-rsbW-sigB-rsbX) is autogenously regulated by σB and (indirectly) by its co-transcribed network partners, V and W 11. In Fig. 4 we focused on the overall contribution of this feedback to the system properties of the network. Here we examine the individual contributions of the two positive loops (upregulation of σB and V synthesis when σB is activated by stress) and the one negative loop (similar upregulation of W synthesis). The available experimental data suggest that σB and its network partners are synthesized in similar stoichiometric ratios before and during the stress response24. Here we investigate why such a design may have emerged in the course of natural selection. Simulations of the steady state performance of the network were done in alternative networks, which are hypothetical mutants in which one of the three genes encoding the partner proteins (σB, V or W) was removed from σB control and placed in a separate, σB-independent transcription unit. Results were then calculated at different levels of constitutive expression for the removed gene. For clarity we performed the simulations under energy stress conditions, in which the RsbX negative feedback loop makes no contribution to the outcome.
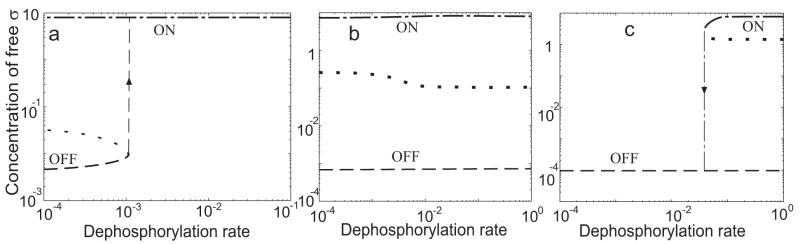
As shown in Fig. 4a of the main text, elimination of all three feedback loops significantly decreases capacity for regulation, i.e. introduces a trade-off between pre-stress and maximum-stress levels of sigma factor. The presence of both positive components of the feedback is required for the wide regulatory capacity characteristic of the wild type network. If the expression of V is removed from σB control, the regulatory capacity of the system is significantly reduced (Fig. 6a); the same effect is obtained if the expression of σB is removed (Fig. 6b).
Fig. 6.
Removal of either positive autocatalytic loop affects steady state performance of the σB network. (a) Elimination of σB control of V expression leads to reduced regulatory capacity. The reference (wild-type) steady state response is shown by a solid line. Dashed and dotted lines correspond to maximum- and pre-stress levels of V expression, respectively. (b) Elimination of σB control of σB expression also leads to reduced regulatory capacity. Line designations are as in panel a, but here dashed and dotted lines correspond to maximum- and pre-stress levels of σB expression.
Notably, eliminating the negative component of the feedback by removing W expression from σB control leads to even more drastic changes in system performance. As shown in Fig. 7, the σB network without W feedback behaves as an ALL-or-NONE bistable switch. The three panels (a–c) correspond to three different values of W synthesis flux, a parameter that significantly affects both the qualitative and quantitative behavior of the mutant network. This parameter would vary depending upon the strength of the promoter controlling the hypothetical σB-independent transcription unit containing the W gene. Fig. 7a depicts the case for low flux – a level of W synthesis only slightly higher than that resulting from priming transcription in wild-type cells, i.e. in the complete absence of any basal σB activity (see Modeling procedure for details). Fig. 7b shows the case for intermediate flux – the level of W synthesis corresponding to the pre-stress level of W in wild-type cells. Here W concentration will be substantially higher than for panel (a) but much lower than for panel (c). Fig. 7c shows the case of high flux -- the level of W synthesis corresponding to the maximum-stress level of W in wild-type cells. Here the flux is comparable to that found in the wild type system when the σB promoter is saturated.
Fig. 7.
Elimination of σB control of W expression results in ALL or NONE bistability in the σB network. Stable steady state solutions are shown by dashed (OFF) and dash-dotted (ON) lines whereas an unstable steady state between the two stable states is shown by the dotted line. The OFF state corresponds to a low level of σB, as would result from expression of its structural gene when the σB–dependent promoter of the sigB operon is not activated. The ON state corresponds to a high level of σB, as would result when the σB–dependent promoter of the sigB operon is fully activated by stress. (a) For low W expression (1.2×10−4 μMs−1) the network displays two stable steady states only at low dephosphorylation rates; at high rates only the ON state exists. An irreversible transition from OFF to ON can be induced by an increasing dephosphorylation rate, as indicated by the up arrow. (b) For intermediate W expression (5×10−4μMs−1) the network displays two stable steady states over the entire range of dephosphorylation rates. (c) For high W expression (3×10−3μMs−1) the network displays two stable steady states only at high dephosphorylation rates; at low rates only the OFF state exists. An irreversible transition from ON to OFF can be induced by a decreasing dephosphorylation rate, as indicated by the down arrow. See text for details.
The two stable steady states in each panel of Fig. 7 are labeled ON and OFF. In the OFF state the concentration of free σB is so low that the genes encoding σB and V are expressed only at minimum levels by means of priming transcription. In the ON state the concentration of free σB is so high that the genes encoding σB and V are expressed at their maximum rate. The intuitive explanation of these results is as follows. For the simulations shown in Fig. 7a, W concentrations were chosen to be just slightly higher than that of σB and V when the latter are expressed via priming transcription. This ratio of W to σB is sufficient to keep sigma inactive at low V dephosphorylation rates. However, with increasing dephosphorylation rates, more σB is released from W and the σB-dependent promoter controlling σB and V gene expression becomes more active. This results in a multifold increase in the flux of σB and V synthesis. Thus, once the network moves to the ON state it becomes nearly insensitive to dephosphorylation rate because the concentration of the W anti-sigma is insufficient to control σB activity. The same explanation would hold for the ON state shown in Fig. 7b, with its intermediate levels of W. However, in contrast to Fig. 7a, the OFF steady state in Fig. 7b is stable for all dephosphorylation rates as there would not be enough dephosphorylated V anti-anti-sigma present initially to counteract the higher level of W anti-sigma factor. So for the parameters chosen in Fig. 7b, variations of dephosphorylation rate will not affect the steady state of the system and it would remain in the initial condition, either ON or OFF. The simulations shown on Fig. 7c are done with high W concentrations, corresponding to the level of W expression in stressed wild-type cells. As might be expected, the above arguments concerning the extreme stability of the OFF state in Fig. 7b are still valid: this state is insensitive to changes in the dephosphorylation rate. On the other hand, the ON state now only exists for high dephosphorylation rates because the concentration of W in this simulation is comparable to the concentrations of σB and V when their genes are expressed from the fully activated σB-dependent promoter of the operon. Therefore, only when enough V is dephosphorylated to attack the W-σB complex will the ON state be achieved. Once the dephosphorylation rate decreases below a certain threshold, the system irreversibly jumps from the ON to the OFF state.
It should be noted that the bistability observed in the σB network, when the negative component of the autocatalytic feedback is eliminated, differs from the hysteretic bistability observed in the σF network because of the self-enforcing formation of the dead-end complex. In the latter case the network displays bistability only for an intermediate range of dephosphorylation rates and, therefore, σF activity can be turned ON and OFF with physiological levels of change in the dephosphorylation rate. Even though the turn OFF kinetics of the σF network are very slow, given enough time after a significant decrease in the dephosphorylation rate the network will go back to the OFF state. In contrast, the bistability observed in Fig. 7 is not hysteretic as a function of the dephosphorylation rate, which is the physiological input signal for this system. ON (panel a), OFF (panel c), or both ON and OFF (panel b) steady states exist for all values of the dephosphorylation rate; transitions out of these states cannot be induced by changes in this rate, although such transitions might still be induced by changes in other parameters or by stochastic fluctuations. In any case, such a design is not easily controllable and will not be physiologically meaningful for the stress response function.
The sum of these simulations shows that the correct balance of the V-W-σB autoregulatory feedback loops is crucial for the proper functioning of the σB network, with its high regulatory capacity and graded response.
Appendix B: Autoregulatory feedback loops in homologous partner switching networks
With the help of mathematical modeling we demonstrated that the presence of autocatalytic feedback loops serves to increase the regulatory capacity of a partner-switching network. We suggest that this increased capacity would be most useful in a network that responds to diverse inputs of various magnitudes, such as those that activate a general stress response. By contrast, increased regulatory capacity is not a requirement for the initial functioning of a partner-switching network that controls a cell fate decision. To ask whether this design principle could be extended to similar networks in other Gram positive bacteria, we conducted a literature survey to correlate the presence of autocatalytic loops with the physiological roles of σB and σF factors and their network partners.
The results of this literature survey are presented in Tables 1 and 2 and in the discussion below. Notably, the structure of the sigB operon varies considerably among the low-GC Gram-positive bacteria, with different numbers of rsb (regulator of sigma-B) genes linked to the sigB structural gene (Table 1). These different linkage arrangements reflect the diversity of mechanisms that control the PP2C input phosphatases. For example, Bacillus licheniformis 68 and Listeria monocytogenes 69 possess the same operon structure as B. subtilis (Table 1). Based on the B. subtilis model, the rsbRST module in these organisms would encode a second partner switch that controls the RsbU environmental phosphatase, and the rsbX gene would encode a feedback phosphatase that damps continued signaling through this switch 11. By contrast, in Staphylococcus aureus the RsbU phosphatase is controlled by a mechanism which remains to be determined, but which clearly differs from the B. subtilis model: the rsbRST module and the rsbX feedback phosphatase are missing from the Staphylococcus operon, and indeed from the entire genome 70; 71. Similar conclusions can be reached for the related S. epidermidis sigB operon 70; 72. In yet another variation, the gene for the input phosphatase of B. cereus, called rsbY, lies in a separate transcription unit downstream from the sigB operon 73; 74. RsbY phosphatase activity is thought to be controlled by a two-component system, with a CheY-like response-regulator domain covalently linked to the phosphatase domain. Consistent with this different input, the B. cereus genome encodes no rsbRST module, and no rsbX feedback phosphatase 75. The related B. anthracis sigB operon has a similar structure76.
For the organisms listed in Table 1, σB activity is known to be induced by diverse stresses, which constitutes the hallmark of a general stress response. Consistent with this role, one striking feature of these operons is the conservation of an apparently irreducible core: the rsbV anti-anti-sigma gene, the rsbW anti-sigma gene, and sigB, all linked in an autocatalytic, σB dependent transcription unit subject to the same feedback loops we modeled here for the B. subtilis network. This conservation is maintained despite the variability of genes both upstream and down from the core. We therefore argue that unless there was selective pressure to maintain this network architecture, it would almost certainly be lost. We conclude from this comparison that for B. subtilis and its close relatives, partner switching networks associated with a general stress response must benefit from the presence of immediate autocatalytic feedback.
By contrast, the two key features of the σF network are the presence of the dead-end complex and the absence of autocatalytic feedback at the time the cell fate decision is made. Neither of these features can be established without experiment. However, to a first approximation, we will take similar promoter and gene arrangement in related bacteria as presumptive evidence for a lack of autoregulation early on. The B. subtilis spoIIA operon (defined here as the spoIIAA-spoIIAB-sigF gene cluster) is initially transcribed from a σH-dependent promoter preceding spoIIAA 19 and subsequently from the σF/σG–dependent dacF promoter further upstream 32; 33; 34. From the work of Park and Yudkin 77 and our own inspection of genomic sequences (not shown), it can be inferred that the spoIIA operons of representative Bacillus, Clostridium and Paenibacillus species are also under σH control (B. coagulans, B. licheniformis, B. megaterium, B. sphaericus, B. stearothermophilus, C. acetobutylicum, C. tetani, and P. polymyxa). Thus for B. subtilis and its close relatives, the networks associated with the control of the first compartment-specific sporulation factor (σF) apparently lack the immediate autocatalytic feedback loop found in the networks associated with the general stress factor (σB).
This correlation between immediate autocatalytic feedback and general stress is strengthened by considering partner switching networks from Streptomyces coelicolor, a high-GC Gram-positive bacterium phylogenetically distant from the low-GC B. subtilis. The complex lifecycle of this bacterium is reflected in the extraordinary signaling and regulatory capability encoded in its large genome, including the structural genes for 66 sigma factors 78; 79. Among these, nine or ten are σB homologs, and four are particularly relevant to our discussion (Table 2). The σB, σL, and σM factors form an interesting regulatory cascade, with σB involved in both the general stress response and differentiation, whereas σL and σM seem to be primarily involved in differentiation 56. Of these, only σB is clearly autoregulated, with the rsbA anti-sigma factor and sigB structural genes in one σB-dependent transcription unit and the rsbV anti-anti-sigma factor gene in another 80. Thus the positive and negative autocatalytic feedback loops are maintained even with the separation of rsbV from its network partners. By contrast, sigL and sigM are apparently not autoregulated, but instead comprise part of a sigma cascade of σB → σL → σM 56. The case of S. coelicolor σH is equally striking. The sigH gene is located in an operon together with the ushX gene encoding its anti-sigma factor 81. This operon is expressed from at least two promoters: P1 is σH-independent and is active during differentiation whereas P2 is σH-dependent and is active during osmotic stress 82. Thus sigH expression appears to be regulated by both positive and negative feedback loops during stress response but not during differentation. It is clear that the differentiation and stress response networks in S. coelicolor are highly interrelated 55; 56, and the mechanisms controlling sigma factor activity are not fully understood. However, one may conclude that sigma and anti-sigma pairs that participate not only in differentiation but also in a broader stress response are subject to autoregulation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wall ME, Hlavacek WS, Savageau MA. Design of gene circuits: lessons from bacteria. Nat Rev Genet. 2004;5:34–42. doi: 10.1038/nrg1244. [DOI] [PubMed] [Google Scholar]
- 2.Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, Zeitlinger J, Jennings EG, Murray HL, Gordon DB, Ren B, Wyrick JJ, Tagne JB, Volkert TL, Fraenkel E, Gifford DK, Young RA. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- 3.Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: Simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. [DOI] [PubMed] [Google Scholar]
- 4.Conant GC, Wagner A. Convergent evolution of gene circuits. Nat Genet. 2003;34:264–266. doi: 10.1038/ng1181. [DOI] [PubMed] [Google Scholar]
- 5.Yeger-Lotem E, Sattath S, Kashtan N, Itzkovitz S, Milo R, Pinter RY, Alon U, Margalit H. Network motifs in integrated cellular networks of transcription-regulation and protein-protein interaction. Proc Natl Acad Sci USA. 2004;101:5934–5939. doi: 10.1073/pnas.0306752101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Savageau MA. Biochemical systems analysis: a study of function and design in molecular biology. Addison-Wesley Pub. Co; Reading, Mass: 1976. [Google Scholar]
- 7.Voit EO. Canonical nonlinear modeling: S-system approach to understanding complexity. Van Nostrand Reinhold; New York: 1991. [Google Scholar]
- 8.Alves R, Savageau MA. Extending the method of mathematically controlled comparison to include numerical comparisons. Bioinformatics. 2000;16:786–798. doi: 10.1093/bioinformatics/16.9.786. [DOI] [PubMed] [Google Scholar]
- 9.Alves R, Savageau MA. Comparing systemic properties of ensembles of biological networks by graphical and statistical methods. Bioinformatics. 2000;16:527–533. doi: 10.1093/bioinformatics/16.6.527. [DOI] [PubMed] [Google Scholar]
- 10.Koonin EV, Avarind L, Galperin MY. A comparative-genomic view of the microbial stress response. In: Storz G, Hengge-Aronis R, editors. Bacterial Stress Responses. ASM Press; Washington, D.C: 2000. pp. 17–444. [Google Scholar]
- 11.Price CW. General stress response. In: Sonenshein AL, Hoch JA, Losick R, editors. Bacillus subtilis and its closest relatives: from genes to cells. ASM Press; Washington, D.C: 2002. pp. 369–384. [Google Scholar]
- 12.Beaucher J, Rodrigue S, Jacques PE, Smith I, Brzezinski R, Gaudreau L. Novel Mycobacterium tuberculosis anti-σ factor antagonists control σF activity by distinct mechanisms. Mol Microbiol. 2002;45:1527–1540. doi: 10.1046/j.1365-2958.2002.03135.x. [DOI] [PubMed] [Google Scholar]
- 13.Kozak NA, Mattoo S, Foreman-Wykert AK, Whitelegge JP, Miller JF. Interactions between partner switcher orthologs BtrW and BtrV regulate type III secretion in Bordetella. J Bacteriol. 2005;187:5665–5676. doi: 10.1128/JB.187.16.5665-5676.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pané-Farré J, Lewis RJ, Stülke J. The RsbRST stress module in bacteria: a signalling system that may interact with different output modules. J Mol Microbiol Biotechnol. 2005;9:65–76. doi: 10.1159/000088837. [DOI] [PubMed] [Google Scholar]
- 15.Hua L, Hefty PS, Lee YJ, Lee YM, Stephens RS, Price CW. Core of the partner switching signalling mechanism is conserved in the obligate intracellular pathogen Chlamydia trachomatis. Mol Microbiol. 2006;59:623–636. doi: 10.1111/j.1365-2958.2005.04962.x. [DOI] [PubMed] [Google Scholar]
- 16.Hecker M, Völker U. General stress response of Bacillus subtilis and other bacteria. Adv Microb Physiol. 2001;44:35–91. doi: 10.1016/s0065-2911(01)44011-2. [DOI] [PubMed] [Google Scholar]
- 17.Völker U, Maul B, Hecker M. Expression of the σB-dependent general stress regulon confers multiple stress resistance in Bacillus subtilis. J Bacteriol. 1999;181:3942–3948. doi: 10.1128/jb.181.13.3942-3948.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Piggot PJ, Losick R. Sporulation genes and intercompartmental regulation. In: Sonenshein AL, Hoch JA, Losick R, editors. Bacillus subtilis and its closest relatives: from genes to cells. ASM Press; Washington, D.C: 2002. pp. 483–518. [Google Scholar]
- 19.Hilbert DW, Piggot PJ. Compartmentalization of gene expression during Bacillus subtilis spore formation. Microbiol Mol Biol Rev. 2004;68:234–262. doi: 10.1128/MMBR.68.2.234-262.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yudkin MD, Clarkson J. Differential gene expression in genetically identical sister cells: the initiation of sporulation in Bacillus subtilis. Mol Microbiol. 2005;56:578–589. doi: 10.1111/j.1365-2958.2005.04594.x. [DOI] [PubMed] [Google Scholar]
- 21.Alper S, Duncan L, Losick R. An adenosine nucleotide switch controlling the activity of a cell-type-specific transcription factor in Bacillus subtilis. Cell. 1994;77:195–205. doi: 10.1016/0092-8674(94)90312-3. [DOI] [PubMed] [Google Scholar]
- 22.Alper S, Dufour A, Garsin DA, Duncan L, Losick R. Role of adenosine nucleotides in the regulation of a stress-response transcription factor in Bacillus subtilis. J Mol Biol. 1996;260:165–177. doi: 10.1006/jmbi.1996.0390. [DOI] [PubMed] [Google Scholar]
- 23.Najafi SMA, Harris DA, Yudkin MD. Properties of the phosphorylation reaction catalyzed by SpoIIAB that help to regulate sporulation of Bacillus subtilis. J Bacteriol. 1997;179:5628–5631. doi: 10.1128/jb.179.17.5628-5631.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Delumeau O, Lewis RJ, Yudkin MD. Protein-protein interactions that regulate the energy stress activation of σB in Bacillus subtilis. J Bacteriol. 2002;184:5583–5589. doi: 10.1128/JB.184.20.5583-5589.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Duncan L, Alper S, Losick R. SpoIIAA governs the release of the cell-type specific transcription factor σF from its anti-sigma factor SpoIIAB. J Mol Biol. 1996;260:147–164. doi: 10.1006/jmbi.1996.0389. [DOI] [PubMed] [Google Scholar]
- 26.Garsin DA, Duncan L, Paskowitz DM, Losick R. The kinase activity of the antisigma factor SpoIIAB is required for activation as well as inhibition of transcription factor σF during sporulation in Bacillus subtilis. J Mol Biol. 1998;284:569–578. doi: 10.1006/jmbi.1998.2202. [DOI] [PubMed] [Google Scholar]
- 27.Lee CS, Lucet I, Yudkin MD. Fate of the SpoIIAB*-ADP liberated after SpoIIAB phosphorylates SpoIIAA of Bacillus subtilis. J Bacteriol. 2000;182:6250–6253. doi: 10.1128/jb.182.21.6250-6253.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Clarkson J, Shu JC, Harris DA, Campbell ID, Yudkin MD. Fluorescence and kinetic analysis of the SpoIIAB phosphorylation reaction, a key regulator of sporulation in Bacillus subtilis. Biochemistry. 2004;43:3120–3128. doi: 10.1021/bi036014+. [DOI] [PubMed] [Google Scholar]
- 29.Igoshin OA, Price CW, Savageau MA. Signalling network with a bistable hysteretic switch controls developmental activation of the σF transcription factor in Bacillus subtilis. Mol Microbiol. 2006;61:165–184. doi: 10.1111/j.1365-2958.2006.05212.x. [DOI] [PubMed] [Google Scholar]
- 30.Magnin T, Lord M, Yudkin MD. Contribution of partner switching and SpoIIAA cycling to regulation of σF activity in sporulating Bacillus subtilis. J Bacteriol. 1997;179:3922–3927. doi: 10.1128/jb.179.12.3922-3927.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kalman S, Duncan ML, Thomas SM, Price CW. Similar organization of the sigB and spoIIA operons encoding alternate sigma factors of Bacillus subtilis RNA polymerase. J Bacteriol. 1990;172:5575–5585. doi: 10.1128/jb.172.10.5575-5585.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.de Lencastre H, Piggot PJ. The Bacillus subtilis spolIA locus is expressed at two times during sporulation. FEMS Microbiol Lett. 1988;51:109–112. [Google Scholar]
- 33.Schuch R, Piggot PJ. The dacF-spoIIA operon of Bacillus subtilis, encoding σF is autoregulated. J Bacteriol. 1994;176:4104–4110. doi: 10.1128/jb.176.13.4104-4110.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wu JJ, Schuch R, Piggot PJ. Characterization of a Bacillus subtilis sporulation operon that includes genes for an RNA polymerase σ factor and for a putative DD-carboxypeptidase. J Bacteriol. 1992;174:4885–4892. doi: 10.1128/jb.174.15.4885-4892.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Steil L, Serrano M, Henriques AO, Völker U. Genome-wide analysis of temporally regulated and compartment-specific gene expression in sporulating cells of Bacillus subtilis. Microbiology. 2005;151:399–420. doi: 10.1099/mic.0.27493-0. [DOI] [PubMed] [Google Scholar]
- 36.Wang ST, Setlow B, Conlon EM, Lyon JL, Imamura D, Sato T, Setlow P, Losick R, Eichenberger P. The forespore line of gene expression in Bacillus subtilis. J Mol Biol. 2006;358:16–37. doi: 10.1016/j.jmb.2006.01.059. [DOI] [PubMed] [Google Scholar]
- 37.Kang CM, Brody MS, Akbar S, Yang X, Price CW. Homologous pairs of regulatory proteins control activity of Bacillus subtilis transcription factor σB in response to environmental stress. J Bacteriol. 1996;178:3846–3853. doi: 10.1128/jb.178.13.3846-3853.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yang X, Kang CM, Brody MS, Price CW. Opposing pairs of serine protein kinases and phosphatases transmit signals of environmental stress to activate a bacterial transcription factor. Genes Dev. 1996;10:2265–2275. doi: 10.1101/gad.10.18.2265. [DOI] [PubMed] [Google Scholar]
- 39.Voelker U, Luo T, Smirnova N, Haldenwang W. Stress activation of Bacillus subtilis σB can occur in the absence of the σB negative regulator RsbX. J Bacteriol. 1997;179:1980–1984. doi: 10.1128/jb.179.6.1980-1984.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chen CC, Lewis RJ, Harris R, Yudkin MD, Delumeau O. A supramolecular complex in the environmental stress signalling pathway of Bacillus subtilis. Mol Microbiol. 2003;49:1657–1669. doi: 10.1046/j.1365-2958.2003.03663.x. [DOI] [PubMed] [Google Scholar]
- 41.Kim TJ, Gaidenko TA, Price CW. A multicomponent protein complex mediates environmental stress signaling in Bacillus subtilis. J Mol Biol. 2004;341:135–150. doi: 10.1016/j.jmb.2004.05.043. [DOI] [PubMed] [Google Scholar]
- 42.Iber D, Clarkson J, Yudkin MD, Campbell ID. The mechanism of cell differentiation in Bacillus subtilis. Nature. 2006;441:371–374. doi: 10.1038/nature04666. [DOI] [PubMed] [Google Scholar]
- 43.Dworkin J, Losick R. Differential gene expression governed by chromosomal spatial asymmetry. Cell. 2001;107:339–346. doi: 10.1016/s0092-8674(01)00528-1. [DOI] [PubMed] [Google Scholar]
- 44.Hlavacek WS, Savageau MA. Rules for coupled expression of regulator and effector genes in inducible circuits. J Mol Biol. 1996;255:121–139. doi: 10.1006/jmbi.1996.0011. [DOI] [PubMed] [Google Scholar]
- 45.Dworkin J, Losick R. Developmental commitment in a bacterium. Cell. 2005;121:401–409. doi: 10.1016/j.cell.2005.02.032. [DOI] [PubMed] [Google Scholar]
- 46.Akbar S, Kang CM, Gaidenko TA, Price CW. Modulator protein RsbR regulates environmental signalling in the general stress pathway of Bacillus subtilis. Mol Microbiol. 1997;24:567–578. doi: 10.1046/j.1365-2958.1997.3631732.x. [DOI] [PubMed] [Google Scholar]
- 47.Bernhardt J, Völker U, Völker A, Antelmann H, Schmid R, Mach H, Hecker M. Specific and general stress proteins in Bacillus subtilis - A two-dimensional protein electrophoresis study. Microbiology. 1997;143:999–1017. doi: 10.1099/00221287-143-3-999. [DOI] [PubMed] [Google Scholar]
- 48.Boylan SA, Rutherford A, Thomas SM, Price CW. Activation of Bacillus subtilis transcription factor σB by a regulatory pathway responsive to stationary-phase signals. J Bacteriol. 1992;174:3695–3706. doi: 10.1128/jb.174.11.3695-3706.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Monod J, Jacob F. Teleonomic mechanisms in cellular metabolism, growth, and differentiation. Cold Spring Harb Symp Quant Biol. 1961;26:389–401. doi: 10.1101/sqb.1961.026.01.048. [DOI] [PubMed] [Google Scholar]
- 50.Ferrell JE., Jr Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr Opin Cell Biol. 2002;14:140–148. doi: 10.1016/s0955-0674(02)00314-9. [DOI] [PubMed] [Google Scholar]
- 51.Davidson EH, McClay DR, Hood L. Regulatory gene networks and the properties of the developmental process. Proc Natl Acad Sci U S A. 2003;100:1475–1480. doi: 10.1073/pnas.0437746100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ptashne M. A genetic switch: phage lambda revisited. 3. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, N.Y: 2004. [Google Scholar]
- 53.Lawrence JG. Gene organization: selection, selfishness, and serendipity. Annu Rev Microbiol. 2003;57:419–440. doi: 10.1146/annurev.micro.57.030502.090816. [DOI] [PubMed] [Google Scholar]
- 54.von Mering C, Zdobnov EM, Tsoka S, Ciccarelli FD, Pereira-Leal JB, Ouzounis CA, Bork P. Genome evolution reveals biochemical networks and functional modules. Proc Natl Acad Sci U S A. 2003;100:15428–15433. doi: 10.1073/pnas.2136809100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Viollier PH, Kelemen GH, Dale GE, Nguyen KT, Buttner MJ, Thompson CJ. Specialized osmotic stress response systems involve multiple SigB-like sigma factors in Streptomyces coelicolor. Mol Microbiol. 2003;47:699–714. doi: 10.1046/j.1365-2958.2003.03302.x. [DOI] [PubMed] [Google Scholar]
- 56.Lee EJ, Karoonuthaisiri N, Kim HS, Park JH, Cha CJ, Kao CM, Roe JH. A master regulator σB governs osmotic and oxidative response as well as differentiation via a network of sigma factors in Streptomyces coelicolor. Mol Microbiol. 2005;57:1252–1264. doi: 10.1111/j.1365-2958.2005.04761.x. [DOI] [PubMed] [Google Scholar]
- 57.Scott JM, Smirnova N, Haldenwang WG. A Bacillus-specific factor is needed to trigger the stress-activated phosphatase/kinase cascade of σB induction. Biochem Biophys Res Commun. 1999;257:106–110. doi: 10.1006/bbrc.1999.0418. [DOI] [PubMed] [Google Scholar]
- 58.Alves R, Antunes F, Salvador A. Tools for kinetic modeling of biochemical networks. Nat Biotechnol. 2006;24:667–672. doi: 10.1038/nbt0606-667. [DOI] [PubMed] [Google Scholar]
- 59.Lord M, Barilla D, Yudkin MD. Replacement of vegetative σA by sporulation-specific σF as a component of the RNA polymerase holoenzyme in sporulating Bacillus subtilis. J Bacteriol. 1999;181:2346–2350. doi: 10.1128/jb.181.8.2346-2350.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rollenhagen C, Antelmann H, Kirstein J, Delumeau O, Hecker M, Yudkin MD. Binding of σA and σB to core RNA polymerase after environmental stress in Bacillus subtilis. J Bacteriol. 2003;185:35–40. doi: 10.1128/JB.185.1.35-40.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schuck P, Minton AP. Kinetic analysis of biosensor data: elementary tests for self-consistency. Trends Biochem Sci. 1996;21:458–60. doi: 10.1016/s0968-0004(96)20025-8. [DOI] [PubMed] [Google Scholar]
- 62.Schuck P, Minton AP. Analysis of mass transport-limited binding kinetics in evanescent wave biosensors. Anal Biochem. 1996;240:262–72. doi: 10.1006/abio.1996.0356. [DOI] [PubMed] [Google Scholar]
- 63.Kim TJ, Gaidenko TA, Price CW. In vivo phosphorylation of partner switching regulators correlates with stress transmission in the environmental signaling pathway of Bacillus subtilis. J Bacteriol. 2004;186:6124–6132. doi: 10.1128/JB.186.18.6124-6132.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wise AA, Price CW. Four additional genes in the sigB operon of Bacillus subtilis that control activity of the general stress factor σB in response to environmental signals. J Bacteriol. 1995;177:123–133. doi: 10.1128/jb.177.1.123-133.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Mendes P. Gepasi - a software package for modeling the dynamics, steady-states and control of biochemical and other systems. Comput Appl Biosci. 1993;9:563–571. doi: 10.1093/bioinformatics/9.5.563. [DOI] [PubMed] [Google Scholar]
- 66.Mendes P. Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem Sci. 1997;22:361–363. doi: 10.1016/s0968-0004(97)01103-1. [DOI] [PubMed] [Google Scholar]
- 67.Mendes P, Kell DB. Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics. 1998;14:869–883. doi: 10.1093/bioinformatics/14.10.869. [DOI] [PubMed] [Google Scholar]
- 68.Brody MS, Price CW. Bacillus licheniformis sigB operon encoding the general stress transcription factor σB. Gene. 1998;212:111–118. doi: 10.1016/s0378-1119(98)00140-1. [DOI] [PubMed] [Google Scholar]
- 69.Glaser P, Frangeul L, Buchrieser C, Rusniok C, Amend A, Baquero F, Berche P, Bloecker H, Brandt P, Chakraborty T, Charbit A, Chetouani F, Couve E, de Daruvar A, Dehoux P, Domann E, Dominguez-Bernal G, Duchaud E, Durant L, Dussurget O, Entian KD, Fsihi H, Garcia-del Portillo F, Garrido P, Gautier L, Goebel W, Gomez-Lopez N, Hain T, Hauf J, Jackson D, Jones LM, Kaerst U, Kreft J, Kuhn M, Kunst F, Kurapkat G, Madueno E, Maitournam A, Vicente JM, Ng E, Nedjari H, Nordsiek G, Novella S, de Pablos B, Perez-Diaz JC, Purcell R, Remmel B, Rose M, Schlueter T, Simoes N, Tierrez A, Vazquez-Boland JA, Voss H, Wehland J, Cossart P. Comparative genomics of Listeria species. Science. 2001;294:849–852. doi: 10.1126/science.1063447. [DOI] [PubMed] [Google Scholar]
- 70.Gill SR, Fouts DE, Archer GL, Mongodin EF, Deboy RT, Ravel J, Paulsen IT, Kolonay JF, Brinkac L, Beanan M, Dodson RJ, Daugherty SC, Madupu R, Angiuoli SV, Durkin AS, Haft DH, Vamathevan J, Khouri H, Utterback T, Lee C, Dimitrov G, Jiang L, Qin H, Weidman J, Tran K, Kang K, Hance IR, Nelson KE, Fraser CM. Insights on evolution of virulence and resistance from the complete genome analysis of an early methicillin-resistant Staphylococcus aureus strain and a biofilm-producing methicillin-resistant Staphylococcus epidermidis strain. J Bacteriol. 2005;187:2426–2438. doi: 10.1128/JB.187.7.2426-2438.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wu S, de Lencastre H, Tomasz A. Sigma-B, a putative operon encoding alternate sigma factor of Staphylococcus aureus RNA polymerase: molecular cloning and DNA sequencing. J Bacteriol. 1996;178:6036–6042. doi: 10.1128/jb.178.20.6036-6042.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Knobloch JK, Bartscht K, Sabottke A, Rohde H, Feucht HH, Mack D. Biofilm formation by Staphylococcus epidermidis depends on functional RsbU, an activator of the sigB operon: differential activation mechanisms due to ethanol and salt stress. J Bacteriol. 2001;183:2624–2633. doi: 10.1128/JB.183.8.2624-2633.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.van Schaik W, Tempelaars MH, Wouters JA, de Vos WM, Abee T. The alternative sigma factor σB of Bacillus cereus: response to stress and role in heat adaptation. J Bacteriol. 2004;186:316–325. doi: 10.1128/JB.186.2.316-325.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.van Schaik W, Tempelaars MH, Zwietering MH, de Vos WM, Abee T. Analysis of the role of RsbV, RsbW, and RsbY in regulating σB activity in Bacillus cereus. J Bacteriol. 2005;187:5846–5851. doi: 10.1128/JB.187.16.5846-5851.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Anderson I, Sorokin A, Kapatral V, Reznik G, Bhattacharya A, Mikhailova N, Burd H, Joukov V, Kaznadzey D, Walunas T, Markd’Souza Larsen N, Pusch G, Liolios K, Grechkin Y, Lapidus A, Goltsman E, Chu L, Fonstein M, Ehrlich SD, Overbeek R, Kyrpides N, Ivanova N. Comparative genome analysis of Bacillus cereus group genomes with Bacillus subtilis. FEMS Microbiol Lett. 2005;250:175–184. doi: 10.1016/j.femsle.2005.07.008. [DOI] [PubMed] [Google Scholar]
- 76.Fouet A, Namy O, Lambert G. Characterization of the operon encoding the alternative σB factor from Bacillus anthracis and its role in virulence. J Bacteriol. 2000;182:5036–5045. doi: 10.1128/jb.182.18.5036-5045.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Park SG, Yudkin MD. Sequencing and phylogenetic analysis of the spoIIA operon from diverse Bacillus and Paenibacillus species. Gene. 1997;194:25–33. doi: 10.1016/s0378-1119(97)00096-6. [DOI] [PubMed] [Google Scholar]
- 78.Bentley SD, Chater KF, Cerdeno-Tarraga AM, Challis GL, Thomson NR, James KD, Harris DE, Quail MA, Kieser H, Harper D, Bateman A, Brown S, Chandra G, Chen CW, Collins M, Cronin A, Fraser A, Goble A, Hidalgo J, Hornsby T, Howarth S, Huang CH, Kieser T, Larke L, Murphy L, Oliver K, O’Neil S, Rabbinowitsch E, Rajandream MA, Rutherford K, Rutter S, Seeger K, Saunders D, Sharp S, Squares R, Squares S, Taylor K, Warren T, Wietzorrek A, Woodward J, Barrell BG, Parkhill J, Hopwood DA. Complete genome sequence of the model actinomycete Streptomyces coelicolor A3(2) Nature. 2002;417:141–147. doi: 10.1038/417141a. [DOI] [PubMed] [Google Scholar]
- 79.Hahn MY, Bae JB, Park JH, Roe JH. Isolation and characterization of Streptomyces coelicolor RNA polymerase, its sigma, and antisigma factors. Methods Enzymol. 2003;370:73–82. doi: 10.1016/S0076-6879(03)70007-X. [DOI] [PubMed] [Google Scholar]
- 80.Lee EJ, Cho YH, Kim HS, Ahn BE, Roe JH. Regulation of σB by an anti- and an anti-anti-sigma factor in Streptomyces coelicolor in response to osmotic stress. J Bacteriol. 2004;186:8490–8498. doi: 10.1128/JB.186.24.8490-8498.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Sevcikova B, Kormanec J. Activity of the Streptomyces coelicolor stress-response sigma factor σH is regulated by an anti-sigma factor. FEMS Microbiol Lett. 2002;209:229–235. doi: 10.1111/j.1574-6968.2002.tb11136.x. [DOI] [PubMed] [Google Scholar]
- 82.Sevcikova B, Benada O, Kofronova O, Kormanec J. Stress-response sigma factor σH is essential for morphological differentiation of Streptomyces coelicolor A3(2) Arch Microbiol. 2001;177:98–106. doi: 10.1007/s00203-001-0367-1. [DOI] [PubMed] [Google Scholar]
- 83.Becker LA, Cetin MS, Hutkins RW, Benson AK. Identification of the gene encoding the alternative sigma factor σB from Listeria monocytogenes and its role in osmotolerance. J Bacteriol. 1998;180:4547–4554. doi: 10.1128/jb.180.17.4547-4554.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Senn MM, Giachino P, Homerova D, Steinhuber A, Strassner J, Kormanec J, Fluckiger U, Berger-Bachi B, Bischoff M. Molecular analysis and organization of the σB operon in Staphylococcus aureus. J Bacteriol. 2005;187:8006–8019. doi: 10.1128/JB.187.23.8006-8019.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.