Temporal maps and informativeness in associative learning

Abstract

Neurobiological research on learning assumes that temporal contiguity is essential for association formation, but what constitutes temporal contiguity has never been specified. We review evidence that learning depends, instead, on learning a temporal map. Temporal relations between events are encoded even from single experiences. The speed with which an anticipatory response emerges is proportional to the informativeness of the encoded relation between a predictive stimulus or event and the event it predicts. This principle yields a quantitative account of the heretofore undefined, but theoretically crucial, concept of temporal pairing, an account in quantitative accord with surprising experimental findings. The same principle explains the basic results in the cue competition literature, which motivated the Rescorla–Wagner model and most other contemporary models of associative learning. The essential feature of a memory mechanism in this account is its ability to encode quantitative information.

Associative learning

The associative aspect of learning can be understood in a broad or a narrow sense. When understood in the broad sense, ’associative’ implies only that the subject has learned a relation between two things. In this sense, we can say that a subject has associated X and Y when they have learned that event Y follows event X at an interval of ∼10 s. When used in this sense, ’associations’ encode information: the brain can recover the exact relation (e.g. temporal) and parameters (duration values) from the structure of the association^*.

When understood in the narrow sense, ’associative’ implies the formation of a signal-conducting connection between the internal representations of two events. The activation of one representation excites or inhibits the other by signals transmitted through the connection. The connection does not specify the nature (e.g. spatial, temporal, causal or categorical) or parameters (e.g. 10 s, 5 km, etc) of the relation between what it connects. An experienced temporal relation between events is often assumed to be essential for the formation of an association in this narrow sense. However, the association thus formed does not encode information [2-4]. The duration of the interval separating the associated events cannot be recovered by ’reading’ or ’transcribing’ the association.

Association formation in the narrow sense is plausibly thought to be realized by changes in synaptic conductance. When understood in the broad sense, however, the possible dependence on changes in synaptic conductances is less clear because it is not clear how synaptic changes might encode the nature and parameters of the different relations that might be learned. If we are to understand associations in this broad sense while maintaining the hypothesis that identifies associations with changes in synaptic conductances, we need to understand how synaptic conductances can encode quantities and relations, for example, the temporal distance between X and Y.

The distinction between the narrow and broad senses of association is important because accumulating experimental evidence has made it clear that time is not only a crucial dimension of the experiences that produce simple temporally conditioned behavior; rather, time is encoded in the ’association’. Simple learned responses, such as the conditioned eye blink and freezing in response to anticipated shock, which play a fundamental part in research on the neurobiological foundations of learning, are mediated by mechanisms that parametrically represent the temporal relation between the predicting event and the predicted event [5-7]. The rabbit not only blinks, it blinks at the right time [8,9]; the rat does not simply become fearful in anticipation of shock, it becomes most fearful around the time at which shock is expected [10,11]. The physical changes in the brain wrought by the conditioning experience of the animal encode the temporal parameters of the experienced relation. They form a temporal map [12].

For millennia, association formation in the narrow, non-representational sense has been thought to depend on close temporal contiguity [4,13-15]. Research with Pavlovian paradigms, such as eye-blink and fear-conditioning paradigms, which are thought to reveal the basic principles of association formation, has raised two formidable challenges to this hypothesis. First, the results from inhibitory conditioning and cue competition protocols show that temporal pairing is neither necessary nor sufficient for association formation in the broad sense (Box 1). Second, it has proved impossible to define empirically what constitutes close temporal contiguity [16,17] (Box 2).

Box 1. Temporal pairing is neither necessary nor sufficient in associative conditioning.

Figure I schematizes the protocols for classic experiments in the associative learning literature. The results obtained using the inhibitory protocol show that the temporal contiguity of the CS and US is not necessary for the development of a CR to a CS. The results obtained with the cue competition protocols (the failure of a conditioned response to develop to a CS repeatedly paired with the US) show that the temporal contiguity of CS and US is not sufficient.

Figure I.

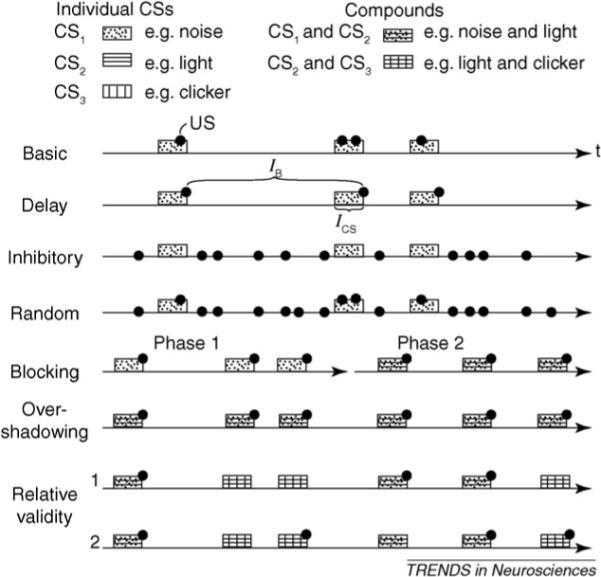
Learning protocols and the behavioral results they produce (a CR to the CS, or not). Basic : the US occurs only during the CS but at unpredictable times within it: leads to a CR. Delay: the US occurs only at the termination of a CS of fixed duration, I_CS: leads to a CR. Inhibitory: the US occurs only when CS is absent (ergo, CS never paired with US): leads to a CR (such as CS avoidance if the US is appetitive or CS approach if the US is aversive). The remaining protocols are cue-competition protocols. Truly random: the times of US occurrence are completely independent; hence, they sometimes occur during CS ’by coincidence’: a CR to the CS does not develop but a strong CR does develop to the experimental chamber (the spatial context), which is a competing cue. Blocking: trained during Phase 1 with CS₁ and then during Phase 2 with CS₂ and CS₁, presented ’in compound’ (together): a CR to CS₂ does not develop. Overshadowing: CS₁ and CS₂ presented in compound from the outset; a CR develops to one or the other CS but not both (Box 4). Relative validity: (1) CS₂ is always presented in compound; half the time it is compounded with CS₁ and half the time with CS₃. The US occurs only when it is compounded with CS₁. A CR develops only to CS₁, despite fact that US is paired with CS₂ on half of all CS₂ occurrences. (2) Same as in RV–1 except that now pairing of US with CS₂ occurs on the half of the trials when it appears in compound with CS₁ and half the trials when it appears in compound with CS₃. CR develops only to CS₂, despite fact that the US is paired with the other two CSs just as frequently (on half of all their occurrences) and with CS₂ no more frequently than in RV–1.

Box 2. The effect of the temporal parameters on the rate of learning.

When the average interval between USs (Ī_B) is fixed and the CS–US interval (I_CS) is increased, trials to acquisition increase (Figure Ia, solid line). When, however,Ī_B is increased in proportion to the increase in I_CS, holding constant the Ī_B/I_CS ratio, the CS–US interval has no effect on the rate of acquisition (Figure 1a, dashed line). The interacting effects of Ī_B and I_CS on the rate of acquisition make it impossible to define a critical interval within which the CS and US must both fall in order to become associated.

When trials to acquisition are plotted against Ī_B/I_CS on double logarithmic coordinates, the slope of the regression line does not differ significantly from −1 (Figure Ib), implying that the rate of acquisition (the inverse of trials to acquisition) is proportional to this ratio. The greater this ratio, the relatively closer CS onset is to US onset. The acquisition-promoting effect of increasing Ī_B while holding I_CS constant is observed even for very large values of Ī_B and Ī_B/I_CS [31].

Figure I.

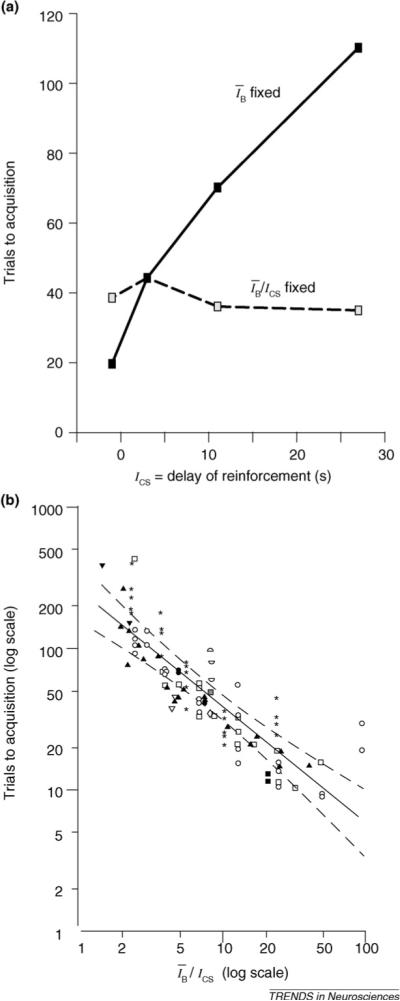
(a) Trials to acquisition (a measure of associability) plotted as a function of the CS–US interval, either when the average interval between USs, Ī_B, is fixed (solid line) or when the ratio of this interval to CS duration, Ī_B/I_CS, is fixed (dashed line). (b) Trials to acquisition versus Ī_B/I_CS on double logarithmic coordinates. The solid line is the best fitting linear regression; the dashed curves are the 95% confidence interval. Both plots adapted, with permission, from Ref. [5].

Here, we review findings that emphasize the crucial role of a temporal map in the emergence of the conditioned response (CR) in widely used associative learning paradigms. We then show that when we consider the Shannon information (Box 3) that the predicting stimulus (CS) provides about the timing of the predicted stimulus (US) we get a unified account of cue competition and temporal contiguity. The CS enables the animal to anticipate the US by virtue of the encoded temporal relation. The principle on which the account rests is that the ‘strength’ of a learning protocol (as measured by the readiness with which exposure to that protocol leads to the emergence of a CR) is determined by one component of the information that the CS provides about the timing of the next US. From this principle we derive both the cue competition results and the quantitative effects of varying the temporal parameters of a protocol on ‘associability’.

Box 3. Computing the Shannon information that a CS provides regarding the timing of the US.

We assume that the temporal map gives subjects a representation of the distributions of possible times of US occurrence, conditioned on the presence or absence of different possibly predictive cues (CSs). The entropy of any such representation (distribution) is a measure of the subject's uncertainty (ignorance) regarding the timing of the next US. The information that a CS communicates, which we call H_com, is the difference between the entropy of the subject's representation of the possible times of US occurrence when not conditioned on the presence or absence of the CS in question and the entropy of the subject's representation of the possible times of US occurrence given the CS.

In the basic protocol (Box 1), the USs are generated by random rate processes, so the distributions of inter-event intervals are exponential. The entropy of an exponential distribution is H_exp = k – log₂λ = log₂Ī + k, where λ is the rate parameter (e.g. USs per unit time), Ī is the average inter-event interval and k = log₂ $\left(\frac{e}{\Delta \tau }\right)$ is a constant whose value depends on the assumed temporal resolution (Δτ). The difference in the two exponential entropies is:

$$H_{\mathrm{com}}=H_{\mathrm{B}}-H_{\mathrm{CS}}={\log }_2{\lambda }_{\mathrm{CS}}-\log {\lambda }_{\mathrm{B}}={\log }_2({\lambda }_{\mathrm{CS}}∕{\lambda }_{\mathrm{B}})$$ [Equation i]

The value assumed for Δτ does not matter, provided it is small relative to the other temporal values, because the constant k drops out when we take the differences in the entropies.

In delay conditioning, the US follows CS onset at a fixed interval, I_CS, which is the duration of a single CS. An extensive experimental literature implies that, at CS onset, the temporal map of the CS–US relation provides the subject with a distribution for the expected time of the US that is Gaussian with mean I_CS and standard deviation σ = wI_CS, where w is the Weber fraction [5]. The empirical value of w is ∼0.15, which is to say that subjects represent an experienced interval with +/− 15% precision [32]. The entropy of a Gaussian distribution is:

$$H_{\mathrm{Gauss}}=1∕2{\log }_2\left[\frac{2\pi e{\sigma }^2}{{\left(\Delta \tau \right)}^2}\right]$$

Substituting wI_CS for s and expanding, we obtain, after some algebra, an expression for the subject's uncertainty about the timing of the next US immediately after CS onset:

$$H_{\mathrm{CS}}={\log }_2{I}_{\mathrm{CS}}+{\log }_{2}w+1∕2{\log }_{2}2\pi e-{\log }_2\left(\Delta \tau \right)$$

As before, the background distribution (the distribution when we ignore the CS) is:

$$H_{\mathrm{B}}=k-{\log }_2{\lambda }_{\mathrm{B}}={\log }_2{\stackrel{‒}{I}}_{\mathrm{B}}+k$$

The difference between the entropies is:

$$H_{\mathrm{com}}=({\log }_2{\stackrel{‒}{I}}_{\mathrm{B}}+{\log }_{2}e-{\log }_2\left(\Delta \tau \right))-({\log }_2{\stackrel{‒}{I}}_{\mathrm{CS}}+{\log }_{2}w+1∕2{\log }_{2}2\pi e-{\log }_2\Delta \tau )={\log }_2({\stackrel{‒}{I}}_{\mathrm{B}}∕I_{\mathrm{CS}})-{\log }_{2}w+k$$ [Equation ii]

(where k is a numerical constant).

In equations (i) and (ii) we see that the information about the timing of the next US communicated to the subject by the onset of the CS always has a component equal to the log of the factor by which CS onset reduces the expected time to the next US (λ_CS/λ_B or Ī_B/I_CS). In the basic protocol, this is the only component; in the delay protocol there is an additional component. Its magnitude depends only on w, the Weber fraction, which measures the precision with which a subject can represent an interval^†. The information in this component does not depend on the temporal parameters of the protocol; it is ∼2 bits whenever there is a previous event at a fixed interval before the US, regardless of how far back. Thus, this component of the information communicated is present (in undiminished magnitude) even when we drop the CS from the protocol and simply fix the duration of the US–US interval.

Protocol intervals are learned at or before appearance of the CR

When subjects repeatedly experience a fixed CS–US interval, they rapidly form a temporally based expectation of the US. A recent study [18] exposed goldfish to an aversive conditioning procedure in which a brief shock (the US) came 5 s after the onset of a light (the CS). On a few trials in each session the light remained on for 45 s and no shock was presented, enabling us to track the timing of the CR both before and after the expected time of the shock. Figure 1 shows the development and timing of the CR over the course of training. The main effect of training was to change the magnitude of peak responding; the time at which the CRs occur did not change. Modeling of the distributions over the course of training confirmed this conclusion. The peak height changes but its location does not. The response is appropriately timed when it first appears. Similar results have been obtained in eyeblink conditioning in rabbits, appetitive head-poking in rats and autoshaping in birds and mice [9,19-21].

Figure 1.

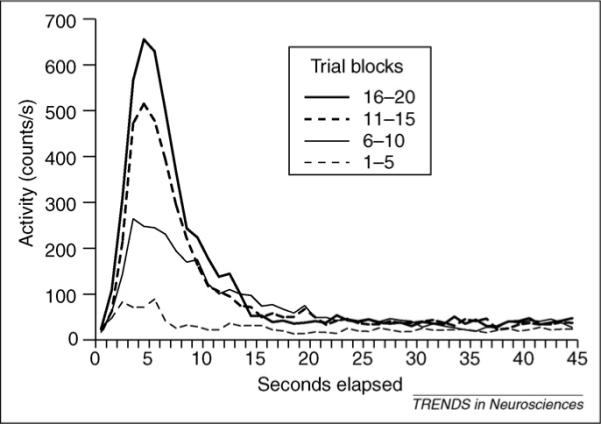
CR timing in goldfish as Pavlovian training progresses. A 5 s visual CS terminated in mild shock (US). Training trials were intermixed with probe trials, during which the CS remained on for 45 s with no US. Movement as a function of time in the CS is shown for blocks of 5 sessions (50 CS–US pairings) during the long unreinforced trials. The amount of anticipatory activity increased as training progressed, but the timing of the CR was appropriate even in the earliest part of training. Modified, with permission, from Ref. [18].

There is even evidence that the CS–US interval is learned before the CR appears. By shortening the delay (I_CS for CS interval) in a rabbit eyeblink protocol from 700 ms to 200 ms shortly before the CR was expected to make its appearance, it has been possible to demonstrate that the rabbits learn the CS–US interval before they begin to respond to the CS [8]. When they did begin to respond, they blinked at 200 ms; but on probe trials, where the CS was prolonged, they also blinked at 700 ms.

This rapid temporal learning has a role in all conditioning phenomena. Blocking and overshadowing (Box 1) are strongest when the compounded CSs maintain the same temporal relation between CS and US [6,22]; the greatest inhibition occurs at the time at which expected reinforcement is omitted [6,23] and the modulation of excitatory value by contextual cues is temporally specific [24]. In trace conditioning, where there is a gap between the termination of the CS and the onset of the US, CRs become more frequent as the gap interval elapses [25].

Rats detect and adjust to a change in random rates of reward as rapidly as is, in principle, possible [26]. What distinguishes two different random rates is only the distribution of their inter-event intervals. The distributions always overlap, even for very different rates. To detect a change in the rate parameter as rapidly as is in principle possible, the subject must track the sequence of recent inter-event intervals and compare their distribution to the distribution expected on the hypothesis that the rate has not changed.

The temporal map

A temporal map [12] represents the temporal distribution of events in such a way that it is possible to infer the distribution of distances between pairs of events that have not been directly paired. A recent study (K.T. Taylor et al., unpublished) demonstrates the integration of separately experienced positive (forward) and negative (backward) intervals. Over two days of training, a forward group received eight pairings of a 16 s white noise followed by a clicker. In the backward group, the order was reversed (clicker followed by noise). Subjects were then were exposed to backward pairings of the clicker with food (food followed by the clicker). If subjects integrate the temporal information gained from the separate phases of training, they would expect food near the end of the noise in the forward group but have no reason to expect food during the noise in the backward group. This was indeed the case. Subjects in the forward group responded significantly more to the noise than subjects in the backward group, despite responding very little to the clicker itself. Similar experiments in other laboratories [6] have repeatedly shown that subjects form a temporal map that enables them to infer temporal relations they have not directly experienced.

We assume that the map represents not simply the distances between the expectations; rather, it represents the expected distributions of event times. For fixed intervals, an extensive experimental literature shows that the variability in the subject's representation of a fixed interval is Gaussian, with a standard deviation proportional to its mean [27,28]. This scalar variability in the representation of intervals is why temporal discriminations obey Weber's law [29].

Informativeness: a crucial parameter

An event informs to the extent that it reduces ignorance. The cue competition results (Box 1) indicate that a predictive cue does not elicit a CR unless it tells the subject something it does not already know about when the next US will occur. In information-theoretic terms, a CS does not elicit a CR unless its onset reduces the subject's uncertainty regarding when to expect the next US. The reduction in the uncertainty is measured by the reduction in the entropy of the subject's representation of the distribution of probable US times. In Box 3, we develop the simple formulae that specify the amount by which CS onset changes the entropy of these distributions.

In the basic protocol (Box 1), the information communicated by the CS is:

$$H_{\mathrm{com}}={\log }_2({\lambda }_{\mathrm{CS}}∕{\lambda }_{\mathrm{B}})$$

This is the log of the ratio between λ_CS (USs per unit CS time) and the background rate, λ_B (USs per unit time). This result immediately yields the results of the simplest cue competition protocol – the truly random control (Box 1). In the truly random protocol λ_CS = λ_B; hence, H_com = log(1) = 0.

The CS communicates no information about the timing of the next US, and so a CR (anticipatory response) should not develop. All of the information available to the subject comes from the context (i.e. being the experimental apparatus).

In the commonly used delay protocol (Box 1), the information communicated by the CS is:

$$H_{\mathrm{com}}={\log }_2({\stackrel{‒}{I}}_{\mathrm{B}}∕I_{\mathrm{CS}})-{\log }_{2}w+k$$

(where k is a numerical constant; Box 3). Because of the entropy introduced by the scalar variability in the brain's representation of a fixed duration, the additional information provided by fixing the interval between CS onset and US occurrence does not depend on I_CS, the duration of the warning interval. In other words, this component of the information does not depend on the temporal parameters of the protocol.

The ratios λ_CS/λ_B and Ī_B/I_CS are essentially the same quantity; they are the factor by which the onset of a CS shortens the expected interval to the next US. We call this factor the informativeness of the temporal relation between the CS and the US. If we measure associability (A) by the reciprocal of the number of trials required before the appearance of a CR, then, from the results in Box 2,we have a simple formula for the CS–US associability in a given protocol:

$$A\left(\mathrm{CS}\right)\propto \text{Informativeness}-1$$

Where:

$$\text{Informativeness}=E\left(t\left(\mathrm{US}\right)\right)∕E\left(t\left(\mathrm{US}\right)\right)\mid \mathrm{CS})$$

In words, the informativeness is the unconditional or purely contextual expected time to the US, divided by the expected time to the US given the CS. The informativeness is equal to the (multiplicative) factor by which the onset of the CS reduces the expected interval to the next US; so, an informativeness of 1 implies no reduction. The CS–US associability in a protocol is proportional to the informativeness of the CS–US relation minus 1, so that, when a CS is uninformative, associability is 0.

This formula explains the quantitative results on the effects of varying the temporal parameters (Box 2). It also yields the results of the cue competition protocols (Box 1). In the blocking protocol:

$$E\left(t\left(\mathrm{US}\right)\right)\mid {\mathrm{CS}}_1\&\sim {\mathrm{CS}}_2)=E\left(t\left(\mathrm{US}\right)\right)\mid {\mathrm{CS}}_1\&{\mathrm{CS}}_2)$$

In words, the expected time to the next US given CS₁ and not CS₂ is equal to the expected time to reinforcement given CS₁ and CS₂. Therefore, the reduction factor for CS₂ (its informativeness) is 1 (no reduction and 0 associability). Arguably (Box 4), in the overshadowing protocol, if either CS is attended to (if its informativeness is computed), then the associability of the other is 0; so, subjects should learn to use only one of two perfectly redundant CSs to anticipate the US. By contrast, in each of the relative validity protocols only one CS can be fully informative. In RV–1 (see bottom of Box 1), if CS₁ is attended to then CS₂ has no associability, whereas in RV–2, if CS₂ is attended to then CS₁ and CS₃ have no associability.

Box 4. Some outstanding questions.

We predict that in the overshadowing protocol, for example, only one of the two cues will elicit a CR. This has been the result in some studies [33,34] but not in others. An outstanding question is whether the instances in which incomplete overshadowing and/or blocking is seen might be explained as either an artifact of group averaging (some subjects responded to one CS, whereas others responded to the other CS [33]) or a consequence of a failure to compare the responding to the blocked or overshadowed CS with appropriate controls for generalization, non-specific response potentiation and secondary conditioning.

Does inverse informativeness determine the rate of inhibitory conditioning? An inhibitory CS increases the expected time to the next US by lowering the rate of reward. Is the number of CS presentations required to elicit an inhibitory CR inversely proportional to the factor by which the inhibitory CS increases the expected time of the next US? If so, then how does this work when there is never a US during the CS? Does cumulative unreinforced CS exposure give a lower bound on the probable expectation of the US–US interval in the presence of a CS?

Our associability formula (and the quantitative results in Box 2) has counter-intuitive implications. The most surprising is that for a protocol of a given duration, the progress of ‘association’ formation at the end of the protocol (as measured either by the average strength or frequency of the CR or by the number of subjects that have begun to make a CR) will be unaffected by the number of trials (CS– US pairings). When the duration of a protocol is fixed, deleting trials by some factor increases the informativeness by the same factor. When there is, for example, an eightfold reduction in the number of trials, then there is an eightfold increase in the informativeness of the CS. Thus, by our formula, there should be no effect of this massive a reduction in the number of trials. Surprising as this prediction is, it has recently been confirmed in an extensive series of Pavlovian conditioning experiments with rats, mice and pigeons [30].

Conclusions

From a simple information-theoretic principle, it is possible to deduce both the results of cue competition experiments and the effects of varying the temporal parameters in a learning protocol. The principle is that a CS is associable with a US within a given protocol only to the extent that it reduces the expected time to the next US. For neuroscientists, perhaps the most important implication of the formula and the experiments whose results it accounts for is that there is no such thing as a window of associability – a critical interval within which two events must occur if they are to become associated. Another important implication is that the emergence of a CR depends on the brain encoding the metric temporal relations within a protocol. Whatever the physical change that underlies the formation of an association (in the broad sense), it must be capable of encoding the duration of a temporal interval. Another startling implication of our formula and of the experimental results that motivated it is that the number of trials is not in and of itself a crucial parameter of a training protocol. The crucial parameter is the informativeness, the factor by which the onset of the CS reduces the expected time to the next US.