Abstract
The partial Fourier gradient-echo echo planar imaging (EPI) technique makes it possible to acquire high-resolution functional MRI (fMRI) data at an optimal echo time. This technique is especially important for fMRI studies at high magnetic fields, where the optimal echo time is short and may not be achieved with a full Fourier acquisition scheme. In addition, it has been shown that partial Fourier EPI provides better anatomic resolvability than full Fourier EPI. However, the partial Fourier gradient-echo EPI may be degraded by artifacts that are not usually seen in other types of imaging. Those unique artifacts in partial Fourier gradient-echo EPI, to our knowledge, have not yet been systematically evaluated. Here we use the k-space energy spectrum analysis method to understand and characterize two types of partial Fourier EPI artifacts. Our studies show that Type 1 artifact, originating from k-space energy loss, cannot be corrected with pure postprocessing, and Type 2 artifact can be eliminated with an improved reconstruction method. We propose a novel algorithm, that combines images obtained from two or more reconstruction schemes guided by k-space energy spectrum analysis, to generate partial Fourier EPI with greatly reduced Type 2 artifact. Quality control procedures for avoiding Type 1 artifact in partial Fourier EPI are also discussed.
Keywords: EPI, partial Fourier reconstruction, fMRI, artifact removal, echo shifting effect
It has been shown in recent works, that for high-resolution functional MRI (fMRI) studies, a partial Fourier acquisition scheme (1-7) is superior to full Fourier acquisition in two ways (8,9). First, the desired echo time (TE) value that provides the optimal BOLD sensitivity may not be achievable with a high-resolution full Fourier echo planar imaging (EPI) scan because of the very long acquisition window of high-resolution EPI. On the other hand, the optimal TE value can be easily achieved with partial Fourier EPI. Second, because of the significant signal decay within the long acquisition window of full Fourier EPI, the reconstructed EPI images are always blurred by the corresponding point spread function (PSF). On the other hand, the PSF of partial Fourier EPI is much sharper and thus the reconstructed images have a better anatomic resolvability.
Successful applications of partial Fourier EPI to high-resolution fMRI studies have been reported in several recent works (9,10). We expect that, partial Fourier EPI will continue to play a major role in future high-resolution fMRI studies especially those performed at high magnetic fields, because the optimal TE will be further shortened at high fields and it will be extremely difficult to acquire short-TE EPI data without using a partial Fourier acquisition scheme.
In order to reliably and properly apply the partial Fourier EPI method to fMRI studies, it is important that we have a good understanding of its technical limitations and artifacts. However, the technical limitations and image artifacts of partial Fourier EPI, to our knowledge, have not yet been systematically investigated. Here, we use the newly developed k-space energy spectrum analysis method (11) to understand and characterize two types of artifacts in partial Fourier EPI. Alternative image reconstruction algorithms and quality control procedures are suggested to further improve the accuracy of partial Fourier EPI based fMRI studies.
A BRIEF REVIEW OF THE K-SPACE ENERGY SPECTRUM ANALYSIS
A brief review of the k-space energy spectrum analysis method (11) is provided here. Unlike spin-echo imaging, the image-domain phase accumulations due to the in-plane susceptibility field gradients cannot be refocused in gradient-echo imaging. The gradients of image domain phase values result in the shift of the k-space echo energy peaks in gradient-echo imaging and gradient-echo EPI (12), which can be understood by the shift theorem of Fourier transformation. The k-space echo-shifting effect may induce EPI geometric distortions (13,14) and a spatial variation of the BOLD sensitivity in fMRI studies (15). As described in our recent work (11), the k-space echo-shifting effect depends on the local susceptibility field gradients and EPI scan parameters (Eqs. [1] and [2] in Ref. 11).
For example, it can be seen from the gradient-echo EPI k-space data shown in Fig. 1a that not all of the k-space energy peaks are located at the center of the k-space, due to the susceptibility induced echo-shifting effect. Even though it is easy to identify the overall k-space energy distribution pattern (i.e., the summation of k-space energy peaks corresponding to all image domain pixels) from Fig. 1a, it is not straightforward to identify the location of a k-space energy peak corresponding to a specific region of interest (ROI), especially when the local field gradient in an ROI is nonlinear (e.g., Fig. 4 in Ref. 11).
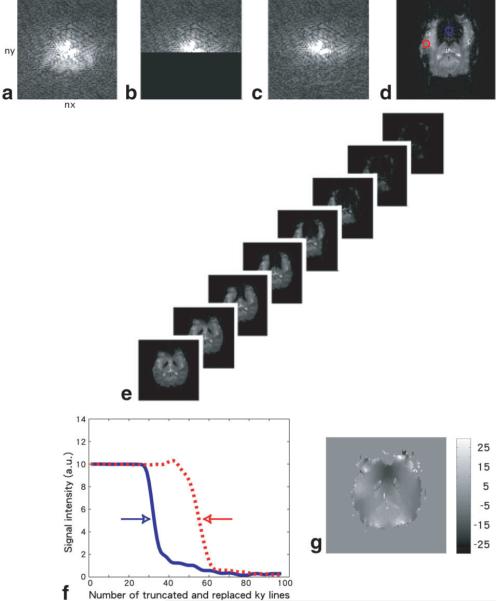
FIG. 1.
A schematic diagram of the k-space energy spectrum analysis: A selected number of ky lines of gradient-echo EPI k-space data (a) are truncated (b) and replaced with values calculated with Cuppen's algorithm (c), using the untruncated k-space data. A partial Fourier image is then obtained with 2D FFT (d). This procedure is repeated for different numbers of truncated and replaced ky lines (e), and the pixel-wise signal intensity as a function of truncated and replaced ky line number (i.e., k-space energy spectrum) is obtained (f). From the k-space energy spectrum, a ky displacement map can be calculated (g). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
We have previously proposed using the k-space energy spectrum analysis algorithm to measure the spatially dependent echo-shifting effect from gradient-echo EPI data. This algorithm is schematically illustrated by Fig. 1, assuming the EPI matrix size is nx • ny (Fig. 1a). First, a number of ky lines are truncated in postprocessing (Fig. 1b) and replaced by values calculated from the untruncated data using Cuppen's algorithm (Fig. 1c). The background phase information required in Cuppen's method is obtained from the original full k-space data. An image is reconstructed with 2D fast Fourier transform (FFT) (Fig. 1d). Steps shown in Fig. 1b to d are then repeated for different numbers of truncated ky lines (from 1 to ny), and ny images are generated (Fig. 1e). The k-space energy spectrum along the phase-encoding direction of any pixel can be obtained from those ny images, by extracting the pixel-wise signal intensities corresponding to different numbers of truncated ky lines. For example, the k-space energy spectra for the blue and red pixels (see Fig. 1d) are shown in Fig. 1f. A sudden change of signal intensity occurs (indicated by arrows) when the peak of the k-space echo signals is being truncated. For the blue pixel, an abrupt signal change occurs when 32 ky lines are truncated and replaced, indicating that the zero ky line is displaced by −15 lines (i.e., 32 – (ny /2) • 1, and ny • 96) due to the local field gradients. For the red pixel, an abrupt signal change occurs when 56 ky lines are truncated and replaced, indicating that the zero ky line is displaced by • 9 lines (i.e., 56 – (ny /2) • 1, and ny • 96) due to the local field gradients along the phase-encoding direction. Thereafter, a ky displacement map can be calculated, which provides the information on the spatially dependent echo-shifting effect along the phase-encoding direction (Fig. 1g). The same approach can be applied along the readout direction to calculate the kx displacement map.
In Ref. 11, we have shown that the k-space energy spectrum analysis is capable of quantifying both linear and nonlinear local field gradients, on a pixel-by-pixel basis, as long as the B0 field within an ROI is smooth and its gradient values can be defined in every pixel. It should be noted that the local field gradient calculated from the k-space energy spectrum analysis represents the spatial variation of the B0 field values between the targeted pixel and its nearest neighboring pixels, rather than the intravoxel field gradient of an isolated pixel. The k-space energy spectrum analysis can actually be used in characterizing artifacts in partial Fourier gradient-echo EPI, as shown in the following sections.
Artifacts Due to the Echo-Shifting Effect in Partial Fourier Gradient-Echo EPI
It has been observed and pointed out by Zhang et al. (6) that partial Fourier EPI data may be degraded by signal loss artifact in areas with pronounced susceptibility field gradients. Zhang et al. (6) have shown that the signal loss artifact in partial Fourier gradient-echo EPI may be reduced, but not completely eliminated, with an improved reconstruction algorithm. Here we use the k-space energy spectrum analysis method to further illustrate that there exist two different types of artifacts that are unique in partial Fourier gradient-echo EPI. Our study shows that (a) both types of artifacts originate from the echo-shifting effect along the phase-encoding direction of gradient-echo EPI, and (b) one of these two artifacts may not be eliminated with any postprocessing algorithm, as illustrated by a simulation study presented in the following paragraphs and Fig. 2. The data shown in Fig. 2 are built with the same simulation program as that in Ref. 11 (Fig. 2a to e), but different reconstruction approaches are used to illustrate different types of artifacts (Fig. 2f).
FIG. 2.
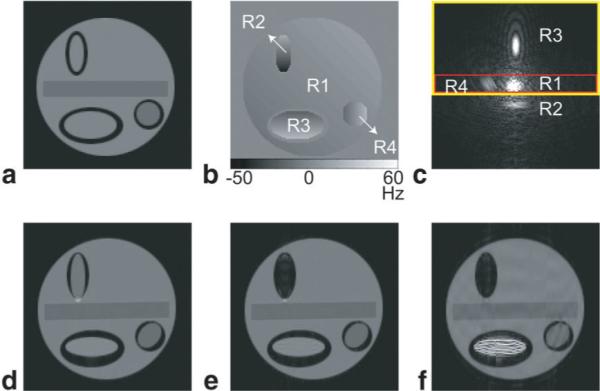
The echo-shifting induced artifact in partial Fourier gradient-echo EPI (simulation). a,b: The proton density map and field inhomogeneity map of the mathematical phantom (i.e., the input of our simulation). c: The full Fourier EPI k-space data. d: The reconstructed full Fourier EPI image. e: An image reconstructed from partial Fourier data (i.e., within the yellow box of c) using Cuppen's algorithm and the full knowledge of image background phase. f: An image reconstructed from partial Fourier data (i.e., within the yellow box of c) using Cuppen's algorithm and low-resolution information of image background phase (i.e., the data within the red box of c). [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]
Type 1 Artifact
Figure 2a and b show the proton density map and field inhomogeneity map of our mathematical phantom (i.e., the input of our simulation), and it can be seen that there exist pronounced field gradients along the phase-encoding direction (vertical) in Region 2 and Region 3. The simulated full Fourier EPI k-space data are shown in Fig. 2c. Echo energy peaks corresponding to Region 2 and Region 3 deviate from the ideal k-space center along the phase-encoding direction due to the local field gradients (i.e., the echo-shifting effect). The reconstructed image is shown in Fig. 2d.
If a partial Fourier acquisition scheme, rather than full Fourier acquisition, is chosen, then it is more likely that echo energy corresponding to certain image domain regions will be shifted outside the chosen k-space sampling window. For example, if only the k-space area within the yellow box is sampled (Fig. 2c), the k-space energy corresponding to Region 2 will not be acquired properly, which in turn results in signal loss in the image reconstructed using a partial Fourier reconstruction algorithm. For example, the reconstructed image shown in Fig. 2e is obtained with Cuppen's partial Fourier reconstruction method (1,5), in which the required image background phase information is measured from the full k-space data. The signal loss artifact shown in Fig. 2e is termed Type 1 artifact of partial Fourier gradient-echo EPI. Type 1 artifact originates from k-space energy loss and thus may not be corrected with any pure post-processing method.
Type 2 Artifact
In conventional partial Fourier MRI reconstruction methods, the required image background phase information can only be estimated from a central ky band (for example, the rectangular area enclosed by red line in Fig. 2c). If the k-space energy peak corresponding to a certain image domain region is located outside the central ky band, then the low-resolution phase image may not provide accurate phase estimation for the corresponding image-domain region. As a result, there may exist additional artifacts in the corresponding region of the reconstructed partial Fourier image. For example, the k-space energy peak corresponding to Region 3 is located outside the ky band used for low-resolution background phase estimation, and thus the reconstructed partial Fourier EPI is degraded by artifact (i.e., artificial signal elevation) in Region 3, as shown in Fig. 2f. This artifact, termed Type 2 artifact of partial Fourier gradient-echo EPI, results solely from improper postprocessing, thus it should be possible to remove Type 2 artifact with an improved postprocessing method.
Our observation of Type 1 and Type 2 artifacts in numerical simulation is also validated in another study based on the k-space energy spectrum analysis of human brain EPI data (Fig. 3). Full Fourier gradient-echo EPI data of multiple axial slices were acquired at 3T (General Electric, Milwaukee, WI, USA) from a healthy subject with the following parameters: FOV • 24 cm • 24 cm, matrix size • 96 • 96, targeted TE value • 42.3 ms, inter-ky echo-spacing time • 0.752 ms, readout bandwidth • 100 kHz, and slice thickness • 4 mm. The image reconstructed from full Fourier EPI data (Fig. 3a) is used as the ground truth in this study. Using the newly developed k-space energy spectrum analysis method, the deviation of ky energy peak from the k-space center are quantified for all pixels, as shown in Fig. 3b. The partial Fourier EPI data of matrix size 96 • 54 were then generated from the acquired full Fourier EPI data, by truncating the most negative 42 ky lines. The image shown in Fig. 3c (96 • 96) was reconstructed from the partial Fourier EPI data and the complete knowledge of image-domain background phase (i.e., the phase image reconstructed from the full Fourier EPI data) using Cuppen's iterative algorithm. Since the complete knowledge of background phase is used in Cuppen's reconstruction, the image shown in Fig. 3c is degraded by only Type 1 artifact (signal loss indicated by an arrow), but not Type 2 artifact. Based on the ky displacement shown in Fig. 3b, the pixels with the corresponding k-space echo energy located outside the partial Fourier EPI acquisition window were identified, as represented by red pixels of Fig. 3d. Observation of Figs. 3c and 3d confirms that 1) the signal loss artifact due to insufficient sampling of the k-space energy peaks (i.e., Type 1 artifact) cannot be corrected even when a complete knowledge of image-domain background phase values is available, and 2) the k-space energy spectrum analysis may quantitatively explain Type 1 artifact in partial Fourier gradient-echo EPI.
FIG. 3.
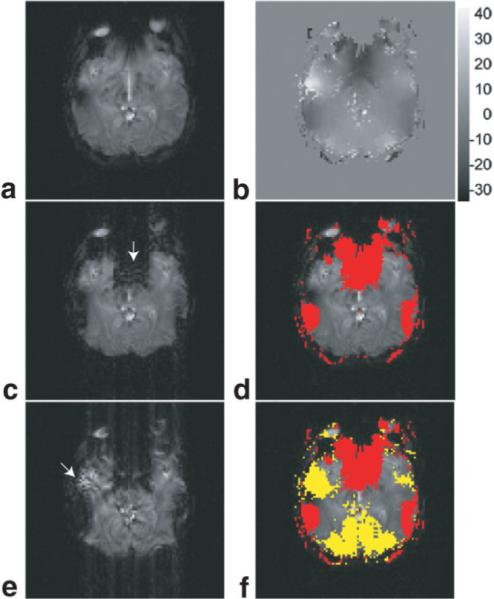
Type 1 and Type 2 artifacts in partial-Fourier gradient-echo EPI of human brain, simulated from the acquired full Fourier EPI data (through data truncation). a: The full Fourier EPI image of matrix size 96 • 96. b: The ky displacement map calculated from full Fourier EPI data using the k-space energy spectrum analysis. c: The partial Fourier EPI image reconstructed with Cuppen's algorithm and the full knowledge of image background phase (that is available from full Fourier EPI data). d: Image pixels susceptible to Type 1 artifact (shown in red) using the information from the ky displacement map (b). e: The partial Fourier EPI image reconstructed with Cuppen's algorithm and low-resolution estimation of image background phase (from the central ky band 96 • 12). f: Image pixels susceptible to Type 1 (shown in red) and Type 2 (shown in yellow) artifacts using the information from the ky displacement map (b).
In actual partial Fourier EPI scans, the background phase values can only be estimated from the central ky band, and thus the reconstructed image may be further degraded by both Type 1 and Type 2 artifacts. The image shown in Fig. 3e (96 • 96) is reconstructed from the partial Fourier EPI data (matrix size 96 • 54) and a low-resolution phase image calculated from the central ky band (matrix size 96 • 12). It can be seen that the reconstructed image is affected by both Type 1 artifact (similar to that in Fig. 3c) and Type 2 artifact (i.e., artificial signal elevation indicated by an arrow in Fig. 3e). Based on the ky displacement shown in Fig. 3b, the pixels with the corresponding k-space echo energy located in the positive ky space, but outside the central ky band used for background phase estimation, were identified, as shown in yellow in Fig. 3f. Comparison of Fig. 3e and f confirms that the artificial signal elevations (i.e., Type 2 artifact) in partial Fourier EPI indeed occurs in pixels with the corresponding k-space energy peaks shifted outside the central ky band used for background phase estimation.
As illustrated in Fig. 3, the information obtained from the k-space energy spectrum analysis of full Fourier EPI data can be used to quantify two different types of artifacts in partial Fourier EPI. However, in actual partial Fourier EPI based fMRI studies, the full Fourier EPI scan of the same TE (and thus with identical echo-shifting effect) usually cannot be achieved. Therefore, one may only perform the k-space energy spectrum analysis of the acquired partial Fourier EPI data in actual scans. Our further study shows that, as expected, the k-space energy spectrum analysis of partial Fourier EPI data enables the identification of pixels susceptible to Type 2 artifact, but not the pixels affected by Type 1 artifact (data not shown). The capability of identifying Type 2 artifact directly from the partial Fourier EPI data makes it possible to design an improved image reconstruction algorithm, as described in the next section.
Reduction of Type 2 Artifact in Partial Fourier Gradient-Echo EPI Using an Improved Reconstruction Procedure
As illustrated in our simulated and human brain EPI data (Figs. 2 and 3), Type 2 artifact can be eliminated if a complete knowledge of background phase information is available. Unfortunately, such information is generally unavailable in partial Fourier EPI scans. Here we propose an improved partial Fourier EPI reconstruction algorithm, in which the information from the k-space energy spectrum analysis of partial Fourier EPI data is used to reduce Type 2 artifact. The improved partial Fourier EPI reconstruction algorithm is schematically illustrated in Fig. 4. Using a conventional partial Fourier EPI scan scheme, portions of the k-space data, i.e., in the positive ky domain (area 2 in Fig. 4a) and the central ky band (area 1 in Fig. 4a), are acquired. The partial Fourier EPI data are first processed with the k-space energy spectrum analysis method to generate a ky displacement map. Pixels with the corresponding k-space energy peaks located in k-space area 1 and area 2 are identified (Fig. 4b).
FIG. 4.
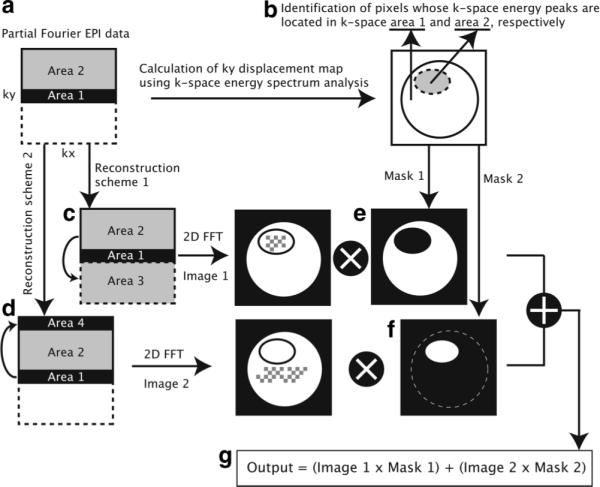
An improved partial Fourier EPI reconstruction algorithm consisting of two schemes. a: The acquired partial Fourier EPI k-space data. b: The k-space energy spectrum analysis is applied to identify pixels with k-space energy peaks located in k-space area 1 and area 2 (a), respectively. c: Partial Fourier reconstruction scheme 1 (i.e., the conventional partial Fourier reconstruction) is designed for pixels whose k-space energy peaks are located in k-space area 1. Data in unacquired area 3 are calculated from data in area 2, with low-resolution background phase information estimated from data in area 1. d: Partial Fourier reconstruction scheme 2 is designed for pixels whose k-space energy peaks are located in k-space area 2. Data in area 4 are calculated from data in area 1, with low-resolution background phase information estimated from data in area 2. e: Mask 1 is generated to identify pixels whose k-space energy peaks are located in k-space area 1. f: Mask 2 is generated to identify pixels whose k-space energy peaks are located in k-space area 2. g: The output of the reconstruction algorithm is the combination of images obtained from two reconstruction algorithms, filtered with different masks.
The acquired data are then processed with two different partial Fourier reconstruction schemes. It should be noted that these two partial Fourier reconstruction schemes are actually based on the same calculation strategy. The full list of the calculation strategies (e.g., Margosian method, homo-dyne detection method, singular value decomposition (SVD) method, and iterative methods) are reviewed in Refs. 5 and 6. In our implementation, we choose Cuppen's iterative method as our partial Fourier calculation strategy (1,5). As described in the next two paragraphs, the two reconstruction schemes in Fig. 4 differ only in their extension of the k-space coverage, which is chosen based on the output of the k-space energy spectrum analysis.
As shown in Fig. 4c, reconstruction scheme 1 is actually the conventional partial Fourier EPI reconstruction scheme, covering k-space area 1, 2, and 3. It is designed for pixels with k-space energy peaks located in k-space area 1 (i.e., the central band of the acquired k-space data). In reconstruction scheme 1, the unacquired k-space data (area 3 in Fig. 4c) are calculated from the acquired k-space data (area 2), based on the low-resolution background phase information estimated from the central ky band (area 1), using partial Fourier Hermitian property. An image is then reconstructed with 2D FFT, in which Type 2 artifacts may appear in pixels whose corresponding k-space energy peaks are located in k-space area 2. Those pixels (susceptible to Type 2 artifact in reconstruction scheme 1) have actually been identified in Fig. 4b with k-space energy spectrum analysis.
Reconstruction scheme 2 (Fig. 4d) covers k-space areas 1, 2, and 4. It is designed for pixels with the corresponding k-space energy peaks located in k-space area 2 (i.e., the positive ky domain of the acquired k-space data). In reconstruction scheme 2, k-space data in area 4 are calculated from the acquired k-space data in area 1, with background phase information estimated from data in area 2, using partial Fourier Hermitian property. An image is then reconstructed with 2D FFT, in which Type 2 artifacts may appear in pixels whose corresponding k-space energy peaks are located in area 1. For pixels whose corresponding k-space energy peaks are located in area 2, the signals can be properly reconstructed with reconstruction scheme 2.
We note that the pixels with the corresponding k-space energy peaks located in k-space area 1 and area 2 can be properly reconstructed with reconstruction scheme 1 and scheme 2, respectively. Therefore, images obtained from reconstruction scheme 1 and scheme 2 need to be properly combined. Based on the information obtained from Fig. 4b, two image-domain masks are generated to identify pixels with the corresponding k-space energy peaks located in k-space area 1 and area 2, as schematically illustrated in Fig. 4e and f. A pixel-by-pixel multiplication of the image obtained from Fig. 4c and the mask obtained from Fig. 4e generates an image with correct signal intensities in pixels with k-space energy peaks located in area 1. On the other hand, a pixel-by-pixel multiplication of the image obtained from Fig. 4d and the mask obtained from Fig. 4f generates an image with correct signal intensities in pixels whose k-space energy peaks are located in area 2. As shown in Fig. 4g, the output of the proposed algorithm is an image with greatly reduced Type 2 artifact, which is the summation of two images obtained from reconstruction schemes 1 and 2 filtered with appropriate image-domain masks.
The algorithm shown in Fig. 4 combines images obtained from two reconstruction schemes, corresponding to different extensions of k-space coverage, to avoid Type 2 artifact. Theoretically, minor residual artifacts may still exist in this two-scheme reconstruction algorithm, since the k-space energy peaks may not be located at the k-space center in either scheme. To further correct for this effect, the two-scheme reconstruction algorithm may be extended to a more general multischeme algorithm.
The k-space coverage of the multischeme reconstruction is illustrated in Fig. 5a and b (which may replace Fig. 4c and d in partial Fourier EPI reconstruction), assuming the matrix size of the acquired k-space data is Nx • Ny. As shown in Fig. 5a, if the k-space energy peak is closer to the most positive acquired ky line, then the reconstructed k-space coverage should be extended along the positive ky domain by Ny–2p lines (where p is the distance between the k-space energy peak and the most positive acquired ky line). On the other hand, if the k-space energy peak is closer to the most negative acquired ky line (Fig. 5b), then the reconstructed k-space should be extended along the negative ky domain by Ny–2q lines (where q is the distance between the energy peak and the most negative acquired ky line). In this way, the k-space energy peak will always be located at the center of the reconstructed k-space for all possible levels of the k-space energy peak displacement.
FIG. 5.
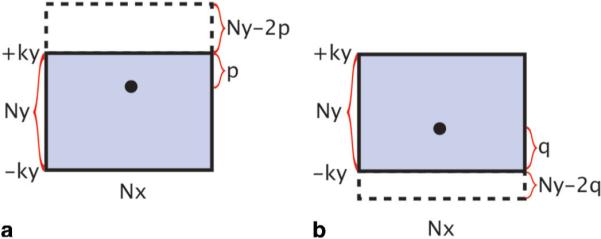
The k-space coverage in the multischeme reconstruction algorithm. a: When the k-space energy peak is closer to the most positive acquired ky lines, the reconstructed k-space coverage should be extended along the positive ky domain by Ny–2p lines, where p is the distance between the energy peak and the most positive acquired ky line. b: When the k-space energy peak is closer to the most negative acquired ky lines, the reconstructed k-space coverage should be extended along the negative ky domain by Ny–2q lines, where q is the distance between the energy peak and the most negative acquired ky line. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]
In the multischeme reconstruction algorithm, Ny images of different reconstruction schemes will first be generated from the acquired k-space data using the partial Fourier Hermitian property. Each reconstruction scheme is appropriate only for certain image pixels, with their corresponding k-space energy peaks located at the k-space center for this scheme. Therefore, those Ny images need to be combined to generate a single output image, using Ny masks produced from the ky displacement map (similar to the procedure shown in Fig. 4e, f, and g). In this process, the signals in the output image will always be obtained from the appropriate reconstruction schemes, in which the corresponding k-space energy peak is located at the k-space center.
EXPERIMENTS AND RESULTS
Application of the conventional and improved partial Fourier EPI reconstruction procedures to human brain EPI data is shown in Fig. 6. Full Fourier gradient-echo EPI data were acquired from healthy subjects with a 1.5 Tesla system (General Electric). Scan parameters included: matrix size • 64 • 64, slice thickness • 4 mm, FOV • 24 cm • 24 cm, inter-ky line echo-spacing time • 0.592 ms, and readout bandwidth • 100 kHz. The reconstruction programs were implemented on our Apple MacPro computer (CPU: 2.66 GHz dual core Intel Xeon; Memory: 4 GB) with Matlab programming language (Mathworks, Natick, MA, USA). Multiple partial Fourier EPI data sets, corresponding to different numbers of acquisition ky lines (34, 36, 38, . . . , 64), were generated from the acquired full Fourier EPI data through k-space truncation. Images of the same reconstruction matrix size (64 • 64) were then reconstructed from data sets corresponding to different numbers of acquisition ky lines using four approaches: 1) Cuppen's algorithm with full knowledge of image background phase (that is available from full Fourier EPI data); 2) the conventional Cuppen's algorithm with low-resolution estimation of image background phase (from the central ky band); 3) the improved two-scheme partial Fourier reconstruction method with low-resolution estimation of image background phase; and 4) the multischeme partial Fourier reconstruction method with low-resolution background phase information. The reconstructed partial Fourier EPI images were then compared with the full Fourier EPI images, and the levels of residual artifacts were calculated. For each 2D EPI image (64 • 64), the reconstruction time was 0.06 s for the conventional Cuppen's algorithm, 2.2 s for the proposed two-scheme reconstruction method, and 4 s for the proposed multischeme reconstruction method.
FIG. 6.
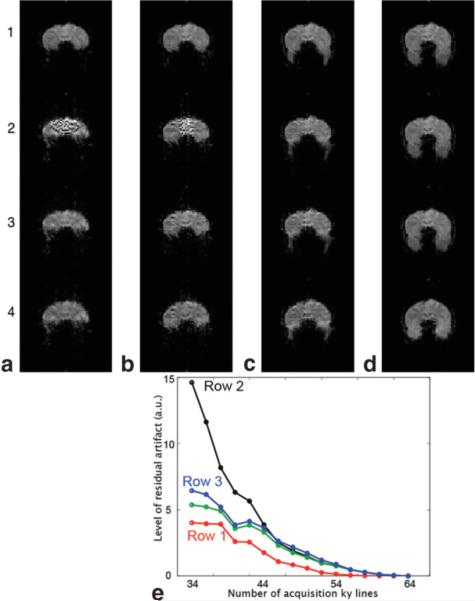
a–d: Partial Fourier gradient-echo EPI with different numbers of acquisition ky lines (36, 40, 46, and 64). Row 1: Cuppen's reconstruction with full knowledge of background phase. Row 2: Cuppen's reconstruction with low-resolution background phase information. Row 3: Improved partial Fourier EPI reconstruction with low-resolution background phase information. Row 4: Partial Fourier EPI after distortion correction. e: The residual artifact in partial Fourier EPI generated from data with different numbers of acquisition ky lines using different reconstruction methods. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]
Images of a selected coronal-plane, corresponding to four different numbers of acquisition ky lines: 36, 40, 46, and 64, are shown in Fig. 6a to d, respectively. Images reconstructed using Cuppen's algorithm with full knowledge of image background phase are shown in row 1. As explained previously (e.g., Fig. 3c), these images are affected by only Type 1 artifact but not Type 2 artifact. The difference between the reconstructed partial Fourier images and the full Fourier images thus indicates the levels of Type 1 artifact corresponding to different numbers of acquisition ky lines, as shown by red data points in Fig. 6e. Residual artifacts in Fig. 6e were calculated by measuring the difference between partial Fourier and full Fourier image on a pixel-by-pixel basis, followed by summing the square of difference for all pixels.
When the background phase values are estimated from the central ky band, the reconstructed partial Fourier EPI is always affected by additional (Type 2) artifacts, as shown in row 2 of Fig. 6a–d. It can be seen that Type 2 artifact (i.e., artificial signal elevation) decreases as the number of acquisition ky line increases. The differences between conventional partial Fourier EPI (based on Cuppen's reconstruction with low-resolution background phase information) and the full Fourier EPI, corresponding to different numbers of acquisition ky lines, are presented by black data points in Fig. 6e.
Using the new two-scheme partial Fourier reconstruction algorithm (Fig. 4), the reconstructed images have significantly reduced Type 2 artifact (row 3 of Fig. 6a–d) in comparison to images obtained with the conventional method (row 2). As shown in Fig. 6e, the residual artifacts seen with the improved method (blue data points) are significantly smaller than those obtained with the conventional method (black data points), when the number of acquisition ky lines is smaller than 44. Using the multi-scheme partial Fourier reconstruction algorithm (raw image not shown), the residual artifacts may be further reduced for data with a very small number of acquisition ky lines (34 and 36), as shown by the green data points in Fig. 6e.
We have shown in our previous work (11) that the field inhomogeneity maps calculated from the k-space energy spectrum analysis can be used to convert EPI images from distorted to nondistorted coordinates. This EPI distortion correction procedure is compatible with the proposed partial Fourier EPI reconstruction. For example, the geometric distortions in EPI (row 3) can be removed, and the corrected EPI data (row 4) can then be directly coregistered with anatomic reference images. It should be noted that uncorrected EPI images shown in row 1 to row 3, are distorted to the same level, since they have an identical inter-ky line echo spacing time (which determines the level of geometric distortions).
DISCUSSION
As described in previous sections, the k-space energy spectrum analysis of partial Fourier gradient-echo EPI provides information on the k-space energy location for all image-domain pixels. Based on this information, we have designed an improved partial Fourier EPI reconstruction algorithm to generate images with reduced Type 2 artifact. On the other hand, Type 1 artifact (i.e., complete signal loss) occurs as a result of the k-space peak energy displacement into the unsampled ky domain, and k-space energy spectrum analysis of partial Fourier EPI data cannot provide any useful information related to Type 1 artifact.
As illustrated by Fig. 6e, both Type 1 and Type 2 artifacts can be decreased by simply increasing the number of acquisition ky lines in partial Fourier EPI scans. However, in order to achieve the optimal TE and BOLD sensitivity in high-resolution fMRI studies, reducing the number of acquisition ky lines is needed and therefore the capability of reducing Type 2 artifacts in postprocessing is important. We would like to emphasize that, the dependence of artifact level on the number of acquisition ky lines, presented in Fig. 6e, is calculated from data of the same TE. In actual partial Fourier gradient-echo EPI scans, a shorter minimal TE may be achieved as the number of acquisition ky lines decreases. Therefore, the levels of both Type 1 and Type 2 artifacts shall be further reduced, when a shorter TE is chosen for partial Fourier EPI.
In order to reduce Type 1 artifact in partial Fourier gradient-echo EPI, one has to perform extra quality control scans in advance and design proper scan strategies for the subsequent partial Fourier EPI scans. The quality control can be achieved in several different ways. For example, one can measure the in-plane field gradients using multiple full Fourier gradient-echo EPI or asymmetric spin-echo EPI with different T2* weightings (16), and then use Eqs. [1] and [2] in reference (11) to predict the k-space energy distribution pattern corresponding to partial Fourier EPI scan with the desired parameters (such as TE, matrix size, number of oversampling ky lines, etc.). The scan parameters (especially the number of acquisition ky lines) should be chosen carefully so that Type 1 signal loss artifact in the targeted brain regions can be avoided. It should be noted that, because the echo-shifting effect and k-space peak energy location directly determine the effective TE (15), it is important that the imaging parameters are chosen in such a way that the effective TE in the targeted brain regions are capable of providing good BOLD sensitivity when performing fMRI studies.
We expect that partial Fourier gradient-echo EPI will play a more important role in future fMRI studies performed at high magnetic fields. Because tissue T2* value and thus the optimal TE value for BOLD contrast decreases with the magnetic field strength, it will be very challenging to achieve optimal BOLD sensitivity for high-field fMRI scans without partial Fourier gradient-echo EPI. The improved partial Fourier EPI reconstruction method (for Type 2 artifact removal) and quality control procedure (for Type 1 artifact reduction) discussed in this work will be helpful for future high field fMRI studies. It should be noted that, parallel imaging is also an important strategy to provide high-resolution gradient-echo EPI data with short TE. The combination of parallel imaging and partial Fourier EPI may also help reduce Type 1 and Type 2 artifacts, and may prove a useful approach for high field fMRI (17,18).
We have demonstrated that the new reconstruction algorithm proposed here (Fig. 4) improves the image quality of partial Fourier gradient-echo EPI. Actually, the same algorithm can also be applied to improve the image quality of partial Fourier gradient-echo imaging, when the partial Fourier scan strategy is applied along the readout direction to reduce the minimal TE of gradient-echo imaging. As noted by Posse (12), the in-plane susceptibility field gradients also induce an echo-shifting effect along the readout direction in gradient-echo imaging. We expect that Type 2 artifact also exists in ultra-short TE partial Fourier gradient-echo imaging, and this artifact can also be reduced using the proposed reconstruction algorithm shown in Fig. 4 (but applied along the readout direction of partial Fourier gradient-echo imaging).
Acknowledgments
Grant sponsor: National Institutes of Health (NIH); Grant numbers: R03EB003902; R21EB005690; U41RR019703.
REFERENCES
- 1.Cuppen JJ, Groen JP, Konijn J. Magnetic resonance fast Fourier imaging. Med Phys. 1986;13:248–253. doi: 10.1118/1.595905. [DOI] [PubMed] [Google Scholar]
- 2.Haacke EM, Lindskog ED, Lin W. A fast, iterative, partial-Fourier technique capable of local phase recovery. J Magn Reson. 1991;92:126–145. [Google Scholar]
- 3.Margosian P, Schmitt F, Purdy D. Faster MR imaging: imaging with half the data. Health Care Instrum. 1986;1:195–197. [Google Scholar]
- 4.Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE Trans Med Imaging. 1991;10:154–163. doi: 10.1109/42.79473. [DOI] [PubMed] [Google Scholar]
- 5.McGibney G, Smith MR, Nichols ST, Crawley A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn Reson Med. 1993;30:51–59. doi: 10.1002/mrm.1910300109. [DOI] [PubMed] [Google Scholar]
- 6.Zhang X, Yacoub E, Hu X. New strategy for reconstructing partial-Fourier imaging data in functional MRI. Magn Reson Med. 2001;46:1045–1048. doi: 10.1002/mrm.1296. [DOI] [PubMed] [Google Scholar]
- 7.Xu Y, Haacke EM. Partial Fourier imaging in multi-dimensions: a means to save a full factor of two in time. J Magn Reson Imaging. 2001;14:628–635. doi: 10.1002/jmri.1228. [DOI] [PubMed] [Google Scholar]
- 8.Jesmanowicz A, Bandettini PA, Hyde JS. Single-shot half k-space high-resolution gradient-recalled EPI for fMRI at 3 Tesla. Magn Reson Med. 1998;40:754–762. doi: 10.1002/mrm.1910400517. [DOI] [PubMed] [Google Scholar]
- 9.Hyde JS, Biswal BB, Jesmanowicz A. High-resolution fMRI using multislice partial k-space GR-EPI with cubic voxels. Magn Reson Med. 2001;46:114–125. doi: 10.1002/mrm.1166. [DOI] [PubMed] [Google Scholar]
- 10.Lu H, Mazaheri Y, Zhang R, Jesmanowicz A, Hyde JS. Multishot partial-k-space EPI for high-resolution fMRI demonstrated in a rat whisker barrel stimulation model at 3T. Magn Reson Med. 2003;50:1215–1222. doi: 10.1002/mrm.10655. [DOI] [PubMed] [Google Scholar]
- 11.Chen NK, Oshio K, Panych LP. Application of k-space energy spectrum analysis to susceptibility field mapping and distortion correction in gradient-echo EPI. Neuroimage. 2006;31:609–622. doi: 10.1016/j.neuroimage.2005.12.022. [DOI] [PubMed] [Google Scholar]
- 12.Posse S. Direct imaging of magnetic field gradients by group spin-echo selection. Magn Reson Med. 1992;25:12–29. doi: 10.1002/mrm.1910250103. [DOI] [PubMed] [Google Scholar]
- 13.Weisskoff RM, Davis TL. Correcting gross distortion on echo planar images.. Society for Magnetic Resonance in Medicine (SMRM) 11th Annual Scientific Meeting; Berlin, Germany. 1992. [Google Scholar]
- 14.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 15.Deichmann R, Josephs O, Hutton C, Corfield DR, Turner R. Compensation of susceptibility-induced BOLD sensitivity losses in echo-planar fMRI imaging. Neuroimage. 2002;15:120–135. doi: 10.1006/nimg.2001.0985. [DOI] [PubMed] [Google Scholar]
- 16.Reber PJ, Wong EC, Buxton RB, Frank LR. Correction of off resonance-related distortion in echo-planar imaging using EPI-based field maps. Magn Reson Med. 1998;39:328–330. doi: 10.1002/mrm.1910390223. [DOI] [PubMed] [Google Scholar]
- 17.Hu HH, Madhuranthakam AJ, Kruger DG, Glockner JF, Riederer SJ. Combination of 2D sensitivity encoding and 2D partial fourier techniques for improved acceleration in 3D contrast-enhanced MR angiography. Magn Reson Med. 2006;55:16–22. doi: 10.1002/mrm.20742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bydder M, Robson MD. Partial Fourier partially parallel imaging. Magn Reson Med. 2005;53:1393–1401. doi: 10.1002/mrm.20492. [DOI] [PubMed] [Google Scholar]