Fast imaging for magnetic resonance electrical impedance tomography

Abstract

In magnetic resonance electrical impedance tomography (MREIT), currents are injected into an object, the resulting magnetic flux density measured using MRI, and the conductivity distribution reconstructed using these MRI data. The relatively long acquisition times of conventional MREIT methods limit the signal averaging rate and are susceptible to motion artifacts. In this study, we reconstructed the conductivity distribution of an agarose gel phantom from data acquired in under a minute using a single shot, spin echo, echo planar imaging (SS-SEPI) pulse sequence. The results demonstrate that SS-SEPI can be used for MREIT data acquisition.

1. Introduction

In electrical impedance tomography (EIT), a conductivity-dependent current density distribution is first generated within an object, either by direct current injection through surface electrodes or induction using external coils. Peripheral voltage measurements are then acquired and used to reconstruct the conductivity distribution within the object. Conventional EIT systems are physically limited by the number of electrodes that can be placed on an object’s surface, thereby restricting the number of measurements that can be acquired. Furthermore, these measurements are taken on the surface of the object and not within the object itself. Boundary potentials suffer from low sensitivity to interior conductivity perturbations. As a result, this modality suffers from poor, non-uniform spatial resolution [1].

A solution to these limitations is to acquire a larger number of measurements from directly inside the object. Interior potentials cannot be acquired non-invasively. However, applied currents generate a conductivity-dependent magnetic flux density distribution, of which the component parallel to the main static field of an MRI scanner (z-component) can be measured by MRI using an appropriate pulse sequence. Such measurements can be made with high spatial resolution and with high sensitivity to interior conductivity perturbations. Mapping of the current-generated magnetic flux density using MRI and conductivity reconstruction using this measurement data form the basis of the technique called magnetic resonance electrical impedance tomography (MREIT).

MRI pulse sequences have been developed to measure the effects of applied currents at various frequencies – DC [2], RF at the Larmor frequency of the scanner [3], and low frequency AC up to 2 kHz [4,5]. These methods all utilize the standard 2D spin echo (SE) pulse sequence, which acquires one line of k-space data per repetition time (TR). The long acquisition times of these methods limit the signal averaging rate, and make them susceptible to motion artifacts during in vivo studies. In this study, we investigated the use of a single shot, spin echo, echo planar imaging (SS-SEPI) pulse sequence for data acquisition in MREIT. This sequence acquires the entire k-space data in a single TR, and thus would be useful in MREIT data acquisition for decreasing the total scan time and reducing susceptibility to motion artifacts.

2. Materials and Methods

2.1 Background

Variations in the main static MRI field alter the Larmor frequency, which effects the phase of MRI measurements. Such perturbations can be the result of injected currents, as well as other sources such as field inhomogeneities and eddy currents. Measurement of such perturbations by MRI was first proposed by Maudsley et al for the purpose of mapping the field inhomogeneity of an MRI system [6].

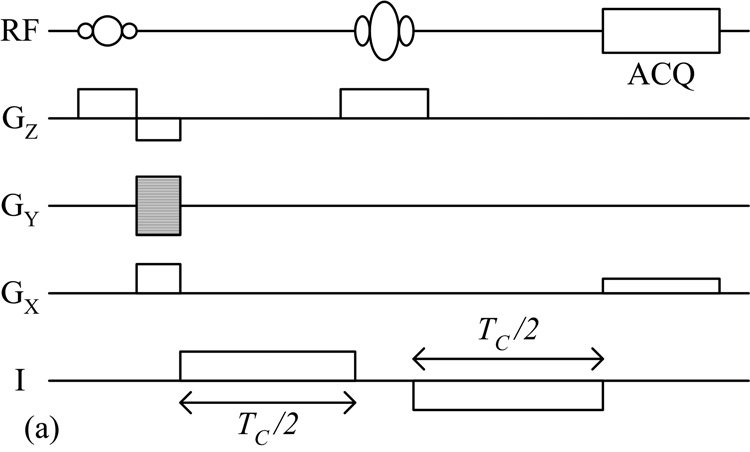
Scott et al later proposed using the standard SE pulse sequence specifically for measuring the effects of applied currents [2]. The injection of a bipolar current pulse was synchronized to the pulse sequence, as shown in Fig. 1a, and the resulting magnetic flux density distribution was encoded into the phase of the MR image as:

$$\phi (\mathbf{r})=\gamma ·T_C·B(\mathbf{r})$$ (1)

where φ(r) is the phase shift at point r, γ is the gyromagnetic ratio, T_C is the total duration of the injected current, and B(r) is the amplitude of z-component current-generated magnetic flux density at point r. A bipolar pulse was utilized so that the phase contributions from current applied before and after the RF refocusing pulse added constructively. Data were collected twice, each with opposite polarities in the applied current waveform. The resulting phase maps were subtracted then divided by two, so as to cancel out contributions from sources other than the injected current.

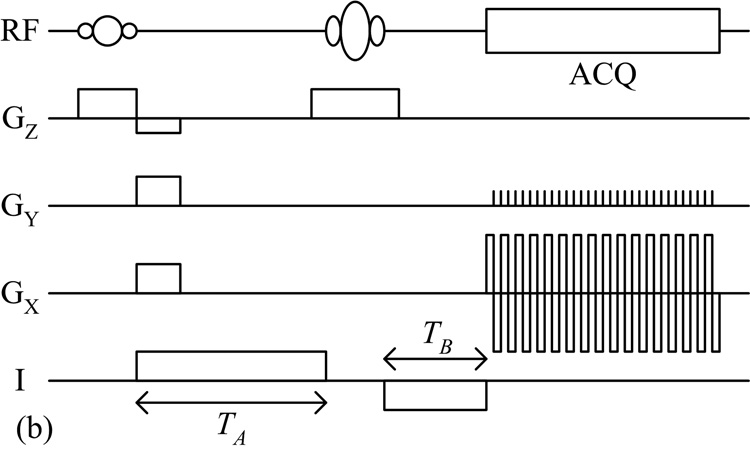
Fig. 1.

(a) Standard SE and (b) SS-SEPI pulse sequences used for MREIT data acquisition.

The noise in magnetic flux density measurements is inversely proportional to both T_C and the signal-to-noise ratio (SNR) of the image [7]. Decreasing the echo time (TE) improves the image SNR, but decreases the maximum possible T_C. Alternatively, increasing TE allows for longer T_C, but decreases the image SNR. Scott et al calculated that the optimum balance between these factors occurs when TE is set close to the T₂ value of the object [7]. As such, gradient echo-based sequences have generally been avoided for magnetic flux density measurements since T₂* decay would significantly reduce the SNR when using typical optimum TE values.

2.2 SS-SEPI MREIT

Reported MREIT studies have all utilized some form the standard SE pulse sequence. In this study, we synchronized the injection of an asymmetric bipolar current pulse to a SS-SEPI pulse sequence, as shown in Fig. 1b. As with the standard SE method, the current-generated magnetic flux density introduced a phase shift as given in Eq. (1), with T_C now equal to T_A plus T_B. To achieve maximum signal (phase shift), current was applied throughout the pulse sequence, except during the application of the slice selective RF pulses and data acquisition. Restricting the current during these periods prevented the current-generated magnetic flux density from perturbing slice selection and distorting the data sampling.

While EPI-based sequences can drastically reduce scan time, its complexity introduces additional challenges. Phase inconsistencies between alternating lines of sampled k-space generate Nyquist ghost artifacts that appear half the field of view (FOV) along the phase encoding direction from the actual object. These artifacts degrade the SNR of the image, and in regions where the ghosts and the original object overlap, the phase becomes convoluted, leading to an inaccurate measurement of the current-generated magnetic flux density. To eliminate Nyquist ghosting, we utilized the correction method of Buonocore and Gao [8]. A 2D phase map was calculated from odd-echo-only and even-echo-only images, and used to correct the corrupted data. In cases where original object and ghost images do not overlap, their method effectively eliminates Nyquist ghosting and restores the SNR of the original object. For this study, we avoided overlap by using a large FOV such that the imaged object spanned less than half the length of the phase encoding direction.

Due to the low sampling bandwidth in the phase encoding direction, EPI-based sequences are also prone to geometric distortions caused by inhomogeneity of the main static MRI field. To correct for such distortions, we utilized the technique of Chiou et al [9]. Additional SS-SEPI data using no applied currents were acquired with the gradient echo time fixed and the spin echo time shifted by integral multiples of the inter-echo spacing. A phase modulation factor was calculated using this data. By modulating the MREIT k-space data with this correction factor, the geometric distortions were removed while preserving the phase information containing the current-generated magnetic flux density distribution.

2.3. MREIT Reconstruction

Given the (z-component) magnetic flux density distribution, several algorithms have been proposed to reconstruct the conductivity distribution. These include the sensitivity matrix method (SMM) [10,11], ∇²B_z algorithms [12,13], and ∇B_z algorithms [14,15]. For this study, we utilized the SMM. The object domain was discretized into a mesh of first order triangular elements, chosen for compatibility with the finite element method (FEM) [16]. A linear relationship between conductivity perturbations and z-component magnetic flux density perturbations was then assumed, such that:

$$\mathrm{\Delta }B=\mathbf{S}\mathrm{\Delta }\sigma$$ (2)

where S is known as the “sensitivity” matrix. Given m measurement points and n conductivity elements, ΔB is an m × 1 vector, Δσ is an n × 1 vector, and S is an m × n matrix. An initial conductivity distribution σ_initial was assumed (e.g. uniform conductivity), and the problem linearized around this initial condition:

$$B_{\mathit{\text{final}}}-B_{\mathit{\text{initial}}}=\mathbf{S}\mathit{(}{\sigma }_{\mathit{\text{final}}}-{\sigma }_{\mathit{\text{initial}}}\mathit{)}$$ (3)

where B_initial is the z-component magnetic flux density distribution given σ_initial and calculated using the FEM and Biot-Savart Law, B_final is the MRI measured z-component magnetic flux density, σ_final is the actual (unknown) conductivity distribution. Use of a uniform conductivity distribution as σ_initial has been applied in previous phantom and in vivo studies [17–20], although selecting a more realistic initial condition based on any a priori information may improve the final reconstruction. The matrix elements of S were calculated using:

$$S_{ij}={\left[\frac{\partial B_i}{\partial {\sigma }_j}\right]}_{\sigma ={\sigma }_{\mathit{\text{initial}}}}\approx {\left[\frac{\mathrm{\Delta }{B}_i}{\mathrm{\Delta }{\sigma }_j}\right]}_{\sigma ={\sigma }_{\mathit{\text{initial}}}}.$$ (4)

A particular element of S is the change in the magnetic flux density of the i^th pixel with respect to the change in the conductivity of the j^th finite element around the initial condition σ_initial. To find S_ij numerically, the conductivity of the j_th finite element was perturbed by a small amount Δσ_j (e.g. 1% change) around σ_initial, and the resulting magnetic flux density calculated using the FEM and Biot-Savart Law. S_ij was then approximated as the change in the magnetic flux density of the i_th pixel divided by the change in the conductivity of the j_th finite element.

In general, S is an ill-conditioned matrix, thus a simple least squares fit cannot be used to solve for σ_final. The equation was solved using the conjugate gradient method with Tikhonov regularization, where σ_final was found by:

$$\underset{{\sigma }_{\mathit{\text{final}}}}{{\displaystyle \text{min}}}\{\Vert \mathbf{S}\mathrm{\Delta }\sigma -\mathrm{\Delta }{B}_z{\Vert }^2+\lambda \Vert \mathrm{\Delta }\sigma {\Vert }^2\}$$ (5)

where λ is a regularization parameter [21]. The regularization parameter λ was chosen such that the calculated z-component magnetic flux density generated by the reconstructed conductivity distribution was closest to the MRI-measured magnetic flux density. After solving the equation, σ_final was assigned as the new, updated σ_initial, and the process was iterated to improve the results. For each iteration, S was recalculated using the updated σ_initial, and a new σ_final was found.

2.4 Experiment

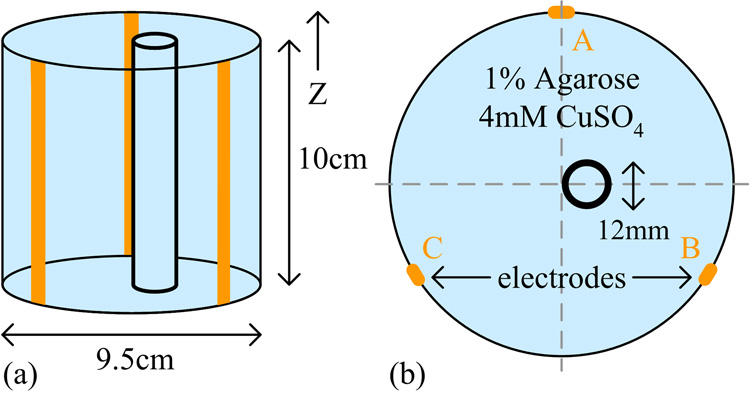
For the test phantom, a hollow acrylic cylinder with an inner diameter of 9.5 cm was filled to a thickness of 10 cm with 4 mM CuSO₄ and 1% (g/100 ml water) agarose. Within this disk, a smaller cylindrical shell of 12 mm diameter was utilized to simulate an electrically insulating region. The interior region was filled with the background gel to generate an MR signal. Three copper strips each 3 mm wide were placed equidistant to each other along the length of the inner wall, and used as electrodes to inject current into the interior region. The phantom was placed within a 4 T MRI system such that its cylindrical axis was parallel to the main static MRI field. A schematic of the phantom is shown in Fig. 2.

Fig. 2.

(a) Side view and (b) top view of the test phantom.

A current source was constructed and used to generate the injected currents [22]. Synchronization of the circuit output with the pulse sequence was controlled by the scanner computer through a digital interface. Wires connecting the current source to the electrodes were aligned parallel to the main static MRI field, so that the magnetic flux density generated by currents passing through them contained no z-component, and thus did not perturb the MRI signal.

A given set of injecting electrodes forms an “injection profile”. Since an infinite number of conductivity distributions can generate a single given magnetic flux density distribution, data from at least two different injection profiles is required to reconstruct a unique solution [23]. For this study, we collected data for two injection profiles, using electrode pairs A & B and A & C of Fig. 2. (The magnetic flux density distribution generated using the third possible electrode pair B & C is a linear combination of the fields generated using the two selected profiles). For each profile, a bipolar current pulse with a 4 mA amplitude was injected into the phantom, and data was acquired using the SS-SEPI pulse sequence with the following parameters: T_A = 28.2 ms, T_B = 1.7 ms, TR = 1 s, TE = 60 ms, slice thickness = 5 mm, FOV = 20 cm, data matrix = 64×64, BW = 167 kHz, and NEX = 10. The TE value was selected to optimize the SNR of the magnetic flux density measurements (TE ≈ T₂ of the agarose gel). In order to calculate the modulation factor for geometric distortion correction, 5 additional SS-SEPI data sets were acquired with the same parameters, except using no applied currents, a gradient echo TE of 60 ms, and spin echo TEs shifted by 0 µs, −864 µs, −1728 µs, −2593 µs, and −3456 µs relative to the gradient echo. For comparison, MREIT data was also acquired using the standard SE method with parameters: T_c = 56.6 ms, TR = 1 s, TE = 60 ms, slice thickness = 5 mm, FOV = 20 cm, data matrix = 64×64, BW = 50 kHz, and NEX = 4. A high resolution SE image was also acquired with parameters: TR = 500 ms, TE = 60 ms, slice thickness = 5 mm, FOV = 20 cm, data matrix = 256×256, BW = 50 kHz, and NEX = 2.

For reconstruction, a circular FEM mesh containing 1024 triangular elements was aligned to the phantom using the magnitude images. Magnetic flux density measurements were then calculated from the phase images. Data from the two injection profiles were used simultaneously in the conductivity reconstruction algorithms by combining the (linear) SMM equations. A total of 10 iterations of the SMM with Tikhonov regularization were utilized.

3. Results and Discussion

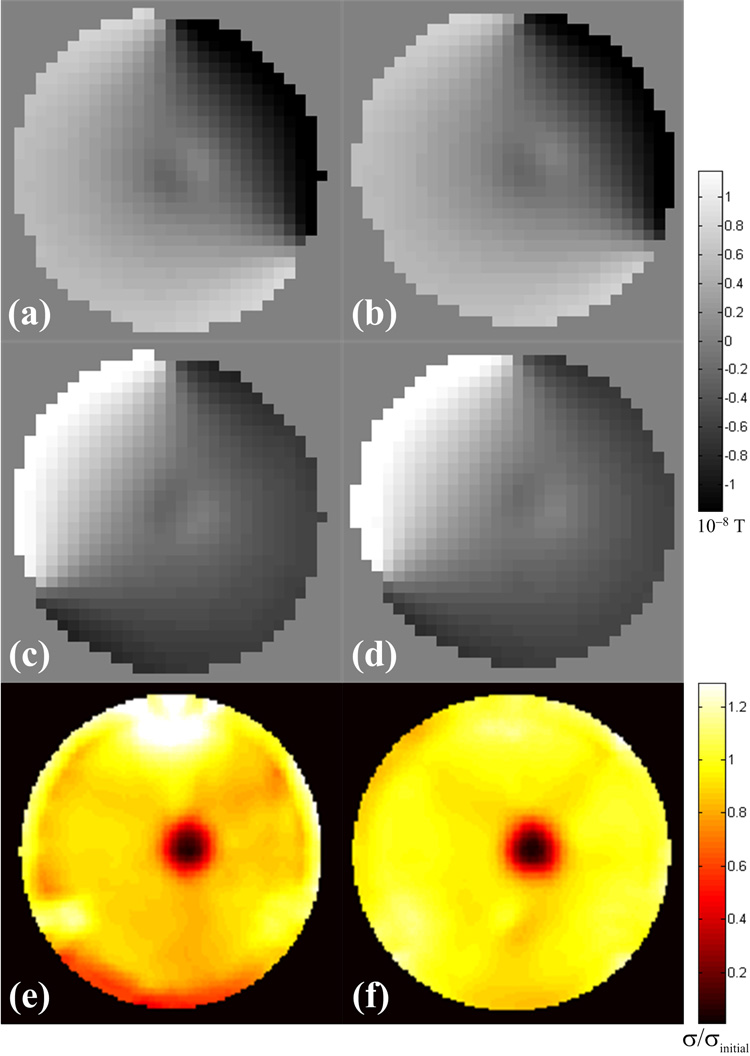
The magnetic flux density distributions and conductivity reconstructions generated from the acquired MRI data are shown in Fig. 3. Comparison with the SE results shows that the SS-SEPI pulse sequence was able to map out the general variation in the magnetic flux density due to the insulating region, and that this data can be used to reconstruct the conductivity distribution.

Fig. 3.

Magnetic flux densities for the (a,b) injection profile using electrodes A & B and (c,d) injection profile using electrodes A & C, and (e,f) reconstructed conductivity distributions of the test phantom for data acquired with the SS-SEPI and SE pulse sequences respectively. Conductivites are given relative to the initial uniform value assigned before iteration.

The uncorrected SS-SEPI data suffers from Nyquist ghosting, as well as significant geometric distortion as see by the large displacement of the inner cylindrical shell along the phase encoding direction in Fig. 4a. Close inspection of Figs. 4a–c shows that while the corrected SS-SEPI data is greatly improved over the uncorrected data, the original geometry of the phantom has not been fully restored. In addition to residual geometric distortion of the magnetic flux density maps, the remaining artifacts caused some misalignment in the boundary conditions for numerical calculation in the reconstruction algorithm. The increased artifacts in the conductivity reconstruction, especially near the periphery, are the result of these errors. The higher conductivity region at the top of the phantom may be the result of the remaining artifacts creating an increase in the apparent current density, while the lower conductivity band at the bottom may be the result of a decrease in the apparent current density.

Fig. 4.

(a) Uncorrected SS-SEPI, (b) corrected SS-SEPI, (c) MREIT SE and (d) high resolution SE magnitude images of the test phantom. The phase encoding direction is horizontal. The copper electrodes generated slight local distortions.

These residual artifacts indicate some limitations in our correction algorithm. To reduce these distortions, we can improve the field homogeneity. While second order shim coils were utilized in this study, additional channels could further improve the uniformity of the main static field. Use of alternate pulse sequences could also reduce these artifacts. For example, multi-shot EPI would increase the phase encoding bandwidth between segments of sampled k-space, thereby reducing the amount of distortion. However, this improvement would come at the expense of scan time, since multiple TRs would be required to acquire the full k-space data. For data processing, alternate geometric distortion correction algorithms may offer improved performance.

For this study, we utilized a large FOV to avoid the complication of overlap of the phantom image and Nyquist ghosts. In some cases, it may be desirable to decrease the FOV, such as when higher resolution is required. The Nyquist correction algorithm used in this study can address such overlap by estimating a linear phase correction in the overlap regions. The advantage of this technique is that no additional references scans are required. However, other correction techniques that utilize reference scans may offer improved performance.

An additional limitation of the SS-SEPI pulse sequence is that larger acquisition matricies require significant increases in the minimum TE and the sampling time, which reduces the image SNR. However, the results of this study demonstrate that conductivity reconstruction is possible with lower MR resolutions, such as the 3.125 mm by 3.125 mm by 5 mm voxels used here. The exact relationship between MR resolution and the minimum detectable conductivity perturbation will be investigated further.

The primary advantage of single shot EPI is that it acquires the entire k-space data in a single scan. This feature makes it potentially useful for in vivo MREIT measurements. Standard SE imaging is susceptible to motion artifact, which severely distorts the phase data required for calculation of the magnetic flux density distribution. We can try to minimize subject motion, but it cannot altogether be eliminated (e.g. circulation, respiration). Gating techniques can help, but require additional hardware/software development and can further increase acquisition times. In SS-SEPI, successive lines of k-space data are collected within a few milliseconds of each other. Since typical subject motion is negligible on this time scale, k-space lines do not experience any significant phase perturbation, and the resulting image is free of motion artifact.

Perhaps the main obstacle to in vivo application of MREIT on humans is that relatively large current injection levels are presently required to obtain accurate conductivity images. Lower current levels result in a decrease in the SNR of the acquired magnetic flux density maps used in the reconstruction process. Oh et al reconstructed conductivity images of a biological tissue phantom in a 3T MRI system using the harmonic B_z algorithm and found a significant degradation in the reconstruction at as high as 12 mA of injected current [24]. We have recently reported MREIT studies using injected currents of around 1 mA [17–20]. Despite this decrease in the applied current, this level still remains above the required safety limits for application in human studies. The IEC 601 standard limits “patient auxiliary currents” to 100 µA at low frequencies. Techniques to increase the SNR of the acquired data and/or improvements to the data processing that will enable accurate reconstruction with lower SNR data are needed.

A simple method to improve the SNR is to increase signal averaging. For our previous studies using the standard SE method, 5–10 minutes were required to collect a sufficient data set (two opposing current polarities times two injection profiles) using 1 mA of injected current. Reducing the current from 1mA down to 100 µA corresponds to a 10 fold decrease in the phase signal amplitude and SNR of the B_z maps. Assuming noise is uncorrelated from one acquisition to the next, 100 signal averages would be needed to recover the SNR, requiring a scan time of over 8 h. In practice, the presence correlated noise also decreases the efficiency of additional averaging [25].

To reduce scan time to accommodate large signal averaging, the SS-SEPI pulse sequence can be used to acquire MREIT data. While the larger readout sampling bandwidth and longer sampling time inherent in EPI-based sequences results in a decrease in the image SNR per acquisition, the increased signal averaging available in an allotted study time may result in a net SNR gain. For example, in this study the bandwidth of the SS-SEPI acquisition was 3.3 times higher than the SE acquisition. The longer sampling time of the SS-SEPI acquisition also contributed to lower SNR due to increased T₂* blurring. However, 64 signal averages could have been acquired with the SS-SEPI pulse sequence in the same time required to obtain a single average of SE data, contributing to an SNR gain of 8. The balance between these SNR factors will be further investigated.

While data from a single SS-SEPI acquisition should produce a motion-free image, a set of images acquired from multiple scans for signal averaging may not generate identical results. While each individual image may be free of motion artifact, the physical location and/or shape of the (moving) object may change between scans. When signal averaging is performed, the addition of these slightly different images will result in blurring in regions where the object position/shape has changed. If each image is spatially transformed to match a common high resolution anatomical template before averaging, then all images will conform to the same position/shape after this morphing. Such morphing may also correct for any residual geometric distortion. The (matching) modified images could then be added together to improve the SNR. While this method may reduce motion blurring, its effect on the resulting magnetic flux density map must be investigated further.

4. Conclusion

We have demonstrated that the SS-SEPI pulse sequence can be used for MREIT data acquisition. As such, we are presently investigating this technique with more complex phantoms and in vivo studies. While the inherent EPI issues of Nyquist ghosting and geometric distortion must be addressed, this method offers a significant reduction in scan time. With its insensitivity to subject motion and ability to perform larger signal averaging in a given study time, this method may address some of the key obstacles limiting in vivo application of MREIT.