Statistical methods for analysis of radiation effects with tumor and dose location-specific information with application to the WECARE study of asynchronous contralateral breast cancer

Summary

Methods for the analysis of individually matched case-control studies with location-specific radiation dose and tumor location information are described. These include likelihood methods for analyses that just use cases with precise location of tumor information and methods that also include cases with imprecise tumor location information. The theory establishes that each of these likelihood based methods estimates the same radiation rate ratio parameters, within the context of the appropriate model for location and subject level covariate effects. The underlying assumptions are characterized and the potential strengths and limitations of each method are described. The methods are illustrated and compared using the WECARE study of radiation and asynchronous contralateral breast cancer.

1. Introduction

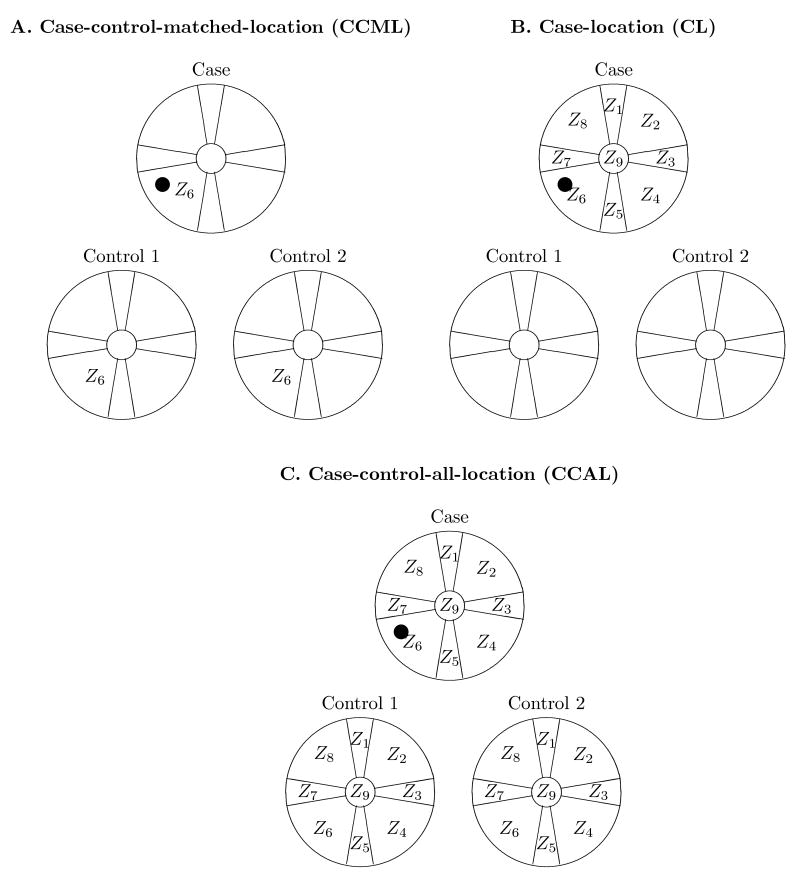
Epidemiologic studies of cancer outcomes after therapeutic radiation exposures are advantageous, compared to many occupational or environmental studies, in that exposures are more accurately known. However, doses to secondary tissues (those not specifically targeted therapeutically) may differ by orders of magnitude and need to be carefully estimated by dose reconstructions (Stovall et al., 2006). Since dose can vary appreciably even within an organ, analyses are based on doses to specific tumor locations within the organ. Studies that use this approach, assigning radiation dose to locations within the breast, lung, bone, and other organs have been used increasingly in recent years (Tucker et al., 1987; Travis et al., 2002, 2003; van Leeuwen et al., 2003; Gilbert et al., 2003). For each of these studies, the data includes information about radiation dose across, and tumor location within, the affected organ. Our interest in this type of data and the motivation for this work is the 1:2 matched case-control WECARE (Women's Environment Cancer And Radiation Exposure) study of radiation and asynchronous contralateral breast cancer (CBC) which has location of CBC within the breast and dose at locations across the breast. The basic location-specific data are illustrated in Figure 1C with region or location of CBC, within the nine location scheme, for the case and radiation dose Z_l within each location.

Figure 1.

Radiation dose comparisons suggested by the WECARE study. Z_l is the dose to the contralateral breast at location l due to treatment of the first breast cancer. The indexing counts around the breast in the direction of the center of the body and thus is “laterality independent.” The • marks a CBC that occurred within location 6 which received a dose of Z₆.

For the substantive analysis of the WECARE study, and has been typical for studies with location-specific tumor and dose information, analysis of radiation effects were performed using conditional logistic regression where dose at the case's CBC location is compared to the control doses at the same location in their contralateral breast (Stovall et al., 2008); what we will call the case-control-matched-location (CCML) approach shown in Figure 1A. The WECARE analyses raised questions about whether more statistical information could be obtained from the available data. In this paper, we address two of these questions by developing new analytic methods and providing a theoretic framework to study them.

First, while dose information is available for all locations, the CCML approach only uses dose at the location of the case's CBC. There are other reasonable dose comparisons. The case-location (CL) approach (Panel B) has the structure of 1:8 case-control data; the comparison is between the case's CBC location dose to the doses at the case's non-cancer locations. The controls are not used in this comparison. The case-control-all-location (CCAL) approach (Panel C) has the structure of 1:26 case-control data; the comparison is between the case's CBC location dose to the doses at each of the case's non-cancer locations and the doses at all the control subject locations. Given the data structures, a natural method of analysis for each is conditional logistic regression. The data structures in Figure 1 and the conditional logistic analysis assume that case's tumor can be assigned to one of the nine locations, so we will call the respective conditional logistic likelihoods the precise location CCML, CL, and CCAL likelihoods. The precise location likelihood methods are described in Section 3. A formal derivation based on counting processes is given in Web Appendix A and shows that precise location likelihoods may be derived as partial likelihoods in the usual sense, and that each is estimating the same radiation effects parameters, subject to different modeling assumptions. The CCAL uses “all the data” but the CCAL model is a submodel of both CCML and CL models so trades-off reduced variance for potential increased bias.

Second, for 15% of the WECARE study cases, the CBC could not be assigned to a single location. In Section 4 and Web Appendix C, we derive natural extensions of the precise location likelihoods with location of tumor assigned to a location-group, the smallest set of locations known to include the location of tumor origin. The location-group likelihood extension provides a valid way to use all of the WECARE data in the analysis, but requires additional assumptions about the spread of tumors. It turned out that the actual WECARE data were not well suited to illustrate these methods so we simulated location of origin and location-group outcomes for our evaluation of the approach.

In Section 5, we discuss how these methods benefited the WECARE study, recommendations for future studies of this type, and other applications.

2. The WECARE study data

The WECARE study is a population-based, 1:2 individually (counter-)matched case-control study designed to examine the joint roles of ATM gene mutations, radiation exposure, and CBC and is described fully elsewhere (Bernstein et al., 2004; Stovall et al., 2008). Briefly, the study design is a nested case-control study from a cohort of unilateral breast cancer patients ascertained by a consortium of five cancer registries, followed for occurrence of CBC (the cases). For each case, two controls were sampled from the time-since-first-breast-cancer risk set (Cox, 1972), matched on age at diagnosis of the first cancer, race, and registry, and counter-matched on registry-reported radiotherapy (RT) treatment. The entire WECARE case-control study consists of 708 CBC cases and 1399 unilateral breast cancer controls with 694 complete triplets. We note that, consistent with previous studies (Boice et al., 1992; Preston et al., 2002), radiation dose effects were only observed among younger women after substantial elapsed time since radiotherapy. Thus, we will particularly focus on the subgroup who were <45 years old at diagnosis of first breast cancer and whose CBC occurred at least five years after the first breast cancer (i.e., “<45, 5+ subgroup”). Since the controls are matched to the case on these factors, these consist of the 133 <45, 5+ subgroup cases and their 257 matched controls.

2.1 Location of second breast cancer in cases

As in Figure 1, we will index locations to account for laterality, with numbering, starting at the 12 o'clock position, toward the center of the body, i.e., the numbering of the nine locations is clockwise around the right breast and counter-clockwise for the left. Figure 1 shows the right breast, the numbering for the left breast is in the opposite direction. The case's CBC location of origin was determined based on the records from the diagnosing physician and a complete review of medical records. Because breast cancer patients are generally carefully and frequently screened for other cancer occurrences and, by definition, all of the WECARE cases were (unilateral) breast cancer patients before CBC occurred, the size of the CBC at diagnosis was usually small. Thus, of the 708 cases, 609 (110 in the <45, 5+ subgroup) case's CBC could be assigned to a single location of origin and, with their matched controls, constitute the precise location data set. For 99 cases (23 in the <45, 5+ subgroup), a location of CBC origin could not be assigned because of single tumors that spanned multiple locations (14), multiple tumors with foci located in different locations (34), or information on location was completely lacking in the medical records (51).

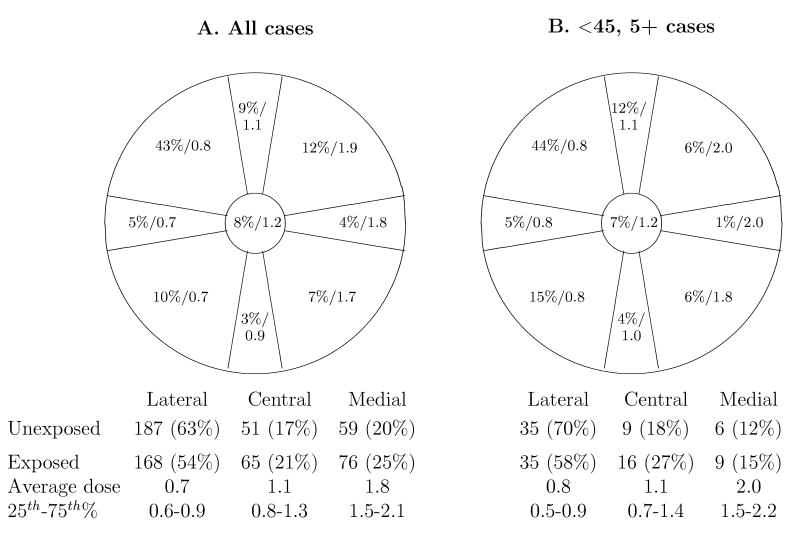
Figures 2A and B show the distribution of CBC over the nine locations for all cases and the <45, 5+ subgroup, respectively. Comparing the proportions of cases in the comparably sized quadrant locations, there is a marked increasing gradient in the density of tumors from the lower-medial locations to the upper-lateral locations. The location distribution is very much dominated by the “upper-outer” location (location 8 in Figure 1) with 43% of second cancers in this location. This distribution is similar to that found for first breast cancers (Spratt and Donegan, 1967).

Figure 2.

Distribution of CBCs (percent) in all cases and the average dose (Gy) among the radiation exposed cases. Restricted to 606 cases with precise location and known dose.

2.2 Dose data

For women who received RT for the first breast cancer, radiation dose to the nine locations on the contralateral breast was estimated based on information given in radiation treatment records using dose reconstruction techniques. The quality of the treatment records was generally very good with only 8 subjects whose dose could not be assigned. Overall there were 1487 women (351 cases and 1136 controls) including 322 (110 cases and 212 controls) in the <45, 5+ subgroup, who have positive therapeutic radiation dose.

A feature of the WECARE data, that will have implications for analysis using the CL approach, is that RT untreated subjects receive zero therapeutic dose to the contralateral breast at all locations while RT treated subjects receive positive therapeutic dose at all locations. Figure 2 shows the numbers exposed and descriptive dose statistics for cases with precise location CBC by the nine locations and summarized over lateral, central, and medial locations among RT treated subjects. There is a strong increasing gradient in dose from lateral to medial portions of the breast.

2.3 Subject level information

For all study participants, information about possible breast-cancer related risk factors was obtained using an extensive questionnaire by telephone interview. For this paper, we included indicators for covariates that were predictive of CBC risk: family history (breast cancer in a first degree relative), number of full term pregnancies (<3,3+), and non-RT treatments (chemo- or hormone- therapy).

3. Analysis using location-specific dose information with precise location of tumor origin information

Without loss of generality, we use notation appropriate to the WECARE study. For the subject i, there is a radiation dose at location l, Z_il, l = 1,…,9 where the numbering is laterality independent and toward the center of the body. Let C_i be subject-level covariates; for the WECARE study those listed in Section 2.3. Let 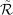be the set of indices for subjects in the case-control set, D be the case index, and L be the location of the case's cancer; for example L = 6 in Figure 1. Heuristically, we can think of (D, L) within 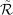as the random outcome of interest and that the natural conditional logistic likelihoods associated with the comparisons in Figure 1 as derived from the probability of (D, L) conditional on (L, 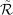), (D, 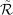), and 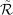for CCML, CL, and CCAL likelihoods, respectively. However, each comparison supports a different rates model structure which we define in the next section. Once defined, the conditional logistic likelihood can then be elucidated and are shown in the “Precise location” column of Table 1.

Table 1. Models and precise-location and location-group likelihoods for case-control-matched-location (CCML), case-location (CL), and case-control-all-location (CCAL) approaches to analysis.

Analysis method	Model for αl,c,s(t)	Likelihood
		Precise location	Location-group
CCMLa	αl,s(t) u(c; γ)	$\frac{u(C_i;\gamma )r(Z_{D,L};\beta )w_D(\stackrel{\sim }{\mathcal{R}})}{{\sum }_{j\in \stackrel{\sim }{\mathcal{R}}}u(C_j;\gamma )r(Z_{j,L};\beta )w_j(\stackrel{\sim }{\mathcal{R}})}$	$\frac{{\sum }_{l\in \text{L}}[x(C_D,l;\eta )r(Z_{D,l};\beta )\rho (\text{L}|l)]w_D(\stackrel{\sim }{\mathcal{R}})}{{\sum }_{j\in \stackrel{\sim }{\mathcal{R}}}{\sum }_{l\in \text{L}}[x(C_J,l;\eta )r(Z_{j,l};\beta )\rho (\text{L}|l)w_j(\stackrel{\sim }{\mathcal{R}})}$
CL	αc,s(t) v(l; δ)	$\frac{v(L;\delta )r(Z_{D,L};\beta )}{{\sum }_{l}v(l;\delta )r(Z_{D,l};\beta )}$	$\frac{{\sum }_{l\in \text{L}}[v(l;\delta )r(Z_{D,l};\beta )\rho (\text{L}|l)]}{{\sum }_{l}v(l;\delta )r(Z_{D,l};\beta )}$
CCAL	αs(t) x(l, c; η)	$\frac{x(C_D,L;\eta )r(Z_{D,L};\beta )w_D(\stackrel{\sim }{\mathcal{R}})}{{\sum }_{j\in \stackrel{\sim }{\mathcal{R}}}[{\sum }_{l}x(C_J,l;\eta )r(Z_{j,l};\beta )]w_j(\stackrel{\sim }{\mathcal{R}})}$	$\frac{{\sum }_{l\in \text{L}}[x(C_D,l;\eta )r(Z_{D,l};\beta )\rho (\text{L}|l)]w_D(\stackrel{\sim }{\mathcal{R}})}{{\sum }_{j\in \stackrel{\sim }{\mathcal{R}}}[{\sum }_{l}x(C_j,l;\eta )r(Z_{j,l};\beta )]w_j(\stackrel{\sim }{\mathcal{R}})}$

^aFor the CCML location-group likelihood, the appropriate model is the CCAL.

3.1 Case-control-all-locations likelihood

Our assumption is that the biological relevant dose at a specific location is radiation dose at that location. Thus, we will define CBC rates in terms of location-specific hazards models. Our primary interest is in the radiation effects, accounting for variation in rates over location and controlling for potential confounding factors. For the CCAL design, there is variation in both location and subject-level covariates across the comparison units, both components need to be modeled. So, consider the general proportional hazards model with t time since first breast cancer, l the location, s the matching factors, c subject-level covariate vector, and z a vector of doses at each location as

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\eta ,\beta \right)={\alpha }_s\left(t\right)x\left(c,l;\eta \right)r\left(z_l;\beta \right)$$ (1)

where α_s is the baseline hazard for matching stratum s, and x(c, l; η) is a parametric model for the joint effects of location and subject-level covariates. The dose-response rate ratio model is given by r(z; β) with β the rate ratio parameters of primary interest. So, for instance, we will consider a three-category dose model where, with d_k, k = 0, 1, 2 three dose ranges, $r\left(z;\beta \right)=exp\left[{\sum }_{k=0}^{2}I\left(z\in d_k\right){\beta }_k\right]$ or, as is typical in radiation studies, a linear excess relative risk (ERR) “trend” model r(z; β) = (1 + zβ). Of course, both the η or β and even “forms of the models” x and r can be modified by s and t but, for simplicity, we will suppress this. The key idea is that rate variation in c and l are modeled using relatively few parameters that can be estimated from the data.

The likelihood contribution is then given by the CCAL likelihood in Table 1 where w_j(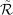) are case-control sampling weights. For “standard” random sampling of controls the w_j(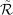) ≡ 1. For the WECARE data, these are the counter-matching weights (Bernstein et al., 2004).

3.2 Case-control-matched-location likelihood

For the CCML approach, location is fixed across all comparison units but subject-level covariates differ and will need to be modeled, so the likelihood will support a model that has a non-parametric location component but requires model structure for the subject-level effects,

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\beta \right)={\alpha }_{s,l}\left(t\right)u\left(c;\gamma \right)r\left(z_l;\beta \right)$$ (2)

i.e., a separate baseline hazard function for each location and stratum and a model u(c; γ) for covariate effects with parameters γ. With α_l,s (t) common across all units, the likelihood contribution is the precise-location CCML entry in Table 1.

3.3 Case-location likelihood

For the CL method, subject-level covariates are constant over the comparison units but location differs, so the likelihood will accommodate a model that has a non-parametric subject-level component but requires a model structure on the location component,

$${\alpha }_{l,c,s}(t)={\alpha }_{c,s}(t)v(l;\delta ).$$ (3)

In this model, the α_c,s(t), are separate baseline hazard functions for confounders c in stratum s for location 1 (i.e., v(1; δ) ≡ 1) and v(l; δ) is a model for location effects with parameters δ. Now since α_c,s(t) is fixed over a given subject (case), it cancels in the likelihood contribution yielding the CL likelihood in Table 1.

3.4 Statistical properties of the estimators

While the Figure 1 comparisons give a heuristic motivation for the methods, they do not provide a framework to study statistical properties. In Web Appendix A, we represent the data as subject-location specific counting processes, derive the associated intensities, and show that each of the likelihoods in Table 1 is a partial likelihood (in the sense of Cox (1972)) based on a different conditioning events. The process framework immediately clarifies a number of issues that might not be apparent based on the intuitive case-control comparisons in Figure 1. First, all of the analytic methods are estimating the radiation effects rate ratio parameter β₀, under the different models given in the previous sections. Second, under the reasonable assumption that CBCs, both across subjects and across locations within subject, do not occur simultaneously, failure occurrence at locations within a given subject are “conditionally uncorrelated” in the usual sense, and there is no need to account for “within-subject correlation” beyond appropriately modeling the location effects in the hazards model (Andersen et al., 1993). Third, in situations like the WECARE study where CBC occurrence is a censoring event, there is no information to assess within-subject location variability in CBC rates, after controlling for effects in the hazard model. Finally, standard counting process/martingale techniques (e.g., Andersen et al., 1993; Borgan et al., 1995) can be used to show that each partial likelihood has the usual basic likelihood properties, i.e., at β₀, that the expectation of the score is zero and variance of the score is the expected information. The conditions for consistency and asymptotic normality for the three likelihoods are standard; with the key assumption that the limiting information matrix under the method specific model is invertible.

The general bias and variance characteristics for the three designs are summarized in Table 2. These can be formalized by consideration of the CCAL model (1) that now explicitly includes s and t modifier parameters in x:

Table 2. Qualitative comparison of the analysis methods with respect to susceptibility to bias due to confounding, design flaws, and statistical information. Statistical information is directly related to radiation dose variability.

	Susceptible to
Analysis method	Location confounding	Subject-level covariate confounding	Design flaws	Statistical information: Source of dose-variability
CCML	No	Yes	Yes	Between-subject
CL	Yes	No	No	Within-subject
CCAL	Yes	Yes	Yes	Both between- and within-subject

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\eta ,\beta \right)={\alpha }_s\left(t\right)x_{s,t}\left(c,l;\eta \left(s,t\right)\right)r\left(z_l;\beta \right)$$ (4)

Models (2) and (3) are “limiting infinite parameter” cases of (4). For the CCML model (2), x_s,t(c, l; η(s, t)) = x_s,l(t) u(c; γ), with x completely unstructured in l (and s), so that α_s,l(t) = α_s(t) x_s,l(t), while for the CL model (3) is unstructured in c (and s) with α_s,c(t) = α_s(t) x_s,c(t). Further, the likelihoods in Table 1 are all non-parametric maximum likelihood (Andersen et al., 1993, Section VII.2.1). Thus, by standard likelihood theory, when the CCAL model represents the data, the CCAL β-information is greater than the CCML or CL, since the CCAL model is a submodel of either, with fewer (nuisance) parameters. On the other hand, the CCAL is susceptible to residual confounding (bias) due to misspecification of location and/or subject-level covariate effects while the CCML is robust to location and CL to subject-level covariate confounding. We also note that, as would be obvious from a case-series analysis, the CL likelihood does not depend on the controls so is not susceptible to study design flaw biases, such as selection bias.

3.5 Comparison of precise location likelihoods using the WECARE study data

In CL and CCAL analyses, we included indicators for each location in a log linear model v(l; δ) = exp(δ_l) with δ₁ ≡ 0. This model assumes that the location effects are the same over stratification factors and time so is not as flexible as the non-parametric model α_s,l(t), appropriate to the CCML analysis. For CCML and CCAL analyses, the potential confounding variables discussed in Section 2.3 were included as a log linear factor $u\left(c;\gamma \right)=exp\left(\sum c_p{\gamma }_p\right)$where p indexes the risk factor covariates. For the CCAL analysis, in which both location and subject-level covariates must be modeled parametrically, we have assumed a multiplicative structure with x = v × u. We fitted radiation dose-response model with r(z; β) as three-category and ERR forms. For the three categories, CCML and CCAL analyses use the RT untreated (therapeutic dose=0) as the baseline dose category with intervals 0.01-0.99 Gy and 1+ Gy. However, a modeling issue for the CL method is that either all locations or no locations are RT exposed. Without zero to non-zero dose comparisons on any single breast, we must use a non-zero baseline category. Thus, we defined a CL low-dose category of 0.01-0.49 Gy. The linear ERR model r(z; β) = 1 + zβ was fitted using all three methods. Thus, the models fitted for the CCML, CL, and CCAL analyses were, respectively,

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\gamma ,\beta \right)={\alpha }_{s,l}\left(t\right)exp\left(c^{\prime }\gamma \right)r\left(z_l;\beta \right)$$ (5)

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\delta ,\beta \right)={\alpha }_{s,c}\left(t\right)exp\left({\delta }_l\right)r\left(z_l;\beta \right)$$ (6)

$$\lambda \left(t,l,s,c,\text{z};\alpha ,\delta ,\gamma ,\beta \right)={\alpha }_s\left(t\right)exp\left({\delta }_l\right)exp\left(c^{\prime }\gamma \right)r\left(z_l;\beta \right)$$ (7)

where r(z_l; β) is either the three-category or ERR model.

Because each likelihood is of the conditional logistic form with weights, standard conditional logistic regression software that accommodates inclusion of an offset in the model can be used without modification. For the WECARE analyses, we used SAS PHREG (SAS Institute, Cary, NC) and, for fitting the ERR model, the Pecan module of Epicure (Hirosoft International, Inc.).

We compared the efficiency of the methods for the WECARE study by computing the expected information for β under model (7) using a simulation technique described in Web Appendix B. We found that the relative information for the CL and CCAL was no more than 30% and 110% compared to the “standard” CCML likelihood (100%), respectively, over a range of plausible β. There are two reasons why the CL analysis has much lower efficiency than the CCML. First, dose comparisons are only among exposed subjects in the CL analysis and unexposed cases contribute only to the estimation of location effects which has only an indirect and limited impact on the efficiency of parameters associated with radiation effects. On the other hand, unexposed subjects contribute directly to the estimation of radiation effects in case-control comparisons exploited by CCML and CCAL methods. Second, the CCML and CCAL methods benefit from the registry-RT counter-matched design, used precisely because it increases the efficiency for estimation of radiation dose parameters (Bernstein et al., 2004). Using all the location-specific information, the information from the CCAL likelihood was a maximum of 10% larger than the CCML. In our substantive analysis, we decided that this modest increase in efficiency was not worth the increased susceptibility to residual location confounding and reported our findings based on the CCML (Stovall et al., 2008).

In Section 3, we discussed how mismodeling of location or confounder effects could result in residual confounding of the radiation effects. Such confounding occurred in the analysis of the WECARE data in the following situation. We fitted models like (5)-(7) with location and subject-level effects, δ, γ, assumed constant over the entire population and estimated from all 609 case-control sets and separate radiation effect parameters β_g estimated for each of the four subgroups g defined by splitting age at first cancer diagnosis at 45 and time since first diagnosis at five years. The estimates from the three-category dose model for the <45, 5+ subgroup are shown in the “Global δˆ, γˆ” column in Table 3. The CCML analysis, which does not require estimation of location effects, indicates a fairly steep trend in CBC risk with a doubling in the 1+ Gy dose category, compared to zero dose. This trend was not seen in either the CL or CCAL analyses with the rate ratio for the highest dose category less than the middle category.

Table 3. Rate ratios for dose categories and estimated ERR (βˆ) for CBC in the < 45, 5+ subgroup using location and covariate effects estimated from all subjects (Global) and from the < 45, 5+ subgroup (Subgroup). CCML: Case-control-matched-location, CL: case-location, CCAL: case-control-all-location.

Analysis method	Dose (Gy)	Number < 45, 5+ casesa	Global δˆ, γˆb RR (95% CI)	Subgroup δˆ, γˆc RR (95% CI)
CCML	0	50	1	1
	.01-1	34	1.36 (0.79-2.34)	1.34 (0.77-2.32)
	1+	26	2.03 (1.08-3.79)	2.03 (1.07-3.85)
CLd	0-.5	57	1	1
	.5-1	27	1.58 (0.50-5.01)	1.74 (0.53-5.70)
	1+	26	1.25 (0.37-4.22)	2.10 (0.52-8.49)
CCAL	0	50	1	1
	.01-1	34	1.67 (1.01-2.78)	1.46 (0.86-2.47)
	1+	26	1.50 (0.86-2.61)	1.78 (0.98-3.20)

^aDose at location of CBC.

^bLocation (δ) and subject-level (γ) parameters were estimated from the full data set, 609 case-control sets.

^cAll parameters estimated from the < 45, 5+ subgroup, 110 case-control sets.

^dCannot use zero as baseline (see text).

We then performed an analysis that included only the 110 case-control sets in the <45, 5+ subgroup so that location and subject-level covariate effects δ and γ are specific to that subgroup. In the “Subgroup δˆ, γˆ” column of Table 3, the CL and CCAL dose category estimates are seen to be consistent with those from the CCML analysis. The explanation for the discrepancy between the global and subgroup analyses is residual confounding of the dose response by location. As seen in Figure 2, the distribution of CBCs over lateral, central, and medial locations for the <45, 5+ subgroup is shifted away from the medial, relative to the overall distribution. In the analysis of <45, 5+ subgroup dose effects with the global estimates of location, the rate ratio for the high dose category (strongly correlated with medial locations), is “reduced” to better represent the lower CBC rates in the medial location compared to the lateral. Thus, the misspecification of the location model resulted in residual confounding of the dose effects in the global model. When the location effects were appropriately modeled as <45, 5+ subgroup-specific, the three analyses show similar dose response patterns.

4. Analysis methods that incorporate any available tumor location information

The precise location analyses do not accommodate the 99 case-control sets whose CBC could not be assigned into one of the nine locations. The question naturally arose as to whether it is possible to incorporate dose information from these subjects.

In order to provide a theoretical framework to develop and investigate methods to incorporate these case-control sets, we need to expand our probabilistic framework to accommodate the possible outcomes. So, define the location-group L as the smallest set of locations known to contain the point of CBC origin, the size of the location-group to be the number of locations in the location-group, imprecise location to mean a location-group of size greater than one, and completely unknown location to mean a location-group of maximum size, i.e., the entire breast. The outcome data are now the case/location-group pair (D, L),

In Appendix C we derive partial likelihoods based on the natural induced location-group model assuming the location-specific rates models given in Section 3. Intuitively, and just like the precise location likelihoods, the CCML, CL, and CCAL location-group likelihoods are obtained as conditional probabilities of (D, L) conditional on (L, 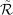), D, and 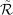, respectively. These are shown in “Location-group” column of Table 1. The location-group likelihoods require inclusion of ρ(L|l), the probability that location-group L would be observed if the tumor originated in location l. Since the actual location of origin is unknown for imprecise location cases, the ρs cannot be estimated from the data. If the tumor spans multiple locations, the ρs should incorporate any knowledge about tumor growth, whereas if the location is unknown because of inadequate medical records, the ρ(l|l) should be equal for l ∈ l. Based on an examination of the location-group likelihood expressions, a number of observations became apparent. First, the contributions from single location location-groups is the same as the precise location likelihood contribution. Second, the location-group CCML likelihood now requires modeling of the location main effects so that the likelihood is based on the same model as the CCAL likelihood. But, we found that location effects could not be estimated. Since only cases with multiple-location location-groups contribute to location parameter estimation, we conjecture that constraints on the parameters are needed. Third, there is no information to the CL likelihood from cases with completely unknown location. Fourth, estimation based on the location-group likelihoods cannot be done using standard software. For our analysis of the WECARE data we used an estimation routine written in R (R Foundation for Statistical Computing) that we have posted at http:\\hydra.usc.edu\timefactors.

A heuristically appealing alternative to the likelihood-based estimators is to use the location-group average dose in a precise location CCML-type likelihood. Let Z̄_j,_l the average of subject j's location-specific doses over location-group l. In this approach, estimation is based on the precise location CCML likelihood (Table 1) except with Z_j,L replaced by Z̄_j,_L. Now, for cases with precise tumor location L, the “averaging” will be over the single location so that Z̄_j,_{L} = Z_j,L and likelihood contribution will be the exactly the CCML contribution. Simple averaging can generally result in systematic misclassification with regard to location of origin dose and thus bias estimates in either exponential or ERR models (Armstrong, 1990; Brenner and Loomis, 1994; Langholz et al., 2007). The magnitude of the bias will depend on the (average) variation in dose across location-group, and the dose response model r(z; β).

4.1 WECARE study analysis based on simulated outcome and location-group

As noted in Section 2.1, there were 99 imprecise location cases in the WECARE study. In the course of our analyses that include these cases, it became evident that these imprecise location cases are “different” and need to be considered separately. These issues are described elsewhere (Stovall et al., 2008) but of relevance here is that the actual data do not serve to illustrate the methods. Thus, we simulated case-location and location-group outcomes from the base WECARE case-control set data as follows: First, fixing the location and covariate parameters to the CCAL estimates from <45, 5+ subgroup and the radiation ERR β₀ = 0.7, we randomly assigned a case and a location of origin from each of the 708 case-control sets based on the CCAL precise location conditional probability using (7) and Web Supplement equation (1). We then simulated location-groups using a Markov-chain growth model in which, starting at the location of origin, tumor could spread to adjacent locations at each step, over a randomly assigned number of steps; details and programs are available from the authors. The Markov-growth simulated data set consisted of 309 precise location cases, 276 with location-group of size 2 or 3, and 123 with location-group of size 4 or more, but only one completely unknown location case (location-group of size 9). To investigate an extreme example, we also created an unknown location data set setting the location-group for all imprecise location cases in the Markov-growth data set to have completely unknown location.

Table 4 shows the estimated ERR with 95% confidence intervals (part A) and null information, the information at β = 0, (part B) for the location of origin, simulated Markov-growth, and unknown location data sets using the different analysis methods. For the location of origin data, the ERR estimates from the precise location CCML, CL, and CCAL likelihoods are within sampling error of β₀ = 0.7 and all are very close to each other with βˆ ≈ 0.9. With precise location known for only 309 cases in the randomly assigned location group data sets, the precise location analyses yield ERR estimates with considerably more variability than the location of origin estimates. For the simulated Markov growth data, the location-group CL and CCAL likelihoods capture 57%[=100%×(0.14-0.094)/(0.17-0.094)] and 88% of the difference between location of origin and precise location null information. In particular, the location-group CCAL information is 94% of the best possible (location of origin CCAL) with estimated βˆ and 95% CI very close that obtained from the location of origin analysis. The location-group average dose analysis also performed well with βˆ = 0.85 just slightly less than the location of origin estimates. For the “extreme” unknown location data set, the location-group CL likelihood provides no improvement over the precise location CL for the reason discussed in the last section. However, the location-group CCAL likelihood is still able to exploit the dose information in the completely unknown location cases, with ERR estimates very close to those from the location of origin CCAL analysis and recapturing 73% of the location of origin null information. Analysis of the unknown location data set using location-group average dose results in some bias toward the null.

Table 4. Estimated ERR (βˆ) and null information at β = 0 for each of the analysis methods using data with case and location outcome and location-group simulated from the WECARE case-control sets. Location-group likelihoods were used for the location-group data sets.

Analysis method	Location of origin data	Location group sim ulation
		Precise location	Markov growth	Completely unknown
A. Estimated ERR/Gy (βˆ) (95% confidence intervalsa)
CCML	0.89 (0.60-1.25)	1.05 (0.59-1.67)	–	–
CL	0.91 (0.10-5.48)	0.34 (-0.10-∞)	0.65 (-0.01-5.00)	0.34 (-0.10-∞)
CCAL	0.88 (0.59-1.24)	1.03 (0.58-1.65)	0.89 (0.59-1.24)	0.88 (0.58-1.25)
Location group average	–	–	0.85 (0.56-1.19)	0.77 (0.52-1.08)
B. Null information per case (Percent relative to location of origin-CCAL)
CCML	0.60 (94%)	0.32 (49%)	–	–
CL	0.17 (27%)	0.09 (15%)	0.14 (22%)	0.09 (15%)
CCAL	0.64 (100%)	0.34 (53%)	0.60 (94%)	0.56 (87%)
Location group average	–	–	0.59 (93%)	0.63 (99%)b

^abased on the profile likelihood.

^bnot valid since estimate is biased.

5. Discussion

The new precise location analysis methods provided additional insight into radiation effects in the WECARE data. After adequate control of location effects, analyses using CCML and CL were in general agreement, providing additional validity to the study results. For the WECARE study, adding the cases with imprecise location information using the location-group likelihoods did not improve on the precise location analysis because the imprecise location cases need to be considered separately (Stovall et al., 2008).

The precise location analysis methods have an intuitive appeal based on the comparisons in Figure 1 and are easy to implement using standard conditional logistic software. The CCML and CL analyses rely on “orthogonal” information; the former on case-control comparisons, the latter on location comparisons within cases. Thus, the bias and variance trade-offs of these approaches are also orthogonal. These methods strongly complement each other, location and subject-level confounding can be addressed separately in CL and CCML analyses with the resulting models combined in the CCAL analysis which incorporates both case-control and location comparisons. However, since the methods do not accommodate cases with imprecise location, the approach is sensitive to the location scheme used; if the size of the locations is decreased, the number of cases dropped from analysis because of imprecise location tumors increases. The location-group analysis methods are not sensitive to the location scheme in this way but requires specification of the ρ(l|l)s. It should not be surprising that inclusion of imprecise location cases requires additional assumptions. The size and direction of the location group are related to dose uncertainty and the need to specify the ρ(l|l)s reflects the need to incorporate the distribution of dose over the component locations within the location-group. We note that if dose generally does not vary much over location group, e.g., tumors are small, then the analysis will not be sensitive to the choice of ρs. In practice, we suggest performing a sensitivity analysis to assess the dependence of the results on the ρs.

As an alternative to the likelihood methods, the location-group average dose method does not require specialized software and we found it performed quite well in the WECARE analyses using the ERR model. However, the bias may be more pronounced when estimating parameters in other models or with other data situations. If the location-group average dose method is used, we suggest validating key results using precise location or location-group CCAL.

In the limiting case of reducing the size of the locations, one can think of dose to a point on the breast and the location-group as surface (or volume) occupied by the tumor. The sums over locations in the location-group likelihoods then become integrals over the smooth surface (or volume). The location-group likelihoods in Table 1 are simply a discrete (and adequate given the precision of dose information) approximation to the integration.

In the WECARE study, the location scheme was dictated by the way CBC location was described in the medical records. Since there is a steep dose gradient in the medial to lateral direction, finer location divisions along this direction would have been desirable, particularly given that about 50% of CBCs were in the lateral portion of the breast. On the other hand, there was little variation in dose from lower to upper part of the breast so collapsing over these locations results in little loss of information (Langholz et al., 2007). Thus, if practical, we recommend using a “fine grid” location scheme for data collection.

While the CL analysis of the WECARE study had much lower efficiency than the CCML or CCAL, the CL analysis requires only cases, a third the number of subjects compared to the case-control CCML and CCAL methods. Thus, the difference in “cost efficiency” is not nearly as great as the difference in “absolute efficiency.” In situations where a large pool of cases is available and a control pool is not, a case-only study with the CL analysis provides a potentially cost effective option.

The methods we have described expand the analysis tools for second (solid) cancer studies after therapeutic radiation and can be adapted to the particular study situation. For instance, in a study of breast cancer and treatments for Hodgkin disease, the CCML approach was used to analyze breast cancer risk after radiotherapy (Travis et al., 2003). Unlike the WECARE study, both breasts are “at risk” for subsequent breast cancer so one might add “laterality” (B) to subject (D) and location (L) as an additional location attribute of the cancer. The three approaches we have described for the WECARE data analysis are special cases conditioning on B. But there are additional valid and useful comparisons including comparing dose at the same location across laterality in the case (i.e., condition on D, L). Such a comparison has advantages similar to the CL, but provides close matching on tissue structure and, possibly, larger dose diversity. Similar opportunities to use location-specific dose and location information would be possible in a study of lung cancer after treatment for Hodgkin's disease (Gilbert et al., 2003). There are potential applications in other situations where the risk factor varies over the organ of interest such as in studies of cell phone use and brain tumors, polyps and colon cancer, and sunlight and skin cancers. Further, the methods can serve as a basis for estimation of location-specific dose effects when the location of tumor cannot be determined, such as for hemopoietic cancers, using the natural whole organ “aggregate model” induced by summing over the component location-specific counting processes (intensities). This approach is discussed in Langholz et al. (2007).

Supplementary Materials: Web Appendices and equations referenced in Sections 1, 3.4, 3.5, 4.1 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.