Precision of Position Signals for Letters

Abstract

Accurate reading of words and text relies on reliable identification of letters in left to right order. Previous studies have shown that people often make letter-reversal errors when identifying strings of letters away from fixation. These errors contribute to a decline in letter identification performance away from fixation. This study tests the hypothesis that these errors are due to decreased precision (increased position noise) in the coding of letter position in the periphery. To test our hypothesis, we measured observers' performance for identifying pairs of adjacent letters presented within 8 letter positions left and right of fixation. The task was to name the two letters of each pair, from left to right. Responses were scored in two ways for each letter position: (1) letters were identified correctly and in the correct position, and (2) letters were identified correctly but in the wrong position. The ratio of these two scores, when subtracted from 1, gives the empirical rate of mislocation errors. Our primary finding shows that the coding of letter position becomes increasingly imprecise with distance from fixation. A model in which the encoded position of each letter is independent and Gaussian distributed, and in which the spread of the distribution governs the precision of localizing the letter accounts for the empirical rate of mislocation errors. We also found that precision of letter position coding scales with letter size but the precision does not improve with the use of a pre-cue.

Introduction

The accuracy of letter identification often suffers when letters are presented in strings, even when each of the letters can be identified correctly when presented alone. This effect is more pronounced when letters are presented outside the foveal region (Bouma, 1970). The difficulty in correctly identifying letters in the presence of other letters is referred to as crowding.

Crowding is ubiquitous in spatial vision and affects a variety of spatial tasks (for a review, refer to Levi, 2008). With respect to letter identification, the hallmark of the crowding effect is a reduction in letter identification accuracy for letters flanked by other letters when compared with the performance for identifying single letters. The reduction in accuracy can be a result of (1) assigning a wrong identity to the target letter (letter-identity errors); and/or (2) assigning the correct identity to the target letter but the wrong position relative to other letters (letter-reversal errors). The latter type of error is often referred to as a “transposition error” (Estes, Allmeyer & Reder, 1976) or a “mislocation error” (Ortiz, 2002; Chung, Legge & Ortiz, 2003; Strasburger, 2005). There is evidence that a significant proportion of the errors made when people identify strings of letters away from fixation is due to mislocation errors, e.g. the string of letters “oae” might be mis-read as “aoe” (Butler & Currie, 1986; Estes et al, 1976; Mewhort, Campbell, Marchetti & Campbell, 1981; Townsend, Taylor & Brown, 1971; Ortiz, 2002; Strasburger, 2005; Strasburger, Harvey & Rentschler, 1991). Given that accurate reading of words and text relies on correct identification of letters in the left to right order, errors in either identification or spatial order of letters may disrupt both word recognition and reading.

In this study, we hypothesized that the accuracy of judging the spatial order (the relative positions) of letters is directly related to the precision of position coding of letters. As such, the goals of this study were to examine the precision of position coding of letters at different distances away from fixation, and to determine whether the imprecision of letter position coding could account for a portion of the errors made in identifying letter strings.

Position judgments can be exquisite under optimal conditions. For example, our ability to judge the relative position of a pair of highly visible lines or dots that are in close proximity to one another (Vernier judgment) can be as precise as a few arc sec (Westheimer, 1975). This exquisite performance has often been attributed to a spatial filter mechanism for mediating relative position judgments. According to this model, the visual system compares the contrast response output from spatially localized oriented filters that straddle the crucial target features, thereby deducing the relative position of the two targets (Klein & Levi, 1985; Wilson, 1986). However, the precision for judging the relative position of two objects decreases dramatically when the two objects are separated by a few arc min (Klein & Levi, 1987; Levi & Klein, 1989; Waugh & Levi, 1993; Williams, Enoch & Essock, 1984). For instance, Williams et al (1984) reported that thresholds for judging the relative position of two dots (a Vernier task) separated by 60 arc min reaches approximately 60 arc sec, an order of magnitude higher than the Vernier threshold for abutting dots. The declining precision in position judgment for widely separated targets is often attributed to the reliance on a less precise mechanism for localization – the local sign mechanism.

Local signs are hypothetical sensory signals that represent stimulus locations in the visual field. According to Lotze (1885) who first proposed the notion of local sign, each retinal receptor stimulated by a target will signal a local sign that can be thought of as a location or position tag. Hering (1899) suggested that for an extended stimulus such as a thin line, positional accuracy of the line can be improved by averaging the local signs along the length of the line. Relative position judgment of a pair of separated Vernier lines could be accomplished by comparing the mean local signs of the two lines. For extended two-dimensional targets, local signs are likely to be computed based on the centroid of each target, because relative position judgment can be equally precise for separated targets that are composed of clusters of dots (Badcock, Hess & Dobbins, 1996; Hess, Dakin & Badcock, 1994; Whitaker & Walker, 1988), irregular shapes (Patel, Bedell & Ukwade, 1999), or have opposite contrast polarity (Levi, Jiang & Klein, 1990; Levi & Waugh, 1996; Levi & Westheimer, 1987; O'Shea & Mitchell, 1990).

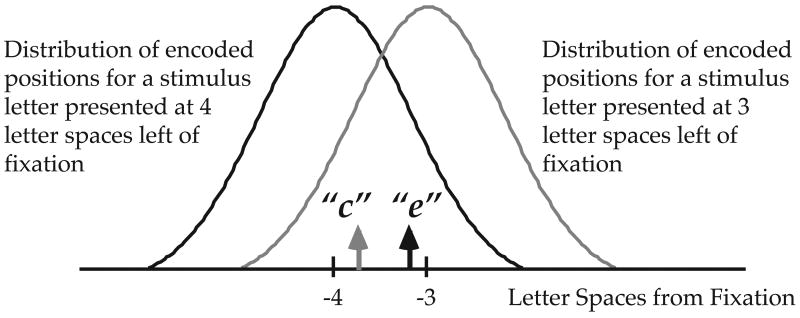
In this study, we were interested in the position coding of letters. Because letter stimuli are two dimensional, often have irregular shapes, and adjacent letters in text usually have center-to-center spacing greater than a few arc min (the mean spacing between 12 point Times Roman letters, viewed from 40 cm, is approximately 17.4 arc min), we reason that positional information for letters is likely to be based on local signs that are computed based on centroids of the letters. The computation of the centroid of a target, if based on features which themselves have some positional imprecision, should follow a normal distribution in which the spread of the distribution represents the precision of localizing the target. A distribution with a smaller spread implies that we could localize the target with higher precision. A pair of adjacent letters would therefore yield two distributions of the centroid signals, one for each letter. If the spread of the distributions is small enough so that there is little or no overlap, then we would be able to determine the spatial order of the two letters with high precision. In contrast, significant overlapping of the two distributions could cause the letters to be localized in the wrong relative position, i.e. in reversed left-to-right order (see Figure 1). This leads to the hypothesis that the imprecision of letter position coding, which is directly related to the spread, or the position noise of the underlying centroid distributions, could account for mislocation errors made in identifying letter strings. This hypothesis predicts that the rate of mislocation errors should increase with the position noise (the width) of the underlying distributions for letter position coding.

Figure 1.

A schematic cartoon depicting how mislocation errors could occur. If samples from the two distributions are drawn with the values indicated by the arrows, then the letter “c”, drawn from the distribution centered on letter position −3 (3 letter spaces left of fixation) would be perceived as on the left of letter “e”, constituting a mislocation error.

In this paper, we first present a simple probabilistic model embodying these concepts. The key parameter of the model is the standard deviation of the underlying distribution of position noise, representing the imprecision of position coding. In Experiment 1, we examined the ability of the model to fit the empirical data on the accuracy of identifying letters at various letter positions, and how the distance from fixation affects the position noise standard deviation. In the experiment, we measured the rate of mislocation errors when the identities of pairs of letters were known to the observers and the task was to indicate the relative position of the two letters. In Experiment 2, we extended the use of the model to account for mislocation errors in the more important case of identifying pairs of unknown letters in the correct order. Experiment 2 included three letter sizes, enabling us to determine the impact of letter size on the model's noise standard deviation. We also examined the potential benefit of a precue for guiding spatial attention to the target location by reducing the position noise.

Our model is similar in its basic concept to the “Overlap Model” recently described by Gomez, Ratcliff and Perea (2008). By assuming position uncertainty, the overlap model accounts for a number of well-known effects observed in the recognition of strings of letters including replacement errors, transposition errors, letter migration errors, insertion errors and repetition of letters. In the Gomez et al. study, subjects saw strings of five briefly presented letters (60 ms), and then tried to choose this target string from a pair of subsequently presented strings (two-alternative forced choice). The foils differed from the target strings in having letter transpositions, letter insertions, etc. Accuracy data were interpreted using the overlap model. This model, with its six free parameters (Experiment 1) did well in modeling most of the types of letter response errors. Gomez et al. were primarily interested in position uncertainty associated with relative position within the string. For example, their results indicate that position uncertainty is least for the leading letter, increasing monotonically so that the final letter exhibits the largest uncertainty (their Table 3). Presumably, these findings are influenced by both bottom-up factors such as crowding and distance from fixation, and top-down factors such as the lexical status of strings (word vs. non-word, their Experiment 2), linguistic and memory effects in matching the target to the two alternatives in the forced-choice procedure. By contrast, our interest was focused primarily on early sensory coding, especially the impact of retinal eccentricity and character size.

Methods

Letter identification accuracy was measured for pairs of letters presented sequentially in two adjacent letter positions, extending 8 letter slots left and right of fixation. Each pair of adjacent letter positions was tested 10 times in a block in a random order, with a total of 160 trials per block. Letters were chosen randomly from the 26 lowercase letters of the alphabet, with the constraint that the two letters of any pair could not be the same. The fixation target consisted of two small green dots that were vertically separated by approximately 1.2°, a separation larger than the largest letter size used in the study, so that the fixation dots would not mask the letters presented at fixation. Previously, Beard, Levi & Klein (1997) showed that when the two elements of a Vernier target were presented sequentially with at least 20 ms inter-stimulus interval between the offset of one and the onset of the other, localization thresholds were independent of stimulus feature characteristics such as contrast polarity and visibility, reflecting the properties of the local sign mechanism but not those of the spatial filter mechanisms. Here, we borrowed their sequential-presentation paradigm and presented letters asynchronously each for 50 ms to isolate the local sign mechanism for position judgments of letters. Our assumption was that position signals for letters in strings are determined by the local sign mechanism and not by the spatial filter mechanism underlying typical measures of Vernier acuity. The order of whether the right or left letter of the pair was presented first was randomized across trials. We included a mask, a row of 21 ‘#’ symbols, that covered up to 10 letter slots left and right of fixation, before and after each letter in order to minimize the contamination of position signals due to motion cues or cues from spatial filters. The mask did not provide information about the position or identity of the target letters.

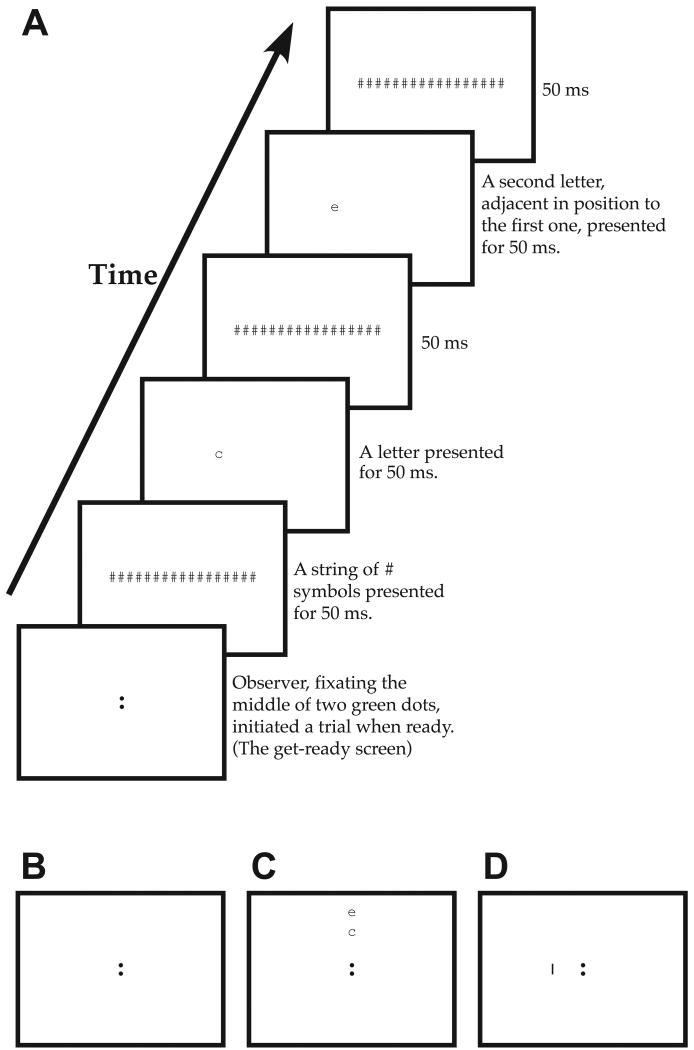
A trial began with the observers fixating midway between the two green fixation dots at a viewing distance of 40 cm. Once initiated by the observers, a trial lasted 250 ms and was comprised of the following sequence: the mask, the first target letter of the pair, the mask, the second target letter of the pair and the mask (Figure 2). Each component (letter or mask) was presented for 50 ms. The observer's task was to identify the pair of letters, from left to right, regardless of which letter was presented first. Feedback on accuracy was not provided to the observers. Testing was binocular.

Figure 2.

(A) A schematic cartoon depicting a sample trial for the different testing conditions. The stimulus letters, from left to right, were “ec”. (B–D) The different looks of the get-ready screen before the observer initiated a trial. In (B), only the pair of fixation dots (green in the actual experiment) was shown. (C) Experiment 1: The two target letters in the upcoming trial were presented above the pair of fixation dots before the trial. The relative position of the two letters was random and did not indicate the spatial or temporal order of the two letters in the trial. (D) Experiment 2: A short green vertical line indicating the mid-point of the two letters in the upcoming trial was shown. This green line served as the precue.

Stimuli were generated using a Silicon Graphics O2 workstation and presented on a Sony monitor (model# GDM-17E21). Letters were rendered in Courier font, a fixed-width font, so that the center-to-center spacing between adjacent letters was constant regardless of the letter identity. For the Courier font, the center-to-center spacing is 1.16× the width of the lowercase letter “x”. When we express the distance of a letter from fixation as letter position in this paper, we use this 1.16× x-width as the width of each letter position. However, in order to be consistent with the conventional expression of letter size, we specify our letter size with respect to the x-height. For the Courier font, we measured the x-width to be 1.35× x-height, in other words, each letter position is equivalent to 1.57× x-height. Letters and masks were presented as high-contrast (ca. 90% Weber contrast), black letters (symbols) on a white background of 45 cd/m².

Six observers, all with corrected-to-normal vision of 20/20 or better in each eye, participated in the study. Written informed consent was obtained from each observer after the procedures of the experiment were explained, and before the commencement of data collection. With the exception of author SC, none of the observers was aware of the purpose of the experiments.

Basic experimental design

In Experiment 1, we measured human performance for judging the relative position of pairs of letters of known identity presented asynchronously, as a function of distance from fixation (measured as the number of letter positions). By allowing the identity of the letters to be known, demands on identification were minimized so that any errors made on the task represented primarily mislocation errors. Letters were 0.8° (x-height). Before each trial, we showed the two letters for the upcoming trial vertically aligned above the fixation target (see Figure 2C). The relative vertical arrangement of the two letters was randomized from trial to trial, and did not indicate the temporal order or the relative spatial location of the two letters. Four of the six observers participated in this experiment. Each of these observers completed four blocks of trials.

In Experiment 2, we examined human performance for letter position coding using a task that more closely resembles the conventional task of identifying strings of letters in words. The identity of the letters was not disclosed before each trial and observers had to identify the letters, in addition to judging their relative position. Because previous studies have shown that coding of position based on stimulus centroid is size dependent, we tested three letter sizes: 0.3°, 0.5° and 0.8°. We also asked whether the spatial uncertainty associated with presenting letter pairs at many possible locations adversely affected our results, given that observers had to distribute their spatial attention to monitor all these locations. To do so, in half of the blocks, a vertical green line (pre-cue) of the same length as the x-height of the letters was presented before each trial, marking the mid-point between the two adjacent letters in the upcoming trial (see Figure 2D). The pre-cue disappeared as soon as the observer initiated a trial, and reappeared (in a different location for the next trial) as soon as the observer's response was recorded. The precue never overlapped with any letter parts spatially or temporally. Potentially, the pre-cue could improve letter identification performance by guiding covert attention to the stimulus location prior to stimulus onset. Each observer completed four blocks of trials for each combination of letter size and the presence or absence of the pre-cue. These blocks were tested in a random order for each observer.

Data Analyses

In each trial, observers named the two letters from left to right. Trials for which the responses for both letters were incorrect were excluded from analysis. For the rest of the trials, we scored the responses in two ways to assess the impact of spatial mislocation errors. The exact method requires that the response letter matches the corresponding stimulus letter in both the identity and the position of the letter within the pair. The either-position method is more forgiving. The response letter is deemed correct as long as it matches either of the two stimulus letters of the pair. The ratio of the proportion-correct scored by these two methods (exact/either-position), which we shall refer to as R_score in this paper, yields the proportion of responses in which letters were localized in the correct positions. By subtracting R_score from 1, we obtained the proportion of responses in which letters were identified correctly but in the wrong position — the empirically determined rate of mislocation errors. This analysis provides an estimate of the mislocation error rate without contamination by the identification accuracy (see Appendix for details). As an example, for letter position 3 to the right of fixation, suppose that the either-position scoring method yields a performance measure of 80% correct, and the exact method yields 60% correct. The corresponding value of R_score is 0.60/0.80 = 0.75. This means that the letter was properly localized on 75% of the trials in which it was correctly identified. The value 1 − R_score, or 0.25 in this example, represents the proportion of mislocations, that is, the letter was mislocalized on 25% of the trials in which it was correctly identified. Table 1 summarizes how we scored the different types of responses to the same stimulus letter pair (“ec” is used as an example). Letter identification performance reported in this paper was corrected for guessing (chance level = 0.0384).¹

Table 1. Types of responses to the stimulus letter pair “ec”, and how the responses were scored according to the exact and either-position criteria.

	Exact		Either-position
Response	Left letter	Right letter	Left letter	Right letter
“ec”	✓	✓	✓	✓
“ce”	✗	✗	✓	✓
“eo”	✓	✗	✓	✗
“oe”	✗	✗	✓	✗
“sc”	✗	✓	✗	✓
“cs”	✗	✗	✗	✓
“so”	trial excluded from analysis		trial excluded from analysis

Model

Our model assumes that the encoded positions of the letters are stochastically independent, Gaussian distributed with a mean equal to the true retinal eccentricity and a standard deviation that increases linearly with distance from fixation. We assume an observer's response in judging the spatial ordering (relative position) of a pair of adjacent letters is based on the magnitudes of the position signals; the letter with the larger position signal is judged to be farther from fixation. Because of the noise in the distributions of position signals (Figure 1), a letter which is physically closer to fixation may be judged farther yielding a mislocation error.

a. Estimating the standard deviation of the Gaussian distribution

The following derivation, culminating in Eq. [3], shows how the model's standard deviation S of the underlying distribution of position signals at a given letter position x is related to the z-score for the empirically measured proportion of mislocation errors (1 − R_score) at that location.

For an adjacent pair of letters at letter positions x and x+1, the standard deviation of the encoded position for each letter can be represented by S(x) and S(x+1). The distribution of the encoded letter position difference is Gaussian, with a standard deviation S_diff given by Eq. [1]. The sign of a sample value taken from this difference distribution indicates whether or not the correct ordering of letters is preserved (+ sign: correct ordering; − sign: reversed ordering).

$$S_{\text{diff}}=\sqrt{S{(x)}^2+S{(x+1)}^2}$$ [1]

For simplicity, we assume that the standard deviations at adjacent letter positions are approximately equal, i.e. S(x) ≈ S(x+1), although as can be seen later, the standard deviation increases slowly with distance from fixation.

The proportion of mislocation errors, given empirically by 1 − R_score, corresponds to the area of the difference distribution to the left of zero. To estimate the standard deviation of the distribution of the position signals, we first converted R_score into its corresponding z-score.² The z-score is related to the presumed standard deviation of the distribution of the position signals according to the following equation:

$$z=\frac{\text{difference between the mean of the two distributions}}{\sqrt{2}S}$$ [2]

where S is the standard deviation at location x.

Since letters were presented in adjacent letter positions, the difference between the mean of the two distributions (i.e. the center-to-center distance between adjacent letters) was always one letter, therefore

$$S=\frac{1}{\sqrt{2}z}$$ [3]

To summarize, the model's standard deviation S at letter position x is estimated from Eq. [3] using the z-score associated with R_score.

b. Linear scaling

Next, we derive expressions for the change in the model's value of S with letter position x from fixation. Beard et al (1997) showed that the imprecision of local signs increases linearly with eccentricity in peripheral vision. Following Beard et al, we assume that S follows a linear scaling law:

$$S=S_0+kx$$ [4]

where S is the model's standard deviation at letter position x from fixation, S₀ is the standard deviation at the fovea and k is a scaling constant. This equation can be rewritten as

$$S=S_0(1+\frac{x}{X_2})$$ [5]

where k = S₀/X₂ and X₂ is the letter position at which the foveal value (S₀) of the standard deviation doubles.

Note that our derivation has used letter position from fixation to represent the distance from fixation. To convert to degrees of visual angle (more commonly used to express scaling laws associated with retinal eccentricity), we simply multiply the values in Eqs [4] or [5] by the letter size in degrees. For instance, if the letter size (x-height) is 0.5°, and the doubling distance X₂ is 3 letters, the corresponding doubling distance in degrees is 3 × 1.57 × 0.5° = 2.36°. When the doubling distance is expressed in degrees, it is commonly referred to as E₂ (Levi, Klein & Aitsebaomo, 1984; 1985).

c. Model prediction and validation

In both Experiments 1 and 2, for each letter position, we first calculated R_score, the ratio of proportion correct for the exact and either scoring methods. We then converted this ratio into a z-score. This z-score was used to estimate a value for the model's standard deviation S using Eq. [3]. S characterizes the breadth of the Gaussian distribution of possible positions for a letter at a given distance x from fixation. By assuming a linear scaling law as detailed above, we generated the two parameters of a linear equation of the form of Eq. [4] showing how SD depends on eccentricity. To improve the quality of the fits, we combined data from the right and left hemifields (justified by statistical analyses, see Results). These procedures allowed us to create a model for describing our data. We then assessed how well the model fit our data. To do so, we reversed the process: with the parameters derived from the scaling law, we first computed the predicted standard deviations for each letter position. From these predicted values, we calculated the predicted z-scores using Eq. [3], which were subsequently converted into the predicted proportion-correct for letters identified in the correct positions. The predicted mislocation error rate was given by subtracting the expected proportion-correct from 1.

Results

Experiment 1: Position judgments for letters with known identity

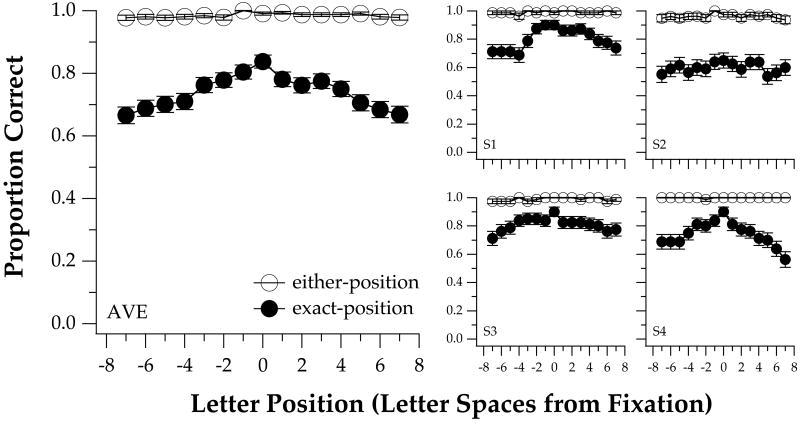
Proportion correct for letter identification, scored by the exact and either-position methods, is plotted as a function of letter position in Figure 3. The large panel presents the averaged data of the four observers, with the small panels showing the individual data. Data were collected for 0.8° letters. In this experiment, the identities of the two letters were disclosed to observers before each trial. For each letter position, half of the trials had the left letter of the pair shown at that position and the other half of the trials had the right letter shown at that position. Averaged across observers, there was no significant difference in letter identification performance for the left versus the right letter for all letter positions, for either of the two scoring methods (paired-t test, exact: t_(df=14) = 0.14, p = 0.89; either-position: t_(df=14) = 0.4, p = 0.70). Hence, for the results of this experiment, the performance reported for each letter position was the performance pooled between trials for the left and right letters.

Figure 3.

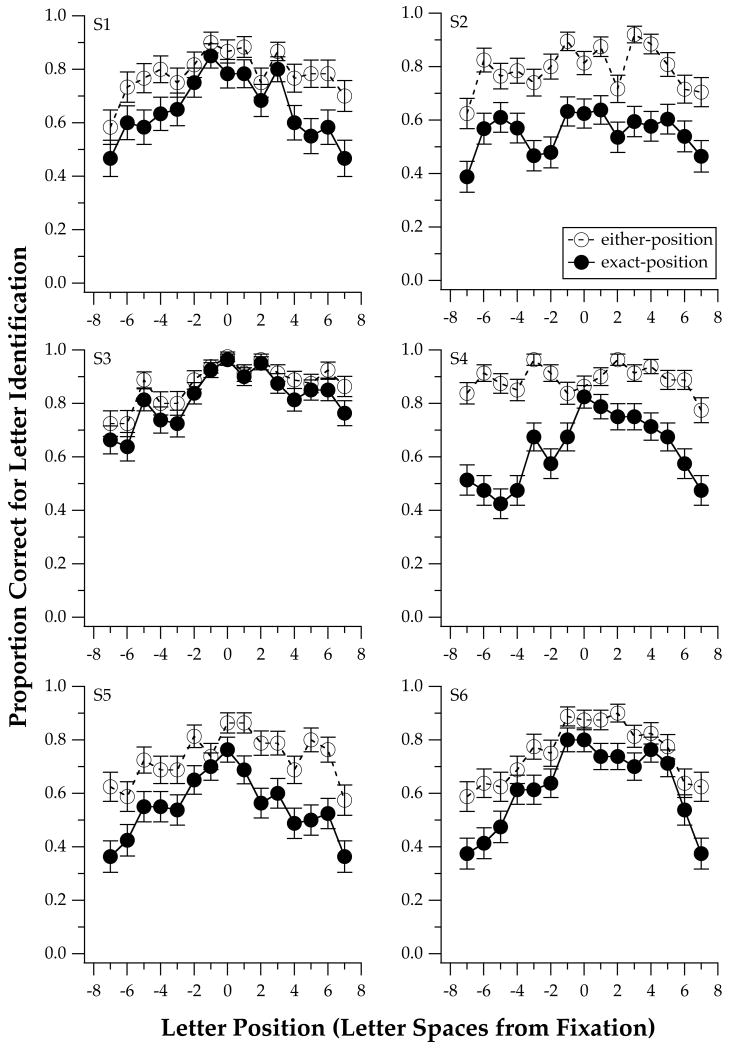
Proportion correct for letter identification is plotted as a function of letter position from fixation (negative values: left of fixation; positive values: right of fixation) for four observers. Individual observers' data are shown in the small panels while the averaged data are shown in the large panel. Data were collected for 0.8° letters the identities of which were disclosed to observers before each trial. Data were scored according to the exact (filled circles) and the either-position (unfilled circles) methods.

Because observers knew the identity of the letters, performance scored by the either-position method was very close to 100%, although observers still made a small number of errors independent of letter position. When performance was scored using the exact method, not surprisingly, performance dropped, but the drop in performance varied with letter position. The best letter identification performance (proportion correct) was obtained at fixation (letter position 0) and averaged 0.84 across the four observers. Performance progressively decreased for letter positions further away from fixation. At seven letter slots away from fixation, accuracy for the exact criterion was approximately 0.67.

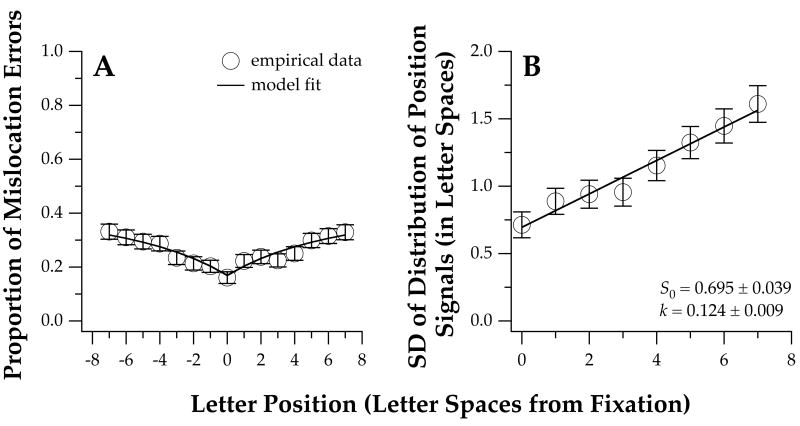
Figure 4A shows that the proportion of mislocation errors (1 − R_score) increases with letter positions from fixation. Note that at fixation, mislocation errors still occurred, although the rate was the lowest (approximately 16%). The rate increases to approximately 33% at seven letter slots away from fixation.

Figure 4.

(A) Proportion of mislocation errors (1 – R_score) for data shown in Figure 3 is plotted as a function of letter position (unfilled circles). The solid line represents the model fit (see text for details). The values for the model fit are based on the estimated standard deviations shown in panel B, converted to z-scores (Eq. 3) and then the rate of mislocation errors. (B) The standard deviation of the distribution of the position signals at each letter position (left and right side of fixation combined) is plotted as a function of letter position (unfilled circles). The solid line represents a regression line (Eq. 4) fit to the data. The fitted parameters are given in the panel.

We estimated the standard deviation of the underlying distribution for position coding at each letter position (see Methods). The estimated standard deviations corresponding to the same letter position in the left and right hemifields were combined, because there was no significant difference in the SDs between the two hemifields (t-test: p = 0.93). A regression line of the form of Eq. [4] was used to fit these data from which the foveal SD and the rate of change of SD with letter position were derived (Figure 4B). Using the fitted parameters, we generated the SD at each letter position as predicted by our model (see Methods). Figure 4A compares the proportion of mislocation errors based on the model fit (smooth lines) with the empirical mislocation error rate (circular symbols). Clearly, our model provides a reasonable description of the empirical data, implying that the SD of the underlying distribution of position signals for the letters can explain the rate of mislocation errors.

Experiment 2: Position judgments for letters with unknown identity

In the previous experiment, the observer knew the identity of the stimulus letters before the trial and needed only to determine the relative position of the two letters. Can our model also predict the mislocation error rate for the more typical task of identifying strings of letters in the correct order when neither the letter identity nor relative position is known ahead? In Experiment 2, we measured letter identification performance when the letter identity was not disclosed to observers before each trial. We also tested the effect of letter size and the use of a precue to guide the deployment of spatial attention.

Figure 5 compares the letter identification performance, scored by the exact and either-position methods, as a function of letter position for the six observers who participated in this experiment. The letter size was 0.5° and the precue was used. As in Experiment 1, for each letter position plotted on the x-axis, half of the trials had the left letter of the pair shown at that position and the other half of the trials had the right letter shown at that position. Averaged across observers and letter positions, there was no significant difference in letter identification performance for the left versus the right letter, for either of the two scoring methods (exact: t_(df=178) = 1.03, p = 0.31; either-position: t_(df=178) = 1.64, p = 0.10). Hence, for the results of this experiment, the performance reported for each letter position was the performance pooled across trials for the left and right letters.

Figure 5.

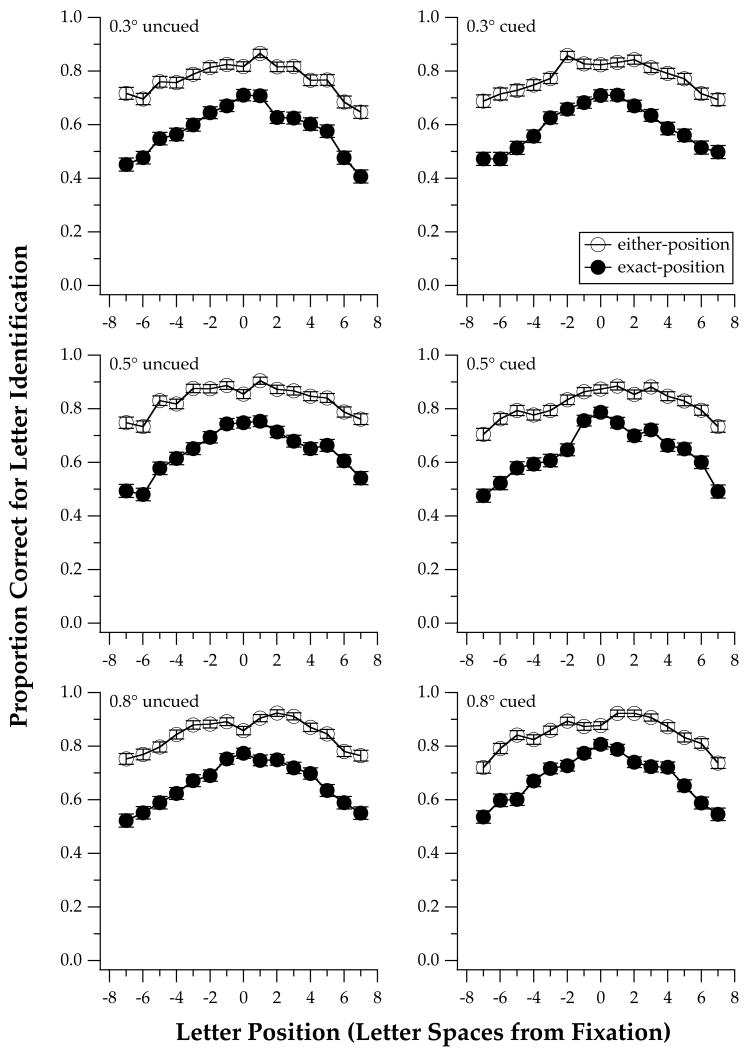
Proportion correct for letter identification is plotted as a function of letter position from fixation (negative values: left of fixation; positive values: right of fixation), for the six observers. Letter size was 0.5° and the precue was used. The two curves in each panel represent the same set of data scored by the exact and the either-position methods.

Figure 6 compares letter identification performance, averaged across the six observers, as a function of letter position for the three letter sizes (0.3°, 0.5° and 0.8°), with and without the pre-cue. The general profile of how letter identification performance changes with letter position is very similar for the three letter sizes and in the presence or absence of the pre-cue. In each panel, results for the two scoring methods are plotted separately. Not surprisingly, performance was always better when data were scored using the either-position method than with the exact method.

Figure 6.

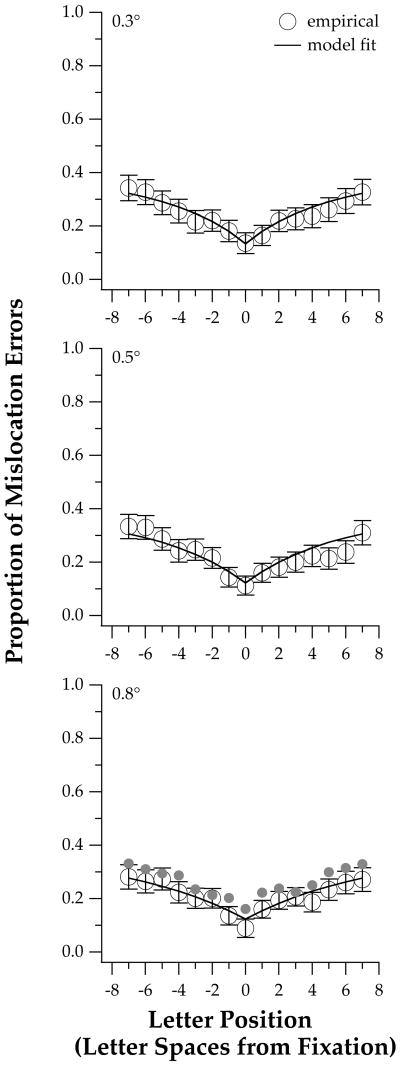
Proportion correct for letter identification, combined across the six observers, is plotted as a function of letter position from fixation (negative values: left of fixation; positive values: right of fixation), for the three letter sizes (0.3°, 0.5° and 0.8°) and the uncued/cued conditions. The two curves in each panel represent the same set of data scored by the exact and the either-position methods.

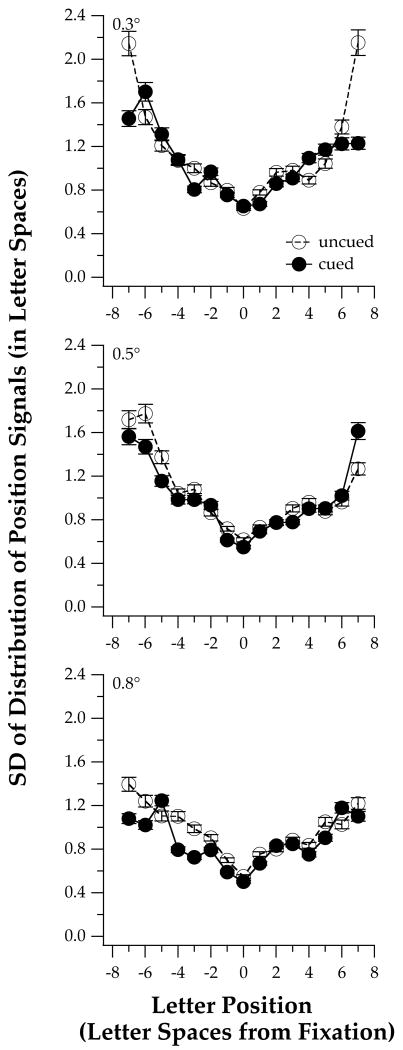
As in Experiment 1, we estimated the model standard deviation S of the distribution of the encoded letter position based on R_score (data shown in Figure 6). These standard deviations are plotted in Figure 7 as a function of eccentricity in units of letter spaces, for the three letter sizes, with and without the pre-cue. A two-factor ANOVA showed that when standard deviations were expressed in letter position units, neither the main effect of letter size (F_{(df = 2,84)} = 2.58, p = 0.08) nor the use of a pre-cue (F_{(df = 1,84)} = 1.48, p = 0.23) affect the estimated standard deviations. The mean values of standard deviations, computed across all letter positions, are 1.16 ± 0.46, 1.04 ± 0.35 and 0.97 ± 0.23 letter positions for 0.3°, 0.5° and 0.8° letters, respectively, for the no-cue condition. In the presence of the pre-cue, the mean standard deviations are 1.06 ± 0.30, 1.00 ± 0.33 and 0.87 ± 0.22 letter positions for the three letter sizes. The virtually constant values of the model standard deviation (in letter position units) for different letter sizes implies that the precision of position signals for letters scales with letter size, consistent with previous findings for the effect of stimulus size on positional accuracy (Patel et al, 1999; Whitaker & Walker, 1988).

Figure 7.

Estimated standard deviation (in letter spaces) derived from the data combined across the six observers, is plotted as a function of letter position, for the three letter sizes and the uncued/cued conditions.

The pre-cue had no significant effect on the value of the model standard deviation. The mean values are 1.06 ± 0.36 and 0.98 ± 0.29 letter positions without and with the pre-cue, respectively. Apparently, guiding the deployment of spatial attention has virtually no effect in enhancing the precision of position coding for letters.

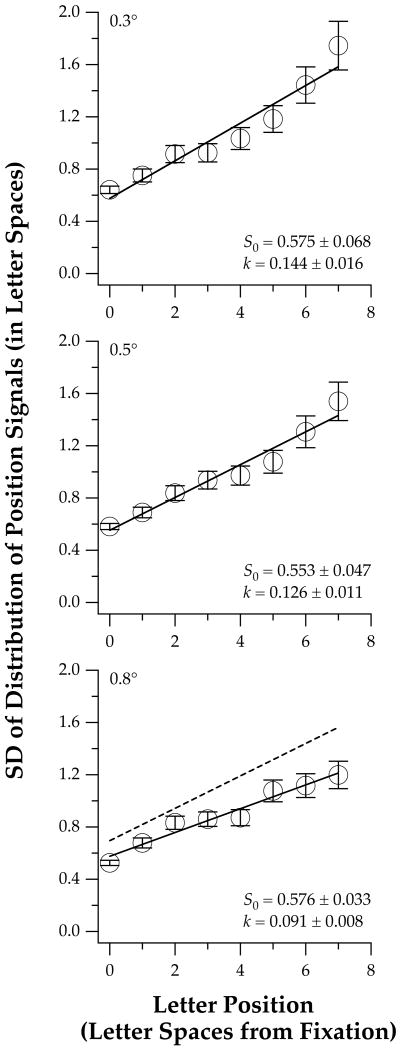
We also compared the empirically determined rate of mislocation errors (1 − R_score) with the model prediction as described in Experiment 1. The predicted model values were generated by first combining the estimated values of standard deviation for the same nominal letter position in the right and left hemifields (unfilled symbols in Figure 8), as we did in Experiment 1, and fitting the data with a regression line of the form of Eq. [4] from which the foveal standard deviation and the rate of change of the standard deviation with letter position (the slope parameter k) were derived. To compare the model predictions for Experiments 1 and 2, we included in the bottom panel of Figure 8 (letter size 0.8°) the regression line fit for the data in Experiment 1, which was shown in Figure 4B. The regression line of Experiment 1 (dashed line) has a steeper slope and was shifted vertically upward when compared with the regression line fit of Experiment 2. The upward shift of the line implies a higher rate of mislocation errors in Experiment 1, which could be due to the fact that in Experiment 2, we excluded from analysis trials in which the identities of both letters were incorrect.

Figure 8.

Estimated standard deviation of the distribution of position coding (in letter spaces) is plotted as a function of letter position, for the three letter sizes. SDs obtained for the same nominal letter position left and right of fixation were collapsed as one single value. A linear regression line (Eq. 4) was fit to each set of data (for each letter size), from which the foveal SD (parameter S₀) and the slope of the line (parameter k) were estimated.

The model prediction for Experiment 2 was then converted into the rate of mislocation errors which are plotted in Figure 9. Even when the letter identity was not disclosed to observers beforehand, our model still provides a reasonable description of the empirical rate of mislocation errors.

Figure 9.

Proportion of mislocation errors is plotted as a function of letter position left and right of fixation (letter position 0). The empirical values are the differences in proportion correct between the two curves in Figure 6, averaged across the six conditions. Values plotted are data combined across the six observers and averaged across the six conditions (3 letter sizes × 2 cueing conditions). The model fit was derived from the linear regression lines depicted in Figure 8.

Discussion

The goal of this study was to examine the precision of position coding for letters, and to determine whether or not the imprecision of letter position coding could account for errors made in identifying letter strings. In two experiments, we measured the accuracy of position signals for letters as a function of eccentricity, with and without the letter identity being disclosed to observers before testing. We also examined the effects of letter size and the deployment of spatial attention on the accuracy of positional signals. We characterized the precision of position signals for letters by the standard deviation of a hypothetical underlying Gaussian distribution centered on the letter position. Our data show that the position signal becomes increasingly imprecise with eccentricity.

Localizing the centroid of a letter

The 26 lowercase letters used in this study do not have regular shapes and each of them contains different letter features. Patel et al (1999) measured Vernier thresholds for pairs of random shapes and compared the thresholds with those obtained for two-dot stimuli. They found that Vernier thresholds for random shapes are generally higher than those for dot stimuli. To account for the difference in thresholds for regular and irregular shapes, Patel et al (1999) proposed that the determination of the centroid of regular shapes may rely on high-level learnt rules of geometry while that for irregular shapes may involve a noisier low-level centroid computation scheme, one that depends on the number of “position detectors” within the stimulus. Based on statistical grounds, the precision of determining the centroid of a stimulus would improve with the number of detectors.

If each letter feature³ has its own local sign, and the centroid of the letter is computed from these component local signs, then two factors could contribute to decreasing precision of letter position outward from fixation — a decrease in the number of features per letter, or increasing imprecision in the local signs of the component features.

Improper binding of letter features has been proposed to play a role in crowding and is a third possible factor underlying decreasing precision of letter-position signals. Levi, Hariharan and Klein (2002) and Pelli, Palomares and Majaj (2004) provided evidence that crowding is not due to a failure of feature detection, but more likely due to imperfect feature integration. According to this view, letters interfere with each other because their component features become jumbled (imperfect feature binding) during pattern recognition. Here, we suggest that in addition to accounting for letter identity errors, misbinding of letter features could also play a role in mislocation errors. The determination of centroid is a weighted computation taking into account the distance of individual features from the centroid, and misbinding of features could result in a change of centroid location. It is possible that the misbinding of letter features could result in identification errors without mislocations, and also mislocations without identification errors.

E₂ for position signals

Thresholds for almost all spatial tasks are known to increase (i.e. worsen) with eccentricity from the fovea. The E₂ parameter (the eccentricity at which threshold is twice the value at the fovea) is commonly used to represent the rate of change of the threshold of interest with eccentricity (e.g. Levi et al, 1984, 1985; Toet & Levi, 1992). A high E₂ value implies that the variable of interest changes slowly with eccentricity whereas a low E₂ value implies that the variable changes quickly with eccentricity. For instance, maximum reading speed decreases with eccentricity with an E₂ of 4.13° (Chung, Mansfield & Legge, 1998), contrast sensitivity, detection and resolution thresholds increase with eccentricity with an E₂ of about 2.5° (Levi & Klein, 1990; Virsu & Rovamo, 1979; Virsu, Näsänen, & Osmoviita, 1987), letter acuity and the critical print size for reading change with eccentricity with an E₂ of about 1.5° (Chung et al, 1998; Herse & Bedell, 1989). However, the most rapid increase in threshold with eccentricity is usually reported for hyperacuity tasks such as bisection, Vernier judgment and spatial interval discrimination, with an E₂ value of 0.6–0.8° (e.g. Beard et al, 1987; Levi & Klein, 1990; Levi & Waugh, 1994; Virsu et al, 1987; Waugh & Levi, 1993; Wilson, 1991).

Previously, Beard et al (1997) reported that for asynchronously presented Vernier targets that are thought to be mediated by the local sign mechanism, thresholds increase in peripheral vision with an E₂ of about 0.8°. Because we postulated that a similar mechanism could underlie the precision of position coding for letters, we asked whether letter position judgment would vary with eccentricity with an E₂ of about 0.8°. An estimation of the E₂ value can be obtained from Figure 8 in which we fit linear regression lines to the SD of the distribution as a function of letter position. The E₂ values obtained were 4.0, 4.4 and 6.3 letter positions from fixation, for 0.3°, 0.5° and 0.8° letters, respectively. When converted to degrees and assuming that adjacent letters were 1.16× the x-width for Courier letters, these E₂ values correspond to 1.88°, 3.45° and 7.91° for the three letter sizes respectively. Clearly, these E₂ values are all substantially greater than the 0.8° reported by Beard et al (1997), for their Vernier judgment task.

An explanation for the higher E₂ values obtained in this experiment than in Beard et al (1997) is probably related to the size scaling we observed. For our task, the E₂ is size-dependent, a likely consequence of the reliance on the centroids of the letters in making judgments of the relative positions of a pair of adjacent letters. The larger E₂ for larger target size is consistent with reliance on coarser features with more gradual dependence on retinal eccentricity. It is known that the crucial band of spatial frequencies for analyzing large letters is shifted toward higher object spatial frequencies (in cycles per letter) compared with smaller letters (Chung, Legge & Tjan, 2002; Majaj, Pelli, Kurshan & Palomares, 2002). Because the change in position threshold with eccentricity is slower for low spatial frequencies (higher E₂ value) than high spatial frequencies (Toet, Snippe & Koenderink, 1988), the change in position signals for letters with eccentricity should be slower for large letters than for smaller ones.

Linking letter position coding to crowding and reading

Letters appear as ordered strings in words. Recent findings indicate that the visual span for reading (the number of adjacent letters that can be recognized reliably on one fixation) limits reading speed (Legge et al, 2007), and that crowding is a major determinant of the size of the visual span (Pelli et al, 2007). To the extent that letter mislocations contribute to crowding and a reduction in the size of the visual span, they will also limit reading speed.

Here, we found that the imprecision of letter position coding accounts for a sizeable proportion of all the errors made on letter identity — approximately one-third of the total letter identity errors at a distance equivalent to seven letter positions from fixation. Even at three letter positions left or right of fixation, our results indicate that there is approximately a 20% chance letters are mislocalized. If these results generalize to reading, a person fixating on the leading letter of “boost” might sometimes read “boots”. While context will often be helpful in overriding such errors, mislocations might be more disruptive in identifying the leading letters of words rightward of fixation (termed parafoveal preview) or in correctly encoding long numbers or unfamiliar names.

Many theories have been proposed to account for the crowding effect, including an optical explanation (Hess, Dakin & Kapoor, 2000; Liu & Arditi, 2000), spatial scale shift (Hess et al, 2000; Chung & Tjan, 2007), its distinction from contrast masking by remote flankers (Chung et al, 2001; Levi et al, 2002; Pelli et al, 2004); loss of position information (Popple & Levi, 2005; Strasburger et al, 1991; Strasburger, 2005); abnormal feature integration (Nandy & Tjan, 2007; Pelli et al, 2004) and a reduced attentional resolution explanation (Intriligator & Cavanagh, 2001; He, Cavanagh & Intriligator, 1996; Strasburger et al, 1991). An extensive review of these theories is outside the scope of this paper (for a review, please refer to Levi, 2008). However, our finding of an increased imprecision of position signal with eccentricity is consistent with at least the loss of position information and the abnormal feature integration theories of crowding. According to our model, the loss of position information would increase the rate of letter-reversal errors whereas abnormal feature integration could cause letter-identity errors as well as errors in localizing the centroid of a letter.

We made two attempts to link letter mislocations to crowding. The first attempt was to compare the E₂ values. The reported E₂ values for crowding are approximately 0.9° for an acuity task (Jacobs, 1979), or 0.74° for the spatial extent of crowding (Chung, unpublished data). In comparison, our estimate of the E₂ for the precision of position coding for letters ranges between 1.88 and 7.91°, depending on letter sizes. The smaller E₂ for crowding than for mislocation errors, along with the fact that crowding is independent of target size (Levi et al, 2002; Pelli et al, 2007) and thus is compatible with the cortical magnification scaling rule, whereas our estimation of the precision of letter position coding shows a dependence on letter size, suggest that mislocation errors and crowding may not share the same underlying mechanism.

Our second attempt was to relate our finding of the rate of change of mislocation errors with distance from fixation to “Bouma's law”. Bouma (1970) first showed that the critical spacing for crowding is proportional to eccentricity. Pelli et al (2004, 2007) elaborated on Bouma's original finding and suggested that the critical spacing at any given eccentricity depends only on the eccentricity, but not the stimulus size. They further quantified Bouma's law to specify the critical spacing as half of the eccentricity, and suggested that a genuine crowding task would follow Bouma's law, i.e., the critical spacing extends to approximately half the eccentricity. With respect to our mislocation errors, Bouma's rule predicts that at a letter position X away from fixation, the critical spacing extends to X±0.5X letter positions. For example, the critical spacing for mislocation errors should be between 2 and 6 letter positions for a letter presented at 4 letter positions away from fixation. When expressed as degrees of visual angle, the critical spacing for mislocation errors becomes larger for a larger letter size. This scaling of mislocation errors with letter size is qualitatively similar to the scaling of critical spacing of crowding, suggesting that the computation underlying mislocation errors could be similar to that of crowding.

Taken together, our two attempts in comparing mislocation errors with crowding imply that we cannot completely rule out the independence of mislocation errors and crowding, although at this stage, the similarities in properties between the two are not strong enough for us to conclude that they share the same underlying mechanism.

Spatial cueing

In this study, we did not find any difference in the precision of position coding for letters with or without the pre-cue, nor did we find any improvement in letter identification accuracy with the pre-cue. This lack of an advantage of using the pre-cue has been reported in the literature. Nazir (1992) measured the effect of lateral masking on the resolution of the gap of a square C-like stimulus at eight possible locations 4° from fixation. In some of the trials, she presented a dot cueing the location of the stimulus preceding the trial and found no systematic differences in her results for the cued and uncued trials. This absence of a precueing effect did not depend on the location of the stimulus or the type of flankers. Shiu and Pashler (1994) suggested that the controversy over the benefit of a precueing effect could be due to whether the target is presented by itself in an otherwise empty field (single-element display) or accompanied by distractors (multi-element display). They showed that a precueing benefit is found when multiple masks are used instead of a single mask following the target, however, the benefit also depends on the validity of the precue. The precueing benefit disappears when the target location is validly cued. Given that our pre-cue always validly cued the locations of the two letters in the upcoming trial, our finding of a lack of the precueing effect is completely consistent with the report of Shiu and Pashler. Another factor that might account for the controversy of the precueing benefit is that the precueing effect is usually reported for stimuli that are very close to the visibility threshold. The traditional explanation for the precueing effect is that the cue helps the observers direct their attention to the target location and that the observers do not have to monitor, or spread their attention across many possible target locations. Presumably, suprathreshold targets can draw and direct observers' attention to the target location easily, especially when there is only a single target presented in an otherwise empty field (as in our experiments). As such, suprathreshold judgment may not be limited by attention and could also explain why we did not find a precueing benefit.

How generalizable is our model?

Given our interest in examining the precision of position coding of letters, in Experiments 1 and 2, we developed a model that specifically deals with position coding of letters. We showed that the model provides a reasonable description of our empirical data on letter identification. Can our model be generalized to other positional judgment tasks?

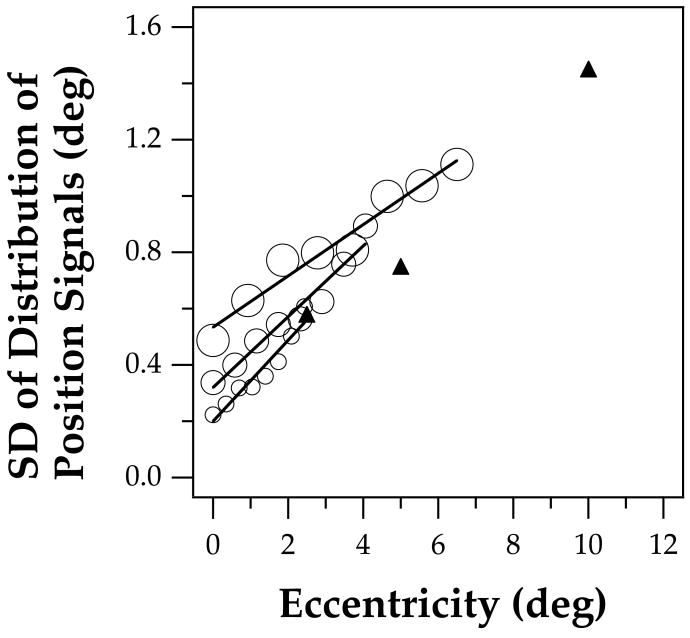
Levi and Tripathy (1996) examined human accuracy for localizing the position of a peripherally presented target, a task that is relevant to ours. Using Gaussian or Gabor patches, they found that when localization thresholds are plotted as a function of the standard deviation (SD) of the stimulus envelope, thresholds remain independent of SD for SD less than 1/5 of the stimulus eccentricity. When SD exceeds a certain critical point, referred to as the intrinsic blur, thresholds increase roughly linearly with increasing SD. The intrinsic blur therefore provides an estimate of the best precision of position coding for a peripheral target. In Figure 10, we replotted their estimated intrinsic blur values (Table 1 in Levi and Tripathy, 1996) as a function of stimulus eccentricity (shown as black triangles). Values plotted were averaged across observers who participated in the same testing condition. To show how their data compare to our model prediction, we included the standard deviations of the distribution of the position signals obtained in Experiment 2, replotted from Figure 8 and converted to degrees of visual angle as unfilled circles. The straight lines are predictions from our model fit. Clearly, even though the task of Levi and Tripathy (1996) differed from our letter identification task, their data follow the trend of our model prediction reasonably well, suggesting that our model, one that relates the standard deviations of the underlying distribution to positional judgment accuracy, could be generalized to account for performance on other positional judgment tasks.

Figure 10.

The SD of the intrinsic blur (in deg) for localizing peripherally presented Gaussian or Gabor patches is plotted as a function of stimulus eccentricity (black triangles; data replotted from Levi & Tripathy, 1996). For comparison, the estimated SD of the distribution of letter position coding as reported in Figure 8, converted to degrees, is plotted as a function of letter position, converted to eccentricity in degrees, for the three letter sizes (open circles). Straight lines represent the model predictions. The data for localizing Gaussian or Gabor patches follow the trend of our model predictions reasonably well.

Conclusions

In this paper, we have presented data showing that subjects make more letter-reversal errors with increasing distance from fixation. We interpret this finding to indicate that the coding of letter position becomes increasingly imprecise with distance from fixation. A simple noise model describes the data. The model assumes that the encoded position of each letter is Gaussian distributed and that the spread of the distribution governs the precision of localizing the letter. The key variable of the model is the standard deviation of the Gaussian distribution of position signals at any given retinal eccentricity. The value of the standard deviation depends on character size, consistent with a computation of pattern position based on a global statistic such as the centroid of component feature locations.

Appendix

Underlying Model

We assume that a stimulus contains a pair of letters L1 and L2 arranged side by side. A stimulus is encoded by the response of “feature detectors” in the visual pathway. A segmentation process divides the feature responses into two bundles of features B1 and B2.

A recognition algorithm is run independently on B1 and B2. Let the probability of a correct identification of L1 from bundle 1 be P1, and the probability of a correct identification of L2 from bundle 2 be P2.

An independent position finding algorithm is run on bundle 1 to estimate its position (e.g., a centroid computation), and also on bundle 2. Let the resulting estimated horizontal positions be H1 and H2. Assume that the probability of a correct spatial relationship between H1 and H2 is H12. The probability of a mislocation would be 1–H12.

Probabilities of Eight Outcomes

Assuming all of the computations are independent, there are eight possible outcomes for the response, determined by whether or not the first letter is right or wrong, the second letter is right or wrong, and whether or not the spatial order is right or wrong:

Case	L1 Identity	L2 Identity	Spatial Order	Probability
1	Correct: P1	Correct: P2	Correct: H12	P1P2H12
2	Correct: P1	Correct: P2	Wrong: 1-H12	P1P2(1-H12)
3	Correct: P1	Wrong: 1-P2	Correct: H12	P1(1-P2)H12
4	Correct: P1	Wrong: (1-P2)	Wrong: 1-H12	P1(1-P12)(1-H12)
5	Wrong: 1-P1	Correct: P2	Correct: H12	(1-P1)P2H12
6	Wrong: 1-P1	Correct: P2	Wrong: 1-H12	(1-P1)P2(1-H12)
7	Wrong: 1-P1	Wrong: 1-P2	Correct: H12	(1-P1)(1-P2)H12
8	Wrong: 1-P1	Wrong: 1-P2	Wrong: 1-H12	(1-P1)(1-P2)(1-H12)

The probabilities listed in the right column have a sum of 1.0.

Exact and Either Scoring

The probability of getting the first letter (L1) correct without regard to letter order (the either scoring), is the sum of the first four cases listed in the table above. As can be easily verified, the four corresponding expressions in the right column add up to P1.

The probability of getting L1 correct and also the correct letter order (the exact scoring) is determined by adding cases 1 and 3, that is, P1P2H12 + P1(1-P2)H12 = P1H12

The ratio of the exact to either scoring is: Ratio = P1H12/P1 = H12

Similarly, for L2: Ratio = P2H12/P2 = H12

From the above analysis, the ratio of the exact and inexact scores provides an estimate of the mislocation rate, given by 1–ratio, without contamination by the identification accuracy.