Abstract
We investigate numerically vortex-induced vibrations (VIV) of two identical two-dimensional elastically mounted cylinders in tandem in the proximity–wake interference regime at Reynolds number Re = 200 for systems having both one (transverse vibrations) and two (transverse and in-line) degrees of freedom (1-DOF and 2-DOF, respectively). For the 1-DOF system the computed results are in good qualitative agreement with available experiments at higher Reynolds numbers. Similar to these experiments our simulations reveal: (1) larger amplitudes of motion and a wider lock-in region for the tandem arrangement when compared with an isolated cylinder; (2) that at low reduced velocities the vibration amplitude of the front cylinder exceeds that of the rear cylinder; and (3) that above a threshold reduced velocity, large-amplitude VIV are excited for the rear cylinder with amplitudes significantly larger than those of the front cylinder. By analysing the simulated flow patterns we identify the VIV excitation mechanisms that lead to such complex responses and elucidate the near-wake vorticity dynamics and vortex-shedding modes excited in each case. We show that at low reduced velocities vortex shedding provides the initial excitation mechanism, which gives rise to a vertical separation between the two cylinders. When this vertical separation exceeds one cylinder diameter, however, a significant portion of the incoming flow is able to pass through the gap between the two cylinders and the gap-flow mechanism starts to dominate the VIV dynamics. The gap flow is able to periodically force either the top or the bottom shear layer of the front cylinder into the gap region, setting off a series of very complex vortex-to-vortex and vortex-to-cylinder interactions, which induces pressure gradients that result in a large oscillatory force in phase with the vortex shedding and lead to the experimentally observed larger vibration amplitudes. When the vortex shedding is the dominant mechanism the front cylinder vibration amplitude is larger than that of the rear cylinder. The reversing of this trend above a threshold reduced velocity is associated with the onset of the gap flow. The important role of the gap flow is further illustrated via a series of simulations for the 2-DOF system. We show that when the gap-flow mechanism is triggered, the 2-DOF system can develop and sustain large VIV amplitudes comparable to those observed in the corresponding (same reduced velocity) 1-DOF system. For sufficiently high reduced velocities, however, the two cylinders in the 2-DOF system approach each other, thus significantly reducing the size of the gap region. In such cases the gap flow is entirely eliminated, and the two cylinders vibrate together as a single body with vibration amplitudes up to 50% lower than the amplitudes of the corresponding 1-DOF in which the gap flow is active. Three-dimensional simulations are also carried out to examine the adequacy of two-dimensional simulations for describing the dynamic response of the tandem system at Re = 200. It is shown that even though the wake transitions to a weakly three-dimensional state when the gap flow is active, the three-dimensional modes are too weak to affect the dynamic response of the system, which is found to be identical to that obtained from the two-dimensional computations.
1. Introduction
Vortex-induced vibrations (VIV) of elastically mounted obstacles are of interest in a broad range of areas of engineering practice. These include, among others, the design of risers and conductor tubes in oil-drilling platforms, civil structures such as bridges and chimney stacks and marine structures in the ocean. In addition to their great practical relevance VIV problems are also important from a fundamental standpoint due to the enormous richness of their underlying vorticity dynamics. For these reasons a large and continuously expanding body of literature is dedicated to the study of VIV; see the recent review by Williamson & Govardhan (2004).
The flow past a single elastically mounted two-dimensional cylinder has served as the generic VIV model problem and has been widely studied both numerically and experimentally. As pointed out in the recent review of Williamson & Govardhan (2004), however, even this relatively simple system exhibits enormous complexity, and several aspects of its fundamental physics are still the subject of vigorous scientific debate and intense research. The complexity of VIV dynamics should thus be expected to increase considerably when two or more elastically mounted cylinders are arranged in close proximity to each other and allowed to vibrate freely as a coupled system. Even though early literature on VIV of two-cylinder configurations dates back to almost a century ago – see the early work by Pannell, Grifiths & Coales (1915) on airplane wires and Biermann & Herrnstein (1933) on airplane twin struts to support the wings – this problem has not been studied nearly as extensively as its single-cylinder counterpart. Yet understanding the VIV dynamics of multi-cylinder configurations is essential for the safety and reliability of various marine structures, where the suppression or minimization of flow-induced structural vibrations is a critical design requirement (Griffin & Ramberg 1982). In this paper we employ numerical simulation to contribute to the understanding of the physics of free vibrations of two elastically mounted, geometrically identical cylinders in tandem arrangement. In what follows, we provide a brief review of previous work on the single-cylinder problem followed by a more comprehensive review of the experimental and numerical literature on two-cylinder configurations. Finally, we present the objectives of our contribution and provide the outline of the paper.
It is well known that when a single elastically mounted cylinder is placed in a free stream, large-amplitude oscillations occur when the shedding frequency synchronizes with the oscillation frequency (Williamson & Roshko 1988). Unlike forced vibrations of a linear oscillator, the synchronization occurs over a range of frequencies, called the ‘lock-in’, ‘lock-on’ or ‘synchronization’ region (Griffin 1985; Sarpkaya 2004; Williamson & Govardhan 2004). The vortex shedding from a single cylinder in the lock-in region is more complex than the standard von Karman vortex street seen behind the rigid cylinder. In their pioneering experimental work Williamson & Roshko (1988) demonstrated that different vortex-shedding modes are associated with the different VIV regimes and characterized each mode by the number of vortices (S for a single and P for a pair of vortices) shed per cycle, e.g. the 2S, 2P and P+S. For a more detailed analysis and comprehensive review of related literature on single-cylinder VIV the reader is referred to the reviews by Griffin (1985), Sarpkaya (2004) and Williamson & Govardhan (2004).
If two cylinders are placed sufficiently close to each other their wakes can interfere, which further adds to the complexity of the problem for the cases of both stationary and elastically mounted cylinders. The distance needed for interference can vary for different arrangements (say tandem, staggered and side by side). Zdravkovich & Pridden (1977) broadly classified the various interference regions for stationary cylinders as follows: When the two cylinders are sufficiently far apart (L/D > 4 where D is the diameter of the cylinder and L is the distance between the cylinder centers), only the rear cylinder will be affected by the wake of the front cylinder (wake interference region). A far more complex situation arises when the rear cylinder is sufficiently close (L/D < 4) so that the wake of the first cylinder is affected by the presence of the rear cylinder. In this flow regime, which Zdravkovich & Pridden (1977) dubbed the proximity–wake interference region, the wake dynamics of both cylinders are coupled, as the presence of one affects the other, and the flow can become very complex and potentially bistable (Zdravkovich & Pridden 1977). Furthermore, experiments and simulations (Meneghini et al. 2001; Mizushima & Suehiro 2005; Tasaka et al. 2006) have shown a critical spacing L/D of about 3.5 exists in which the flow patterns undergo an abrupt change.
Vibrations of two elastically mounted cylinders in tandem (see figure 1) have been studied before albeit not nearly as extensively as single-cylinder vibrations – see Zdravkovich (1988) for a review of the vibrations of two cylinders in different interference regions and discussion of the underlying vibration mechanisms. In most experiments both cylinders were elastically mounted and free to vibrate except in the works of Bokaian & Geoola (1984a,b) in which one of the two cylinders was always held fixed. Bokaian & Geoola (1984b) reported that when the upstream cylinder is fixed the downstream cylinder exhibited, depending on the gap size and its structural properties, a VIV, a galloping, a combination of VIV and galloping or separated VIV and galloping. By ‘galloping’ they referred to what Zdravkovich (1985) called ‘fluid-elastic oscillations’. Other researchers have used different terms for the same phenomenon, such as ‘interference galloping’ (Ruscheweyh 1983) and ‘wake galloping’ (Brika & Laneville 1999). However, the term galloping can be misleading, since galloping instabilities are typically vibrations caused by the variation of the hydrodynamic forces due to the motion of the structure in the flow when the force is in the direction of the motion and increases as the structure moves away from the equilibrium position (Blevins 1990). In fact, in the tandem arrangement it has been shown that the force is restoring in nature; i.e. the force tends to restore the cylinders back to their initial rest (equilibrium) position (King & Johns 1976; Bokaian & Geoola 1984b; Blevins 2005). Fontaine et al. (2006) have classified hydrodynamic interference between two risers in two categories: (1) VIV and (2) wake-induced oscillations (WIO). In WIO, the velocity gradients in the wake of an upstream bluff body impose forces on the downstream bluff body that induce vibration (Blevins 1990, 2005; Wu, Huang & Barltrop 2003).
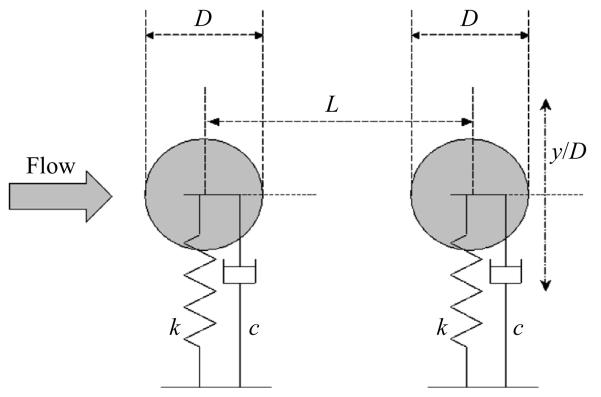
Figure 1.
Tandem arrangement of two identical, elastically mounted cylinders.
Zdravkovich (1985) observed that in some cases the amplitude of the upstream cylinder can be larger than the downstream one, while for other cases the opposite is true. Allen & Henning (2003), King & Johns (1976) and Laneville & Brika (1999) had similar observations. Fontaine et al. (2006) reported that in some cases the amplitude of the downstream cylinder can be more than twice as much as that of the upstream cylinder.
The focus of all previously reviewed experiments with two elastically mounted cylinders, including the most recent ones, has been for the most part on the cylinder response (amplitude) and to a lesser extent on the forces exciting the VIV. No experiments aimed at identifying the flow patterns associated with the modes and characteristics of the vibrations have been reported to date. Yet and as pointed out by Sumner, Price & Paidoussis (2000), flow visualization and identification of the flow patterns are critical prerequisites for understanding the fluid mechanics of multi-cylinder arrangements. Sumner et al. (2000) made this comment in relation to fixed cylinders, but the need for systematically studying the flow patterns should be even more pressing when the cylinders are free to vibrate, and the complexity of the problem increases dramatically. This need is clearly underscored by the often confusing and unclear terminology used to describe various phenomena observed in experiments (see previous literature review) and the apparent lack of conclusive understanding of the important physics of two-cylinder VIV. Numerical simulations can provide the necessary physical insights, but to the best of our knowledge only two numerical studies have been reported to date focusing on VIV of two-cylinder configurations (Mittal & Kumar 2001; Jester & Kallinderis 2004). Mittal & Kumar (2001) carried out two-dimensional simulations for two elastically mounted cylinders in tandem for Re = 100 and L/D = 5.5. Jester & Kallinderis (2004) simulated two-dimensional free vibrations for the tandem configuration for Re = 1000 and L/D = 5. For such spacings (L/D ≈ 5) the flow will fall into the wake interference region as classified by Zdravkovich & Pridden (1977). Therefore, the upstream cylinder behaves as an isolated single cylinder, while the downstream cylinder experiences large, flow-induced vibration over a wide range of flow velocities.
In this paper we employ the recently developed fluid–structure interaction (FSI) method of Borazjani, Ge & Sotiropoulos (2008) (see also Gilmanov & Sotiropoulos 2005 and Ge & Sotiropoulos 2007) to carry out two- and three-dimensional FSI simulations for two elastically mounted cylinders in tandem, placed L/D = 1.5 apart. This spacing places the problem in the proximity–wake interference region, which to the best of our knowledge has never before been studied numerically, and consequently many important aspects of its underlying physics remain largely unexplored or poorly explained (see table 1 for the list of simulations performed in this work). For example an important feature of this flow regime, which has been observed in experiments but has yet to be conclusively explained, is the fact that depending on the governing parameters either the front or the rear cylinder could exhibit the largest oscillation amplitude. As previously mentioned, King & Johns (1976) have argued that this phenomenon occurs because the vortex shedding from the front cylinder sometimes strengthens and sometimes weakens that from the rear cylinder. As we will show in this paper, this explanation, however, is far too broad and somewhat simplistic. Other aspects of the flow in the proximity–wake interference region that are virtually unexplored and will be addressed in this work are the specific flow patterns and the vorticity dynamics during vibrations. Furthermore, we also consider the effect of the number of degrees of freedom of the motion of the two cylinders on the dynamics of the VIV. We carry out and report calculations with both one (only vertical motion) and two (vertical and horizontal) degrees of freedom.
Table 1.
List of simulations performed for this study.
| Arrangement | Re | L/D | 3-D vs 2-D | DOF | Mred | ξ | Ured |
|---|---|---|---|---|---|---|---|
| Isolated | 150 | NR | 2-D | 1 | 2 | 0 | 3, 4, 5, 6, 7, 8 |
| Isolated | 200 | NR | 2-D | 1 | 2 | 0 | 3, 4, 5, 6, 7, 8 |
| Tandem | 200 | 1.5 | 2-D | 0 (fixed) | NR | NR | NR |
| Tandem | 200 | 4 | 2-D | 0 (fixed) | NR | NR | NR |
| Tandem | 200 | 1.5 | 2-D | 1 | 2 | 0 | 3, 4, 5, 6, 7, 8, 10, 14 |
| Tandem | 200 | 1.5 | 2-D | 2 | 2 | 0 | 3, 4, 5, 6, 7, 8, 10 |
| Tandem | 200 | 1.5 | 3-D (width = 5D) | 1 | 2 | 0 | 4, 8 |
| Tandem | 200 | 1.5 | 3-D (width = 5D) | 2 | 2 | 0 | 6, 7 |
Re: Reynolds number; L/D: distance between cylinder centres and diameters; 2-D: two-dimensional; 3-D: three-dimensional; DOF: degrees of freedom; Ured: reduced velocity; Mred: reduced mass; ξ: non-dimensional damping coefficient; NR: not relevent.
Our simulations are carried out for Re = 200. This value of Reynolds number is widely considered in the literature to be the upper threshold for which the wake flow remains two-dimensional and laminar (Carmo & Meneghini 2006; Papaioannou et al. 2006; Ryan, Thompson & Hourigan 2007), and as such two-dimensional simulations should be appropriate. To examine the validity of this broadly accepted hypothesis for the problem under consideration, we also carry out several three-dimensional FSI simulations by considering two-dimensional cylinders of finite span. Our results will show that even though weakly three-dimensional instabilities are excited in the wake of the second cylinder, and in some cases even within the gap region, these instabilities are not sufficiently strong to alter the dynamic FSI response of the system, which for all simulated cases is found to be essentially identical to that observed for the two-dimensional system.
It is important to note that most of the available experimental observations are at significantly higher Reynolds number. Our results will show, however, that important aspects of the VIV dynamics observed in the experiments are also reproduced numerically at lower Re. This finding is not surprising given the large body of previous numerical work with a single, freely vibrating cylinder, which has shown that low Re simulations can capture and adequately explain a wide range of VIV phenomena (Williamson & Govardhan 2004). Furthermore, given the current state of understanding of two-cylinder VIV – especially in the proximity–wake interference region – simulations at low Reynolds number should be a useful first step towards elucidating the mechanisms responsible for excitation of cylinders to large amplitudes (Mittal & Kumar 2001).
This paper is organized as follows. In § 2 we present the governing equations and a brief description of the FSI numerical algorithm. In § 3 we verify and validate the numerical method by applying it to simulate flow past stationary cylinders in tandem and VIV of a single elastically mounted cylinder. The results are compared with experimental observations and other benchmark simulations reported in the literature. In § 4 we present the results of the two-dimensional FSI simulations for the tandem arrangement with one and two degrees of freedom with emphasis on both the dynamic response of the system and the flow patterns. We also present the results of the three-dimensional FSI simulations and compare the computed solutions with their two-dimensional counterparts. In § 5 we discuss and summarize the vibration excitation mechanisms emerging from our simulations.
2. Governing equations and numerical method
We consider flow of an incompressible, viscous, Newtonian fluid in a domain containing an arbitrary number of identical, rigid, elastically mounted cylinders that are free to vibrate in response to flow-induced forces. The fluid flow is governed by the unsteady incompressible Navier–Stokes equations, which in compact tensor notation read as follows:
| (2.1) |
| (2.2) |
where ui are the velocity component along the xi direction; p is the pressure divided by the fluid density ρ; Re is the Reynolds number based on the diameter of the cylinder D, the approach flow velocity U and the kinematic viscosity of the fluid ν (Re = UD/ν); and D/Dt is the material derivative defined as (D/Dt)(·) = (∂/∂t)+ uj (∂/∂xj ).
The equation of motion of an elastically mounted cylinder is obtained from Newton's second law of motion and reads in compact tensor notation as follows (i = 1, 2):
| (2.3) |
where m is the mass of the cylinder; Qi is the ith component of the position vector of the center of the cylinder; c is the parameter governing the damping of the system; k is the stiffness of the spring; and Fi is the ith component of the force imparted by the flow on the cylinder (see figure 1). The natural frequency f and the critical damping factor ccr of the elastically mounted cylinder are given as follows:
| (2.4) |
| (2.5) |
Equation (2.3) can be formulated in a non-dimensional form, using the diameter D and the free stream velocity U as length and velocity scales, respectively, as follows (Qi is now used to denote the non-dimensional coordinates of the position vector):
| (2.6) |
The various non-dimensional parameters in the above equations are defined as follows: non-dimensional damping coefficient
| (2.7) |
reduced velocity
| (2.8) |
reduced mass
| (2.9) |
non-dimensional force coefficient
| (2.10) |
Equation (2.6) comprises a system of second-order ordinary differential equations, which are solved numerically by first transforming them into a system of first-order ordinary differential equations as follows:
| (2.11) |
| (2.12) |
The Navier–Stokes equations ((2.1) and (2.2)) are closed with the no-slip and noflux boundary conditions for the velocity field, which need to be prescribed on the instantaneous location of the fluid/solid interface Γ (t). Assuming that a set of K material points are used to describe the shape and track the position of the surface Γ (t) of the body, and letting xk(t) be the position vector of the kth material point at time t, the boundary conditions at the rigid fluid/solid interface can be formulated as follows:
| (2.13) |
Equation (2.13) couples the Eulerian velocity field of the fluid with the Lagrangian description of the motion of the solid surface and closes the FSI problem, consisting of (2.2), (2.6) and (2.13), which needs to be solved numerically.
The FSI numerical algorithm we employ in this work has been described in detail in Borazjani et al. (2008). Only a brief overview of the key aspects of the method are presented here for the sake of completeness.
The method for solving the Navier–Stokes equations ((2.1) and (2.2)) in a domain containing moving rigid objects is the sharp interface, hybrid Cartesian/immersed boundary methodology of Gilmanov & Sotiropoulos (2005) enhanced with the algorithmic improvements reported by Ge & Sotiropoulos (2007). This method employs an unstructured, triangular mesh to track the motion of three-dimensional, arbitrarily complex, moving immersed boundaries. The immersed boundaries are treated as sharp interfaces by reconstructing boundary conditions for the velocity field at grid nodes in the immediate vicinity of the moving boundary – the so-called immersed boundary (IB) nodes – by interpolating along the local normal to the boundary. The reconstruction method has been shown to be second-order accurate on Cartesian grids with moving immersed boundaries (Gilmanov & Sotiropoulos 2005) and can easily handle situations involving multiple moving objects with large amplitudes of motion. The IB nodes are identified using an efficient node-classification algorithm described in detail in Borazjani et al. (2008). The Navier–Stokes equations are discretized on the background mesh, using the second-order accurate curvilinear/immersed boundary (CURVIB) method of Ge & Sotiropoulos (2007). The convective terms are discretized with the second-order accurate quadratic upstream interpolation for convective kinematics (QUICK) scheme, while three-point central differencing is used for the viscous and pressure gradient terms. The discrete equations are integrated in time via the second-order accurate fractional step formulation of Ge & Sotiropoulos (2007). The momentum equations are solved implicitly with a Newton–Krylov solver (Ge & Sotiropoulos 2007). The Poisson equation is solved with a generalized minimal residual algorithm (GMRES) solver enhanced with multigrid as preconditioner, and the discrete divergence of the velocity is driven to machine zero at every time step usually within 30 GMRES iterations (Ge & Sotiropoulos 2007).
The FSI solver adopts the partitioned FSI solution approach, and both loose coupling (LC-FSI) and strong coupling (SC-FSI) strategies are implemented. Numerical experiments and theoretical stability considerations presented in Borazjani et al. (2008) suggest that both the properties of the structure (mass, geometry) and the local flow conditions can play an important role in determining the stability of the FSI algorithm. Under certain conditions unconditionally unstable FSI iterations result even when SC-FSI is employed. For such cases, however, combining SC-FSI with under-relaxation in conjunction with the Aitken acceleration technique (Irons & Tuck 1969) was shown to effectively resolve the stability problems. As shown in Borazjani et al. (2008) for the range of reduced mass values Mred considered in this work (Mred = 2), both the LC-FSI and SC-FSI (without under-relaxation) algorithms yield robust FSI iterations and results that are essentially indistinguishable from each other. Therefore, LC-FSI was used for the three-dimensional simulations, which are computationally very expensive compared to the two-dimensional simulations, while SC-FSI was used for all the two-dimensional simulations. The SC-FSI is declared to be converged when the difference in the velocity and position of each cylinder between two successive iterations drops about four orders of magnitude to 10−6. Such a level of convergence is usually achieved within four to five SC-FSI iterations. For more details on our FSI numerical method, the reader is referred to Borazjani et al. (2008).
3. Validation and verification of the FSI algorithm
The fluid solver has been thoroughly validated for flows with prescribed motion in Gilmanov & Sotiropoulos (2005) and Ge & Sotiropoulos (2007). The FSI algorithm has also been extensively validated in Borazjani et al. (2008) for VIV of an elastically mounted cylinder and pulsatile, physiologic flows through a bileaflet mechanical heart valve. The ability of the method to accurately calculate the total force imparted by the flow on the moving boundary, including its pressure and viscous components, has also been demonstrated in Borazjani & Sotiropoulos (2008) by simulating inline forced vibrations of a single cylinder and comparing with benchmark numerical results and experimental data. In this section we further demonstrate the accuracy of our numerical method by applying it to simulate two test cases, which are relevant to the problem of interest in this work and for which benchmark simulations and experiments have been reported in the literature: (1) flow past two fixed cylinders in tandem and (2) VIV of a single elastically mounted cylinder. The first case seeks to validate the temporal and spatial accuracy of the solver for the fixed cylinder configuration. The unsteady periodic flow state obtained from these simulations also provides the initial condition for the two-cylinder FSI simulations reported in §4. Some results for the second case have already been presented in Borazjani et al. (2008), where our method was shown to reproduce benchmark computational data with good accuracy. Additional results for this case are included in this paper in order to compare the vibrations of the two tandem cylinders with an isolated cylinder under the same conditions.
3.1. Flow past two stationary cylinders in tandem
This test case is identical to that studied numerically by Meneghini et al. (2001), using a fractional-step, Galerkin, finite element method, and Slaouti & Stansby (1992), using a point-vortex methodology. Two tandem arrangements of two identical cylinders are considered, with L/D = 1.5 and 4, respectively. For both cases simulations are carried out for Re = 200. The inlet of the computational domain is placed 7.5D upstream of the first cylinder, while the outlet is placed 24D from the second cylinder. The upper and lower boundaries are respectively placed 8D above and below the horizontal axis of symmetry. The background Cartesian domain is discretized with 281 × 241 grid nodes for L/D = 1.5 and 401 × 209 for L/D = 4 in the horizontal and vertical directions, respectively. The mesh is uniform and isotropic with spacing h = 0.022D in a square with dimensions 30 × 30, containing the two cylinders in the L/D = 1.5 case. Two such squares, each containing one cylinder, are used in the L/D = 4 case. Outside the region near the two cylinders the mesh is stretched to the boundaries of the computational domain, using the hyperbolic tangent stretching function. The non-dimensional time step for all simulations is Δt = 0.02. Extensive numerical sensitivity studies showed that these mesh and time step sizes are adequate for obtaining grid-independent solutions.
For the L/D = 1.5 case, the simulations reveal the presence of two quasi-steady vortices in the gap area between the two cylinders. The drag force on the front and rear cylinders is positive and negative, respectively, while the lift force on the rear cylinder is larger than on the front one. The calculated values of the time-averaged drag and lift forces and the Strouhal number are all found to be smaller than the corresponding values for a fixed isolated cylinder at the same Reynolds number. All these findings are in good qualitative agreement with the experimental data of Zdravkovich & Pridden (1977) for the same cylinder spacing but higher Reynolds numbers. In table 2 the results of our simulations are tabulated and compared with the results of Meneghini et al. (2001) and Slaouti & Stansby (1992). It is evident from these comparisons that our computed results are in good overall agreement with the simulations of Meneghini et al. (2001) (note that the lift coefficients reported here in the table have been extracted to plotting accuracy from figure 8 of their paper) and in reasonable agreement with simulations of Slaouti & Stansby (1992) as shown in table 2. A striking discrepancy that is evident from table 2 is that the lift coefficients for both cylinders calculated by Slaouti & Stansby (1992) are one order of magnitude larger than our predictions and those by Meneghini et al. (2001). It is not clear whether this discrepancy is possibly due to a typographical error in the paper of Slaouti & Stansby (1992) or due to some other inherent numerical error. The overall consistency of our results with those of Meneghini et al. (2001), however, does suggest that the two studies yield reliable results of comparable accuracy. Even though some quantitative differences between our predictions and those of Meneghini et al. (2001) are observed, the overall level of agreement of the two studies is well within the range of what has been reported in previous numerical studies of related flows. For example the computed values for the drag coefficient of a single cylinder at Re = 200 have been reported to be in the range of 1.17 to 1.58 (see table 2 of Liu, Zheng & Sung 1998), while, for a more closely related test case, the drag coefficient of the first cylinder in a two-cylinder tandem arrangement at L/D = 3.5 spacing has been reported to be in the range 0.85 to 1.27 (see table 1 of Papaioannou et al. 2006).
Table 2.
Mean drag coefficient (Cd), lift coefficient fluctuations (Cl) and the Strouhal number (St) for two stationary tandem cylinders with L/D = 1.5 and Re = 200 are compared with the results of Meneghini et al. (2001) and Slaouti & Stansby (1992). The subscripts 1 and 2 refer to the front and the rear cylinders, respectively. The values before and after ± represent the mean value and the above-the-mean fluctuation amplitude, respectively
| L/D = 1.5 | Cd1 | Cl1 | St1 | Cd2 | Cl2 | St2 |
|---|---|---|---|---|---|---|
| Present | 1.1121 | 0.024 | 0.174 | −0.216 | 0.05 | 0.174 |
| Meneghini et al. (2001) | 1.06 | 0.03* | 0.167 | −0.18 | 0.06* | 0.167 |
| Slaouti & Stansby (1992) | 0.83 ± 0.05 | 0.2 | 0.14 | −0.17 ± 0.15 | 0.3 | 0.14 |
represents uncertainty in the measurement.
Figure 8.
Phase portrait of the transverse force relative to the transverse motion for the 1-DOF tandem system (Re = 200, Mred = 2, ξ = 0). Black and grey colors correspond to the front and the rear cylinders respectively. (a) Ured = 3; (b) Ured = 4; (c) Ured = 5; (d) Ured = 6; (e) Ured = 7; (f) Ured = 8; (g) Ured = 10; (h) Ured = 14.
The cylinder spacing (L/D = 4) for the second test case is very close to the critical spacing for which previous experiments and simulations (Meneghini et al. 2001; Mizushima & Suehiro 2005) have shown that the flow patterns undergo an abrupt change. The exact value of the critical spacing depends on the Reynolds number of the flow with all available experimental and numerical results scattered around (L/D)crit = 3.5 (Mizushima & Suehiro 2005). In the vicinity of the critical spacing the flow is dominated by the competition of two states (Mizushima & Suehiro 2005; Tasaka et al. 2006). The first state is characterized by the formation of two quasi-steady vortices in the gap region and periodic vortex shedding from the rear cylinder. The second state is far more complex, as it is characterized by the onset of vortex shedding from the first cylinder and the emergence of a dynamically rich flow state in the wake of the second cylinder.
Our numerical simulations for L/D = 4 capture the competition of these two flow states as shown in figure 2, which depicts the time variation of the drag coefficient of the second cylinder. After approximately 100 units of simulation time, the vortex shedding from the second cylinder reaches a statistically stationary state with the drag force oscillating periodically above a constant mean value. The typical flow pattern for this state is shown in the corresponding inset in figure 2 and consists of a quasi-steady gap flow with periodic vortex shedding from the second cylinder. This flow state is sustained in the computation for approximately 430 time units at which point the flow undergoes an abrupt change. Both the magnitude and fluctuation amplitude of the drag force increase sharply and no periodic state is achieved for as long as we continue the simulation (approximately an additional 500 time units beyond the onset of the flow transition; see figure 2). The characteristic flow patterns for this new state are dominated by vortex shedding from the first cylinder and a complex flow in the wake of the second cylinder.
Figure 2.
Drag coefficient time history for the rear cylinder of two stationary cylinders in tandem with L/D = 4. At about 430 time units an abrupt change in the drag coefficient is observed. The insets show the flow state before and after the abrupt change. The shedding from the front cylinder causes the abrupt change in the forces. It also disrupts the shedding from the rear cylinder; therefore, periodic steady state was not reached for the rear cylinder.
Comparisons between our simulations and the results of Slaouti & Stansby (1992) and Meneghini et al. (2001) are shown in table 3. As seen from this table the lift force on both cylinders is higher than the L/D = 1.5 case with the rear cylinder experiencing higher lift force than the front one; the drag force on both cylinders is positive; and the Strouhal number is still smaller than that for an isolated cylinder. These trends are in qualitative agreement with the experimental data (Zdravkovich & Pridden 1977) and in reasonable overall quantitative agreement with the numerical results (Slaouti & Stansby 1992; Meneghini et al. 2001). The sharp flow transition indicated in figure 2 was also observed in the numerical simulations of Meneghini et al. (2001). The only difference between our simulations and their results is that in their work the transition occurred after approximately 120 time units instead of the 430 time units it took for the transition to occur in our simulation. Note, however, that Meneghini et al. (2001) employed a finite-element method; so the numerical disturbances that are implicitly embedded in the two simulations due to discretization and other numerical errors are drastically different, and this could explain the differences in the transition times. Slaouti & Stansby (1992) did not observe such a transition. The most significant discrepancies between the three results shown in table 3 are observed in the quantities predicted for the rear cylinder. The observed spread for the differences in predicted quantities could be due to the fact that neither the present simulation nor that of Meneghini et al. (2001) reached a periodic state, and consequently they may have not achieved the same level of statistical convergence.
Table 3.
Mean drag coefficient (Cd), lift coefficient fluctuations (Cl) and the Strouhal number (St) for two stationary tandem cylinders with L/D = 4 and Re = 200 are compared with the results of Meneghini et al. (2001) and Slaouti & Stansby (1992). The subscripts 1 and 2 refer to the front and the rear cylinders, respectively. The values before and after ± represent the mean value and the above-the-mean fluctuation amplitude, respectively
| L/D = 4 | Cd1 | Cl1 | St1 | Cd2 | Cl2 | St2 |
|---|---|---|---|---|---|---|
| Present | 1.29 | 0.745 | 0.185 | 0.6 | 1.9 | 0.185 |
| Meneghini et al. (2001) | 1.18 | 0.75* | 0.174 | 0.38 | 1.5* | 0.174 |
| Slaouti & Stansby (1992) | 1.11 ± 0.05 | 0.7 | 0.19 | 0.88 ± 0.4 | 1.8 | 0.19 |
represent uncertainty in the measurement.
3.2. VIV of an isolated cylinder
In this section we report numerical simulations of VIV for an isolated elastically mounted cylinder in order to verify the FSI solver with benchmark data and also establish the baseline case for analysing the VIV of the cylinders in tandem arrangement. The grid used here is the same as the L/D = 1.5 test case discussed above with 281 × 241 grid nodes except that the cylinder is positioned 8D from the inlet and at the center of the 3D × 3D uniform mesh box.
We investigate the effect of the reduced velocity Ured on the dynamic response of the cylinder by fixing Re, Mred and ξ (Re = 150, Mred = 2, ξ = 0) and systematically varying Ured in increments of one (starting from Ured = 3) to find the lock-in region. The calculated response curve (vibration amplitude plotted against reduced velocity) is shown in figure 3, which also includes the recent results of Ahn & Kallinderis (2006) for comparison. As seen in figure 3, the two numerical results are in excellent agreement with each other. It should be pointed out that the comparisons shown in figure 3 have also been included and discussed in detail in Borazjani et al. (2008). We chose, however, to also include this figure in the present paper for the sake of completeness, since the single-cylinder VIV case provides the basis for comparison for the tandem configuration.
Figure 3.
The calculated response curve (maximum vibration amplitude vs reduced velocity) of an isolated cylinder at Re = 150 and 200 compared with the published results of Ahn & Kallinderis (2006) at Re = 150 (Mred = 2, ξ = 0).
To compare the oscillations of the tandem cylinders, which will be presented in §4, with the isolated-cylinder case at the same Reynolds number, we also carried out VIV simulations for the isolated-cylinder case at Re = 200 (Mred = 2, ξ = 0). The results for this Reynolds number are similar to those for the Re = 150 case except that the lift force and displacement become out of phase, and the oscillation amplitude is reduced at a lower reduced velocity (Ured = 7) as can be observed in figure 3. Figure 4 shows the corresponding phase portrait for different reduced velocities. It can be observed that at Ured = 3 the phase portrait is in the first and third quadrants, and the lift coefficient and displacement are in-phase. As the reduced velocity is increased the phase portrait rotates counterclockwise, and at Ured = 7 it is located in the second and fourth quadrants; i.e. lift coefficient and displacement become out of phase.
Figure 4.
Phase portraits of displacement vs lift coefficient at different reduced velocities for an isolated cylinder (Re = 200, Mred = 2, ξ = 0). The phase angle rotates counterclockwise by increasing the reduced velocity and becomes out-of-phase at higher reduced velocities (Ured ≥ 7). (a) Ured = 3; (b) Ured = 4; (c) Ured = 5; (d) Ured = 6; (e) Ured = 7; (f) Ured = 8.
Figure 9 shows the root mean square (r.m.s.) of drag and lift coefficients, ratio of frequency of oscillation to the natural frequency of the system, and the phase angle between the lift force and cylinder oscillations for an isolated elastically mounted cylinder as a function of reduced velocity. The r.m.s. quantities are calculated from an ensemble of about 4000 to 5000 time steps corresponding to about 20 cycles in the quasi-steady state. The early transitional data were carefully removed before calculating the various quantities. Note that figure 9 also includes the same results for the tandem arrangement, but these results will be discussed later in § 4.1.1. For the time being, we focus our discussion exclusively on the response of the single-cylinder system. It can be observed from figure 9(a,b) that the r.m.s. drag coefficient of an isolated cylinder is maximized at Ured = 4, where the vibration amplitude is maximum, while the r.m.s. lift coefficient is minimized at Ured = 6, where the frequency of the oscillation is the same as the natural frequency. The simulated behaviour of lift and drag coefficients is similar to that in Blackburn & Henderson (1999) and Zhou, So & Lam (1999), who reported computational results for VIV of an isolated cylinder at Re = 200 with Mred = 10, ξ = 0.01 and Mred = 1, ξ = 0.01, 0.1, 1.0, 10.0, respectively.
Figure 9.
Vibrations of two tandem cylinders at different reduced velocities (1-DOF, Re = 200, Mred = 2, ξ = 0). (a) CXr.m.s.: r.m.s. drag coefficient; (b) CYr.m.s.: r.m.s. lift coefficient; (c) f/fN: oscillation frequency to natural frequency; (d) ϕ: phase angle between the lift coefficient and cylinder oscillations. Solid line: 1-DOF system; dashed lines: 2-DOF system; open symbols: front cylinder; filled symbols: rear cylinder.
It is also worth noting in figure 9(c) that within the lock-in region, the oscillation frequency does not exactly match the natural frequency of the system. This phenomenon is referred to as ‘soft’ lock-in by Mittal & Kumar (2001) and has been observed by different researchers (Moe & Wu 1989; Khalak & Williamson 1997, 1999). As pointed out by Mittal & Kumar (2001) this is one of the mechanisms through which the nonlinear oscillator self-limits the vibration amplitude.
We also observe in figure 9(d) that for Ured > 6 the phase angle between the lift force and cylinder oscillations jumps sharply by almost 180°. The change in the phase angle is linked to the change in the timing of the vortex shedding as shown in figure 5, which shows the vortex-shedding patterns for Ured = 3 and 8 at the maximum bottom position (ymin). Such change in the phase angle has also been observed in the experiments. Depending on whether the flow velocity is increased or decreased, two response types (called initial branch and lower branch) have been documented experimentally, which have different phase angles (Williamson & Govardhan 2004). Zdravkovich (1982) was the first to show via flow visualization that the phase angle jump between the initial and lower branches is linked to the change in the timing of the vortex shedding. The same phenomenon has also been observed in the forced-vibration simulations of Meneghini & Bearman (1993, 1995) and Blackburn & Henderson (1999), among others.
Figure 5.
Snapshots of vorticity contours from two isolated cylinders (Re = 200, Mred = 2, ξ = 0): (a) Ured = 8 and (b) Ured = 3 when at the maximum bottom position (ymin). The phase angle variation is linked to such changes in the timing of vortex shedding. The dashed lines represent negative vorticity.
It is evident from the above discussion that our numerical approach yields results in very good quantitative agreement with previous simulations and captures all qualitative trends of the single-cylinder system response as observed in previous experimental and computational studies. Having established the accuracy of our FSI method we now proceed to tackle the main objective of this work, namely the study of induced vibrations of two identical, elastically mounted cylinders in tandem arrangement.
4. Flow-induced vibrations of two cylinders in tandem
4.1. Two-dimensional simulations
In this section we report the results of two-dimensional numerical simulations and analyse the physics of the flow past two elastically mounted cylinders in tandem. The cylinders are placed at L/D = 1.5 apart, and the Renolds number is Re = 200. The non-dimensional parameters governing the response of the structures are the same as for the single-cylinder simulation (Mred = 2, ξ = 0), and the reduced velocity is systematically varied in the range 3 ≤ Ured ≤ 14. The damping coefficient ξ is assigned to be zero to obtain the most intense vibrations, as damping has been shown to decrease the vibration amplitude (Zhou et al. 1999; Fontaine et al. 2006). We carry out simulations for both one (only vertical motion is allowed) and two (both vertical and horizontal motion is allowed) degrees of freedom (1-DOF and 2-DOF, respectively) to investigate the effect of the degrees of freedom on the ensuing VIV dynamics. For all cases, the size of the computational domain, the density and distribution of the grid and the size of the time step are identical to those used for the stationary tandem arrangement discussed in § 3.1. Also all FSI computations reported in this section are initialized from the same instantaneous snapshot of the solution we obtained in § 3.1 for the stationary tandem arrangement. The simulations are continued until the quasi-steady state is reached.
In what follows, we begin by discussing the 1-DOF system in terms of its dynamic response and the underlying vorticity dynamics. Subsequently we discuss the results of our simulations for the 2-DOF system. Finally, we discuss the three-dimensional results.
4.1.1. 1-DOF
Response curve and VIV dynamics
As expected from the single-cylinder results, the dynamic response of the system is found to depend strongly on the reduced velocity. Figure 6 shows the temporal variation of the position of the two cylinders for four different values of Ured, which are selected to highlight representative dynamical responses in the various VIV regimes. For Ured = 3 (see figure 6a) the oscillation amplitudes are small, i.e. out of lock-in, but the front cylinder exhibits larger oscillation amplitude than the rear cylinder with (where and denote the maximum vibration amplitudes for the front and rear cylinders, respectively). For the sake of our discussion we shall refer to the vibration state for which the statistically stationary solution is such that as state 1. When the reduced velocity is increased to Ured = 4 (see figure 6b), a different dynamic response is observed as the two cylinders now oscillate out of phase and the overall oscillation amplitudes increase considerably, reaching nearly 50% of the cylinder diameter. During the early transients both cylinders oscillate at comparable amplitudes, but beyond a certain time the oscillation amplitude of the second cylinder is reduced, and the first cylinder is still oscillating at higher amplitude than the second one; i.e. the flow is still in state 1.
Figure 6.
Time history of transverse vibrations (y/D) of two 1-DOF cylinders in tandem (Re = 200, Mred = 2, ξ = 0) for four different values of Ured. (a) Ured = 3; (b) Ured = 4; (c) Ured = 5; (d) Ured = 8.
At Ured = 5 (see figure 6c) the cylinders continue to oscillate out of phase, but their relative oscillation amplitudes undergo a dramatic transition, as the rear cylinder is now seen to exhibit somewhat larger oscillation amplitude than the front cylinder. This trend is found to persist and intensify for Ured > 5 as shown in figure 6(d). In general, further increase in the reduced velocity was found to cause large-amplitude oscillations with the second cylinder always having the largest amplitude : we shall refer to this state of the vibration as state 2. Furthermore, increasing the reduced velocity is also seen to increase the overall transient time required for the system to attain its statistically stationary state.
Based on figure 6(c), Ured = 5 appears to be very close to the critical level of the reduced velocity that delineates states 1 and 2, i.e. when the magnitude of the oscillation amplitude of the rear cylinder overtakes for the first time that of the front cylinder. For this reason and to facilitate our subsequent discussion we shall refer to the solution obtained for Ured = 5 as the critical state. As we have already discussed in the introduction, similar transition from state 1 to state 2 for two vibrating cylinders in tandem has also been observed experimentally (King & Johns 1976; Ruscheweyh 1983; Allen & Henning 2003). To the best of our knowledge, however, no conclusive explanation has been offered to date for this intriguing phenomenon. This issue will be further pursued in § 5.
Figure 7(a) shows the response curve for the two-cylinder system over the entire range of simulated reduced velocities. For reference, the response curve of the single-cylinder case is also included in this figure. It is evident from this figure that the lock-in region for the tandem arrangement is much wider than that for the isolated-cylinder case, which is in agreement with the experimental findings (King & Johns 1976; Ruscheweyh 1983; Brika & Laneville 1999). It is also evident that the state 2, persists for all Ured > 5 with no signs of this trend reversing even for reduced velocities as high as Ured = 14. This finding is also in agreement with the experimental measurements of King & Johns (1976), who reported that the downstream cylinder in their experiment continued to oscillate with the highest amplitude regardless of how much the reduced velocity was increased; in their experiment they studied reduced velocities as high as Ured = 18. In our simulations if the maximum vertical separation between cylinders exceeded one diameter state 2 was observed. To reinforce this point, we plot in figure 7(b) the variation of the maximum vertical separation of the two cylinders with Ured. Figure 7(b) shows clearly that the large-amplitude oscillations of the rear cylinder are not excited before the vertical separation of the two cylinders exceeds one cylinder diameter.
Figure 7.
(a) Response curve (maximum vibration amplitude vs reduced velocity) of two 1-DOF cylinders in tandem compared with an isolated cylinder. A much wider lock-in region is observed for the tandem cylinders relative to an isolated one in similar flow conditions. (b) Maximum vertical separation of the 1-DOF tandem system at different reduced velocities. For reduced velocities greater than five, when the rear cylinder has higher amplitude of motion, the separation is more than one diameter (Re = 200, Mred = 2, ξ = 0).
The form of the response curve and the wider lock-in region shown in figure 7(a) have important practical implications for designing structures for which preventing VIV is an important consideration (Griffin & Ramberg 1982). It follows from figure 7 that even if a structure is designed to be outside of the lock-in region as an isolated structure, it might still be in the lock-in region if placed in tandem with another similar structure. The results shown in figure 7(a), however, suggest that the lock-in region for the tandem arrangement is extended mainly on the higher end of reduced velocities. Therefore, if each structure is designed as an isolated structure to be out of the lock-in region on the low end of reduced velocities (Ured < 4 based on the results shown in figure 7a), the structure will not be in the lock-in region if another structure is placed in tandem.
To further elucidate the dynamic response of the system, we plot in figure 8 the phase portrait of the transverse force with the transverse displacement of the cylinders as a function of the reduced velocity. There are several new and important features of the problem that are revealed by the plots in figure 8. First, for all cases the phase portraits are symmetric with respect to the origin, which implies that only one half of the cycle is enough to analyse the dynamics, as the other half-cycle is the mirror image of the first half. Another feature is that the phase portraits remain single-valued only up to Ured < 5. This implies that in state 2 the force at a certain position is different, depending on whether the cylinder is moving upwards or downwards; e.g. the force at y = 0 is positive if the cylinder is going up and negative if it is going down for Ured ≥ 5. Another striking dynamical feature that follows from figure 8 is thus the variation of the phase angle between force and displacement, similar to the isolated-cylinder case in § 3.2. Up to Ured = 6 the phase portraits are located in the first and the third quadrant; i.e. the lift force and the displacement are in phase and generally in the same direction. For Ured > 6, the phase portraits are in the second and forth quadrants, i.e. out of phase, and the force and displacement are generally in the opposite direction. This is in agreement with the experimental observations that the force is a restoring one in tandem arrangement; i.e. the force tends to restore the cylinders back to initial rest (equilibrium) position (King & Johns 1976; Bokaian & Geoola 1984b; Blevins 2005).
More quantitative insights into the dynamic response of the tandem system can be obtained by revisiting figure 9, which, as discussed above, shows various r.m.s. quantities (lift and drag coefficients, oscillation frequency and the phase angle between the lift force and cylinder oscillations) as functions of the reduced velocity for the front and rear cylinders in tandem along with the corresponding quantities for an isolated cylinder. As seen in figure 9(d), the phase angle between the lift coefficient and the cylinder position jumps sharply by 180° for both cylinders in tandem at exactly the same reduced velocity as the isolated cylinder. As discussed in § 3.2, for the isolated cylinder this sharp jump in the phase angle is linked to the change in the timing of vortex shedding (see also figure 5). Apparently the same mechanism is at work in the tandem arrangement as well, but in this case the change in the timing of vortex shedding alone cannot possibly be the only mechanism that dominates the dynamic response of the system. Note that the out-of-phase force produced by the change in the timing of vortex shedding does not excite large-amplitude oscillations in the isolated cylinder, which is obviously not the case for the tandem arrangement (see figure 7). Comparing the phase portraits of the isolated (figure 4) and tandem systems (figure 8), it is further observed that the magnitude of the so-resulting out-of-phase force is much larger in the latter than the former case. This is also apparent from figure 9(b), which shows that for Ured > 3 the r.m.s. of the lift force CY r.m.s. for the tandem system is significantly higher than the corresponding value for the single-cylinder system. Therefore, it is reasonable to postulate that for the tandem system some mechanism other than vortex shedding should produce a large out-of-phase force that acts to enhance and further amplify the effect of vortex shedding.
A rather striking finding that emerges from figure 9(b), and which further points to the excitation of a new physical mechanism in the tandem system, is that while for sufficiently small reduced velocities the lift force on the rear cylinder is smaller than that on the front cylinder this trend is reversed at approximately Ured = 5. As seen in figure 9(b), for Ured > 5 the lift force on the rear cylinder exceeds that on the front cylinder, attaining values roughly 1.5 to 2 times higher throughout the simulated range of reduced velocities. This sharp transition in the relative magnitude of the lift force on each cylinder coincides exactly with and appears to signal the transition from state 1 to state 2. Increased lift force on the rear cylinder obviously suggests a sharp change in the underlying flow patterns, which should now give rise to a more asymmetric pressure field around the rear cylinder. It is worth noting that the drag force is not affected by this apparent change in flow patterns, since, as seen in figure 9(a), the r.m.s. of the axial force on the rear cylinder remains lower than that on the front cylinder regardless of the value of the reduced velocity. This trend, however, should not be surprising, since the rear cylinder always operates within the wake of the front cylinder, and as such on average it is always exposed to lower streamwise velocities. The nature of the apparent change in flow patterns and the associated mechanism that increases the lift force on the rear cylinder and gives rise to the large amplitude of oscillations in the tandem system will be discussed in detail in the subsequent section.
As was also discussed for the single cylinder, figure 9(d) shows that the oscillation frequency of the tandem system does not exactly match the natural frequency, and there is a slight detuning, i.e. ‘soft’ lock-in. ‘Soft’ lock-in has been previously observed for tandem cylinders by Mittal & Kumar (2001) and has also been reported for an isolated cylinder by several researchers, e.g. Moe & Wu (1989) and Khalak & Williamson (1997, 1999), as already discussed in§ 3.2. Figure 9(d) shows that the ratio f/fN increases as Ured increases for both the isolated and tandem cylinders, but the rate of increase and overall values are clearly higher for the isolated cylinder. As mentioned before, Mittal & Kumar (2001) have pointed out that soft lock-in is one of the mechanisms of the nonlinear oscillator to self-limit its oscillation amplitude. The oscillation amplitude of an elastically mounted cylinder does not change significantly even if the mass and damping of the system are reduced by a factor of 100 (Mittal & Kumar 2001; Govardhan & Williamson 2006). Other mechanisms to self-limit the vibrations include the reduction in the amplitude of the forces and the introduction of an additional frequency component that acts like an effective fluid-dynamic damping (Mittal & Kumar 2001). An introduction of another frequency component causes low-frequency modulations in the lift force and cylinder oscillations as can be observed in figure 6(b,c). The figures showing the time history of lift force and cylinder oscillations in Mittal & Kumar (2001) also show similar modulations. Such modulations have been frequently observed in the isolated cylinder VIV by Griffin (1972), Moe & Wu (1989), Al-Jamal & Dalton (2004) and Blackburn & Henderson (1999), among others. Similar modulations in the drag force of a normal, stationary flat plate have been observed (Lisoski 1993; Najjar & Balachandar 1998). Najjar & Balachandar (1998) provided a physical interpretation of the modulations, which is that the flow gradually varies between two different regimes: a regime H of high mean drag and a regime L of low mean drag. They observed that in regime H the shear layer rolls up closer to the plate to form coherent spanwise vortices, while in regime L the shear layer extends farther downstream, and the rolled-up von Karman vortices are less coherent (Najjar & Balachandar 1998). Obviously the modulations observed in our simulations are mainly due to the self-limiting behavior of the vibrations and not due to different three-dimensional flow regimes as was the case for vortex shedding past a fixed flat plate.
Vorticity dynamics
In this section we analyse the calculated flow fields in terms of instantaneous velocity, pressure and vorticity fields in order to elucidate the mechanisms that trigger the previously discussed complex dynamic response of the two-cylinder system. Wherever possible in our subsequent discussion we will adopt the classical terminology of Williamson & Roshko (1988) to identify vortex-shedding patterns (2S, 2P, etc.). The calculated flow fields will also be shown to exhibit a number of vortical interactions that are similar to those identified by Sumner et al. (2000) for various arrangements of two stationary cylinders. For that, we will also make use of the terminology introduced by these researchers to describe such interactions, e.g. vortex pairing and enveloping (see figure 10).
Figure 10.
Schematic of different vortex interaction for two cylinders in staggered arrangement. Taken from Sumner et al. (2000).
Our simulations suggest that the previously discussed dynamic transition of the system from state 1 to state 2 is accompanied by a sharp transition in the vorticity dynamics characterizing each state. To highlight this transition, we show in figures 11, 12 and 13 the results for Ured = 4 (representative state 1), 8 (representative state 2) and 5 (critical state), respectively. For each reduced velocity we show instantaneous flow fields at several time instants within half a period. The specific time instants are marked with letters (A, B, C, . . . ) and with points on the plots at the bottom of each set of figures, showing the variation of the cylinder displacement, velocity and lift force within one half of the oscillation period.
Figure 11.
Velocity vectors with pressure contours (left column) and streamlines with vorticity contours (right) for two tandem cylinders (1-DOF, Re = 200, Mred = 2, ξ = 0) at Ured = 4. The horizontal dash-dotted lines in A–D indicate the initial rest positions of the cylinders. The time instants (A, B, C, ...) are specified by the dash-dotted lines on the accompanying time history for the visualized portion of the cycle at the bottom of the figure. The superscripts F and R refer to the front and the rear cylinders, respectively; y/D is the position of the cylinder; V is the velocity of the cylinder; and CL is the lift coefficient.
Figure 12.
Velocity vectors with pressure contours (left column) and streamlines with vorticity contours (right) for two tandem cylinders (1-DOF, Re = 200, Mred = 2, ξ = 0) at Ured = 8. The horizontal dash-dotted lines in A–F indicate the initial rest positions of the cylinders. The internal captions identify the important vorticity interactions discussed in the text. The time instants (A, B, C, ...) are specified by the dash-dotted lines on the accompanying time history for the visualized portion of the cycle at the bottom of the figure. The superscripts F and R refer to the front and the rear cylinders, respectively; y/D is the position of the cylinder; V is the velocity of the cylinder; CL is the lift coefficient.
Figure 13.
Velocity vectors with pressure contours (left column) and streamlines with vorticity contours (right) for two tandem cylinders (1-DOF, Re = 200, Mred = 2, ξ = 0) at Ured = 5. The horizontal dash-dotted lines in A–F indicate the initial rest positions of the cylinders. The internal captions identify the important vorticity interactions discussed in the text. The time instants (A, B, C, ...) are specified by the dash-dotted lines on the accompanying time history for the visualized portion of the cycle at the bottom of the figure. The superscripts F and R refer to the front and the rear cylinders, respectively; y/D is the position of the cylinder; V is the velocity of the cylinder; and CL is the lift coefficient.
Figure 11 shows the typical flow patterns for state 1 at Ured = 4. It can be observed that the vortices shed from the top and bottom of the front cylinder do not enter the gap region but wrap around the top and bottom sides, respectively, of the rear cylinder, disrupting its vortex shedding. The gap flow velocities remain small, as recirculating flow is present for most of the cycle in this region. The fact that the flow does not directly impinge on but rather passes around the rear cylinder causes drastically different pressure distributions around the two cylinders. Unlike the pressure field around the front cylinder, which is characterized by the continuous presence of high-(stagnation flow) and low-pressure pockets, the pressure field around the second cylinder never develops a stagnation region. Consequently no high-pressure pocket emerges, resulting in relatively small vertical force, which explains the previously discussed smaller lift force and smaller amplitude of oscillations of the rear cylinder relative to those of the front cylinder. Therefore, the main characteristic of the state 1 flow patterns is that the rear cylinder remains always within the wake of the front cylinder and as such is never exposed to a region of high (stagnation) pressure, since the gap region is for the most part occupied by slow, recirculating flow. The combined downstream wake is a regular von Karman street (2S mode).
Figure 12 shows the typical flow pattern for state 2 at Ured = 8. In this case a strong gap flow is initiated with velocities as high as the free stream velocity, which pushes one of the front cylinder shear layers (upper and lower in the first and second halves of the cycle, respectively) to pass through the gap region. As we will subsequently show, the passage of the shear layer through the gap region triggers a sequence of very complex vortex-to-vortex and vortex-to-cylinder interactions that dominate the dynamics of the flow. This is a fundamental difference between the state 1 and state 2 flow patterns and the main cause for the change in the relative oscillation amplitude of the two cylinders. With reference to the time instants A through F in the accompanying time history plot at the bottom of figure 12 the underlying flow patterns and key physics in the gap region can be summarized as follows:
(a) In A the gap flow initiates when the rear cylinder is close to its top maximum position and when the front cylinder is almost at the initial position. The vertical separation between the two cylinders is sufficiently large to expose the rear cylinder to the free stream velocity field, which leads to the formation of a pocket of high stagnation pressure at its upper front. This pocket of stagnation pressure deflects part of the flow impinging on the rear cylinder downward, giving rise to a strong gap flow, which induces a pocket of separated flow (denoted as ‘induced separation’ in the figure) and the associated region of low pressure underneath the front part of the rear cylinder. The resulting pressure distribution on the rear cylinder is such that the flow-induced force is negative (restoring) and thus out of phase with the positive displacement of the cylinder.
(b) In B the gap flow is now sufficiently strong to begin to push the upper shear layer from the front cylinder into the gap region (‘gap push’) and cause the front cylinder vortex shedding and the associated low-pressure core to be advected further downstream along the lower side of the rear cylinder. The lift force on the rear cylinder has decreased due to the decrease of its upper front high stagnation pressure, since the upward motion has stopped and the cylinder is accelerating downward.
(c) In C the upper shear layer of the front cylinder has now been completely displaced by the flow into the gap region underneath the rear cylinder, where it pairs (‘vortex pairing’) and begins to interact with positive vorticity from the lower shear layers of both the front and rear cylinders, which have now merged. By this interaction the low-pressure core from the front cylinder vortex shedding has now been advected further downstream and merged with the low-pressure pocket from the rear cylinder shedding, right underneath the rear cylinder, increasing the lift force on that cylinder. Also the low-pressure pocket on top of the front cylinder from the vortex shedding has become stronger by the gap push and the accelerated flow in the gap region. The direction of the lift force on both cylinders is restoring; i.e. the force tends to restore the cylinders back to initial rest (equilibrium) position.
(d) In D the ‘vortex pairing’ process causes the ‘enveloping’ of the negative vorticity from the displaced upper shear layer of the front cylinder by positive vorticity of the lower shear layers of both cylinders. The ensuing very complex vortex-to-vortex interactions lead to the rapid growth of the low-pressure region, which is now at the rear of the descending rear cylinder, and its size is comparable to the size of the cylinder. This increases further the lift force that accelerates the rear cylinder, which has almost reached the initial position (y = 0) while travelling downward.
(e) In E the ascending front cylinder now passes the descending rear cylinder. The gap flow has seized to exist, as the gap region is now occupied by a cell of recirculating, low-velocity flow. A pocket of high (stagnation) pressure has started forming at the lower front of the rear cylinder, as the cylinder is now outside of the wake of the front cylinder and is again exposed to the free stream velocity. The upper half of the gap region is in fact now occupied by a large pocket of low pressure, which results in a force that tends to accelerate the ascending front cylinder and retard the descending rear cylinder, eventually causing the rear cylinder to stop and reverse its direction of motion. The front cylinder shear layers have reattached to their respective sides of the rear cylinder, but the complex vortex pairing and enveloping phenomena in the wake of the second cylinder still continue albeit at diminishing intensity.
(f) The time instant F marks the end of the first half of the cycle and is essentially the mirror image of the time instant A. The pocket of high stagnation pressure at the lower front of the rear cylinder has grown in size, driving a strong upward gap flow. The previously described displacement process of the front cylinder shear layer (A, B, etc.) is about to be repeated again, only this time for the lower (positive vorticity) shear layer of the front cylinder, which will be displaced into the gap region and begin to interact with the negative vorticity from the upper side. A notable feature in the near wake of the second cylinder is the complete destruction of the negative vorticity that was previously enveloped by the positive shear layers.
Insofar as the combined wake flow is concerned, it is clear from figure 7 that for Ured = 8 the 2P vortex-shedding mode (i.e. two vortex pairs shed per cycle) emerges in the wake. This new finding for the tandem arrangement is worth noting, since the 2P mode has not been observed in the past in two-dimensional VIV simulations of an isolated cylinder but has been observed in three-dimensional simulations (Blackburn, Govardhan & Williamson 2001). It should be pointed out, however, that for our case and according to the vortex-shedding mode map of Williamson & Roshko (1988) the 2P mode is well within the range of possible vortex-shedding modes, since the amplitude of motion we observe in our simulations in the lock-in region is about one diameter. Furthermore, Brika & Laneville (1999) have also observed the 2P mode in their experiments for two tandem cylinders with the front cylinder fixed and the rear cylinder free to vibrate. Even though not shown herein, similar vortex-shedding patterns are also found in our simulations for all reduced velocities in the state 2 regime.
The flow patterns for the critical state (Ured = 5) are shown in figure 13. In general the flow phenomena in the gap region are similar to those observed for Ured = 8 in figure 12. The initiation of the gap flow also occurs when the rear cylinder reaches its maximum displacement and pushes one of the front cylinder shear layers into the gap region, giving rise to phenomena such as induced separation, vortex pairing and enveloping. These phenomena in turn produce pockets of high and low pressure around the rear cylinder with timing such that, unlike state 2, they result in a large non-restoring force (in-phase with cylinder displacement) that excites the vibrations. Major differences are observed, however, between the flow patterns of the critical state and those of state 2 in the wake of the rear cylinder. In fact the combined wake flow for Ured = 5 is far too complex to be described using the terminology of Williamson & Roshko (1988). The vorticity dynamics are characterized by merging of vortices of the same sense of rotation and intense interaction and deformation of vortices of opposite signs. This is due to the fact that faster moving vortices reach the previously shed slower ones and interact and merge with them.
4.1.2. 2-DOF
The results in the previous section point to the conclusion that the onset or not of the gap flow can be used to explain the different dynamic responses of the 1-DOF tandem two-cylinder system (states 1 and 2). To further reinforce this conclusion we carry out numerical simulations for the same initial geometrical configuration but allowing now both cylinders to move elastically along both spatial directions (2-DOF system) such that all structural parameters in the in-line direction are exactly the same as those in the transverse direction.
We attempted to carry out simulations for 3 ≤ Ured ≤ 10 so that the simulated flow physics could be directly compared with the corresponding results of the 1-DOF system. For Ured = 3 and similar to the 1-DOF case the oscillation amplitudes are weak, i.e. out of lock-in, and for that these results are not shown herein. For Ured ≥ 8, on the other hand, the front cylinder collides with the rear cylinder very early in the simulation. Therefore, simulations for Ured ≥ 8 were not pursued further. The vibration time histories for the remaining reduced velocities (4 ≤ Ured ≤ 7) are shown in figure 14. The displacements in the x and y directions in this figure are measured from the initial rest position of the front cylinder.
Figure 14.
Time history of transverse (y/D) and in-line (x/D) vibrations of two cylinders in tandem for four different values of Ured (2-DOF, Re = 200, Mred = 2, ξ = 0). The x/D and y/D displacements are with reference to an inertial frame positioned at the initial rest position of the front cylinder. The superscripts F and R refer to the front and rear cylinders, respectively. (a) Ured = 4; (b) Ured = 5; (c) Ured = 6; (d) Ured = 7.
The response of the 2-DOF system for the Ured = 4 case is broadly similar to that obtained for the same reduced velocity for the 1-DOF system (compare figures 6b and 14a). The main difference between the 1-DOF and 2-DOF simulations is that in the latter case the amplitude of vertical oscillation for both cylinders is reduced by 5% relative to the former case. In-line oscillations are also excited, but their amplitude is much weaker than that for the vertical vibrations (less than 1.5% of D). Also the two cylinders do come closer together compared to their initial L/D = 1.5 distance. This trend is expected however, as the cylinders are now free to move in the direction of the drag force. The reduction in the streamwise separation length, however, is minor for Ured = 4, as the statistically stationary equilibrium position of the two cylinders is about L/D = 1.4.
The effect of the second degree of freedom is far more pronounced at higher Ured, when both the dynamic response of the system and underlying vorticity dynamics are drastically different than those for the 1-DOF system. For Ured = 5 and 6 no statistically stationary states are reached, and the dynamic response is very complex with large-amplitude oscillations in the transverse direction (see figure 14b,c). Even though not shown herein, instantaneous vorticity contour plots for the Ured = 5 case show that the gap flow is excited intermittently. The onset of the gap flow coincides in figure 14(b) with time intervals when large-amplitude oscillations are excited both in the transverse and in-line directions. For Ured = 6 large-amplitude oscillations are excited after 250 time units, reaching the overall oscillation amplitudes observed for the 1-DOF system at the same reduced velocity. As shown in figure 15, this sharp increase in the oscillation amplitudes is accompanied by the onset of the gap flow which is now present throughout the simulated interval for t > 250.
Figure 15.
Vorticity countours for the 2-DOF tandem cylinder arrangement at Ured = 6 (Re = 200, Mred = 2, ξ = 0). (a) A snapshot at t = 113.2 when the cylinders oscillate together without the gap flow present. (b) A snapshot at t = 329.2 when the gap flow is present and when the vortex pairing in the gap is visible. The oscillations in the vertical direction increase significantly when the gap flow is present.
Interestingly and as shown in figure 6(d), for Ured = 7 the system returns to a much simpler, essentially periodic, dynamic state. The in-line oscillations are weak (less than 2% of D), and the amplitude of vertical oscillations for both cylinders is now approximately 50% less than that observed in the corresponding 1-DOF system. Furthermore, the reduction in the horizontal separation of the two cylinders is greater at this reduced velocity, reaching L/D = 1.2. As seen in figure 16, the two cylinders come closer together, thus greatly reducing the gap size, and vibrate together primarily in the vertical direction as a single bluff body. The resulting shedding pattern in the wake is a standard 2S von Karman vortex street, which is in stark contrast with the 2P shedding mode obtained for the 1-DOF counterpart (see figure 16).
Figure 16.
Streamlines and vorticity contours for two 2-DOF tandem cylinders at Ured = 7 (Re = 200, Mred = 2, ξ = 0). The horizontal dash-dotted lines in A–F indicate the initial rest positions of the cylinders. The snapshots show the steady stationary state, in which the cylinders come close to each other and shed as a single body (2S mode).
As discussed in the previous section, figure 9 shows the r.m.s. values of different flow quantities. Here we will discuss the 1-DOF vs 2-DOF results of this figure. Note that the r.m.s. quantities for the 2-DOF case with Ured = 5 are not reported in this figure, since a quasi-steady state was not reached. Results are reported in this figure, however, for Ured = 6 for t > 250 when the gap flow was observed. It can be observed from this figure that the r.m.s. drag coefficient for the 2-DOF cases are all lower than their 1-DOF counterparts. For the Ured = 4 and 6 2-DOF cases, for which the cylinder spacing (L/D) is only slightly smaller than the corresponding 1-DOF case, the drag is only slightly reduced, but for Ured = 7 in which the cylinders are much closer to each other (L/D ≈ 1.2) the drag is significantly reduced in the 2-DOF case relative to the corresponding 1-DOF case. This trend is to be expected, however, since when the cylinders come closer to each other the flow sees an effective more elliptical and streamlined shape, which has a lower drag (Mittal & Balachandar 1996). The lift coefficient, on the other hand, is lower for the Ured = 4 and 7 2-DOF cases, when the gap flow is not present, but higher at Ured = 6 relative to the 1-DOF. The lift coefficient is higher in the Ured = 6 2-DOF case because the addition of the second degree of freedom allows the cylinders to move under the action of the low-pressure pockets caused by the gap flow in the horizontal direction and use these pockets for a longer period of time. In figure 9 soft lock-in is observed for the 2-DOF cases as well, and similar to the 1-DOF case the phase angle between the lift coefficient and cylinder position changes at the same Ured as for the isolated cylinder.
To summarize, for Ured = 5 and 6 the onset of large-amplitude oscillations is accompanied by the onset of the gap flow. For these reduced velocities the overall vibration amplitudes in the transverse direction, the underlying excitation mechanism (gap flow) and the overall state of the system (state 2 is also excited) are similar to those observed for the corresponding 1-DOF systems. This trend should be attributed to the fact that for these reduced velocities the distance between the two cylinders is only marginally reduced, which allows suefficient vertical separation for the gap flow to be excited. For Ured = 7, on the other hand, the two cylinders come close to each other, thus suppressing the gap flow and drastically reducing, relative to the corresponding 1-DOF system, the amplitude of the vibrations. For this case, the in-line oscillations are negligible, and the dynamic response of the system in the vertical direction is a simple periodic oscillation with the second cylinder vibrating at larger amplitude than the first cylinder. That is even though at this reduced velocity the 2-DOF system exhibits significantly smaller oscillation amplitude than its 1-DOF counterpart, state 2 still persists. This can be explained by the fact that when the cylinders are so close to each other, the front cylinder shedding is suppressed, and the two cylinders shed as a single body.
4.2. Three-dimensional simulations
Our discussion of the VIV dynamics of the tandem arrangement has thus far been based on the key assumption that for Re = 200 the underlying flow phenomena can be adequately described by two-dimensional computations. The flow around an isolated cylinder, however, has been shown to transition to three-dimensional at Re = 188 (Karniadakis & Triantafyllou 1992). Placing a second cylinder in the wake of a single cylinder drastically changes the flow behavior, and consequently the transition to three-dimensional flow might also be affected. Given the very complex dynamics identified by our two-dimensional computations, especially when the gap flow is excited, one might reasonably argue that for the tandem arrangement we considered herein the transition to three-dimensional flow could very well occur at Re < 200. Carmo & Meneghini (2006), however, have found that for a stationary tandem arrangement with L/D = 1.5 (smaller than the critical value), two-dimensional and three-dimensional computations yield identical results in terms of the Strouhal number for Re as high as 320 – see figures 4 and 8 of Carmo & Meneghini (2006). Even though Carmo & Meneghini (2006) did report that three-dimensional structures emerged at Re = 270 in their computations, such structures formed far downstream from the rear cylinder at this Re, while the flow in the gap region remained essentially two-dimensional. For values of L/D greater than the critical value of 3.5, however, Carmo & Meneghini (2006) reported that two-dimensional simulations are not adequate for resolving the time scale of vortex shedding for Re > 190. In other words, for the fixed tandem arrangement if the second cylinder is placed closer than the critical spacing the flow in the far wake is likely to be three-dimensional for Re = 200, but the ensuing three-dimensionality is weak and does not affect the time scale of vortex shedding, which for Re as high as 320 is found to be identical to that obtained from the two-dimensional computations. The results of Carmo & Meneghini (2006) for the tandem system along with previous results for the single cylinder (Karniadakis & Triantafyllou 1992) do suggest, therefore, that the presence of the second cylinder has a stabilizing effect on the dynamics of the flow, provided of course that it is placed sufficiently close to the first cylinder. The recent results by Papaioannou et al. (2006), who reported two-dimensional and three-dimensional numerical simulations for two stationary cylinders in tandem, have shown similar stabilizing effect of the rear cylinder when placed at a distance less than the critical spacing. The following quote from their paper (Papaioannou et al. 2006) is particularly revealing: ‘Comparison with the single cylinder case reveals that the presence of the downstream cylinder at spacings lower than the critical value has a stabilizing effect on both the primary and secondary enstrophy. Systematic quantification of three-dimensionalities involves finding measures for the intensity of the spanwise fluctuations of the forces. This also verifies the stabilization scenario, suggesting that when the second cylinder is placed at a distance smaller than the critical one, three-dimensional effects are suppressed compared to the single-cylinder case. However, when the spacing exceeds the critical value, the upstream cylinder tends to behave like a single cylinder, but three-dimensionality in the flow generally increases’. Finally, the earlier work of Mittal & Balachandar (1995) who carried out two-dimensional and three-dimensional numerical simulations for flow over elliptical cylinders is also relevant to our work especially for the 2-DOF system, when the two cylinders come close together and effectively shed as a single ‘elliptical’ cylinder. Mittal & Balachandar (1995) reported that there tends to be higher discrepancy between the drag force from the two-dimensional and three-dimensional computations for bluffer cylinders, which also suggests that perhaps an effective elliptical shape tends to reduce (or at least delay for higher Re) the importance of three-dimensional effects.
All these results collectively suggest that in the proximity–wake interefence region studied in this paper, the assumption of two-dimensional flow is likely adequate to describe the dynamic response of the system. However, all evidence presented above, conclusive as they may be, are for stationary cylinders. Consequently, the potential role of the cylinder motion and the ensuing nonlinear VIV dynamics, especially when the gap flow is excited, on the emergence of three-dimensionality in the flow is not known and to the best of our knowledge has never been examined before in the literature. In this section we carry out full, three-dimensional FSI simulations to examine the suitability of the two-dimensional assumption at Re = 200 for both the 1-DOF and 2-DOF tandem arrangements.
We consider two two-dimensional, finite-span cylinders in tandem, mounted normally between two vertical slip walls located 5D apart in the spanwise direction (z-axis). This spanwise length is considered adequate to capture the emergence of three-dimensional structures in the wake, since the spanwise wavelength of three-dimensional structures in the wake of a circular cylinder is typically of the order of one cylinder diameter (Karniadakis & Triantafyllou 1992; Mittal & Balachandar 1996). The use of slip-wall boundary conditions at the two side walls introduces three-dimensional disturbances in the computations, which can be thought of as being analogous to the end-wall effects that are known to complicate the interpretation of experimental results for such flows (Williamson 1996). The presence of such disturbances, however, does not pose a problem in the context of our work, which only seeks to examine the adequacy of the two-dimensional assumption for describing the VIV dynamics at Re = 200 rather than to determine the Re at which the flow past the purely two-dimensional (infinite span) geometry transitions to three-dimensional flow.
The computational domain and grid at z = constant planes are identical to those used for the two-dimensional simulations. Namely 281 × 241 grid nodes, distributed as described in § 4.1, are used to discretize the transverse planes. To examine the sensitivity of the computed results to the spanwise grid resolution, we carried out simulations with 51 and 101 grid nodes distributed uniformly along the span and found essentially identical results. All subsequently reported simulations, however, have been obtained on the finest mesh consisting of 281×241×101 grid nodes (approximately 6.8 million) in the streamwise, vertical and spamwise directions, respectively. The time step and other numerical parameters used for all three-dimensional simulations are identical to those used for the two-dimensional computations. We carry out three-dimensional simulations for both the 1-DOF and 2-DOF tandem systems. For the 1-DOF system, we consider two representative cases: one in state 1 (Ured = 4) and one in state 2 (Ured = 8). For the 2-DOF case, we select two values of the reduced velocity: Ured = 6, for which the two-dimensional computations reveal a dynamically rich, chaotic response; and Ured = 7, for which the two-dimensional system reaches a simple quasi-steady state.
Figure 17 compares the results of the two-dimensional and three-dimensional simulations in terms of the time history of oscillations of the front and the rear cylinders for all four simulated cases. As seen in figure 17(a,b), for the 1-DOF system the two-dimensional and three-dimensional oscillation amplitudes are close to each other especially for the Ured = 8 case. Some discrepancies are only observed for the Ured = 4 case in which there is a slight, albeit clear, phase shift between two-dimensional and three-dimensional results in the amplitude of oscillations of the first cylinder and somewhat more pronounced differences in the response of the second cylinder. As seen in figure 17(a), the low-frequency amplitude modulations that characterize the system response at Ured = 4, although present both in two-dimensional and three-dimensional, are clearly weaker in the three-dimensional simulations. These small discrepancies notwithstanding, however, it is obvious from figure 17(a,b) that both two-dimensional and three-dimensional computations yield essentially identical VIV response and that the three-dimensional system remains in its respective dynamical state (state 1 or 2) determined by the two-dimensional simulations.
Figure 17.
Comparison between the vertical vibrations of the 1-DOF and 2-DOF tandem systems obtained from two-dimensional (dotted lines) and three-dimensional (solid lines) simulations (Re = 200, Mred = 2, ξ = 0). The superscripts F and R refer to the front and the rear cylinders, respectively. (a) 1-DOF Ured = 4; (b) 1-DOF Ured = 8; (c) 1-DOF Ured = 6; (d) 1-DOF Ured = 7.
Similar conclusions are derived from figure 17(c,d), regarding the response of the two-dimensional and three-dimensional 2-DOF systems. For the dynamically rich Ured = 6 case, the results are very similar, and the only difference between the two-dimensional and three-dimensional computations are in the time it takes for the system to transition to large-amplitude oscillations. For the two-dimensional case this transition occurs at t ≈ 250, while for the three-dimensional case it takes place a bit earlier at t ≈ 200. Nevertheless, for both the two-dimensional and three-dimensional computations the initial and final amplitudes of oscillations for Ured = 6 are essentially identical. Finally, for the Ured = 7 case both two-dimensional and three-dimensional computations reach practically the same statistically stationary, periodic state with some small discrepancies between the two results observed only during the early transients of the simulations.
The state of three-dimensionality of the wake for each simulated case is visualized in figures 18-21 in terms of isosurfaces of (a) spanwise velocity component uz; (b) the streamwise component of the vorticity field Ωx; and (c) the spanwise vorticity component Ωz. Obviously for two-dimensional flow both uz and Ωx should be identically zero. It is evident from these figures that for the cases for which the gap flow is not excited (Ured = 4 and 7 for the 1-DOF and 2-DOF systems, respectively) the three-dimensionality of the flow is very weak and is restricted primarily in the immediate vicinity of the cylinders in the mid-span region. The picture that emerges, however, is quite different for the other two cases for which the gap flow mechanism is active. The structure of the contours of uz and Ωx reveal a complex and three-dimensional flow both within the gap region and downstream of the rear cylinder. Three-dimensionality emerges in the form of pairs of counter-rotating, rib-like structures of streamwise vorticity braided together with the spanwise rollers. The overall wake structure is qualitatively very similar to that reported by Carmo & Meneghini (2006) in their three-dimensional simulations of flow past two stationary, tandem cylinders for L/D = 1.5 and Re = 270 (see figure 11 in their paper). Note, however, that, unlike the highly three-dimensional wake structure shown in Carmo & Meneghini (2006) in which the streamwise and spanwise vorticity components are of the same magnitude, in our simulations the magnitude of the streamwise vorticity component is, for all cases, one order of magnitude smaller than the magnitude of the dominant spanwise vorticity component. Consequently, the flow even for the cases for which the gap flow is active is only weakly three-dimensional at Re = 200. This is clearly evident in figures 19 and 20, for instance, by the fact that the spanwise vorticity iso-surfaces develop only a weak three-dimensionality manifested by low-amplitude, spanwise waviness of the cylindrical vortex tubes. Furthermore, the three-dimensional distortion of the vortex tubes becomes pronounced only several diameters downstream of the rear cylinder.
Figure 18.
Vibrations of the 1-DOF system for the Ured = 4 case (Re = 200, Mred = 2, ξ = 0). The three-dimensional wake structure is visualized by (a) iso-surfaces of spanwise velocity uz = ±0.05, (b) iso-surfaces of y component of vorticity Ωy = ±0.1 and (c) iso-surfaces of z component of vorticity Ωz = ±1.
Figure 21.
Vibrations of the 2-DOF system for the Ured = 7 case (Re = 200, Mred = 2, ξ = 0). The three-dimensional wake structure is visualized by (a) iso-surfaces of spanwise velocity uz = ±0.05, (b) iso-surfaces of y component of vorticity Ωy = ±0.1 and (c) iso-surfaces of z component of vorticity Ωz = ±1.
Figure 19.
Vibrations of the 1-DOF system for the Ured = 8 case (Re = 200, Mred = 2, ξ = 0). The three-dimensional wake structure is visualized by (a) iso-surfaces of spanwise velocity uz = ±0.05, (b) iso-surfaces of y component of vorticity Ωy = ±0.1 and (c) iso-surfaces of z component of vorticity Ωz = ±1.
Figure 20.
Vibrations of the 2-DOF system for the Ured = 6 case (Re = 200, Mred = 2, ξ = 0). The three-dimensional wake structure is visualized by (a) iso-surfaces of spanwise velocity uz = ±0.05, (b) iso-surfaces of y component of vorticity Ωy = ±0.1 and (c) iso-surfaces of z component of vorticity Ωz = ±1.
To summarize, the three-dimensional computations we presented in this section show that the flow for both the 1-DOF and 2-DOF systems at Re = 200 transitions to a weakly three-dimensional state when the gap flow mechanism is excited. The intensity of the ensuing three-dimensionality, however, is too weak to disrupt the primary mode of vortex shedding, which is dominated by strong spanwise vortices. Consequently, the three-dimensional disturbances in the flow do not alter the dynamic response of the vibrating cylinders, which is essentially identical to that obtained from the two-dimensional computations.
5. Discussion and conclusions
The wider lock-in region and the higher amplitudes of oscillation for the 1-DOF system suggest a mechanism for vibrations in tandem arrangement other than the vortex shedding, which is the primary mechanism for the vibrations of an isolated cylinder. As seen in figure 7, when vortex shedding does not excite the isolated cylinder (e.g. Ured = 3) the vibrations do not build up for the tandem arrangement either. This suggests that the vortex shedding is an important mechanism for the tandem arrangement especially for initiating the vibrations. The other vibration mechanisms should be related to the special arrangement of the cylinders, hence related to the interference effects.
The instantaneous flow patterns discussed in § 4.1.1 clearly show the emergence of a gap flow at higher reduced velocities (Ured ≥ 5) at which larger amplitudes of motion occur. The gap flow causes the passage of the front cylinder shear layer through the gap, which triggers a sequence of very complex vortex-to-vortex and vortex–cylinder interactions that assist the force created by the vortex shedding, especially when it is weak and out-of-phase at higher reduced velocities. By such processes, the gap flow mechanism induces a large oscillatory force, which maintains the large-amplitude, low-frequency oscillations of the cylinders well beyond the lock-in range of an isolated cylinder. Perhaps the most striking evidence of the importance of the gap flow follows from our simulations for the 2-DOF case at high reduced velocity Ured = 7. For this case the in-line degree of freedom causes the gap to become smaller, seizes the flow through it and suppresses the amplitude of the vibrations for reduced velocity values for which large-amplitude vibrations are excited in the 1-DOF system. In such a case the tandem cylinders move close to each other and shed as a single body, which reduces the oscillation amplitude of both cylinders significantly. Furthermore, when the gap flow is present in the 2-DOF case, the oscillation amplitude reaches the same level as the corresponding 1-DOF system.
It is important to re-emphasize, however, that although the gap flow is found to be important for sustaining the large amplitude of vibration, this mechanism by itself cannot excite the cylinders in a tandem arrangement. The vortex-shedding mechanism plays an important role in the process, as it initiates the excitation of the system and produces a vertical separation between the two cylinders large enough to trigger the gap flow mechanism. In all simulations if the maximum vertical separation between cylinders exceeds one diameter the gap flow is observed. To reinforce this point, we have plotted in figure 7 the variation of the maximum vertical separation of the two cylinders with Ured for the 1-DOF system next to the response curve. Figure 7 shows clearly that the gap flow (i.e. large-amplitude oscillations) is not excited before the vertical separation of the two cylinders exceeds one cylinder diameter.
The oscillation amplitude and r.m.s. of the lift force of the rear cylinder were larger than those of the front cylinder when the gap flow was present, i.e. state 2 . This was explained by the fact that the gap flow increases the asymmetry of the pressure field around the rear cylinder, causing large pockets of low pressure. For reduced velocities less than 5, for which the vortex shedding was the only mechanism of vibration, the 1-DOF systems was in state 1 . This is explained by the fact that the vortices shed from the upstream cylinder disrupt the vortex shedding behind the downstream cylinder, which reduces the oscillatory force and the resultant vibration amplitude.
All the findings reported in this work are for two cylinders in tandem in the proximity–wake interference region. It is thus appropriate to briefly discuss the validity of our findings in other interference regions, such as the proximity and the wake interference regions, and present a comprehensive picture of the underlying VIV mechanisms for these regions. We have essentially reported computational results for the proximity interference region (small L/D) while studying the dynamics of the 2-DOF system at reduced velocities for which the two cylinders come close together and shed as a single body (see results for Ured = 7 in figure 16 and discussion in § 4.1.2). Our results show that in this case no gap flow is excited; the overall amplitudes of motion are lower than those in the proximity–wake interference region; and state 2 emerges. These findings can be explained by the fact that when the cylinders are so close to each other, the front cylinder shedding is disrupted, and the two cylinders shed as a single body. Most shedding occurs in the wake of the rear cylinder, which naturally develops larger amplitude vibrations than the front cylinder.
In the wake interference region (typically L/D > 4) the wider lock-in range has also been observed for the rear cylinder (King & Johns 1976; Mittal & Kumar 2001; Jester & Kallinderis 2004), while the front cylinder has the same lock-in range as an isolated cylinder. The vortex shedding is the primary mechanism of vibration for the front cylinder. On the other hand, the rear cylinder vibrations are excited by the wake vortices shed from the front cylinder even when the front cylinder oscillations are weak (King & Johns 1976; Mittal & Kumar 2001; Jester & Kallinderis 2004; Fontaine et al. 2006) or when the front cylinder is held stationary (Bokaian & Geoola 1984b). Zdravkovich (1988) used the term ‘wake-displacement’ mechanism for such vibrations of the rear cylinder. Nevertheless, the vibration amplitudes in the wake interference region are much weaker than in the proximity–wake interference region, where the most intense vibrations have been observed (King & Johns 1976; Bokaian & Geoola 1984b; Zdravkovich 1985). As we have shown in this paper, the cause of such intense vibrations is clearly the gap flow mechanism present in the proximity–wake interference region.
In this work we have reported simulations for a single reduced mass value Mred = 2, which is in the range in which most marine structures are found (Fontaine et al. 2006). Exploring the effect of varying Mred on the vibrations of the tandem system is out of the scope of this study and will be pursued in future investigations. Nevertheless, the detrimental effects of low Mred values on the stability of the FSI algorithms have been discussed extensively in Borazjani et al. (2008), where it has been shown in the limit of Mred → 0 stable FSI iterations can be achieved only by using under-relaxation and the Aitken acceleration technique. Furthermore, the physics of the VIV for an isolated cylinder with low Mred has been addressed in Govardhan & Williamson (2000). They found that for low Mred the lock-in region becomes wider, and the oscillation frequency can be much larger than the natural frequency of the system. They also reported that below a critical reduced mass the upper-branch vibrations continued to the limit (in flow speed) of their facility. These findings suggests that the response of the tandem cylinders at low Mred could be quite different from what was observed herein.
Gap flow switch has been previously suggested as an excitation mechanism by Zdravkovich (1974, 1988), but that mechanism is very different than the gap flow explained herein. In the experiments by Zdravkovich (1974) the oscillations were not excited when the cylinders were in tandem, but only when the downstream cylinder was mechanically displaced for 20% of diameter in the transverse direction, large-amplitude oscillations were maintained. The onset of the vibrations was explained by the existence of a bistable flow in the gap region with two modes, one with a gap flow and the other without it, and the hysteretic mode exchange of the flow between these modes. Quoting Zdravkovich (1974): ‘the observed large-amplitude low-frequency vibration of the rear cylinder may be attributed to the hysteresis of the flow switch through and around the gap between the cylinders’. The results we have presented herein have clearly shown, however, that the gap flow in our case has no connection with bistable flow modes or hysteresis.
Our three-dimensional simulations have shown that two-dimensional computations are adequate for capturing the VIV dynamics of the tandem arrangement in the proximity–wake interference regime at Re = 200. Even though at this Reynolds number the flow does transition to a weakly three-dimensional state, the three-dimensional modes are not sufficiently intense to affect the dynamic response of the system, which for all simulated cases is essentially identical to that obtained from the two-dimensional computations. The simulations do show, however, that the relative strength of the three-dimensional perturbations grows rapidly for reduced velocities for which the gap flow is excited. In such cases, three-dimensional disturbances grow both within the gap region and in the wake of the rear cylinder. This finding points to the conclusion that for Re > 200 full three-dimensional FSI computations could very well be required to accurately resolve the dynamic response of the system especially for reduced velocities for which large-amplitude oscillations are excited by the gap flow mechanism.
Acknowledgments
This work was supported by the NIH Grant RO1-HL-07262, the NSF Grant 0625976 and the Minnesota Supercomputing Institute. We thank the anonymous reviewers whose insightful comments helped improve the quality of the manuscript.
REFERENCES
- Ahn HT, Kallinderis Y. Strongly coupled flow/structure interactions with a geometrically conservative ale scheme on general hybrid meshes. J. Comput. Phys. 2006;219(2):671–696. [Google Scholar]
- Al-Jamal H, Dalton C. Vortex induced vibrations using large eddy simulation at a moderate reynolds number. J. Fluids. Struct. 2004;19(1):73. [Google Scholar]
- Allen DW, Henning DL. Vortex-induced vibration current tank tests of two equal-diameter cylinders in tandem. J. Fluids Struct. 2003;17(6):767. [Google Scholar]
- Biermann D, Herrnstein W. The interference between struts invarious combinations. (Technical Report 468).National Advisory Committee for Aeronautics. 1933 [Google Scholar]
- Blackburn HM, Govardhan RN, Williamson CHK. A complementary numerical and physical investigation of vortex-induced vibration. J. Fluids Struct. 2001;15(3–4):481. [Google Scholar]
- Blackburn HM, Henderson RD. A study of two-dimensional flow past an oscillating cylinder. J. Fluid Mech. 1999;385:255–286. [Google Scholar]
- Blevins RD. Flow-Induced Vibration. 2nd ed. Van Nostrand Reinhold; 1990. [Google Scholar]
- Blevins RD. Forces on and stability of a cylinder in a wake. J. Offshore Mech. Arctic Engng. 2005;127(1):39–45. [Google Scholar]
- Bokaian A, Geoola F. Proximity-induced galloping of two interfering circular cylinders. J. Fluid Mech. 1984a;146:417. [Google Scholar]
- Bokaian A, Geoola F. Wake-induced galloping of two interfering circular cylinders. J. Fluid Mech. 1984b;146:383. [Google Scholar]
- Borazjani I, Ge L, Sotiropoulos F. Curvilinear immersed boundary method for simulating fluid structure interaction with complex three-dimensional rigid bodies. J. Comput. Phys. 2008;227(16):7587–7620. doi: 10.1016/j.jcp.2008.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borazjani I, Sotiropoulos F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Exp. Biol. 2008;211:1541–1558. doi: 10.1242/jeb.015644. [DOI] [PubMed] [Google Scholar]
- Brika D, Laneville A. The flow interaction between a stationary cylinder and a downstream flexible cylinder. J. Fluids Struct. 1999;13(5):579. [Google Scholar]
- Carmo BS, Meneghini JR. Numerical investigation of the flow around two circular cylinders in tandem. J. Fluids Struct. 2006;22(6–7):979. [Google Scholar]
- Fontaine E, Morel J, Scolan Y, Rippol T. Riser interference and VIV amplification in tandem configuration. Intl J. Offshore Polar Engng. 2006;16(1):33–40. [Google Scholar]
- Ge L, Sotiropoulos F. A numerical method for solving the three-dimensional unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 2007;225:1782–1809. doi: 10.1016/j.jcp.2007.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmanov A, Sotiropoulos F. A hybrid Cartesian/immersed boundary method for simulating flows with three-dimensional, geometrically complex, moving bodies. J. Comput. Phys. 2005;207(2):457. [Google Scholar]
- Govardhan R, Williamson C. Defining the ‘modified griffin plot’ in vortex-induced vibration: revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 2006;561:147–180. [Google Scholar]
- Govardhan R, Williamson CHK. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000;420:85–130. [Google Scholar]
- Griffin OM. Flow near self-excited and forced vibrating circular cylinders. J. Engng Industry: Trans. ASME B. 1972;94(2):539. [Google Scholar]
- Griffin OM. Vortex shedding from bluff bodies in a shear flow: a review. J. Fluids Engng: Trans. ASME. 1985;107(3):298. [Google Scholar]
- Griffin OM, Ramberg SE. Some recent studies of vortex shedding with application to marine tubulars and risers. J. Energy Resour. Technol.: Trans. ASME. 1982;104(1):2. [Google Scholar]
- Irons BM, Tuck RC. A version of the Aitken accelerator for computer iteration. Intl J. Numer. Meth. Engng. 1969;1(3):275–277. [Google Scholar]
- Jester W, Kallinderis Y. Numerical study of incompressible flow about transversely oscillating cylinder pairs. J. Offshore Mech. Arctic Engng. 2004;126(4):310. [Google Scholar]
- Karniadakis G, Triantafyllou G. Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 1992;238:1–30. [Google Scholar]
- Khalak A, Williamson CHK. Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 1997;11(8):973–982. [Google Scholar]
- Khalak A, Williamson CHK. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 1999;13(7–8):813–851. [Google Scholar]
- King R, Johns DJ. Wake interaction experiments with two flexible circular cylinders in flowing water. J. Sound Vib. 1976;45(2):259. [Google Scholar]
- Laneville A, Brika D. The fluid and mechanical coupling between two circular cylinders in tandem arrangement. J. Fluids Struct. 1999;13(7–8):967–987. [Google Scholar]
- Lisoski D. Nominally 2-dimensional flow about a normal flat plate. California Institute of Technology; Pasadena, California: 1993. PhD thesis. [Google Scholar]
- Liu C, Zheng X, Sung CH. Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 1998;139(1):35–57. [Google Scholar]
- Meneghini J, Bearman P. AIAA Shear Flow Conf. Orlando, Florida: 1993. Numerical simulation of high amplitude oscillatory-flow about a circular cylinder using a discrete vottex method. [Google Scholar]
- Meneghini JR, Bearman PW. Numerical simulation of high amplitude oscillatory flow about a circular cylinder. J. Fluid Struct. 1995;9(4):435. [Google Scholar]
- Meneghini JR, Saltara F, Siqueira CLR, Ferrari JJA. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 2001;15(2):327. [Google Scholar]
- Mittal R, Balachandar S. Effect of three-dimensionality on the lift and drag of nominally two-dimensional cylinders. Phys. Fluids. 1995;7(8):1841–1865. [Google Scholar]
- Mittal R, Balachandar S. Direct numerical simulation of flow past elliptic cylinders. J. Comput. Phys. 1996;124(2):351–367. [Google Scholar]
- Mittal S, Kumar V. Flow-induced oscillations of two cylinders in tandem and staggered arrangements. J. Fluids Struct. 2001;15(5):717. [Google Scholar]
- Mizushima J, Suehiro N. Instability and transition of flow past two tandem circular cylinders. Phys. Fluids. 2005;17(10):104107. [Google Scholar]
- Moe G, Wu ZJ. Proc. of the Intl Offshore Mech. and Arctic Engng Symp. The Hague, The Netherlands: 1989. Lift force on a vibrating cylinder in a current. [Google Scholar]
- Najjar F, Balachandar S. Low-frequency unsteadiness in the wake of a normal flat plate. J. Fluid Mech. 1998;370:101–147. [Google Scholar]
- Pannell J, Grifiths E, Coales JD. Experiments on the interference between pairs of aeroplane wires of circular and lenticular cross section, British Advisory Committee for Aeronautics Reports and Memoranda No. 208. Ann. rep. 1915;7:219–222. 1915–1916. [Google Scholar]
- Papaioannou GV, Yue DKP, Karniadakis GE, Triantafyllou MS. Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 2006;558:387. [Google Scholar]
- Ruscheweyh HP. Aeroelastic interference effects between slender structures. J. Wind Engng Ind. Aerodyn. 1983;14(1–3):129. [Google Scholar]
- Ryan K, Thompson MC, Hourigan K. The effect of mass ratio and tether length on the flow around a tethered cylinder. J. Fluid Mech. 2007;591:117–144. [Google Scholar]
- Sarpkaya T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004;19(4):389. [Google Scholar]
- Slaouti A, Stansby PK. Flow around two circular cylinders by the random-vortex method. J. Fluids Struct. 1992;6(6):641. [Google Scholar]
- Sumner D, Price SJ, Paidoussis MP. Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 2000;411:263. [Google Scholar]
- Tasaka Y, Kon S, Schouveiler L, Gal PL. Hysteretic mode exchange in the wake of two circular cylinders in tandem. Phys. Fluids. 2006;18:084101. [Google Scholar]
- Williamson CH, Roshko A. Vortex formation in the wake of an oscillating cylinder. J. Fluid Struct. 1988;2:355–381. [Google Scholar]
- Williamson CHK. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996;28(1):477–539. [Google Scholar]
- Williamson CHK, Govardhan R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004;36:413. [Google Scholar]
- Wu W, Huang S, Barltrop N. Multiple stable/unstable equilibria of a cylinder in the wake of an upstream cylinder. J. Offshore Mech. Arctic Engng. 2003;125(2):103–107. [Google Scholar]
- Zdravkovich MM. Flow-induced vibration of two cylinders in tandem arrangements, and their suppression; Proceedings of the International Symposium on Flow Induced Structural Vibrations; Karlsruhe: Springer; 1974. pp. 631–639. 1972. [Google Scholar]
- Zdravkovich MM. Modification of vortex shedding in the synchronization range. J. Fluids Engng: ASME Trans. 1982;104:513–517. [Google Scholar]
- Zdravkovich MM. Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 1985;101(4):511–521. [Google Scholar]
- Zdravkovich MM. Review of interference-induced oscillations in flow past two parallel circular cylinders in various arrangements. J. Wind Engng Ind. Aerodyn. 1988;28:183–200. [Google Scholar]
- Zdravkovich MM, Pridden DL. Interference between two circular cylinders, series of unexpected discontinuites. J. Ind. Aerodyn. 1977;2(1977):255–270. [Google Scholar]
- Zhou C, So R, Lam K. Vortex-induced vibrations of an elastic circular cylinder. J. Fluids Struct. 1999;13(2):165–189. [Google Scholar]