High b-value Apparent Diffusion-Weighted Images from CURVE-ball DTI

Abstract

Purpose

To investigate the utility of a proposed clinical diffusion imaging scheme for rapidly generating multiple b-value diffusion contrast in brain MRI with high SNR.

Materials and Methods

Our strategy for efficient image acquisition relies on the invariance property of the diffusion tensor eigenvectors to b-value. A simple addition to the conventional DTI data acquisition scheme used for tractography yields diffusion-weighted images at twice and three times the conventional b-value. An example from a neurosurgical brain tumor is shown. Apparent diffusion-weighted (ADW) images were calculated for b-values 800, 1600 and 2400 s/mm², and a map of excess diffusive kurtosis was computed from the three ADW's.

Results

High b-value ADW images demonstrated decreased contrast between normal gray and white matter, while the heterogeneity and contrast of the lesion was emphasized relative to conventional b-value data. Kurtosis maps indicated the deviation from Gaussian diffusive behavior

Conclusion

DTI data with multiple b-values and good SNR can be acquired in clinically reasonable times. High b-value ADW images show increased contrast and add information to conventional DWI. Ambiguity in conventional b-value images over whether hyperintense signal results from abnormally low diffussion, or abnormally long T₂, is better resolved in high b-value images.

INTRODUCTION

Diffusion-weighted MRI (DWI) has shown increasing potential as a probe of tissue microstructure due to its sensitivity to the restricted diffusion caused by structural barriers that limit water mobility in vivo. The level of diffusion weighting is indicated by the b-value, a parameter that reflects the length and strength of the field gradients applied in the pulse sequence. For free (or Gaussian) diffusion, the DWI signal, S(b) is described as a decaying exponential: S(b) ∝ e^-bD where D is the diffusion constant. This behavior does not generally characterize diffusion in porous media or biological tissues, a fact which forms the basis for research into compartmental dimensions using q-space diffusion analysis (1), and drives the search for additional information from high b-value DWI. Nevertheless, fitting neural tissue DWI data to this decaying exponential in order to find the diffusion constant, is empirically acceptable as long as two facts are kept in mind:

1. This diffusion “constant” is not constant - it is not only a function of b, but of both the factors contributing to b, i.e., the gradient pulse length and strenght, and can also depend on TE.

2. The measured diffusion reflects complex intrections of water in different cellular compartments with barrier at different lenght scales. It is thus not an intrinsic tissue property and will depend on the time scale of the measurenment and the partial volume effects in the voxel, prompting its customary notation as “apparent” diffusion.

Because models of water diffusion in neural tissue cannot fully simulate the complexity of water interactions in tissue, they cannot accurately predict the dependence of the diffusion signal on pathological states of the tissue. However, it is clear that high b-value DWI emphasizes the effect of restricted diffusion on the signal, and can have higher contrast.

Early detection of hyperacute stroke was the first clinical application of DWI, and has remained the most important (2,3). The accepted b-value for this application is in the vicinity of b≈1000s/mm². Higher b-value have been shown to yield higher contrast and contrast-to-noise ratios that improved accuracy in early diagnosis of stroke (4, 5). High b-value DWI has been shown to be useful for assessment of histopathological grading in tumors (6,7) - Seo et al. concluded that DWI at b=3000 s/mm² is more useful than DWI at b=1000s/mm² in terms of discriminating high-grade and low-grade gliomas at 3T. High b-value DWI was also shown to be more sensitive to tissue changes in Alzheimer's disease than conventional DWI (8), and to provide a superior definition of the leading edge of the lesion in progressive multifocal leukoencephalopathy (9)

Diffusion MRI scans of the brain often include acquisition of multiple diffusion directions distributed on spherical shell which enabbles delineation of white matter fiber direction and tract tracing, by utilizing difusion tensor analysis (10) or its offshoots. Optimally, multiple b-values, each with many direction whould be acqired so that both DTI tractography and tissue characterization could be performed. Given the limited gradient strenght of in-vivo MRI, if all the measurements are performed in the same acquisition scan, the (relatively long) echo time (TE) is determined by the highest b-value measurement, resulting in lower than optimal SNR for the other measurements. If the shells are acquired in different scans, spatial misregistration may be a problem. In either case, when multiple shells are acquired, the scan time is usually too long for clinical applicability, from tens of minutes to hours, depending on the number of slices and shells acquired - see examples in (11,12). A need exists for faster high b-value DTI acquisition, particularly for preoperative and intraoperative use.

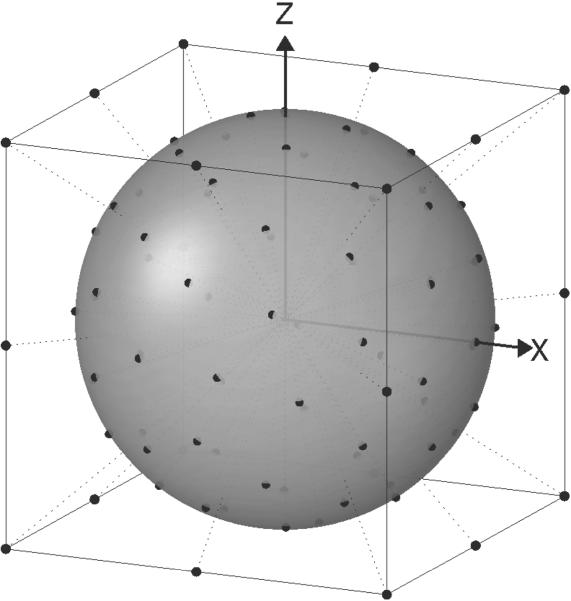
In order to obtain DTI data with multiple b-values and acceptable SNR in clinically reasonable times, a new acquisition method is proposed - CURVE-ball (CUbe Rays to Vertices and Edges) DTI. The analysis of CURVE-ball DTI data is based on the assumed independence of the principal diffusion axes in the tissue on the b-value at which the diffusion data is acquired. Thus the eigenvectors can be calculated from a conventional multi direction, DTI acquisition using a single b-value on a spherical shell, as schematically shown in Fig. 1. Tensors fitted to higher b-values are then constrained to the same eigenvectors. Within the same TE, 6 gradient directions at strengths twice the basic value are acquired, based on gradient directions to the edges of the enclosing cube, i.e. {1,1,0} etc. as first implemented for DTI in Ref.(13). Note that a gradient strength increase of √2, doubles the b-value. Four additional gradient directions at even higher b-values are obtained by utilizing the maximum gradient on all axes (i.e. {1,1,1} etc.) giving three times the basic b-value as first suggested for optimizing SNR in Ref. (14). One of the main advantages of this acquisition is the fact that TE is determined by the length of the gradient pulses required for the low b-value, isotropically distributed measurements on the sphere surface, and is thus short, resulting in high SNR for all measurements. The shorter TE also allows more slices to be acquired per unit time. In order to use this acquisition strategy the slice, frequency, and phase encode directions should be aligned with the physical X,Y,& Z field gradients.

1.

CURVE-ball gradient directions.

When multiple b-value data is available, it becomes possible to assess the deviation from Gaussian diffusive behavior by expanding the fundamental exponential relationship to include a metric called the excess diffusional kurtosis (15). In this case the DWI signal in each voxel is fit to: S(b) ∝ exp(-bD+b²D²K/6) resulting in a map of excess kurtosis, K. Although this is a model-free, empirically derived parameter and does not directly correspond to any particular physiological phenomenon, it can yield noval contrast. Bi-exponential fitting of the diffussion curve is another commonly used technique to extract more information from the diffusion curve (16).

METHODS

Data Acquisition

CURVE-ball acquisition was implemented on a General Electric 3T scanner with 36 isotropic directions at a basic b-value of b_base=800 s/mm², 6 directions with b=1600 s/mm², and 4 direction with b=2400 s/mm², the latter with 2 averages for increased SNR. The scan also acquired at ^b=0, giving a total of 51 measurements for every slice location. FOV was 25.6 cm with phase FOV 0.75 and acquisition matrix 128 × 96 reconstructed to 256 × 192; TE was 80.7ms, TR was 4s, slice thickness 3mm, with other image acquisition parameters being typical for EPI-based dual echo (17) DTI. A patient was scanned preoperatively under an existing human research protocol that optimizes techniques for image-guided neurosurgery, including both fMRI and DTI. The patient was later diagnosed on the basis of fresh tissue histopathology with grade II oligoastrocytoma with focal anaplastic features.

Due to the rotational invariance of the diffusion tensor, in order to calculate the mean diffusivity, or apparent diffusion constant, only three diffusion-weighted measurements, in which the diffusion gradient directions are orthogonal, are actually required. The maximum length of three orthogonal vectors of equal length within a cube enclosing a sphere of radius r is √2r, yielding in this case a b-value of 2·b_base. The implication of this is that only 7 gradient directions actually need to be sampled in order to acquire data at b=b_base and b=2·b_base. In this case, in order to calculate an ADW image at b=3·b_base, an additional scan would be required (potentially adding spatial misregistration issues), or the diffusion gradients would have to be lengthened, with a corresponding increase of TE and decrease in SNR in all the images. In the CURVE-ball strategy it is assumed that tensors need to be computed for white matter tracing. Although the scan time is lengthened by acquiring a sufficient number of low b-value gradients directions for accurate tensor determination and tractography, the additional benefits include the ability to compute the fractional anisotropy (FA) map and the ability to generate data at b=3·b_base in the same scan with the same diffusion gradient timing.

Analysis

The diffusion-weighted images are separated into three groups according to b-values, in this case: 800, 1600, and 2400 s/mm². The analysis effectively finds the diffusion image for each b-value as follows:

1. Fit the b=b_base=800 and b=0 data in each voxel to a tensor, using the linear equation for computational speed:

$$\log \left(S_{\mathrm{lo}}\right)=\log \left(S_0\right)-b_{\mathrm{base}}{\widehat{\mathbf{g}}}_{\mathrm{lo}}\cdot {\mathbf{D}}_{\mathrm{lo}}\cdot {\widehat{\mathbf{g}}}_{\mathrm{lo}},$$ [1]

where S_lo is the signal and ĝ_lo are the unit gradient directions. This yields estimates of the non-diffusion-weighted signal amplitude s₀, the diffusion tensor, D_lo, and its eigenvectors {ê₁, ê₂, ê₃}.

2. Use these eigenvectors to constrain the tensors fitted to higher b-value data, fitting one tensor to the data acquired at medium b-values (b=0 & 2b_base), and a second tensor to the data acquired with b=0 & 3b_base. Practically, this can be done by transforming the gradient directions into the coordinate system defined by the eigenvectors, and then constraining the calculated diffusion tensors to be diagonal, for example in the case of the medium b-value:

$$\log \left(S_{\mathrm{med}}\right)=\log \left(S{’}_0\right)-2b_{\mathrm{base}}{\widehat{\mathbf{G}}}_{\mathrm{med}}\cdot {\mathbf{D}}_{\mathrm{med}}\cdot {\widehat{\mathbf{G}}}_{\mathrm{med}},$$ [2]

where Ĝ_med are the unit gradient directions at b-value 2b_base in the coordinate system defined by {ê₁, ê₂, ê₃}.

Calculation of the three tensors takes approximately 2 seconds per slice (256×256 pixels) in Matlab® on a workstation with 8 dual-core AMD Opteron 880 processors, running at 2.4ghz with 64GB of ram and 750GB of local fast file storage space. Although linear fitting of the logarithm emphasizes the noise, particularly at high b-values, it was used here for simplicity and speed.

3. Calculate Apparent Diffusion-weighted Images (ADW) for each b-value:

$$\begin{array}{cc}\hfill & {\mathrm{ADW}}_{\mathrm{lo}}=S_0\exp (-b_{\mathrm{base}}{\mathrm{ADC}}_{\mathrm{lo}}),\hfill \\ \hfill & {\mathrm{ADW}}_{\mathrm{med}}=S{’}_0\exp (-b_{\mathrm{med}}{\mathrm{ADC}}_{\mathrm{med}}),\hfill \\ \hfill & {\mathrm{ADW}}_{\mathrm{hi}}=S{"}_0\exp (-b_{\mathrm{hi}}{\mathrm{ADC}}_{\mathrm{hi}}),\hfill \end{array}$$ [3]

where ADC = Trace(D)/3 is the average apparent diffusion coefficient. Thus the ADW for each b-value is effectively a diffusion weighted image that is independent of diffusion direction. It is a convenient way of viewing DWI images, mainly because the CSF signal is very low which enables a wider range of contrast in the brain parenchyma.

4. Computer the excess kurtosis by fiting the three ADW signal intensities on a voxel-by-voxel basis to the formula from Ref.(15):

$$\mathit{ADW}\left(b\right)=\sqrt{{\eta }^2+{\left[S_0\exp \left(-\mathrm{bD}+\frac{1}{6}{\mathrm{b}}^2{\mathrm{D}}^2\mathrm{K}\right)\right]}^2}$$ [4]

where η² is the variance of the background noise.

RESULTS

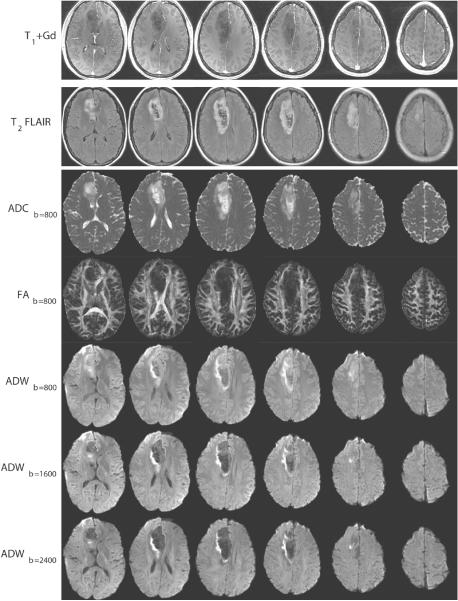
The CURVE-ball acquisition time was 3.5 minutes for 14 slices on a GE 3T scanner. The SNR at b=0 in brain parenchymal regions was approximately 30 (the signal was averaged from a mixed area of gray and white matter, while the noise was computed from the standard deviation of the signal in an artifact-free area outside the brain). Imaging results are in Figure 2 for slices #1,3,5,7,9 out of 14. Conventional imaging (T₁+Gd and T₂ FLAIR) exhibited minimal enhancement and central necrotic areas. The ADC at low b-value showed an area of low diffusivity at the right lateral aspect of the lesion. Brief inspection of the ADW images indicated that gray/white matter contrast decreased (previously observed, e.g. in (18)), and intra-lesion contrast increased as the b-value increased.

2.

Conventional scans and diffusion maps of slices {1,3,5,7,9,11}.

Figure 3 shows a comparison between raw diffusion-weighted image with b-value 2400 s/mm², acquired using: A. a conventional sequence (within a spherical shell), and B. all three gradients. The TE/SNR for the former was 102ms/6.9, and for the latter was 82ms/9.3, a 35% gain in SNR in this case.

3.

Comparison of diffusion-weighted images with b=2400 s/mm² using two different acquisition strategies. A. Conventional high b-value DTI. B. CURVE-ball sparse acquisition with full gradient strength on all 3 axes. Boxes show regions of interest from which SNR was calculated.

Figures 4A and 4B show the ADW calculated forb=800 and b=2400 s/mm² respectively. The gray/white matter contrast existing at b=800 had almost disappeared at b=2400. In order to compare the information from low and high b-value diffusion metrics, Figs. 4C and 4D show the high b-value ADW₂₄₀₀ contours (from Fig 4B) overlaid on the ADC and FA grayscale images calculated from b=800. Red contours indicate high ADW, while blue contours show low ADW. The middle range contours were removed for clarity. Some relative intensity level differences between the maps are demonstrated in regions of interest #1-3 in Fig 4B. ROI's #1 and #2 are moderately hyperintense on both the ADC₈₀₀ grayscale map in Fig. 4C, and the ADW ₈₀₀ map in Fig. 4A. However, on the ADW₂₄₀₀ map, ROI#1 became hypointense while ROI#2 became isointense with healthy tissue. This may indicate less pathology in ROI#2 than in ROI's #1 and #3, a hypothesis supported by the higher FA₈₀₀ value there. (Although high FA often indicates healthy white matter, low FA need not indicate pathology and can be due to partial voluming with gray matter, or with an area of crossing tracts in white matter, so should be used with caution as an indicator of tissue structural integrity) The excess kurtosis map in Fig. 5 shows some gray/white matter contrast as expected, and low values in all three ROI's. Its contrast distribution on the right lateral aspect of the lesion differs from the other diffusion maps.

4.

A comparison of low and high b-value diffusion. A. ADW₈₀₀ from slice #5 (from b=800 s/mm² data). B. ADW₂₄₀₀ (from b=2400 s/mm² data). C. Contours of ADW₂₄₀₀ overlaid on ADC at b=800. D. Contours of ADW₂₄₀₀ overlaid on Fractional Anisotropy map (FA) at b=800. TO generate the contours, the ADW images were smoothed with a 2D Gaussian Kernel, of width σ=1 pixel. The mid-level contour lines are not shown in order to focus attention on the lesion.

5.

Excess Kurtosis map with overlaid contours. The contours were smoothed with a 2D Gaussian kernel of width σ=2 pixels.

DISCUSSION

We have shown that high b-value DWI data can be acquired quickly and efficiently and can increase image contrast and lesion conspicuity. At high b-values, the apparent diffusion weighted images show lower contrast between healthy gray matter and healthy white matter and in this case, higher contrast between distinct parts of a brain tumor, different from the contrast exhibited at a lower b-value. The T₂ shine-through phenomenon in DWI, where long T₂ may be confused with low diffusion, is much reduced in the high b-value images. This phenomenon may be particularly helpful for differentiating tumor vs. abscess, or hyperacute stroke from the subacute stages. Diffusive kurtosis maps add another dimension to the data interpretation by reflecting the degree of non-exponential diffusive behavior as a function of b-value.

A neurosurgical glioma patient was scanned for this study. Based on visual inspection of the CURVE-ball DTI images, there are brain areas in which all the diffusion metrics indicate pathology, and areas in which the high and low b-value maps provide different and complementary information. ROI#2 in Fig. 4B may be an example of tissue that, based on the high b-value data and the FA, should be spared excision, with the abnormally high ADC at the low b-value possibly resulting from vasogenic edema. Schwarcz et al. have previously measured a large change in the diffusion at low b-values and no significant change in the so-called slow diffusion constant (derived from the slope of the diffusion curve at high b-values) in areas of vasogenic edema (19).

The difficulty of DWI interpretation increases with the number of variables that can be isolated but more information may lead to increased specificity. Ultimately the objective would be to understand the tissue characteristics that give rise to a certain diffusion behavior with the potential gain being a better diagnostic characterization of pathology. Modeling can yield insight into the relationship between tissue ultrastructure and DWI signal. For example, Monte Carlo simulations have suggested that the remaining signal at high b-values (ADW₂₄₀₀ here) reflects the size of the population of water molecules that exhibits bounded diffusion, i.e. is restricted to spatial compartments on a cellular length scale (1920). Thus high ADW₂₄₀₀ could be interpreted as an indication of hypercellularity and low ADW₂₄₀₀ as a lack of cellular structure.

In conclusion, in order to obtain DTI data with multiple b-values and good SNR in short scan times, a new data acquisition strategy is proposed and implemented. The basis of the method is the invariance of eigenvector directions to b-value. High b-value images can provide different contrast and additional information when compared to conventional DWI. This acquisition strategy, accompanied by straightforward analysis, may help enable routine clinical high b-value DTI.