Limiting unwanted cues via random rove applied to the yes-no and multiple-alternative forced choice paradigms

Abstract

When a random rove is used in a perceptual task to control the influence of an unwanted cue that may confound the decision strategy of primary interest, the effectiveness of the rove is determined by its range. Green [Profile Analysis (Oxford University Press, Oxford, 1988)] provided a formula which allows experimenters to determine the roving range required to ensure that the listeners relying on the unwanted cue cannot exceed a pre-defined percentage of correct responses in a two-interval, two-alternative forced-choice experiment. Here, Green’s analysis is extended to the yes-no and m-alternative, forced-choice paradigms (m>2).

Introduction

In designing an auditory detection or discrimination experiment, the researcher often faces the possibility that multiple decision strategies, or perceptual cues, are available to the listeners in performing the task. For example, in a spectral-shape discrimination experiment, the primary interest of the researcher is the listeners’ ability to detect a change in the relative level of different frequency components. However, a change in the relative level is always accompanied by changes in the absolute level of certain frequency components. As a result, the task can also be performed based on the absolute level of a single component, without having to monitor the relative level of different frequency components at all. Unless the influence of the change in absolute level on the listener’s decision is under control, the outcome of such an experiment will not have any definitive implication on the listeners’ ability to discriminate spectral shapes. Any cue other than the cue of primary interest is denoted as an unwanted cue in this paper. (Thus, in the above example the absolute-level cue is an unwanted cue). One approach to limiting the influence of an unwanted cue is to apply random rove to the stimulus dimension associated with that cue, de-correlating the cue from the primary cue. For example, by randomly varying the absolute overall stimulus level upon each stimulus presentation independent of changes made to spectral shape, any change in absolute level will be an unreliable indication of a change in spectral shape. For this reason, random rove has been an essential component in studies of spectral-shape discrimination (e.g., Spiegel et al., 1981; Green, 1988). Aside from its role in studies of spectral-shape discrimination, the randomization technique has had a long history in auditory research, and has been applied in a wide range of studies and tasks to control the influence of various unwanted cues, including frequency discrimination or pitch perception (e.g., Henning, 1966; Moore and Glasberg, 1989; Emmerich et al., 1989; Dai et al., 1994; Shackleton and Carlyon, 1994; Carlyon and Shackleton, 1994; Moore et al., 2006; Micheyl and Oxenham, 2007; Oxenham et al., 2009), binaural hearing (e.g., Koehnke and Colburn, 1987; Wightman and Kistler, 1999; Zahorik, 2002; Stellmack et al., 2006; Fan et al., 2008), and cases where multiple cues were controlled in a single task (e.g., Richards et al., 1989; Lutfi, 2001).

The extent to which an unwanted cue is controlled by a random rove is directly determined by the range of the rove. For the two-interval, two-alternative forced-choice (2I-2AFC) paradigm, Green (1988) (pp. 19–21) provided a quantitative analysis of the limit that the random rove imposed on the discrimination performance that can be achieved on the basis of an unwanted cue. Specifically, for a given size of the change in the variable associated with the unwanted cue, Δ, and a range of rove, R, the upper limit of percent correct based on the unwanted cue is given by PC(Δ)=0.5+Δ∕R−0.5(Δ∕R)². Green’s formula can be used as a guideline in several ways for applying the randomization technique. For example, suppose the experimenter in a spectral-shape discrimination experiment applies a rove of R=20 dB to limit an unwanted absolute-level cue of Δ=1 dB. According to Green’s formula, the unwanted cue alone can produce a percent correct of PC=54.9% at the best. In another example, suppose the experimenter wants to determine the range of rove needed to limit a 1-dB unwanted cue to a percent correct of PC=52%. According to Green’s formula, the rove must have a range of $R=\Delta ∕[1-\sqrt{2(1-\mathrm{PC})}]=49.5\mathrm{dB}$ to accomplish that objective.

Green’s formula was derived specifically for applications with a 2I–2AFC paradigm; to the authors’ best knowledge, it has not been extended to other psychophysical paradigms. Because different paradigms have their own special merits (Macmillan and Creelman, 2005), there are occasions when the experimenter wants to apply the randomization technique under other paradigms than the 2I–2AFC option. For example, Versfeld and Houstma (1991, 1995) applied random rove to spectral-shape discrimination under a 3AFC paradigm. Therefore, it is useful to provide a theoretical analysis of the limit imposed by randomization on the performance that can be achieved based on an unwanted cue in other paradigms than 2–I2AFC. The primary purpose of this note is to extend the analysis by Green (1988) to the yes-no and general multiple-alternative, forced-choice (mAFC) paradigms. The analysis addresses random roves applied to both continuous and discrete variables.

Analysis and discussion

Random rove applied to continuous variables

The following analysis is limited to randomizations based on uniform distributions which have been used in most applications of the randomization technique in auditory-perception research. Among different distributions of a fixed range, the uniform distribution has been shown to produce the lowest limit on percent correct (Dai, 2008). Let x be the stimulus variable associated with the unwanted cue, upon which randomization is applied. For the standard-alone condition, the distribution has a probability density function of y_n(x)=f(x)=1∕R, defined within the range R>x>0, and is zero elsewhere. For the standard-plus-signal condition, it is y_S(x)=f(x−Δ), defined within R+Δ>x>Δ, and is zero elsewhere.

In the yes-no task, the optimum decision rule based on likelihood ratio is to respond “yes” if the magnitude of the observation is greater than a fixed criterion. The criterion is unbiased if it corresponds to a likelihood ratio of unity (assuming that equal number of no-signal and signal trials are included). The proportion of correct responses is identical to the proportion of yes responses over the trials when the signal is presented. Given this decision rule and the two density functions f(x) and f(x−Δ), the proportion of correct and unbiased responses for Δ can be expressed as a weighted sum of two PCs:

$${\mathrm{PC}}_{\text{yes}\text{-}\text{no}}\left(\Delta \right)=(1-\frac{\Delta }{R}){\mathrm{PC}}_0+\frac{\Delta }{R}{\mathrm{PC}}_1,$$

in which PC₀=50% represents the chance performance when the observation or sample of x falls into the overlapping region (i.e., where the likelihood ratio is unity) of the two distributions, and PC₁=100% represents the perfect performance when the sample falls into the non-overlapping region (i.e., where likelihood ratio is infinity) of the shifted distribution. Combin-ing the above expressions, we obtain

$${\mathrm{PC}}_{\text{yes}\text{-}\text{no}}\left(\Delta \right)=\frac{1}{2}+\frac{1}{2}\frac{\Delta }{R}.$$ (1)

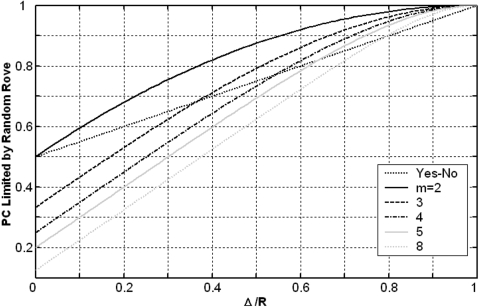
This function is plotted as the dark dotted line in Fig. 1.

Figure 1.

Percentage of correct responses (PC) based on unwanted cues (Δ), which is limited by random rove implemented with continuous uniform distributions, as a function of the ratio between Δ and the range of the rove (R). Different curves represent the results computed for different psychophysical paradigms, including the yes-no (dark dotted line) and mAFC paradigms with m=2–8 (as indicated by the legends). The intercepts of the curves on the y axis (i.e., Δ=0) represent the chance performances for the specific paradigms.

In a mAFC paradigm, in which the random rove is implemented with a uniform distribution, the optimum decision rule is to respond to the interval in which the magnitude of the observation variable is greater than that in any of the other m−1 intervals. Given that the sample drawn from the standard-plus-signal distribution equals x=η, the probability that every sample drawn from the m−1 standard-alone distributions is less than η would be ${\left[{\int }_{-\infty }^{\eta }{y}_N\left(\zeta \right)d\zeta \right]}^{m-1}$. This probability integrated over all possible values of η, therefore, would be the PC value, which can be expressed generally as (Green and Swets, 1966) (p. 47):

$${\mathrm{PC}}_m\left(\Delta \right)={\int }_{-\infty }^{\infty }{y}_S\left(\eta \right){\left[{\int }_{-\infty }^{\eta }{y}_N\left(\zeta \right)d\zeta \right]}^{m-1}d\eta .$$ (2)

By plugging in the above-defined probability density functions into Eq. 2, PC can be further expressed as

$${\mathrm{PC}}_m\left(\Delta \right)={\int }_{\Delta }^{R+\Delta }f(\eta -\Delta ){\left[{\int }_0^{\eta }f\left(\zeta \right)d\zeta \right]}^{m-1}d\eta .$$ (3)

Substituting the expression for f(x) into Eq. 3 and integrating, we have

$${\mathrm{PC}}_m\left(\Delta \right)=\frac{1}{m}[1-{\left(\frac{\Delta }{R}\right)}^m]+\frac{\Delta }{R}.$$ (4)

The first term of Eq. 4 represents the performance when the sample falls into the overlapping region of the shifted signal distribution and the m−1 un-shifted non-signal distributions. The second term represents the perfect performance when the sample falls into the non-overlapping region of the shifted signal distribution. This function is plotted in Fig. 1 for m=2, 3, 4, 5, and 8.

Figure 1 shows for different paradigms the limit imposed by a uniformly distributed random rove on the percent-correct performance that can be achieved based on an unwanted cue. For each paradigm, the proportion of correct responses (PC) attainable using the unwanted cue is calculated using Eq. 1 (for the yes-no paradigm) or Eq. 4 (for mAFC paradigms), and is plotted as a function of the ratio between the size of an unwanted cue (Δ) and the range of the rove (R). Given that a uniform distribution will be used to limit the unwanted cue in the yes-no or mAFC tasks, the researcher can use Eq. 1 or 4 to determine how big a range is sufficient to keep performance based on the cue from reaching a certain value. For relatively small ratios of Δ∕R, mAFC paradigms with greater m values produced lower limits on PC, largely due to the lower baseline or chance performance level for these paradigms. While the yes-no and 2I–2AFC paradigms share the same chance performance at 50%, random rove implemented with the yes-no paradigm produced percent correct values below those of the 2I–2AFC paradigm at all values of Δ∕R. As the ratio Δ∕R increases, random rove implemented with the yes-no paradigm becomes increasingly more effective relative to that implemented with the mAFC paradigms. Beyond about Δ∕R=0.7, the yes-no paradigm produces the lowest percent correct values than all the mAFC paradigms shown.

Random rove applied to discrete variables

Thus far, the analysis has been carried out for continuous variables. However, in experimental applications of the randomization technique, the experimenter may choose to draw samples from a discrete distribution. Although discrete distributions can be approximated by continuous ones when their probability mass functions have a very large number of bins, the results obtained with continuous and discrete distributions become clearly different when the bins are sparse. Thus, in general, randomization applied to discrete variables should not be treated as a special case of that applied to continuous variables. In particular, Eqs. 1, 4 will lead to sizable error when the number of bins is small. In practice, a small number of bins in discrete distributions can happen when the range of randomization (R) is comparable to the size of the signal (Δ), which may result from either a severely limited range to apply randomization (as with hearing impaired ears) or an unusually large signal size (as with an extremely difficult task, e.g., Dai and Green, 1992). Therefore, we need to derive for discrete variables the equations relating PC to Δ and R, which is the purpose of this section.

For analyzing random rove applied to discrete variables, we define the probability mass function of the random rove as having n bins spaced at equal inter-bin intervals of b=R∕(n−1), with each bin representing a probability of p=1∕n. Note that the amount of shift of the distribution caused by the unwanted cue, Δ, is allowed to take only integer numbers of the inter-bin intervals; other values of Δ will produce no overlap of bins between the distributions, leading to a percent correct of 100%, and rendering the application of random rove useless. With a shift of Δ between the two distributions for the non-signal and signal events, the number of bins that do not overlap will be Δ∕b=(n−1)Δ∕R, which amounts to a probability of pΔ∕b=[(n−1)∕n]Δ∕R. Note that for continuous distributions the probability of the non-overlapping portion is simply Δ∕R. Thus, the expressions for the limits on PC imposed by random rove for discrete variables can be obtained by replacing Δ∕R with [(n−1)∕n]Δ∕R in Eqs. 1, 4. We have

$${\mathrm{PC}}_{\text{yes}\text{-}\text{no}}^{\text{discrete}}\left(\Delta \right)=\frac{1}{2}+\frac{1}{2}\frac{n-1}{n}\frac{\Delta }{R},$$ (5)

for the yes-no paradigm, and

$${\mathrm{PC}}_m^{\text{discrete}}\left(\Delta \right)=\frac{1}{m}[1-{\left(\frac{n-1}{n}\frac{\Delta }{R}\right)}^m]+\frac{n-1}{n}\frac{\Delta }{R},$$ (6)

for the mAFC paradigms. These results may be interpreted as if, by implementing the random rove with discrete instead of continuous distributions, the size of the unwanted cue is effectively reduced by a factor of (n−1)∕n.

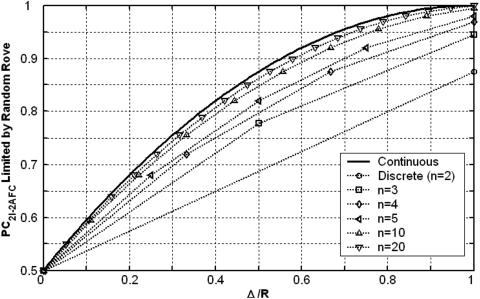
To illustrate the different outcomes of random rove applied to discrete and continuous variables, the limit on the percent-correct performance for the 2I–2AFC paradigm is computed as a function of Δ∕R using Eq. 6, for discrete variables with several values of the number of bins. Figure 2 presents the results obtained with n=2 (circles), 3 (squares), 4 (diamonds), 5 (right triangle), 10 (up triangle), and 20 (down triangle) bins. For comparison, the solid dark curve from Fig. 1, which represents the result obtained using a continuous distribution with the 2I–2AFC paradigm, is re-plotted here. A general summary of the results is that, for all possible values of Δ∕R where the discrete distributions are available, random rove leads to lower percent correct values, thus is more effective, when implemented with discrete than with continuous distributions. The advantage of discrete distributions is most pronounced for distributions with five or fewer bins. For example, with n=2 and a shift of Δ=R, the percent correct is 100% with a continuous distribution, but is limited to PC=87.5% with a discrete distribution. With continuous distributions, to limit the unwanted cue to the same PC=87.5% would require a rove range twice the size of Δ, i.e., Δ∕R=0.5. Thus, when Δ=R, implementing random rove with the discrete distribution effectively reduces the size of the unwanted cue by half (or equivalently, effectively increases the rove range by a factor of 2) relative to that with the continuous distribution. The advantage of discrete distributions over continuous distributions diminishes as the number of bins increases. For distributions with more than n=20 bins, the outcomes are closely approximated by the function obtained with the continuous distribution.

Figure 2.

Same format as in Fig. 1, but for the 2I–2AFC paradigm only. The symbols represent the percent correct values limited by random rove implemented with discrete uniform distributions with n=2 (circles), 3 (squares), 4 (diamonds), 5 (right triangles), 10 (up triangles), and 20 (down triangles) bins. The solid line represents the function obtained with continuous uniform distributions in Fig. 1, which is replotted her for comparison.

Depending on the specific experimental situation, the experimenter may opt for discrete distributions with sparse bins over continuous distributions to maximize the effect of randomization. This approach may prove to be a useful addition to techniques developed for experimental conditions where the range of rove is limited to not much greater than the size of the unwanted cue (e.g., Kidd and Mason, 1992; Kidd and Dai, 1993), helping us deal with special cases such as when there is a severely limited dynamic range due to hearing impairment, or when the perceptual task is extremely difficult.