Abstract
Circular dichroism (CD) is an excellent tool for examining the interactions and stability of proteins. This protocol covers methods to obtain and analyze circular dichroism spectra to measure changes in the folding of proteins as a function of denaturants, osmolytes or ligands. Applications include determination of the free energy of folding of a protein, the effects of mutations on protein stability and the estimation of binding constants for the interactions of proteins with other proteins, DNA or ligands, such as substrates or inhibitors. The experiments take 2-5 h.
INTRODUCTION
Circular dichroism (CD) is an excellent technique to study the folding and interactions of proteins. Machines capable of obtaining measurements below 250 nm, where the protein backbone amides absorb light, first became available commercially about forty years ago. At that time, very little was known about the structure of proteins, and the principal application of CD was to determine the secondary structure of newly isolated proteins. However, CD is more valuable as a rapid method to study protein folding and interactions.
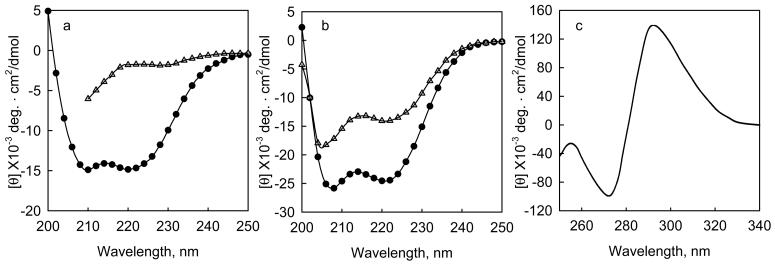
When the amide polypeptide bonds are aligned in regular arrays, such as α-helices or β-pleated sheets, they have characteristic spectra. For example, proteins with high contents of α-helices have characteristic bands at 222 and 208 nm. Two examples of such proteins are shown in Figure 1. The addition of ligands, denaturants, or stabilizing agents, such as osmolytes, to proteins often changes their CD spectra. Thus CD can be used to study the effects of denaturants or osmolytes on protein folding, or to determine ligand binding constants. Figure 1a illustrates how the addition of guanidine-HCl (Gn-HCl) to a helical protein causes a loss of the characteristic helical CD bands1, which can be used to determine the free energy of folding of the protein. Figure 1b illustrates how the addition of calcium to the calcium binding subunit of troponin (TnC) causes an increase in its ellipticity due to an increase in helical content2. The change in ellipticity can be used to determine the calcium binding constants. In addition, when ligands with chromophores bind to proteins they may develop strong extrinsic CD bands that can be used to determine binding constants. Figure 1c shows the CD bands that are induced when folate binds to dihydrofolate reductase from E coli3. The induced extrinsic ellipticity can be used to determine the binding constant of the ligand.
Figure 1. Changes in intrinsic and extrinsic circular dichroism bands upon the interaction of proteins with denaturants and ligands.
a, The change in mean residue ellipticity when Gn-HCl is added to a fragment of tropomodulin 1, Tmod1160-3591, 0.24 mg/ml (10 μM) in 100 mM NaCl, 10 mM sodium phosphate, pH 6.5 at 10 °C. (o) native protein, (Δ) protein + 3.6 M Gn-HCl. b. The change in mean residue ellipticity when calcium binds to the calcium binding subunit of cardiac troponin, TnC, 0.2 mg/ml, at 2 °C in 50 mM NaC1, 2 mM HEPES, pH 7.0, 0.5 mM DTT, with (Δ) 2mM EDTA, or (•) 3 mM CaCl22. c, Induced molar ellipticity when saturating sodium folate binds to dihydrofolate reductase from e coli.3. The enzyme is 18 μM in 100 mM NaCl, pH 7.2 at 27 °C.
Sources of spectrometers and cuvettes, setting up CD machines to collect data and the procedures for obtaining high quality, reproducible data have been covered previously4. This protocol will cover how to obtain data as a function of titrants, including denaturants, osmolytes and ligands, and how to analyze data to determine the free energy of protein folding and the binding constants of protein-ligand (or protein-protein) interactions. This protocol will only cover the basics of each application. For more detailed information, there are several reviews and illustrative papers which cover the use of CD spectroscopy to determine the free energy of folding using denaturants or osmolytes5-13 and to study interactions of proteins with ligands, other proteins and polynucleotides14-19.
Description of methods
The two methods that will be described are how to determine the free energy of protein folding from changes in CD as a function of denaturants or osmolytes (A) and how to determine binding or dissociation constants from changes in CD as a function of ligand concentration (B).
(A) Determination of the free energy of folding by following changes in the ellipticity of a protein as a function of denaturants or osmolytes
The free energy of folding of a protein can be determined from CD measurements as a function of denaturants or osmolytes if the change in CD is due to a two-state transition between folded and unfolded states. To a first approximation the free energy is linearly dependent on the concentration of denaturants, such as urea or guanidine, which cause a loss of ellipticity, or osmolytes, such as trimethylamine N-oxide (TMAO) or sucrose, which increase the stability of proteins and cause an increase in ellipticity12,20. Note, if this method is to be used to determine true thermodynamic parameters, the unfolding of a protein must be reversible; i.e. the folding at each concentration of denaturant must be identical whether the denaturant is added to the folded protein or the denaturant is diluted out of the solution by added denaturant-free protein in buffer. The folding constant, KF of a monomeric protein or polypeptide can be evaluated by the equation:
| (1) |
where [F] is the concentration of folded protein and [U] is the concentration of unfolded protein. The folding constant at any concentration of denaturant, [D]i can be calculated from the ellipticity, [θ]i, at the ith concentration of denaturant, using equations 2 and 3 for a monomer and equations 2 and 4 for a multimeric protein with equivalent subunits, or equations 2 and 5 for a multimeric protein where all the subunits are unique. The fraction folded is:
| (2) |
where [θ]F is the ellipticity at which the molecule is fully folded and [θ]U is the ellipticity of the fully unfolded molecule. The folding constant for a monomeric protein is:
| (3) |
where Pt is the total protein concentration. For a multimeric protein with identical chains the equation is:
| (4) |
where Pt is the molecular concentration of the multimeric protein when all the protein is folded, i.e. the total concentration of chains/n. For a multimeric protein where all the chains are unique the equation is:
| (5) |
The free energy of folding of a protein, ΔGF, can be evaluated from the equation:
| (6) |
where R is the gas constant =1.98 cal/mole and T is the absolute temperature. In this protocol, the free energy is calculated in terms of moles of folded protein, e.g. one mole of a folded homodimeric protein, A, unfolds to give two moles of unfolded chains, B. For many proteins, the free energy of folding is a linear function of the amount of titrant added8,12,20.
| (7) |
where ΔGi is the free energy of the protein in the presence of the ith concentration of denaturant, ΔGo is the free energy of the folded protein in the absence of denaturant, m is the slope and [Di] is the concentration of denaturant.
To determine the free energy of folding using linear regression: (1) determine KFi of folding at each concentration of titrant, [D]i using equations 2 and 3 for a monomer or 2 and 4 or 5 as appropriate for multimers; (2) calculate the free energy at each condition using equation 6; (3) plot ΔGFi (y) as a function of denaturant (x) and fit the data to a straight line, y=mx+b, where m is the slope and b is the y intercept. The free energy of folding, ΔGo, is equal to the y intercept. The unfolding curves can also be evaluated directly from the ellipticity, [θ]i, as a function of denaturant, [D]i, using non-linear regression routines such as the Levenberg-Marquardt algorithm21 found in many graphics programs as shown below. For a monomer:
| (8) |
| (9) |
| (10) |
where M is the slope.
| (11) |
where R is the gas constant, which equals 1.98 cal/mol, and T is the absolute temperature.
| (12) |
| (13) |
The theoretical ellipticity, Y is fit to the observed data, [θ]i, using non linear least squares analysis. One inputs initial values of Go, M, [θ]F, and [θ]U and allow the program to find the best fit to the data. For a heterodimer equation 12 is replaced by:
| (14) |
where Pt is the total protein concentration when it is fully folded as a dimer. For a homodimer equation 12 is replaced by
| (15) |
Occasionally, there will be small changes in the CD spectrum of a protein as a linear function of perturbant preceding and/or following the major unfolding transition. Large linear changes in the spectral parameters of the folded and unfolded state of proteins are often seen when folding is monitored by changes in the fluorescence of the aromatic residues or difference spectroscopy in the aromatic region of the spectrum. These changes result from interaction of the perturbing substance with exposed chromophores in the folded and unfolded proteins, rather than from conformational changes. When there are such linear changes, correction terms are applied to the equations used to fit the data8. When the change in ellipticity is fit directly, equation 13 is replaced by equation 16, which contains a correction for the linear changes in the ellipticity of the fully folded and unfolded proteins as a function of perturbant.
| (16) |
Here m1 and m2 are the slopes of the linear pre-transition and post-transition changes, respectively. They are input as additional parameters in the curve fitting routines. The linear correction terms should only be applied when it is clear that there are true linear changes in ellipticity of the fully unfolded and folded forms of the protein as a function of the titrant. Fits of raw data are almost always improved when the number of parameters to be fit is increased, but the parameters often become highly dependent on one another and the results may be misleading. In addition, the pre- and post-transition “linear” changes in CD may indicate that the unfolding transitions are not two-state between a single folded and unfolded form. There may be small local unfolding transitions that contribute to the total free energy of unfolding.
Denaturation studies can be used to determine the association constants of protein-protein complexes if the folding is reversible and the proteins only bind to each other when folded. In the simplest case both proteins (e.g. X and Y) are monomers. The constant of folding of protein X is kFX=[XF]/[XU] and the constant of folding of protein Y is kFY=[YF]/[YU]. The constant of folding of the dimer is kFXY=[XYF]/[XU][YU]. The association constant KA=[XYF]/[XF][YF]. Making the substitutions: KA=kFXY/kFXkFY. To determine the binding constants of a dimer, first determine the free energies of folding of the free proteins and the protein complex from the linear plots of the free energies of folding ΔGi as a function of [D]i and extrapolate to zero denaturant concentration to obtain values of ΔGo. Calculate the folding constants in the absence of denaturant using the relationship kF=e−Go/RT. R is the gas constant and T is the absolute temperature. Divide the kF of folding of the dimer by the product of the kF values of folding of the two monomers to get the binding constant, KA, for dimer formation.
In some cases the free energy of folding is not strictly a linear function of the concentration of denaturant. Such non-linearity is most often seen when proteins are denatured using Gn-HCl, and may arise from charge-charge interactions between the protein and denaturant22. A complete discussion of these cases is beyond the scope of this protocol, but there are several papers in the literature that discuss the treatment of non-linear data in detail22-24.
The free energy of folding of a protein that is intrinsically disordered can be determined by adding osmolytes such as TMAO, sucrose, sorbitol or glycerol13,25, which induce folding. In this case, increasing concentrations of osmolytes are added to the protein solution until there is no further increase in ellipticity. The final ellipticity value corresponds to [θ]F. Wu and Bolen13 have pointed out that if the native protein is not completely unfolded in the absence of osmolytes, its ellipticity is not equal to [θ]U and the linear extrapolation method will not give the correct ΔG of folding. They suggest titrating the protein solution in the absence of osmolytes with urea to determine the parameter corresponding to the completely unfolded protein (in this case [θ]F), which can then be used to determine the fraction folded using equation 2.
Routines for fitting the change in ellipticity as a function of denaturant or osmolytes to determine the free energy of folding are in SUPPLEMENTAL MATERIALS in SigmaPlot format in the file Unfolding.doc.
(B) The determination of binding or dissociation constants from changes in ellipticity as a function of ligands, nucleic acids or other proteins
The general theory of binding equilibria has been discussed in several classical papers and books26-30 and a complete analysis is beyond the scope of this protocol. There are also several detailed reviews about how to use CD and spectroscopy in general to measure protein-protein and protein-ligand interactions14,15,18,19,31-35 so only illustrative examples will be given here.
If one titrates a protein, P, with another protein or a ligand, A, the concentration of product [PA] formed is in equilibrium with free [P] and [A]. The dissociation constant of the complex is defined as KD and the association constant KA is equal to 1/KD.
| (17) |
[Pt] and [Ao] are the initial concentrations of protein, P, and ligand, A, and [PA] is the concentration of complex formed. The saturation fraction, s, is defined as [PA]/[Pt].
If there is a change in the intrinsic or extrinsic CD accompanying binding, the change, Δ[θ], is proportional to the amount of complex formed.
| (18) |
where ε is the proportionality constant. When all of protein P is bound by the ligand or protein A
| (19) |
Case 1. Weak Binding (or where the free concentration of ligand may be determined independently)
If one titrates a protein P with a ligand with a total concentration [Ao] and the dissociation constant >> protein concentration, [Pt], then [A], the free ligand concentration, is approximately equal to [Ao] and the data can be fit by equations such as those described by Scatchard36, Hill37 or McGhee-von Hipple30.
In the Scatchard plot the change in ellipticity as a function of free ligand concentration, [A], is transformed into a linear plot, shown in equation 20.
| (20) |
To determine the binding constant and the proportionality constant, one plots Δ[θ]/[Pt][A] as a function of Δ[θ]/[Pt]. The slope is the association constant and the x-intercept is ε.
In the Hill plot, the change in ellipticity as a function of ligand concentration is described by equation 21 which is not linear.
| (21) |
The Hill equation is a generic equation for describing the binding of multiple ligands to a protein. Here, KA is the association constant and “h” is the Hill constant that describes the cooperativity of binding. C is a constant to offset the data if the ellipticity in the absence of ligand is not equal to zero. To determine KA, h and Δ[θ]max from plots of Δ[θ] versus total ligand, [Ao], one estimates their initial values and uses non-linear least squares to find the values that best fit the equation.
One may also estimate ligand binding constants by performing denaturations of the protein in the absence and presence of varying concentration of ligands or other proteins5,7. In this case:
| (22) |
Where ΔGo(ligand) is the free energy of folding, determined by titration with denaturants in the presence of ligand, ΔGo is the free energy of folding determined in the absence of substrate, KA is the association constant and [A] is the free ligand concentration.
Case 2 -Tight Binding
When binding is tight, and one only knows the total concentration of ligand, [Ao] rather than the free, and the dissociation constant Kd is less than or close to that of the total protein concentration, [Pt], one must correct the concentrations of protein and ligand for the amount bound38. In this treatment the ellipticity, [θ]i, at any total ligand concentration [Ao]i is defined by equation 23.
| (23) |
where n is the 1/number of binding sites. The equation can be solved by estimating initial values of KA, and n and [θ]max and finding the best fits using non-linear least squares curve fitting procedures.
Curve fitting files in SigmaPlot™ format for fitting the Hill equation and the Scatchard equation for the case of tight binding are in SUPPLEMENTAL MATERIALS in the file binding.doc.
Comparisons with other methods
Circular dichroism, like all other spectroscopic methods, is an indirect way of determining the free energy of folding of proteins and protein binding interactions. The advantage of CD is that one gets information about the structural changes of the protein in response to perturbants and ligands and CD is a relatively rapid method of studying folding and binding. However, as with all other spectroscopic techniques, the values that are obtained are model dependent. For example, when a protein is titrated to determine binding or dissociation constants, the assumption is made that the maximal change in ellipticity corresponds to maximal binding. For accurate determinations of either folding or binding constants, the stoichiometry of the reaction (i.e. number of binding sites, and/or oligomeric state of the protein) must be confirmed by independent methods such as equilibrium dialysis or ultracentrifugation. In addition, CD is most useful for determining dissociation constants ranging from 0.01 to 1 μM, since CD measurements are usually obtained on samples ranging from 0.005 mg/ml in a 1 cm cell to 1 mg/ml in a 0.1 cm cell. If a protein has a molecular weight of 20,000 the lowest practical concentration would be 0.1 μM, which would give a lower limit for the determination of a dissociation constant of 0.01 μM. The binding of more tightly bound ligands would be almost linear with concentration until saturation was reached (i.e. almost stoichiometric). Thus CD is often not as sensitive as other spectroscopic methods, such as fluorescence.
Applications
Chemical perturbation of protein circular dichroism has many applications. Perusal of the “PubMed” data base (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?DB=pubmed) shows that there have been over 1000 papers published on following the interactions of proteins with Gn-HCl using CD. A primary application is to examine the effects of naturally occurring mutations on protein stability. In addition, as detailed above, the technique can be used to determine the binding constants of protein-protein, protein-DNA and protein-ligand interactions. Similarly, there are many applications of following titrations of proteins with ligands. The principal applications are examining the interaction of proteins with drugs19,39 and examining the effects of mutations on ligand binding.
PROCEDURE
Equipment
Circular dichroism equipment, machine setup and cells (cuvettes) suitable for CD use have been described previously4.
Small stirring bars that will fit inside a rectangular 1 cm x 1 cm cuvette.
Equipment setup
Procedures for setting up the machine to collect data, i.e. flushing with N2, turning on the lamp, setting the temperature, the wavelength range, the band width, the step size, etc. have been described previously4. Make sure that the instrument is flushed with nitrogen before firing the lamp. Turn on the lamp before turning on the instrument and computer to avoid damaging electronics when the lamp is fired. Make sure that circulating water baths or water supply if they are needed for cooling the lamp or acting as a heat trap for the temperature controllers are turned on before the CD machine is started. Some CD machines have automatic titrating accessories that work with cells with 1cm path lengths and will remove solutions from the sample compartment when the cell starts to get full so that one does not have to change samples during a titration, when the volume of titrant exceeds the volume capacity of the cuvette. Before using such attachments, however, test them with water to make sure that they do not leak and that they deliver accurate volumes.
Software
A commercial graphics program which allows user-defined non-linear least squares curve fitting. Most of the commonly available commercial programs use the Levenberg-Marquardt algorithm21 for fitting curves to non-linear equations. Graphic packages include: GraphPad, http://www.graphpad.com/; Psi-Plot, http://www.polysoftware.com/aboutpsi.htm; Origin, http://www.originlab.com; and SigmaPlot, http://www.systat.com.
Reagent Setup
For these experiments, four solutions are required: (1) a protein solution, (2) a solution containing both protein and either the denaturant, osmolyte or ligand of interest (3), buffer without protein and (4) ligand without protein. The protein concentration range and path lengths of the CD cells depend on the type of experiment. Case 1 and 2 cover the reagent setups for following the interaction of proteins with denaturants or osmolytes in the far UV and near UV to visible regions of the spectrum respectively. Case 3 and 4 cover the reagent setups for following the titration of proteins with ligands in far UV or in the near UV and visible regions, respectively.
Case 1. Measuring the interactions of the protein amide backbone with denaturants, osmolytes or other perturbants to follow changes in secondary structure
Most proteins have strong CD bands arising from the peptide backbone between 220 and 190 nm. Denaturants such as urea and Gn-HCl, however, absorb strongly below 220 nm. For the best signal to noise, when the absorption of the perturbant plus protein is relatively high, i.e. > 1 in a 1 cm cell at 218-222 nm, the protein concentration should be 0.1 to 0.2 mg/ml protein and CD spectra should be obtained in cuvettes with path lengths of 0.05 - 0.2 cm to maintain the total absorbance below one.
Case 2. Measuring the interactions of the aromatic amino acids or prosthetic groups with denaturants or osmolytes to follow changes in tertiary structure
The CD bands arising from aromatic amino acids (between 350 and 250 nm) and prosthetic groups such as flavins and hemes (in the visible region of the spectrum) are 100 fold weaker than the ellipticity of the peptide backbone. However, the absorbance of most denaturants and osmoytes are negligible above 250 nm. Protein concentrations of ∼ 1 to 2 mg/ml are usually required and measurements should be made in 1 cm cuvettes.
Case 3. Determining titration curves of proteins with ligands by following changes in the ellipticity of the amide backbone
Many ligands including substrates, inhibitors, oligomers of DNA or RNA, metals or other proteins have very low absorption bands between 218 to 222 nm, or have absorptions comparable to that of the protein to be titrated. In these cases it is preferable to prepare solutions of 0.01 to 0.02 mg/ml protein and examine the spectral changes in cells with 1 cm path lengths. The use of lower protein concentrations and larger volumes makes it easier to determine binding constants for ligands with high affinities. It is also easier to aliquot precise volumes of the solution containing the titrant and mix the solutions thoroughly when larger volumes are used.
Case 4. Determining titration curves of proteins with ligands by following changes in the aromatic region or induction of extrinsic CD bands upon ligand binding
Since CD bands of the aromatic groups and most bound ligands are weak, studies should be performed using 1 to 2 mg/ml solutions in cells with 1 cm path lengths.
Solution 1A (Case 1)
0.2 - 0.4 ml of a 0.1 to 0.2 mg/ml solution of protein dissolved in a buffer with low absorbance between 260 and 200 nm. The absorption properties of buffers has been described previously4.
Solution 1B (Case 2)
2-4 ml of 1 to 2 mg/ml protein dissolved in a buffer that does not absorb in the near UV or visible region (most buffers).
Solution 1C (Case 3)
2-4 ml of 0.01 to 0.02 mg/ml protein dissolved in a buffer with low absorbance4 between 260 and 200 nm.
Solution 1D (Case 4)
2-4 ml of 1 to 2 mg/ml protein dissolved in a buffer that is transparent in the near UV and visible region.
Solution 2A (Case 1)
0.5 to 1 ml of a stock solution containing the same concentration of protein as solution 1A plus a denaturant such as urea, 8M (Fluka, 51456 (http://www.sigmaAldrich.com) or guanidine-HCL (Gn-HCl), 6M (Sigma G7153 http//www.sigmaaldrich.com), osmolytes such as Trimethylamine N-oxide, 5M (Aldrich 317594 http//www.sigmaaldrich.com), ligands with high absorption in the amide backbone region, or metals, such as calcium or aluminum. These solutions can contain buffering systems to regulate the free concentrations of metals40-42.
Solution 2B (Case 2)
2 to 5 ml of a stock solution containing the same concentration of protein as solution 1B with denaturants, osmolytes, or ligands as described for solution 2A.
Solution 2C (Case 3)
2 to 5 ml of a stock solution containing the same concentration of protein as solution 1C plus a 5 to 10 fold molar excess of ligand (e.g. substrate or inhibitor), 5 to 10 fold excess of a second protein or polynucleotide if the ligand has a high affinity, or high concentrations, ∼ mM, of ligands, if the binding is very weak.
Solution 2D (Case 4)
2 to 5 ml of a stock solution containing the same concentration of protein as solution 1D plus a 5 to 10 fold molar excess of ligand (e.g. substrate or inhibitor).
Solution (3)
Buffer used to prepare solutions 1A, 1B, 1C or 1D
Solution (4)
Ligand at same concentration used to prepare solution 2C or 2D.
Preliminary experiments
Before beginning any titration experiments make sure that the protein to be studied gives a high quality CD spectrum4 and that the spectrum changes upon addition of a denaturant, osmolytes or ligand.
Obtain a background spectrum of water in the appropriate cell. For solution 1A collect the spectrum in a 0.1 cm cell between 260 and 190 nm. For solution, 1C obtain the spectrum of the water blank in a 1 cm cell between 260 and 200 nm. For 1B or 1D collect the spectrum of water in a 1 cm cell between 350 and 250 nm for aromatic groups, or at the wavelength range where the prosthetic group or colored ligand absorbs light.
Obtain the spectrum of the protein without ligand (solutions 1A, 1B, 1C or 1D).
Obtain the spectrum of solution (4) if performing a titration with an asymmetric, optically active ligand, such as a nucleotide or oligonucleotide.
Obtain the spectrum of solution 2A, 2B, 2C or 2D using the same conditions as the spectrum of the protein alone to determine whether the addition of the denaturant or ligand has an effect on the protein structure, or induces the appearance of an extrinsic CD band before starting a titration.
If the ligand has a spectrum, subtract the sum of the CD spectra of the ligand and the free protein from the spectrum of the protein-ligand mixture, to make sure that there is a measurable change upon interaction.
Protocol Timing 2-5 hours
1 Collect the spectrum of water in the CD cell to use as a blank. Use a 0.1 - 0.2 cm cell for solutions 1A and a 1 cm cell for solutions 1B, 1C and 1D.
Troubleshooting.
| Step | Problem | Solution |
|---|---|---|
| 1 | The baseline is not flat. | Run a spectrum without a cell to make sure the baseline with N2 is flat. Clean the cell as described in previously4. |
| 2 | The protein sample has very low ellipticity between 250 and 200 nm, |
Check that the protein concentration is correct as described previously4 |
| 3 | There is no change in ellipticity upon mixing the ligand or titrant with the protein. |
Not all ligands will become optically active or change the conformation of a protein upon binding. In addition, some proteins are resistant to denaturants such as urea. If this is the case, check if the addition of ligand or titrant changes the stability to thermal denaturation and use this method to determine the binding constants or free energy of folding47 |
| The ellipticity changes as a function of time. |
The protein may equilibrate very slowly. Try preparing samples with various concentration of ligand or titrant and incubate overnight. This uses more protein solution that serial additions but may solve the problem. |
|
| 5 | The change in ellipticity does not plateau, when corrected for the ellipticity of ligand, even at very high ligand to protein ratios. |
The concentration of protein in the pure solution and in the solution containing ligand plus protein may not be equal. If one is using Teflon stoppered cells and mixing by inverting the cells, the solution may be leaking. Try redoing the titration at lower concentrations in a cell that is stirred with a magnetic stirring bar. Alternatively, the protein-ligand or protein in the presence of titrant may not be at equilibrium. Try incubating the mixtures for longer periods of time. |
| 6 | The ellipticity of the ligand is not linear function of its concentration. |
The ligand may self associate or may have too high and absorbance. Make sure that the dynode voltage is below 5004. Try titrating samples of a fixed concentration of ligand with increasing concentrations of protein, if the ellipticity of the protein is linear as a function of concentration. |
| 10 | Plots of the free energy of folding are not a linear function of denaturant or osmolyte. |
There may be unfolding intermediates or the samples may not be at equilibrium. Try incubating the samples for a longer period of time before obtaining the spectra. However in some cases the changes are intrinsically non-linear and require more complicated analyses11,12,22 |
| 11 | The ellipticity change saturates at a low ligand to protein ratio, but the data cannot be fit by equation (23) using non-linear least squares curve fitting programs. |
First, make sure that the initial parameters for maximal change, protein concentration and KD are close to what would be expected from the raw data. If changing the initial parameters does not work, the protein may have more than one class of tight binding sites and the binding may be cooperative and require more complicated approaches to describe the binding curves30,37,48. |
2 Wash and dry the cells. If collecting data in a 1 cm cell, add a small magnetic stirring bar to the cell before adding the protein sample.
3 Collect the spectrum of the protein alone, 0.2 ml of solution 1A in a 0.1 cm cell, or 0.4 ml in a 0.2 cm cell or 2 ml of solution 1B, 1C, or 1D in a 1 cm cell.
4 Titrate the protein solution with perturbant.
Option 1. Measuring the interactions of the peptide backbone with denaturants or osmolytes to follow changes in secondary structure
Many 0.1 cm CD cuvettes have a maximum capacity of 0.35 ml and more than one sample must be used to cover the entire desired concentration range of the perturbant. Start with.0.2 ml of solution 1A and add a small aliquot of solution 2A, e.g. 0.01 to 0.05 ml. After the addition, seal the cell tightly with a Teflon stopper and carefully mix the solutions. Then take the spectrum of the mixture. It is suggested to take 2-3 multiple spectra to make sure that the protein is equilibrated with the perturbant and that the spectrum is not changing as a function of time. Save the spectra. Alternatively, set the machine to record data at a single wavelength as a function of time. Collect data for 1 to 2 minutes at 1 second intervals at 260 or 250 nm and save the data and at 222 nm (or other wavelength with high ellipticity) and save the data. Calculate the difference of the average values of the ellipticity at the two wavelengths. (Note that some CD machines have functions to allow one to automatically compute the average value and slope of the data collected as a function of time.) Continue adding aliquots and taking CD measurements until the cell is filled. Then make a fresh sample of a mixture containing 0.2 ml of a mixture of sample 1A and 2A and then add aliquots of 2A to the fresh solution. An example of a scheme for titrating a protein with denaturant is given in Table 1.
Table 1.
Example Scheme for Titrating of a Protein with Guanidine-HCl*
| 1A Tmod1160-359, 10 μM, ml |
2A Tmod1160-359, 10 μM + Gn-HCl, 4.8 M, ml |
Total Volume, ml |
Gn-HCl, M | θ222 nm, mdeg |
[θ]/l000 deg. · cm2/ dmol |
|---|---|---|---|---|---|
| 0.20 | 0.00 | 0.20 | 0.00 | −30.1 | −14.7 |
| 0.20 | 0.05 | 0.25 | 0.96 | −30.0 | −14.6 |
| 0.20 | 0.10 | 0.30 | 1.60 | −27.5 | −13.4 |
| 0.20 | 0.15 | 0.35 | 2.06 | −23.6 | −11.5 |
| 0.10 | 0.10 | 0.20 | 2.40 | −17.6 | −8.6 |
| 0.10 | 0.15 | 0.25 | 2.88 | −10.9 | −5.3 |
| 0.10 | 0.20 | 0.30 | 3.20 | −6.5 | −3.2 |
| 0.10 | 0.25 | 0.35 | 3.43 | −5.4 | −2.6 |
| 0.00 | 0.20 | 0.20 | 4.80 | −4.3 | −2.1 |
In this example, a fragment of tropomodulin 1, an actin and tropomyosin binding protein, (Tmod1160-359), is titrated with guanidine-HCl (Gn-HCl)1. Solution 1A contains Tmod1160-359, 0.24 mg/ml (10 μM), in 100 mM NaCl, 10 mM sodium phosphate, pH 6.5. Solution 2A, contains 0.24 mg/ml Tmod1160-359 in 100 mM NaCl, 10 mM sodium phosphate and 4.8 M Gn-HCl, pH 6.5. The titration is performed in a cuvette with a 0.1 cm path length and a sample volume capacity of 0.35 ml.
Option 2. Measuring the interactions of the aromatic amino acids or prosthetic groups with denaturants or osmolytes to follow changes in tertiary structure
Use a strategy similar to that shown in Option 1. Add 0.1 to 0.5 ml aliquots of sample 2B to 2 ml of solution 2A and mix with a magnetic stirring bar. Take a spectrum or record the ellipticity at two different wavelengths after each addition of sample 2B as described in Option 1. When the total volume equals 3 ml, the mixture of solutions 1B and 2B may be carefully removed from the cuvette, and saved, the cell cleaned and dried and 2 ml of saved solution added back to the cell and the titration continued. Alternatively, a fresh mixture of solution 1B and 2B totaling 2 ml can be prepared and the titration continued.
Option 3. Titrate a protein with a ligand to examine changes in the backbone conformation when the absorption of the ligand + protein at 218-222 nm < 1 in a 1 cm cell
Add small aliquots, 0.01 to 0.05 ml, of solution 2C to solution 2C as described in Option 2 and collect the data after each addition described in Option 1.
Option 4. Titrate a protein with a ligand or denaturant to examine changes in the aromatic region of the spectrum between 320 and 250 nm or the induction of extrinsic ellipticity in the near UV or visible regions of the spectrum
Add small aliquots, 0.01 to 0.05 ml, of solution 4B to solution 4A and measure the spectrum between 350 and 250 nm to detect changes in the aromatic spectrum of the protein or at higher wavelengths to detect the induction of intrinsic CD bands in ligands that absorb in the visible region. Mix the solutions as described in Option 2 and collect data as described in Option 1
5 Continue adding aliquots of solution 2A, B, C or D until there is no change in the spectrum of the backbone, aromatic or prosthetic groups or until the change in ellipticity as a function of the titrant is a linear function of the titrant concentration.
6 If the ligand is optically active, e.g. a substrate, inhibitor, polynucleotide or another protein, repeat the titration by adding solution (4) to pure buffer. The change in ellipticity should be a linear function of the concentration of the ligand.
7 Correct the spectra of the protein-ligand mixture for the contributions of the pure ligand.
8 Save the calculated smoothed corrected data as individual files for each sample.
9 If full spectra were collected at each ligand or perturbant concentration, examine the spectra sets and pick the wavelength where the ellipticity change is the greatest, or the signal to noise the highest and create a file of the ellipticity at the desired wavelength (y) as a function of ligand or titrant (x).
10 If one has determined changes in the backbone folding due to addition of denaturants or osmolytes, analyze the data to determine the free energy of folding. In the case of monomers or dimers the data may be fit directly by nonlinear least squares analysis using equations 8-16. For proteins with more than two subunits it is easier to calculate the free energies of folding at each concentration of titrant using equations 2 - 7 and determine the free energy of folding by plotting the free energy as a function of titrant and extrapolating to zero additions.
11 Analyze data collected as a function of ligand concentration to estimate binding constants using equations 21 and 22, if the concentration of free ligand is known, or if the binding is weak, and equation 23 if the binding is tight and only the total ligand concentration is known.
Expected Results
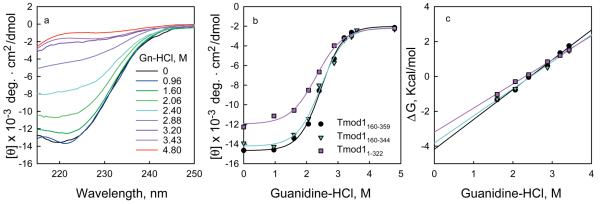
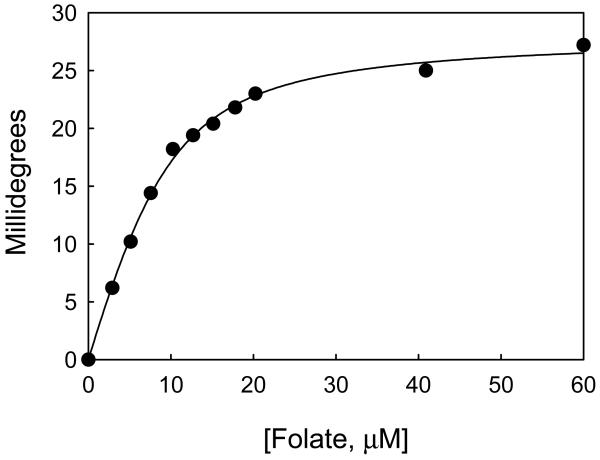
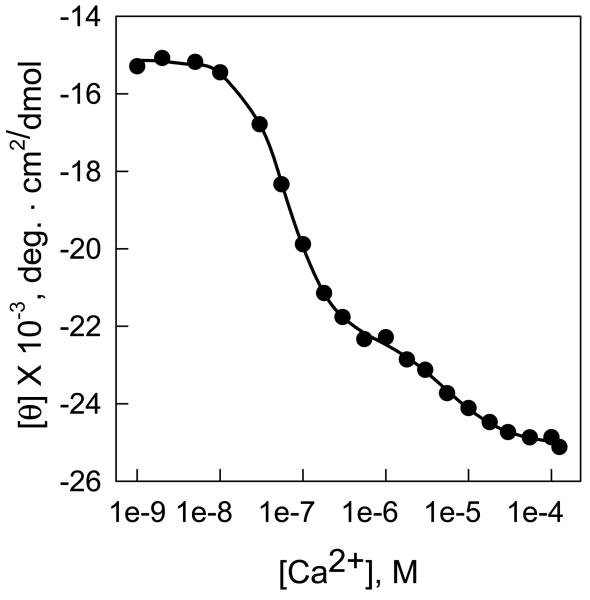
Figures 2-4 illustrates typical results of how CD can be used to determine the free energy of folding of proteins as well as the enzyme-ligand binding constants. Figure 2 shows the unfolding of three monomeric fragments of an actin capping protein, tropomodulin1, as a function of increasing Gn-HCl concentrations. Figure 2a shows how the spectrum of one of the fragments, Tmod1160-359, changes between 260 and 215 nm as a function of Gn-HCl. (The scheme used to collect the data for this fragment is given in Table 1). The high absorbance of guanidine precludes accurate CD measurements below 215 nm. Figure 2b shows the change in ellipticity at 222 nm of all three fragments. The data were fit by equations 8 to 13 using nonlinear least squares analysis21. Figure 2c shows the plots of ΔG versus Gn-HCl. ΔG was calculated using equations 2, 3 and 7. The free energies of folding of the three fragments, calculated by direct fitting of the unfolding curves, and by transforming the data to a plot of the free energy of folding as a function of denaturant concentration are almost identical and are summarized in Table 2. Figure 3 illustrates the titration of a recombinant subunit of troponin, Troponin C, with Ca2+2. Measurements were made in a solution containing a mixture of nitrilotriacetic acid and EGTA, which act as a calcium buffering system. Increasing amounts of a 9.01 mM CaCl2 stock were added to the buffered protein and the pH was maintained by adding an equimolar amount of KOH after each Ca2+ addition. The free Ca2+ concentrations corresponding to the total calcium added were calculated from the binding constants of Ca2+ for nitrilotriacetic acid and EGTA40 using the computational method of Perrin and Sayse41,43,44. The protein has two classes of binding sites, which each bind two molar equivalents of calcium. The data were fit by the sum of two independent Hill equations (equation 21) to determine the binding affinities and the Hill coefficients (a measure of cooperativity) for each site37. 65 ± 8.5% of the ellipticity change was caused by binding to the first class of sites and 35 ± 8% by binding to the second class of sites. The dissociation constants were 0.086 ± 0.007 and 4.1 ± 0.9 μM, respectively, and the Hill coefficients were 2 ± 0.7 and 1.0 ± 0.05, respectively45. Figure 4 illustrates the titration of a protein with a ligand where the binding is tight and only the total ligand concentration is known. In this figure, dihydrofolate reductase is titrated with one of its substrates, folate. When folate binds to the enzyme the ligand binds asymmetrically and large extrinsic CD bands are induced, one with a positive band near 292.5 nm and one with a negative band near 270 nm (ref 3) (Figure 1c). Folate by itself has almost no ellipticity at these concentrations. The change in ellipticity between 292.5 and 270 as a function of ligand was fit assuming their was tight binding38 (equation 23) using the Levenberg-Marquardt algorithm21 to determine the maximal ellipticity change (28 millidegrees), the number of binding sites (0.95) and the dissociation constant of the enzyme-substrate complex (3.1 μM). These values agree with those estimated from linear transformation of the data using the method of Kurganov et al.3,46.
Figure 2. Determining the free energy of folding from changes in CD as a function of denaturant.
a, The mean residue ellipticity of three fragments of tropomodulin 11 as a function of Gn-HCl in 100 mM NaCl, 10 mM sodium phosphate, pH 6.5 at 10 °C. a, (black circles), Tmod1160-359, 0.24 mg/ml; (magenta triangles), residues Tmod1160-344, 0.17 mg/ml; (cyan squares), Tmod11-322, 0.22 mg/ml. The data were fit to equations 9-12 by non-linear least squares analysis. b, The data in panel a were transformed using equations 2, 3 and 5 to give a linear plot of ΔG as a function of denaturant. The free energy of folding equals the value of the y intercept.
Figure 4. Determination of affinity constants and number of binding sites from the induction of extrinsic CD bands upon enzyme-ligand interactions.
When folate binds to Dihydrofolate reductase from E. coli its absorption bands become optically active3. (•) The change of the difference in ellipticity between 292.5and 270.0 nm of dihydrofolate reductase from E. coli as a function of increasing folate concentration. (line) The data fit by equation (23)38 to determine the number of binding sites/mole (0.95), the maximal ellipticity change, 28 millidegrees, and the dissociation constant, 3.1 μM. The enzyme was 9.2 μM in 0.1 N NaCl, pH 7.2, at 27 °C.
Table 2.
Estimates of Free Energy of Folding Calculated from Direct Fits of Unfolding Data and by Linear Extrapolation*
| Free Energy of Folding, Kcal/Mol | ||
|---|---|---|
| Sample | Direct Fit1 | Linear Extrapolation2 |
| Tmod1160-359 | −4.2 ± 0.3 | −4.2 ± 0.1 |
| Tmod1160-344 | −3.8 ± 0.5 | −3.8 ± 0.2 |
| Tmod11-322 | −3.1 ± 0.3 | −3.2 ± 0.1 |
The data in Figure 2b were fit by equations 8-13 using the Levenberg-Marquardt 21 algorithm implemented in SigmaPlot (Systat Software, Point Richmond, CA).
The data in Figure 2c were fit to the line y=mx +b, where y is the free energy at each concentration of Gn-HCl, x is the concentration of Gn-HCl, m is the slope and b, the y intercept equals the free energy in the absence of denaturant. The data were fit using the Levenberg-Marquardt algorithm21. In both cases the estimated errors in the free energies are the standard errors of the parameters estimated from the curve fitting (one determination for each curve).
Figure 3. Determination of affinity constants from changes in the intrinsic CD of the polypeptide backbone as a function of increasing ligand concentration.
0.4 ml of chicken muscle Troponin C (TnC), 0.1 mg/ml, in 100 mM KCl, 50 mM Tris-HCl, pH 7.5, 0.9 mM EGTA, 0.9 mM nitriloacetic acid, pH 7.5 at 25 °C, in a 0.2 ml cuvette was titrated with Ca2+.
Supplementary Material
Acknowledgements
The research was supported by a NIH grant, GM-36326 to NJG and Dr. Sarah E. Hitchcock-DeGregori and by the Circular Dichroism Facility at Robert Wood Johnson Medical School (UMDNJ).
Footnotes
SUPPLEMENTAL MATERIAL
Two files with equations for determining the free energy of folding from chemical perturbation studies and for estimating binding constants for use with curve fitting programs are in the files Unfolding.doc and Binding.doc respectively. The equations are in SigmaPlot (Systat Software, Inc. Point Richmond, CA) format, but can easily be modified for use with other graphics programs.
REFERENCES
- 1.Fowler VM, Greenfield NJ, Moyer J. Tropomodulin contains two actin filament pointed end-capping domains. J. Biol. Chem. 2003;278:40000–9. doi: 10.1074/jbc.M306895200. [DOI] [PubMed] [Google Scholar]
- 2.Smith L, Greenfield NJ, Hitchcock-DeGregori SE. The effects of deletion of the amino-terminal helix on troponin C function and stability. J. Biol. Chem. 1994;269:9857–63. [PubMed] [Google Scholar]
- 3.Greenfield NJ, Williams MN, Poe M, Hoogsteen K. Circular dichroism studies of dihydrofolate reductase from a methotrexate-resistant strain of Escherichia coli. Biochemistry. 1972;11:4706–11. doi: 10.1021/bi00775a011. [DOI] [PubMed] [Google Scholar]
- 4.Greenfield NJ. Using circular dichroism spectra to estimate protein secondary structure. Nature Protocols. 2006;1:2876–90. doi: 10.1038/nprot.2006.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schellman JA. Macromolecular Binding. Biopolymers. 1975;14:999–1018. [Google Scholar]
- 6.Schellman JA. The effect of binding on the melting temperature of biopolymers. Biopolymers. 1976;15:999–1000. [Google Scholar]
- 7.Pace CN, McGrath T. Substrate stabilization of lysozyme to thermal and guanidine hydrochloride denaturation. J. Biol. Chem. 1980;255:3862–5. [PubMed] [Google Scholar]
- 8.Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1. Unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 9.Scholtz JM, et al. Calorimetric determination of the enthalpy change for the alpha-helix to coil transition of an alanine peptide in water [published erratum appears in Proc Natl Acad Sci U S A 1991 Aug 1;88(15):6898] Proc. Natl. Acad. Sci. U.S.A. 1991;88:2854–8. doi: 10.1073/pnas.88.7.2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Santoro MM, Liu Y, Khan SM, Hou LX, Bolen DW. Increased thermal stability of proteins in the presence of naturally occurring osmolytes. Biochemistry. 1992;31:5278–83. doi: 10.1021/bi00138a006. [DOI] [PubMed] [Google Scholar]
- 11.Santoro MM, Bolen DW. A test of the linear extrapolation of unfolding free energy changes over an extended denaturant concentration range. Biochemistry. 1992;31:4901–7. doi: 10.1021/bi00135a022. [DOI] [PubMed] [Google Scholar]
- 12.Yao M, Bolen DW. How valid are denaturant-induced unfolding free energy measurements? Level of conformance to common assumptions over an extended range of ribonuclease A stability. Biochemistry. 1995;34:3771–81. doi: 10.1021/bi00011a035. [DOI] [PubMed] [Google Scholar]
- 13.Wu P, Bolen DW. Osmolyte-induced protein folding free energy changes. Proteins. 2006;63:290–6. doi: 10.1002/prot.20868. [DOI] [PubMed] [Google Scholar]
- 14.Greenfield NJ. Enzyme ligand complexes: spectroscopic studies. CRC Crit. Rev. Biochem. 1975;3:71–110. doi: 10.3109/10409237509102553. [DOI] [PubMed] [Google Scholar]
- 15.Lacey JC, Jr., Pruitt KM. Drug-biomolecule interactions: interactions of mononucleotides and polybasic amino acids. J. Pharm. Sci. 1975;64:473–7. doi: 10.1002/jps.2600640335. [DOI] [PubMed] [Google Scholar]
- 16.Kelly SM, Price NC. The use of circular dichroism in the investigation of protein structure and function. Curr. Protein. Pept. Sci. 2000;1:349–84. doi: 10.2174/1389203003381315. [DOI] [PubMed] [Google Scholar]
- 17.Allenmark S. Induced circular dichroism by chiral molecular interaction. Chirality. 2003;15:409–22. doi: 10.1002/chir.10220. [DOI] [PubMed] [Google Scholar]
- 18.Greenfield NJ. Circular dichroism analysis for protein-protein interactions. Methods Mol. Biol. 2004;261:55–78. doi: 10.1385/1-59259-762-9:055. [DOI] [PubMed] [Google Scholar]
- 19.Zsila F, Bikadi Z, Fitos I, Simonyi M. Probing protein binding sites by circular dichroism spectroscopy. Curr. Drug Discov. Technol. 2004;1:133–53. doi: 10.2174/1570163043335135. [DOI] [PubMed] [Google Scholar]
- 20.Bolen DW, Santoro MM. Unfolding free energy changes determined by the linear extrapolation method. 2. Incorporation of delta G degrees N-U values in a thermodynamic cycle. Biochemistry. 1988;27:8069–74. doi: 10.1021/bi00421a015. [DOI] [PubMed] [Google Scholar]
- 21.Marquardt DW. An algorithm for the estimation of non-linear parameters. J. Soc. Indust. and Appl. Math. 1963;11:431–441. [Google Scholar]
- 22.Ibarra-Molero B, Sanchez-Ruiz JM. A model-independent, nonlinear extrapolation procedure for the characterization of protein folding energetics from solvent- denaturation data. Biochemistry. 1996;35:14689–702. doi: 10.1021/bi961836a. [DOI] [PubMed] [Google Scholar]
- 23.Gupta R, Yadav S, Ahmad F. Protein stability: urea-induced versus guanidine-induced unfolding of metmyoglobin. Biochemistry. 1996;35:11925–30. doi: 10.1021/bi961079g. [DOI] [PubMed] [Google Scholar]
- 24.Ferreon AC, Bolen DW. Thermodynamics of denaturant-induced unfolding of a protein that exhibits variable two-state denaturation. Biochemistry. 2004;43:13357–69. doi: 10.1021/bi048666j. [DOI] [PubMed] [Google Scholar]
- 25.Somero GN. Environmental adaptation of proteins: strategies for the conservation of critical functional and structural traits. Comp. Biochem. Physiol. A. 1983;76:621–33. doi: 10.1016/0300-9629(83)90464-4. [DOI] [PubMed] [Google Scholar]
- 26.Tanford C. Physical chemistry of macromolecules. John Wiley; New York: 1961. [Google Scholar]
- 27.Deranleau DA. Theory of the Measurement of Weak Molecular Complexes. II. Consequences of Multiple Equilibria. J. Am. Chem. Soc. 1969;91:4044–4049. [Google Scholar]
- 28.Deranleau DA. Theory of the measurement of weak molecular complexes. I. General considerations. J.Am. Chem. Soc. 1969;91:4044–4049. [Google Scholar]
- 29.Deranleau DA. Theory of weak molecular complexes. III. Observation equations for multiple equilibria and an application to protein charge-transfer titrations. J. Am. Chem. Soc. 1975;97:1218–24. doi: 10.1021/ja00838a042. [DOI] [PubMed] [Google Scholar]
- 30.McGhee JD, von Hippel PH. Theoretical aspects of DNA protein interactions: cooperative and non cooperative binding of large ligands to a one dimensional homogeneous lattice. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- 31.Siligardi G, Hussain R. Biomolecules interactions and competitions by non-immobilised ligand interaction assay by circular dichroism. Enantiomer. 1998;3:77–87. [PubMed] [Google Scholar]
- 32.Tetin SY, Hazlett TL. Optical spectroscopy in studies of antibody-hapten interactions. Methods. 2000;20:341–61. doi: 10.1006/meth.1999.0927. [DOI] [PubMed] [Google Scholar]
- 33.Wallace BA, Janes RW. Circular dichroism and synchrotron radiation circular dichroism spectroscopy: tools for drug discovery. Biochem. Soc. Trans. 2003;31:631–3. doi: 10.1042/bst0310631. [DOI] [PubMed] [Google Scholar]
- 34.Greenfield NJ. Analysis of circular dichroism data. Methods Enzymol. 2004;383:282–317. doi: 10.1016/S0076-6879(04)83012-X. [DOI] [PubMed] [Google Scholar]
- 35.Tan WB, Bhambhani A, Duff MR, Rodger A, Kumar CV. Spectroscopic identification of binding modes of anthracene probes and DNA sequence recognition. Photochem. Photobiol. 2006;82:20–30. doi: 10.1562/2005-05-24-RA-539. [DOI] [PubMed] [Google Scholar]
- 36.Scatchard G. The attractions of proteins for small molecules and ions. Ann. N.Y. Acad. Sci. 1949;51:660–72. [Google Scholar]
- 37.Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. (Lond.) 1910;40:iv–vii. [Google Scholar]
- 38.Engel G. Estimation of binding parameters of enzyme-ligand complex from fluorometric data by a curve fitting procedure: seryl-tRNA synthetase-tRNA Ser omplex. Anal. Biochem. 1974;61:184–91. doi: 10.1016/0003-2697(74)90344-3. [DOI] [PubMed] [Google Scholar]
- 39.Pacifici GM, Viani A. Methods of determining plasma and tissue binding of drugs. Pharmacokinetic consequences. Clin. Pharmacokinet. 1992;23:449–68. doi: 10.2165/00003088-199223060-00005. [DOI] [PubMed] [Google Scholar]
- 40.Sillen LG, Martel AE. Stability Constants of Metal Complexes. 2nd ed. The Chemical Society; Burlington House, London: 1964. [Google Scholar]
- 41.Perrin DD, Sayce JG. Computer calculation of equilibrium concentrations in mixtures of metal ions and complexing species. Talanta. 1967;14:833–842. doi: 10.1016/0039-9140(67)80105-x. [DOI] [PubMed] [Google Scholar]
- 42.Leavis PC, Kraft EL. Calcium binding to cardiac troponin C. Arch. Biochem. Biophys. 1978;186:411–5. doi: 10.1016/0003-9861(78)90453-8. [DOI] [PubMed] [Google Scholar]
- 43.Leavis PC, Rosenfeld SS, Gergely J, Grabarek Z, Drabikowski W. Proteolytic fragments of troponin C. Localization of high and low affinity Ca2+ binding sites and interactions with troponin I and troponin T. J. Biol. Chem. 1978;253:5452–9. [PubMed] [Google Scholar]
- 44.Dobrowolski Z, Xu GQ, Hitchcock-DeGregori SE. Modified calcium-dependent regulatory function of troponin C central helix mutants. J. Biol. Chem. 1991;266:5703–10. [PubMed] [Google Scholar]
- 45.Smith L, Greenfield NJ, Hitchcock-DeGregori SE. Mutations in the N- and D-helices of the N-domain of troponin C affect the C-domain and regulatory function. Biophys. J. 1999;76:400–8. doi: 10.1016/S0006-3495(99)77206-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kurganov BI, Sugrobova NP, Yakovlev VA. Estimation of dissociation constant of enzyme-ligand complex from fluorometric data by “difference” method. FEBS Lett. 1972;19:308–310. doi: 10.1016/0014-5793(72)80067-x. [DOI] [PubMed] [Google Scholar]
- 47.Greenfield NJ. Using circular dichroism, collected as a function of temperature, to determine the thermodynamics of protein folding and binding interactions. Nature Protocols. 2006;1:2527–35. doi: 10.1038/nprot.2006.204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ray A, Maiti M, Nandy A. SCATPLOT: a computer program for determination of binding parameters of non-linear non-cooperative ligand-substrate interactions. Comput. Biol. Med. 1996;26:497–503. doi: 10.1016/s0010-4825(96)00034-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.