Characterisation of the passive permeability barrier of nuclear pore complexes

Abstract

Nuclear pore complexes (NPCs) restrict uncontrolled nucleocytoplasmic fluxes of inert macromolecules but permit facilitated translocation of nuclear transport receptors and their cargo complexes. We probed the passive barrier of NPCs and observed sieve-like properties with a dominating mesh or channel radius of 2.6 nm, which is narrower than proposed earlier. A small fraction of diffusion channels has a wider opening, explaining the very slow passage of larger molecules. The observed dominant passive diameter approximates the distance of adjacent hydrophobic clusters of FG repeats, supporting the model that the barrier is made of FG repeat domains cross-linked with a spacing of an FG repeat unit length. Wheat germ agglutinin and the dominant-negative importin β^45-462 fragment were previously regarded as selective inhibitors of facilitated NPC passage. We now observed that they do not distinguish between the passive and the facilitated mode. Instead, their inhibitory effect correlates with the size of the NPC-passing molecule. They have little effect on small species, inhibit the passage of green fluorescent protein-sized objects >10-fold and virtually block the translocation of larger ones. This suggests that passive and facilitated NPC passage proceed through one and the same permeability barrier.

Introduction

Nuclear pore complexes (NPCs) are embedded into the nuclear envelope and allow passive as well as active exchange between the nuclear and the cytoplasmic compartments (for review see Mattaj and Englmeier, 1998; Görlich and Kutay, 1999; Adam, 2001; Tran and Wente, 2006; D'Angelo and Hetzer, 2008). Active or facilitated nuclear transport requires very specific interactions with the NPC. They are typically mediated by importin β-type nuclear transport receptors (NTRs), which bind cargo molecules, shuttle rapidly between both compartments, and cooperate with the RanGTPase system to achieve a directional transport even against gradients of chemical activity. They accelerate NPC passage of cargoes as small as green fluorescent protein (GFP) (≈27 kDa) or as large as ribosomal subunits (≈2.5 MDa). Passive NPC passage, in contrast, appears rapid only for small molecules and is already clearly delayed for GFP-sized proteins (Ribbeck and Görlich, 2001). Objects that can traverse NPCs only in the passive mode will in the following be referred to as ‘inert'.

It was proposed earlier that NPCs accommodate not only a large central channel for active receptor-mediated transport, but also eight peripheral ones for passive exchange of ions, metabolites and small non-nuclear proteins (Hinshaw et al, 1992; see also Naim et al, 2006). However, this ‘separate channel hypothesis' is in conflict with other models of NPC function (Feldherr et al, 1984; Feldherr and Akin, 1997; Keminer and Peters, 1999) and in particular with those assuming that FG repeat domains form a common barrier for passive and facilitated exchange (Macara, 2001; Ribbeck and Görlich, 2001; Rout and Aitchison, 2001). Resolving this issue is crucial for the understanding of NPC function.

If NPCs were equipped with just a single barrier, then one could use inert objects to probe the properties of that universal barrier. One would also predict that NTR·cargo complexes not only compete with other receptor-mediated nuclear transport pathways, but also affect passive transport. In the case of separate channels, however, one should expect the two different channel systems to have very different permeability properties and very different affinities for NTRs. Also, it should be possible to generate reagents that block the central ‘active' channel, and leave the passive ones unaffected, and vice versa.

The suggestion of separate channels was based on electron micrographs from detergent-extracted negatively stained NPCs that showed not only a central channel wide enough for transporting ribosomes, but also eight peripheral ones with a radius of ≈5 nm that were thought to constitute the passive diffusion channels (Hinshaw et al, 1992). Reports on wheat germ agglutinin (WGA), a potent inhibitor of receptor-mediated NPC passage, were seemingly consistent with the separate channel hypothesis.

WGA is a tetravalent lectin (Nagata and Burger, 1974) that targets N-acetyl glucosamine (GlcNAc) moieties in several FG repeat nucleoporins of higher eukaryotes, in particular of the central Nup62 complex (Davis and Blobel, 1986; Finlay et al, 1987; Hanover et al, 1987). It strongly inhibits signal- and receptor-mediated nucleocytoplasmic transport (Finlay et al, 1987; Newmeyer and Forbes, 1988). Although its effects on passive NPC passage have not yet been assessed comprehensively and conclusively, it is generally believed that WGA leaves passive NPC passage unaffected (Finlay et al, 1987; Yoneda et al, 1987). Inhibition by this reagent was even widely used as a criterion to distinguish between passive and active nuclear transport of a given macromolecule.

Another inhibitor of NPC passage crucial for this study is the dominant-negative Importin β^45-462 fragment (Kutay et al, 1997). It is deficient in binding to RanGTP and imposes a general block on receptor-mediated NPC passage. Its inhibitory effect was so far explained by its resistance to RanGTP-mediated release from its high affinity binding sites at nuclear pores. Here, we elucidated further details of its inhibitory mechanism.

As the dominant-negative Impβ^45-462 fragment is derived from a bona fide NTR, it should inhibit transport only along the path of facilitated passage. Its effects on passive diffusion have not been thoroughly tested. However, Impβ^45-462 should inhibit passive NPC passage only if inert material diffused through the same channel system as importin β complexes.

In this study, we used a size series of 11 inert permeation probes with masses between 0.6 and 40 kDa to explore the permeability barrier of NPCs. The data obtained suggest a sieve-like barrier with a heterogeneous mesh size and a prevalent mesh radius of ≈2.6 nm. This is far more narrow than the earlier assumed 4.5 nm (Paine et al, 1975; Keminer and Peters, 1999). However, the new number now plausibly explains why NPC passage of GFP-sized proteins with a Stokes radius of 2.4 nm is already strongly delayed. We discuss why earlier studies arrived at larger numbers. The extremely slow, but still detectable, NPC passage of larger inert proteins suggests a small percentage of wider passive diffusion paths. We further observed that passive NPC passage is not independent of facilitated fluxes. Instead, the presence of NTRs slowed down the passive NPC passage of inert macromolecules. Similar, but much stronger, effects were observed with the established inhibitors of facilitated NPC passage, WGA and Impβ^45-462. This strongly argues in favour of a common channel system for facilitated and passive NPC passage.

Results

Strategy to determine the widths of the passive diffusion channels of NPCs

To correlate the properties of the passive diffusion barrier with structures within NPCs, we wanted to determine the apparent widths of the passive diffusion channels. The experimental system of choice for such a quest are permeabilised cells, which have leaky plasma membranes but intact nuclei, that is, fluorescent probes can be easily introduced into these cells and their uptake into nuclei followed by fluorescence microscopy (Adam et al, 1990; Ribbeck and Görlich, 2001). During the permeabilisation, the cells are depleted of their soluble contents (including shuttling NTRs), and this allows testing the effects of exogenously added NTRs on facilitated or passive NPC passage.

The passive (i.e. non-receptor mediated) influx of a given species into nuclei follows first-order kinetics and can therefore be described by:

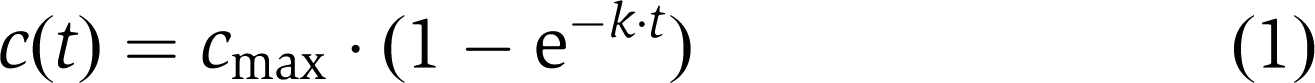The rate constant k depends on several parameters, namely on the diffusion constant D, the nuclear volume V, the Stokes radius r of the diffusion species, the radius R of the channels, the length L of the channels, the number of NPCs per nucleus, and the number of channels per NPC. Assuming perfect mixing inside the nuclear and cytoplasmic compartments and further assuming that no binding of the diffusing species within either nucleus or cytoplasm occurs, k can be expressed as follows:

The term (1−(r/R))² describes steric hindrance of entry into the channel and extends the validity of the equation from the diffusion of point-like objects to objects with the Stokes radius r.

With η being the viscosity of the medium within the channel, k_B being the Boltzmann constant and T the absolute temperature, the diffusion constant D can be expressed as the Stokes–Einstein relation:

Substitution and simplification of equation (1) for the non-trivial case (r<R) then yields:

We wanted to elucidate R. However, equation (4) contains additional unknown constants, such as the number of channels per pore, the length of the passive channels and the viscosity inside the channels, which are unknown and cannot be easily derived. In addition, the volume of the nuclei is not constant, but varies considerably between individual cells, as does the number of NPCs per nucleus.

The straightforward solution to these problems is not to consider individual rate constants, but to compare the rate constants of a series of molecules (1,…i,…n) to that of a reference molecule. Dividing the rate constant of species i by the rate constant of the reference molecules eliminates all unknown parameters from equation (4), except for the channel diameter R:

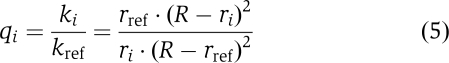Determining the quotient q_i for a series of molecules with different Stokes radii should therefore provide a robust estimate of R, independent of uncertain guesses, for example, about channel length and pore numbers.

Our passive probes had to meet a number of criteria: First, we only used proteins with a single, compactly folded domain and nearly spherical shape. Second, we verified by bead-binding assays that none of the passive probes interacted with NTRs. And third, we excluded candidates that showed an NTR-like behaviour and bound at physiological conditions to FG nucleoporin repeats or to the FG repeat mimic Phenyl-Sepharose (Ribbeck and Görlich, 2002). Ten proteins passed all these tests, namely human insulin, bovine aprotinin, bovine ubiquitin, human profilin 1, a z-domain from Staphylococcus aureus Protein A, Escherichia coli thioredoxin, bovine α-lactalbumin, the enhanced GFP, the phosphate-binding protein from E. coli (PBP), and the maltose-binding protein from E. coli (MBP).

To detect these proteins within permeabilised cells, we exploited either their intrinsic fluorescence (GFP) or we labelled them at a ≈1:1 stoichiometry with Alexa488. Alexa568-labelled thioredoxin (13.9 kDa) was included in all measurements as the above-mentioned inert reference molecule. The series was complemented by an Alexa488-labelled 11 amino acids long peptide and fluorescein-labelled cysteine. These are certainly more probes than needed to estimate the apparent radius of a diffusion channel. However, we not only wanted to obtain such an estimate, but also test whether the diffusion model from equation (5) plausibly describes the process of passive NPC passage and account for the possibility of heterogeneity in the widths of the diffusion channels.

Probing the passive barrier of NPCs in permeabilised HeLa cells

To follow the influx of the fluorescent probes into nuclei of permeabilised HeLa cells (strain CCL2), we used time-resolved confocal laser scanning microscopy. Figure 1 shows representative examples of such a time series, whereas Figure 2 displays the corresponding quantifications, in which the rates of nuclear accumulation had been fitted to single exponential curves (see equation (1)). As expected, the equilibration time of the nuclear fluorescence depended on the size of the diffusion substrate. MBP as the largest diffusion marker did not equilibrate within the time range of the experiments, whereas the 8.5 kDa protein ubiquitin equilibrated with a half time of ≈20 s.

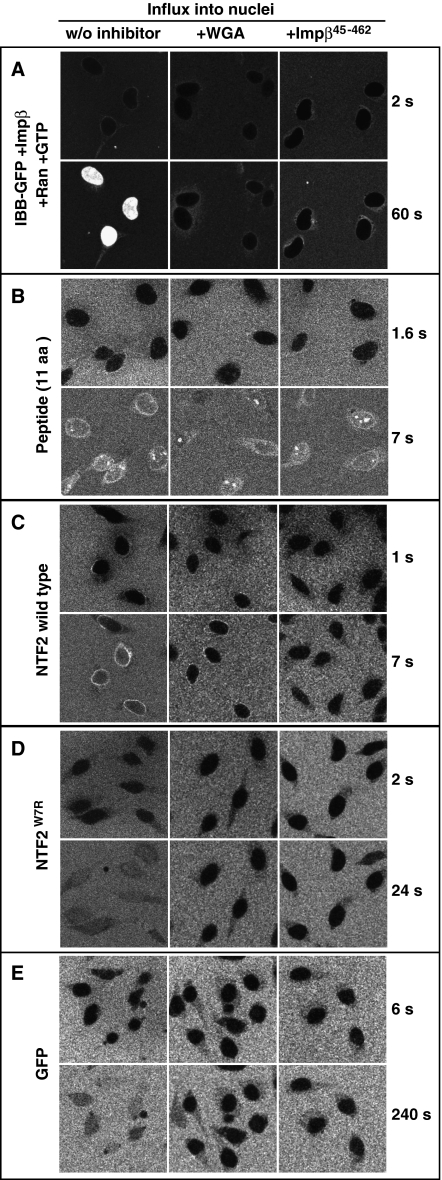
Figure 1.

Time course of diffusion for various inert substrates into nuclei. Alexa488-labelled ubiquitin, lactalbumin or MBP as well as GFP were each pre-mixed with Alexa568-labelled thioredoxin. Entry of the substrate pairs into nuclei of permeabilised cells was followed by confocal laser scanning microscopy in separate fluorescence channels. Four time points each are shown. For quantitation see Figure 2. Post-experimental controls show nuclear exclusion of Alexa647-MBP and active import of IBB-GFP (see main text as well as Materials and methods).

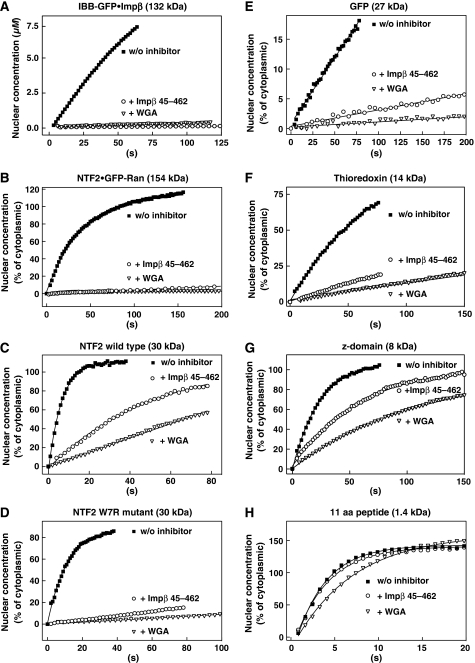
Figure 2.

Quantitation of passive entry into nuclei. Graphs show evaluations of the time series from Figure 1. Nuclear substrate concentrations are plotted versus time. Each graph shows the indicated diffusion substrate (⧫) and thioredoxin as a control (□). Data points were fitted to c(t)=a+k·t for MBP and GFP, and to c(t)=c_max·(1−e^−k·t) for all other proteins. Averages of analysed cells are shown. Nuclear entry rates depend on the size of these inert substrates. Although nuclear entry of ubiquitin, lactalbumin and thioredoxin occurred rapidly, influx of GFP (27 kDa) was slow and that of MBP (40 kDa) was very slow.

To exclude any damaged nuclei, we performed two post-experimental controls for each measurement. First, after each passive diffusion experiment we verified that a large diffusion marker (Alexa647-labelled MBP) remained excluded from the nuclei. And second, we tested whether the nuclei were still able to actively accumulate an IBB-GFP fusion in a Ran-, GTP-, and importin β-dependent manner (see Figure 1; Görlich et al, 1996a; Weis et al, 1996). Nuclei that failed either test were excluded from further analysis.

A sieve-like passive permeability barrier with a dominant mesh radius of 2.6 nm

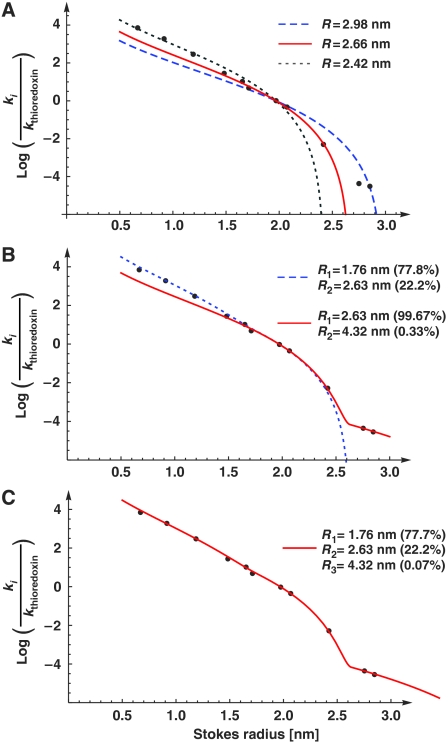
As explained above, the most informative numbers for estimating the radius of the passive channels are the ratios of the nuclear entry rate constants k_i to that of our internal reference, thioredoxin k_ref. We determined these ratios on the level of individual nuclei, averaged them for a given passive permeation probe (see Table I), and fitted the data points [Stokes radius r_i; q_i=(k_i/k_ref)] to equation (5) to obtain an estimate for the apparent channel radius. As seen from Figure 3A, we obtained a best fitting value of R=2.66 nm (red curve).

Table 1.

Molecules used to probe the passive diffusion channels of NPCs

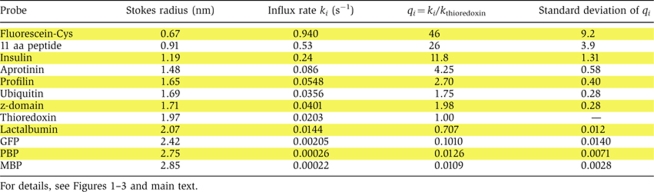Figure 3.

Estimation of passive pore radii from passage rates. Graph shows a plot of Stokes radii (r_i) versus the natural logarithm of k_i/k_thioredoxin, the ratios of nuclear entry rates. The following probes were included: a fluorescein maleimide-cysteine adduct (0.67 nm Stokes radius), a labelled 11 aa peptide (0.9 nm), insulin (1.19 nm), aprotinin (1.48 nm), profilin 1 (1.65 nm), a z-domain from Protein A (1.71 nm), thioredoxin (1.97 nm), lactalbumin (2.07 nm), GFP (2.42 nm), the phosphate-binding protein PBP (2.75 nm) and the maltose-binding protein MBP (2.85 nm). The data were parameter-fitted to different models for passive passage through NPCs (see equations (5) and (7)). A faithful model, consistent with all data points, could only be obtained with the assumption of heterogeneity in channel width. A smaller residuum indicates a better fit of the data (see below). For details see main text and Materials and methods. (A) ‘Uniformly sized channel model', as detailed in equation (5). The best fit was obtained for R=2.66 nm with a residuum of 3.58 (red curve). This fit, however, does not explain the very slow NPC passage of PBP and MBP. The panel also shows a simulated blue dashed curve with R=2.98 nm (residuum=5.87), which predicts best the flux ratio for MBP and thioredoxin. The gray dotted curve was obtained for R=2.42 (residuum=4.46); it predicts the flux ratios for small probes best. (B) ‘Two radii model' (with n=2 according to equation (7), Materials and methods). The radius combination of 1.76 and 2.63 nm gave a near-perfect fit for small and medium-sized probes (blue dotted line, residuum=2.75), whereas the combination 2.63 and 4.32 nm gave an excellent fit for medium sized and larger probes (red line, best global fit, residuum=1.51). (C) ‘Three radii model' (with n=3, equation (7)), which gave an excellent fit for small, medium sized and large probes (residuum=0.39).

Heterogeneity in the widths of passive diffusion channels

The predicted passive channel radius of 2.66 nm is smaller than the Stokes radii of our largest test molecules PBP (2.75 nm) and MBP (2.85 nm). Thus, this uniformly sized channel model cannot explain the very slow, but still detectable translocation of these molecules into the nucleus. In fact, this discrepancy points towards a heterogeneity of channel widths also predicted by current models of NPC function (see Discussion below). Consistent with that, modelling the permeability barrier as a mixture of two differently sized channels improved the fit considerably and yielded as best fit parameters a predominant channel radius of 2.63 nm (99.7% of the channels) and 0.33% channels with a radius of 4.32 nm (see red curve in Figure 3B). The introduction of the second channel width improved the residuum of the fit from 3.58 to 1.51 (compare red curves of panels 3A and 3B).

However, the fluxes predicted by the two-radii model were too slow for very small permeation probes such as insulin, small peptides or the fluorescein-cysteine conjugate (by factors of 2–3), in turn pointing towards additional channels with a smaller radius than 2.63 nm. Indeed, the simplest numerical model of passive fluxes through NPCs, which gave a satisfying fit for the entire range of permeation probes, included three distinct channel radii, namely, ≈78% of channels with a radius of 1.76 nm, ≈22% of channels with a radius of 2.63 nm and 0.07% of 4.32 nm channels. The best global fit with a residuum 0.39 is shown in Figure 3C. Note that the radii of the two larger channel types, 2.63 and 4.32 nm, as well as their mixing ratio of ≈300:1 is virtually identical to the best two-channel model. This reflects the fact that the small 1.76 nm channels do not contribute to fluxes of thioredoxin, lactalbumin, GFP, PBP or MBP.

The quality of the three-radii fit is very sensitive to even small changes in the radius of the medium-sized channel (the 2.63 nm channel). In contrast, deviations in the radii of the smaller and the larger channels are tolerated much better and can reasonably well be compensated for by changes in the mixing ratios (as long as the larger channels are >3.5 nm and the smaller ones <1.9 nm in radius). We therefore argue that the channels of 2.63 nm radius dominate the selectivity of the passive permeability barrier of NPCs. It is important to emphasise that the three-radii model is merely the simplest model consistent with the data set. In reality, we would expect a continuous distribution of channel widths, with a peak around R=2.63 nm. However, for the sake of simplicity, we will stick in the following to the three-radii model.

How many of these passive channels (at the estimated mixing ratio) might a single NPC contain? For a first estimation, we assume that the passive channel system completely fills the large central channel of the NPCs (see below) and that the central channel has a radius of 25 nm. The cross-sectional area of the central channel would then leave space for up to ≈120 channels with a radius of 1.76 nm and ≈35 channels of 2.63 nm radius, whereas at any given time only one out of nine NPCs would possess a 4.32 nm channel. Note, however, that these numbers represent upper limits, because this very simple estimate neglects the (unknown) cross-sectional areas of the passive channel ‘walls'.

Interestingly, an independent estimate gave a similar order of magnitude. With a nuclear entry rate constant of 0.02 s⁻¹ for thioredoxin, a Stokes radius of 1.97 nm, a 50 nm long path through the permeability barrier, 3000 NPCs per nucleus, a nuclear volume of 1200 μm³, and an intra-channel viscosity three-fold higher than that of water, equation (4) suggests that a single NPC might contain ≈80 channels at 1.76 nm radius, 24 channels at 2.63 nm radius and 0.08 channels at 4.32 nm radius. This would be consistent with a central channel entirely filled with a densely packed subchannel system as described by the FG hydrogel model (Ribbeck and Görlich, 2001; Frey and Görlich, 2007).

Inhibitors of facilitated NPC passage also inhibit passive passage of GFP-sized inert objects

Next, we addressed the question in how far NPC ligands, which target the ‘facilitated path' through NPCs, also affect NPC passage of inert molecules. For that, we first confirmed that WGA and the dominant-negative importin β^45-462 fragment inhibited importin β-mediated import of IBB-GFP into nuclei of permeabilised cells by a factor of at least 200 (Figures 4A and 5A; Table II).

Figure 4.

Effects of WGA and Impβ^45-462 on facilitated and passive NPC passage. Permeabilised cells were either left untreated (left row) or pre-incubated with 0.1 mg/ml wheat germ agglutinin (middle row) or with 3 μM of the dominant-negative importin β^45-462 fragment (right row). Thereafter, indicated influx experiments were performed. Import of IBB-GFP was performed in the presence of importin β, Ran and a GTP-regenerating system. All other import mixtures comprised only the fluorescent proteins. WGA and Impβ^45-462 inhibited both, facilitated NPC passage (of IBB-GFP·importin β or NTF2) and passive nuclear entry of e.g. GFP. The inhibitory effects were strongest towards the large (132 kDa) IBB-GFP·importin β complex, strong towards GFP-sized objects (NTF2, NTF2^W7R, GFP), and non-significant towards the smallest substrate, an 11 amino acid long peptide. For quantitation, see Figure 5.

Figure 5.

Quantitative analysis of the effects imposed by WGA and Impβ^45-462. Graphs compare the entry kinetics of a given substrate into untreated nuclei (▪) with entry into nuclei pre-incubated with either WGA (▿) or Impβ^45-462 (○). See also Figure 4 and Table II.

Table 2.

Quantitation of the inhibition of NPC-passage by the lectin wheat germ agglutinin (WGA) and the dominant-negative importin β^45–462 fragment

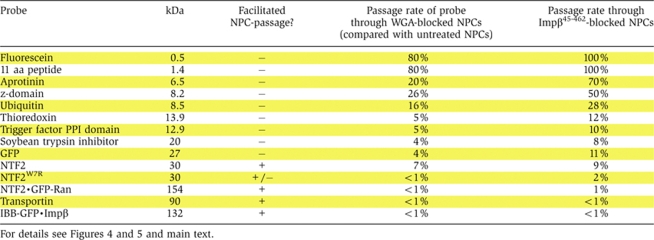We then compared the inhibitors' effects on NPC passage of two similarly sized molecules, namely GFP and NTF2. GFP is a typical inert molecule with a slow but still well measurable NPC passage rate. The NTF2 homodimer is slightly larger. It functions as the nuclear import receptor of Ran, is therefore capable of facilitated translocation and crosses NPCs ≈100-times faster than GFP (Ribbeck et al, 1998; Smith et al, 1998; Ribbeck and Görlich, 2001). If the inhibitors targeted facilitated translocation only, then they should only inhibit influx of NTF2, but not of GFP. The data, however, clearly show that neither WGA nor Impβ^45-462 could discriminate between the species. Instead, WGA inhibited the influx of NTF2 and GFP by similar factors, namely 15-fold and 25-fold, respectively (see Figures 4C, 4E, 5C and 5E as well as Tables II and III). Likewise, Impβ^45-462 diminished the nuclear entry rate of NTF2 11-fold and that of GFP nine-fold. This strongly argues against the view that inert material and NTRs cross NPCs through separate channel systems. Instead, the data suggest that both species take a similar path through the NPC, traverse the same permeability barrier and solely differ in the way they interact with the barrier.

Table 3.

Absolute numbers for nuclear influx rates of GFP, NTF2 and NTF2^W7R through untreated NPCs, WGA-blocked NPCs and Impβ^45-462-blocked NPCs

The inhibitory effects of WGA and Impβ^45-462 increases with the size of the translocating species

The observation that WGA and Impβ^45-462 inhibit NPC passage of NTF2 more weakly (11–15-fold) than that of Impβ·IBB-GFP (>200-fold) could point to a peculiarity of the NTF2-dependent import pathway. However, the fact that the inhibitors completely blocked NPC passage of the 154 kDa NTF2·GFP–RanGDP complex (Figure 5B; Table II) suggests a more probable explanation, namely that the magnitude of inhibition depends primarily on the size of the substrate of facilitated translocation and not on the transport pathway used.

We then tested the effects of the inhibitors on passive NPC passage of a size series of inert substrates (Figure 5; Table II). The effect of WGA on very small substrates, such as fluorescein was small (Table II), but steadily increased with substrate size, reaching a 20-fold inhibition for the 14 kDa protein thioredoxin (Figure 5F; Table II) and a 25-fold inhibition for GFP (Figure 5E; Table II), whereas nucleocytoplasmic flux of larger inert molecules, such as MBP, was suppressed to values below the limit of detection. The inhibitory effect of Impβ^45-462 showed a similar size dependence, but was generally somewhat weaker than WGA (Figure 5; Table II).

Multimerisation apparently contributes to the strong inhibitory potential of Impβ^45-462

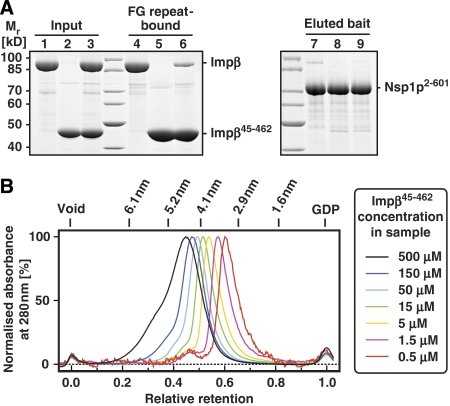
Importin β·cargo complexes typically arrest at NPCs until RanGTP dissociates the complex and releases the cargo into the nucleus (Moore and Blobel, 1993; Görlich et al, 1996b). RanGTP also promotes the release of importin β from high affinity binding sites at the NPC (Kutay et al, 1997; Shah et al, 1998; Ben-Efraim and Gerace, 2001; Walther et al, 2003). Thus, the failure of Impβ^45-462 to bind RanGTP is certainly crucial for its inhibitory potential (Kutay et al, 1997). However, this is only part of the explanation. Even in the absence of RanGTP, Impβ^45-462 binds more avidly to FG repeats (Figure 6A) and diminishes influx of transportin into nuclei ≈50-times more strongly than full-length importin β (Supplementary Figure S1). Indeed, the gel filtration experiments from Figure 6B reveals another property of the mutant that is relevant for these effects, namely that Impβ^45-462 forms dynamic oligomers. At low sample concentrations, a peak around 3.3 nm Stokes radius was observed, which corresponds to a dimer or monomer. At high concentrations, however, a peak around 4.6 nm and a shoulder around 5.5 nm were evident, roughly corresponding to tetramers or up to octamers. As Impβ^45-462 strongly accumulates at NPCs (Kutay et al, 1997), it probably oligomerises there. Its exceptionally strong binding to NPCs can therefore at least in part be explained by an avidity effect caused by this oligomerisation.

Figure 6.

Impβ^45-462 multimerises and binds FG repeats more strongly than full-length importin β. (A) Nickel-Sepharose beads coated with the His-tagged FG/FxFG repeat domain of Nsp1p were incubated with an excess of untagged Impβ (lanes 1, 4, 7), untagged Impβ^45-452 (lanes 2, 5, 8) or a mixture of both proteins at physiological salt conditions. Bound NTRs and bait proteins were sequentially eluted and analysed by SDS–PAGE and Coomassie staining. Loaded material corresponds to 0.75% of input material or 3% of the eluted material. In comparison to the single incubations, binding of Impβ was drastically diminished in the presence of Impβ^45-452, whereas binding of the Impβ mutant itself was virtually unaffected. This indicates that Impβ^45-452 has an increased affinity for FG repeat domains. (B) Impβ^45-452 was mixed with plasmid DNA and GDP as markers for void volume and total volume, respectively, diluted to the indicated concentrations and subjected to analytical gel filtration. Absorbance profiles acquired at 280 nm were normalised to the maximal optical density. Note that the observed peak positions and shapes greatly depend on the protein concentration of the applied sample. Higher order oligomeric forms are observed at higher protein concentrations. The gradual decrease of apparent molecular weight with higher dilutions indicates dynamic association/dissociation equilibria between multiple association states.

Even NPCs blocked by WGA or Impβ^45-462 are selective and show the phenomenon of facilitated passage

According to two criteria, NTF2 traverses even WGA-blocked NPCs in a facilitated manner. First, also in the presence of WGA, its passage is ≈200-times faster than that of GFP (Table III). Second, the passage of NTF2 through WGA-treated NPCs is strongly impaired by the W7R mutation in NTF2 (Table III). This mutation was earlier shown to disable the major FG repeat binding site in NTF2 and to abolish the capacity of NTF2 to stimulate nuclear influx of RanGDP through untreated NPCs (Bayliss et al, 1999). We can thus conclude that WGA does not generally block facilitated translocation; it only imposes a very strict upper size limit for the translocating species. Similar conclusions apply to the dominant-negative Impβ^45-462 fragment (see Table III and Discussion below).

Facilitated transport load also affects the passive permeability properties of NPCs

The above-described inhibition experiments strongly suggest common channels for passive and facilitated NPC passage. Nevertheless, one could argue that WGA and the Impβ^45-462 fragment generate a very special situation inside nuclear pores. We therefore tested whether loading NPCs with wild-type transport receptors and functional NTR·cargo complexes would affect the passive permeation properties of NPCs. As seen from Table IV, pre-incubation of nuclei with 1 μM transportin already diminished nuclear influx of thioredoxin to 60% of the original rate, and, together with 1 μM importin β, to 25%. As permeabilised cells still contain significant amounts of endogenous NPC-bound transport receptors, the magnitude of the effect is probably still underestimated.

Table 4.

Effect of functional NTRs and importin β fragments on passive NPC-passage

We recently reconstituted the permeability barrier of NPCs as a saturated FG hydrogel that not only suppresses the passive influx of inert material, but also allows facilitated entry of NTRs and their cargo complexes (Frey and Görlich, 2007). In the accompanying study (Frey and Görlich, 2009), we describe that NTRs tighten such FG hydrogel against the passive influx of GFP-sized objects. Thus, NTRs enhance the performance of the barrier in both systems, in the in vitro assembled hydrogel as well as in authentic NPCs from intact cell nuclei.

Discussion

A common channel system for passive and facilitated NPC passage

In this study, we have characterised the passive permeation properties of NPCs and tested the model that NPCs use separate channels for passive and facilitated exchange. Our data do not support this model. Instead, four arguments speak in favour of a common barrier that controls passive as well as facilitated translocation.

First, a strict ‘separate channel scenario' should assume a central channel of ultimate selectivity, that is, a channel that allows only receptor-mediated passage, but completely blocks inert material. It is hard to envision what a proteinaceous barrier could possibly look like that is absolutely tight against passive passage of even ions and at the same time allows facilitated passage of ribosomes. It is even harder to envision, how selective pressure could have enforced the evolution of such a super-tight structure, if its tightness must be bypassed by additional passive diffusion channels.

The second argument concerns the basis of the original suggestion, namely 3D reconstructed electron micrographs of negatively stained, detergent-extracted NPCs. Besides the large central channel, these showed eight peripheral ones with a radius of ≈5 nm, which were assumed to conduct inert material (Hinshaw et al, 1992). Later reconstructions of membrane-embedded NPCs, however, revealed that these channels are no continuous connections between cytoplasm and nucleus (Akey and Radermacher, 1993; Stoffler et al, 2003). Instead, they terminate on the lipid bilayer and therefore cannot contribute to nucleocytoplasmic exchange.

Third, recent attempts to reconstitute the permeability barrier as an FG hydrogel have shown that such gels not only exclude large inert molecules and allow facilitated entry of NTR·cargo complexes, but also permit entry of small inert proteins. The influx of GFP, for example, occurs at a rate similar to that found in authentic NPCs (Frey and Görlich, 2007). Such FG hydrogel can therefore explain both, the facilitated and the passive permeability properties of NPCs.

Finally, if separate channels were used, then passive passage should be insensitive to ligands or inhibitors that target the active channel system. In contrast to the earlier belief, however, we now found that WGA or the Impβ^45-462 fragment not only block facilitated NPC passage, but also inhibit the passive one. This strongly suggests that facilitated passage and the bulk of passive transport occur through the same channel system and lead through the same barrier. Besides this main barrier, additional channels might exist within the rigid framework of NPCs. However, to be consistent with our data, these channels should be rather narrow and contribute only little to the transport of macromolecules. Their conductance for ions and metabolites should also be small compared with the enormous capacity expected for a main selectivity barrier based on FG repeats.

Why were the inhibitory effects of WGA on passive NPC passage overlooked so far? One reason is that the effects of e.g. WGA on very small substrates are weak and easy to miss without a quantitative time-course experiment. Likewise, given that these inhibitors block the passage of a typical NTR·cargo complex (of at least 130 kDa in mass) much more strongly than NPC passage of small inert molecules (⩽30 kDa), it was probably tempting to attribute these different sensitivities to the differences in the mode of passage. In fact, however, it is the difference in size that matters. When comparing passive and facilitated substrates of similar size, similar levels of inhibition are observed.

Naim et al (2006) concluded that passive and facilitated transport through NPCs are largely uncoupled and use separate routes. These conclusions were based on the observation that microinjection of a BSA-NLS conjugate into HeLa cells had little effect on passive NPC passage. NPCs of living HeLa cells must, however, already sustain a facilitated mass flow of >14 MDa per pore and second just to guarantee the biosynthetic transport of RNAs, histones, ribosomal and hnRNP proteins (Ribbeck and Görlich, 2001). As the microinjected cargo increased this number by no more than 4%, no significant impact on passive NPC passage could be expected. The authors also observed that nuclear influx of a very small 9.5 kDa dextrane was not significantly diminished by the NTR transportin. This is consistent with our observation that NPC ligands, such as WGA or Impβ^45-462 clearly delay passive NPC passage of GFP (27 kDa), but have only negligible effects on small inert objects.

The dominating radius of the NPCs' passive diffusion channels is smaller than previously thought

From the kinetics of NPC passage for a wide range of inert molecules, we could estimate that NPCs behave towards inert material like a sieve with a dominating mesh radius of ≈2.63 nm. Earlier studies suggested a radius of 4.5 nm for the passive diffusion channels (Paine et al, 1975; Keminer and Peters, 1999). This difference needs to be explained.

Perhaps the most misleading earlier assumption was that of a uniform radius of all passive diffusion channels (Paine et al, 1975). Given that, for example, BSA with a radius of 3.5 nm can—extremely slowly though—cross the nuclear envelope (Bonner, 1978), this assumption suggested uniform pores with a radius larger than 3.5 nm. We would argue, however, that only a very small fraction of the passive diffusion channels is that wide.

Another potentially misleading factor is the use of non-spherical probes. We observed that a deviation from a spherical form results in a faster NPC passage than expected from the mass of the diffusing species. One example for such a non-spherical probe is a GFP–GFP fusion, which behaves non-spherically during gel filtration, has a mass of ≈54 kDa and yet crosses NPCs 3.5-times faster than the smaller 43 kDa maltose-binding protein (data not shown). A probable explanation for this effect is that elongated molecules might enter channels in a preferred orientation and then appear narrower than a spherical one of the same mass. Most previous probings of the passive permeability barrier were performed with dextranes, which are not rigid spheres either, but essentially linear polymers that also show an anomalous behaviour during gel filtration. Therefore, they also pass NPCs faster than expected from their mass.

Another straightforward explanation for previous over-estimations of the passive channel radii is that these earlier studies (Paine et al, 1975) introduced an inappropriate correction factor into the equation that describes diffusion through narrow channels. This correction factor originated from the description of a very different process, namely the gravity-driven movement of a sphere inside a liquid-filled tube that is closed at its ends and whose wall is impermeable to the liquid (Ladenburg, 1907). Under such conditions, the movement of the sphere causes a counter flow of the liquid, which builds up pressure in front of the sphere, increases friction between sphere and liquid and thereby hinders the sphere's movement. These conditions, however, do not apply to NPCs, because the relevant channels through NPCs are open-ended (otherwise no nucleocytoplasmic transport would occur), and because they are composed of hydrated protein structures that are per se permeable to the solvent.

Our new results are in prefect agreement with common experience. For example, that NPC passage of GFP-sized objects (radius of 2.4 nm) is already significantly delayed and BSA (3.5 nm) is essentially excluded from passage.

The need to retain the RanGTP gradient might have dictated the passive exclusion limit of NPCs

It is quite an interesting question as to why NPCs show the characteristic passive limit of ≈2.6 nm Stokes radius. We would assume this number to be a compromise between two key requirements. Active transport relies on the nucleocytoplasmic RanGTP gradient and therefore the barrier must prevent the dissipation of this gradient. Such dissipation would not only result in a waste of metabolic energy, but also in a frequent abortive disassembly of importin·cargo complexes in the cytoplasm. The system would only be effective if Ran alone crossed NPCs more slowly than RanGTP·NTR complexes. Ran has approximately the same Stokes radius as GFP (≈2.4 nm). Thus, the passive efflux of RanGTP from nuclei should be well restricted, whereas NTF2 ensures rapid, facilitated influx of RanGDP into nuclei. If the passive limit were significantly higher, then it would be impossible for the permeability barrier to suppress the dissipation of the RanGTP gradient. A significantly lower limit could, however, mean that NTRs might experience problems in translocating larger cargoes. As the size of Ran is well conserved, one should expect similar passive exclusion limits in different species, despite the fact that the presumably barrier-forming modules, FG repeats, show little sequence conservation (see below).

Correlation between passive NPC permeability and the FG hydrogel model of NPC function

Of all the current models of NPC function, our data correlate best with the selective phase or FG hydrogel model, which assumes a sieve-like permeability barrier created by reversible cross-links between individual repeat units of FG repeat domains (Ribbeck and Görlich, 2001; Frey and Görlich, 2007). The mesh size of the sieve determines the passive exclusion limit, that is, inert molecules larger than the meshes are excluded from passage. NTRs bind the FG motifs, thereby transiently opening meshes and catalysing their own entry into the gel. The diameter of the meshes should roughly correspond to the unit length of FG repeats, which is in the order of 3–6 nm. This nicely fits the observation that NPCs behave like a sieve with meshes of ≈3.5–5 nm in diameter (1.76 and 2.6 nm in radius, see Figure 3). The FG hydrogel model, therefore, predicts the correct order of magnitude for the passive channel width. The hydrogel model also predicts the observed heterogeneity in the channel diameters, simply because the lengths of individual repeats are heterogeneous and because meshes can combinatorially form from two, three or even more repeat units. The larger (4.3 nm) radii might also originate from spontaneous opening of inter-repeat contacts or from a small fraction of NPCs that have been damaged or whose assembly has not yet been completed.

Finally, we could not only estimate the size distribution of the passive channels, but we also concluded that ≈100 parallel channels fill the central channel of the NPC. This density is suspiciously similar to the mesh-density predicted by the FG hydrogel model. We, therefore, argue that the passive diffusion channels are no straight cylinders, but describe allowed paths through the porous meshwork that constitutes the FG hydrogel.

Mechanism of inhibition by WGA and Impβ^45-462

The strong inhibitory effect of WGA on NPC passage, in particular of larger objects, begs the question of the mechanism of inhibition. WGA possesses four independent binding sites for O-GlcNAc. It has only a low affinity for monomeric O-GlcNAc, but binds oligomeric O-GlcNAc derivatives with high avidity. Examples for such high avidity WGA ligands are chitin, the nucleoporin p62, which carries multiple mono-O-GlcNAc modifications on serine and threonine residues within its non-globular (FG/FN repeat) region, or indeed entire NPCs. We propose that the multivalent binding mode of WGA is crucial for its impact on NPCs. WGA probably cross-links GlcNAc-containing FG repeats, thereby introducing additional mesh contacts and consequently creating smaller meshes with a lower exclusion limit. A numerical evaluation of the inhibition data (analogous to Figure 3) indeed revealed that WGA decreased the apparent dominant radius of the passive NPC diffusion channels from ≈2.6 to ≈1.6 nm, with only ≈1% of the original 2.6 nm channels persisting. This would explain why very small objects (such as fluorescein or peptides) can still rapidly pass WGA-blocked NPCs and why the passage of GFP-sized or even larger objects is severely hindered. These additional WGA-generated meshes cannot be resolved by transport receptors, explaining why large NTR·cargo complexes fail to pass through. Such a WGA-clotted permeability barrier is most likely a composite structure with numerous inter-FG repeat contacts, which makes the barrier very tight towards GFP, but still permits a facilitated passage of the very small transport receptor NTF2 (Tables II and III).

Impβ^45-462 is a potent inhibitor of nucleocytoplasmic transport. It is derived from a bona fide transport receptor and binds FG repeats. However, the observations that Impβ^45-462-clotted NPCs still allowed facilitated passage of NTF2 and that this facilitated passage required an intact FG-binding site of NTF2 (Tables II and III) suggests that the mere occupation of binding sites for NTRs is not sufficient to fully explain the inhibition. Impβ^45-462 can be expressed in high yield and solubility in E. coli (Kutay et al, 1997), which is actually surprising in the light of the facts that (1) importin β is built from a single domain that spans the entire sequence of 876 residues (Cingolani et al, 1999) and (2) that a domain represents the fundamental folding unit, which, in the case of the Impβ^45-462 fragment, is obviously fragmented. Importin β is built from HEAT-repeats (Cingolani et al, 1999; Vetter et al, 1999), and the Impβ^45-462 fragment apparently complements its missing parts by forming the oligomers that we observed in the gel filtration experiments. The oligomeric form can simultaneously contact a greater number of FG motifs and therefore binds FG repeats or entire NPCs more avidly than a monomeric derivative. And like WGA, the oligomerisation of the mutant introduces additional non-covalent cross-links into the FG hydrogel, which decrease the mesh size and pose additional obstacles that cannot be dissolved by functional NTRs.

In Supplementary Figure S1, we pentamerised importin β with the help of a pentameric cargo. We observed that transportin flux through NPCs was diminished by this pentamer ≈10-times more strongly than by a monomeric species at identical importin β concentration. Nevertheless, Impβ^45-462 is still a more potent inhibitor than the rigid importin β pentamer (Supplementary Figure S1). We suggest that the dynamic association equilibrium between Impβ^45-462 molecules is crucial for this effect. As an initial monomer, Impβ^45-462 can fill the available space inside the permeability barrier probably more efficiently than the rigid 600 kDa cargo·importin β pentamer. Subsequent multimerisation inside the FG repeat meshwork will greatly stabilise the FG·Impβ^45-462 interactions. In addition, it is possible that the fragmentation of the NTR favours a conformation with an increased affinity of individual binding pockets for FG motifs.

Correlation of NPC function with properties of FG repeat hydrogels

NTRs suppress passive NPC passage probably by a similar mechanism as the NPC inhibitors WGA and Impβ^45-462, though in a fully reversible manner. They bind FG repeats multivalently, thereby increasing the degree of non-covalent cross-linking and consequently decreasing the mesh size. In the accompanying paper (Frey and Görlich, 2009), we show that in vitro reconstituted FxFG and GLFG hydrogels not only reproduce normal passive barrier function and facilitated entry of NTRs, but also that NTRs and the dominant-negative Impβ^45-462 fragment tighten these gels considerably against passive influx. This perfect correlation strongly suggests that the hydrogel model indeed has the potential to faithfully describe the permeability barrier of NPCs.

Materials and methods

Fluorescent probes and nuclear transport factors

Aprotinin, ubiquitin, α-lactalbumin and WGA were purchased from Sigma-Aldrich. Profilin, PBP, MBP, IBB-GFP, NTF2, transportin and importin β constructs and IBB-nucleoplasmin^1-149 core protein were expressed and purified as described (Görlich et al, 1994; Kutay et al, 1997; Ribbeck and Görlich, 2001).

To obtain Impβ^45-462 for competition assays (Figure 6), His₁₄-TEV-Impβ^45-462 was expressed in E. coli and purified on Nickel-Sepharose. The untagged protein was obtained after cleavage with TEV-protease followed by two passages over Nickel-Sepharose.

IBB-core and importin β were mixed at a monomer ratio of 1:2 and the IBB-core·importin β complex was purified through gel filtration (Superdex 200, Amersham Biosciences). Other proteins were expressed in E. coli from the following vectors: z-domain of protein A from pQE-60-z, a derivative of pQE60 (Qiagen), thioredoxin as a fusion protein with a C-terminal His- and S-tag from pET32a (Novagen), GFP from a pQE80 (Qiagen) derivative providing a N-terminal His and zz tag, His₁₀-GFP-Ran from pQE80. Proteins were purified on Ni-NTA-agarose followed by gel filtration on Superdex 75 or 200 (Amersham Bioscience). The His- and zz-tags of GFP and the S-tag of thioredoxin were removed by TEV protease or Thrombin treatment, respectively. The PPI domain of Trigger factor was a kind gift of Dr Bernd Bukau. The 11 amino acid peptide was chemically synthesised and had the sequence NH₂-CQARRQHTRKK-COOH.

All proteins except for thioredoxin were labelled with Alexa488 (Molecular Probes) using either its maleimide form or the succinimidyl ester. Thioredoxin represented a control protein in the diffusion assays and was therefore labelled with another fluorophore, namely Alexa568 maleimide (Molecular Probes) allowing detection in another channel. MBP used as an internal control for nuclear integrity was labelled with Alexa647 maleimide (Molecular Probes). Labelling with the maleimide form of the fluorophore was performed in Tris/HCl buffer pH 7.5 on ice, whereas Hepes/KOH buffer pH 7.5 was used for the succinimidyl ester.

Nuclear import assays and quantifications

HeLa cells (European Cell Culture collection, strain CCL2, ECACC code: 93021013) were grown on coverslips to about 30–50% confluence, washed in cold buffer A (20 mM HEPES-KOH pH 7.5, 120 mM potassium acetate, 5 mM magnesium acetate, 250 mM Sucrose), permeabilised for 2.5–3 min in buffer A supplemented with 60 μg/ml digitonin, washed five times in buffer A and used immediately. Focal plane adjustment and reaction start were performed as described (Ribbeck and Görlich, 2002). Each diffusion reaction consisted of the following protein mixture: protein of choice labelled with Alexa488, Thioredoxin-Alexa568 and MBP-Alexa647. Recordings were made directly on the non-fixed samples using time-lapse confocal laser scanning microscopy as described (Ribbeck and Görlich, 2002), the difference being that three separate channels were used for fluorescence detection.

After completion of the diffusion experiment, an import reaction with 0.5 μM IBB-GFP·importin β complex, Ran and an energy mix (Ribbeck and Görlich, 2002) was started by directly adding the import mixture onto the coverslip. After 2 min, a single scan was recorded with reduced photomultiplier sensitivity.

For inhibition experiments, permeabilised cells were pre-incubated with WGA (Sigma, 0.1 mg/ml in buffer A) or Impβ^45-462 (3 μM in buffer A) for 5 min.

Quantification of the nuclear signal over time was essentially done as described (Ribbeck and Görlich, 2002) with the following modifications: the nuclear signal was evaluated with the quantification module of the Leica TCS SP2 software package. Fitting of data points to linear functions or single exponential curves was performed with GraphPad^® Prism.

Table I shows the standard deviations of the flux ratios q_i between individual experiments, which was larger than any of the corresponding ‘intra-experiment' standard deviations between individual cells of an individual measurement. For each probe, 3–9 independent experiments with 2–10 cells per experiment and a total of 21–43 cells were performed. The WGA and Impβ^45-462 inhibition data include 2–7 independent measurements with a total of 9–43 cells for each probe and each inhibitor. WGA or Impβ^45-462 treated nuclei showed less variability than untreated nuclei. The deviation in the ‘inhibition factors' is therefore dominated by the variability of untreated nuclei. Quantifications in Figures 2 and 5 are averages over all (undamaged) cells in the respective experiments. Tables and Figure 3 show averages of all relevant experiments.

Parameter fit to single radius models of passive NPC channels

Optimisation was based on the Stokes radii of the specified diffusion probes (r₁,…r_i,…r_n) and the ratios of their nuclear entry rates to the entry rate of thioredoxin q_i=(k_i/k_thioredoxin). The simplest model with a homogenous channel radius R is given by equation (5). The FindMinimum function of Mathematica 6.0.3.0 was used to minimise the deviation of predicted flux ratios from experimental data. The relative error to be minimised is given as a function of R by:

Parameter fit to models with heterogeneous channel radii

In the diffusion models with heterogeneous channel sizes, the total flux was considered a linear combination of fluxes through n differently sized channels. The simulated flux ratio is then given by:

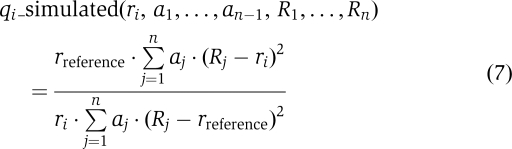The residuum to be minimised was computed analogously to equation (6). As attempts of a global fit for the 2n−1 unknown parameters with the FindMinimum function typically ended in local minima, we first generated a complete set of reasonable channel radii (0.67–5 nm at 0.1 nm resolution) and subsequently computed the optimal mixing ratio of channels (given by a₁ … a_n with Σⁿ_j=1 a_j=1) for each channel combination using the FindMinimum function. In subsequent rounds, the resolution was refined to <0.01 nm.

More sophisticated numerical evaluation procedures, which also considered that the concentrations of the diffusing species close to the channels are not identical to the bulk concentration in the respective compartments (imperfect mixing) and which weighted the experimental data according to their standard deviation, yielded virtually identical best fits in the two and three radii models (not shown).

Determination of Stokes radii

Stokes radii of permeation probes were estimated by gel filtration on an analytical Superdex 200 column, calibrated with the markers plasmid DNA (to determine the void volume) and GDP (to determine the total column volume), aprotinin (r=1.48 nm), myoglobin (2.04 nm), chymotrypsinogen (2.22 nm), GFP (2.4 nm), ovalbumin (2.83 nm) and BSA (3.41). The Stokes radii of the marker proteins were determined by analytical ultracentrifugation (performed at NANOLYTICS GmbH, Dallgow, Germany).

Assay for oligomerisation of Impβ^45-462

Impβ^45-452 in buffer AD (130 mM NaCl, 20 mM Tris–HCl pH 7.5, 2 mM MgCl₂, 0.2 mM EDTA, 5 mM DTT) was mixed with plasmid DNA and GDP as markers for void volume (V₀) and total volume (V_tot), respectively, and diluted to the indicated concentrations. A measure of 400 μl of each dilution was analysed on a Superdex 200 10/30 column (GE Healthcare). Absorbance profiles at 280 nm were normalised to the maximum optical density. Relative retention (R_r) values were determined from the absolute retention volumes (V_abs) according to: R_r=(V_abs−V₀)/(V_tot−V₀). Ferritin (r=6.1 nm), Catalase (5.2 nm), dsRed (4.1 nm), MBP (2.85 nm), mCherry (2.4 nm) and Cytochrome C (1.6 nm) were used to calibrate the column.

Competitive binding of Impβ^45-462 and wild-type importin β to FG repeats

A measure of 20 μl Nickel-Sepharose beads coated with 100 μg of His₁₀-tagged FG/FxFG repeat domain of Nsp1p (Nsp1p^2-601) were incubated with 200 μg of untagged full-length Impβ, 200 μg of Impβ^45-452 or a mixture of 200 μg Impβ and 200 μg Impβ^45-452 in buffer AD. After extensive washing, bound NTRs were eluted with 50 mM Tris/HCl pH 8.5, 130 mM NaCl, 5% SDS, 5 mM DTT followed by a second elution with SDS sample buffer containing 300 mM imidazole to recover the baits. Aliquots corresponding to 0.75% of input material or 3% of the eluted material were analysed by SDS–PAGE and Coomassie stained. Control reactions confirmed that background binding to the matrix was negligible and that the amount of NTRs used exceeded the binding capacity of the coated matrix by a factor of at least 1.5 (not shown).

Supplementary Material

Supplementary Figure S1

Review Process File