Evolution of Stochastic Switching Rates in Asymmetric Fitness Landscapes

Abstract

Uncertain environments pose a tremendous challenge to populations: The selective pressures imposed by the environment can change so rapidly that adaptation by mutation alone would be too slow. One solution to this problem is given by the phenomenon of stochastic phenotype switching, which causes genetically uniform populations to be phenotypically heterogenous. Stochastic phenotype switching has been observed in numerous microbial species and is generally assumed to be an adaptive bet-hedging strategy to anticipate future environmental change. We use an explicit population genetic model to investigate the evolutionary dynamics of phenotypic switching rates. We find that whether or not stochastic switching is an adaptive strategy is highly contingent upon the fitness landscape given by the changing environment. Unless selection is very strong, asymmetric fitness landscapes—where the cost of being maladapted is not identical in all environments—strongly select against stochastic switching. We further observe a threshold phenomenon that causes switching rates to be either relatively high or completely absent, but rarely intermediate. Our finding that marginal changes in selection pressures can cause fundamentally different evolutionary outcomes is important in a wide range of fields concerned with microbial bet hedging.

EVOLUTIONARY adaptation is the process of phenotypic change across generations due to which organisms are more likely to survive and reproduce in their environments. In the standard population genetic framework, the underlying mechanism of adaptation is genetic change caused by random mutations or recombination. In the past few decades, epigenetic change has been described as an additional mechanism to induce phenotypic change without modification of the genotype. Phenotypic change mediated by epigenetic change can be inherited across generations and can lead to phenotypic heterogeneity among genetically identical individuals. While the exact molecular mechanisms underlying epigenetic change are not yet fully understood, the phenomenon has been described in a variety of species, from unicellular organisms such as Saccharomyces cerevisiae, Escherichia coli, or Bacillus subtilis to plants and animals (Rakyan et al. 2002; Henderson and Jacobsen 2007).

An intriguing example of such a process is stochastic switching, whereby individual cells randomly switch among a number of different inheritable phenotypes. Phenotypic variation (often referred to as phenotypic noise) in clonal populations caused by stochastic switching is generally understood to be a bet-hedging strategy in uncertain environments (Stumpf et al. 2002; Thattai and van Oudenaarden 2004; Kussell and Leibler 2005): In the absence of a reliable sensing mechanism, it might be beneficial to spread the risk of being maladapted in future environments among phenotypically variable offspring, each of whom stands a chance of being well adapted to a future environment. Bet hedging is a general phenomenon thought to be responsible for phenotypic variability at all levels of the tree of life, ranging from stochastic switches in unicellular organisms to variable seed morphologies in desert plants that must survive recurrent droughts (Evans and Dennehy 2005). Like every risk-diversifying strategy, however, bet-hedging comes at a cost, generated by the production of potentially maladapted phenotypes. Under which circumstances the benefits outweigh the costs of stochastic switching is a question tackled by both experimental (Acar et al. 2008) and theoretical studies (Leigh 1970; Ishii et al. 1989; Lachmann and Jablonka 1996; Thattai and van Oudenaarden 2004; Kussell and Leibler 2005).

Stochastic switches often rely on feedback loops in genetic networks. Stochasticity in gene expression due to internal fluctuations in mRNA transcription or protein translation can be sufficient to cause transition between two or more different regulatory states, resulting in bi- or multistability (Smits et al. 2006). For example, the galactose-utilization network in S. cerevisiae consists of three feedback loops that allow for bistability of two distinct expression states that reflect past galactose exposure (Acar et al. 2005). The soil bacterium B. subtilis relies on a positive feedback loop to generate bistability between competence and noncompetence states, where the bacterium can incorporate exogenous DNA into its genome when in the competence state (Maamar et al. 2007). More recently, multistability in gene expression in E. coli has been described as an example of an epigenetic switch that does not rely on feedback loops, but instead is based on methylation (Lim and van Oudenaarden 2007). While there may be many different mechanisms underlying stochastic switching, they are relevant to this study only insofar as they produce switching rates that are inherited and malleable and thus subject to natural selection. If the rate at which the switching occurs is an evolvable trait, understanding the ecological and genetic parameters that determine the evolutionarily stable phenotypic switching rate is important to understanding the general phenomenon of bet hedging. Theoretical studies have shown that the evolutionarily stable switching rate is expected to evolve to be in tune with the rate of environmental change (Leigh 1970; Ishii et al. 1989; Lachmann and Jablonka 1996). Experimental data have indeed suggested that cells may tune interphenotype switching rates to the frequency of environmental changes (Acar et al. 2008). Furthermore, evidence that phenotypic variation can be selected for has been provided recently (Freed et al. 2008).

We address the evolution of stochastic switching rates using an explicit population genetic model with a modifier gene that determines the rate of switching to explore the conditions under which stochastic switching is adaptive. Our results indicate that switching rates will reflect the rate of environmental change only under very limited conditions. In particular, we find that unless selection is very strong, the maintenance of nonzero rates of stochastic switching depends crucially on the symmetry of the fitness landscape: If the fitness cost of being maladapted varies among environments, stochastic switching cannot be maintained. Our findings suggest that pure bet hedging as a strategy in an uncertain world is constrained by very stringent fitness symmetry conditions.

METHODS

To address the evolution of phenotypic switching rates we use a population genetic model that tracks the frequency of haploid genotypes over time in an infinitely large population. Each genotype consists of a major locus under selection and a modifier locus. The allele at the major locus determines the phenotype and thus the fitness of the genotype in a given environment (see below). The allele at the modifier locus determines the rate at which the allele at the major locus switches to an alternative allele; the modifier alleles are otherwise selectively neutral. There are two possible alleles at the major locus (0 and 1) and two possible alleles at the modifier locus (m and M). Thus, there are four possible genotypes: 0m, 0M, 1m, and 1M.

The phenotype of an individual is given solely by the allele at the selection locus, and hence there are only two phenotypes in the model, p₀ and p₁. The fitness of these phenotypes depends on the environment in which they find themselves. At any given time, the environment is in one of two possible states, e₀ and e₁. Phenotypes p₀ and p₁ have maximal fitness (i.e., 1) in environments e₀ and e₁, respectively. The fitness of phenotype p₀ in environment e₁ is 1 − s₀, and the fitness of phenotype p₁ in environment e₀ is 1 − s₁.

The population is initiated with random allele frequencies at the major locus. At the modifier locus, only the wild-type allele m is present initially. The initial environment is randomly chosen to be either e₀ or e₁. After initiation, the following processes occur at each time step: clonal reproduction, selection, and mutation (i.e., switching of allelic states at the major locus). The frequency of the genotype with allele i at the major locus after selection in environment j is given by f_i′, where

w_i = f_iw_ij, and w_ij = 1 if i = j and w_ij = 1 − s_i otherwise.

Mutation occurs only at the major locus. The rate at which mutation occurs is given by the allele at the modifier locus. Thus, there are two mutation rates, μ_m and μ_M. Unless noted otherwise, mutation at the major locus occurs at the same rate in both directions: i.e., the rate of mutation from allele 0 to allele 1 (μ_[0→1]) is equal to the rate of mutation from allele 1 to allele 0 (μ_[1→0]). We can relax this assumption and allow for μ_[0→1] ≠ μ_[1→0]. In that case, the allele at the modifier has two distinct rates associated with it, μ_[0→1] and μ_[1→0]. Because we are concerned mainly with the change of phenotype, we generally use the term switching rate, rather than mutation rate.

Environmental change is simulated by switching from environment e₀ to environment e₁ and vice versa after an average waiting time of n generations, where the waiting times are either sampled from a gamma distribution with parameters a and b (with a as the shape parameter and b as the scale parameter), or where the waiting time is always exactly n. In the first case, the mean waiting time is n = ab, corresponding to the average rate of environmental change, and the variance is ab². In the second case, the variance is zero, reflecting a situation where the environment changes periodically every n generations (we refer to this as the periodic case). The gamma distribution allows us to test a whole range of distributions by modifying the variance while holding the mean constant. The exponential distribution, which is a special case of the gamma distribution with a = 1, is used in a number of studies where the environment changes with an instantaneous rate of 1/n at every time point (we refer to this as the exponential case).

After a burn-in period of 1000 generations, the modifier allele M is introduced at frequency f_M = 10⁻⁴. A simulation run is stopped 100,000 generations after the introduction of the allele M or if f_M = 1 or f_M = 0. We consider an invasion successful if f_M > 10⁻⁴ after the simulation has stopped; if the invasion is successful, we say that μ_M is the selected switching rate, and otherwise μ_m is the selected rate. In most cases, the two frequencies (i.e., f_M before and after the simulation) differ by many orders of magnitude, in particular when the selection coefficients (s₀ and s₁) and the difference between μ_m and μ_M are not small. In such cases, allele M will reach fixation (f_M = 1) if it has a selective benefit over allele m.

To find the evolutionarily stable switching rate, we perform the following invasion trial procedure: a simulation run is started with randomly chosen values between 0 and 0.1 for the wild-type switching rate μ_m and the mutant switching rate μ_M. After the simulation run, the selected switching rate is then used as the new wild-type switching rate (μ_m) in a follow-up simulation, and a new modifier switching rate (μ_M) is chosen such that μ_M = μ_m × ∂, where ∂ is a randomly chosen number from an exponential distribution with mean 1 (in the case where we allow for μ_[0→1] ≠ μ_[1→0], we simply choose two random numbers, ∂₁ and ∂₂, from an exponential distribution with mean 1, and μ_M[0→1] = μ_m[0→1] × ∂₁ and μ_M[1→0] = μ_m[1→0] × ∂₂). This process is repeated 500 times, and the selected switching rate after 500 sequential simulation runs, each of up to 100,000 generations, is considered to be the evolutionarily stable switching rate.

Although the formulation of the model is in purely genetic terms, the generality of the model also allows for its interpretation in epigenetic or behavioral terms. For example, one can think of a gene x with two possible expression states (e.g., low and high expression levels), giving rise to two different phenotypes. In that case, the expression level (low or high) is given here by the allele at the major locus (0 or 1), and the rate of switching between the two expression levels is given by the allele at the modifier locus. It is important to note that the one-locus/two-allele formulation is chosen solely for modeling convenience, with the aim of capturing any type of vertical transmission of a bimodal phenotypic trait, and even though a given system might not involve an actual genetic locus with two alleles (e.g., the expression example given above), our model will still capture the dynamics of that system.

RESULTS

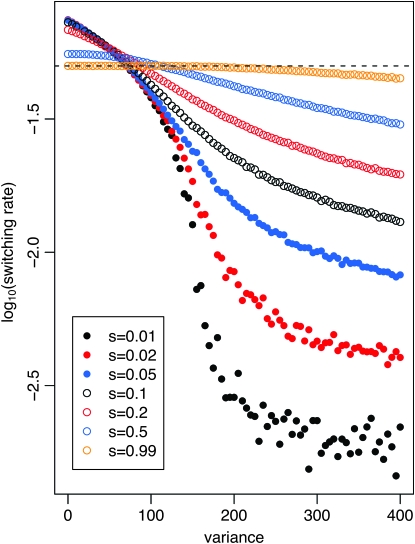
We first explore the behavior of the model in a symmetric fitness landscape, i.e., where the fitness cost of expressing the maladapted phenotype is independent of the environment (s₀ = s₁). If the environment changes periodically every n generations, we find the evolutionarily stable switching rate to be on the order of 1/n, confirming results of earlier studies (Leigh 1970; Ishii et al. 1989; Lachmann and Jablonka 1996). However, in stochastic environments where the environment changes with an instantaneous rate of 1/n at every time point, we find that the evolutionarily stable switching rates can be up to two orders of magnitude lower, depending on the selection coefficient (Figure 1). Interestingly, while the switching rates decrease substantially when selection is not very strong (s < 0.1), the decrease does not occur gradually over the full range of variances, but is confined to a rather narrow, intermediate region.

Figure 1.—

Evolution of stochastic switching rates in symmetric fitness landscapes, i.e., s = s₀ = s₁. The log₁₀ evolutionarily stable switching rate on the y-axis depends both on the fitness cost of being maladapted in both environments (s) and on the variance of the distribution of waiting times. The mean waiting time is fixed at n = 20 and the variance ranges from zero, which corresponds to a periodic environment where the environment changes exactly every 20 generations, to 400, which corresponds to an exponential distribution (a = 1, b = 20) where the environment changes with probability 0.05 at each generation. Different values of s are plotted using the colored open and solid circles. The expectation that switching rates evolve to be in tune with the rate of environmental change (1/n) is given by the dashed line.

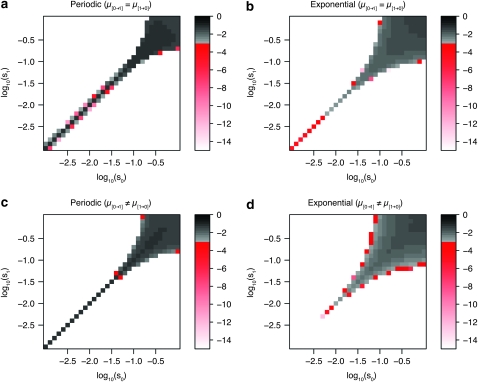
Next, we turn our attention to the behavior of the model in an asymmetric fitness landscape, i.e., where the fitness cost of expressing the maladapted phenotype is dependent on the environment (s₀ ≠ s₁). In such a landscape, we observe a hitherto undescribed threshold phenomenon: If the two selection coefficients are similar in strength, switching rates evolve to levels observed in symmetric fitness landscapes; however, if the difference between the coefficients reaches a certain threshold value, the switching rates quickly evolve toward zero. Figure 2, a and b, shows the log₁₀ values of the evolutionarily stable switching rates for the periodic and the exponential case, respectively, with various combinations of selection coefficients s₀ and s₁ between (and including) 0.001 and 1. Figure 2, a and b, demonstrates that nonzero switching rates in asymmetric fitness landscapes cannot be maintained unless selection is very strong in both environments. In the periodic case, switching rates on the order of 1/n can be maintained—provided s₀ and s₁ are identical—even when selection is weak. In the exponential case, the parameter range in which nonzero switching rates can be maintained is slightly larger, but when selection is not very strong, switching rates drop dramatically even when s₀ = s₁. In Figure 2, c and d, we relax the condition that the switching rates have to be identical in both directions and allow for μ_[0→1] ≠ μ_[1→0], but the general conclusion remains the same. Figure 2, c and d, shows the lower of the two switching rates. The areas where one of the switching rates will evolve to zero (the white areas) are almost identical to the case where μ_[0→1] = μ_[1→0] (i.e., Figure 2, a and b).

Figure 2.—

Evolution of stochastic switching rates in asymmetric fitness landscapes. The plot shows the log₁₀ of the evolutionarily stable switching rates. In c and d, the smaller of the two rates (μ_[0→1] and μ_[1→0]) is shown. The threshold phenomenon is clearly visible as a sudden drop from switching rates at high levels (shown by the gray color gradient) to rates ≤10⁻¹⁵ (shown in white). Intermediate rates are almost nonexistent (shown by the red color gradient). (a–d) The periodic (a and c) and the exponential case (b and d). Each of the 900 points shows the average of 50 invasion trials. s₀ and s₁ vary from 0.001 to 1, and the mean waiting time is n = 20. In principle, the plots should be perfectly symmetric along the diagonal s₀ = s₁. The slight deviations from perfect symmetry are due to the stochastic nature of the simulations. The condition that the switching rates are equal in both directions is relaxed in c and d, where the two rates are allowed to evolve independently (i.e., μ_[0→1] ≠ μ_[1→0]). In c and d, only the lower of the two rates is shown.

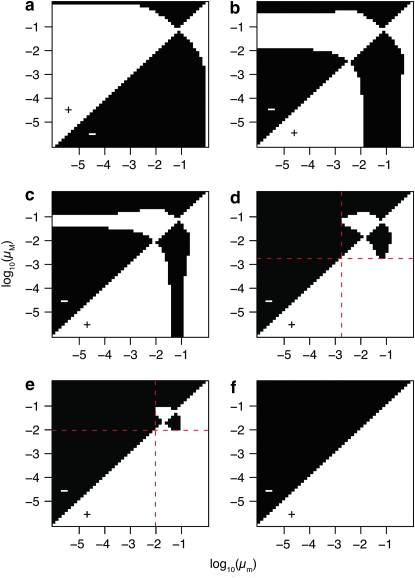
The threshold phenomenon observed in Figure 2 substantially limits the circumstances under which stochastic switching can be maintained. To understand the cause of this phenomenon, we looked at the invasion dynamics of modifier alleles for different combinations of selection coefficients in Figure 3 (for simplicity, we assume again that μ_[0→1] = μ_[1→0]). The panels in Figure 3 are pairwise invasibility plots, where the horizontal axis represents the value of the wild-type switching rate μ_m and the vertical axis represents the mutant switching rate μ_M. The modifier allele M cannot invade the population in the black regions, whereas in the white regions M invades. In all panels, s₀ is kept constant at 0.1, but s₁ varies from 0.1 to 0.25. Figure 3a shows that when s₀ = s₁, the evolutionarily stable switching rate is on the order of 1/n. However, as soon as s₀ ≠ s₁, we observe a qualitative change in the range of switching rates that are < ∼0.01 (Figure 3b). In that range, any mutant modifier allele that causes an even lower switching rate can invade. Thus, there is a potential for the switching rates to evolve to zero (in Figure 3b, the smallest value for the switching rate is 10⁻⁶, but the results in Figure 2 show that the switching rate will evolve to values <10⁻¹⁵). Notably, however, modifier alleles that cause substantially higher switching rates (μ_M > 0.01) may always invade. This means that although the switching rate might steadily evolve toward zero, it will always be prone to invasion by higher switching rates. Whether such an invasion can occur once the switching rate is very low depends on the availability of mutations that cause such dramatic changes in switching rates. On the other hand, the equilibrium at ∼1/n is resistant to invasion by mutant switching rates of any size; i.e., it is globally evolutionarily stable. Hence, under the assumption that all mutations are available with some nonzero probability, switching rates are expected to evolve to a value on the order of 1/n in the long run (given the settings used here, i.e., a periodically changing environment), but for large periods of time, they may be dramatically lower. A slight increase in s₁ (Figure 3c) increases the parameter range where very low switching rates are temporarily selected for, and while the globally evolutionarily stable switching rate is still on the order of 1/n, it becomes increasingly hard for a mutation causing high switching rates to invade as long as the wild-type switching rate is very low.

Figure 3.—

These pairwise invasibility plots show which modifier switching rate μ_M can invade a population with wild-type switching rate μ_m. (a) A symmetric fitness landscape with s₀ = s₁ = 0.1. (b–f) Asymmetric fitness landscapes with s₁ > s₀ = 0.1 and the following values for s₁: (b) 0.11, (c) 0.13, (d) 0.15, (e) 0.18, and (f) 0.23. Each of the 2500 points on each panel shows the average of 10 invasion trials (one invasion trial corresponds to 500 consecutive simulation runs, each up to 100,000 generations; see main text). If the modifier switching rate invades, the area is white (also indicated by a plus sign); otherwise it is black (also indicated by a minus sign). In all simulations, the environment changes periodically every n = 20 generations. The panels show how a departure from a symmetric fitness landscape (a) causes a fundamental change in the invasion dynamics. In particular, the parameter range in which a globally evolutionarily stable nonzero switching rate exists becomes increasingly smaller (b and c) and will eventually disappear altogether (d–f). In d and e, the nonzero switching rate is locally evolutionarily stable only and cannot be maintained in the long run: The red dashed lines indicate the threshold values of μ_m below which a modifier allele with switching rate μ_M can invade only when μ_M < μ_m. A population with a wild-type switching rate μ_m below this threshold will ultimately evolve its switching rate toward zero.

By further increasing s₁, a threshold will eventually be reached where the previously globally evolutionarily stable switching rate will become locally evolutionarily stable only: Once a mutant appears that causes a switching rate below a certain threshold value (red dashed lines in Figure 3, d and e), the rate will ultimately evolve toward zero. Thus, at this point the dynamic behavior is opposite to that described above: The switching rates are expected to evolve to zero in the long run, but, for a period of time, they may be on the order of 1/n. Indeed, when we look at the data of invasion trials underlying Figure 2 at this parameter range (e.g., s₀ = 0.1, s₁ = 0.15), we find that most stable switching rates are <10⁻¹⁵ but, in a very few cases, the rates are still on the order of 1/n (data not shown). An even further increase of s₁ will eliminate the locally evolutionarily stable switching rate of 1/n, and only mutations decreasing the switching rate can invade, rapidly driving the switching rates toward zero (Figure 3f).

DISCUSSION

The idea that stochastic switching of phenotypes is an adaptive strategy to cope with changing environments has gained ground in the past two decades. Empirical studies have demonstrated the ubiquity of stochastic switching in clonal populations, and theoretical advances have shown that such a bet-hedging strategy can in principle be advantageous even in comparison to environmental sensing (Kussell and Leibler 2005). However, all modeling efforts aimed at understanding the phenomenon have assumed fitness symmetry such that the fitness cost of being maladapted is equal in all environments. Here, we have used a population genetic model to investigate the evolution of stochastic switching rates, and while our model can reproduce previously reported results, we find dramatic changes in the behavior of the model once we relax the fitness symmetry conditions. In particular, we discovered a threshold phenomenon where minor changes in selection result in the loss of stochastic switching unless selection against maladaptation is strong in all environments.

Stochastic switching is generally seen as an adaptive bet-hedging strategy to create phenotypic variability in an otherwise uniform population (but alternative explanations exist; see, for example, Ackermann et al. 2008). The main rationale is that the variability would confer a fitness benefit to the population, and both theoretical and empirical work (see, e.g., Dubnau and Losick 2006) have demonstrated this effect repeatedly. Our results confirm this notion in principle but indicate that the details of environmental change, and in particular the associated fitness costs in all environments, can dramatically alter the outcome and cause strong and consistent selection against stochastic switching. An influential theoretical analysis (Kussell and Leibler 2005) has suggested that stochastic switching is an optimal strategy only if the environment does not change too quickly and that otherwise environmental sensing would be more beneficial. Here, we have focused exclusively on stochastic switching, and it remains to be seen if the observed selection against stochastic switching in asymmetric fitness environments would automatically lead to a competitive advantage for environmental sensing. For example, it is possible that asymmetric fitness landscapes will also make environmental sensing more difficult to evolve, especially if the relative fitness cost of the sensing mechanism is uniform across environments. However, if the relative fitness cost of sensing is low compared to the weakest selection coefficient and if sensing is fairly responsive, then it is conceivable that sensing could be selected for under a wide range of conditions. Studying these issues quantitatively is an important next step in this work.

Our results may be helpful to interpret differences in findings from populations of cells in the wild and in the laboratory. For example, wild strains of B. subtilis enter the competence state at a much lower rate than laboratory strains (Dubnau and Losick 2006). Both periodic environments and perfectly symmetric fitness landscapes are arguably more likely to be maintained in the laboratory than in the wild. Thus, it is possible that switching rates of laboratory strains are higher than those found in the wild due to small differences in the selective pressures imposed by the different environments or due to a difference in the variance of environmental change.

Stochastic phenotype switching has attracted considerable attention in the study of microbial pathogens, where it is commonly referred to as phase variation (van der Woude and Bäumler 2004). The resulting phenotypic variability has been proposed to facilitate immune evasion and colonization of new niches within a host. Bet hedging might even be an adaptive strategy in between-host dynamics. For example, static latency of the herpes virus has been suggested to be a bet-hedging strategy when the number of susceptible hosts (i.e., the environment of the virus) fluctuates over time (Stumpf et al. 2002). Microbial pathogens have such short generation times that evolutionary considerations are of importance during the lifetime of their human hosts, and thus understanding the evolutionary dynamics of stochastic switching might hold a key to developing efficient strategies for their control.