Age Structure, Changing Demography and Effective Population Size in Atlantic Salmon (Salmo salar)

Abstract

Effective population size (N_e) is a central evolutionary concept, but its genetic estimation can be significantly complicated by age structure. Here we investigate N_e in Atlantic salmon (Salmo salar) populations that have undergone changes in demography and population dynamics, applying four different genetic estimators. For this purpose we use genetic data (14 microsatellite markers) from archived scale samples collected between 1951 and 2004. Through life table simulations we assess the genetic consequences of life history variation on N_e. Although variation in reproductive contribution by mature parr affects age structure, we find that its effect on N_e estimation may be relatively minor. A comparison of estimator models suggests that even low iteroparity may upwardly bias N_e estimates when ignored (semelparity assumed) and should thus empirically be accounted for. Our results indicate that N_e may have changed over time in relatively small populations, but otherwise remained stable. Our ability to detect changes in N_e in larger populations was, however, likely hindered by sampling limitations. An evaluation of N_e estimates in a demographic context suggests that life history diversity, density-dependent factors, and metapopulation dynamics may all affect the genetic stability of these populations.

THE effective size of a population (N_e) is an evolutionary parameter that can be informative on the strength of stochastic evolutionary processes, the relevance of which relative to deterministic forces has been debated for decades (e.g., Lande 1988). Stochastic forces include environmental, demographic, and genetic components, the latter two of which are thought to be more prominent at reduced population size, with potentially detrimental consequences for average individual fitness and population persistence (Newman and Pilson 1997; Saccheri et al. 1998; Frankham 2005). The quantification of N_e in conservation programs is thus frequently advocated (e.g., Luikart and Cornuet 1998; Schwartz et al. 2007), although gene flow deserves equal consideration given its countering effects on genetic stochasticity (Frankham et al. 2003; Palstra and Ruzzante 2008).

Effective population size is determined mainly by the lifetime reproductive success of individuals in a population (Wright 1938; Felsenstein 1971). Variance in reproductive success, sex ratio, and population size fluctuations can reduce N_e below census population size (Frankham 1995). Given the difficulty in directly estimating N_e through quantification of these demographic factors (reviewed by Caballero 1994), efforts have been directed at inferring N_e indirectly through measurement of its genetic consequences (see Leberg 2005, Wang 2005, and Palstra and Ruzzante 2008 for reviews). Studies employing this approach have quantified historical levels of genetic diversity and genetic threats to population persistence (e.g., Nielsen et al. 1999b; Miller and Waits 2003; Johnson et al. 2004). N_e has been extensively studied in (commercially important) fish species, due to the common availability of collections of archived samples that facilitate genetic estimation using the temporal method (e.g., Hauser et al. 2002; Shrimpton and Heath 2003; Gomez-Uchida and Banks 2006; Saillant and Gold 2006).

Most models relating N_e to a population's genetic behavior make simplifying assumptions regarding population dynamics. Chiefly among these is the assumption of discrete generations, frequently violated in practice given that most natural populations are age structured with overlapping generations. Here, theoretical predictions still apply, provided that population size and age structure are constant (Felsenstein 1971; Hill 1972). Ignored age structure can introduce bias into temporal genetic methods for the estimation of N_e, especially for samples separated by time spans that are short relative to generation interval (Jorde and Ryman 1995; Waples and Yokota 2007; Palstra and Ruzzante 2008). Moreover, estimation methods that do account for age structure (e.g., Jorde and Ryman 1995) still assume this structure to be constant. Population dynamics will, however, likely be altered as population size changes, thus making precise quantifications of the genetic consequences of acute population declines difficult (Nunney 1993; Engen et al. 2005; Waples and Yokota 2007). This problem may be particularly relevant when declines are driven by anthropogenic impacts, such as selective harvesting regimes, that can affect age structure and N_e simultaneously (Ryman et al. 1981; Allendorf et al. 2008). Demographic changes thus have broad conservation implications, as they can affect a population's sensitivity to environmental stochasticity and years of poor recruitment (Warner and Chesson 1985; Ellner and Hairston 1994; Gaggiotti and Vetter 1999). Consequently, although there is an urgent need to elucidate the genetic consequences of population declines, relatively little is understood about the behavior of N_e when population dynamics change (but see Engen et al. 2005, 2007).

Here we focus on age structure and N_e in Atlantic salmon (Salmo salar) river populations in Newfoundland and Labrador. The freshwater habitat in this part of the species' distribution range is relatively pristine (Parrish et al. 1998), yet Atlantic salmon in this area have experienced demographic declines, associated with a commercial marine fishery, characterized by high exploitation rates (40–80% of anadromous runs; Dempson et al. 2001). A fishery moratorium was declared in 1992, with rivers displaying differential recovery patterns since then (Dempson et al. 2004b), suggesting a geographically variable impact of deterministic and stochastic factors, possibly including genetics. An evaluation of those genetic consequences thus requires accounting for potential changes in population dynamics as well as in life history. Life history in Atlantic salmon can be highly versatile (Fleming 1996; Hutchings and Jones 1998; Fleming and Reynolds 2004), as exemplified by the high variation in age-at-maturity displayed among and within populations (Hutchings and Jones 1998), partly reflecting high phenotypic plasticity (Hutchings 2004). This diversity is particularly evident in the reproductive biology of males, which can mature as parr during juvenile freshwater stages (Jones and King 1952; Fleming and Reynolds 2004) and/or at various ages as anadromous individuals, when returning to spawn in freshwater from ocean migration. Variability in life history strategies is further augmented by iteroparity, which can be viewed as a bet-hedging strategy to deal with environmental uncertainty (e.g., Orzack and Tuljapurkar 1989; Fleming and Reynolds 2004). Life history diversity and plasticity may allow salmonid fish populations to alter and optimize their life history under changing demography and population dynamics, potentially acting to stabilize N_e. Reduced variance in individual reproductive success at low breeder abundance (genetic compensation) will achieve similar effects and might be a realistic aspect of salmonid breeding systems (Ardren and Kapuscinski 2003; Fraser et al. 2007b). Little is currently known about the relationships between life history plasticity, demographic change and N_e, partly due to scarcity of the multivariate data required for these analyses.

Our objective in this article is twofold. First, we use demographic data for rivers in Newfoundland to quantify how life history variation influences age structure in Atlantic salmon and hence N_e and its empirical estimation from genetic data. We find that variation in reproductive contribution by mature parr has a much smaller effect on the estimation of N_e than is often assumed. Second, we use temporal genetic data to estimate N_e and quantify the genetic consequences of demographic changes. We attempt to account for potential sources of bias, associated with (changes in) age structure and life history, by using four different analytical models to estimate N_e: a single-sample estimator using the linkage disequilibrium method (Hill 1981), the temporal model assuming discrete generations (Nei and Tajima 1981; Waples 1989), and two temporal models for species with overlapping generations (Waples 1990a,b; Jorde and Ryman 1995) that differ principally in assumptions regarding iteroparity. A comparison of results from these different estimators suggests that iteroparity may often warrant analytical consideration, even when it is presumably low. Although sometimes limited by statistical power, a quantification and comparison of temporal changes in N_e among river populations suggests a more prominent impact of demographic changes on N_e in relatively small river populations.

MATERIALS AND METHODS

Life history:

Atlantic salmon life history represents the classical example of anadromy. Juveniles (called parr) typically spend their first few years in freshwater. They then undergo physiological changes (known as smoltification) and migrate out to sea (at which point they are called smolts). Anadromous adults, after spending one (one-sea winter or grilse) or several years (multisea winter) feeding in the ocean environment, return to spawn in freshwater, typically in the river of origin. Many die after spawning (semelparity), but some migrate out to sea again to return and breed again in future years (iteroparity). Alternately, males can mature in freshwater (as mature male parr) before undertaking any ocean migration.

Molecular genetic analyses:

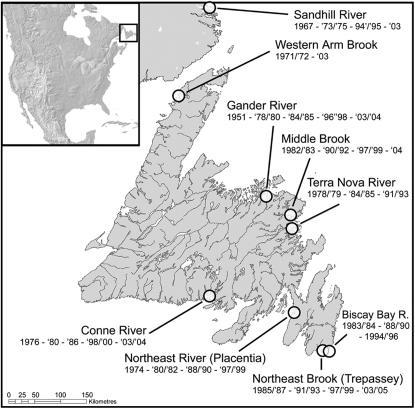
Atlantic salmon samples (N = 2758, scales or fin clips) were collected nonlethally from anadromous adult salmon runs between 1951 and 2004 in nine rivers, distributed throughout Newfoundland and in southern Labrador (Figure 1). Exceptions are samples consisting of smolts (Western Arm Brook, 2004) or postspawning adults returning to the sea (Northeast Brook Trepassey). Scales were kept in dry paper envelopes and fin clips were stored in 95% ethanol. Where possible, we pooled samples from 2–3 consecutive years in an attempt to obtain samples representative of the entire population at a given point in time (e.g., Waples 1990a), i.e., to reduce the effect of age structure on measures of temporal genetic variance and provide more accurate estimates of population allele frequencies (see supporting information, Table S1). Our sampling design thus corresponds to plan I (Waples 1989), and temporal genetic N_e estimators involving such a design usually require a correction term inversely related to population size (1/N; e.g., Waples 1989; Jorde and Ryman 1995), but here we assumed census population sizes were large enough for this correction to be ignored in statistical analyses.

Figure 1.—

Map of Newfoundland and Labrador, showing study river locations and years sampled. See Table S1 for sample details.

Two different DNA extraction protocols were applied, depending on the age of the samples. For archived scale samples collected prior to 1990, DNA extraction was performed using a phenol-chloroform extraction protocol (Taggart et al. 1992), followed by a concentration step using microconcentrators (Amicon, Danvers, MA) (Nielsen et al. 1999a). For fin-clip samples and post-1990 scale samples, DNA was extracted following a glass milk protocol (Elphinstone et al. 2003). Genetic polymorphism was examined in a suite of 14 microsatellite loci specific for Atlantic salmon (see Palstra et al. 2007 for details), chosen on the basis of product size range (<300 bp to reduce occurrence of large allele dropouts), scoring convenience, and variability for the region of study.

Sample statistics:

Basic descriptives for each sample and locus (allele frequencies, number of alleles, and observed and expected heterozygosity) were obtained using FSTAT (version 2.9.3.2; Goudet 1995). Temporal genetic methods for estimating N_e assume that variance in allele frequency arises solely as a consequence of genetic drift (and sampling). Technical artifacts thus need to be eliminated as a potential source of temporal genetic variance; markers should be selectively neutral and unlinked, whereas sampled individuals should represent random samples from a population. Departures from Hardy–Weinberg equilibrium (HWE) were assessed for each locus and sample by testing for significant departure of F_is from neutral expectations as implemented in FSTAT (based on 5600 randomizations). Fisher's exact test (Sokal and Rohlf 1991) was used to evaluate overall sample HWE conditions by combining probabilities from individual loci (Ryman et al. 2006). The occurrence of genotyping errors [resulting from technical artifacts (null alleles) or DNA quality (large allele dropouts)], as well as linkage disequilibrium among loci, was assessed as in Palstra et al. (2007). Where irregularities were suspected, samples were rescored and amplification procedures (if possible) repeated.

Estimating effective population size:

We used four analytical approaches to estimate N_e (denoted 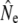hereafter), all based on neutral genetic marker data, while accounting for overlapping generations and age structure. These estimators require detailed knowledge of demographic parameters, such as age structure and average generation interval, which we first calculated using life table analyses.

Life table analyses:

We performed life table analyses to estimate age-specific survivorship (l_x) and fecundity (b_x), information needed to account for the effects of overlapping generations and age structure. This information is used directly to estimate N_e in the analytical approach of Jorde and Ryman (1995), but is also essential for other estimation models. Since we used demographic data on anadromous runs as a basis for life table analyses, some complications arise from uncertainties regarding freshwater survival and reproduction. Particularly, male parr maturation will affect (male) freshwater mortality and can bias the age composition of breeders when ignored. We evaluated the consequences of mature male parr reproduction in life table analyses as follows.

We estimated age-specific survival rates (s_i) by combining estimates of survival for all potential life history stages (parr, mature parr, smolts, virgin anadromous fish, and repeat spawners) present in at the previous age (i − 1). We ignored survival at the egg-to-fry stages, as the genetic correlations in age-structured populations depend on differences in survival among the reproductive age classes (Jorde and Ryman 1996). Thus, for nonmature male and female parr, we assumed a constant annual freshwater survival (s_fw) to the smolt stage of 0.38 (median value of estimates for Canadian rivers) (Symons 1979; Evans et al. 1984; Myers 1984; Cunjak and Therrien 1998; Cunjak et al. 1998; Locke 1998). The majority of smolts in Newfoundland rivers spend one winter in the ocean before returning to spawn (O'Connell et al. 2006a). We therefore used information on the age composition of virgin one-sea winter adults returning to rivers to spawn (p_anad) (N ranging from 658 to 3689 per river) to estimate, for both sexes, percentages of individuals smoltifying (p_smolt) at age i as

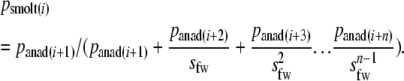We used empirical values for Newfoundland rivers (Dempson et al. 2004a; O'Connell et al. 2005) of smolt-to-grilse survival (s_smolt, assumed to be 5% when no river-specific data were available) and iteroparity (s_anad, calculated from empirical data), which were both assumed to be age independent. For each year i, age-specific survival rates (s_i) were calculated for females as

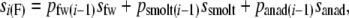where p_{y(i − 1)} are the relative proportions of each life history stage y surviving from age i − 1 to age i.

The equation for annual survival of males requires inclusion of mature parr as an additional life history stage. Estimates of the survival of mature parr relative to nonmaturing fish (s_rel) range from 0.29 to 0.80 (Myers 1984; Hutchings and Myers 1994; Whalen and Parrish 1999) and we assumed s_rel = 0.35 for subsequent analyses. We further used empirical estimates of mature parr incidence for rivers in this region (Dalley et al. 1983; Myers et al. 1986) as a basis for life table analyses. The biological plausibility of assumptions about mature parr was assessed through simulations (see File S1). Although male parr can mature at various freshwater ages (e.g., L'Abée-Lund 1989; Heinimaa and Erkinaro 2004), maturation generally occurs about halfway through the freshwater stage. In Newfoundland, male parr typically mature at ages 1+ and 2+ (Dalley et al. 1983; Myers et al. 1986; Hutchings 2002). Therefore we estimated the average age of precocious parr maturation by halving the average (female) smolt age and assumed mature parr to be present in two age classes (1+ and 2+ for the majority of rivers). Hence, age-specific survival rates for males were calculated as

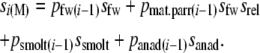Age-specific survivorship values (l_x) were then calculated as 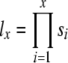, for each sex and age class x in a population.

For anadromous fish, age- and sex-specific birth rates (b_x) were estimated, using proportions of adults in the various age classes, weighted by body size (wet weight), as a proxy for relative fecundity (Fleming et al. 1997; Mjølnerod et al. 1998; Garant et al. 2001; but see O'Connell et al. 2008). We attempted to account for the influence of male parr maturation on age-specific reproductive contribution of males as follows. In the absence of data for the rivers, we used empirical values from observations under natural (Jordan and Youngson 1992; Martinez et al. 2000; Garant et al. 2001; Taggart et al. 2001) and experimental conditions (Hutchings and Myers 1988; Moran et al. 1996; Thomaz et al. 1997; Garcia-Vazquez et al. 2001; Jones and Hutchings 2001, 2002). These studies suggest that mature male parr account for ∼30% of the fertilizations in direct competition with anadromous fish, over a wide range of operational sex ratios. We used this average as a baseline estimate for the reproductive contribution by mature parr, the remainder (70%) being accounted for by the anadromous male year classes. We considered scenarios with larger (Northeast River Placentia, 50%) and smaller (Sandhill River, 25%) parr reproduction, on the basis of empirical estimates of parr incidence and spawning ground surveys (F. Palstra, personal observation). These percentages do not apply to b_x but to p_x, since they should reflect the probability that progeny genes are inherited from a male parent of age x (cf. Felsenstein 1971). Reproduction among anadromous (male) age classes was allocated on the basis of age composition (weighted by body size). For the (two) mature parr age classes, we assumed a slight reproductive advantage for older parr (60%), since male parr size can affect reproductive success (Thomaz et al. 1997; but see Jones and Hutchings 2002). Using these criteria, we estimated the projected reproductive contribution of each age class as p_x = l_xb_x, after adjusting b_x values to generate a constant population size (Σl_xb_x = 1). Age-specific values of l_x, b_x, and p_x were then used to estimate the age structure of breeders, as well as the average generation interval G (in years) following Felsenstein (1971).

Temporal models assuming discrete generations:

We applied a discrete temporal model to estimate N_e over the longest time span between two samples available for each river, using three different temporal genetic variance estimators. First, we used the standardized temporal allelic variance measure of Pollak (1983) [denoted F_k and N_e(k)]. Second, we applied the unbiased, but possibly less precise measure of Jorde and Ryman (2007) [denoted F_s and N_e(s)]. Finally, we employed the pseudo-maximum-likelihood approach of Wang (2001), assuming N_e = 25,000 as an upper limit. This latter method was also applied to account for gene flow, which should not a priori be ignored, given Atlantic salmon life history (e.g., Stabell 1984; Jonsson et al. 2003). We therefore evaluated the impact of gene flow on effective population size by applying Wang and Whitlock's (2003) model incorporated in MLNE, which jointly estimates N_e and gene flow (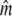). For these latter analyses we considered all other sampled rivers in regional proximity as pooled source populations.

N_e/N ratios were calculated whenever sufficient demographic data (O'Connell et al. 2006b) were available and corresponding census sizes (N) were calculated as follows. First, age information of anadromous adults was used to estimate proportional reproductive contributions of breeders (X_i) for each cohort i in the time period to which the genetic estimates of N_e apply (Waples 2005). X_i values were then used to calculate census size following Ryman and Laikre (1991) and intergenerational census size N (see Waples 2002).

Pacific salmon model assuming semelparity:

Second, we applied a model developed specifically for semelparous Pacific salmonids (Waples 1990a,b). Under the Pacific salmon model, the signal of genetic drift (F_k, Pollak 1983) between cohorts inversely reflects the effective annual number of breeders (N_b) in given breeding seasons. We incorporated the effects of age structure into estimation of N_e by calculating b (the slope of the regression of 2F_k on 1/N_b) following Tajima (1992), on the basis of the age distribution of projected reproductive output (p_x values). Given uncertainties regarding what precisely is estimated when using a sample of adults derived from various cohorts (plan I, Waples 2005), we reconstructed age cohorts, on the basis of age determined from scale readings. Cohort samples (with S > 10) were then used to calculate year-specific N_b estimates using the software SALMONNb (Waples et al. 2007). Corresponding N_b/N ratios were calculated whenever annual anadromous run sizes were known. Additionally, we inferred effective population size from 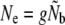, where 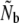is the harmonic mean of the annual N_b estimates as calculated by SALMONNb.

Cohort model for iteroparous species:

Third, we applied the cohort model of Jorde and Ryman (1995) for iteroparous species with variable age at maturity. This model assumes populations with a constant age structure, where N_e fluctuates around a mean value. For each river, we estimated cohort effective population size (N_e(J&R)), by calculating the average standardized temporal allele frequency variance (F_k, Pollak 1983) based on consecutive cohorts (with harmonic mean sample size 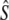>10) as

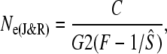which includes generation interval (G) and correction factor C. This C term is independent of population size and allele frequency, determined exclusively by l_x and b_x values, thus correcting for genetic covariance among cohorts attributable to age structure (Jorde and Ryman 1995). Given uncertainty about reproductive contributions by mature parr, we used simulations to assess the sensitivity of C and G to variance in male parr maturation and reproductive contribution. On the basis of simulation results, we calculated C and G as the average of sex-specific values. A similar approach was also used to estimate N_e before and after the commercial fishery closure in 1992, as this closure may have altered population dynamics. For this purpose, life tables were adjusted on the basis of demographic data pertinent to each time period. N_e/N ratios were estimated on the basis of the harmonic mean of corresponding annual counts of anadromous fish (Waples 2002, 2005).

Linkage-disequilibrium method:

We applied the linkage-disequilibrium method to neutral genetic data derived from single temporal samples (Hill 1981), using the program LDNe (Waples and Do 2008). Briefly, this method estimates the effective number of parents contributing to a sample, assuming no immigration occurred. Estimates for samples derived from a single cohort thus reflect N_b, whereas samples of adults of mixed ages (plan I) are intermediate between N_b and N_e (Waples 2005). Here, we used individual cohort samples to estimate the effective number of breeders in any given year (N_b), as well as temporal samples of consecutive years of adults pooled to estimate N_e.

Changes in demographic factors underlying N_e:

We used genetic estimates of N_b (from the Pacific salmon model, referring to the number of breeders in a season) to explore the scope for temporal changes in the demographic and reproductive parameters of a population, as indirect genetic estimates can be expected to be inclusive of all the demographic properties affecting effective size. Using river-specific demographic data, the seasonal inbreeding effective female size (N_bf) was approximated following Lande and Barrowclough (1988), where the average (k) and variance (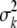) of progeny size for number of adult females (N) is used to estimate

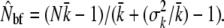Here, progeny size was approximated by a correlation between wet weight and the number of eggs (O'Connell et al. 2008). The inbreeding effective number of males (N_bm) in a given breeding season was then estimated as

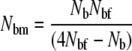(Wright 1938). A comparison of the relative magnitudes of N_bm and N_bf can then provide some indications of changes in reproductive biology.

RESULTS

Genetic marker characteristics:

DNA was successfully extracted from 2514 of 2758 samples (91.4%). Genetic analyses on these samples yielded consistently high amplification success, ranging from 98.5% (SSsp1605) to 99.8% (SSsp2215). Locus gene diversity for these samples was high, varying from 0.64 (Ssa12) to 0.93 (SSsp2216). Gene diversity per sample ranged from 62.0% (1997, Northeast Brook) to 83% (1951, Gander; 1991, Terra Nova), with corresponding average number of alleles ranging from 7.1 (1997, Northeast Brook) to 14.8 (1991, Terra Nova). No consistent patterns of loss of genetic diversity were observed (in gene diversity or allelic richness) in any of the temporal comparisons, including that spanning over 5 decades (the longest time span available in the present study, Gander 1951–2003). Overall, 329 alleles were available for subsequent analyses, ranging from 85 (1997, Northeast Brook) to 208 (1991, Terra Nova) independent alleles per river sample (see Table S1).

Fifty-one of 1064 locus-by-sample comparisons were out of HWE, a result expected by chance alone (4.8% of comparisons significant at α = 0.05, 0.9% of comparisons significant at α = 0.01). None of these deviations were consistent across loci or samples. MICRO-CHECKER analyses suggested that 7 of these could be attributed to a lack of heterozygotes, possibly indicating the presence of null alleles. Only one locus (SsaF43) in one river (Conne) showed such signatures in multiple temporal replicates and was hence removed from further analyses involving this river. As previously shown (Palstra et al. 2007), these loci likely are unlinked and do not display strong signatures of selective sweeps in tests for selective neutrality.

Genetic estimates of effective population size:

Life table simulations (see File S1 for details) suggested s_rel = 0.35 as a reasonable assumption for mature parr survival in the majority of life table analyses, along with male parr maturation rates that result in anadromous age structures compatible with empirical observations. See below for an evaluation of the genetic consequences of variation in parr maturation incidence on 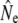in the cohort model. Estimates of generation interval (G) from life table analyses (Table 1) ranged from 4.5 years [Northeast River (Placentia)] to 6.7 years (Sandhill River) and were subsequently used to scale measures of temporal genetic variance to .

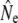TABLE 1.

Temporal estimates of N_e assuming discrete generations, using two temporal samples (with harmonic sample size 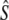) separated by time t (measured in generation intervals)

River	Period	G (yr)	t		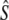		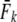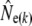95% C.I.		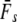	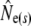95% C.I.
Biscay Bay River	1983–1994	4.9	2.4	72	0.0159	629	(213–∞)	0.0177	331	(119–∞)
Conne River	1976–2003	4.8	5.7	57	0.0188	2547	(476–∞)	0.0177	∞	(558–∞)
Gander River	1951–2003	5.4	10.2	87	0.0141	1933	(880–18,394)	0.0138	2097	(828–∞)
	1951–1978		5.4	72	0.0203	417	(243–891)	0.0224	306	(157–6,405)
	1978–2003		4.8	80	0.0144	1305	(468–∞)	0.0152	934	(324–∞)
Middle Brook	1982–2004	5.2	3.9	84	0.0143	836	(336–∞)	0.0158	529	(208–∞)
Northeast Brook	1985–2003	5.2	3.3	52	0.0238	376	(133–∞)	0.0245	336	(174–∞)
Northeast River	1974–1997	4.5	5.3	61	0.0187	1197	(356–∞)	0.0188	1204	(279–∞)
Sandhill River	1967–2003	6.7	5.7	85	0.0152	825	(408–3,399)	0.0148	783	(321–∞)
	1967–1994		4.3	73	0.0172	628	(289–4,704)	0.0173	585	(267–∞)
	1973–2003		4.6	84	0.0147	836	(379–8,286)	0.0155	520	(235–∞)
Terra Nova River	1978–1991	5.1	2.7	76	0.0142	1371	(328–∞)	0.0142	1531	(368–∞)
Western Arm Brook	1971–2004	5.4	6.3	60	0.0185	1657	(498–∞)	0.0202	781	(295–∞)

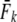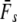Given are point estimates plus 95% confidence intervals using the moment-based estimators of Pollak (1983) [ and ] and Jorde and Ryman (2007) [ and ].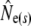

Table 1 shows genetic estimates of N_e for nine rivers in Newfoundland and Labrador, assuming closed populations, characterized by discrete generations. Although these estimates display variation among methods in magnitude, patterns of relative magnitude remain fairly constant across rivers. 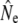_(k) ranged from 376 (Northeast Brook) to 2547 (Conne River), whereas 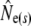ranged from 331 (Biscay Bay River) to infinity (Conne River). These results confirm that F_s may be less precise than F_k, as confidence intervals associated with 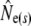were often wider (cf. Jorde and Ryman 2007). The likelihood method of Wang (2001) gave estimates ranging from 490 (Northeast Brook) to infinity (Terra Nova River) (Table 2). For all three estimator models, corresponding confidence intervals often, but not always, included infinity. Given the relative consistency, in particular for the smaller rivers, we conclude that our results may not be strongly biased by the estimator of temporal genetic variance applied.

TABLE 2.

Temporal estimates of N_e assuming discrete generations, considering closed () and open populations (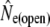), using Wang and Whitlock's (2003) approach

River	Period	t		95% C.I.		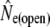95% C.I.		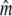95% C.I.
Biscay Bay River	1983–1994	2.4	756	(314–∞)	404	(220–1042)	0.0135	(0.0098–0.0256)
Conne Rivera	1976–2003	5.7	1396	(524–∞)	—	—	—	—
Gander River	1951–2003	10.3	1262	(754–3531)	1038	(531–2958)	0.0200	(0.0070–0.0411)
	1951–1978	5.4	1394	(887–2627)	557	(292–1731)	0.0251	(0.0075–0.0495)
	1978–2003	4.8	5230	(1457–∞)	1026	(397–7670)	0.0169	(0.0014–0.0451)
Middle Brook	1982–2003	3.9	759	(369–∞)	730	(306–4012)	0.0126	(0.0008–0.0326)
Northeast Brook	1985–2003	3.3	493	(235–3599)	∞	(463–∞)	0.0002	(0–0.0003)
Northeast River	1974–1997	5.3	1990	(521–∞)	∞	(8083–∞)	0.0001	(0–0.0002)
Sandhill River	1967–2003	5.7	1334	(619–∞)	514	(316–1222)	0.0144	(0.0060–0.0246)
	1973–2003	4.6	702	(393–2023)	452	(244–871)	0.0164	(0.009–0.0331)
	1967–1994	4.3	1033	(438–∞)	364	(225–860)	0.0182	(0.007–0.0315)
Terra Nova River	1978–1994	2.7	∞	(673–∞)	389	(137–∞)	0.1230	(0.0083–0.4728)
Western Arm Brook	1971–2004	6.3	1329	(548–∞)	683	(327–2219)	0.0171	(0.0024–0.0252)

Given for each river are estimates of effective population sizes and incoming gene flow (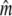) plus their confidence intervals, for two samples separated by time t (in generation intervals). Estimates of infinity indicate 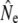> 2 × 10⁵.

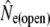^a was not calculated for Conne River as no putative source populations were deemed to be sampled.

Considering gene flow in the likelihood method (Wang and Whitlock 2003), results changed in two distinct ways (Table 2). For the majority of rivers, empirical N_e estimates are reduced, with Terra Nova showing the most dramatic reduction (from ∞ to 389), suggesting the sustained influence of migration from a large source population, which masked a signal of genetic drift when ignored. Other rivers, such as Northeast Brook (Trepassey) or Northeast River (Placentia) show the opposite pattern, where allowing for gene flow in the model results in an increase in N_e estimates, with very low estimates of gene flow. Such results suggest the presence of sporadic and intermittent gene flow among those rivers (see Wang and Whitlock 2003). In general, N_e estimates that account for gene flow appear to be smaller and (thus) more precise (narrower confidence intervals). These discrete generation N_e estimates apply to relatively long time spans (2.4–10.3 generations), over which bias due to age structure may be reduced and therefore be suitable for comparisons with N_e estimates derived from the Pacific salmon and cohort models.

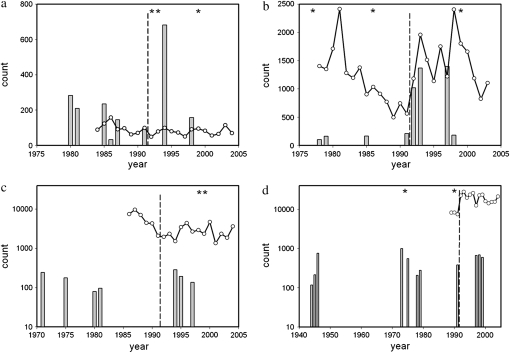
The Pacific salmon model yielded N_e estimates that are large relative to estimates derived from the discrete generation model, although qualitative patterns among rivers remain mostly consistent (Table 3). Genetic estimates of the annual number of breeders (N_b) range from 172 [Northeast Brook (Trepassey)] to ∞ (Western Arm Brook). Transformation of N_b to N_e by multiplication with generation interval yields estimates ranging from 813 (Conne) to 61,053 (Terra Nova River). Year-specific N_b estimates (Figure 2) show considerable annual and river-by-river variation. Temporal trends in N_b in two comparatively small rivers [Northeast Brook (Trepassey), Figure 2a; Middle Brook, Figure 2b] suggest increases in N_b estimates after the fishery closure in 1992. These temporal trends are less apparent in larger rivers such as Conne and Gander (Figure 2, c and d), although statistical power to infer changes in these two larger rivers may have been limited (see discussion).

TABLE 3.

Comparison of genetic N_e estimates using three different analytical models (all assuming closed populations) along with estimates of N_e for census population size N

		Discrete generations					Cohort model					Pacific salmon model
River	Iteroparity		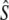	95% C.I.	N		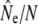n		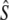	95% C.I.		n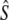
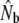Biscay Bay River	0.012	72	629	(213–∞)	3,121	0.20	7	19	1,734	(274–∞)	0.56	10	19	602	2,915
Conne River	0.053	57	2,547	(476–∞)	12,573	0.20	4	27	646	(256–∞)	0.05	9	24	167	813
Gander River	0.095	87	1,933	(880–18,394)	—	—	8	24	1,145	(194–∞)	—	10	22	759	4,117
Middle Brook	0.065	84	836	(336–∞)	2,300	0.36	7	23	429	(197–∞)	0.19	9	22	684	3,527
Northeast River	0.109	52	1,197	(356–∞)	1,262	0.95	7	23	∞	(3329–∞)	—	11	21	∞	∞
Northeast Brook	0.063	61	376	(133–∞)	400	0.94	7	19	283	(117–∞)	0.71	11	18	172	895
Sandhill River	0.095	84	825	(408–3,399)	21,971	0.04	7	24	582	(201–∞)	0.03	12	22	465	3,115
Terra Nova River	0.029	76	1,371	(328–∞)	5,243	0.26	6	21	2,970	(348–∞)	0.57	9	20	11,927	61,053

reflects discrete generations, is the harmonic mean of 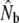estimates derived from SALMONNb multiplied by G, and estimates are derived from the model of Jorde and Ryman (1995), on the basis of harmonic mean sample sizes 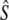. n refers to the number of consecutive cohort comparisons (cohort model) or to the total number of individual cohorts (Pacific salmon model). Demographic estimates of anadromous iteroparity incidence are also provided.

Figure 2.—

Annual trends in anadromous run sizes (open circles, solid lines) and N_b estimates (shaded bars) for four Newfoundland rivers, (a) Northeast Brook, (b) Middle Brook, (c) Conne River, and (d) Gander River, in relation to the marine fishery closure of 1992 (dashed vertical line). Note the logarithmic scale for count in Conne River and Gander River. Annual N_b estimates were obtained with SALMONNb (Waples et al. 2007). Asterisks refer to estimates of infinity.

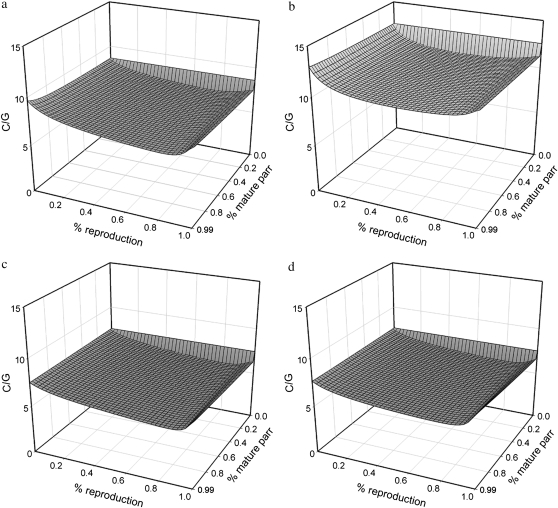
We employed Jorde and Ryman's (1995) method to estimate N_e while accounting for age structure. First, we used simulations to evaluate the consequences of varying parr maturation and reproductive contribution for model parameters C and G, i.e., for the strength of genetic fluctuations for a given survival and reproduction schedule. Simulations suggest both parameters are much more sensitive to variation in reproductive contribution of mature male parr than to variation in maturation incidence. Increased male parr reproduction tends to increase the genetic covariance between cohorts (reducing C) and reduce generation interval G. However, it is the C/G ratio that determines the genetic consequences for 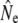; when considering C and G jointly (Figure 3), the effects of mature parr on N_e estimation appear limited. Mature parr reproductive contribution has a weak, buffering effect on fluctuations, with the exception of increases at very high levels of parr reproductive contribution (>90%). Although biologically plausible, these latter increases may mainly reflect a modeling artifact, related to assumptions about the age structure and reproductive contribution of the mature parr age classes. Second, the genetic consequences of age structure vary among rivers (Figure 3), reflecting differences in the river-specific age composition of adults, but the mildly buffering effect of mature parr reproduction remains fairly constant. Summarizing, these simulation results suggest that the assumption of 30% reproductive contribution by mature parr appears reasonable. Unless mature male parr reproductive success is very low (<10%) or very high (>90%), subsequent genetic N_e estimates derived from the cohort model can thus expected to be fairly robust to variation in mature male parr reproductive contribution.

Figure 3.—

Genetic consequences of parr maturation (% mature parr) and reproductive contribution by mature male parr (% reproduction) for the estimation of N_e from the magnitude of genetic fluctuations among consecutive cohorts, expressed as C/G, calculated following Jorde and Ryman (1995). Results are shown for four representative rivers: (a) Northeast River, (b) Conne River, (c) Gander River, and (d) Sandhill River.

The cohort model yielded empirical 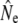values (Table 3) that are qualitatively consistent with the trends among rivers derived from the other genetic estimators. N_e(J&R) estimates are somewhat smaller, but usually closer to estimates from the discrete generation model, than those derived from the Pacific salmon model. The discrete model yielded smaller 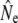than the cohort model in Northeast River and Biscay Bay, which for the latter may have been caused by the comparatively short time span between temporal samples (2.4 generations). Conversely, for Conne River the discrete model yielded higher 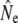values than the other models. These results may suggest that the Pacific salmon model generally does not appear to be a good predictor of N_e for species with low iteroparity such as Atlantic salmon. Alternately, iteroparity in Atlantic salmon may be higher than suggested by the incidence of repeat spawning in anadromous fish.

Changes in effective population size over time:

Temporal changes in effective sizes were evaluated in two different ways. First, we used single sample estimates based on linkage disequilibrium (Table 4). We find that linkage disequilibrium (LD)-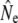 can fluctuate considerably, with some indications of increases after 1992 in Middle Brook and Northeast Brook. Furthermore, this method frequently yielded N_e estimates of infinity for larger rivers such as Gander River, suggesting limitations in statistical power to infer N_e there. However, results from these analyses are difficult to interpret, as they are derived from plan I samples, reflecting a value anywhere between N_b and N_e (Waples 2005). Therefore, next we performed a more detailed comparison of N_b estimates on the basis of cohort samples, limited to two smaller rivers where sampling may have been more appropriate considering census sizes (Table 5). Again, these results show that annual N_b estimates can fluctuate widely (e.g., Middle Brook). Nevertheless, N_b estimates for Northeast Brook appear to have somewhat increased after the closure of the marine fishery (1992). In both rivers, 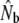are accompanied by wide confidence intervals.

TABLE 4.

Temporal trends in genetic N_e estimates

	Linkage disequilibrium (LD)				Cohort model
River	Yr		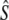LD-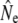	95% C.I.	G	C	n		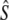	95% C.I.
Biscay Bay	1983	64	567	(330–1,842)
	1988	73	467	(307–933)
	1994	81	∞	(1,203–∞)
Conne	1976	40	488	(205–∞)
	1980	45	345	(186–1,761)	4.8	53.8	1	22	804	(281–∞)
	1986	49	3,342	(446–∞)
	1998	67	2,729	(582–∞)
	2003	96	2,008	(728–∞)	4.8	60.9	3	29	791	(305–∞)
Gander	1951	76	2,774	(786–∞)
	1978	67	1,300	(522–∞)	5.4	33.8	6	22	1,766	(311–∞)
	1984	76	∞	(1,409–∞)
	1996	68	∞	(986–∞)	5.4	36.5	2	31	1,270	(389–∞)
	2003	100	∞	(1,838–∞)
Middle Brook	1982	70	417	(269–879)	5.2	41.2	4	19	331	(147–∞)
	1990	50	237	(159–450)
	1997	81	498	(322–1,041)	5.1	41.7	3	27	1,616	(334–∞)
	2004	101	318	(248–435)
Northeast River	1974	50	∞	(1,141–∞)
	1980	74	400	(243–1,017)
	1988	81	46	(42–51)
	1997	77	149	(121–192)
Northeast Brook	1985	50	42	(35–51)	5.1	37.9	4	17	251	(96–∞)
	1991	65	43	(38–50)
	1997	65	143	(101–227)	5.2	39.2	3	23	438	(142–∞)
	2003	52	222	(127–712)
Sandhill	1967	63	2,418	(571–∞)	6.7	44.8	5	20	1,215	(191–∞)
	1973	64	3,784	(688–∞)
	1994	85	∞	(1,855–∞)	6.7	44.8	2	35	1,050	(390–∞)
	2003	127	1,588	(837–11,712)
Terra Nova	1978	71	∞	(4,464–∞)
	1984	74	1,020	(503–90,655)
	1991	80	622	(402–1,317)
Western Arm Brook	1971	42	∞	(477–∞)
	2004	100	∞	(1,702–∞)

LD-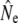 refers to estimates based on single samples using the program LDNe (Waples and Do 2008) and reflects estimates for cohorts grouped before and after the marine fisheries closure (1992). estimates are based on n cohort comparisons (and period-specific parameters G and C).

TABLE 5.

Genetic estimates of the annual number of breeders (LD-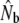) based on the linkage disequilibrium method, for samples with harmonic mean sample size (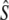) as inferred with the program LDNe (Waples and Do 2008)

River	Yr	N		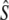LD-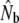	95% C.I.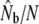
Middle Brook	1977	—	12	∞	(54–∞)	—
	1978	1403	24	∞	(203–∞)	—
	1979	1350	24	289	(104–∞)	0.21
	1985	904	13	437	(58–∞)	0.48
	1986	1036	11	792	(49–∞)	0.76
	1991	562	25	200	(94–∞)	0.36
	1992	1182	26	457	(144–∞)	0.39
	1993	1959	15	∞	(109–∞)	—
	1997	1221	22	∞	(236–∞)	—
	1998	2405	48	190	(131–329)	0.08
	1999	1802	25	410	(128–∞)	0.23
Northeast Brook	1980	—	16	65	(28–∞)	—
	1981	—	19	190	(48–∞)	—
	1985	124	11	35	(15–∞)	0.28
	1986	158	20	13	(10–17)	0.08
	1987	91	28	208	(76–∞)	2.28
	1991	99	14	43	(19–∞)	0.43
	1992	49	14	∞	(49–∞)	—
	1993	79	17	773	(53–∞)	9.78
	1994	99	13	939	(36–∞)	9.49
	1998	91	41	196	(100–1494)	2.15
	1999	95	31	435	(118–∞)	4.58

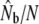ratios are based on the size of annual anadromous runs (N).

We repeated the cohort model on cohorts grouped before and after 1992. The closure of the marine fishery in 1992 may have influenced the genetic behavior of rivers differently, with a possible relation to river size (Table 4). First, the fishery closure had little impact on life table parameters that relate age structure to N_e within rivers, suggesting that population dynamics may not have been strongly altered after 1992. However, we document small increases in C after 1992, although assumptions about mature parr reproduction were kept constant in life table analyses. Estimates derived from the cohort model suggest that N_e may have increased in smaller census size rivers (Northeast Brook, Middle Brook), but possibly not in larger ones (Gander, Conne, Sandhill). Again, these conclusions have to be qualified by the low precision of N_e estimates: confidence intervals often include infinity. Thus, a lack of observed changes in N_e in larger rivers may have been caused by limited statistical power (sample size limitations) for detecting such changes.

Changes in demographic factors underlying N_e:

Finally, an exploratory analysis of reproductive factors underlying N_b (Table 6) suggests that some temporal changes may have occurred in breeding ecology. Due to the limited availability of demographic data, these calculations were performed only for two rivers. As female fecundity was the only factor considered, N_bf estimates are likely biased upward; subsequent N_bm estimates will be biased downward and we suggest some caution in interpreting results. Demographic estimates of the effective number of females (N_bf) remained relatively stable over time; hence changes in genetic estimates of N_b may be mainly attributable to fluctuations in N_bm. Analyses suggest N_bm estimates may have increased after 1992, both absolutely and relative to N_bf, although relationships with census male size vary. Annual male census sizes (N_m) have remained stable or decreased in Northeast Brook, but have increased in Middle Brook, whereas N_bm may have increased in both rivers. Moreover, there may be a positive relation between N_bm and N_m in Middle Brook (r = 0.61, p = 0.15, n = 8), but not in Northeast Brook (Trepassey, r = 0.02, p = 0.96, n = 7).

TABLE 6.

Demographic estimates of the annual effective number of male breeders (N_bm), derived from 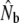(Pacific salmon model), and demographic estimates of the effective number of females (N_bf)

River	Yr	Census	Nm	Nf		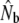Nbf	Nbm	Nbm/Nbf
Middle Brook	1978	1403	117	1286	104	1225	27	0.02
	1979	1350	270	1080	163	1022	42	0.04
	1985	904	168	736	167	700	44	0.06
	1991	562	241	321	210	285	64	0.23
	1992	1182	220	962	1019	919	353	0.38
	1993	1959	440	1519	1369	1423	451	0.32
	1997	1221	234	987	1396	931	559	0.60
	1998	2405	172	2233	180	2089	46	0.02
Northeast Brook	1985	124	21	103	235	95	154	1.62
	1986	158	35	123	33	107	9	0.08
	1987	91	37	54	145	52	119	2.27
	1991	99	11	88	97	86	34	0.39
	1992	49	9	40	2367	39	∞	∞
	1994	99	13	86	682	84	∞	∞
	1998	91	3	88	158	85	74	0.87

Results are shown only for rivers with sufficient genetic data and demographic data; the latter include census size information of annual cohorts, divided into males (N_m) and females (N_f).

DISCUSSION

All genetic models make simplifying assumptions about populations, but this study reemphasizes the potential complexity of life history, age structure, and demography that underlie N_e and hence affect its empirical estimation in fluctuating populations. Iteroparity, even when presumably low, may have to be accounted for in genetic estimation models. On the other hand, variance in reproductive contribution by mature male parr may affect age structure more so than 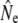estimation. Accounting for potential changes in age structure and population dynamics, we document temporal changes in N_e in some rivers. These changes may reflect abundance increases of breeders as well as breeding system alterations and possibly effects of density-dependence and metapopulation dynamics. We start by discussing the limitations arising from our sampling design.

Sampling limitations:

An important element of any genetic method of estimating N_e is adequate sampling, both in terms of sample size and in terms of representation of the entire population. These concerns are especially relevant when actual effective population sizes are large, as all (temporal) methods measure a signal that scales to 1/N_e. Our conclusions may hence be affected by sampling error: for example, the sample sizes of individual cohorts were often small (minimum S = 12, Table 3). Similarly, the number of consecutive cohort comparisons was often small (Table 3, Table 5), which may have affected the accuracy of the cohort model, in particular under strong demographic perturbations (Jorde and Ryman 1995). Considerations of sampling efforts required to obtain sufficient statistical power (e.g., Palstra and Ruzzante 2008) suggest that appropriate sample sizes for larger rivers (e.g., Gander, Conne) might have been well in excess of 100 individuals. Thus, we limited some of our genetic analyses to smaller river populations. Nevertheless, sampling limitations are evident in the wide confidence intervals (C.I.'s) associated with many 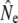. This affects the strength of inferences on comparisons between 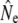from different estimator methods, as well as changes in 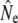over time. Sampling efforts to reliably infer N_e and detect temporal changes may have to be (considerably) larger than those underpinning this study (N = 2758).

Second, genetic estimates derived from models for overlapping generations are sensitive to the confidence with which individuals could be assigned back to their cohorts, on the basis of age determination of fish scales. Random errors in this assignment will likely introduce an upward bias into 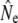, since a mixture of individuals of different ages present in the presumed “cohorts” will dilute signals of genetic differentiation present among the actual cohorts (Palm et al. 2003). This source of bias may explain why genetic estimates derived from the Pacific salmon model are often larger than those from the discrete generation model, but not the differences between N_e estimates from the semelparous Pacific salmon and cohort models.

Age structure and N_e estimation:

Age structure and reproductive biology are important determinants of N_e (Felsenstein 1971; Hill 1972; Nunney 1991, 1993, 1996; Frankham 1995) with consequences for its empirical estimation (Jorde and Ryman 1995; Engen et al. 2007; Waples and Yokota 2007). The discrete generation model has so far been most commonly applied, but will be (downwardly) biased, when applied to temporal samples taken over short time spans for species with overlapping generations (Waples and Yokota 2007; Palstra and Ruzzante 2008). This bias arises mainly because signals of genetic drift (related to N_e) will be strongly affected by genetic (co)variances generated by age structure (Jorde and Ryman 1995). Under these circumstances, genetic estimators designed specifically for overlapping generations (Waples 1990a,b; Jorde and Ryman 1995) will be preferable to discrete temporal methods. Previous empirical investigations of (fish) species with low iteroparity have tended to use either one of these methods (e.g., Palm et al. 2003; Consuegra et al. 2005; Fraser et al. 2007a). This study is the first to simultaneously apply two models that differ principally in the assumption of iteroparity, facilitating an investigation of the importance of low iteroparity for N_e estimation.

On the one hand, whenever individuals can reproduce more than once, the semelparous Pacific salmon model can be expected to overestimate N_e. This upward bias will be caused by genetic contributions of iteroparous individuals that will tend to buffer genetic fluctuations among years and thus reduce the strength of interannual genetic signals on which estimates of N_e are based in the Pacific salmon model. Conversely, the cohort model may underestimate N_e when survival depends strongly on previous reproduction (and total mortality in the population is low) (Jorde and Ryman 1995). Unfortunately, the reproductive biology of Atlantic salmon may incorporate both of these aspects. A comparison of N_e estimates derived from these two models to discrete temporal estimates (Table 3) suggests that the upward bias in the Pacific salmon model may be more serious than the risk of downward bias in the cohort model. Although were often lower than , their general similarity may suggest that total mortality rates in Atlantic salmon populations are generally low enough for bias due to reproduction-dependent mortality to be small (cf. Figure 4 in Jorde and Ryman 1995). On the other hand, in six of eight rivers, the Pacific salmon model results in larger N_e estimates than the other two models (Table 3).

This upward bias may arise mainly because of the calculation of from the harmonic mean of annual N_b estimates. Using demographic data, Waples (2002) found that effective population size in fluctuating salmon populations can be (much) smaller than the product 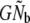. This reduction (40–60%) was attributed to relative discrepancies between the size of cohorts and their reproductive contribution to a given generation. Cohort and discrete generation models directly estimate N_e and may thus be less sensitive to this source of bias. Demographic analyses (following Waples 2002) suggest that this reduction may be weak to moderate in the populations studied (5–59%). Nevertheless, remain relatively high after correcting for this bias, suggesting that even low iteroparity can bias N_e estimation in a strictly semelparous model. Extended analyses, comparing annual N_b estimates from the Pacific salmon model with discrete generation temporal estimates of N_b, tend to support this conclusion (see Table S2). Although the interpretation of N_e estimates derived from different estimator models is complicated by differing sampling efforts in space and time, as well as wide C.I.'s (Table 3), these findings thus suggest that ignoring low iteroparity is generally not recommended.

These results might also imply that iteroparity in Atlantic salmon populations is higher than suggested by estimates of iteroparity in anadromous fish (Table 3), possibly due to contributions by resident nonanadromous salmon, including mature parr. Nonanadromous salmon probably have higher rates of iteroparity than anadromous salmon and can be common in some Newfoundland systems (Leggett and Power 1969; Hutchings 2002). Mature male parr might also contribute to iteroparity, given that similar discrepancies between the salmon and the discrete generation model are evident in empirical studies on systems where nonanadromous salmon are presumably absent (e.g., Consuegra et al. 2005; Fraser et al. 2007a). A substantial mortality cost associated with parr maturation (s_rel = 0.35) does not preclude iteroparity, either again as mature parr or as anadromous adults. For example, although less abundant and often older than females, many males that previously matured as parr are present in smolt runs in Newfoundland (Chadwick 1981; Dalley et al. 1983; Myers 1984; Hutchings 1986; Hutchings and Myers 1994). This uncertainty regarding the general incidence of iteroparity in males may make the cohort model preferable over the Pacific salmon (semelparity assumed) model for N_e estimation in Atlantic salmon.

Single sample estimators of N_e may be less influenced by assumptions of iteroparity and thus prove useful, provided that careful attention is paid to what these estimates apply to (see Waples 2005). LD-N_e estimates based on plan I temporal samples (Table 5) should be interpreted with some caution, as variance in the magnitude of LD-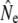 will also be generated by variable age composition of samples (see Table S1). These difficulties emphasize that, regardless of the genetic methods applied, empirical N_e studies should be founded on detailed knowledge of life history and age structure.

Consequences of gene flow:

Our study adds to a growing number of empirical investigations of N_e in salmonid fish (e.g., Østergaard et al. 2003; Shrimpton and Heath 2003; Lage and Kornfield 2006; Fraser et al. 2007b; Vähä et al. 2008). Using various temporal genetic methods, we document relatively high estimates of N_e as well as increases in 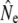in small populations over time. Gene flow as inferred from Wang and Whitlock's (2003) approach may provide one explanation for this observation, as gene flow might often be more prevalent into effectively smaller salmonid populations, thus maintaining genetic diversity (Consuegra et al. 2005; Fraser et al. 2007a; Hansen et al. 2007). Indeed, in many (but not all) rivers a marked decrease in 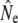was observed once gene flow was considered. The approach of Wang and Whitlock (2003) has been criticized on the biological reality of its migration model (Hoffman et al. 2004; Fraser et al. 2007b). Nevertheless, temporal estimates of gene flow (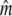) agree with contemporary genetic estimates of migration into these rivers (Palstra et al. 2007) and direct estimates of migration from tagging studies in Atlantic salmon in general (Stabell 1984; Jonsson et al. 2003). On the other hand, our results also caution against generalizations, as we occasionally found very limited evidence for gene flow among regionally (very) proximate rivers.

It is less clear whether temporal changes in gene flow underpin those observed in 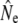in some (smaller) rivers. Current analytical limitations complicate investigating effects of gene flow on N_e over short time spans. Removal of putative immigrants from samples prior to N_e estimation may have been one solution, but would have reduced (already limited) sample sizes, particularly for the cohort and Pacific salmon models. These sampling concerns may, however, be less important for single sample estimators. As an exploratory analysis, we removed putative migrants from two temporal samples (Middle Brook, 1982 and Middle Brook, 1997), using assignments tests (Paetkau et al. 2004), and then repeated linkage-disequilibrium analyses on truncated samples. For the corrected 1982 sample this results in LD- 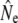= 384 (95% C.I.: 235–974, 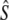= 59.6), whereas the corrected 1997 sample yields LD- 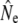= 234 (95% C.I.: 172–360, 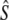= 63.8). Although these assignment tests yield estimates of migration that are relatively high compared to other approaches (Table 2) or those reported in the literature (e.g., Stabell 1984), the measure of interest here is relative change over time. Hence, whereas both samples show a decrease in 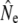(see Table 4) when individuals putatively identified as migrants were excluded, this decrease is stronger for the 1997 sample (52%) than for the 1982 sample (8%). These results may thus indicate temporal changes in the strength of gene flow that might be causally linked to changes in 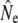in some rivers over time.

Life history diversity and N_e:

Stability of N_e in the context of demographic changes may be attributable to life history diversity, as this facilitates maximization of lifetime reproductive success under various environmental and demographic conditions. Mature male parr reproduction has been speculated to be beneficial for N_e (Saunders and Schom 1985; L'Abée-Lund 1989; Martinez et al. 2000; Valiente et al. 2005; Juanes et al. 2007), although mature parr may “increase” effective size only in the sense that 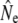is increased compared to when mature parr are ignored in analyses (e.g., Jones and Hutchings 2002; Saura et al. 2008). Nevertheless, the reasoning implies that parr reproductive contribution increases N_e by reducing the variance in (male) individual reproductive success. Empirical investigations have often applied theory for discrete generations, through the influence of mature parr on sex bias (e.g., L'Abée-Lund 1989; Consuegra et al. 2005) or individual reproductive success in a single breeding season (e.g., Martinez et al. 2000; Taggart et al. 2001). Both approaches may not correctly reflect processes in age-structured populations with overlapping generations. First, the consequences of sex bias for N_e are expected to be much reduced (Nunney 1991, 1993), in particular when sex bias reflects survival (rather than recruitment) differences. Second, the genetic effects of annual variance in individual reproductive success will be buffered under iteroparity, since individuals that failed to breed in one year may succeed in the future (Nunney 1993). Indeed, individual parr often obtain very little reproductive success in (experimental) spawning events (e.g., Thomaz et al. 1997; Jones and Hutchings 2001, 2002; Weir et al. 2005) as mature parr also establish dominance hierarchies during spawning (Hutchings and Myers 1988; Fleming 1996). Instead, N_e may be mainly affected by the reproductive variance of anadromous males (Mjølnerod et al. 1998; Jones and Hutchings 2002). We find some support for this assertion through a positive relation between annual N_b estimates and the number of anadromous males in Middle Brook. Moreover, total reproductive success by mature male parr may be highest when few anadromous males are present (Jones and Hutchings 2002). For example, Northeast Brook, characterized by anadromous runs with relatively few males, also has the highest N_e/N ratios observed in this study (Table 3), which might be interpreted as a positive effect of mature male parr reproduction on N_e. However, the biological relevance of N_e/N ratios is questionable when N does not accurately reflect the potential number of breeders. If this is indeed the case in Northeast Brook, then our results may simply imply that males in this population maximize their lifetime reproductive success by predominantly maturing and reproducing as parr.

Our life table simulations suggest variance in male parr reproduction has limited influence on the empirical estimation of N_e. While we very likely would have overestimated N_e had we ignored mature parr reproduction (i.e., increased values of C/G, Figure 3), N_e estimation appears more sensitive to age skew in anadromous breeders. Genetic fluctuations among cohorts are already buffered by variable anadromous age at maturity. Furthermore, genetic effects of mature parr reproduction are reduced (or more precisely, halved), since half the alleles in the progeny will descend from females, which are usually obligatory anadromous. As previously reported by Juanes et al. (2007), mature male parr reproduction reduces the strength of genetic fluctuations (i.e., increases the genetic covariance) among consecutive cohorts. That by itself does not increase N_e, because of the concomitant decrease in generation time. Thus, higher levels of mature male parr reproductive success may concentrate breeders in a given generation into a shorter time span, without strongly affecting N_e. This could, however, render such populations more sensitive to environmental stochasticity (Gaggiotti and Vetter 1999) and may actually increase the pace at which genetic variance is lost (e.g., Ryman et al. 1981; Allendorf et al. 2008). These conclusions partly depend on the cohort model assumption of constant population size (Σl_xb_x = 1). Our simulations may therefore be interpreted as a quantification of the effects of parr reproduction on age structure and genetic fluctuations, for a given value of N_e. Mature parr reproduction may be more appropriately viewed as one of a few strategies utilized by male Atlantic salmon to maximize their lifetime reproductive success, the ultimate genetic contribution a stabilization of N_e rather than an absolute increase. The demographic and genetic consequences of this reproductive strategy may be more important, through changing the age structure of a population.

Demography, density dependence, and temporal trends in N_e:

A major goal of this study was to evaluate temporal trends in N_e in populations that have likely undergone demographic fluctuations. Changing population size does not affect the standard, discrete-generation temporal method, which estimates the harmonic mean N_e over the time between samples (Waples and Yokota 2007), but many models for overlapping generations do assume constant population size (e.g., Felsenstein 1971; Hill 1972; Nunney 1993; Jorde and Ryman 1995). Jorde and Ryman (1995) discuss the analytical consequences of demographic perturbations in the cohort model and argue that it may be accounted for by monitoring a population over time, i.e., by calculating F as the mean of several cohort comparisons. In our study this requirement is fulfilled by for the longest time spans per river (Table 3, minimum n = 4). Similarly, for cohorts before and after 1992 usually consist of multiple comparisons, with the exception of Conne River (Table 4). Moreover, these latter analyses were performed using life tables based solely on demographic information pertinent to each time period, to account for potential temporal changes in age structure. Despite the various limitations arising from our analytical approach, results suggest temporal changes in N_e in some, but not all, river populations, that correlate poorly with demographic trends. Concomitantly, the observed temporal and spatial differences in 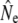provide a poor explanation for differential recovery patterns in abundance observed among rivers after the closure of the commercial fishery (Dempson et al. 2004a). Thus, genetic stochasticity has likely not been a major force impeding population recovery in these rivers, despite very high exploitation rates in the marine fishery prior to the closure (Dempson et al. 2001).

As pointed out previously, sampling limitations likely reduced the ability to detect changes in N_e in larger census size populations. Nevertheless, larger populations may be innately more resistant to changes in N_e. First, effective population size in larger systems may be more prominently influenced by metapopulation dynamics: in Atlantic salmon, larger rivers (including some in Newfoundland) often appear to be genetically substructured (e.g., Beacham and Dempson 1998; Verspoor and Cole 2005; Vähä et al. 2007, 2008). Under these conditions, the reproductive factors reducing N_e within a subpopulation are modulated by processes acting among subpopulations. Population subdivision likely reduces overall N_e (Whitlock and Barton 1997; Nunney 1999), thereby also providing one explanation for lower N_e/N ratios in some large rivers (Table 3). Yet, population (sub)structuring has also been invoked to explain greater demographic stability (Einum et al. 2003). Atlantic salmon in larger river systems tend to display higher life history diversity (Klemetsen et al. 2003) that may enable maximization of lifetime reproductive success under a wider range of demographic and environmental conditions, hence conveying an increased genetic stability. Whether larger populations are generally characterized by this apparent paradox of lower N_e/N ratios and higher genetic stability (i.e., stable N_e) remains to be investigated.

Density dependence may affect the relationships between life history, demography, and N_e. First, density dependence (operating at the freshwater stage) can influence the expression of life history phenotypes (Kokko and Rankin 2006; Einum et al. 2008), either directly through genetic changes or indirectly through phenotypic plasticity modulated by growth rates (Gardiner and Shackley 1991; Jonsson et al. 1998; Nordwall et al. 2001). For example, population dynamics in Northeast Brook display signs of density dependence (Klemetsen et al. 2003), and declining anadromous runs here have also tended to become more female biased. Whether plastic or genetically based (Piche et al. 2008), such trends may indicate a shift to earlier maturation as male parr in this system. Second, density dependence is also a prerequisite for genetic compensation, where reduced variance in individual reproductive success underpins increased N_e/N ratios at low population size (Pray et al. 1996; Ardren and Kapuscinski 2003; Fraser et al. 2007b; Watts et al. 2007). We observed such relationships in both rivers considered in demographic detail. Finally, under endogenous population regulation, the total reproductive value of a salmonid population (and hence N_e) may depend mainly on the availability of suitable habitat, as observed in Chinook salmon (Shrimpton and Heath 2003). Freshwater habitat in Newfoundland has remained relatively pristine, hence providing an additional explanation for the observed resilience of N_e in the face of population declines. When considered from this angle, increases in N_e in some rivers after the marine fishery closure may indicate that the high exploitation rates kept these populations below their carrying capacity.

Life history evolves to maximize the lifetime reproductive success of individuals in a population and this in turn is the principal determinant of effective population size. The life history plasticity evident in Atlantic salmon and other salmonid fish (Hutchings 2004) may convey resilience against declines in N_e through enabling optimization of fitness under a range of environmental conditions. Age structures characterized by overlapping generations and multiple mating opportunities (iteroparity) may thus be more resistant to the detrimental genetic consequences of years with poor recruitment and low numbers of breeders (Warner and Chesson 1985; Nunney 1993; Ellner and Hairston 1994; Gaggiotti and Vetter 1999) and render a population less sensitive to environmental stochasticity (Gaggiotti and Vetter 1999). Some support for this comes from empirical studies on long-lived fish species (e.g., Diaz et al. 2000; Lippe et al. 2006). Resilience against genetic stochasticity afforded by life history may, however, not protect against other stochastic factors or against declines driven by deterministic factors. A particular value of N_e can reflect a large variety of age structures with markedly different sensitivities to environmental and genetic stochasticity (Ryman et al. 1981; Gaggiotti and Vetter 1999). As age structures become more complex, sensitivity to environmental stochasticity and the pace at which genetic diversity is lost may both decrease, but so may the pace of a population's response to natural selection. The evolutionary implications of effective population size therefore depend on detailed knowledge of its interactions with life history and population dynamics. These insights may be attained only through carefully considering age structure in empirical investigations of N_e.