Mapping in Structured Populations by Resample Model Averaging

Abstract

Highly recombinant populations derived from inbred lines, such as advanced intercross lines and heterogeneous stocks, can be used to map loci far more accurately than is possible with standard intercrosses. However, the varying degrees of relatedness that exist between individuals complicate analysis, potentially leading to many false positive signals. We describe a method to deal with these problems that does not require pedigree information and accounts for model uncertainty through model averaging. In our method, we select multiple quantitative trait loci (QTL) models using forward selection applied to resampled data sets obtained by nonparametric bootstrapping and subsampling. We provide model-averaged statistics about the probability of loci or of multilocus regions being included in model selection, and this leads to more accurate identification of QTL than by single-locus mapping. The generality of our approach means it can potentially be applied to any population of unknown structure.

A number of experimental strategies for genetic mapping of complex traits in model organisms involve the use of highly recombinant populations derived from inbred lines. Examples are advanced intercross lines (AILs) (proposed by Darvasi and Soller 1995), where a pair of inbred progenitors are intercrossed for three or more generations, and heterogeneous stocks (HS) (Demarest et al. 1999), where a number, usually eight, of inbred strains are intercrossed for many generations. In theory, these strategies can achieve much higher-resolution mapping than is obtainable with standard inbred strain crosses because they accumulate a greater density of recombinants.

It is often assumed that these populations can be analyzed as if the individuals were equally related, as in an F₂ cross, or unrelated, as in the case of a carefully ascertained human case–control association study. The simplifying assumptions are that family relations may be ignored and that each locus can be analyzed independently. However, it can easily be shown, for example by simulation, that these assumptions are false.

What makes genetic association in an AIL or HS more complicated than in an F₂ cross? Advanced intercross lines are bred in maintenance populations of small to moderate size, typically between 20 and 50 mating pairs for n − 1 generations, and then bred out in a final generation to achieve a larger mapping population. The breeding strategy employed during the maintenance phase is usually chosen to minimize loss of genetic diversity and is similar to schemes used in the preservation of rare species. Completely random mating is inappropriate because, owing to the small number of individuals, it gives rise to an unacceptable number of matings between full sibs. Mating maximally unrelated individuals after Wright (1921) is optimal in the first few generations but rapidly contracts the network of unrelateds, making consanguineous breeding in later generations inevitable. More often schemes are chosen to balance convenience with minimal long-term inbreeding. In pseudorandom mating, mates are chosen at random, although mating to close relatives is forbidden. In regular systems such as circular mating, the population is maintained in a number of separate groups and males are transferred between groups in a predetermined pattern (Kimura and Crow 1963). Other more complex schemes based on minimizing coancestry are a sophistication of Wright's method and may guard better against inbreeding (Caballero and Toro 2000) but are not to our knowledge used in the generation of populations bred for experimental mapping. Rockman and Kruglyak (2008) recently compared breeding schemes for the generation of recombinant inbred AILs (RIAILs) in terms of their ability to guard against allele-frequency drift and promote map expansion, finding that random-pair mating is superior to circular or random mating for producing panels of inbred lines for QTL mapping.

One important consequence of these breeding schemes applied over multiple generations in a finite outbred population is the emergence of long-range correlations between genetic markers, such that, for example, it is sometimes possible to predict the genotype of a marker on chromosome 1 by the genotype on chromosome 5. These are due to partial fixation of pairs of haplotype blocks within subsets of the population. The exact pairings are stochastically determined, but some breeding designs are more susceptible to this effect than others. Consequently a single causal variant segregating in the cross will be confounded not only with neighboring loci [due to short-range linkage disequilibrium (LD)] but also with distant loci.

HS populations have used similar breeding schemes to AILs (Valdar et al. 2006a) but differ from AILs in that they are descended from more than two inbred strains: typically, though not necessarily, eight. This adds a further level of complexity. Because the markers used for genotyping will have fewer alleles than the number of haplotypes segregating in the cross, individual markers typically do not unambiguously identify the underlying strain haplotype. In particular, unless all variants are genotyped, QTL will be missed by single-marker association analysis (Mott et al. 2000).

Large-scale studies of HS, AILs, and similarly structured populations are also particularly susceptible to environment–genotype confounds that are avoidable in F₂'s, backcrosses, and simpler designs. With limited laboratory resources, inclusion of siblings in a genetic mapping study is often unavoidable. However, doing so introduces a level of clustering that can result in, for example, some families and alleles being oversampled in summer and undersampled in winter, which in turn can produce spurious genetic or family associations. The complex correlation structures present in AILs, HS, and related populations cause simplistic association methods to misclassify false signals as true QTL.

These highly recombinant structured experimental populations resemble those found in plant and animal breeding where it is common to model the multiple levels of relatedness through variance components parameterized by the kinship matrix. Specifically, to account for effects from the rest of the genome the effect of a single locus is estimated simultaneously with one or more random intercept terms whose expected correlation structure is fixed given the pedigree and models the effects of overall genetic relatedness (Kennedy et al. 1992; Jannink et al. 2001; Zhao et al. 2007). Such approaches are highly applicable to HS and AIL populations, and control the false positive rate of association by diminishing the estimated effect and significance of loci that are predictive of family structure.

However, two loci that are associated with the phenotype can be correlated with each other in a way that is not well explained by overall genetic relatedness. Moreover, it is plausible that a causal locus happens to be predictive of family structure and so is hard to detect under polygenic modeling. It is therefore useful to have complementary approaches that characterize the correlation structure between loci but that do not make strong assumptions about the relationship between the underlying population structure and the trait of interest.

In this article we describe single-locus and multilocus approaches for dealing with both the detection and the subsequent characterization of location uncertainty of QTL segregating in structured populations. We expect our method to be particularly helpful in cases where the founders are known but the pedigree is not and where the population structure is expected to be smooth in the sense that any major structural features, such as gross environmental effects or strong subpopulation effects arising from combining separate populations at a late stage, are known or absent. We argue that when it comes to detecting QTL, a single-locus approach is inferior to one that models multiple loci, a view that has been advocated by several groups in animal and plant genetics (Jansen 1993; Zeng 1993; Sillanpaa and Arjas 1998; Broman and Speed 2002), and is one increasingly taken in human association (Balding 2006 and refs therein; Servin and Stephens 2007; Fridley 2008 and refs therein).

METHODS

We describe first an approach to single-locus modeling that reduces false positives by more conservative estimation of significance thresholds, but at the cost of increasing false negatives. We then describe a preferable way to model the confounding elements of the population, doing so explicitly in a multilocus framework. Finally we describe alternative single-locus approaches included for illustrative comparison in our simulations.

Modeling single loci:

The approach that follows is applicable to a wide range of trait distributions including binary (case–control), binomial (count), gamma, and survival (time-to-event) distributions, and these have been implemented in our software (see end of discussion). For clarity though we restrict our focus to normally distributed traits. Let the phenotype of individual i when affected by a single genetic locus m be modeled as

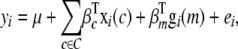(1)

where 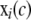is the value of the covariate c for individual i, C is the set of all known (or suspected) covariates, which we define to include environmental covariates and any gross components of population structure (e.g., subpopulations of a mapping population sourced from different distributors or breeders or other “obvious” subpopulation indicators), g_i(m) specifies the genetic predictor at locus m in individual i, μ is the trait mean, β is used generically to describe a predictor's effect, and e_i ∼ N(0, σ²). A nominal P-value for the association of the locus m with the phenotype can be calculated as the probability that a more extreme test statistic would be observed under the null hypothesis that β_m = 0, as judged by a partial F-test (or more generally a likelihood-ratio test for the model in Equation 1 against one without the locus term).

We define g_i(m) in terms of the HAPPY statistical model (Mott et al. 2000), where a locus is defined as the interval between two observed loci and the genotype for the individual is described as the estimated descent of founder haplotypes within that interval. Because this model uses identity by descent, in some literature it would be classified as linkage disequilibrium mapping (e.g., Meuwissen and Goddard 2000) to distinguish it from pure association with observed genotypes. However, because our approach generalizes trivially to the case where g_i(m) is coded as an observed genotype, and because the distinction between “LD mapping” and “association” is defined inconsistently across and within plant, human, and animal literature (cf. Hastbacka et al. 1992; Kruglyak 1999; Clark 2003; Mackay and Powell 2007), we use the general term “association.” (We note that any method that computes these quantities could be substituted for HAPPY. Specifically, g_i(m) is a vector of expected haplotype proportions for mouse i at marker interval m defined as follows. Let D be an h × h matrix of expected diplotype proportions for marker interval m in individual i, such that element D_st is the expected proportion of the interval that is composed of the phased haplotype pair {s, t}, where s and t are founder haplotypes. Then under an additive plus dominance (i.e., full) genetic model, g_i(m) = vec(D); under a full model where phase is unknown, 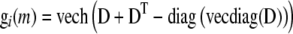, where 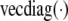extracts the diagonal elements of a matrix and other functions are defined as in, for example, Gentle (2007); and under an additive model where the 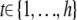th element of g_i(m) is the expected number of haplotypes from strain t over the interval, 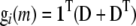(see also appendix a). For marker intervals on the X chromosome, males are treated as homozygous for their hemizygous allele. In the simple case of a single additive effect modeled with no covariates in a two-founder system, such as an F₂ cross or an advanced intercross, Equation 1 simplifies to

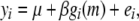(2)

where g_i(m) is the expected proportion of t haplotypes in marker interval m of individual i, where t is one of the two founders.

Significance thresholds: parametric bootstrapping from a multilevel sibship model:

It is useful to have a genomewide significance threshold by which to judge how unusual an observed association would be under the null hypothesis of no QTL effect. However, in a population with a complex genetic and family correlation structure, it is sometimes unclear how to identify the exchangeable structure of the data under the null hypothesis (Churchill and Doerge 2008). For example, if the phenotype is influenced by environmental covariates, then members of the population are exchangeable only conditional on those covariates. The permutation is then valid only if it is within environment groups or if the phenotype is corrected for the effect of the environment before permutation. On this principle, sibship-specific effects may be removed by either permuting within sibship or correcting the phenotype for sibship effects prior to permutation. However, in populations with family structure, the sibship-specific and allele-specific effects are confounded: removing one also removes the other, causing loss of power.

A compromise is to correct the phenotype at an early stage in the analysis with the sibship effect (and some or all of the environmental effects) estimated using partial pooling (Gelman and Hill 2007), also known as best linear unbiased prediction (BLUP) or shrinkage (McCulloch and Searle 2001), or using the related approach of fitting animal models (Henderson 1974; Lynch and Walsh 1998; Aulchenko et al. 2007). Nonetheless, if the phenotype is influenced by multiple genetic loci of small effect, even the shrinkage estimate of the sibship effect will be confounded with the cumulative effect of several QTL, and so correcting for this will still reduce power.

Consequently, it is worth considering an alternative approach of simulating null phenotypes by parametric bootstrap from a hierarchical sibship model. Let 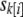denote the effect of sibship k containing individual i (all individuals from the same sibship share the same effect); then we fit the null model

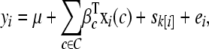(3)

where 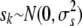, to obtain point estimates 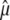, , 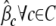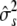and 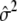. To generate null model phenotypes we first sample hierarchically from

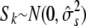and then from

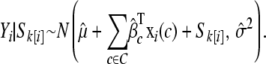This generates a set of phenotypes whose correlation structure reflects the grouping of environments and sibships in the observed population, but not necessarily the correlation structure between sibships that might be due to the segregation of specific alleles since the rank order of sibship effects is scrambled, in effect, sampling between and within sibships. The single-locus model in Equation 1 is then applied to each simulated data set (see appendix b) and the resulting distribution of genomewide maximum P-values is taken as the distribution of maximum P-values expected under the null hypothesis of no QTL. This null distribution is then fitted to a generalized extreme value (GEV) distribution and a suitable quantile is estimated as the genomewide significance threshold (Dudbridge and Koeleman 2004; Valdar et al. 2006a).

Modeling multiple loci:

Genotype correlations between loci mean that some seemingly independent associations will be confounded. Multiple-QTL modeling can clarify these relationships. The mutlilocus version of Equation 1 is

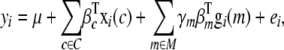(4)

where M is the set of all genetic predictors, and 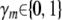is an indicator variable for each genetic predictor m denoting its inclusion (γ_m = 1) or exclusion (γ_m = 0) from the model, with γ hereafter denoting the vector of γ_m's for all m. Identifying the true set of QTL (or rather the set of genetic predictors that best capture the true causal signals) means finding the correct assignment of ones and zeros to γ, a model selection problem (Broman and Speed 2002).

Resample model averaging: bootstrap aggregation and subsample aggregation:

Traditional methods of model selection aim to find an assignment of ones and zeros to γ that produces a parsimonious model with good explanatory power. However, choosing a single model (which we call discrete selection) does not characterize the uncertainty of model choice and leads to an estimate of γ that is unstable in the sense that observing a slightly different data set can result in a quite different model being chosen (and where a causal interpretation is sought, a different conclusion) (e.g., Sillanpaa and Corander 2002). Not only do such estimates have high variance, but also there is no standard function for determining the variance of the estimator.

Bootstrap aggregation (bagging) and subsample aggregation (subagging) are resample model averaging (RMA) procedures that have been shown to produce more accurate predictions of quantities related to multiple predictor models, especially when the standard estimators of those quantities have high variance (Breiman 1996; Buhlmann and Yu 2002). Here we adopt a strategy of inferring γ that minimizes risk under quadratic loss, aiming to find an estimate 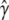with low mean squared error, . Under this loss structure, RMA should therefore produce an estimate 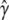that is more stable than that from discrete selection and one that leads to greater predictive accuracy. A probabilistic interpretation is that if 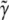is the estimate of γ given by discrete model selection applied to a new sample drawn from the underlying population model, then 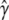from RMA estimates 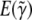, the long run expectation of .

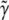The suitability of resampling for assessing frequentist variability in model choice depends on how well the resample procedure mimics the ideal of sampling from the population (i.e., of repeating the experiment many times). If we knew the true model γ in advance and wanted to measure properties of the inference process, such as how often the model selection procedure included particular subsets of loci or how well 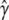matched true γ, then it would be appropriate to resample by parametric bootstrapping, first fitting the true model and then applying the inference procedure to data sets generated by draws from it. Since in this context we do not know the true model, we use nonparametric resampling, by which we mean generating a new data set by drawing a fraction p individuals at random from the population either with or without replacement. In doing this we assume infinite exchangeability among only the rows in the data, where each row represents trait, covariate, and genetic data for a single individual. Additional constraints are required (e.g., block resampling) for time series and other data structures where the order of row labels may be important.

Sampling with replacement is otherwise referred to as nonparametric bootstrapping, sampling without replacement when p < 1 is subsampling (Politis et al. 1999), whereas sampling without replacement when p = 1 recovers the original data set. “Bagging” is model averaging based on nonparametric bootstrapping [from “bootstrap aggregation” (Breiman 1996)] and “subagging” is when it is based on subsampling [from “subsample aggregation” (Buhlmann and Yu 2002)].

Within each resample we use forward selection to select the multiple-QTL model because it is fast, has predictable convergence (relative to, say, stepwise selection), and scales to any number of loci (unlike backward selection), making it highly practical in this context. For the objective function that compares nested models we use the negative log₁₀ P-value (log P) of the partial F-test (or likelihood-ratio test for non-least-squares problems) and we terminate selection when the highest log P from adding a predictor fails to exceed the 5% genomewide significance threshold that would be given by naive permutation. Model selection is conceptually distinct from the test of a null hypothesis (e.g., Raftery 1995) and so specifying a looser threshold than that for single-locus inference does not imply a contradiction. Moreover for this purpose we prefer the genomewide permutation threshold to the more traditional “Akaike information criterion” (AIC) (Akaike 1974) or “Bayes information criterion” (BIC) (Schwarz 1978) because it scales with the effective number of tests and has an interpretation when only one locus is chosen. Where the proportion resampled is p < 1, we adjust the threshold downward so that a signal of a constant effect size that is borderline significant in the full data set would also be borderline significant in the subsample (see appendix c).

Calculating model inclusion probabilities:

Applying model selection to each of R resamples of the observed population yields the R × n(M) matrix 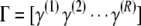^T, where γ^(r) is the column vector of indicators describing the predictors chosen by model selection on the rth resample. The expected proportion of times genetic locus m would be included in a multilocus model is then given by the Monte Carlo estimate

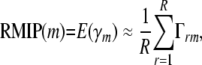which we term the resample model inclusion probability (RMIP), because it is an estimate of a binomial probability it is asymptotically normally distributed with variance RMIP(1 − RMIP)/R.

Range probabilities and other useful statistics:

The expected number of chosen marker intervals within a subset of marker intervals M*, where for example this set could describe a chromosome, a small genomic region, or even a noncontiguous set of loci, is

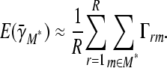The empirical “range probability” of q or more chosen marker intervals within region M* is

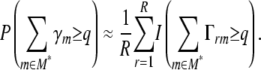(5)

For example, if the range probability of one or more chosen marker intervals within the region 80–90 Mb is estimated at 0.6, then in 60% of resamples one or more loci from the region entered the multilocus model, or equivalently there is a ∼60% probability of one or more loci being chosen within that region in multilocus model selection of a future resample of the data. The conditional probability of m being chosen in models containing any of M* where 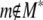is

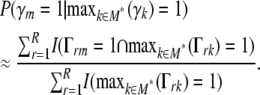More generally, any other statistic T that can be defined for a multilocus model, such as the variance explained by the whole model or one of its predictors, may be estimated as by model averaging as

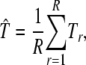where T_r is the statistic calculated for the model in resample r.

Alternative mapping methods 1: correcting the phenotype before mapping for family effects using hard, soft, and pedigree correction:

An intuitive approach to mitigate the effects of population structure is to correct the phenotype for family effects before subsequent analysis, with a more sophisticated variant being to “correct” the phenotype for polygenic effects estimated with the help of the pedigree (Aulchenko et al. 2007; Barendse et al. 2007). To illustrate the impact of this general approach on mapping small-effect QTL in structured populations of related individuals of known descent, we consider three types of correction to the phenotype. Let y_i* be the corrected phenotype for individual i used in the single-locus model

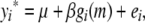with other parameters defined as for Equation 2. For “hard correction,” we define 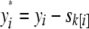, where 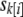is the mean phenotype of sibship k, to which individual i belongs. This is equivalent to using the residuals from a least-squares fit to the phenotype with sibship as a fixed effect or equivalently subtracting the sibship. We term “soft correction” as using 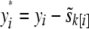, where 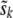is the shrinkage estimate of the sibship effect from fitting 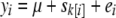, with 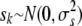. Finally, when the full pedigree is known, we define “pedigree correction” as 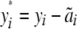, where 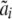is the estimate of the polygenic effect [i.e., the individual's BLUP (Lynch and Walsh 1998)] from previously fitting the pedigree model 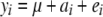, with 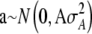and A as the additive genetic relationship matrix derived from the full pedigree. Under the assumptions of these models, once corrected the phenotypes of individuals in different families are exchangeable under permutation and derivation of empirical genomewide thresholds are valid (Aulchenko et al. 2007). When fitting these models we therefore estimate significance thresholds by permutation of y_i*.

Alternative mapping methods 2: mixed model with a sibship random intercept:

A more computationally intensive approach used traditionally in animal and plant breeding is to estimate single-locus effects simultaneously with a random polygenic effect (Kennedy et al. 1992). We approximate this by fitting the multilevel model

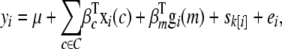with terms defined as in Equations 1 and 3, obtaining a nominal P-value for the locus effect via a likelihood-ratio test against the model in Equation 3, and calculating a genomewide significance threshold using the parametric bootstrapping approach described earlier, where trait values are simulated from a multilevel sibship that excludes the locus effect.

Pedigree correction models were fitted by restricted estimate maximum likelihood, using WOMBAT (Meyer 2007) with standard settings. All other models were fitted in R (R Development Core Team 2007) with extensive use of the add-on packages lme4 (Bates et al. 2008) for multilevel models and evd (Stephenson 2002) for fitting null GEV distributions.

SIMULATIONS

To test how well our method distinguished true from false associations in structured populations we simulated two breeding designs commonly used for high-resolution mapping in model organism genetics: the AILs and the HS.

F₁₈ advanced intercross:

We simulated 1000 populations of 500 F₁₈ individuals. Each individual comprised a simplified genome of two chromosomes and each chromosome comprised 50 diallelic markers spaced evenly over 100 cM. Chromosome 1 contained 2 additional markers hidden from further analysis that acted as QTL at 25 and 75 cM. Recombination was simulated using the Haldane model (Lynch and Walsh 1998). The F₁₈ was bred from 60 F₂'s maintained in a circular mating system (see Valdar et al. 2006a and references therein) of 25 mating pairs for 15 generations, with a final outbreeding of 20 sibs from each F₁₇ mating pair. Simulated QTL were additive and acted in the same direction in the founders, and each accounted for 5% of the phenotypic variance, with the remaining variance simulated as a normal deviate.

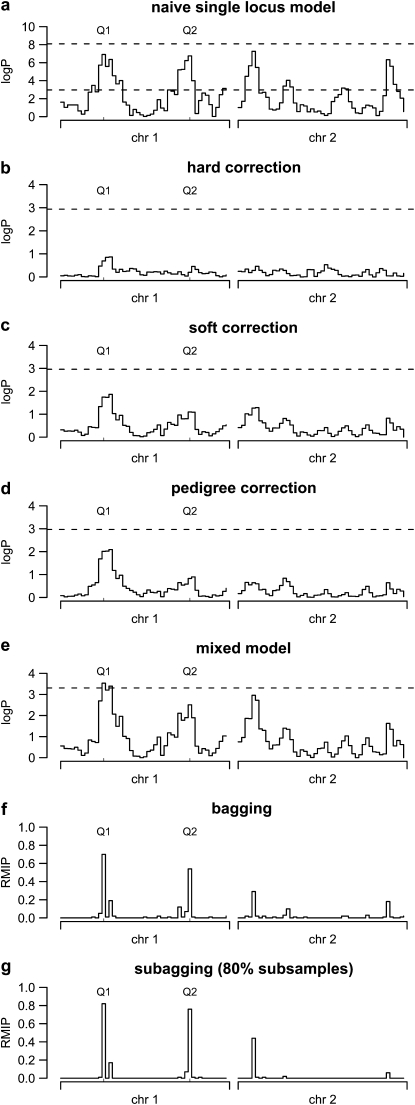
Figure 1 shows genome scans from a single simulated population with the positions of the simulated QTL labeled. A naive single-locus analysis (fitted using Equation 1 with no covariates) and permutation thresholds (Figure 1a) suggest at least four highly significant associations, two of which are on the control chromosome [chromosome (chr) 2]. These false associations are due to correlation between the simulated QTL and chr 2 markers arising through population structure (among all 1000 trials, the maximum 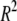between a chr 2 marker and a QTL was >0.3 in 182 trials and >0.4 in 32 trials). Correcting the phenotype for sibship effects before mapping provides an overconservative analysis that detects no QTL (Figure 1, b–d). The mixed model (Figure 1d) performs better but still attributes higher significance to a ghost peak than to one of the true QTL. The multilocus methods bagging and subagging (Figure 1, f and g) allow associations across the genome to compete with one another for a place in the model and in this example results in the true QTL ranking higher than all ghost peaks.

Figure 1.—

Single-locus and multilocus genome scans for a simulated F₁₈ advanced intercross. (a–d) The single-locus HAPPY model applied to a simulated two-chromosome F₁₈ population. (a) The single-locus model with permutation (bottom dashed line) and parametric bootstrap (top dashed line) thresholds. (b–d) The effect of correcting the phenotype for family, with dashed lines marking permutation thresholds. (e) The single-locus model including a sibship variance component with a threshold derived by parametric bootstrap. (f and g) Resample model inclusion probabilities (RMIPs) for each marker interval derived from bagging (f) and subagging (g). The positions of the two simulated QTL are marked Q1 and Q2.

To compare the performance of the single and multilocus approaches for identifying QTL in all 1000 simulated populations, we first divided the genome into nonoverlapping segments of 10 cM such that there were 20 segments in total with the segments at 20–30 cM and 70–80 cM covering Q1 (at 25 cM) and Q2 (at 75 cM). For each segment we then recorded the maximum log P (for the single-locus approaches) or the range probability (for the multilocus approaches). We examined the ability of the segment score for each method to discriminate segments that contained QTL from those that did not. Defining segments in this way allowed us to focus on the problem of discriminating confounded associations without being distracted by uncertainty in precise genomic location.

Table 1 reports performance statistics for single- and multilocus methods. At a given threshold we define power as the proportion of QTL-containing segments that exceed the threshold (i.e., detected), false discovery rate (FDR) as the proportion of detected segments that did not contain QTL, and chromosome 2 associations as the proportion of marker intervals on chr 2 that were predicted to be QTL. Statistics were calculated separately for each simulated population (trial) and Table 1 reports the averages over the 1000 trials. In the first section of Table 1 each trial has its own set of thresholds for 5% genomewide significance, as derived in methods. Under the null model assumed by each combination of method and threshold type, chr 2 associations exceeding the threshold are therefore expected ∼2.5% of the time. Permutation is seen to be anticonservative for the naive single-locus approach, leading to more than half of the declared associations being false and almost 10% of loci detected on chr 2. Parametric bootstrap provides a threshold that is overconservative on chr 2 but nonetheless leads to a high FDR, mainly because of the relative abundance of false peaks on chr 1 and, in the case of the single-locus method, poor discrimination. In these simulations, the combination of phenotype correction and permutation thresholds leads to low power and a complete abolition of signal in the case of correcting for sibship means (hard correction).

TABLE 1.

Performance of single-locus and multilocus methods in mapping two QTL in 1000 simulated F₁₈ advanced intercross populations

	Single locus or multilocus	Threshold				False discovery rate (%)e	Chromosome 2 associations (%)f
Methoda			Typeb	Units	Valuec			Power (%)d
Naive single locus	Single	Permutation	Log P	3.01 (2.67, 3.38)	94.8 (±0.49)	65.4 (±0.66)	9.68 (±0.13)
Naive single locus	Single	Parametric bootstrap	Log P	6.79 (3.01, 12.4)	70.1 (±1.1)	21.1 (±0.83)	1.3 (±0.051)
Hard correction	Single	Permutation	Log P	3.02 (2.66, 3.4)	0.8 (±0.2)	0.05 (±0.05)	0 (±0)
Soft correction	Single	Permutation	Log P	3.01 (2.65, 3.39)	28.2 (±1)	1.75 (±0.3)	0 (±0)
Pedigree correction	Single	Permutation	Log P	3.01 (2.63, 3.42)	25 (±1)	1.92 (±0.32)	0 (±0)
Mixed model	Single	Parametric bootstrap	Log P	3.23 (2.83, 3.63)	83 (±0.86)	26 (±0.82)	0.318 (±0.025)
Single locus	Single	∼80% power	Log P	5.27	80 (±0.99)	37.6 (±0.96)	2.38 (±0.069)
Hard correction	Single	∼80% power	Log P	0.536	80 (±0.9)	62.5 (±0.65)	4.63 (±0.095)
Soft correction	Single	∼80% power	Log P	1.68	80 (±0.89)	23.4 (±0.81)	0.259 (±0.023)
Pedigree correction	Single	∼80% power	Log P	1.55	80 (±0.91)	24.2 (±0.8)	0.29 (±0.024)
Mixed model	Single	∼80% power	Log P	3.45	80 (±0.92)	22.3 (±0.81)	0.216 (±0.021)
Bagging	Multilocus	∼80% power	Range probability	0.65	80.6 (±0.93)	1.83 (±0.36)	0.00204 (±0.002)
Subagging (40%)	Multilocus	∼80% power	Range probability	0.6	80.1 (±0.93)	1.6 (±0.35)	0.00204 (±0.002)
Subagging (50%)	Multilocus	∼80% power	Range probability	0.65	80.5 (±0.94)	1.52 (±0.33)	0.00204 (±0.002)
Subagging (60%)	Multilocus	∼80% power	Range probability	0.7	80.6 (±0.93)	1.82 (±0.37)	0.00612 (±0.0035)
Subagging (70%)	Multilocus	∼80% power	Range probability	0.76	80.2 (±0.95)	1.78 (±0.37)	0.0122 (±0.005)
Subagging (80%)	Multilocus	∼80% power	Range probability	0.82	80.4 (±0.94)	2.35 (±0.42)	0.0143 (±0.0054)
Subagging (90%)	Multilocus	∼80% power	Range probability	0.91	80.2 (±0.96)	2.72 (±0.45)	0.0143 (±0.0054)
Subagging (80%, medium stopping rule)	Multilocus	∼80% power	Range probability	0.06	81.6 (±1)	5.78 (±0.54)	0.939 (±0.044)
Subagging (80%, strict stopping rule)	Multilocus	∼80% power	Range probability	0	100 (±0)	90 (±0)	100 (±0)
Forward selection	Multilocus	NA	NA	NA	90.4 (±0.71)	8.51 (±0.66)	0.147 (±0.017)
Bagging	Multilocus	∼90.35% power	Range probability	0.46	90.5 (±0.69)	5.73 (±0.55)	0.0224 (±0.0068)
Subagging (80%)	Multilocus	∼90.35% power	Range probability	0.5	90.4 (±0.71)	6.72 (±0.6)	0.0571 (±0.011)

^aSubagging (p%) refers to resample model averaging using p% subsamples. “Strict stopping” refers to use of a stopping rule based on thresholds from parametric bootstrap of a multilevel sibship model; “medium stopping” refers to using the mean of that threshold and one derived by permutation; all other stopping rules are based on permutation.

^bHow the threshold for calculating performance statistics was determined and applied. Permutation: genomewide 5% significance thresholds were calculated separately for each simulation. Parametric bootstrap: thresholds were calculated separately for each simulation. “∼n% power”: scores were pooled for all simulations and the threshold was calibrated to give ∼n% power.

^cFor the permutation and parametric bootstrap results, threshold values are given as “median (lowest, highest).” Otherwise the numbers are the range probability thresholds required to achieve ∼n% power.

^dThe proportion of segments containing QTL that had scores above the threshold, averaged over simulations (SE in parentheses).

^eThe proportion of 10-cM segments with scores above the threshold that did not contain a QTL, averaged over simulations (SE in parentheses).

^fThe proportion of marker intervals on chromosome 2 predicted to contain QTL, averaged over simulations (SE in parentheses).

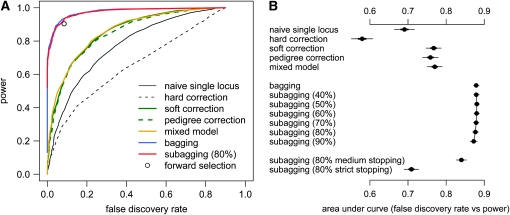
To allow a purer assessment of discriminatory power, the remaining sections of Table 1 fix the threshold of each method to that required to achieve 80% power over all simulations and include the multilocus methods. The second section shows that the mixed model is most discriminatory among single-locus approaches, but that bagging and subagging achieve an order of magnitude lower FDR. Varying the proportion subsampled for subagging makes little difference to performance, but it does change the range probability cutoff associated with a given detection rate. This is because increasing the proportion reduces the variability between subsamples, which acts to polarize the inclusion probabilities such that in the limit, where 100% is equivalent to forward selection, a binary measure is produced. The third section of Table 1 considers departures from the loose permutation-based threshold used as a stopping rule for forward selection in our implementation of subagging. In particular, we consider using the conservative parametric bootstrap threshold (strict) and a threshold that is midway between that and the loose permutation threshold (medium), finding that imposing a strict threshold abolishes all power. Figure 2 compares the discriminatory power of the methods by power and FDR for all possible thresholds (Figure 2A) and summarizes those curves by their area against the x-axis (Figure 2B). Like the related receiver–operator characteristic (ROC) curves (e.g., Sing et al. 2005), a perfect classifier would trace a right angle at the top left corner of the plot and have an area under the curve of 1. For clarity Figure 2A plots mean statistics from 1000 simulations. In Figure 2B we show the sampling variability associated with those means with error bars representing 50 and 95% confidence intervals for the area under each curve.

Figure 2.—

Performance of single-locus and multilocus methods in mapping two QTL in 1000 simulated F₁₈ advanced intercrosses. (A) Plot of predictions at a range of cutoffs for the maximum log P in a segment (single-locus model and hard, soft, and pedigree correction, mixed model) or the range probability over a segment (subagging with 80% subsamples, bagging). Forward selection is a discrete classifier, has no applicable threshold, and so is represented as a single point. (B) Plot of the area under the curves in plot (A), including results for variants of subagging in which the proportion of data subsampled varies (40–90%) and the stopping rule used in forward selection is made stricter (see simulations for details). Area estimates, calculated via the trapezium rule over a grid of values, are plotted with 50 and 95% confidence intervals (thick and thin horizontal bars).

The bottom section of Table 1 compares subagging (with 80% subsamples) and bagging with forward selection, for which segments are predicted to contain a QTL if one or more loci within the segment are included in the multiple-QTL model. Forward selection produces a hard classification of QTL status for a segment and so it does not require (or enable use of) a detection threshold: we therefore adjust the range probability thresholds of bagging and subagging to achieve the same power (90.35%).

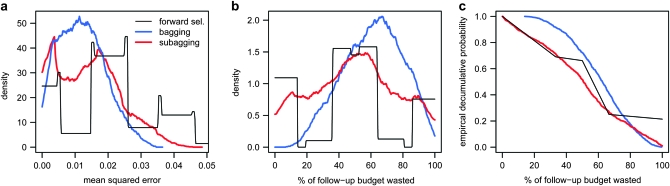
What is the advantage of nesting forward selection within a resampling procedure if doing so achieves only modest gain in power or FDR? Figure 3a plots empirical densities of the mean squared error of individual locus assignments (where the predicted assignment is 0 or 1 for forward selection or the RMIP for bagging and subagging). Consistent with theoretical studies, bagging and subagging give a lower average MSE (1.2 × 10⁻² ± 2.1 × 10⁻⁴ and 1.3 × 10⁻² ± 3.1 × 10⁻⁴, respectively, with 1 being the maximum possible if all locus assignments were wrong) than forward selection (1.9 × 10⁻² ± 4.5 × 10⁻⁴). Moreover, because it is a discrete classifier, the density of forward selection is trimodal (corresponding approximately to finding both, one, or no QTL) and has a mass of probability in the upper tail where bagging and subagging do not. To see why this matters, consider the following hypothetical scenario: suppose a finite budget were available for following up the results of mapping and money was allotted to investigate each marker interval in proportion to the probability that that interval was included in the multilocus model, with the probability being one or zero for forward selection or equal to the RMIP for bagging and subagging. Figure 3b plots the empirical density for the percentage of the budget spent on investigating markers that do not contain QTL (i.e., the budget wasted). Averaged over the 1000 simulations, spending money in accordance with forward selection seems least wasteful (45.4 ± 1.14%), with subagging slightly more wasteful (49.5 ± 0.853%) and bagging the most wasteful (61.3 ± 0.58%). However, as illustrated by the decumulative probabilities in Figure 3c, the high variance of the discrete classifier means that within a simulation there is a considerable risk (21.4%) that the classification is completely wrong and the entire budget is wasted, whereas this would be an unlikely prospect with bagging (∼0%) or subagging (1%).

Figure 3.—

Comparison of forward selection, bagging, and subagging in predicting QTL status of loci in 1000 simulated F₁₈ mapping experiments. Plots show error statistics relating to the assignment of QTL status to each of 98 marker intervals in the two-chromosome genome of the simulated F₁₈'s, where the correct assignment is 1 for the two intervals containing QTL and 0 for the remaining 96, and the predicted status is the vector 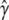of RMIPs from subagging with 80% subsamples and bagging or 0's and 1's from forward selection. (a) The mean squared error of assignment . (b and c) The percentage of money wasted if follow-up funding is spent on each marker interval in proportion to the predicted QTL status. Each data series is fitted to 1000 points, with series in a and b fitted as rectangular-kernel density estimates.

Heterogeneous stocks:

To test our method on a more complex population with ambiguous descent, we simulated 100 populations of 500 F₅₃ heterogeneous stock individuals derived from eight inbred lines. Again modeling a minimal two-chromosome genome, we used marker genotypes from the HS study of Valdar et al. (2006b). This comprised 870 markers spanning 98.6 cM on chromosome 1 and 759 markers spanning 103.7 cM on chromosome 2. All markers were diallelic with minor alleles distributed variously among the eight founder strains (see http://gscan.well.ox.ac.uk/ for more information). We simulated two diallelic QTL on chr 1 and, to allow the simulation to focus on discrimination of signals rather than on power, we positioned these in marker-dense regions at 29 and 68 cM with additive effects each accounting for 10% of the phenotypic variance. The QTL acted in the same direction in the founders, had alleles split equally among the eight inbreds, but had strain distribution patterns that differed from those of their flanking markers. Each population was generated by a single funnel of four two-way crosses, two four-way crosses, and one eight-way cross, giving rise to a mating population of 100 individuals that was then circular-mated for 50 generations, with the mating pairs in the penultimate generation bred to produce 10 offspring each (see Valdar et al. 2006a and references therein). Performance was assessed as for the advanced intercross trials by defining genome segments. Because the HS are more recombinant, segments were 6 cM wide and defined such that each QTL sat at a segment midpoint.

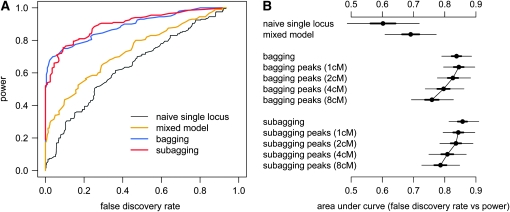
Table 2 reports performance statistics for the single- and multilocus methods applied to the 100 HS populations. The first section of Table 2 shows that the combination of a naive single-locus model and permutation results in most detections (92.3%) being false and leads to more than half the associations on the control chromosome (chr 2) exceeding the supposed 5% significance threshold. The parametric bootstrap controls the number of chr 2 associations somewhat (although is anticonservative) for the naive single-locus model and to an appropriate level for the mixed model (2.41%, suggesting ∼5% false positives for a two-chromosome genome). The second section of Table 2 fixes the threshold for detection at that necessary to achieve 80% power and compares the FDR of single- and multilocus methods. Figure 4 summarizes the discriminatory power of these methods and their variants. Consistent with the AIL simulations, the mixed model outperforms the naive single-locus model and the best discriminatory power is seen for bagging and subagging. In addition to subagging with 80% subsamples and bagging, we consider the two-step strategy of choosing representative “peak” loci, defined as maxima from a naive single-locus scan that exceed a low threshold and are more than d cM apart, followed by performing resample model averaging on those peaks. This strategy was originally adopted by Valdar et al. (2006b), using bagging. Although choosing among a smaller set of peaks incurs fewer computations and so is faster, we would expect it to be also inferior to using all loci because it does not allow for the fact that the identity of the marker acting as the strongest surrogate for a QTL can vary between resamples (e.g., Visscher et al. 1996), whereas using all loci does. Figure 4B illustrates this trend clearly, showing that the smaller the minimum separation of representative loci is, and thus the greater the number of constituent loci that can contribute to the range probability of a 6-cM segment, the more powerfully bagging or subagging discriminates segments containing QTL from those that do not.

TABLE 2.

Performance of single-locus and multilocus methods in mapping two QTL in 100 simulated eight-founder heterogeneous stock populations

	Single locus or multilocus	Threshold				False discovery rate (%)e	Chromosome 2 associations (%)f
Methoda			Typeb	Units	Valuec			Power (%)d
Naive single locus	Single	Permutation	Log P	3.65 (3.43, 3.99)	99.5 (±0.5)	92.3 (±0.28)	52.4 (±0.18)
Naive single locus	Single	Parametric bootstrap	Log P	9.48 (5, 15.5)	90 (±2.2)	73.5 (±2.3)	9.87 (±0.11)
Mixed model	Single	Parametric bootstrap	Log P	3.91 (3.59, 4.33)	89.5 (±2.3)	69.5 (±2.1)	2.41 (±0.056)
Single locus	Single	∼80% power	Log P	9.88	80 (±3.4)	63.3 (±3.5)	7.39 (±0.095)
Mixed model	Single	∼80% power	Log P	5.13	80 (±2.9)	46.6 (±3)	0.702 (±0.03)
Bagging	Multilocus	∼80% power	Range probability	0.39	80 (±2.8)	22.4 (±2.6)	0 (±0)
Bagging peaks 1 cM	Multilocus	∼80% power	Range probability	0.39	80 (±2.8)	12.8 (±2.5)	0.0584 (±0.041)
Bagging peaks 2 cM	Multilocus	∼80% power	Range probability	0.34	80 (±2.9)	23.5 (±2.8)	0.54 (±0.16)
Bagging peaks 4 cM	Multilocus	∼80% power	Range probability	0.29	80.5 (±2.8)	30.4 (±2.7)	1.92 (±0.37)
Bagging peaks 8 cM	Multilocus	∼80% power	Range probability	0.23	80.5 (±2.7)	43.1 (±2.5)	7.95 (±0.95)
Subagging	Multilocus	∼80% power	Range probability	0.4	80 (±3)	16 (±2.8)	0.00264 (±0.0019)
Subagging peaks 1 cM	Multilocus	∼80% power	Range probability	0.34	80 (±2.8)	19.8 (±2.8)	0.204 (±0.077)
Subagging peaks 2 cM	Multilocus	∼80% power	Range probability	0.27	80 (±2.8)	23.3 (±2.9)	0.585 (±0.16)
Subagging peaks 4 cM	Multilocus	∼80% power	Range probability	0.22	80.5 (±2.9)	28.7 (±3)	2.42 (±0.41)
Subagging peaks 8 cM	Multilocus	∼80% power	Range probability	0.14	80 (±2.8)	35.9 (±2.9)	7.33 (±0.91)

^aAll subagging uses 80% subsamples. The suffix “peaks p cM” denotes where model selection chose among representative peaks from a naive single locus scan rather than among all loci (see simulations).

^bHow the threshold for calculating performance statistics was determined and applied. Permutation: genomewide 5% significance thresholds were calculated separately for each simulation. Parametric bootstrap: thresholds were calculated separately for each simulation. “∼n% power”: scores were pooled for all simulations and the threshold was calibrated to give ∼n% power.

^cFor the permutation and parametric bootstrap results, threshold values are given as “median (lowest, highest).” Otherwise the numbers are the range probability thresholds required to achieve ∼n% power.

^dThe proportion of segments containing QTL that had scores above the threshold, averaged over simulations (SE in parentheses).

^eThe proportion of 6-cM segments with scores above the threshold that did not contain a QTL, averaged over simulations (SE in parentheses).

^fThe proportion of marker intervals on chromosome 2 predicted to contain QTL, averaged over simulations (SE in parentheses).

Figure 4.—

Performance of single- and multilocus methods in mapping two QTL in 100 simulated HS populations. (A) Plot of predictions at a range of cutoffs for the maximum log P in a segment (naive single-locus model, mixed model) or the range probability over a segment (subagging with 80% subsamples, bagging). Forward selection is represented as a single point. (B) Plot of the area under the curves in a, including results for variants of bagging and subagging in which model selection is applied to only a representative set of peaks, spaced a minimum distance apart (in parentheses), rather than to all loci. Area estimates are plotted with 50 and 95% confidence intervals (thick and thin horizontal bars; see Figure 2 legend for more details).

DISCUSSION

We describe a way to characterize model uncertainty in a genomewide association study that is particularly useful for outbred populations where the founders are known or can be inferred and where the outbreeding phase results in complex population structure. When the founders are not known or inferable, the genetic predictors can be the genotypes or some other numeric formulation. When the population structure is not complex, the method has no disadvantage over other strategies other than running time. The method is applicable to any situation in which population structure is present or suspected. Moreover, it does not require pedigree information and so is widely applicable to many existing data sets where such information is missing or untrustworthy.

In contrast to methods that impose a genomewide significance threshold to determine whether or not a locus has been identified, our model averaging approach uses such a threshold only as a stopping rule. Locus identification is based instead on the frequency with which it recurs in the resampling. This is not to say that the choice of threshold is unimportant: lowering the stopping rule to a pathological degree will clearly increase the number of spurious loci entering the multilocus model, whereas a similarly pathological raising of the threshold will lead to a loss in power. Nonetheless, the multilocus analysis is far more robust to a loose threshold than a single-locus approach.

For single-locus analysis, we consider a method to generate thresholds based on parametric bootstrap from a multilevel model that is appropriate when loci from the whole genome are not available for a multilocus analysis. This more accurately models a null distribution of a normally distributed phenotype in the presence of a multilevel structure than a permutation test and results in a lower FDR for single-locus analysis. However, in our simulated scenario of two QTL segregating in a highly structured AIL we find that, consistent with studies from mapping in livestock, either correcting the phenotype for partially pooled family or polygenic effects or estimating such effects simultaneously in a mixed model leads to a more discriminatory single-locus approach, albeit with lower power to detect small effects. We show that better discrimination still is available through a multilocus approach that can be ignorant of family structure.

Our assessment of polygenic modeling is illustrative but far from comprehensive (e.g., see Hoeschele et al. 1997). In our simulations, we do not generate polygenic effects explicitly because doing so is unnecessary to demonstrate confounding. However, because our method uses marker information from the whole genome, simulating such effects would also confuse assessment of detection if simulated through multiple scattered small-effect QTL or require a nongenetic justification if simulated by adding correlated noise to the phenotype. In our modeling, we do not estimate polygenic parameters because they are unnecessary to demonstrate unconfounding, although we expect that including them as simultaneously estimated parameters could improve discrimination, albeit it at some computational expense, making our method a frequentist analog to some existing Bayesian approaches that do this (e.g., Bink et al. 2008). We do not, however, consider it desirable to remove polygenic effects from the phenotype before subsequent modeling, such as in the pedigree correction based on Aulchenko et al. (2007). If the goal is to dissect the genetic component of the trait into a potentially large number of small-effect loci as it often is in medical genetics, rather than to detect only large-effect loci helpful for phenotype prediction and subsequent selection as is often the goal in QTL mapping of livestock and plants (Bernardo 2001), then a strategy of removing polygenic effects before mapping discards potentially valuable between-family information that would otherwise add power to a multilocus analysis (see also Crooks et al. 2009). It is also undesirable for our purposes because subtracting the BLUP point estimate from the phenotype involves conditioning on an unknown: uncertainty relating to the polygenic estimates is lost and this potentially biases subsequent characterization of the uncertainty among locus-specific associations. Nonetheless, when there are major structural features within the population that are not first removed, such as distinct subgroups arising through admixture, our method risks picking up loci that are correlated with those components. Our approach is therefore most useful as a way to characterize model uncertainty once such major structural features have been removed.

Aggregating models by bootstrapping (bagging) or by subsampling (subagging) is simple to understand and easy to implement. How does it compare to the increasingly common practice of Bayesian model selection and Bayesian model averaging (Kilpikari and Sillanpaa 2003; Yi 2004; Ball 2007; Yandell et al. 2007; Bink et al. 2008)? In the Bayesian paradigm the inclusion of predictors is specified in terms of a formal hierarchical model in which inclusion probabilities are modeled as the outcome of higher-order processes that loosely specify the number of parameters to be included. The Bayesian approach then conditions on the data to characterize the uncertainty in the inferred parameters, modeling the inclusion probabilities as posterior distributions. This requires integrating over the space of possible multilocus models, which in practice will usually involve exploring different configurations of γ in a Monte Carlo Markov chain.

Bayesian measures of uncertainty relate to personalized probabilistic statements of degrees of belief in a certain event occurring, such as a genetic variant affecting a phenotype (Bernardo and Smith 1994; Maliepaard et al. 2001). In contrast, frequentist measures, such as bagging or subagging, seek to address uncertainty in an estimator (such as forward selection) due to finite sample size, although the choice of model selection procedure, though uncontroversial, is subjective, and the choice of the stopping rule even more so. It is thus necessary to calibrate the RMIP by simulation to interpret it as a probability of a QTL and different mapping populations require individual calibration (although note that calibration is usually required in a Bayesian setting also). Moreover, compared with the Bayesian approach, resampling could be seen as wasteful in that the inferences based on each subsample use a percentage of the data, and those based on bootstrapping use on average ∼63% of the data (Davison and Hinkley 1997). However, for those unprepared or unwilling to specify subjective priors, our method offers a much improved approach to multiple-marker selection, and one that is also simple to apply to a wide range of distributions, such as survival models and generalized linear models.

Our resampling procedure is applicable to any model selection method that seeks to return an estimate of 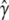. Here we use forward selection and consider only additive genetic models. However, model selection strategies that are more sophisticated or thorough, such as stepwise regression or exhaustive search, that consider a broader range of genetic models, such as dominance and interactions, or that use more specialized stopping rules (e.g., see Zou and Zeng 2008 for a review) all fit into the resampling paradigm we describe, allowing substantial scope for future development.

In summary, we describe a method to deal with problems inherent in certain forms of structured populations: specifically, highly recombinant maintained populations with known founders, where the pedigree may be unknown, and where the population structure is expected to be smooth in the sense that any gross environmental factors or subpopulation indicators are known and can be removed. The generality of our solution means it can also be applied to other outbred populations, including those that use different representations of genotype. In particular we believe that the general approach will be applicable to human populations where major strata have been removed. In agreement with others (Churchill and Doerge 2008), we show that single-locus modeling using permutation thresholds is anticonservative, consider a more conservative alternative based on parametric bootstrap, and compare these with methods for correcting the phenotype for family effects. We then show in simulations that regardless of the threshold chosen, multilocus modeling is superior to single-locus approaches in discriminating between true causal signals and confounding ghost associations.

We provide software to perform single-locus association, estimation of significance thresholds via parametric bootstrap and permutation, and multlilocus association in our program BAGPHENOTYPE provided free at http://www.well.ox.ac.uk/∼valdar/software/. BAGPHENOTYPE is based on the R-library HAPPY, also free at http://www.well.ox.ac.uk/happy/.

APPENDIX A: HANDLING MULTICOLLINEARITY IN REGRESSIONS ON THE HAPPY MATRIX

The 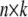matrix 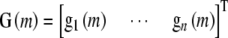for n individuals is by definition overspecified in the kth column but is often also multicollinear in some of the remaining columns owing to some haplotypes being near indistinguishable at some loci. Where our chosen regression software does not handle this ill-conditioning automatically through the QR factorization (see appendix b), we replace 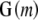by the orthogonal 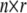matrix 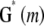, whose 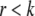columns are those principal components of scaled and centered 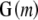whose eigenvalues exceed an orthogonality parameter 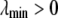, which is chosen to be small and determined empirically for a given genetic data set.

APPENDIX B: EFFICIENT PERMUTATION AND PARAMETRIC BOOTSTRAP TESTS FOR THE SINGLE-LOCUS LINEAR MODEL

In the case of linear models, establishing significance thresholds by performing genome scans of repeated parametric bootstraps or permutations is made several orders of magnitude faster by exploiting the fact that the slowest step in ordinary least-squares fitting, i.e., inversion or decomposition of the design matrix, is independent of the response. We illustrate this below using the QR factorization (e.g., Venables and Ripley 2002) of the normal equations for least squares, which in addition to being efficient implicitly handles the common case of collinearity leading to nonidentifiability among the predictors. Let X be the N × p design matrix for the entire linear model including covariates and marker intervals and 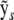be the sth simulated (or permuted) version of the response such that the normal equations for 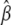are 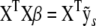. Applying the QR decomposition 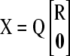, where Q is n × n orthonormal and R is p × p upper triangular, the normal equations become 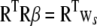, where 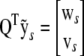with p-vector w_s and (n − p)-vector v_s. Crucially, the residual sum of squares (RSS) is 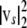, which means that once the QR factorization has been performed for a given design matrix, the RSS and therefore trivially the log P can be rapidly computed for any number of new response vectors 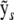. For S permutations or parametric bootstrap replicates on L loci this reduces the complexity from O(SLdr) to O(Ld + Sr), where the time taken for matrix decomposition and RSS calculations is d and r units, respectively.

APPENDIX C: ADJUSTING THE STOPPING RULE FOR FORWARD SELECTION IN A P% SUBSAMPLE

In subagging, forward selection is applied to a set of predictors conditional on a p% subsample of the N data points. If p = 100%, then a stopping rule for deciding whether to include a further predictor in the model is to accept only if the logP of its partial F-statistic (or likelihood-ratio statistic) is both greater than the α% genomewide significance threshold τ^α,N and greater than that of any other of the unselected predictors. However, if p < 100%, and especially when p ≪ 100%, then τ^α,N becomes inappropriately strict: all predictors are penalized due to the drop in sample size. We prefer a stopping rule that reflects the size of the effect rather than the size of the subsample. Therefore to retain power but avoid the computational burden of determining new thresholds empirically, we adjust τ^α,N for sample size N to τ^α,n for sample size n = pN/100% as follows. Consider a predictor in a linear regression on N data points that is borderline significant at τ^α,N and explains a fraction of the variance q = FSS/(RSS + FSS), where FSS and RSS are, respectively, the fitting and residual sums of squares about the regression. If k is the number of fitted parameters in the single-locus model, then the corresponding F-statistic is

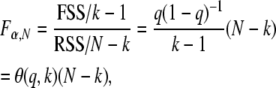where θ is a function of q and k. If q and k are unchanged in the subsample of size n < N, as would be expected if q is robust to resampling, then the F-statistic corresponding to τ^α,n is

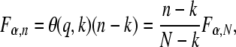such that, given τ^α,N, N, n, and k, we can approximate τ^α,n as

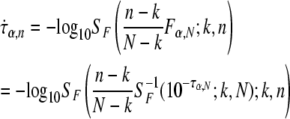where S_F and S_F⁻¹ are survivor and inverse survivor functions for the F-distribution.