Influence of paced maternal breathing on fetal–maternal heart rate coordination

Abstract

Pregnant mothers often report a special awareness of and bonding with their unborn child. Little is known about this relationship although it may offer potential for the assessment of the fetal condition. Recently we found evidence of short epochs of fetal–maternal heart rate synchronization under uncontrolled conditions with spontaneous maternal breathing. Here, we examine whether the occurrence of such epochs can be influenced by maternal respiratory arrhythmia induced by paced breathing at several different rates (10, 12, 15, and 20 cycles per minute). To test for such weak and nonstationary synchronizations among the fetal–maternal subsystems, we apply a multivariate synchronization analysis technique and test statistics based on twin surrogates. We find a clear increase in synchronization epochs mostly at high maternal respiratory rates in the original but not in the surrogate data. On the other hand, fewer epochs are found at low respiratory rates both in original and surrogate data. The results suggest that the fetal cardiac system seems to possess the capability to adjust its rate of activation in response to external—i.e., maternal—stimulation. Hence, the pregnant mothers' special awareness to the unborn child may also be reflected by fetal–maternal interaction of cardiac activity. Our approach opens up the chance to examine this interaction between independent but closely linked physiological systems.

Prenatal development involves increased neural integration as pregnancy progresses. Among other things, this neural integration is indicated by the increasing coincidence of fetal heart rate and fetal motor activity in the second and third trimester (1). Apart from such intrafetal coordination of function, the fetus also interacts with its environment. This interaction can often be documented in the fetal heart rate, which remains one of the primary descriptors of fetal physiological activity accessible to systematic study.

The mother is central to the fetal environment. Her condition sets the framework for the state and development of the fetus. So far, however, only anecdotal evidence exists for maternal perception of the condition of the fetus. Physiologically, prenatal interaction between mother and fetus has been postulated and various studies confirm a relationship between maternal and fetal conditions on the basis of fetal heart rate. These studies show changes in fetal heart rate and heart rate variability (HRV) associated with altered maternal arterial oxygen content (2, 3), maternal hypothermia (4) and maternal exercise (5). Furthermore, links between maternal and fetal heart rate have been examined. A positive correlation between these rates has been found over periods of 1 and 24 h (6) and the entrainment of the fetal heart rate rhythm to the maternal diurnal rhythm has been observed (7). However, short-term interaction between fetal and maternal heart rate is elusive.

In previous work we have examined a large number of mother–fetus pairs on the basis of short, simultaneously acquired magnetocardiographic measurements (8). Apart from requesting the mother to remain in a quiet, supine position for 5 minutes after a period of adaptation, we did not control the maternal or fetal condition in any way. The heart rates were accordingly recorded under spontaneous conditions. Quantifying relative fetal–maternal R-wave timing by using synchrograms, we found many episodes of heart rate coordination. However, the analysis of surrogate data suggested that such episodes may result from spurious fetal–maternal heart rate coupling due to naturally changing frequencies of 2 independent cardiac oscillators. Nonetheless, we did find indirect evidence of occasional nonspurious heart rate coordination by considering the occurrence of the phase relationship of the fetal and maternal R waves. In the original data, we found a preference for specific phases which could not be found in the surrogate data.

In their work examining the short-term relationship between maternal and fetal heart rate in large samples, Dipietro, et al. (1, 9) could find no reciprocal influence on the basis of cross-correlation analysis over 50 min of data. They concluded that, should association between fetal and maternal cardiac activity indeed exist, it will likely be generated by secondary processes that mediate both fetal and maternal heart. On the other hand, other work using cross-spectral analysis has shown that maternal respiratory sinus arrhythmia may also be correlated to changes in fetal heart rate in the high-frequency band related to maternal breathing (10).

We thus postulate in this paper that conditions conducive to physiological cardiac interaction between mother and fetus might be achieved by controlling maternal heart rate via regulation of her respiratory sinus arrhythmia. As in our previous work (8), we examine healthy pregnant women and their unborn children toward the end of gestation by using magnetocardiography, allowing us to register their respective heartbeats simultaneously with high precision. In contrast to our prior uncontrolled recordings, we paced the mother's breathing during acquisition, enabling us to modulate her heart rate. We speculate that this modulation will have an influence on the prerequisites for the entrainment of the fetal cardiac oscillator to that of the mother. The heartbeat time series of both mother and child acquired under different breathing conditions are used to construct synchrograms, and we assess fetal–maternal interaction on the basis of these synchrograms by identifying synchronization epochs (SE). We then compare the characteristics of the SE in these data to those obtained in surrogate data produced by the twin surrogate technique. A more detailed description of the procedures used can be found below in Materials and Methods.

In essence, we aim to assess the occurrence of fetal–maternal heart rate synchronization under conditions of spontaneous and controlled breathing of the mother. This study offers the unique opportunity to examine the interaction between independent but closely linked physiological systems by means of innovative data-analysis approaches.

Results

All of the 6 mothers were able to complete the study protocol without any discomfort and none reported difficulty in maintaining the timed inspiration and expiration cycles. Spectral analysis of the magnetocardiogram (MCG) signals in the datasets in which respiration was cued shows clear peaks at 0.167 Hz, 0.2 Hz, 0.25 Hz, and 0.333 Hz corresponding to the respiratory rates of 10, 12, 15, and 20 cpm, respectively: For each peak, the corresponding full width at half maximum is 0.069 ± 0.001 Hz, 0.068 ± 0.004 Hz, 0.066 ± 0.007 Hz, 0.097 ± 0.009 Hz. In the spontaneous breathing recordings before and after the controlled breathing acquisitions, broad spectral bands with multiple peaks are visible, indicating variable respiratory rates.

The examination of HRV in the heartbeat (RR interval) time series acquired during the 4 paced breathing conditions shows an influence of respiratory rate in the frequency domain and approximate entropy (ApEn) values of the mother (Table 1). The fetal HRV values, apart from ApEn, do not show this influence. The heart rate in both the mothers and the fetuses is clearly higher at the respiratory rates of 15 cpm than at the other rates.

Table 1.

Maternal and fetal for heart rate variability measures

Heart Rate Variability	Maternal Respiratory Rate				P value	Maternal Respiratory Rate				P value
	20 cpm	15 cpm	12 cpm	10 cpm		20 cpm	15 cpm	12 cpm	10 cpm
	Maternal Heart Rate Variability					Fetal Heart Rate Variability
mRR, ms	682 ± 63	645 ± 67	697 ± 81	679 ± 57	0.018	434 ± 25	417 ± 22	444 ± 27	434 ± 28	0.011
SDRR, ms	40 ± 20	26 ± 11	43 ± 19	41 ± 19	0.127	26 ± 11	26 ± 12	29 ± 9	29 ± 6	0.939
RMSSD, ms	14.3 ± 7.5	12.2 ± 6.9	17.6 ± 9.0	20.5 ± 11.0	0.067	5.9 ± 2.2	7.4 ± 5.8	7.6 ± 2.8	7.8 ± 3.9	0.198
LF, ms2	73 ± 41	58 ± 27	79 ± 31	85 ± 35	0.009	54 ± 22	43 ± 19	54 ± 12	49 ± 21	0.512
HF, ms2	56 ± 37	53 ± 35	86 ± 45	95 ± 51	0.017	27 ± 11	23 ± 10	35 ± 17	28 ± 10	0.084
LF / HF	1.40 ± 0.61	1.23 ± 0.44	1.09 ± 0.56	0.97 ± 0.24	0.111	2.01 ± 0.39	1.89 ± 0.44	1.74 ± 0.52	1.72 ± 0.21	0.513
ApEn	0.91 ± 0.08	0.86 ± 0.08	0.89 ± 0.07	0.89 ± 0.04	0.004	0.66 ± 0.26	0.53 ± 0.24	0.78 ± 0.22	0.68 ± 0.29	0.031

Values are mean ± SD. cpm, cycles per minute; mRR, mean RR interval; SDRR, standard deviation (RR interval); RMSSD, root mean square of successive differences; LF, low-frequency power (0.04–0.15 Hz); HF, high-frequency power (0.15–0.4 Hz); ApEn, approximate entropy. P values based on the Friedman test for dependent variables; values < 0.05 are in bold type.

With respect to the surrogate data, we compare the heart rate and its variability of original maternal and surrogate maternal RR interval time series. The results show that the linear properties of the time series are generally well retained in the surrogate data, apart from a lower variance as expressed by the standard deviation in the surrogate data (Table 2). Also, the complexity is slightly reduced. Inspection of the surrogate maternal RR interval time series shows that in some of the reconstructed data, a reduced RR interval range and/or a repetition of specific subseries of RR interval is present. This is to be expected but should not negatively influence a test for synchronization (11).

Table 2.

Differences between the heart rate properties of the original and the surrogate maternal RR interval time series

Difference	nr beats	mRR, ms	SDRR, ms	RMSSD, ms	LF, ms2	HF, ms2	LF / HF	ApEn
Mean	4.2	−1.4	−5.5	0.3	−1.3	−1.0	−0.01	−0.042
SD	12.8	16.3	6.4	2.4	11.2	12.2	0.20	0.020
P value*	0.004	0.109	0.000	0.329	0.679	0.931	0.891	0.000

For each original–surrogate pair, the value of the original RR interval time series was subtracted from the mean value of the 20 surrogate RR interval times series. Values are mean ± SD. nr, number; mRR, mean RR interval; SDRR, standard deviation (RR interval); RMSSD, root mean square of successive differences; LF, low-frequency power; HF, high-frequency power; ApEn, approximate entropy. *, P values based on the Wilcoxon test for paired samples, values < 0.05 are in bold type.

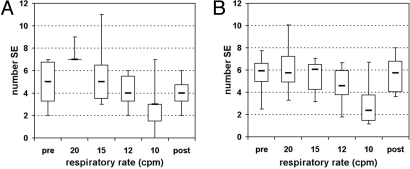
The main point of this study is the analysis of SE among mother and fetus. In each of the fetal–maternal pairs of RR interval time series, the SE are identified for each of the respiratory conditions. In the original data, the number of SE found in the datasets of spontaneous breathing is 4.8 ± 2.2 before the controlled breathing and 4.0 ± 1.5 after. The numbers are similar at the respiratory rates of 15 and 12 cpm: 5.7 ± 1.6 and 4.2 ± 1.6, whereas at the highest rate (20 cpm) more SE are present (7.3 ± 0.9) and at the lowest rate (10 cpm) there are fewer SE (2.8 ± 2.6) (see also Fig. 1A). In the surrogate data, the number of SE lies in the mid-range for all conditions except for the slow rate of 10 cpm (prior, 5.6 ± 2.0; 20 cpm, 6.2 ± 2.6; 15 cpm, 5.4 ± 1.6; 12 cpm, 4.6 ± 1.9; 10 cpm, 3.0 ± 2.3; and after, 5.6 ± 1.9. See also Fig. 1B).

Fig. 1.

Box plots showing the number of SE at different respiratory rates in the original (A) and surrogate (B) data. Note that at 20 cpm in the original data (A), five of the six subjects have 7 SE and one had 9 SE and therefore the interquartile box consists of a line at the value 7. Also, as there were 20 surrogate datasets for each original, the number of SE found in the surrogate data for each respiratory condition was divided by 20 for comparability. (pre, post: datasets of spontaneous breathing before and after controlled breathing.)

The duration of the SE is similar for all 6 respiratory conditions, both in the original and in the surrogate data (Table 3). In the original data, the n:m combination 3:2 occurs most frequently (46%), followed by 5:3 (23%) and 4:3 (17%). The other combinations (2:1, 5:4, and 7:4) each have less than 10% of the SE. The result for the surrogate data are similar (3:2 had 45%; 5:3 had 24%; and 4:3 had 16%).

Table 3.

Duration of the synchronization epochs found in the original and surrogate data under the different respiratory conditions

Synchronization epochs	Respiratory rate
	pre	20 cpm	15 cpm	12 cpm	10 cpm	post
Original
Number of epochs	29	44	34	25	17	24
Duration, s	18.4 ± 9.5	16.1 ± 10.3	14.7 ± 5.8	16.9 ± 6.7	17.0 ± 10.1	15.1 ± 4.9
Surrogate
Number of epochs/20	33.6	37.1	32.6	27.5	18.0	33.7
Duration, s	14.8 ± 6.2	16.7 ± 8.9	15.0 ± 6.4	14.5 ± 6.2	21.4 ± 16.6	15.1 ± 6.7

Values are mean ± SD. pre, post: datasets of spontaneous breathing prior to and following controlled breathing.

Examination of the phase of the fetal R peaks relative to the maternal RR cycles in the 3 n:m combinations which contained at least 10% of the number of SE shows that, in the original data, phase preferences are evident in the 20 cpm data, particularly for the combinations 4:3 and 5:3 (Fig. 2). Furthermore, a phase preference is also visible at the respiratory rate of 12 cpm in the 3:2 combination. It is important to emphasize that none of the surrogate data show a similar preference.

Fig. 2.

Distribution of the SE over the maternal beat phases in the original and surrogate data with respect to the n:m combinations 3:2, 4:3, and 5:3 in the different respiratory conditions. For the original data, the number of SE found is given at the top left of each graph. As there were 20 surrogate datasets for each original, the number of SE found in the surrogate data were divided by 20 for comparability. The arrows indicate clear phase preferences. P values are given for histograms containing at least 6 SE. (pre, post: datasets of spontaneous breathing before and following controlled breathing.)

Comparing the results of the 1 mother–fetus pair that was examined in both the 37th and 39th week using a different order of respiratory rates revealed no obvious differences, so that the order of the respiratory interventions is not considered relevant.

Discussion

The main finding of this study is that the presence or absence of interaction between fetal and maternal cardiac activity may be influenced by maternal respiration. In particular, higher paced breathing rates led to a greater number of SE when compared with normal or slower paced rates or to varying rates found in spontaneous breathing. Furthermore, at these higher respiratory rates we found a tendency for the SE to occur with a higher frequency at specific times of the maternal cycles. The fact that the surrogate data displayed neither an increased number of SE at 20 cpm respiratory rate nor a phase preference of these SE suggested that in the original data a physiological mechanism leading to coupling of the heart rate frequencies was present. The modulation of the maternal heart rate via respiratory sinus arrhythmia induced by higher respiratory rates may thus have created conditions in which the fetal cardiac system was led to couple its timing to that of the maternal system.

Cardiorespiratory coupling has been well documented (12), and we may presume that this occurred in the mothers. It is conceivable that the fetal–maternal coupling was not necessarily mediated by maternal cardiac activity but rather induced directly via the respiratory movements of the mother. To discern this, we examined the HRV of both the mother and the fetus over the complete 5-minute acquisitions in each the respiratory conditions. In the maternal HRV, we found a drop in both low-frequency (LF) and high-frequency (HF) power with faster breathing cycles. This effect has been widely observed and is attributed in particular to the progressive decline in the frequency transfer function of vagal cardiac innervation at higher respiratory rates (13). A similar consistent neural innervation of the fetal cardiac system could not be identified in the fetal 5-minute HRV. Thus we found no evidence of a direct effect of maternal breathing movements on fetal heart rate, and this would not seem to be suited to explain the short-term coupling we observed.

Previous work in our group has shown that in uncontrolled fetal–maternal heart rate acquisitions, most of the SE found could be attributed to the naturally changing frequencies of 2 independent cardiac oscillators and did not necessarily represent true physiological interaction (8). Nonetheless, examination of a large number of subjects and acquisitions showed evidence of occasional physiological synchronization on the basis of nonuniform distribution of the phase preferences of the fetal beats found in the original but not the surrogate data. Although the maternal respiratory rate was not determined in those data, we may presume that a normal spontaneous rate ≈12 cpm was predominant. It is therefore to be expected that some synchronization will occur at normal breathing rates. Our present results suggest that the phase preference found in the data recorded at a relatively normal respiratory rate of 12 cpm (Fig. 2) may have been due to this kind of spontaneous interaction. However, it is clear from Fig. 1 and the relative numbers of SE found in the specific phases (given in Fig. 2) that synchronization occurred more consistently at 20 cpm, suggesting that fast maternal breathing rates are more conducive to initiating coupling between the fetal and maternal heart rates.

We also found a lower probability for SE at the respiratory rates of 10 cpm (Fig. 1). The fact that this occurred not only in the original but also in the surrogate data suggests that breathing at low rates may have created conditions in which the spurious occurrence of fetal–maternal heart rate coupling was hindered. We reasoned that coincidental coordination between the rates could have been inhibited by high, short-term beat-to-beat variability associated with the higher respiratory modulation amplitude found at slow rates of breathing. We did indeed find that the root mean square of successive differences (RMSSD) and HF power values were higher at a respiratory rate of 10 cpm when compared with those of the other rates.

Note that the synchrograms enable us to identify the difference between the n:m ratio of the instantaneous phases of 2 signals at the same time, but do not include time delays that might exist between the 2 signals. To include such a delay in the analysis, the method recently proposed in ref. 14, based on the cross-correlation of phase increments, could be adapted to quantify n:m synchronization. Nevertheless, the adaptation of that method is beyond the scope of this paper and will require further discussion.

With respect to the reliability of the approach used to generate surrogate data, the results indicate that most of the descriptors of heart rate variability were similar between the original and the surrogate datasets. The reduction of variance and complexity in the surrogate data were most likely due to the repetition of specific subseries of RR intervals in the surrogate data, which was to be expected for this kind of block bootstrap. However, it has been argued that this should not invalidate the test for synchronization (11). We conclude that the “twin surrogate” approach generates dependable surrogate data.

If, as our results suggest, fetal–maternal heart rate entrainment may have been induced by high maternal respiratory rates, the question as to how the coupling between maternal and fetal heartbeats was mediated remains. We have previously suggested how the fetus' heart rate may synchronize to external stimuli from the mother. Studies have shown that in adults, subjects exposed to a weak forcing signal in the form of acoustic stimuli with a frequency close to the subject's heart rate, the heart rate frequency locked to the external signal (15). Considering that by midgestation the fetal auditory system is sufficiently developed and capable of perceiving the frequency range of vessel pulsation (16), it is conceivable that the maternal cardiac oscillator has a detuning effect on the fetal rhythm. Such an effect may depend on the changes in the rate of the oscillator. Fast maternal respiration leads to smaller beat-to-beat differences that keep the maternal RR intervals in a range where the conditions for the induction of fetal beat initiation are possible and/or favored.

In summary, the fetal cardiac system seems to possess the capability to adjust its rate of activation in response to external stimulation. Further work needs to be done to elucidate the nature of the influence of the maternal cardiac oscillator on the fetal cardiac system. A better understanding of how these 2 independent cardiac systems interact under various physiological conditions will lead to improved insight into normal prenatal development and shed light on the reciprocal perception between the mother and her child. This in turn may be beneficial for fetal surveillance and the detection of pathological conditions during pregnancy.

Materials and Methods

We examined 6 women in healthy singleton pregnancies, aged 33 ± 4 years (range 27–37). The data from these mothers and their fetuses were collected between the 34th and 40th week of gestation (37.0 ± 2.3). In one case, 2 acquisitions were done (37th and 39th week). The study was approved by the local ethics committee and all mothers gave written informed consent.

Data Acquisition.

Maternal and fetal cardiac activity was recorded by using a Magnes 1300C multichannel biomagnetometer (4D Neuroimaging). The method permits the registration of the magnetic fields produced by the electrical activation of the heart and delivers a relatively noise-free signal similar to that of an ECG, with high temporal resolution. It is particularly useful in the prenatal setting where the ECG has limited applicability (17). Using large array biomagnetometers allows the simultaneous registration of maternal and fetal magnetocardiographic signals. The system used in this study consists of 61 sensing channels arranged concentrically on a slightly curved surface with 825 cm² area of coverage (18). Coil diameter is 28 mm with a spacing of ≈38 mm. The coil distance to the outer surface is ≤16 mm. Environmental noise cancellation is possible on the basis of ambient noise detectors. Intrinsic system noise is specified as ≤10 fT/√Hz average over frequency and across all channels. The measurements were performed in a shielded room (AK3b, Vakuumschmelze, Hanau, Germany) to reduce the influence of electromagnetic artifacts.

For data registration, the subjects were placed in a resting, supine condition. The concave sensor was placed just above the mother's abdomen, the lower rim over the pubis, and the upper rim approximately over the xyphoid. Data were recorded for 5 min at a sampling rate of 1 kHz and a band pass of 1–200 Hz. All recordings took place between 10 a.m. and 4 p.m. In each pregnancy, we obtained 6 consecutive 5-min simultaneous fetal and maternal MCGs. After an adaptation period of 10–15 min, a baseline MCG was recorded with the mother breathing spontaneously. This was followed by 4 acquisitions in which the mother was asked to adapt her respiratory rate by coordinating her inspiration to an auditory cue. The repetition rates of the cues for the 4 acquisitions were 15 cpm, 10 cpm, 20 cpm, and 12 cpm, in that order. This was followed by a sixth and final acquisition in which the mother again breathed spontaneously. The single acquisitions were separated by a 2–3 min. pause without regulated breathing. The total duration of the registration of the 6 MCGs was ≈40 min.

Data Analysis.

In each of the resulting 5-min MCG datasets using respective QRS templates, fetal and maternal R peaks were identified on the basis of template-matching to an accuracy of 1 ms, and the corresponding RR interval time series were constructed (18). On the basis of the relative timing of the fetal and maternal R peaks, synchrograms were created by using the stroboscopic technique described by Schäfer, et al. (19). Accordingly, the phases of the fetal R peaks were plotted on a time axis with respect to m maternal RR interval cycles whereby 1 ≤ m ≤ 4. Horizontal groupings of data points indicate phase synchronization and the number of parallel lines (n) in an epoch of such horizontal groupings embedded in m maternal RR intervals indicates the coupling ratio n:m. On the basis of the occurrence of such groupings, we set 2 ≤ n ≤ 7 and examined 6 nonredundant n:m ratios: 2:1, 3:2, 4:3, 5:3, 5:4, and 7:4. These grouping were identified as SE according to an algorithm developed by Toledo, et al. (20). For an SE to be considered as representing possible fetal–maternal interaction, its duration needed to be 10 s or longer (for details, see ref. 8).

For each dataset in the original data (i.e., each pair of fetal–maternal RR interval time series), the number of SE, as well as their duration and n:m combination, were determined. These results were examined with respect to the 6 respiratory conditions. Furthermore, to investigate whether there was a preference in the timing of the fetal R peaks relative to the maternal RR cycle, the phase of each SE found in each dataset was determined in all datasets. The distributions of these phases over all subjects were examined for those n:m combinations for which the number of SE found was ≥10% of the total number of SE found over all combinations. These were 3:2, 4:3 and 5:3. For each of these n:m combinations, the number of histogram bins was set to 8 × m, corresponding to a resolution of 8 classes per maternal beat. The distributions were examined for a systematic bias for specific phases under each of the 6 respiratory conditions.

To distinguish epochs resulting from physiological interaction and those due to spurious combinations of heart rates, so-called “twin surrogate datasets” of the maternal MCGs were constructed (details in ref. 21). The algorithm used to generate twin surrogates is based on the so-called recurrence matrix

where Θ(·) denotes the Heaviside function, ‖·‖ a norm (e.g., Euclidean or maximum norm), and ε is a predefined threshold.x⃗(i) denotes the point of the trajectory of the system in phase space at time t = iΔt with Δt being the sampling time of the trajectory and i = 1, … , N. If only a scalar time series has been observed, as in the case of MCG data, the trajectory of the system has to be reconstructed by using, e.g., delay coordinates (22). For a review about time series analysis methods based on the recurrence matrix, see ref. 23.

To visualize the recurrences of a dynamical system, one can plot a black dot at the coordinates (i, j) of a N × N matrix if the distance between x⃗(i) and x⃗(j) is smaller than or equal to ε. This representation is called a recurrence plot. These plots exhibit patterns that are characteristic for the type of dynamics of the system under study. For example, long diagonal lines are characteristic for deterministic systems. In fact, it has been shown (23) that many dynamical invariants can be readily estimated from these recurrence plots. Very recently, it has been proven that the recurrence matrix contains all information about the dynamics of a system (24); i.e., systems with the same recurrence matrix are dynamically equivalent.

The main objective behind the method of twin surrogates is to change the structures in a recurrence plot consistently with the ones produced by the underlying dynamical system and then reconstruct the trajectory from the modified recurrence plot. We use the fact that in a recurrence plot there are identical columns, i.e., R_k,i = R_k,j ∀k. These columns may be considered identical because 2 different points of the trajectory can have exactly the same set of neighbors with respect to the threshold ε. Thus, there are points that are not only neighbors but also share the same neighborhood. These points are called twins. Twins are special points of the time series. Despite being distinct points in phase space, they are dynamically indistinguishable considering their neighborhoods; they have different pasts and different futures. The key idea regarding how to introduce the randomness needed for the generation of surrogates of a deterministic system is that one can jump randomly to one of the possible futures of the twins. A surrogate trajectory x⃗^S(i) of x⃗(i) with i = 1, … , N is then generated as follows.

1. Identify all pairs of twins, i.e., all pairs x⃗(i) and x⃗(j) such that R_i,k = R_j,k for k = 1, … , N.

2. Choose an arbitrary starting point x⃗(l) and set x⃗^S (1) = x⃗(l).

3. Generate the twin surrogate iteratively. The jth entry of the surrogate is denoted by x⃗^S (j) = x⃗(m). If x⃗(m) has no twins, set x⃗^S (j + 1) = x⃗(m + 1). If, on the other hand, x⃗(n) is a twin of x⃗(m), set x⃗^S (j + 1) = x⃗(m + 1) or x⃗^S (j + 1) = x⃗(n + 1) with equal probability. If triplets or multiplets occur proceed analogously.

Iterate step iii until the surrogate time series has the same length as the original one.

This algorithm creates twin surrogates which are shadowed (25) by typical trajectories of the system in the limit of an infinitely long original trajectory. Therefore, the twin surrogates mimic both the linear and nonlinear dynamical properties of the system. For any original series, a very large number of surrogate series can be produced. For each dataset, the fetal MCG signals were combined with 20 surrogate maternal MCG signals. These 20 fetal–maternal pairs were then processed and analyzed by using the same procedure as used in the original data. The results of the analyses of the original and surrogate data were compared.

Furthermore, we compared the heart rate properties of the pairs of original and surrogate datasets as follows. For each dataset, the following linear and nonlinear heart rate variability (HRV) measures were calculated for the original maternal RR interval time series and the corresponding 20 surrogate RR interval time series: the number of beats, the mean RR interval, their standard deviation (SD) and RMSSD, their LF and HF power, as well as their ratio (26), and finally the ApEn (27). In each dataset, the mean value of each heart rate measure was calculated in both the original and the corresponding 20 surrogate RR interval time series. The 20 surrogate values were averaged, and the difference (surrogate value minus original value) was determined.

We also considered the direct effect of controlled maternal breathing not only on the maternal but also on the fetal heart rate. To assess these effects, we determined the HRV measures mentioned in the previous paragraph for the original data of each of the respiratory conditions for both mother and child.

Statistics.

Values are expressed as means ± SD and/or quantiles, as appropriate. The uniformity of the HRV measures in the controlled breathing recordings was examined by ANOVA by using a nonparametric equivalent, the Friedman test, for dependent variables. Differences between the maternal heart rate measures in the original and surrogate data were tested by using the Wilcoxon test for paired samples. The distribution of the phases in the histograms was tested by fitting partial Fourier series to the data by using the general linear least-squares model and the significance of the fit was estimated by the zero-amplitude test (F-statistic) (28). This was done only for histograms containing at least 6 SE. All statistics were interpreted in a descriptive manner.