Latitudinal variation in lifespan within species is explained by the metabolic theory of ecology

Abstract

Many ectotherms exhibit striking latitudinal gradients in lifespan. However, it is unclear whether lifespan gradients in distantly related taxa share a common mechanistic explanation. We compiled data on geographic variation in lifespan in ectotherms from around the globe to determine how much of this intraspecific variation in lifespan may be explained by temperature using the simple predictions of the metabolic theory of ecology. We found that the metabolic theory accurately predicts how lifespan varies with temperature within species in a wide range of ectotherms in both controlled laboratory experiments and free-living populations. After removing the effect of temperature, only a small fraction of species showed significant trends with latitude. There was, however, considerable residual intraspecific variation indicating that other, more local factors are likely to be important in determining lifespan within species. These findings suggest that, given predicted increases in global temperature, lifespan of ectotherms may be substantially shortened in the future.

Many phenotypic traits covary with latitude, particularly among ectotherms. For instance, relative to individuals from low latitudes, high-latitude individuals tend to have higher growth rates and larger body size (1, 2), produce larger eggs (3), have relatively shorter extremities (4), and more vertebrae (5). Lifespan also varies with latitude in a wide variety of ectotherms. For example, lifespan increases with latitude in the yellow clam (Mesodesma mactroides) (6), oegopsin squid (suborder Oegospina) (7), and many fish species (8–11). One example is particularly striking: pearl mussels (Margaritifera margaritifera) found in Spain (43°N) have maximum lifespans of 29 years, whereas those in Russia (66°N) live nearly 200 years (12, 13). The purpose of our study is to determine whether this ubiquitous geographical variation in lifespan has a common physiological basis in temperature.

Temperature has long been known to influence lifespan (14, 15). For example, Drosophila melanogaster from Brazil raised at 31.2 °C lived up to 29 days, whereas flies from the same population reared at 12 °C lived up to 247 days (16). Although the temperature-lifespan relationship has been known for nearly a century, most of our knowledge on this relationship is derived from laboratory experiments on short-lived invertebrates (e.g., 17). Studies on natural variation in lifespan with temperature have largely been limited to cross-taxa comparisons (18, 19). As a consequence, the role of temperature in controlling geographic variation in lifespan within species is unclear. It is easy to imagine how geographic variation in the abundance of predators, availability of resources, fluctuations in environmental conditions, and local adaptation might obscure any relationship between temperature and lifespan in wild populations.

The metabolic theory of ecology (MTE) (20) has been used to link metabolism to a wide range of physiological and macroecological processes. Growth trajectories and life histories (21), population dynamics (22), geographic patterns in species richness (23), and community dynamics (24) all scale with body size and temperature in a manner surprisingly consistent with predictions made by the MTE. Since metabolism is known to influence lifespan (25), the MTE makes strong, quantitative predictions about the relationship between lifespan and temperature. In fact, Gillooly and colleagues (18, 26) have already used the MTE to predict variation in lifespan across species. However, the MTE has been criticized by many authors because it appears to lack predictive power at lower taxonomic levels (27), possibly because of the relatively small range of sizes within species. Nonetheless, many species exist over a wide range of temperatures, suggesting the MTE may yet be useful for predicting intraspecific patterns even in the absence of body size variation. In support of this, pelagic larval duration within marine fish and invertebrate species was found to be tightly coupled to temperature and accurately predicted by an MTE-based model (28). Here, we hypothesize that geographic variation in lifespan within species may be explained by temperature using the MTE.

To evaluate whether intraspecific variation in lifespan can be explained by the MTE and whether the temperature-lifespan relationship is apparent in natural populations, we synthesized all available data on intraspecific variation in lifespan from a diverse group of ectothermic taxa. Because field estimates of lifespan may be influenced by many factors including variation in predation, food availability, local adaptation, population density, and sampling variability, we began by testing the MTE using lifespan data from controlled laboratory experiments in which individuals from a single source population were reared under various temperatures. We then evaluated whether variation in temperature affects lifespan in wild populations as predicted by the MTE.

In keeping with previous work (18), we expect lifespan, l, to scale as

where m is body mass, E is activation energy, k is Boltzmann's constant (8.62 × 10⁻⁵ eV/K), and T is temperature in K. The chief unknown in this model is the activation energy which, based on previous work, is presumed to range from 0.2 to 1.2 eV (18, 29).

We tested the MTE by multiple regression of log-lifespan on log-mass and inverse temperature, fitting

to the 29 species for which we found intraspecific data on both size and temperature. However, temperature but not size data were found for an additional 38 species. By dropping mass from the model, we found that the inclusion of mass does not generally affect the slope for temperature, allowing us to analyze this much larger dataset (n = 67 wild species). Given the range of values for E (0.2 to 1.2 eV), we consider the MTE supported if slopes (β) of the regression of ln(l) on 1/kT are not significantly outside of this range.

Results

We compiled data for 30 species under laboratory conditions and for 67 free-living species (1,081 populations). These data represent 4 phyla and 23 orders from around the globe. The dataset contained representatives from terrestrial, freshwater, and marine environments, and of widely different average longevities [minimum average lifespan 11.6 d (Acartia tonsa), maximum 190.0 yrs (Margaritifera margaritifera)]. Latitude and lifespan were positively correlated in 85% of the species, although the relationship was statistically significant in only 39% of the cases. It is worth noting that under a null model without a latitudinal gradient in lifespan, the chances of obtaining 85% positive slopes are exceedingly small (χ² = 27.597, P < 0.0001). Moreover, for all species with significant regressions, lifespan increased with latitude. As discussed below, it appears that much of this latitudinal variation may be explained by temperature using the MTE.

Body size had no apparent influence on lifespan. Among the 29 species for which we had population-specific estimates of body size, 70% exhibited no significant variation in lifespan with size. The temperature slopes (β) estimated for these species did not change significantly when mass was excluded from the regression in all cases except Stizostedion canadense. Importantly, this species is also known to exhibit a latitudinal gradient in the genetic capacity for growth (30), which can potentially generate an interaction between the effects of temperature and mass that is not accounted for in standard MTE analyses. All subsequent results refer to regressions including only temperature.

Laboratory Species.

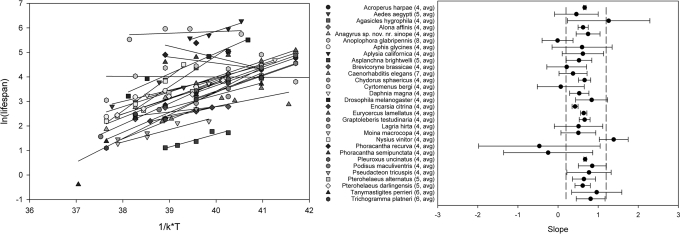
For the 30 species examined to test the MTE under controlled laboratory experiments, 80% of temperature-log lifespan slopes were within the predicted range (mean slope = 0.57) (Fig. 1 and Table 1) and none were significantly outside the range, strongly validating its use at the intraspecific level.

Fig. 1.

The relationship between mean lifespan of single-population individuals of 30 species raised at various temperatures (Left). Slope and 95% confidence intervals for these species are shown (Right), along with the MTE predicted range (dashed lines).

Table 1.

Summary of results for both laboratory and wild species

	Laboratory species (model I regressions)	Wild species (model II regressions)
N	30	67
Mean slope (SD)	0.57 (0.38)	0.55 (0.92)
Mean r2 (SD)	0.82 (0.27)	0.39 (0.34)
Percent within range	80	69
Percent not significantly outside	100	87

Wild Species.

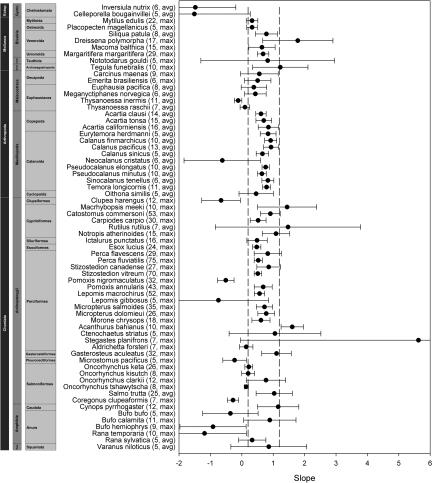
Having shown that the MTE accurately predicts intraspecific variation in lifespan under controlled conditions, we tested the MTE on field data from 67 species. Wild populations also showed predictable and consistent variation with temperature. Lifespan in 87% of the species studied varied as predicted by the MTE (Fig. 2 and Table 1, Table S1). Forty-six species (69%) fit precisely within the MTE-specified interval of slopes, 12 (18%) were outside the range but their slopes did not significantly differ from the predicted range, and 9 (13%) were significantly outside of the predicted range. As expected, coefficients of determination for wild populations were much smaller than those for laboratory populations (wild spp. ${\overline{r}}^2$ = 0.39, SD = 0.34, lab spp. ${\overline{r}}^2$ = 0.82, SD = 0.27). Overall, 70% of the species sampled had slopes that were significantly different from zero. Of these, 89% were within the range predicted by the MTE, 2% were significantly greater, and 9% were significantly less than predicted.

Fig. 2.

Point estimates and 95% confidence intervals for the temperature-log lifespan slopes for 67 ectotherms from natural populations. Vertical bars to the left indicate phylum, family, and order; parentheses after the species name are number of populations and whether lifespan estimate was average or maximum. *, estimates that are significantly outside of the predicted range. See Fig. S1 for plots of the raw data.

Because some studies reported maximum lifespan (n = 43) whereas others reported average lifespan (n = 24), we determined whether this difference had any effect on the estimated slope. There was no significant difference between them: mean slope = 0.463 (SD = 0.717) for average lifespan data and 0.596 (SD = 1.031) for maximum lifespan data (ANOVA: F-ratio = 0.321, df = 1, P = 0.573). However, r² values were substantially greater for the average lifespan data (${\overline{r}}^2$ = 0.58) than for maximum lifespan data (${\overline{r}}^2$ = 0.28). This is not surprising given the much greater sampling variance for maxima than for means.

To further explore the observed variation among species, we regressed the slopes of the temperature-log lifespan regression on the geographic range, mean temperature, average lifespan, and number of populations included in the analysis. We found a significant correlation between mean temperature and β (r² = 0.186, P < 0.001). Geographic range, as measured by the latitude and temperature range for each species, was not significantly correlated with β (lat.: r² = 0.001, P = 0.835; temp.: r² = 0.022, P = 0.230), nor was average lifespan (r² = 0.001, P = 0.784) or number of populations sampled (r² = 0.005, P = 0.576).

We also examined whether there was any consistent pattern in the slopes arising from phylogeny (i.e., class) or environment (i.e., terrestrial, freshwater, marine). Because of limited samples across these 2 factors (e.g., there are very few marine insects), we addressed both of these factors via 1-way ANOVA. We found that there was no significant taxonomic variation in slopes (F = 2.05, df = 8, P = 0.056). The almost-significant difference arises solely due to differences between the Gymnolaemata, an encrusting bryozoan, and all other taxa (Games–Howell pairwise multiple comparison test). We further explored this question accounting for phylogenetic nonindependence by partitioning variance within species, genera, families, orders, classes and phyla via a nested ANOVA (31). None of the nested sets significantly explained the observed variation (all P values >0.05). There were also no significant differences in slopes across environments (F = 0.726, df = 2, P = 0.488).

After accounting for temperature, only 8 species showed significant residual variation with latitude, and multiple regression models that included both latitude and temperature had significant effects of latitude in only 7 cases.

Discussion

In this study, we show that the ubiquitous observation that ectotherms live longer at higher latitudes can be primarily explained by temperature in a manner remarkably consistent with the MTE. Studies have suggested that the MTE lacks predictive power at the intraspecific level because of the relatively small range of body sizes found within species (27). Our analyses show that variation in lifespan at this taxonomic level is well explained by the MTE's Arrhenius model for thermal scaling both in laboratory studies and in wild populations but independent of mass. It appears, therefore, that within species temperature is a more important driver of population-level variation than mass. This is to be expected, because intraspecific variation in body mass tends to be relatively small (32).

Others have noted that the Arrhenius temperature dependence of the MTE is not the only model that could be used (33). We found that alternative regressions using temperature, and log-temperature as independent variables were statistically indistinguishable from the Arrhenius model using the sample size corrected version of AIC (34). These simpler models were always better than one with a quadratic temperature dependence. Our main finding, that the temperature dependence of lifespan within species is highly consistent across widely different taxa, remains valid regardless of the model used. Moreover, the overall mean slopes for lab and wild species (0.57 and 0.55) are not significantly different from the value of 0.65 predicted under the MTE (35). However, although the slopes are remarkably consistent with the MTE, it should be noted that considerable residual variation remains (Fig. S1), indicating that other, local, factors are likely to be important in determining lifespan within species.

Given the general success of the MTE, we suggest that departures from it may, in fact, be quite informative. Assuming that other environmental gradients are of secondary importance, this framework might be used to assess local adaption in lifespan. For instance, the fact that species whose slopes are outside of the predicted range all occur at relatively low temperatures is consistent with the metabolic cold adaptation hypothesis; that is, cold-adapted populations tend to have higher metabolic rates than warm-adapted populations (36), reducing the slope of the apparent temperature-log(lifespan) relationship. Moreover, temperature compensation is thought to evolve in response to size-dependent winter mortality (37, 38) and several of the species with significantly flatter slopes (e.g., Coregonus clupeaformis, Clupea harengus) do, in fact, exhibit this type of winter mortality (39, 40). Another relevant outlier is Stizostedion canadense for which there appeared to be a significant interaction between temperature and mass. We suspect that this result arises from local adaptation in growth rate (30) which is currently unaccounted for in applications of the MTE.

Given the intense current interest in the effects of climate change, it is interesting to consider how lifespan is likely to change, especially given that small changes in temperature will result in relatively large changes in lifespan because of their exponential relationship. Under extremely conservative climate change scenarios, temperatures are expected to rise by 1.1 to 2.9 °C in the next 100 years (41). Based on this temperature change and the 0.2 to 1.2 slope predicted by the MTE, ectotherm lifespans may be expected to shorten by 3–19% (under a 1.1 °C increase) to 8–42% (2.9 °C increases). These changes in lifespan among ectotherms may have widespread consequences, including compensatory responses in life history (42) and higher extinction risk (43). Further, and given the importance to food web dynamics of the interaction between ectotherms and endotherms (44, 45), our results suggest that substantial changes to ecosystem structure and stability are likely if the generation times of ectotherms shift to accommodate changes in climate whereas generation times of endotherms do not.

Materials and Methods

To construct our dataset, we queried all major databases (Web of Science, Google Scholar, PubMed, and Biological Abstracts) with appropriate combinations of keywords. We extended this initial collection with additional citations from sampled papers. We first collected data from controlled laboratory experiments in which individuals from a single source population were reared until natural death under at least 4 temperatures. Average lifespan was reported for all lab data. We then reviewed literature for wild populations in which estimates of either maximum lifespan or average lifespan were provided. After all data for a given species were identified, we screened them against the following criteria: (i) species studied was ectothermic, and (ii) longevity data were reported for at least 5 populations spanning at least 0.25° of latitude. We also collected all other biological (e.g., body size) and physical (e.g., elevation) information, as well as numbers of individuals assayed, when available. We aimed to include the largest possible range of taxa; however, longevity estimates in some groups are scarce (e.g., reptiles) (46).

Annual average temperatures experienced by populations were gathered directly from the source when available. When not presented, geographic coordinates were obtained from the source publication or author and 30-year temperature averages estimated from the NCEP Reanalysis Database (47) for marine species and the National Climatic Data Center (http://www.ncdc.noaa.gov/oa/ncdc.html) database for freshwater and terrestrial species. Because the species in our study were all ectotherms, we assumed that the local ambient temperature was a reasonable approximation to the individual body temperature. Given the uncertainty associated with these estimates of temperature, we evaluated the dependence of lifespan on temperature for wild species with reduced major axis (model II) regression (48).

Because intra-annual variation in temperature typically varies with latitude, we tested whether including variation within a year in our model would yield different results than mean annual temperature alone. Mean annual temperature and the second-order approximation proposed by Savage (49), which includes intra-annual variance in temperature, yielded very similar results. We compared Boltzmann's factors calculated with our gathered annual temperatures as exp[E/kT] and using the approximation exp[E/kT]{1+[E/kT(E/kT − 1)]Var(T)} with variances we obtained for 354 sites. Because of a high correlation between the 2 Boltzmann's factors (correlation coefficient = 0.959) and a paucity of annual temperature variance data, we used 30-yr mean annual temperatures.

To test that body size could be safely omitted, we compared estimated temperature-log lifespan slopes with and without body mass information for 29 species. For some taxa, sizes were only available in terms of length and were converted to mass using species-specific conversions. Temperature slopes for models with and without mass were obtained through multiple regression analysis. We then created 100 bootstrap lifespan, mass, and temperature datasets for each species and calculated regression slopes for each. We compared the original temperature slope obtained without accounting for body mass to the 95% confidence interval of the bootstrapped sample of slopes. For only 1 species, Stizostedion canadense, was the estimated temperature dependence significantly different when mass was included.

We also compared the relationship between ln(lifespan) and temperature assuming a variety of other models. The models we evaluated via second order Akaike Information Criterion (AICc; 34) included the inverse temperature model presented above, a log-log model [ln(l) = a + b ln(T)] (33), a quadratic model [ln(l) = a + (b/kT) + (c/kT²)], and a linear one [ln(l) = a + bT]. All first order models were statistically indistinguishable and the estimated slopes were highly correlated (r > 0.98). The quadratic model was never best under AICc.