Short-Term Memory, Working Memory, and Executive Functioning in Preschoolers: Longitudinal Predictors of Mathematical Achievement at Age 7 Years

Abstract

This study examined whether measures of short-term memory, working memory, and executive functioning in preschool children predict later proficiency in academic achievement at 7 years of age (third year of primary school). Children were tested in preschool (M age = 4 years, 6 months) on a battery of cognitive measures, and mathematics and reading outcomes (from standardized, norm-referenced school-based assessments) were taken on entry to primary school, and at the end of the first and third year of primary school. Growth curve analyses examined predictors of math and reading achievement across the duration of the study and revealed that better digit span and executive function skills provided children with an immediate head start in math and reading that they maintained throughout the first three years of primary school. Visual-spatial short-term memory span was found to be a predictor specifically of math ability. Correlational and regression analyses revealed that visual short-term and working memory were found to specifically predict math achievement at each time point, while executive function skills predicted learning in general rather than learning in one specific domain. The implications of the findings are discussed in relation to further understanding the role of cognitive skills in different mathematical tasks, and in relation to the impact of limited cognitive skills in the classroom environment.

Children's performance in mathematics and reading achievement in schools is influenced by a number of contributing factors. Higher level achievement will depend to some extent on the basic skills that feed into more complex reading and mathematical abilities. Tymms (1999) referred to these as “general developed abilities,” which includes skills (at school entry) such as letter recognition, spelling, and phonemic awareness as precursors to reading, and number recognition, magnitude understanding, and counting as precursors to mathematics (see Geary, Hamson, & Hoard 2000; Geary, Hoard, & Hamson, 1999). Clearly, these predictor variables are a simplified form of the complex skill they are predicting, and Gathercole, Pickering, Knight, and Stegman (2004) argued that such basic skills represent crystallized knowledge (or what Cattell referred to as crystallized intelligence (Gc)) built up on the basis of experiences in the home, nursery school, and other social settings, and referenced by over-learned skills and knowledge such as vocabulary. However, such learning opportunities also interact with a basic cognitive capacity for learning, and Gathercole et al. pointed out that it is essential to assess these fluid cognitive capacities, skills that are not knowledge based and generally less determined by socioeconomic factors, but which allow us to engage in complex cognitive operations. Such abilities can also be referred to as fluid intelligence (Gf) and represent a biologically based ability to acquire skills and knowledge during the lifespan (see Geary, 2007 for a review). As such, it is argued that such fluid cognitive capacities (or Gf) should predict learning in evolutionarily novel contexts such as school and the workplace.

Cognitive studies of mathematical achievement and disorder provide a valuable insight into the deficits that might underlie difficulties in learning mathematics. Many studies have used the working memory model of Baddeley and Hitch (1974, see also Baddeley, 1996, 2000) as a framework within which to study a range of cognitive skills, and recent work indicates that working memory is a core mechanism underlying individual differences in Gf. The two “slave” systems of working memory, the phonological loop and the visual-spatial sketch pad, are specialized for processing language-based and visuo-spatial information, respectively. Assessment of these slave systems is typically made using short-term memory tasks where small amounts of material are held and reproduced in a sequential fashion, with minimal resources needed from long-term memory to interpret the task and no additional competing cognitive demands (e.g., digit span, word recall, Corsi blocks, visual-patterns task). The central executive controls the allocation of resources between the phonological loop and the visual-spatial sketch pad, schedules multiple cognitive activities, and is able to revise the content of memory in light of new and relevant information. Experimental tasks assessing the central executive typically attempt to obtain a measure of the participants' abilities to combine concurrent processing and storage by using measures such as listening span (Daneman & Carpenter, 1980), counting span (Case, Kurland, & Goldberg, 1982) or backward digit span.

More recent conceptualizations of the central executive (e.g., Baddeley, 1996; Miyake et al., 2000) support the idea of distinct executive functions, some of which are more strongly related to general fluid abilities (or Gf) than others. These distinct executive functions include inhibition (suppression of dominant action tendencies in favor of more goal-appropriate behavior), shifting (disengagement of an irrelevant task set or strategy and the subsequent activation of a more appropriate one), and updating (encoding and evaluation of incoming information for relevance to the task at hand and subsequent revision of the information held in memory, most closely associated with complex span tasks). Friedman et al. (2006) reported that in healthy adults, updating (or what others would refer to as working memory) is most closely related to intelligence, whereas the links between inhibition and shifting to intelligence were much lower and significantly mediated by the variance shared with updating. However, where frontal lobe functioning is compromised (as we might expect early in development), executive function skills may not be so easily differentiated, resulting in higher and more general executive function- intelligence correlations.

Many studies have examined the relationship between working memory subsystems, executive functioning, and arithmetic or mathematics ability. Some studies have attributed individual differences in mathematical problem solving (particularly arithmetic) to inefficiencies in the utilization of the phonological system (e.g., Furst & Hitch, 2000; Gathercole & Pickering, 2000; Gathercole et al., 2004; Geary, Brown, & Samaranayake, 1991; Siegel & Ryan, 1989; Swanson & Sachse- Lee, 2001), with the role of the phonological loop being to encode and retain verbal codes used for counting and/or retain interim solutions. However, a number of studies of children with poor mathematical skills have revealed no significant limitations in verbal short-term memory, or limitations being due to a third factor such as processing speed or co-occurring reading difficulties (e.g., Bull & Johnston, 1997; Geary et al., 1999; Geary et al., 2000).

Recent research is placing more emphasis on the important role of the visual- spatial sketch pad in children's early arithmetical skills (McKenzie, Bull, & Gray, 2003; Holmes & Adams, 2006). Visual-spatial skills and visual-spatial working memory have been found to be related to children's early counting ability (Kyttala, Aunio, Lehto, van Luit, & Hautamaki, 2003), and to mathematics ability in children aged 10 years (Maybery & Do, 2003), 11 years, and 14 years (Jarvis & Gathercole, 2003). Studies of children with specific mathematical difficulties have shown that they typically perform poorly on visuo-spatial span measures (McLean & Hitch, 1999; van der Sluis, van der Leij, & de Jong, 2005; White, Moffitt, & Silva, 1992). One of the identified subtypes of mathematical learning disabilities includes those individuals believed to have deficits in visual-spatial skills (Geary, 1993). Visual-spatial skills may impact math at various levels-number inversions and reversal, misalignment of column digits, problems in visual attention and monitoring such as ignoring signs or changing operation part-way through completion of problem, and acquiring concepts of borrowing and carrying. The visual- spatial system also supports other aspects of non-verbal numerical processing such as number magnitude, estimation, and representing information in a spatial form, as in a mental number line (Dehaene, 1997; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Zorzi, Proftis, & Umilta, 2002). Therefore, spatial visualization and understanding and manipulation of spatial relations appear to be particularly important in math skill development (Dark & Benbow, 1990; Geary et al., 2000; McGrew, Flanagan, Keith, & Vanderwood, 1997).

Many studies now also report a direct association between executive functioning and children's early emerging and developing mathematical skills across a wide age range (e.g., Bull, Johnston, & Roy, 1999; Bull & Scerif, 2001; Espy, McDiarmid, Cwik, Stalets, Hamby, & Senn, 2004; Gathercole & Pickering, 2000; Gathercole et al., 2004; McLean & Hitch, 1999; Passolunghi & Siegel, 2001). Many of these studies choose to focus on span tasks thought to measure updating within working memory. However, a number of studies have tried to specify the functional relations between different aspects of executive functioning (e.g., inhibition, shifting, and updating) and their relationship to a range of numerical and mathematical skills. These studies show that in young preschool children (Espy et al., 2004), and in children aged around 7 (Bull & Scerif, 2001) and 11 years (St Clair-Thompson & Gathercole, 2006) inhibitory skills are predictive of mathematics ability, although the relationship may be less clear cut in older children (van der Sluis, de Jong, & van der Leij, 2004). More complex shifting skills have been found to be predictive of performance in children aged 7 years and older (Bull et al, 1999; Bull & Scerif, 2001; McLean & Hitch, 1999; van der Sluis et al., 2004). Finally, whereas some studies report a specific relation between executive functioning and mathematics independent of reading skills (e.g., Bull & Scerif, 2001), it is clear that executive functioning skills have been implicated in many aspects of learning, including language comprehension, reading, and writing (e.g., Gathercole, Alloway, Willis, & Adams, 2006; Gathercole & Pickering, 2000; Gathercole et al., 2004; Swanson & Jerman, 2007). Therefore, one of the aims of this study is to determine the specificity of the relationship between early cognitive and academic skills (in this case reading and mathematics).

Although evidence has amassed for the link between working memory, executive functioning, and mathematics, it is not clear whether these fluid abilities would actually contribute to the prediction and identification of later mathematical skills and difficulties, that is, would they provide teachers with a useful diagnostic tool that could be administered in the early school years. Given the evidence noted earlier that central executive functions predict concurrent and longitudinal mathematical achievement in older children, and appear to be related to mathematics proficiency even in very young preschool children (Espy et al., 2004), can short- term memory, working memory, and central executive functions measured in preschoolers be used to identify those children who go on to develop specific difficulties in mathematics or more general difficulties in learning both reading and math? Tasks assessing cognitive skills like short-term memory or executive functioning do not directly index the component skills needed for mathematics or reading. Therefore, lack of ability in these tasks is not due to a lack of knowledge relevant to the assessment domain, but because they are unable to inhibit, flexibly shift, and hold and manipulate information in short-term or working memory (Gathercole, Brown, & Pickering, 2003). One of the difficulties in assessing such skills in a young sample is finding age-appropriate tasks that do not result in ceiling or floor effects. The current study uses a combination of traditional and newly developed tasks chosen on the basis of their use in other studies with children aged approximately 5 years (e.g., backward digit span), or their recent development and standardization for young samples (e.g., Tower of London and the Shape School).

Many of the previous studies have been conducted with children aged 7 years and older. However, for children just entering school many of the tasks they are faced with are completely novel and as such may place particularly heavy demands on cognitive processes such as short-term, working memory, and executive functioning. The need for supporting cognitive competencies may change as children become more skilled in numerical understanding. In the current study, 124 preschool children (mean age of 4.5 years) were administered a battery of cognitive tasks. This is an unselected sample making the results more applicable to understanding cognition and learning in general rather than being restricted to those children with recognized learning difficulties. Mathematic proficiency was measured by the Performance Indicators in Primary School (PIPS; Tymms, 1999). The PIPS is conducted on entry to the first year of primary school (age 4-5), then again at the end of the first (age 5-6), third (age 7-8), fifth (age 9-10), and the seventh year (11 years). Data will be reported for the first three of these testing periods. Growth curve analyses were conducted to examine the significant unique predictors of mathematics and reading ability over the duration of the study. Correlational and regression analyses also examined the specific and generic cognitive predictors of math and reading achievement within each time point.

Method

Participants

At the outset of the study 124 children attending 4 local nursery schools in Aberdeenshire were tested on the battery of executive function and short-term and working memory measures. All nursery schools were attached to associated primary schools, with the transition for most children being within the same school. At the beginning of testing the mean age of the children was 4 years 6 months (SD = 4 months), with all children being in their preschool year. All children were native English speakers, and were representative of the general population in that geographical location in regard to socioeconomic status (mainly working to middle class), and ethnicity (approximately 95% European Caucasian).

When the children entered primary school in August, they were tested on Performance Indicators in Primary School (PIPS), which assesses children's basic number, phonics, and reading skills at entry into primary school. PIPS data were collected for 111 children from the original sample. PIPS assessments were also conducted at the end of the first year of primary school (June, N = 108) and again at the end of the third year of primary school (June, N = 88). For 7 children, missing data in the executive function battery prevented their inclusion in growth curve modeling analyses. For the remaining 104 children, the pattern of attrition was examined to determine its relation to mathematics performance. Initial PIPS scores were compared among children for whom there was available data versus those for whom it was missing at P3 (N = 82 vs. N = 22) and at P1 (N = 101 vs. N = 3). There was no difference in initial PIPS scores among missing groups at each time point (all ps > .40), consistent with the missing at random assumption (Schafer, 1997) required for the statistical analyses used here. The final sample included 54 girls and 50 boys.

Measures

Mathematics outcome measure. PIPS assessment

At the first two time-points, testing was conducted individually by the teacher with each child using a computerized assessment system. Skills measured included ideas about mathematics (e.g., biggest, smallest, most, least, tallest, shortest), counting, simple arithmetic (e.g., 3 + 2, 3 - 1), number recognition (up to hundreds), shape, and more complex mathematics procedures, for example, what is 3 less than 7, 8 more than 13, ½ of 6, and more complex arithmetic involving larger numbers. At the third time of testing (end of P3), testing was conducted on a group basis, with children recording their responses in a booklet. Skills assessed included more complex mathematical procedures described earlier, along with number sequencing, and graphical representation of data. Note that this instrument includes different item sets for different ages, therefore comparing among raw scores at different ages that would allow understanding of skill growth is not possible. Therefore, the standardized score (M = 50, SD = 10) was used. In this case, the expectation is “flat” growth (children maintain their relative position compared to one another).

Predictor Variables

All predictor measures were administered once during the preschool year. All tasks were administered individually across 3 sessions lasting approximately 20 minutes, with all children being tested by the first author. Children were tested in a quiet corner of the classroom or in a small adjoining room.

Central executive tasks. Shape School

The Shape School was developed by Espy (1997; see also Espy, Bull, Martin, & Stroup, 2006 for conceptualization and psychometric properties of the task), designed to assess different aspects of executive control in young children by using bright colorful, affectively engaging stimuli presented in an age appropriate format of a story book. The story begins by setting up the premise, showing stimulus figures as colored squares and circles with cartoon faces, arms, and legs, playing on a playground. The child is introduced to one class of children, whose “names” are their color, where the child names each stimulus figure color, in order to assess whether the child can reliably recognize and name color. As the story continues, the child is told that the story figures are lining up to go into the play yard. In this control condition, Condition A, the child had to name the color of each figure (arrayed in 3 lines of 5 across the page). This condition served two purposes; to get a baseline measure of naming speed, and more importantly, to set up the prepotent naming response to identify stimulus figure color.

In the next condition, Condition B (Inhibition), children were told that now it was time for lunch, but not all of the story figures had finished their work. “Happy” and “Sad/frustrated” expressions were added to the stimulus figures' faces to depict figures who had completed their work and those who had not, respectively. After 6 practice stimuli to ensure that children understood the task rule, children were instructed to call the names of the children who had finished their work and were ready for lunch, and not to call the names of those who were not ready (similar to a Go No-Go task). In the same configuration of 3 rows of 5 figures each, there were 9 happy-faced stimuli, requiring the color naming response, and 6 sad/frustrated faced stimuli, requiring response suppression.

Finally, another classroom was introduced in Condition C (Switching), where the stimulus figures wore hats. Children were instructed that names of the hatted pupils were the stimulus figure shapes, and the names for the hatless pupils remained the stimulus figure color. After practice with 6 stimulus figures, children again were told that the figures were in line to go to story time, where the child had to name the shape of the figures with hats and color of the hatless figures in the 3 row by 5 figure configuration. There were 8 figures without hats and 7 with hats interspersed randomly, such that the child had to shift between naming hatted figure color and hatless figure shape as cued, respectively.

Children were not allowed to continue with the condition test unless they had successfully named the characters on the practice pages, in order to ensure adequate rule knowledge prior to application in the test conditions. The experimenter recorded the response time and number of stimuli correctly identified (according to the pertinent rule) in each condition from when the child began naming the first figure, to when they finished naming the last figure in the array. For the more challenging B and C conditions only, an efficiency score was calculated by subtracting the number of errors from the number of stimuli correctly named and dividing by the latency to complete each condition. For growth curve analyses, these efficiency scores were regressed on response time in the Control condition and the residuals were saved, to control for basic naming speed.

Tower of London (Korkman, Kirk, & Kemp, 1998)

This task uses a piece of apparatus with three pegs on which three colored balls can be placed. Each peg is a different size allowing only a certain number of balls to be placed on each peg. The child is presented with pictures of the balls arranged in different positions, and asked to move the balls from their resting positions, following certain rules, to create an identical arrangement. The rules included only being able to move one ball at a time, all balls staying on the pegs when they are not being moved, and not being able to change a move once the child had taken their hand off the ball. Children were told the minimum number of moves that would be needed to make the tower match that presented in the book. The task is a measure of children's ability to make moves that initially go against the end-goal state (i.e., inhibiting the tendency to go straight for the end-goal positions), but which ultimately result in completing the task in the minimum number of moves. It is also thought to be a measure of planning, monitoring, and problem-solving ability (e.g., Culbertson and Zillmer, 1998), although previous research suggests that, with young children at least, success on the more complex trials of the Tower of London is best predicted by shifting ability whereby the child has to shift between different subgoals for task completion (Bull, Espy, & Senn, 2004). The maximum score possible on this task was 20.

Short-term memory and working memory tasks

Corsi Blocks (forwards and backwards). This task requires children to watch the experimenter pointing to a series of blocks that are arranged randomly on a board, and then to copy them and point to the blocks in the same order. The series starts with only two blocks, and progresses to more blocks until the child fails to correctly copy the order on two consecutive trials with the same number of blocks. The second stage of the task requires the child to point to the blocks in the opposite order to the experimenter. Backward span tasks are typically seen as working memory tasks as they require the storage of information whilst additional cognitive processing is being undertaken (in this case, reversing the sequence of moves).

Digit span (forward and backward)

This task is identical in procedure to the Corsi Blocks, but instead of copying a sequence of pointing, the child has to repeat a sequence of numbers that have been spoken to the child by the experimenter, first forward and then backward. Forward recall provides a measurement of basic storage capacity of the phonological loop, whereas backward recall, requiring storage and manipulation of the information prior to recall, is thought to tax working memory.

Note that for both Corsi and digits backwards there was too much missing data to allow inclusion in the growth curve analysis. Although backward span tasks have been used successfully with children as young as 4 or 5 years in previous studies (e.g., Alloway, 2007; Gathercole et al., 2003) many children in the current study were unable to recall two items in reverse order, severely limiting variability on these tasks. Therefore, these tasks are included in the correlational analyses only with an indication of the number of children who completed the task.

Results

Descriptive data for mathematics outcome and predictor variables are shown in Table 1. Initial analyses were undertaken to examine for sex differences in performance on the predictor variables and math outcome. Sex differences occurred for only one measure, the Tower of London, where girls scored significantly higher than boys, t(102) = 2.43, p = .02. Examination of sex*time interactions (for math outcome) and of sex*predictor variable (those retained in the final growth curve models) revealed no significant interactions (all ps > .18).

Table 1.

Demographic Information and Descriptive Statistics for Mathematics Outcomes and Predictor Variables

Variable	M	SD	Minimum	Maximum	N
Age at PIPS Wave 1 testing	4.99	0.31	4.25	5.59	104
Age at PIPS Wave 2 testing	5.70	0.31	4.95	6.29	101
Age at PIPS Wave 3 testing	7.71	0.31	6.95	8.29	82
Age at executive function testing	4.49	0.32	3.75	5.09	104
PIPS Mathematics, Wave 1	49.34	9.27	30.64	74.26	104
PIPS Mathematics, Wave 2	49.20	8.02	31.13	67.66	101
PIPS Mathematics, Wave 3	50.67	9.10	31.00	68.00	82
Short-term memory:
Corsi Span Forward (max = 9)	3.06	0.65	2.00	4.00	104
Digit Span Forward	3.54	0.79	2.00	5.00	104
Working memory:
Corsi Span Backward	1.94	1.14	0.00	5.00	78
Digit Span Backward	0.68	1.08	0.00	3.00	84
Executive functioning:
Shape School Inhibit (Efficiency)	0.59	0.28	0.05	1.15	104
Shape School Shift (Efficiency)	0.17	0.14	-0.19	0.55	104
Tower of London (max = 20)	6.87	3.62	1.00	17.00	104

Two forms of analysis are shown in an attempt to understand the relation between the predictor variables and academic achievement. The first, growth curve modeling of the longitudinal data, reflects the overall findings from the entire observation period, and examines the advantages gained in math and reading by having better cognitive skills at Time 1, and whether those cognitive skills help children to gain more math and reading proficiency than would be expected based on their initial standing relative to the standardization sample. The second set of analyses, correlations and regression, examines the cognitive predictors of performance within each time point. This is important given the changing nature of mathematical skills across the time period, and the change in assessment format.

Hierarchical linear modeling results of the growth in PIPS mathematics and reading scores are presented in Tables 2 and 3. In these models to best fit the sampling strategy, change across the assessment waves (P1 beginning, P1 end, and P3) was modeled, and age at testing was controlled statistically. A backwards trimming procedure was used to select the best fitting unconditional (with no predictors) model, where parameters without variability were removed, and then those that did not differ from zero. The intercept was set at the P3 assessment, representing the final level of academic performance relative to normative expectations. When the final unconditional model was selected to model the shape of the trajectory across the observation period, the predictors of interest were included to understand the individually varying growth parameters. Corsi and digit span were centered at the lowest span, and other predictors were centered at their respective sample means. Because the outcome measures being used are normative referenced and use standardized scores, the average linear rates of change were not expected to be significant (which would indicate that the subjects are gaining ground across time relative to the standardization sample).

Table 2.

Growth Curve Modeling-Results of the Unconditional Models

	$\tilde{a}$	SE	Estimated Variance
PIPS Mathematics
Intercept	50.51*	0.95	58.09*
Slope	0.51	0.38	7.09*
PIPS Reading
Intercept	49.55*	0.75	46.26*

Analyses were conducted using PIPS t-scores. The intercept parameter represents expected PIPS t-scores at the final assessment (Wave 3).

^*p < .0001.

Table 3.

Growth Curve Modeling-Results of the Conditional Models

	Mathematics		Reading
	γ	SE	γ	SE
Effects on intercept parameter
Intercept	40.19*****	3.23	44.84*****	1.49
Age at PIPS 3 testing	-4.18	2.97	-	-
Digit Span (Forward)	2.01**	0.82	3.05****	0.86
Corsi (Forward)	2.39**	1.04	-	-
Shape School Inhibit	4.91*	2.53	5.28**	2.70
Shape School Switch	-	-	-	-
Tower of London	0.53***	0.18	0.61***	0.19
Effects on slope parameter
Slope	0.49	0.36	-	-
Age at PIPS 3 testing	-4.20****	1.13	-	-

γ is the relevant parameter estimate. Analyses were conducted using PIPS t-scores. All growth parameters are centered at the final PIPS assessment. Corsi and digit span were centered at the lowest span, and other predictors were centered at their respective sample means.

^*p ≤ .10

^**p ≤ .05

^***p ≤ .01

^****p ≤ .001

^*****p ≤ .0001

In the unconditional models, there was significant individual variation in the level (intercept) of mathematics and reading performance (estimated σ² = 58.09 for Mathematics and 46.26 for Reading), and in the rate of linear change in mathematics performance (estimated σ² = 7.09), accounting for a substantial portion of total variance, pseudo-R² = 0.55, 0.57, and 0.36, respectively (pseudo-R² indexes the proportion of variation in the outcome measure for a multilevel model and is calculated by looking at what proportion of the residual variance in a model is explained by adding additional predictors; Singer & Willett, 2003). Individual variation in the linear rate of change in reading skills was too small to be estimated properly and hence was set to zero for modeling purposes. As expected, children obtained a t-score of 50 on average on both the PIPS Mathematics and Reading subtests at P3, which was stable across the observation period (slope parameter for Mathematics, γ = 0.51, did not differ from 0, and for reading, the slope parameter was too small to be estimated). Although average growth was in fact flat, the linear slope parameter was retained in the Mathematics models to determine whether any of the predictors of interest related to change in mathematics proficiency across the period because there was substantial individual variability in slope. When the covariate, age at the P3 assessment, was included in the model, it was related to both the level and rate of growth of mathematics performance, where children who were younger relative to their grade started off as lower performing at the P1 assessment period and then demonstrated larger “catch-up” growth over the observation period. The age covariate was unrelated to reading proficiency.

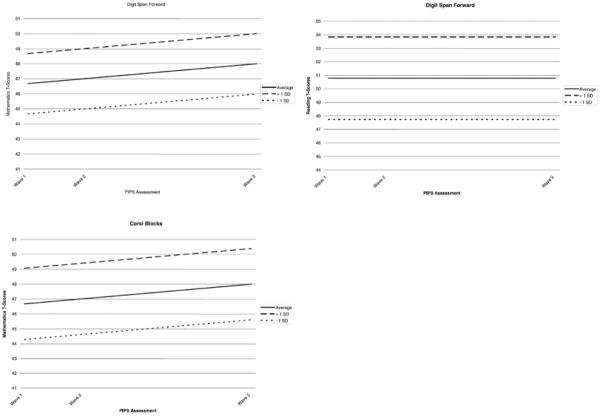
As predicted in the conditional models, several of the cognitive tasks were related to the level of mathematics and reading proficiency, centered here at the final P3 assessment wave. Retention span of verbal (Digit Span) information assessed at the initial P1 assessment was related to the level of PIPS math and reading score. Each increase in verbal span length of 1 digit at the P1 assessment was associated with a 2.01 point higher PIPS math score and a 3.05 point higher PIPS reading score at the P3 assessment. Note that the relative difference in achievement related to retention of verbal information was constant across the observation period, as maximal digit span length recalled at the baseline P1 assessment was unrelated to linear growth, p > .15, shown in the top two panels of Figure 1. That is, children who were able to retain longer digit strings at the beginning of Primary 1 maintained the degree of proficiency in mathematics and reading performance relative to their peers across the entire observation period. A similar pattern of results was evident for retention of non-verbal information assessed by Corsi Blocks, but here, the effect was significant only for mathematics skills. For each additional chunk of non-verbal information maintained online at the initial P1 assessment, PIPS mathematics scores were higher by an additional 2.39 points at the P3 assessment nearly 3 years later. Again, the magnitude of the difference in mathematic performance as a function of non-verbal information maintained was constant across the observation period (all ps > .40). This relation is shown in the bottom panel of Figure 1.

Figure 1.

Effects of short-term memory span on PIPS mathematics and reading scores.

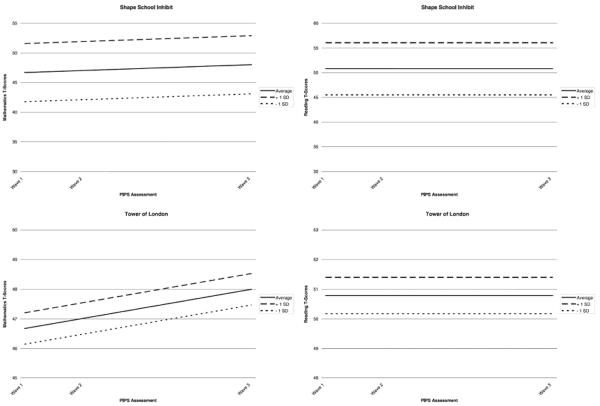
Among the central executive skills, Shape School B (Inhibit) Condition performance assessed at the baseline P1 assessment was related to both mathematics (p < .10) and reading performance (p < .05) at the P3 measurement occasion. Children with a Shape School Inhibit efficiency score 1 unit above the mean obtained an additional 4.91 points on PIPS mathematics and 5.28 points on PIPS reading tests, which was constant across the observation period. Similarly, children who succeeded on one additional trial on TOL (indicating an ability to succeed on more complex trials requiring an increasing number of moves and more counterintuitive moves away from the end-state) scored .53 and .61 points higher on the PIPS Mathematics and Reading outcome measures, respectively (see Figure 2).

Figure 2.

Effects of central executive processes on PIPS mathematics and reading scores.

Correlational analyses examined the pattern of relationships between the predictor variables and PIPS mathematics scores within each time-point. To identify those skills that are specific to the prediction of mathematics ability, the correlations to PIPS reading scores were also examined (see Table 4). At the earliest PIPS assessments conducted at the beginning and end of the first year of primary school, all of the cognitive measures correlated significantly with PIPS mathematics. By the end of the third year of primary school, neither of the short-term memory span tasks (digit or Corsi span) were significantly correlated with math achievement, whereas all central executive measures (working memory span tasks, inhibition, shifting, and Tower of London) significantly correlated with mathematics ability, the strongest correlation being with visual-spatial working memory span. Examination of reading achievement during P1 reveals that all cognitive tasks (with the exception of Corsi span at Wave 1) significantly correlated with reading ability. By the end of P3 both short-term memory tasks (digit and Corsi span) remained significantly correlated with reading achievement, along with Corsi backward span and Shape School Switching. Backward digit span, inhibition, and Tower of London did not significantly predict reading achievement at this stage, although correlations indicated that higher reading achievement was associated with better performance on all cognitive tasks.

Table 4.

Correlations between Predictor Variables and PIPS Mathematics and Reading Scores

	PIPS Correlations Mathematics			PIPS Correlations Reading
Predictor	Wave1	Wave 2	Wave 3	Wave1	Wave 2	Wave 3
Short-term memory:
Corsi Span Forward	.40**** (104)	.36**** (101)	.13 (82)	0.19* (104)	0.27*** (101)	0.28*** (83)
Digit Span Forward	.36**** (104)	.32**** (101)	.12 (82)	0.32**** (104)	0.35**** (101)	0.25** (83)
Working memory:
Corsi Span Backward	.34*** (78)	.36**** (75)	.39*** (58)	0.37**** (78)	0.55**** (75)	0.27** (58)
Digit Span Backward	.52**** (84)	.37**** (81)	.32*** (62)	0.45**** (84)	0.39**** (81)	0.23* (63)
Executive functioning:
Shape School Inhibit (Efficiency)	.42**** (104)	.43**** (101)	.23** (82)	0.40**** (104)	0.46**** (101)	0.21* (83)
Shape School Switch (Efficiency)	.38**** (104)	.31*** (101)	.29*** (82)	0.45**** (104)	0.33**** (101)	0.29*** (83)
Tower of London	.46**** (104)	.30*** (101)	.26** (82)	0.41**** (104)	0.35**** (101)	0.17 (83)

Number of observations included in each correlation are provided in parentheses.

^*p ≤ .10

^**p ≤ .05

^***p ≤ .01

^****p ≤ .001

If certain cognitive skills place general, rather than specific, constraints on reading and mathematics abilities, associations between the cognitive predictors and, for example, mathematics should be abolished when differences in reading ability are taken into account (and vice versa). Regression analyses shown in Table 5 indicate the percentage variance in math achievement predicted by the cognitive tasks once reading ability at each wave of testing has been accounted for (or variance in reading achievement once math ability is accounted for). The first thing to note is the degree of overlap in the variance of math and reading achievement, at its lowest accounting for 36% of the variance at time 3, and at its highest 53% of the variance at Time 2 (end of first year of primary school). Considering first the results from Time 1, controlling for reading ability eliminated some of the previously significant associations between the cognitive skills and math ability (Corsi backward span and Shape School Switching). However, all other measures continued to predict significant unique variance in math ability once reading ability had been accounted for, most notably Corsi span (8.3%), backward digit span (7.1%) and Tower of London (5%). Controlling for math ability removed virtually all significant associations with reading achievement with Shape School Inhibit and Shape School Switch remaining as significant predictors of reading over and above mathematics ability.

Table 5.

Percentage Variance Accounted in Math Controlling for Reading Achievement at Each Time Point (or Reading Controlling for Math Achievement at Each Time Point)

	PIPS Correlations Mathematics			PIPS Correlations Reading
Predictor	Wave1	Wave 2	Wave 3	Wave1	Wave 2	Wave 3
Math/Reading outcome	39***	52.8***	35.7***	39***	52.8***	35.7***
Short-term memory:
Corsi Span Forward	8.3***	2.7*	.20	.40	.00	4.4*
Digit Span Forward	2.9*	.50	.10	1.1	1.6	3.0*
Working memory:
Corsi Span Backward	1.7	.10	5.5*	3.1	10.3***	.20
Digit Span Backward	7.1**	1.0	3.2	1.9	1.9	.20
Executive Functioning:
Shape School Inhibit	3.3*	1.1	1.1	2.5*	2.8*	.60
Shape School Switch	1.3	.60	1.3	5.4*	1.1	2.0
Tower of London	5.0**	.30	2.3	2.1	1.7	.10

Measures from the Shape School are efficiency scores taking into account accuracy and response time.

^*p ≤ .05

^**p ≤ .01

^***p ≤ .001

The pattern of results changes somewhat for the outcome measures at Time 2. Again Corsi span significantly predicts math achievement beyond the variance accounted for by reading ability. All other previously significant associations are reduced to non-significant. Corsi backward span and Shape School Inhibit remain as significant predictors of reading ability once math achievement has been controlled, with all other previously significant associations being eliminated.

Finally, controlling for mathematics or reading ability at Time 3 removes all significant associations between the executive function measures (Inhibit, Switch, and Tower of London) and outcome measures, suggesting thatat this stage the variance accounted for by executive functioning is similar in math and reading achievement. Corsi backward span remains as a significant predictor of math achievement, whereas both short-term memory measures (digit and Corsi span) remain as predictors of reading achievement.

Discussion

One of the main aims of the current study was to examine changes in the pattern of cognitive predictors to mathematical skills over time and to address whether the cognitive skills assessed specifically predicted mathematics achievement, or whether they were more general indicators of the capacity to learn. The correlational and longitudinal analyses showed that virtually all cognitive skills assessed correlated significantly with both mathematics and reading achievement at the beginning and end of the first year of primary school. Results from the regression analyses show that although there was a high degree of overlap in the variance of cognitive skills to both math and reading, certain cognitive skills contributed unique variance that was specific to each academic domain. Notably for math achievement in Primary 1, visual-spatial short-term memory span (Corsi Blocks) was a significant predictor of performance. Significant but smaller contributions at the start of primary school were made by verbal short-term memory (digit span), verbal working memory (digits backward), inhibition (Shape School inhibit), and planning and monitoring (Tower of London). By 7 to 8 years of age (end of third year of primary school), math skills were predicted by visual-spatial working memory (Corsi backward) while reading achievement was predicted by short-term memory capacity (verbal and visual-spatial).

Verbal working memory (backward digit span) and skills under the control of the central executive such as shifting attention, inhibition, and goal planning and monitoring appear to be generic to learning rather than specific to learning in one particular domain. Controlling for either reading or math resulted in no unique prediction to the remaining outcome measure suggesting substantial overlap in the shared variance among these skills. Furthermore, the growth curve analysis indicated that better executive functions skills (inhibition and planning) in preschool already provide children with a building block for math and reading resulting in better academic skills early in development, an advantage that is maintained throughout their first three years of formal schooling. Use of equivalent tests across the different time points and use of raw scores would allow an examination of whether cognitive skills at preschool also predict differential rates of growth in academic skills. Swanson (2003) found that skilled readers showed age-related increases in working memory, whereas the growth trajectory for children with reading difficulties showed minimal age-related change. Such an analysis would allow us to identify whether continued difficulties in math are due to continued lack of development of cognitive skills or whether just starting out with lower levels of cognitive skill but showing the same developmental trajectory, albeit at a lower level, is sufficient to keep math skills below the levels of those who have “normal” cognitive skills.

The importance of executive function and working memory skills in academic achievement has been highlighted in a number of recent studies across a wide age range. Blair and Razza (2007) found that inhibitory control aspects of executive functioning were uniquely related to a range of measures of academic ability (mathematics, phonemic awareness, and letter knowledge). Children who are poor at reading comprehension or at solving mathematical word problems have been found to have poorer inhibition, shown by poorer recall of critical task information and better recall of irrelevant information compared to their more able peers (see e.g., De Beni, Palladino, Pazzaglia, & Cornoldi, 1998; Passolunghi, Cornoldi, & De Liberto, 1999). Recent longitudinal findings from Mazzocco and Kover (2007) of children aged 6 to 11 years also showed that executive functioning (measured using the contingency naming test) was predictive of both math calculations and phonological decoding skills. In a study of 11 year olds, St Clair-Thompson and Gathercole (2006) found that working memory and inhibition both uniquely predicted curriculum attainment in mathematics and English indicating that these skills support general academic learning rather than the acquisition of skills and knowledge in specific domains. Finally, longitudinal findings from Gathercole, Tiffany, Briscoe, Thorn, and the ALSPAC team (2005) also provided strong evidence that scores on complex span tasks were highly related to learning achievement across the curriculum suggesting that capacity to process and store material in working memory significantly constrain a child's ability to acquire skills during the early period of formal education (see also Gathercole et al., 2006).

The current study found that the ability to shift between mental set (as assessed by Shape School switching, also referred to as cognitive flexibility) did not predict achievement over the course of study, but did predict achievement in reading and math at each individual time point. Previous studies have failed to find a relationship between shifting and math in preschool children (e.g., Espy et al., 2004). Measuring cognitive flexibility in preschool children has proven to be challenging, as reversal task performance (as used in many previous studies) may discriminate only those with severe disturbances in flexibly shifting between response sets, such as children diagnosed with severe disorders Other measures that focus on concept formation may prove to be more useful in this regard (e.g., Smidts, Jacobs, & Anderson, 2004), and clearly in the current study the use of the Shape School (Espy, 1997; Espy et al., 2006) has provided a good range of variability in scores. Findings from older school age children (Bull et al., 1999; Bull & Scerif, 2001; McLean & Hitch, 1999; van der Sluis et al., 2004) suggest that the ability to shift flexibly, or consciously inhibit certain procedures or information, may be more critical for performance on more complex mathematical problem solving that is not assessed until later in primary school. More proficient performance on the simple problems such as counting and number recognition assessed in the early PIPS assessments likely requires more basic inhibitory control or maintenance in a short-term storage system, potentially with the central executive performing the role of coordinating representations of the information being held in the slave systems. Indeed, Geary and his colleagues have recently argued that executive functioning may be involved at the earliest stages of construction of linear representations of number (Geary, Hoard, Bryd-Craven, Nugent, & Numptee, 2007). Using multiple measures of numerical and mathematical abilities, and assessing mathematic proficiencies longitudinally and later in development clearly is critical to determine how central executive functions are related to the dynamic development of mathematics skills.

The specific prediction of visual-spatial short-term memory in Primary 1 and subsequently visual-spatial working memory in Primary 3, coupled with the findings from the growth curve analysis showing visual-spatial STM span to specifically predict only math achievement, emphasizes the importance of a good understanding of spatial relations and the importance of being able to manipulate visual-spatial material in working memory as critical to mathematical achievement. These results support those of Jarvis and Gathercole (2003) who also found a relationship between visuo-spatial working memory and National Curriculum mathematics attainment. Deficits in the ability to represent visual-spatial information in working memory may be particularly detrimental to early developing non-verbal numerical skills such as estimation and manipulation of visual representation of magnitude using a number line, skills found to be predictive of later achievement in school (see e.g., Booth & Siegler, 2006; Jordan, Hanich, & Kaplan, 2003).

Visual-spatial deficits are characteristic among children and adults with mathematical learning difficulties (Geary, 1993). The importance of the visual-spatial sketch pad at this young age is in line with recent research suggesting that before the age of 7, and particularly before the onset of spontaneous verbal rehearsal, children rely heavily on visual-spatial representations to support the maintenance of information in short-term storage (McKenzie et al., 2003). Results from Holmes and Adams (2006) showed that visual-spatial short-term memory (as assessed by the Mazes task) uniquely predicted all aspects of mathematics achievement after controlling for the variance associated with age, phonological memory, and central executive functioning. However, this only applied to 8-year-old children, whereas for 10 year olds, visual-spatial short-term memory only predicted performance on more difficult math questions. Based on this they argue that older children may revert to earlier developing visual-spatial strategies for arithmetic where symbolic- linguistic arithmetic or direct retrieval strategies cannot be applied. The role of the visual-spatial sketch pad in early development of mathematical skills may be to provide a foundation for representing abstract problems in a concrete form (Holmes & Adams, 2006), providing a workspace to support the links between children's informal concrete knowledge and the abstract language and symbolism necessary for children's mathematics in school. Continuation of our longitudinal study may reveal that as children become older and more practiced in mathematical knowledge and procedures, the pattern of significant predictors may change.

Not all studies find a direct association between visual-spatial short-term memory or working memory and math achievement. Gathercole et al. (2006), in failing to find such a relationship in a study of 6-11 year olds, did find a relationship between phonological short-term memory and mathematics. Findings from the current growth curve analyses also highlight that better verbal short-term memory span in preschool results in a maintained advantage in math and reading scores throughout early schooling. Holmes and Adams (2006) also found that verbal short-term memory span was related to mental arithmetic (although not other skills such as number and algebra, shape, space and measures, and data handling) in 8-10 year olds, although this was accounted for by age-related variance. They argued that verbal short-term memory may be used on simple auditorily presented arithmetic questions where children used subvocal rehearsal processes to support the retention of problem information and direct retrieval of arithmetic facts from long-term memory. Other findings from adults using dual-task paradigms have suggested that the phonological loop is involved in temporary storage of partial solutions whereas the central executive controls access to and execution of computational algorithms (e.g., Logie, Gilhooly, & Wynn, 1994), but is not involved in the verification of either simple addition or multiplication problems (De Rammelaere, Stuyven, & Vandierendonck, 2001). Geary et al., (2007) argue that while the central executive is a core component to learning difficulties in mathematics, the phonological loop and visual-spatial sketch pad may contribute to more specific math cognition deficits, dependent on what aspects of mathematical skill are being assessed.

Contrasting findings clearly highlight that the relationship between short-term memory/working memory and mathematics is highly flexible, with the resulting pattern of associations influenced by presentation format of the task (auditory vs. visual, horizontal versus vertical; timed versus untimed, answer production versus verification, and complexity of the calculations) and how the cognitive skills themselves are assessed. Trbovich and LeFevre (2003) provide a review of some of these factors, and in their own study showed that vertical versus horizontal visual presentation of arithmetical problems resulted in the recruitment of different cognitive resources. Problems presented in vertical format resulted in increased reliance on visual resources compared to problems presented in horizontal format, which relied more on phonological resources. Trbovich and LeFevre argued that differential recruitment of phonological versus visual memory in horizontal and vertical problems may be related to variability in the solution procedures that individuals select as a function of format. In progressing with understanding of the role of specific cognitive resources in mathematics, there is clearly a need for more systematic experimental studies that highlight the supporting cognitive competencies under different presentation conditions. That way, children identified as having a limitation in some aspects of cognitive functioning but strengths in others can have mathematical problems presented in a format that reduces the reliance on weaker cognitive skills.

These results clearly have implications for classroom practice. Good short-term memory, working memory, and particularly executive functioning skills provide children with an immediate advantage in the school learning environment, providing them with a head-start in mathematics and reading that is maintained throughout the first few years of primary schooling. Children with poor functioning of these cognitive skills may make errors in a range of learning activities due to difficulty remembering and carrying out instructions, inhibiting irrelevant information and staying focused on task, and planning and monitoring progress of individual steps of the task as it progresses. On the basis of this Gathercole et al., (2006) have argued that such children may fail to meet the routine demands of many structured learning activities in the classroom, resulting in missed opportunities to learn and practice skills and achieve normal incremental progress in complex skill domains. Those children who also present with poor visual-spatial short-term memory and working memory may be particularly disadvantaged given that these skills appear to be critical specifically in the early development of mathematical skills, or as a resource to be used for more complex mathematical problem solving. A combination of knowledge-based assessment plus cognitive measures may provide a good estimate of the child's ability to learn and hence their future academic success. Awareness of cognitive limitations and methods of reducing the cognitive processing demands of tasks may overcome some of these difficulties.