Abstract
An exploratory factor analysis (EFA) and a series of confirmatory factor analyses were conducted on 17 variables designed to assess different cognitive abilities in a sample of healthy older adults. In the EFA, four factors emerged corresponding to language, memory, processing speed, and fluid ability constructs. The results of the confirmatory factor analyses suggested that a five-factor model with an additional Attention factor improved the fit. The invariance of the five-factor model was examined across three groups- a group of cognitively-healthy older adults, a group of patients diagnosed with questionable dementia (QD), and a group of patients diagnosed with probable Alzheimer’s Disease (AD). Results of the invariance analysis suggest that the model may have configural invariance across the three groups, but not metric invariance. Specifically, preliminary analyses suggest that the memory construct may represent something different in the QD and AD group as compared to the healthy elderly group, consistent with the underlying pathology in early AD.
Keywords: Alzheimer’s disease, questionable dementia, cognition, structural equation modeling, invariance
Alzheimer’s disease (AD) is a progressive neurodegenerative disease characterized by impairments in cognitive abilities and activities of daily living. Although normal aging is associated with age-related declines across a variety of cognitive abilities (e.g. Salthouse, in press), AD-related declines in functioning are different because the declines interfere with daily life. Questionable dementia (QD) is a categorization designed to characterize individuals who demonstrate mild cognitive impairment beyond what is expected by age and education but whose cognitive and/or functional impairment is not sufficient for the diagnosis of dementia.
There is overwhelming evidence that there are changes in performance in tests of cognitive functioning across groups of older adults categorized as being either healthy, diagnosed with QD, or diagnosed with probable AD. Specifically, patients with QD and AD perform worse on memory and other tests designed to measure cognitive functions such as attention, language, and executive function than do cognitively-healthy older adults. Although it is clear that there are quantitative differences in the cognitive tests (i.e. demented patients perform worse), it is unclear whether there are consistent qualitative differences across these three diagnostic groups. Qualitative differences refer to differences in relations among variables and differences in what the variables may be measuring. In this paper we used two techniques to address this question: invariance analyses, and comparison of the structure through separate exploratory factor analysis (EFA). Examining whether the structure of variables is the same (invariant) across groups is important because comparisons are often made with the assumption that the differences across groups are quantitative, when the differences may be qualitative. If there are qualitative differences (such that the model is not invariant), then differences across groups are difficult to interpret because the meaning of the construct may be changing (Horn & McArdle, 1992). However, the first step is to determine what exactly the variables are measuring, and how the variables relate to one another. This can be addressed with analyses such as EFA and structural equation modeling (SEM) which asks questions like “What is the factor structure of the variables of interest?” and “What model is the best representation of the data?” This paper addressed these questions using a cross-sectional, archival data set derived from healthy older adults as well as those with QD and AD.
The first step involved conducting an exploratory factor analysis to identify the factor structure underlying a set of 17 neuropsychological variables in a sample of cognitively-healthy adults. The factor structure that emerged from the EFA was then examined in the context of a structural model in a confirmatory factor analysis (CFA), in which each variable loaded only on to the factor on which it had the highest loading. This model was examined in a CFA to determine whether it fit the data well and whether it demonstrated convergent and discriminant validity (i.e., construct validity). Because the neuropsychological variables are designed to measure specific cognitive abilities, the fits of a series of theory-based models were compared to the model developed from the EFA. The best-fitting model from all the models was selected to be examined in invariance analyses.
Invariance analyses are one way to explicitly test whether there are qualitative differences in a model across different diagnostic group (i.e. cognitively-healthy older adults, patients diagnosed with QD, and patients diagnosed with AD). Measurement and structural invariance refer to two different types of invariance. Measurement invariance refers to the tests of model invariance that involve the relations among the measured variables, whereas structural invariance refers to the tests of model invariance that involve the relations among the latent variables (Byrne, Shavelson, & Muthén, 1989; Nyberg, 1994). Configural and metric invariance are two different levels of measurement invariance. For a model to demonstrate configural invariance the relations among the latent constructs and measured variables should be the same across different groups (Horn, McArdle, & Mason, 1983). That is, the structure of the model should be invariant. Metric invariance is established when the magnitude of the unstandardized coefficients are not significantly different across groups (Horn & McArdle, 1992) and is tested by constraining the loadings to be the same across the groups and comparing the fit of the constrained (metric invariance) model to a baseline (configural) model. If the metric model does not fit significantly worse then it can be argued that the model demonstrates metric invariance. In this paper structural invariance refers to a test of invariance in which both the loadings and the inter-factor correlations are constrained to be the same across the groups.
The second method used to determine if there are differences in the factor structure of the variables is to compare the results of an EFA across the different diagnostic groups. Although such an approach is data-driven, rather then theory-driven, the results can nonetheless be informative, especially when addressing a fairly novel question.
Although the factor structure of neuropsychological variables in healthy adults has been a fairly common topic of research, the factor structure of variables in patients diagnosed with different types of dementia has been a less frequent topic of inquiry.
Some researchers have hypothesized that one general factor underlies cognitive function in patients with probable AD. This is a compelling explanation because it is parsimonious, and there is evidence that a large proportion of AD-related effects are shared among different cognitive variables (Salthouse & Becker, 1998). Loewenstein and Rubert (1992) have argued that there is an underlying global impairment in memory functioning as well as a general decline in overall cognition. Likewise, Morris and Kopelman (1986) hypothesized that AD-related deficits were the result of deteriorating memory ability and a general deficit in information-processing.
If one (or two) common factors are responsible for AD-related cognitive decline, one would expect that an individual’s performance on one cognitive test would be highly correlated with performance on all other cognitive variables. However, research has indicated that there is great diversity in the clinical manifestation of AD such that patients often present with deficits in some cognitive domains, but not all. Loewenstein, et al. (2001) explicitly tested the one-factor hypothesis by comparing the fit of three models in a sample of patients with AD with a set of variables that encompassed the eight domains specified by the NINCDS-ADRDA as relevant cognition domains in the diagnosis of AD. Lowenstein, et al. found that the one-factor model fit the data relatively poorly and that a six-factor theory-based model that distinguished between a verbal, spatial, memory, executive functioning, Independent Activities of Daily Living and an Activities of Daily Living factor fit the data the best.
Davis, Massman, and Doody (2003) specifically examined the factor structure of the WAIS-R in a moderately large sample of patients diagnosed with probable AD. They compared the fit of a series of different models and found that a three-factor model comprised of a Verbal Comprehension, Perceptual Organization factor and an Attentional factor fit the data the best. Further, Davis, et al. examined the multigroup invariance of the structure across two age groups (< 75 and > 75), three groups divided by dementia severity (mild, moderate, and severe), two education groups (< 12 and > 12), and across men and women. In all of these groups, the same three-factor model provided the best fit to the data. This finding is important because it demonstrates that the factor structure remains the same across different demographic and disease variables within the sample of patients with AD. The current study extends these findings by investigating the factor structure of neuropsychological variables between different diagnostic group (i.e. cognitively-normal older adults, patients with QD, and patients with AD).
Kanne, Balota, Storandt, McKeel, and Morris (1998) examined the factor structure of a set of nine neuropsychological variables in a sample of subjects that were divided into nondemented control subjects (i.e. Clinical Disease Rating (CDR) = 0), those with “very mild” AD (i.e., CDR = .5, and sometimes referred to as QD as in the current study), and those with mild AD (i.e. CDR = 1). Kanne, et al. conducted a principal components analysis (PCA) of 9 neuropsychological variables for each diagnostic group. Kanne, et al. (1998) reported that a one-factor solution was the best representation of the data for the nondemented control group whereas a three-factor solution was the best representation of the data in the very mild and mild AD groups. Although Kanne, et al. did not specifically test for invariance of the factor structure between groups, the different structure that emerged across the three groups from the PCA suggest that there may be differences in how the variables relate to one another, and what they represent, across the three groups.
The goals of this paper were to examine the factor structure of a core battery of variables, to determine whether the emergent model has construct validity, and to examine whether the factor structure remains invariant across diagnostic group.
Method
Participant selection and classification
Subjects for this analysis were selected from the Alzheimer’s Disease Research Center (ADRC) at Columbia University Medical Center. This research center protocol has been in existence for 18 years, and is approved by the Columbia University / New York State Psychiatric Institute Institutional Review Board. Subjects were recruited either due to memory complaints or were recruited as controls. All subjects gave informed consent prior to inclusion in the study.
All subjects received a comprehensive standardized neurological evaluation, including medical history, medical and neurological examination, and performance of physician-rated measures of daily functioning including the Blessed Dementia Rating Scale (BDLS; Blessed, Tomlinson, & Roth, 1968) and the England Activities of Daily Living Scale (Schwab & England, 1969) completed with the subject, an informant, or both. All patients received a CDR score. Nearly all subjects received blood testing and brain imaging study such as CT or MRI. A neuropsychological evaluation was administered as part of the diagnostic evaluation. As is standard procedure for many ADRCs across the country, diagnosis of dementia was made at a clinical consensus conference (which included neurologists, psychiatrists and neuropsychologists) according to DSM-IV-TR (American Psychiatric Association, 2000) criteria, which requires evidence of neuropsychological impairment and functional impairment determined by formal assessments or patient history (or both). At the clinical consensus meeting the evaluating neurologist typically presents the case to the committee and the neuropsychologist presents information from the neuropsychological evaluation. The committee is there to ensure that standardized procedures are being used to diagnose each subject. As such, a diagnosis of probable AD was made based on the NINCDS-ADRDA criteria. Probable AD patients could have CDR of 1 through 5.
A diagnosis of QD was also determined by consensus when a subject had either sufficient cognitive impairment for a diagnosis of dementia but no functional impairment or had insufficient cognitive impairment for a dementia diagnosis but had been assigned a CDR of 0.5 by the examining neurologist because of some impairment.
Participants who scored within the normal range from their age and education were classified as “cognitively-healthy” older adults, and had CDR 0.
To be included in the current analyses, subjects had to be over the age of 40, and had to have been tested in English. All subjects spoke English but of those subjects whose predominant language spoken at home is known, there is a subset of who speak Spanish predominantly at home (4.9% of the healthy elderly, 2.1% of the QD subjects, and 1.9% of the probable AD subjects). There is also a subset of subjects who predominantly speak another language (such as German or Russian) at home (5.6%, 8.3%, and 10.6% across the health elderly, QD, and probable AD subjects respectively). The data from subjects with major medical, non-Alzheimer neurological (e.g. stroke, depression, brain tumor, epilepsy, Parkinson’s disease, Korsakoff’s syndrome), or significant psychiatric disorders (e.g. depression) were excluded from the analyses. Subject groups included cognitively-healthy older adults (N = 322), those diagnosed with QD (N = 701), and those diagnosed with probable AD (N = 535). Subject characteristics are presented in Table 1. Mean age, F (2, 1506) = 57.71, and education, F (2, 1501) = 61.89, were significantly different across the groups.
Table 1.
Demographic characteristics across the healthy, QD, and AD groups.
| Group | ||||||
|---|---|---|---|---|---|---|
| Healthy | range | QD | range | AD | range | |
| Number | 511 | 878 | 639 | |||
| Age | 66.44 (11.27) | 40–91 | 71.84 (9.72) | 42–100 | 74.63 (10.14) | 41–100 |
| Years of Education | 15.91 (3.39) | 1–20 | 14.55 (3.63) | 0–20 | 13.17 (4.13) | 0–20 |
| % Female | 0.58 | 0.56 | 0.63 | |||
| Ethnicity | ||||||
| % Caucasian | 85.1 | 86.2 | 86.3 | |||
| % African American | 6.5 | 8.1 | 9.3 | |||
| % Native American/Indian | 0.3 | 0.0 | 0.2 | |||
| % Asian/Pacific Islander | 1.2 | 1.0 | 0.2 | |||
| % Other | 3.4 | 2.4 | 2.6 | |||
| % Not reported | 2.4 | 2.3 | 1.4 | |||
| % Hispanic | 4.31 | 2.85 | 3.44 | |||
Note. Values are means or percentages and standard deviations are reported in parenthesis.
Neuropsychological Evaluation
All subjects were administered a battery of 17 tests designed to assess a broad range of cognitive functioning such as memory, language, visual-spatial ability and reasoning (see Stern, et al., 1992 for details on the development of the core battery). Subject performance on these tasks is presented in Table 2. This battery is a subset of the full diagnostic battery.
Table 2.
Means scores, standard deviations, and ranges of scores on the neuropsychological tests across the healthy, QD, and AD groups.
| Group | ||||||
|---|---|---|---|---|---|---|
| Healthy | range | QD | range | AD | range | |
| Variables | ||||||
| Total Recall | 45.04 (11.61) | 0–68 | 31.45 (9.34) | 2–63 | 17.75 (8.75) | 0–66 |
| Delayed Recall | 6.77 (2.94) | 0–12 | 2.78 (2.53) | 0–12 | 0.51 (1.06) | 0–6 |
| Delayed Recognition | 11.35 (1.52) | 2–12 | 9.69 (2.41) | 0–12 | 6.23 (2.76) | 0–12 |
| Benton Recognition | 8.57 (1.62) | 1–10 | 7.27 (1.52) | 1–10 | 5.18 (2.08) | 0–10 |
| Similarities Raw | 18.84 (5.93) | 0–27 | 14.31 (6.67) | 0–26 | 6.94 (5.79) | 0–23 |
| Identities/OdditiesTotal | 15.22 (1.17) | 9–16 | 14.71 (1.50) | 5–16 | 12.82 (2.57) | 0–16 |
| Naming Total | 14.27 (1.66) | 2–15 | 13.31 (2.34) | 0–15 | 10.51 (3.57) | 0–15 |
| Letter Fluency Mean | 14.35 (7.01) | 0–97 | 10.93 (4.76) | 1–43 | 6.91 (4.06) | 0–23.7 |
| Category Fluency Mean | 19.01 (5.83) | 0–34 | 13.76 (4.85) | 0–30 | 8.13 (4.47) | 0–27.6 |
| Repetition | 7.75 (0.85) | 0–8 | 7.68 (.75) | 2–8 | 6.89 (1.58) | 0–8 |
| Comprehension | 5.66 (0.88) | 0–6 | 5.47 (.90) | 0–6 | 4.17 (1.67) | 0–6 |
| Rosen | 3.66 (1.13) | 0–5 | 3.16 (1.07) | 0–5 | 2.36 (1.22) | 0–5 |
| Shape Time | 58.3 (24.01) | 27–240 | 79.34 (37.97) | 23–240 | 121.01 (58.67) | 32–240 |
| Shape Omits | 4.60 (3.67) | 0–18 | 5.94 (4.07) | 0–19 | 8.07 (5.28) | 0–20 |
| TMX Time | 68.09 (26.34) | 26–240 | 86.07 (36.20) | 33–240 | 123.34 (57.95) | 32–240 |
| TMX Omits | 1.05 (1.80) | 0–12 | 1.56 (2.41) | 0–19 | 3.51 (4.00) | 0–19 |
| Benton Matching | 9.46 (1.23) | 0–10 | 8.97 (1.38) | 1–10 | 7.44 (2.43) | 0–10 |
Note. Values are means and standard deviations are reported in parenthesis.
In the Selective Reminding Test (SRT; Buschke & Fuld, 1974) subjects are read a list of the same 12 words and asked to recall the words after each of the 6 trials administered. After each recall attempt, subjects are reminded of the words they failed to recall. SRT total recall refers to the total number of words out of a possible 72 that the subject was able to remember. After a 15-minute delay subjects are asked to recall the 12 words. The SRT delayed recall score refers to the number correct (out of 12). After the delayed recall portion, subjects are administered a SRT delayed recognition test in which each of the 12 words are presented with 3 distracters.
In the modified 15-item Boston Naming Test (Kaplan, Goodglass, & Weintraub, 1983) subjects are presented with 15 line drawings and asked the name of each object. If a subject is unable to name the object, the examiner gives the subject a semantic hint after 20 secs, followed by a phonemic hint after 15 secs. The Naming Total variable refers to the total number of objects named spontaneously or with semantic cuing.
Two tests of verbal fluency were administered. In the Letter fluency test subjects are given three letters (i.e. C, F, L) and asked to generate as many words as they can that begin with each letter in 60 secs (within specific guidelines). Total number of words named across the three letters was used as the score. In the Category fluency test subjects are given a category (e.g. animals) and asked to generate as many items as they can that are a member of the given category in 60 secs. The total number of words generated across the categories was used as the score.
The Benton Visual Retention Test (BVRT; Benton, 1955) is comprised of two parts- the recognition test and the matching test. In the BVRT Recognition test subjects view a non-verbal design for 10 secs and are then asked to select the design from an array with three distracters. In the BVRT Matching test subjects are asked to match each non-verbal design to an identical design in an array of four smaller designs. In both cases the total number correct was used as the score.
In the Rosen Drawing Test (Rosen, 1981) subjects copy 5 visual designs on to a piece of paper. No partial credit is given and drawings are scored as either correct or incorrect. The Rosen variable refers to the total number of designs correctly copied.
The Similarities test is a subtest of Wechsler Adult Intelligence Scale-Revised (WAIS-R; Wechsler, 1981) and requires subjects to articulate similarities in a set of items. The total raw score was used in the analyses.
The Identities and Oddities test is a subtest of the Mattis Dementia Rating Scale (Mattis, 1976) and requires the subject to examine three items and select which two are alike in the first 8 trials. In the second 8 trials the same items are shown and the subject is required to select which item is different. The total number of items correct across trials was used as the measure.
The Repetition task is a subtest of the Boston Diagnostic Aphasia Evaluation (BDAE; Goodglass, 1983) which requires participants repeat phrases read by the examiner. Only the high probability phrases were used. The total number of phrases correct was used as the score.
In the Cancellation Test subjects are presented with one sheet of paper and target stimuli are presented at the top of the page. In the shape condition the paper is filled with different shapes and subjects are instructed to cross out the target stimulus (i.e. the diamond shape) as quickly as possible. Shape Time refers to the time to complete the task and Shape Omits refers to the number target stimuli the subject failed to cross out. In the letter version of the task the sheet of paper is filled with letters and the subjects is instructed to cross out the target letter triad (TMX) as quickly as possible. TMX Time refers to the time required to complete the task and TMX Omits are the numbers of target letters omitted. In all four of these tasks greater numbers indicated poorer performance (slower speed to complete, and more omission errors).
Analyses
All confirmatory and invariance analyses were conducted with Amos 5.0 (Arbuckle, 2003) using raw scores. To identify the underlying factor structure, an exploratory factor analysis was performed with the 17 variables of interest. Although PCA and EFA are similar in that they are performed by examining the pattern of correlations between the observed measures, PCA is generally used as a data reduction technique and EFA is used to identify factors that underlie performance on a set of measured variables. The purpose of PCA is to account for the variance in measured variables and importantly, PCA does not differentiate between common and unique variance. PCA therefore identifies principal components that are linear combinations of the variables containing both common and unique variance. EFA, however, is used to identify latent constructs with the goal of understanding the structure of correlations among the measured variables. To this end, EFA differentiates between common and unique variance so that the factors represent what the variables have in common (see Fabrigar, Wegener, MacCallum, & Strahan, 1999 for a comprehensive review of EFA in psychological research).
Confirmatory factor analysis was performed on the emergent factor structure to evaluate whether a model in which each variable loaded only on to the factor on which it had the highest loading fit the data well. This model was then compared to a series of theory-based models that were created based on which latent ability each task was designed to measure.
The theory-based models included a one-factor model, a five-factor model, and a six-factor model. A one-factor model, in which all 17 variables loaded on to the same factor, was tested since some researchers hypothesize that one general factor underlies cognitive function. The five-factor model was comprised of a Language factor (which the Naming total, Repetition, Comprehension, Letter fluency and Category fluency variables loaded on), a Memory factor (comprised of the SRT total recall, SRT delayed recall, SRT delayed recognition, and the BVRT recognition variables), a Reasoning factor (comprised of the Similarities and Identities/Oddities subtests), a Visual-spatial factor (comprised of the Rosen and BVRT Matching tasks) and a Speed/Attention factor (comprised of the Shape time, Shape omits, and TMX time and TMX omits variables). These factors correspond to the latent abilities thought to be measured by these tasks. A six-factor model in which the speed (Shape time and TMX time) and attention (Shape omits, TMX omits) factors were separated was also examined.
Subsequent analyses were conducted on the best-fitting model to determine whether the model exhibited invariance across different diagnostic groups. As recommended by Hu & Bentler (1998), model fit is generally evaluated by examining multiple fit indices such as the chi-square (X 2), Bentler’s comparative fit index (CFI), the critical ratio (X 2/df) (Bollen, 1989) and the root mean square error of approximation (RMSEA) (see Hu & Bentler, 1998 for a detailed discussion of fit indices). Greater CFI values signify a better fit to the data and therefore numbers closer to 1.0 indicate better fit. CFI values of > .90 (Bentler, 1992) or > .95 (Hu & Bentler, 1999) have been used to indicate a good fit to the data. RMSEA values of < .06 are indicative of a good fit (Hu & Bentler, 1999) with values between .8 and .1 suggestive of a mediocre fit (MacCallum, Browne, & Sugawara, 1996). RMSEA values > .1 are generally indicative of a poor fit.
Typically, the change in chi-square per change in degrees of freedom between the models is used to determine whether the fit of the invariance models are significantly different. The chi-square statistic is used because it is based on a known sampling distribution (and therefore significance can be determined.) However, it is well known that the chi-square statistic is affected by sample size such that large differences between the observed and hypothesized covariance matrix in a model with a small sample will not be significant (in chi-square, significance indicates a poor fit) but small or trivial differences in a model with a large sample size can yield a highly significant chi-square. Recent work by Cheung and Rensvold (2002) indicates that a 0.01 change in CFI may be an adequate and appropriate cut-off to use when determining differences in model fit in invariance analyses and can be used to supplement the Δ X2/ Δ df test. They recommend that a change in CFI >- 0.01 be used as an indication that the difference in the models are substantial.
As described above, three levels of invariance were examined – configural, metric, and structural. A model exhibits configural invariance if the structure of the model is the same across groups. To exhibit metric invariance the magnitude of the unstandardized coefficients (i.e. the loadings) should be equal across groups. To demonstrate structural invariance the unstandardized coefficients and the inter-factor covariances are not significantly different across groups.
Results
Exploratory Factor Analysis
Only cognitively-healthy subjects without missing data (N = 185) were used in the EFA in order to generate a factor structure for the healthy “controls” that could be used as a baseline measure to compare the factor structure of QD subjects and probable AD subjects against.
Because the data did not meet criteria for multivariate normality and because the variables were correlated with one another, principal axis factoring extraction and oblique rotation were employed in the EFA. Communality of a measured variable is the amount variance accounted for by the factors. If a variable has low communality it could indicate that it is not related to the other variables, or it could be due to low reliability. Including variables with low communality in the analysis may create considerable distortion in the factor solution (MacCallum, Widaman, Zhang, & Hong, 1999) and studies have indicated their inclusion may reduce the probability of replicating the factor pattern (cf. Velicer & Fava, 1998). Both the Rosen drawing subtest and the Shape Omits test had low communalities (< .20) and were therefore excluded from the analysis.
Several methods were used to determine the number of factors to retain. First the scree plot was inspected, but since a large proportion of the variance was accounted for by the first factor it was difficult to interpret. The Kaiser eigenvalue > 1 rule suggested 4 factors. Although the eigenvalue > 1 rule can often lead to over-factoring, inspection of the factor solution (presented in Table 3) showed that the four factors yielded an interpretable solution that was consistent with research on neuropsychological variables. From the EFA the factors of processing speed, memory, language, and fluid ability (gF) were identified. Two timed tests (Shape time and TMX time) loaded on to the speed factor. The three SRT variables loaded on to the memory factor. The language factor was comprised of the Naming total variable and the WAIS-R subtests of Comprehension and Repetition. The gF factor was comprised of the category and letter fluency variables, the BVRT Recognition and Matching variables, the TMX Omits test and the WAIS-R subtests of Identities/Oddities and Similarities.
Table 3.
Pattern Matrix from the EFA
| Factor | ||||
|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 |
| Shape Time | −1.00 | 0.15 | −0.02 | 0.10 |
| TMX Time | −0.94 | 0.01 | −0.01 | 0.22 |
| Naming Total | 0.06 | 0.52 | 0.17 | 0.02 |
| Repetition | −0.14 | 1.11 | −0.10 | −0.27 |
| Comprehension | −0.04 | 0.51 | 0.17 | 0.17 |
| SRT Total Recall | 0.01 | 0.19 | 0.73 | 0.04 |
| SRT Delayed Recall | −0.02 | −0.14 | 0.96 | −0.07 |
| SRT Delayed Recog | 0.06 | 0.16 | 0.56 | 0.06 |
| BVRT Recognition | 0.15 | −0.03 | 0.14 | 0.48 |
| Similarities Raw | 0.20 | 0.19 | −0.10 | 0.54 |
| Identities/Oddities | −0.04 | −0.03 | 0.17 | 0.49 |
| Letter fluency | 0.24 | 0.22 | −0.16 | 0.39 |
| Category Fluency | 0.23 | 0.21 | −0.01 | 0.35 |
| BVRT Matching | 0.00 | −0.21 | 0.01 | 0.70 |
| TMX Omits | 0.35 | 0.12 | 0.04 | −0.73 |
| Speed | Language | Memory | gF | |
Confirmatory Factor Analyses1
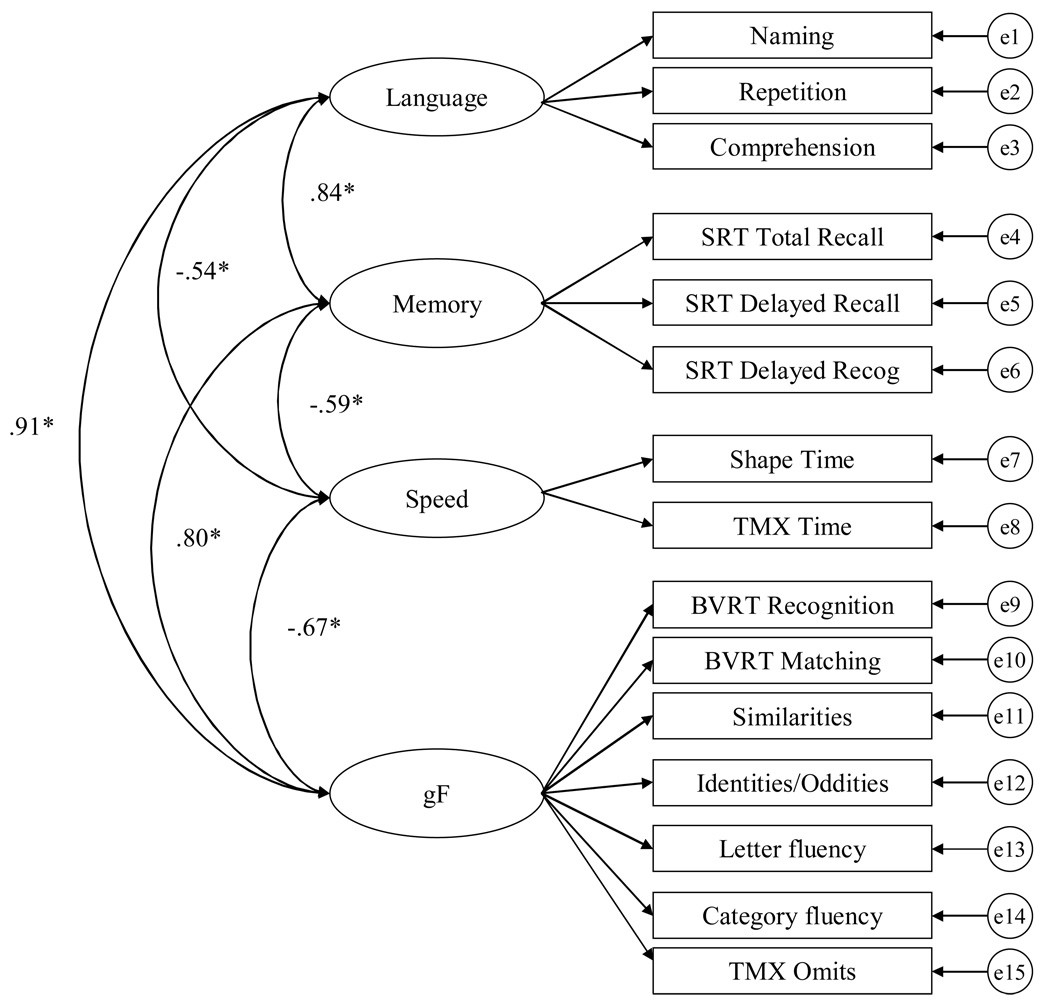
The fit of the four-factor model, depicted in Figure 1, was examined in a context of a CFA with the cognitively-healthy subjects. In this model, the variables were only allowed to load on to the factor in which they had the highest loading. The four-factor model fit the data adequately (X2 = 327.58, df = 84; CFI = .89; RMSEA = .095). One consequence of the data not meeting criteria for multivariate normality is inflated fit statistics (e.g. Chou & Bentler, 1995; West, Finch & Curran, 1995). Although the Bollen-Stine bootstrap was significant (p < .05), the mean X2 from the bootstrap was reduced to 155.71.
Figure 1.
Four-factor model with inter-factor correlations (Model A).
Construct validity can be examined by evaluating convergent validity (i.e. the extent to which the variables hypothesized to represent a construct have substantial variance in common as reflected by moderate to high loadings) and discriminant validity (i.e. the extent to which the factors are distinct from one another with correlations significantly less than 1.0). All the loadings were in the moderate to large range (standardized coefficients ranged from .48 – .92) and all those not set to 1.0 (to provide a metric to the latent factor) were significantly different from zero at the p < .01 level. Although the correlations among the factors were fairly large, they were significantly different then 1.0 as determined by examining the 99% confidence intervals around the correlations (see Table 4).
Table 4.
Inter-factor correlations and 99% confidence intervals among the factors in the 4-factor model
| r | 99% Confidence Interval | ||
|---|---|---|---|
| Lower | Upper | ||
| Speed <−> Language | −0.54* | −0.65 | −0.43 |
| Speed <−> Memory | −0.59* | −0.70 | −0.48 |
| Speed <−> gF | −0.67* | −0.77 | −0.57 |
| Language <−> Memory | 0.84* | 0.77 | 0.90 |
| Language <−> gF | 0.91* | 0.85 | 0.96 |
| Memory <−> gF | 0.80* | 0.74 | 0.87 |
Note. p < .01; r is the inter-factor correlations
Model Comparisons
We next compared several alternate models as explained above. Model A is the four-factor model identified through the EFA (described above). The following models are theory-based models. Model B is the one-factor model in which all the variables loaded on to one general factor. Model C is the five-factor model comprised of a language, memory, reasoning, visual-spatial and a combined speed/attention factor. Model D is a six-factor model in which the speed and attention factors are separated. The results of the model comparisons are presented in Table 5.
Table 5.
Goodness-of-fit statistics for the model comparisons
| Model | X2 | df | X2/df | CFI | RMSEA (90% CI) |
|---|---|---|---|---|---|
| Model A: 4-factor from EFA | 327.58 | 84 | 3.90 | 0.89 | .095 (.084 – 1.06) |
| Model B: 1-factor | 648.35 | 119 | 5.45 | 0.77 | .118 (.109 – .126) |
| Model C: 5-factor | 491.32 | 109 | 4.51 | 0.84 | .104 (.094–.114) |
| *Model D: 6-factor | 366.97 | 104 | 3.53 | 0.89 | .089 (.079–.099) |
| Model E | 382.34 | 109 | 3.51 | 0.88 | .088 (.079–.098) |
| Model F: 5-factor with spilt loading | 327.65 | 108 | 3.03 | 0.91 | .079 (.070 –.089) |
Note. indicates the model solution is inadmissible.
First, it is important to note that model D had an inadmissible solution because the covariance matrix was not positive definite. This is likely a result of the correlation estimate between the Reasoning and Visual-spatial factors being very large (r = .95). Therefore a subsequent model was examined in which the reasoning and visual-spatial factors were combined and the fit is listed in the bottom row of Table 5 for Model E. This five-factor model fit the data better then both the one-factor model and the original five-factor model (model C) that combined the speed and attention factors. The fit of model A (the 4-factor from the EFA) and model E are fairly comparable. Although model A has a slightly better fit as indicated by the CFI value, model E has a slightly better fit as indicated by X2/df and the RMSEA. Therefore, there is no clear best-fitting model.
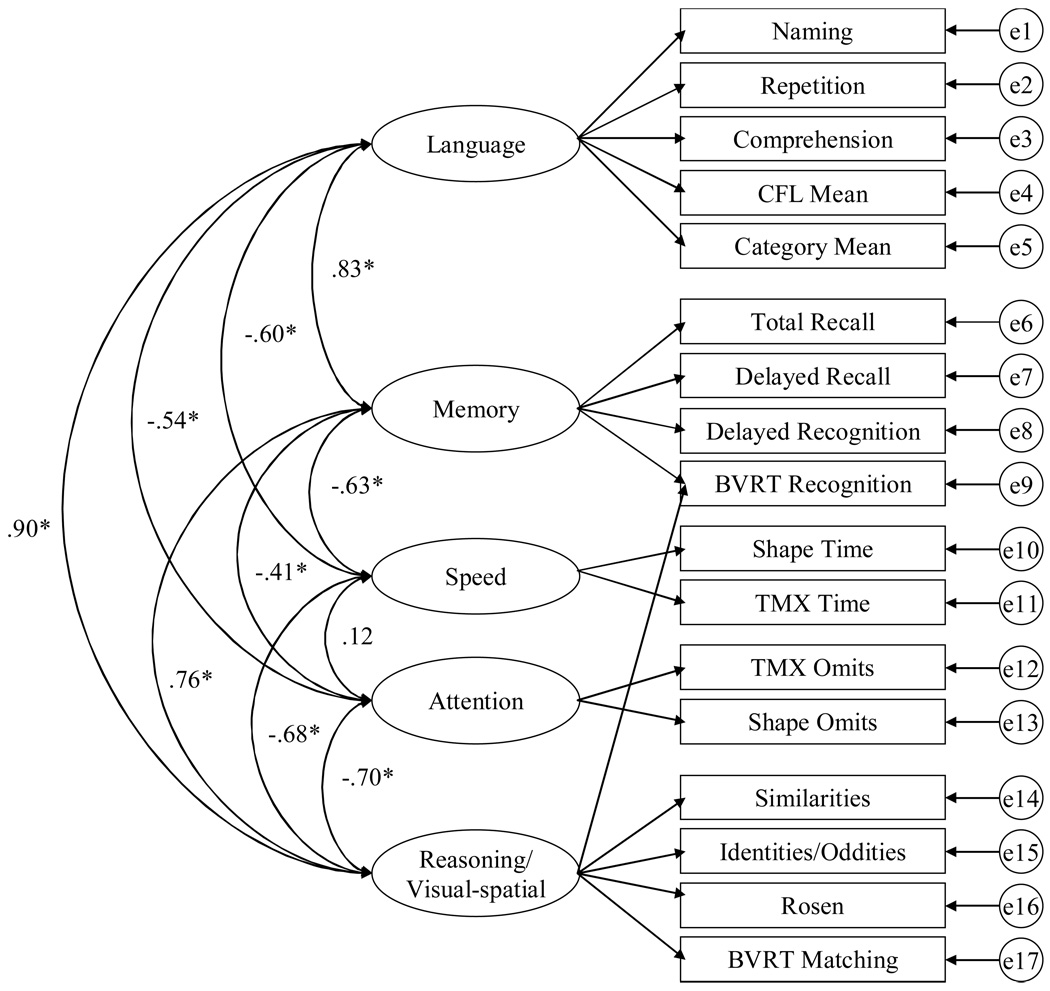
However, it should be noted that Model A and Model E are very similar. The fifth-factor in Model E is the attention factor which does not exist in Model A (in part due because the Shape omits variable was eliminated from the EFA due to low communality). In Model A the fluency variables load on the gF factor whereas in Model E they load with the language variables. Finally, in Model A the BVRT Recognition variable loads with the other visual-spatial tasks but in Model E it loads with the memory variables. Although the BVRT recognition test was designed to measure memory, it is clear that it also has a visual-spatial component. Prior research has indicated that verbal memory may be distinct from visual and spatial memory (e.g. Siedlecki, 2007) suggesting that including the BVRT recognition test with verbal memory tests may not be the most appropriate. For that reason, Model F was examined in which the BVRT recognition test had a split loading on both the memory factor and the reasoning/visual-spatial factor (see Figure 2).
Figure 2.
Model F, the five-factor model with a split loading with inter-factor correlations.
As indicated by the fit statistics reported in Table 5, Model F fit the data the best. Model F had the lowest X2/df and RMSEA, as well as the greater CFI (and the only CFI above the .90 cut-off value indicating an adequate fit). Although not as parsimonious as Model A, Model F is theory-driven and therefore it is less likely that that factor structure is caused by idiosyncrasies of the sample. Model F also demonstrated construct validity since all but one of the variables hypothesized to reflect the same latent construct were all significantly different from zero at the p < .01 level (except those set to 1.0 to provide a metric for the latent factor), and 1.0 was not included in the 99% confidence intervals in any of the inter-factor correlations. For that reason, Model F was selected for the invariance analyses.
Invariance Analyses
To evaluate whether Model F was invariant across the different diagnostic groups, a series of invariance analyses were conducted2. Complete results are presented in Table 6. Configural invariance, which specifies that the structure is the same across groups, is often considered a type of baseline invariance and is evaluated by examining overall fit. The fit of the configural model is adequate. Although the CFI value is below the > .90 cut-off (.89), the RMSEA value (as well as the 90% confidence intervals) is below the .06 cut-off (.039) for a good fit. This result would therefore suggest that there may be some evidence for configural invariance. However, there is no evidence for metric invariance or structural invariance because the change in X 2 per change in df was significantly different then the baseline configural fit. Further, the change in CFI was also greater than the .01 cut-off value suggested by Cheung and Rensvold (2002). This indicates that constraining the loadings to be the same across groups (i.e. metric invariance) and constraining the loadings and inter-factor correlations to be the same across group (i.e. structural invariance) results in a significantly worse fit for the model. These findings therefore imply that those values are changing across the groups.
Table 6.
Invariance analyses of the five-factor model with the spilt loading across three diagnostic group (i.e. cognitively-healthy, QD, and probable AD subjects).
| Model | X2 | df | X2/df | CFI | RMSEA | Δ X2 | Δ df | p < .01 | Δ CFI |
|---|---|---|---|---|---|---|---|---|---|
| Configural | 1078.61 | 324 | 3.33 | 0.89 | .039 (.037 – .042) | Baseline | |||
| Metric | 1509.80 | 350 | 4.31 | 0.83 | .047 (.044 – .049) | 316.63 | 22 | yes | 0.06 |
| Structural | 1737.99 | 370 | 4.70 | 0.80 | .049 (.047 – .052) | 572.07 | 34 | yes | 0.09 |
Additional EFA
Although invariance analyses are one approach to the examining qualitative differences across groups, exploratory analyses can also be informative. To that end, separate EFA with principal axis factoring and oblique rotation were conducted for each group, using the eigenvalue > 1 rule to determine the number of factors to retain. These results are presented in Table 7. It should be noted that some variables were removed from the analyses due to low communality and therefore each group had slightly different variables included in the EFA. In the cognitively-healthy group the Rosen and Shape Omits variables were removed and in the QD group, the Naming total variable was removed from the analyses (all the variables were included in the EFA with the probable AD group).
Table 7.
Results of factor analyses of the neuropsychological variables across the three samples.
| Probable AD patients (N= 193) | QD subjects (N= 366) | Cognitively-healthy controls (N =185) | |||
|---|---|---|---|---|---|
| Factor 1 (Language) | Factor 1 (Language) | Factor 1 (Speed) | |||
| (Eignevalue = 4.27; 26.70%) |
(Eignevalue = 4.34; 27.11%) |
(Eignevalue = 5.9; 39.34%) |
|||
| Similarities | 0.80 | Similarities | 0.78 | Shape Time | −1.00 |
| Identities/Oddities | 0.43 | Identities/Oddities | 0.32 | TMX Time | −0.94 |
| Letter Fluency | 0.57 | Letter Fluency | 0.65 | ||
| Naming Total | 0.46 | Category Fluency | 0.67 | ||
| Comprehension | 0.65 | Repetition | 0.39 | ||
| Comprehension | 0.52 | ||||
| Factor 2 (Visual-Spatial) | Factor 2 (Speed) | Factor 2 (Language) | |||
| (Eignevalue =1.95; 12.17%) |
(Eignevalue = 1.96; 12.23%) |
(Eignevalue = 1.55; 10.30%) |
|||
| Benton Recognition | 0.52 | Shape Time | −0.78 | Naming Total | 0.52 |
| Benton Matching | 0.62 | TMX Time | −0.98 | Repetition | 1.11 |
| Rosen | 0.59 | Comprehension | 0.51 | ||
| Shape Omits | −0.50 | ||||
| TMX Omits | −0.68 | ||||
| Factor 3 (Immediate Memory) | Factor 3 (Memory) | Factor 3 (Memory) | |||
| (Eignevalue =1.45; 9.06%) |
(Eignevalue = 1.42; 8.88%) |
(Eignevalue = 1.32; 8.79%) |
|||
| Category Fluency | 0.68 | SRT Total Recall | 0.64 | SRT Total Recall | 0.73 |
| *Letter Fluency | 0.56 | SRT Delayed Recall | 0.92 | SRT Delayed Recall | 0.96 |
| Repetition | 0.53 | SRT Delayed Recog | 0.56 | SRT Delayed Recog | 0.56 |
| SRT Total Recall | 0.68 | ||||
| Factor 4 (Speed) | Factor 4 (Visual-Spatial) | Factor 4 (gF) | |||
| (Eignevalue = 1.13; 7.06%) |
(Eignevalue = 1.15; 7.2%) |
(Eignevalue = 1.01; 6.75%) |
|||
| Shape Time | −0.83 | Benton Matching | 0.42 | Benton Recognition | 0.48 |
| TMX Time | −0.74 | Benton Recognition | 0.28 | Benton Matching | 0.70 |
| Rosen | 0.30 | Similarities | 0.54 | ||
| Shape Omits | −0.52 | Identities/Oddities | 0.49 | ||
| TMX Omits | −0.68 | Letter fluency | 0.39 | ||
| Category Fluency | 0.35 | ||||
| TMX Omits | −0.73 | ||||
| Factor 5 (Delayed Memory) | |||||
| (Eignevalue = 1.00; 6.24%) |
|||||
| SRT Delayed Recall | 0.63 | ||||
| SRT Delayed Recog | 0.52 | ||||
The most striking difference across the groups was that in the probable AD group the memory variables spilt into two different factors. The SRT Total Recall variable loaded with Category Fluency, Letter Fluency, and Repetition variables on to Factor 3 which we labeled Immediate Memory and the two delayed memory variables loaded on to a separate fifth factor we labeled Delayed Memory. Whereas the Repetition variable appears to be a language variable for the QD and cognitively-healthy groups, it is more correlated with memory in the probable AD group.
Despite some differences in the variables used in the EFA, the factor solution for the QD and cognitive-healthy samples were fairly similar. For both groups a four-factor structure yielded an interpretable solution and included a speed factor and a memory factor. The main difference between the two was where the Similarities, Identities/Oddities, and the Fluency variables loaded. In the cognitively-healthy group those four variables correlated more so with the BVRT Recognition, BVRT Matching, and the TMX Omits variables to form a gF factor. In the QD group those variables loaded with the Repetition and Comprehension variables to form a factor we labeled Language. As can be seen in Figure 1, the Language and gF factors in the cognitively-healthy group are highly correlated suggesting that those variables have considerable variance in common.
The factor structure of the QD group was also similar to the factor structure of the AD group. In many ways the QD structure may be thought of an intermediary between that of the cognitively-healthy and AD groups. In addition to the speed factor that was stable across all three groups, both groups’ factor structures included a Visual-Spatial factor comprised of all the same variables, and a Language factor comprised of many of the same variables. Most of the differences were between the Memory factors. Namely, the probable AD had both immediate and delayed memory factors whereas the QD group had one unitary memory factor.
Discussion
As seen in Table 1, there are clear differences in performance across diagnostic groups, with cognitively-healthy older adults performing better on all the tasks than the QD and probable AD groups. Further, the QD group performed better on all the tasks as compared to the probable AD group. Since diagnoses of these disorders are typically based in part on scores on these tasks, it is not surprising that performance on these tasks decline with disease severity. This is an important point because in this study group membership was determined via clinical consensus by a group of study neurologists, neuropsychologists, and psychiatrists who partially based their assessment on the neuropsychological functioning of the subjects (although diagnosis was also made based on assessment of daily functioning, and evaluation of brain scans when available). As a result, one could argue that there is some circularity in the current analyses (examining group differences in the relations among the neuropsychological variables) since group membership was based partly on neuropsychological functioning. In fact, this paper substantiates empirically the finding often anecdotally reported by neuropsychologists looking for patterns of change in neuropsychological tests. For instance, when a patient has intact immediate memory scores and impaired delayed memory scores it is often said that that patient “fits the pattern” of AD. Although the existence of differences in neuropsychological patterns frequently identified by neuropsychologists may not be surprising, it is important because it supports with data what is presumably known intuitively.
It is well-known that there are quantitative differences across the groups, therefore the main goal of this paper was to determine whether there are qualitative differences across the groups. Several steps were taken to address this question.
First, it was important to determine what the tests were measuring. In a sample of cognitively-healthy older adults without any major co-morbidities, it appears that the neuropsychological variables of interest were measuring the latent abilities of speed, memory, language, and fluid ability (as determined by an EFA). To determine whether this four-factor model was an appropriate representation of the data, it was subsequently examined in the context of a CFA. The fit of the model was adequate and it demonstrated both convergent and discriminant validity. However, a theory-based five-factor model comprised of speed, attention, memory, language, and a combined reasoning and visual-spatial factor was selected for subsequent invariance analyses since it fit the data the best.
A formal test of invariance was conducted across the three groups with the five-factor model. The invariance analyses indicated there may be some configural invariance but no metric or structural invariance (as determined by both the change in X 2 by df and change in CFI).
Although the results of invariance analyses could be interpreted as evidence for configural invariance, a second approach was used to determine whether there were qualitative differences across groups. Additional exploratory factor analyses were conducted and the results indicated that the probable AD group had a different factor structure, with the greatest difference being the creation of two separate memory factors. In the probable AD group the SRT total recall variable loaded with the Category fluency, Letter fluency and Repetition variables on to an Immediate Memory factor. The fluency variables have an episodic memory component in the sense that the subject must remember which words they have already generated since one of the rules of the task is to not repeat words. It therefore makes sense that due to memory difficulties, the fluency variables would be more correlated with the SRT Total Recall variable in the probable AD patients than in the other groups. In addition, the repetition variable requires subjects to repeat phrases to the examiner. In the cognitively-healthy and QD groups this task could reflect one’s language ability but in the probable AD group it could be considered a memory task.
The factor structure of the probable AD group also differed because it included a fifth factor labeled delayed memory that was comprised of the SRT delayed recall and SRT delayed recognition variables. Essentially, the two delayed variables split off into their own factor. This finding is consistent with work completed by Delis, Jacobson, Bondi, Hamilton, and Salmon (2003) who conducted two experiments examining the relations among immediate and delayed memory variables from the California Verbal Learning Test (CVLT; Delis, Kramer, Kaplan, & Ober, 1987; 2000). In Experiment 1, they reported that in a sample of healthy controls and in a sample of Huntington’s disease patients the correlation between the immediate memory measure and delayed memory measure of the CVLT was significant at the p < 0.01 level, but in an AD sample the correlation was not significant. In Experiment 2, they compared the factor structure of the CVLT across three groups comprised of probable AD patients, subjects from the CVLT normative sample, and a group of patients with mixed neurological disorders. They reported that the factor structure of the CVLT was “markedly” different across the groups. Namely, the immediate-recall, delayed-recall, and delayed-recognition memory variables loaded on to a single factor for the normative sample group and mixed neurological group, but these measures loaded on to separate factors in the probable AD group. The authors suggest this finding is likely due to the pathological changes in the brain during the earliest phase of AD which typically affects the mesial temporal lobe including the hippocampus. This region has been shown to be integral in the transference of information form short-term to long-term memory. Therefore if immediate memory is intact but delayed memory is not, the relations among these tasks will change as a result.
These findings are also consistent with earlier work suggesting that relative to immediate recall, delayed recall may be more sensitive to damage in the temporal lobe regions in amnesic patients with localized damage such as in the famous case of the amnesic HM (Milner, Corkin, & Teuber, 1968) and others (e.g. Graf, Squire, & Mandler,1984; Zola-Morgan, Squire, & Amaral, 1989), as well as in AD patients (for a review see Butters, Delis, & Lucas, 1995).
In summary, we took two parallel approaches to examining the factor structure of a battery of neuropsychological variables across three different diagnostic groups. First, invariance analyses were conducted on a theory-based five-factor model. The results of the invariance analyses suggest that there may be some configural invariance across the different groups but there was no evidence for either metric or structural invariance across either model. That is, there was some evidence that the structure (or configuration) of the model was the same across groups but the magnitude of the unstandardized coefficients and covariances were changing. However, the fit of the configural invariance models was only adequate because while the RMSEA indicated a good fit, the CFI was below the typical cut-off used to indicate a good fit. The baseline five-factor model only fit adequately as well. The lack of a great fit of any of the models is likely due to the non-normality of the data since one consequence of non-normal data are poorer fit indices.
The second approach involved examining the differences in the factor structures after conducting a separate EFA for each diagnostic group. The main difference across the groups was a fifth, delayed memory factor emerged in the AD group that was not evident in either the cognitively-healthy or QD group. This result was consistent with findings by Delis, et al. (2003) in which the delayed memory variables were not significantly correlated with an immediate memory measure and in fact, loaded on to a different factor within a sample of probable AD subjects but not in a sample of normal controls.
Although the results of the two approaches may seem somewhat inconsistent, the findings are compatible. The fit of the configural invariance analysis was interpreted to only be adequate and lacked strong evidence for invariance. This is likely because a) the fit of the baseline model was only adequate (likely due to non-normality of the data) and b) the factor structure was changing somewhat across the groups. We can see from the EFA that there were slightly different factor structures across the groups with a fifth factor emerging in the probable AD group.
Some new questions emerge from these findings. For example, why was the model suggested by the EFA different from the best-fitting confirmatory model? One explanation for this finding is that the factor structure suggested by the EFA allows for variables to load on all existing factors whereas the 4-factor model tested in the CFA only allowed the variables to load on to one factor. Although CFA is necessary to conduct invariance analyses, moving from EFA to CFA changes the model substantially. As a result, what may be the best representation of the data in factor space is no longer the best representation when examined in the context of confirmatory analyses.
Another question that emerges is whether quantitative comparisons should be made across different diagnostic groups. Some researchers argue that if the structure is changing across groups, and the variables are measuring different constructs, quantitative comparisons of memory performance, for example, may not be justified. One example of a measure whose meaning may be changing across groups is the “Draw-a-Man” test (Goodenough, 1926) which requires subjects to sketch a picture of a person. In young children this test is a measure of IQ and is correlated with school performance (e.g. Coleman, Iscoe, & Brodsky, 1959). However, the upper age norms for this test and those similar to it end at age 15 (Lezak, 1995) because there is a leveling off of scores. Presumably in teenagers this same test is more of an indicator of artistic ability than intelligence. In this case, comparing performance across age groups on this test may not be warranted since the test is measuring a different construct. In this study, since there is a lack of metric invariance (and possibly configural invariance) of the factor structure across the different diagnostic groups examined in the current study, it can be argued that any quantitative comparisons on these variables should be supplemented with qualitative comparisons. Before strong recommendations can be made regarding these comparisons, it is important that these findings be replicated in additional samples.
A limitation of this study is that we did not address the heterogeneity within diagnostic groups. For example, a subject is diagnosed with QD if they present with impairment within any cognitive domain (either sufficient for dementia but without functional impairment, or insufficient for a dementia diagnosis). Therefore, it is likely that there are subgroups within the QD group that have different growth trajectories – some are likely to develop AD, some may be labeled cognitively healthy at their subsequent visits, and others may remain with a QD diagnosis throughout the duration of the study. This assessment if also true of the probable AD group since subjects may have different levels of severity of disease, may have different patterns of symptoms, and may show different rates of change. Therefore, an important continuation of the current analyses (which may obscure difference in subgroups) is to evaluate potential differences within the diagnostic group.
Acknowledgements
We acknowledge the support of the Alzheimer Disease Research Center Grant from NIH/NIA, P50AG08702 (P.I. Michael Shelanski). KLS is supported as a trainee by a grant (T32MH020004-09) from the National Institute of Mental Health.
Footnotes
Note: This article may not exactly replicate the final version published in the APA journal. It is not the copy of record. Copyright 2008 of the American Psychological Association; DOI: 0.1037/0894-4105.22.3.400; http://www.apa.org/journals/neu/
Full information maximum likelihood (FIML) estimation was used in all confirmatory factor analyses to deal with missing data.
Age and education differed by group, and these variables were therefore included as covariates in the invariance analyses. However, since no substantive differences were found when they were included (i.e. there was still evidence for configural invariance, but not evidence for metric or structural invariance), they were excluded from the models for the sake of parsimony and ease of presentation.
References
- Arbuckle JL. Amos 5.0. Chicago, IL: SPSS; 2003. [Google Scholar]
- Bentler PM. On the fit of models to covariances and methodology to the Bulletin. Psychological Bulletin. 1992;112:400–404. doi: 10.1037/0033-2909.112.3.400. [DOI] [PubMed] [Google Scholar]
- Benton AL. The Visual Retention Test. New York: The Psychological Corporation; 1955. [Google Scholar]
- Blessed G, Tomlinson BE, Roth M. The association between quantitative measures of dementia and of senile change in the cerebral grey matter of elderly subjects. British Journal of Psychiatry. 1968;114:797–811. doi: 10.1192/bjp.114.512.797. [DOI] [PubMed] [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York: Wiley; 1989. [Google Scholar]
- Buschke H, Fuld PA. Evaluating storage, retention, and retrieval in disordered memory and learning. Neurology. 1974;24:1019–1025. doi: 10.1212/wnl.24.11.1019. [DOI] [PubMed] [Google Scholar]
- Butters N, Delis DC, Lucas JA. Clinical assessment of memory disorders in amnesia and dementia. Annual Review of Psychology. 1995;46:493–523. doi: 10.1146/annurev.ps.46.020195.002425. [DOI] [PubMed] [Google Scholar]
- Byrne BM, Shavelson RJ, Muthén B. Testing for the equivalence of factor covariance and mean structures: The issue of partial invariance. Psychological Bulletin. 1989;105:456–466. [Google Scholar]
- Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal. 2002;9:233–255. [Google Scholar]
- Chou C-P, Bentler PM. Estimates and test in structural equation modeling. In: Hoyle RH, editor. Structural Equation Modeling: Concepts, Issues, and Applications. Newbury Park, CA: Sage; 1995. pp. 37–55. [Google Scholar]
- Coleman JM, Iscoe I, Brodsky M. The “Draw-A-Man” test as a predictor of school readiness and as an index of emotional and physical maturity. Pediatrics. 1959;29:275–281. [PubMed] [Google Scholar]
- Davis RN, Massman PJ, Doody RS. WAIS-R factor structure in Alzheimer ’s disease patients: A comparison of alternative models and an assessment of their generalizability. Psychology and Aging. 2003;18:836–843. doi: 10.1037/0882-7974.18.4.836. [DOI] [PubMed] [Google Scholar]
- Delis DC, Kramer JH, Kaplan E, Ober BA. The California Verbal Learning Test. San Antonio, Texas: The Psychological Corporation; 1987. [Google Scholar]
- Delis DC, Kramer JH, Kaplan E, Ober BA. The California Verbal Learning Test. Second Edition. San Antonio, Texas: The Psychological Corporation; 2000. [Google Scholar]
- Delis DC, Jacobson M, Bondi MW, Hamilton JM, Salmon DP. The myth of testing construct validity using factor analysis or correlations with normal or mixed clinical populations: Lessons from memory assessment. Journal of the International Neuropsychological Society. 2003;9:936–946. doi: 10.1017/S1355617703960139. [DOI] [PubMed] [Google Scholar]
- Fabrigar LR, Wegener DT, MacCallum RC, Strahan EJ. Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods. 1999;4:272–299. [Google Scholar]
- Goodglass H. The assessment of aphasia and related disorders. 2nd ed. Philadelphia: Lea & Febiger; 1983. [Google Scholar]
- Goodenough FL. Measurement of Intelligence by Drawings. Chicago: World Book Company; 1926. [Google Scholar]
- Graf P, Squire LR, Mandler G. The information that amnesic patients do not forget. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10:164–178. doi: 10.1037//0278-7393.10.1.164. [DOI] [PubMed] [Google Scholar]
- Horn JL, McArdle JJ. A practical and theoretical guide to measurement invariance in aging research. Experimental Aging Research. 1992;18:117–144. doi: 10.1080/03610739208253916. [DOI] [PubMed] [Google Scholar]
- Horn JL, McArdle JJ, Mason R. When is invariance not invariant: A practical scientist’s look at the ethereal concept of factor invariance. The Southern Psychologist. 1983;1:179–188. [Google Scholar]; Hu L-T, Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods. 1998;3:424–453. [Google Scholar]
- Hu L-T, Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods. 1998;3:424–453. [Google Scholar]
- Hu L-T, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal. 1999;6:1–55. [Google Scholar]
- Kanne SM, Balota DA, Storandt M, McKeel DW, Jr, Morris JC. Relating anatomy to function in Alzheimer‘s disease: Neuropsychological profiles predict regional neuropathology 5 years later. Neurology. 1998;50:979–985. doi: 10.1212/wnl.50.4.979. [DOI] [PubMed] [Google Scholar]
- Kaplan E, Goodglass H, Weintraub S. The Boston Naming Test. Philadelphia: Lea & Febiger; 1983. [Google Scholar]
- Lezak MD. Neuropsychological assessment. 3rd ed. New York: Oxford University Press; 1995. [Google Scholar]
- Loewenstein DA, Ownby R, Schram L, Acevedo A, Rubert M, Arguelles T. An evaluation of the NINCDS-ADRDA neuropsychological criteria for the assessment of Alzheimer’s disease: A confirmatory factor analysis of single versus multi-factor models. Journal of Clinical and Experimental Neuropsychology. 2001;23:274–284. doi: 10.1076/jcen.23.3.274.1191. [DOI] [PubMed] [Google Scholar]
- Loewenstein DA, Rubert MP. The NINCDS-ADRDA neuropsychological criteria for the assessment of dementia: Limitations of current diagnostic guidelines. Behavior, Health, & Aging. 1992;2:113–121. [Google Scholar]
- MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size of covariance structure modeling. Psychological Methods. 1996;1:130–149. [Google Scholar]
- MacCallum RC, Widaman KF, Zhang S, Hong S. Sample size in factor analysis. Psychological Methods. 1999;4:84–99. [Google Scholar]
- Mattis S, editor. Mental status examination for organic mental syndrome in the elderly patient. New York: Grune & Stratton; 1976. [Google Scholar]
- Milner B, Corkin S, Teuber HL. Further analysisof trhe hippocampal amnesic syndrome: 14-year follow-up study of H.M. Neuropsychologia. 1968;6:215–234. [Google Scholar]
- Morris RG, Kopelman MD. The memory deficits in Alzheimer-type dementia: a review. The Quarterly Journal of Experimental Psychology. 1986;38:575–602. doi: 10.1080/14640748608401615. [DOI] [PubMed] [Google Scholar]
- Nyberg L. A structural equation modeling approach to the multiple memory systems question. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:485–491. [Google Scholar]
- Nyberg L, Maitland SB, Ronnlund M, Backman L, Dixon R, Wahlin A, Nilsson L-G. Selective adult age differences in age-invariant multifactor model of declarative memory. Psychology and Aging. 2003;18:149–160. doi: 10.1037/0882-7974.18.1.149. [DOI] [PubMed] [Google Scholar]
- Rosen W. The Rosen Drawing Test. Bronx, NY: Veterans Administration Medical Center; 1981. [Google Scholar]
- Salthouse TA. Executive functioning. In: Park DC, Schwarz N, editors. Cognitive Aging: A Primer. New York: Psychology Press; in press. [Google Scholar]
- Salthouse TA, Becker JT. Independent effects o Alzheimer’s disease on neuropsychological functioning. Neuropsychology. 1998;2:242–252. doi: 10.1037//0894-4105.12.2.242. [DOI] [PubMed] [Google Scholar]
- Schwab RS, England AC. Projection technique for evaluating surgery in Parkinson's disease. In: Gillingham FJ, Donaldson IML, editors. Third symposium on Parkinson's disease. Edinburgh, Scotland: Livingstone; 1969. [Google Scholar]
- Siedlecki KL. Investigating the structure and age invariance of episodic memory across the adult lifespan. Psychology and Aging. 2007;22:251–268. doi: 10.1037/0882-7974.22.2.251. [DOI] [PubMed] [Google Scholar]
- Stern Y, Andrews H, Pittman J, Sano M, Tatemichi T, Lantigua R, Mayeux R. Diagnosis of dementia in a heterogeneous population: Development of a neuropsychological paradigm-based diagnosis of dementia and quantified correction for the effects of education. Archives of Neurology. 1992;49:453–460. doi: 10.1001/archneur.1992.00530290035009. [DOI] [PubMed] [Google Scholar]
- Velicer WF, Fava JL. Effects of variable and subject sampling on factor pattern recovery. Psychological Methods. 1998;3:231–251. [Google Scholar]
- Wechsler D. Wechsler Adult Intelligence Scale-Revised. New York: The Psychological Corporation; 1981. [Google Scholar]
- West SG, Finch JF, Curran PJ. Structural equations with nonnormal variables: Problems and remedies. In: Hoyle RH, editor. Structural Equation Modeling: Concepts, Issues, and Applications. Newbury Park, CA: Sage; 1995. pp. 56–75. [Google Scholar]
- Zola-Morgan S, Squire LR, Amaral DG. Human aneisa and the medial temporal region: Eduring memory impairment following a bilateral lesion limited to the field CA1 of the hippocampus. The Journal of Neuroscience. 1989;6:2950–2967. doi: 10.1523/JNEUROSCI.06-10-02950.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]