Structures that Contribute to Middle-Ear Admittance in Chinchilla

Abstract

We describe measurements of middle-ear input admittance in chinchillas (Chinchilla lanigera) before and after various manipulations that define the contributions of different middle-ear components to function. The chinchilla’s middle-ear air spaces have a large effect on the low-frequency compliance of the middle ear, and removing the influences of these spaces reveals a highly admittant tympanic membrane and ossicular chain. Measurements of the admittance of the air spaces reveal that the high-degree of segmentation of these spaces has only a small effect on the admittance. Draining the cochlea further increases the middle-ear admittance at low frequencies and removes a low-frequency (less than 300 Hz) level dependence in the admittance. Spontaneous or sound-driven contractions of the middle-ear muscles in deeply anesthetized animals were associated with significant changes in middle-ear admittance.

1.0 INTRODUCTION

Chinchillas (Chinchilla lanigera) are nocturnal foragers that lived in communal burrows and are native to the rocky slopes of the high Andes. However, wild chinchillas are endangered, having been over-hunted by humans for food and their fur, and preyed upon by European species introduced into their habitat. Captive chinchillas have been successfully bred in the USA and Russia over the last 80 years. Since the 1950s, chinchillas have become a common animal model in hearing and other research areas (Price 1953; Tibbitts and Hillemann 1959); Peters 1965; Henderson 1969; Lupien and McCay 1960; Bismark and Pfeiffer 1967; Trautwein & Helmboldt 1967; Strike and Seigneur 1969; Dallos 1970; Miller 1970).

The high Andes is an open and arid environment and chinchillas show some adaptations that are similar to those seen in other animals adapted to open and arid areas including a few distinctive features of the middle ear:

1. large middle-ear air spaces ( total volume ≥ 1.5 cc) that are segmented into multiple sub-cavities (Browning and Granish 1978; Vrettakkos et al. 1988).

2. large tympanic-membrane (TM) and ossicular dimensions for an animal of its size (Vrettakkos et al. 1988; Rosowski 1991a&b, 1994), and

3. increased mechanical sensitivity to low-frequency (f < 1000 Hz) acoustic stimuli relative to other animals with similar hearing ranges (Ruggero et al. 1990).

When viewed in light of the relatively sensitive low-frequency auditory thresholds in this species (Fay 1988; Miller 1970), the chinchilla middle ear appears specialized for low-frequency hearing. While preliminary acoustic admittance (Dear 1987)¹, cochlear potential (Dallos 1970) and ossicular-motion measurements (Ruggero et al. 1990) are all consistent with this view, past studies have not determined which middle-ear structures contribute to the sensitivity to low-frequency sound.

There is a history of work on other species specialized for arid climates, typically deserts, that suggests that relatively large tympanic membranes, voluminous middle-ear spaces and good sensitivity to low-frequency sounds are a common theme in such environments (e.g. Heim de Balsac 1936; Legouix and Wisner 1955). The families and species most investigated in this regard are the Heteromyidae (kangaroo rats and their relatives (Webster 1961, 1962; Webster and Webster 1975, 1984; Webster and Plassman 1992)), Gerbillinae (Lay 1972, 1974; Ravicz, Rosowski and Voigt 1992) and the sand cat, Felis margarita (Huang et al. 2002). These studies found a consistent association between anatomical specializations, i.e. large tympanic membranes and middle-ear air spaces, with middle and inner ears that are highly sensitive to low-frequency sound (Webster 1962; Webster and Webster 1975, 1984; Ravicz and Rosowski 1997, Huang et al. 2002).

While there are many examples of the association of certain middle-ear structures with sensitivity to auditory stimuli of different frequencies (e.g. Heim de Balsac 1936; Fleischer 1978, Rosowski and Graybeal 1991; Rosowski 1992), others have questioned the degree of influence of middle-ear mechanical and acoustical processes on hearing range. Ruggero and Temchin (2002) point out that the high-frequency limits of hearing in many vertebrates seem to be set by the limits of inner-ear sensitivity. Ruggero and Temchin (2002) also point out (as others have before them, e.g., Dallos 1970; Rosowski et al. 1985) that the helicotrema within the inner ear plays a role in limiting sensitivity to very low-frequency sounds (< 100 Hz in mammals). Nonetheless the data presented in Figure 1 of Ruggero and Temchin and the work of many others (Dallos 1973; Zwislocki 1975; Rosowski et al. 1986; Rosowski and Graybeal 1991; Rosowski 1992; Puria et al. 1997) support a large role of the middle ear in determining the sensitivity of the ear to the lower and middle decades of the audible range.

Figure 1.

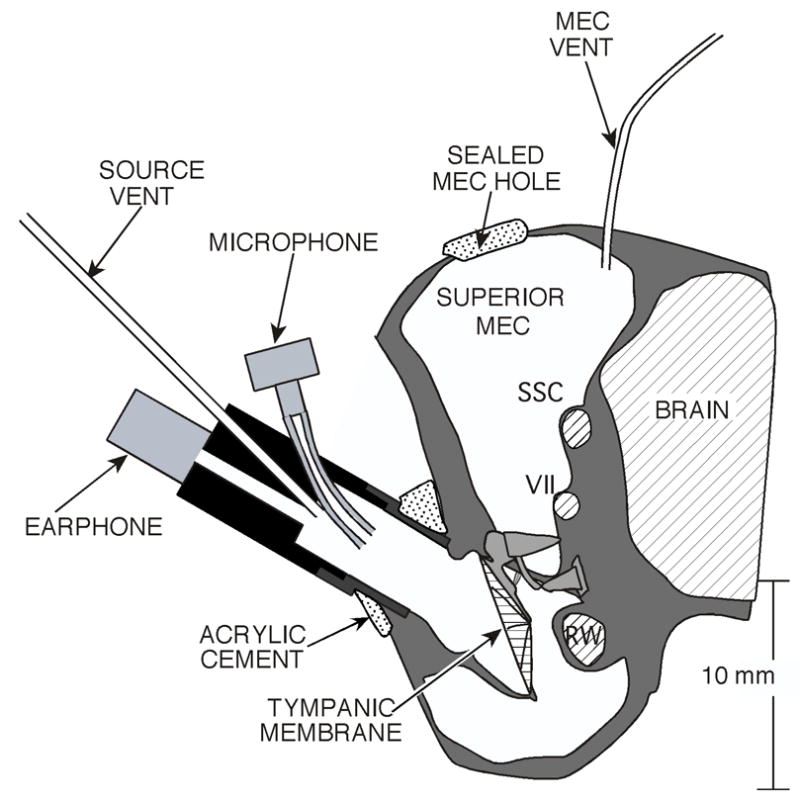
A schematic coronal section of the middle- and external ear of a chinchilla. The large middle-ear air spaces, the remnants of the long bony ear canal and the relatively large tympanic membrane and ossicles are illustrated. The schematic also shows the placement of the sound source in the ear canal, the location of the vent in the superior cavity and the location of the hole in the superior cavity wall. The hole is shown as if it were sealed with ear-mold material. The superior semicircular canal (SSC), the tendon of the tensor tympani (attached to the malleus) and the facial canal (VII) are accessible via the superior hole. The round window (RW) is seen within the middle ear.

The primary purpose of the work described in this report is to separate out the contribution of the middle-ear air spaces, the tympanic membrane, ossicles and the cochlear load in limiting middle-ear function in chinchilla. In gathering the functional data some unusual phenomena were observed: a tympanic membrane and ossicular system that is extremely sensitive to low-frequency sound, a low-frequency inner-ear derived non-linearity in middle-ear mechanics that was previously noted by Kim et al. (1980) and Ruggero et al. (1996), as well as uncontrolled changes in middle-ear admittance in the anesthetized chinchilla linked to activation of the middle-ear muscles. Descriptions of these phenomena are part of this report.

2.0 METHODS

2.1 Animal Preparation

All measurements in animals were performed using protocols approved by the Institutional Animal Care and Use Committee of the Massachusetts Eye and Ear Infirmary and meet the standards set by the State of Massachusetts and the Federal government for animal studies. Twenty-four adult female chinchillas were anesthetized with ketamine hydrochloride (45 mg/kg) and sodium pentobarbitol (50 mg/kg) injected into the parietal peritoneum. Heart rate was monitored and body temperature was maintained at 36 ± 2 degrees C. Periodic toe-pinches were applied to test for depth of anesthesia, and supplements of 1/3 the surgical dose of either ketamine hydrochloride (intramuscularly) or sodium pentobarbital (intraperitoneally) were administered when called for. The surgical preparation of the animal included (i) tracheotomy and insertion of a tracheal cannula, (ii) resecting the pinna and cartilaginous ear canal at the tympanic bone (Figure 1), (iii) exposure of the outer walls of the superior and posterior bulla (the bone that surrounds the middle-ear air spaces), (iv) opening a 3–4 mm diameter hole in the superior bullar wall, (v) placement of a 10 cm long 0.1 mm id vent tube into the superior air space, (vi) exposure and removal of the lateral wall of the bony external canal, and (vii) cementing a brass coupler tube to the bony canal remnant and the tympanic ring to allow easy placement and replacement of our sound generation and measurement system (Figure 1).

A few additional surgical procedures were performed in subsets of animals. In all but four animals the tendon of the tensor-tympani muscle was sectioned at its junction with the manubrium of the malleus via a fine knife inserted through the superior bullar hole. In 15 animals, the tensor tendon was sectioned as above and the labyrinthine portion of the facial nerve was sectioned in its bony canal just distal to its genu (Figure 1) in order to denervate the stapedius muscle, and a second hole (2 mm in diameter) was made in the posterior bullar wall for measurements of cochlear potential in a separate study (Songer and Rosowski 2005). In two other animals the middle-ear muscles were immobilized by intramuscular injections of tubocurare (0.1 mg/kg). (After curare administration the animals were ventilated using a small animal ventilator and regular supplements of anesthesia were performed such that heart rate was maintained at pre-curare baseline.) In three animals (one with the tensor tendon cut and two with the tendon and facial nerve sectioned) the superior semicircular canal was opened with a fine micro-chisel and suction applied to drain the inner ear of fluid. In three animals (another with the tendon cut and the same two with the tendon and facial nerve sectioned) the incudo-stapedial joint was interrupted and the stapes dislocated via the ‘second’ hole in the posterior bullar wall.

2.2 Sound Stimulation and Measurement

A custom-built stimulus and measurement assembly that included a Knowles Acoustics (Itasca IL) hearing-aid receiver (#ED1913) as a sound source and a Knowles hearing-aid microphone (#EK3027) was coupled to the brass tube sealed in the shortened bony ear canal (Figure 1). The microphone was coupled to the system via a probe tube (0.4 mm id and 18 mm in length). The sound sensitivity of the microphone and probe tube were determined by calibration against a 1/4 inch reference microphone (Larson Davis, Provo UT, #2530). Measurements of the microphone voltage produced by the sound source and measurement assembly in known reference loads were used to determine the Norton equivalent source parameters of that assembly (Rosowski et al. 1984; Lynch et al. 1994). Knowledge of these source parameters permitted us to calculate the acoustic admittance at the measurement site within the ear canal coupler Y_EC. The admittance at the tympanic membrane Y_TM was calculated from the ear-canal admittance using a transmission-line correction based on the dimensions of the ear coupler and post-experiment fluid-filling measurements of the residual ear-canal volume between the coupler and the TM (Møller 1965; Rabinowitz 1981; Lynch et al. 1994). The units of acoustic admittance are siemens (S), where 1 S equals 1 Pa-s-m⁻³.

The acoustic stimuli were either broad-band (12 to 25000 Hz) or low-pass (12–300 Hz) multi-harmonic stimuli, which sound like chirps, produced by a PC-controlled Ariel DSP16+ board (Ariel Corp, Cranbury, New Jersey) with SYSid software (SYSid Labs, Richmond CA). The computer controlled DSP16+ synchronously generated the stimulus signal and measured the microphone response. The stimulus output from the DSP16+ board was attenuated to produce sound stimuli (Figure 2) with rms sound levels between 60 and 105 dB SPL. Because of the high output-impedance of our acoustic assembly, the sound pressure produced by our stimuli depended greatly on the acoustic load of the middle ear. For instance, the relatively low sound pressures measured at frequencies less than 1000 Hz in Figure 2 are due to the high admittance of the chinchilla ear when the middle-ear air space is opened. The low sound pressures at frequencies above 10000 Hz are due to the limited volume-velocity output of our sound source above that frequency. Because of these limitations the frequency range of accurate admittance measurement was from 50 to 10000 Hz. (The range of accurate admittance estimation was determined from measurements in test loads of varied admittance, e.g. Ravicz et al. 1992).

Figure 2.

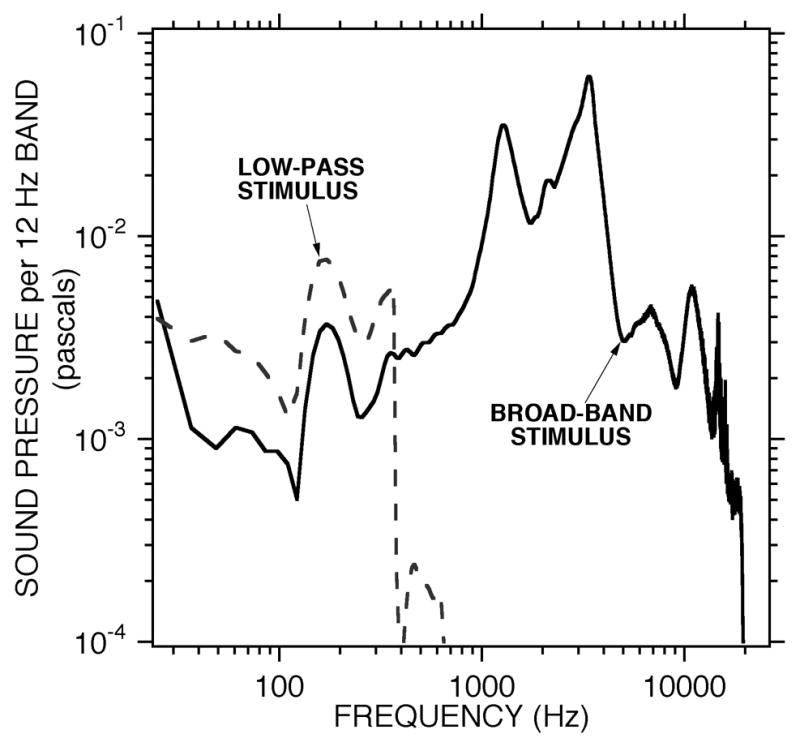
Spectra of the acoustic responses to the broadband and low-pass stimuli with earphone inputs of 0.1 volt rms. The response were measured in the ear canal of a chinchilla in the open-cavity hole condition. The solid line shows the sound pressure spectrum produced by a synthesized electrical stimulus containing components from 12 to 25000 Hz. The dashed line shows the response produced by the low-pass stimulus with stimulus energy at frequencies of 400 Hz and less. Estimates of spectral levels less than 3×10⁻⁴ pascals are contaminated by electrical noise in the microphone response. The sound pressure of the illustrated broad-band stimulus is 88 dB SPL re 2×10⁻⁵ Pa. The sound pressure of the low-pass stimulus is 62 dB SPL.

Complications introduced by the use of the broad-band chirps were limited stimulus energy at low frequencies and the potential for low-frequency distortion produced by the large 1000 – 5000 Hz stimulus and response components. These complications were averted by the use of the low-pass stimulus.

2.3 Measurement Protocol

The admittance at the tympanic membrane Y_TM was measured in three base conditions: i) intact $Y_{TM}^I$: with the superior bullar hole sealed with ear-mold impression material but with a vent to prevent the build up of static pressure, ii) open bullar hole $Y_{TM}^H$: with the 3–4 mm diameter hole in the superior bullar wall opened, and iii) perforated TM $Y_{TM}^P$: with the air spaces sealed and vented but with a 4 mm or larger diameter perforation created in the tympanic membrane. (Since the primary contributor to the $Y_{TM}^P$ measurements was the middle-ear air spaces, the perforated TM measurements were sometimes performed post-mortem.) In several ears, measurements of the open-hole and intact admittance were also performed under different conditions: after curarizing the animal, after cutting the tensor-tympani tendon alone, after immobilizing both middle-ear muscles via sectioning the tensor tendon and the facial nerve, after draining the inner-ear lymphs, after interrupting the incudo-stapedial joint, and after euthanasia via anesthetic overdose.

2.4 Statistical Methods

Two different types of statistical analyses were performed on the data. The first analysis was a computation of the mean and 95% confidence interval of the mean of the data measured at each frequency point in each condition. These means are generally plotted as heavy solid lines in the illustrated frequency responses. The second analysis consisted of the determination of characteristic features of the individual frequency responses, e.g. low-frequency slope, maximum magnitude and the frequency of the maximum. The means and standard deviations of these features are presented in Table 1. Because of differences in the shape and location of maxima and minima in the individual data, the mean of the individual features can differ significantly from the features of the mean data.

TABLE 1.

	Mean ± StDev	Median
Intact
$C_{TM}^I$	1.60 ± 0.32 cc	1.64 cc
Corner Frequency, Intact	1160 ± 240 Hz	1200 Hz
|Y| at Corner Frequency	(7.65 ± 1.84) × 10−8 S	7.17 × 10−8 S
Frequency of Cavity Notch	2630 ± 197 Hz	2550 Hz
|Y| at Cavity notch	(2.67 ± 1.20) ×10−8 S	2.31 × 10−8 S
Bullar Hole Open
$C_{TM}^H$	8.6 ± 4.5 cc	9.9 cc
Frequency at First Angle Zero Crossing	328 ± 194 Hz	232 Hz
|Y| at First Zero Crossing	(1.23 ± 0.56) × 10−7	1.17 × 10−7
Frequency of Hole Anti-Resonance	1370 ± 215 Hz	1340 Hz
|Y| at Anti-Resonance	(8.32 ± 3.57) × 10−9 S	7.18 × 10−9 S
TM Perforated
$C_{TM}^P$	2.00 ± 0.40 cc	2.09 cc
Frequency of Cavity Resonance	1470 ± 300 Hz	1400 Hz
|Y| at Cavity Resonance	(1.10 ± 0.44) × 10−6 S	1.22 × 10−6 S
Frequency of Cavity Anti-Resonance	2450 ± 480 Hz	2600 Hz
|Y| at Cavity Anti-Resonance	(4.01 ± 1.48) × 10−8 S	4.03 × 10−8 S
YTOC
CTOC	6.9 ± 10.cc	4.02 cc
1/Resistance	(6.27 ± 1.93) × 10−8 S	5.66 × 10−8 S
YASBH
Acoustic Mass of Bullar Hole	2130 ± 6150 kg/m4	2840 kg/m4
Frequency of Hole Anti-Resonance	1367 ± 216 Hz	1343 Hz
|Y| at Hole Anti-Resonance	(9.51 ± 4.92) × 10−9 S	7.59 × 10−9 S

Comparisons of descriptors of the measurements of middle-ear input admittance in the intact, bullar hole open and TM perforated conditions, along with estimates of Y_TOC and Y_ASBH from the 9 ears of Figures 3, 5 and 6. The compliances ( $C_{TM}^I,C_{TM}^H,C_{TM}^P$ and C_TOC ) are fit to the low-frequency admittances and are expressed as cubic centimeters (cc) of equivalent air volumes. The Corner Frequency in the intact case (the frequency where the admittance angle first crosses zero) and the admittance magnitude |Y| at the corner describe the frequency where the admittance first becomes approximately resistive, and the magnitude of the reciprocal of that resistance. The Notch, Anti-Resonance and Resonance Frequencies and the admittance magnitudes |Y| at these frequencies quantify the magnitude and frequency of the notch and other extrema produced by resonances and antiresonances in the admittance of the air-spaces in the different measurement states. The Compliances, Resistances and Acoustic Masses computed from the calculations of Y_TOC and Y_ASBH describe the frequency dependence of those calculated admittances.

3.0 RESULTS

3.1 Broadband measurements of middle-ear admittance in the three base conditions: The effects of manipulating the middle-ear air spaces and the tympanic membrane

3.1.1 The intact condition, $Y_{TM}^I$

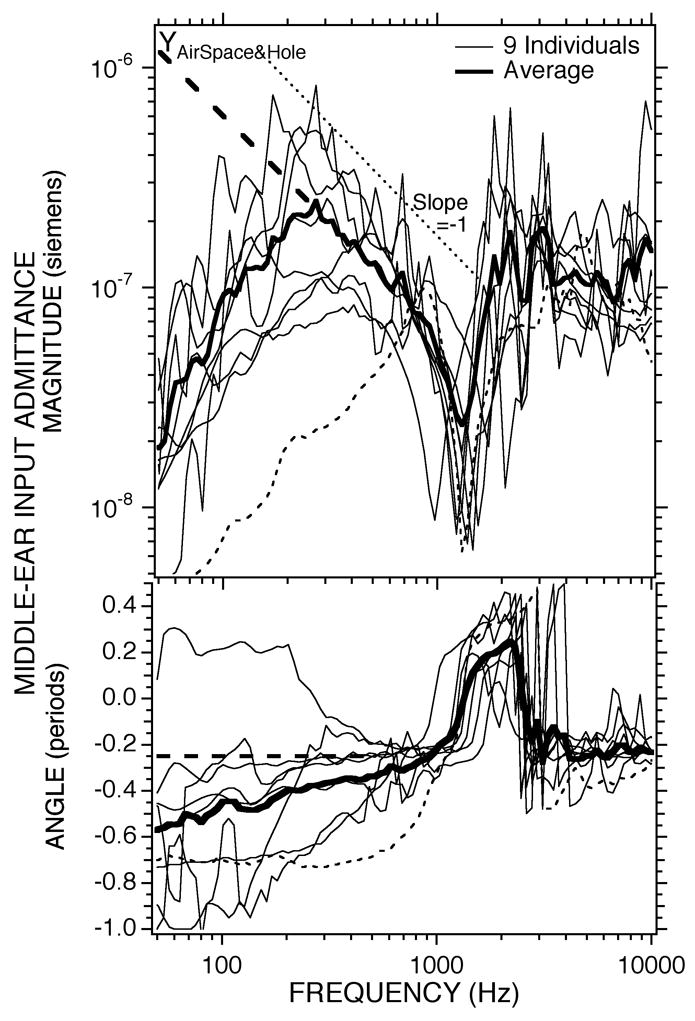
The middle-ear input admittance in the intact chinchilla ear $Y_{TM}^I$ varied little among the nine individuals in which it was measured. (The nine ears are collected in Figure 3A; the averages of the characteristic features of the data are also summarized in Table 1.) With a sealed and vented middle ear, the admittance is dominated by compliance at frequencies less than 600 Hz (Figure 3A), in that the magnitude of the admittance grows proportionally with frequency (i.e. parallel to the thin dashed line illustrating a log-log slope of 1) and the phase angle is between 0.125 and 0.25 periods. The mean low-frequency compliance in the 9 ears is that of an equivalent air volume² of 1. 6 cc with a standard deviation of ± 0.32 cc (Table 1). At some middle frequency (1160 ± 240 Hz) the admittance angle goes through 0 and magnitude flattens out at a value of (7.65 ± 1.84) ×10⁻⁸ S. Near 2600 Hz there is a small notch in the admittance magnitude (at the arrows in Figure 3A) associated with a zero crossing in the angle just before a small angle maximum. The mean and standard deviation of the frequency of this magnitude notch and angle change in the 9 ears is 2630 ± 197 Hz (Table 1).

Figure 3.

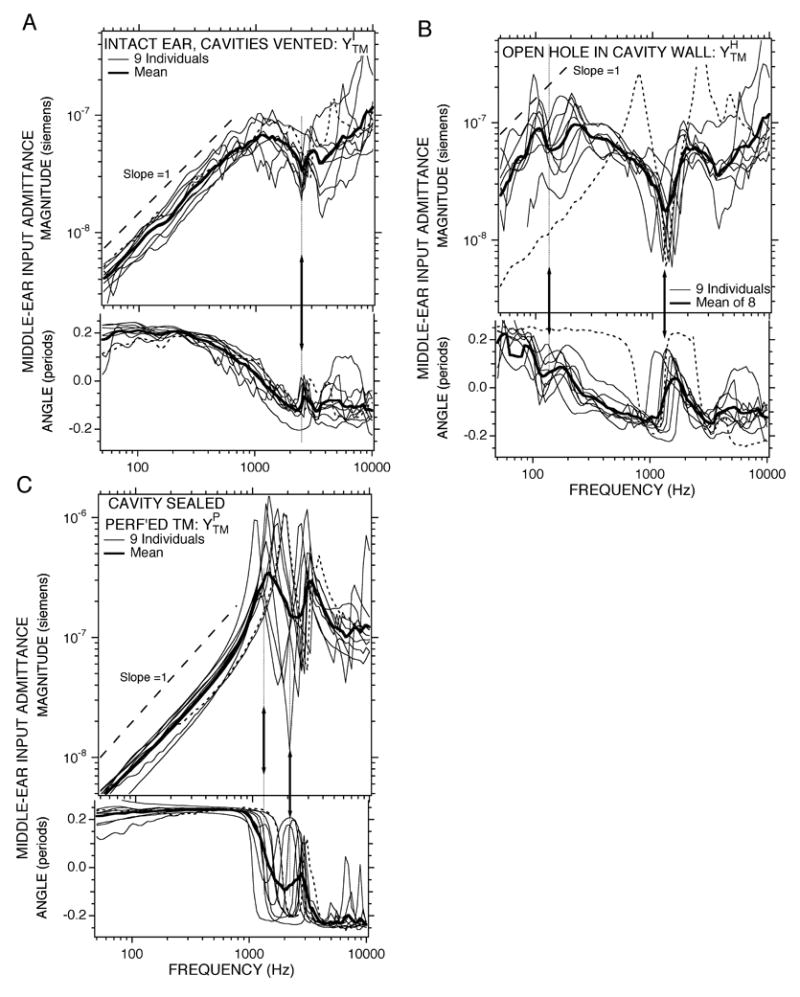
Middle ear input admittance Y_TM measured with broad-band stimuli under three conditions in 9 ears: (A) $Y_{TM}^I$: intact the middle-ear cavities are sealed and vented, (B) $Y_{TM}^H$: open hole in the cavity wall, (C) $Y_{TM}^P$: perforated TM with the cavity sealed. The thin lines are from individual ears, while the thick dark line shows the mean of the individuals. The thin dotted data lines are from Ear #102. Each panel contains a plot of magnitude (upper plot) and phase angle (lower plot) vs. frequency. The magnitude is scaled in acoustic siemens, where 1 S = 1 m³-s⁻¹-Pa⁻¹. The dashed lines and arrows in each panel are described in the text.

3.1.2 The open bullar-hole condition, $Y_{TM}^H$

Opening a 3–4 mm diameter hole in the bullar wall of the same nine ears led to a factor of 4–5 increase in the admittance magnitude at low-frequencies in eight of the nine ears (Figure 3B). The admittance with the hole open $Y_{TM}^H$ is only approximately compliant at frequencies below 100 Hz (the slope is not constant and the angle usually only approaches 0.25 periods at the lowest frequencies). Our best estimate of the mean equivalent volume of this increased compliance is 8.6 ± 4.5 cc (Table 1). Between 100 and 300 Hz the admittance varies with frequency, with six of the nine ears showing a local minimum in magnitude and phase near 150 Hz (at the lower-frequency arrow in Figure 3B). At 328 ± 14 Hz the admittance angle goes through zero and the magnitude is (1.23 ± 0.56) × 10⁻⁷ S. At 1370 ± 215 Hz there is a deep minimum in the admittance magnitude associated with a zero crossing in admittance angle just before a prominent angle peak (at the higher-frequency arrow in Figure 3B). The mean value of this magnitude minima is (8.32 ± 3.57) × 10⁻⁹ S.

All of the data curves presented in Figure 3B were measured within 30 minutes of initiating measurements. As the experiment proceeded, e.g. measurements made with varied levels and frequency ranges, we sometimes saw changes in the frequency dependence where the later data curves had a decreased low-frequency admittance (an increased stiffness) and looked more like the single outlier (Ear #102, the dashed line) in Figure 3B. (This outlier is also illustrated in Figure 3A, where its admittance magnitude tends to be just a little larger than the mean.) These changes could sometimes, but not usually, be reversed by moistening the middle ear and the tympanic membrane with normal saline. We did not see such time dependences in a later series of animals, discussed in section 3.5, where we sectioned the tensor-tympani muscle and denervated the stapedius muscle.

3.1.3 The perforated TM condition, $Y_{TM}^P$

Resealing the bullar hole and making a 4 mm diameter or larger perforation in the TM leads to a decrease in the admittance relative to the open bullar-hole condition at low frequencies, f < 800 Hz, consistent with a decrease in the compliance over the open bullar-hole state (Figure 3C). The average value of the new compliance is 2.00 ± 0.40 cc, which is somewhat larger than the 1.6 ± 0.32 cc compliance in the intact condition (Table 1). In the 800 to 5000 Hz range, $Y_{TM}^P$ has a complex frequency dependence with a pair of magnitude maxima bracketing a single minimum. Each of these three magnitude extrema is associated with a zero crossing in the angle. The extrema occur at varied frequencies in the different ears with the result that much of the frequency dependence is smoothed out in the mean of the measurements (illustrated by the thick line in Figure 3C); because of such smoothing while meaning, the frequencies, magnitudes of the extrema and angles of the extrema in the mean curve vary significantly from the mean of these features in the individual curves noted in Table 1. For example, Table 1 notes the frequency of the lower-frequency maxima is 1470 ± 300 Hz (the lower-frequency arrow in Figure 3C), while the frequency of the minima is 2450 ± 480 Hz (the higher-frequency arrow in Figure 3C). The average magnitude at the first maxima is (1.10 ± 0.44) ×10⁻⁶ S, and the average magnitude of the minima is (4.01 ± 1.48) ×10⁻⁸ S.

3.1.4 Relationships between middle-ear air space structure and the admittance in the three base conditions

The effects of opening the middle-ear air spaces and perforating the TM with the air spaces sealed in two individual ears are illustrated in Figure 4. All of the trends visible in the grouped data sets of Figure 3 are apparent in Figure 4, while the presentation of the individual data allows easy comparisons of the frequencies and magnitudes of the different extrema seen in the different conditions. In this section we address how the two manipulations of the air spaces (opening the hole, and sealing the spaces and perforating the TM) help isolate the effects of the air spaces on the admittance.

Figure 4.

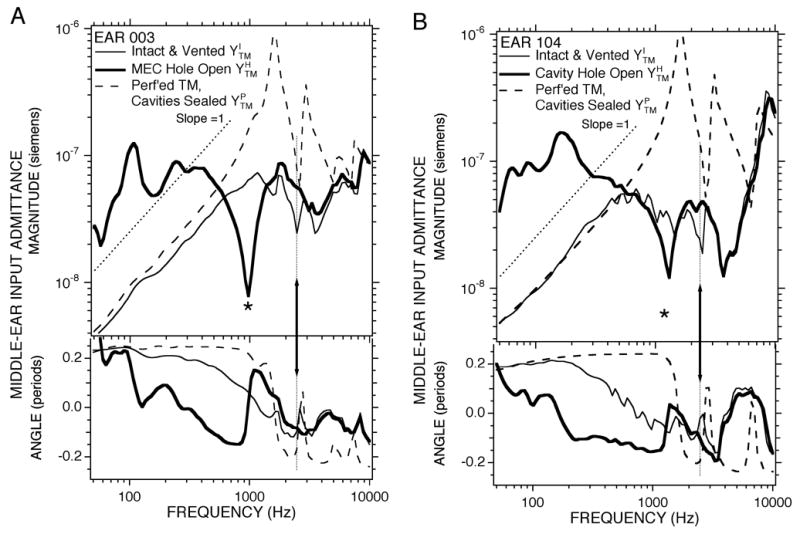
Middle ear input admittance Y_TM measured with broad-band stimuli under three conditions in 2 ears. Each panel shows measurements in a single ear. (A) Ear 004. (B) Ear 104. The thinner solid lines shows results from the $Y_{TM}^I$ intact condition. The thicker solid line shows results from the $Y_{TM}^H$ open cavity hole condition. The dashed lines shows results from the $Y_{TM}^P$ perforated TM condition. The thin dotted lines describe log-log slopes of 1. The arrows point to features associated with a middle-ear cavity antiresonance. The *s mark features associated with a cavity-hole antiresonance.

Voss et al. (2001) demonstrated that the middle-ear input admittance measured in human temporal bones with TM perforation diameters larger than 4 mm approximated the admittance of the middle-ear air spaces, at least at frequencies less than 4000 Hz. Our admittance measurements in the perforated TM state $Y_{TM}^P$ can therefore be used to estimate the admittance of the sealed middle-ear air spaces, and our measurements of compliance in the perforated TM state are estimates of the compliance of the air spaces. The similar magnitude of the compliance-like admittances measured at f < 500 Hz in the perforated and intact conditions $Y_{TM}^I$ (Figures 3A, 3C and 4) suggests that the compliance of the middle-ear air spaces is a dominant factor in the intact measurements. This dominance is supported by the large increase in low-frequency admittance when the impedance of the air spaces is “shorted-out” (Møller 1965; Guinan & Peake 1967; Dallos 1970) by the open hole in the bullar wall (Figures 3B and 4). Similar large-increases in middle-ear mobility linked to opening the chinchilla middle-ear air spaces have been noted before (Dallos 1970; Drescher & Eldredge 1974; Ruggero et al. 1990).

There are other features of the data in the intact and open-holed conditions that may be attributed to the condition of the middle-ear air spaces. Table 1 and Figures 3A, 3C and 4 point out that the mid-frequency notch in the intact admittance magnitude (Fig. 3A) occurs at a frequency that is similar to the deeper mid-frequency minimum in the admittance measured in the perforated condition (Fig. 3C & 4). This similarity suggests a causal relationship between the minimum in the air-space admittance and the notch in the intact state. Such air-space induced admittance minima in intact ears have been described in domestic cats and other felids (Møller 1965; Guinan and Peake 1967; Huang et al. 1997; Huang et al 2000).

The middle-ear air spaces also contribute to the admittance in the open bullar-hole condition. The magnitude minima and the angle changes near 1300 Hz that are seen in the admittance with the open bullar hole (Fig 3B- the lower arrows, and Fig 4- the asterisks) are consistent with an anti-resonance between the compliance of the air space and the acoustic and radiation mass associated with the bullar hole. Similar phenomena have been observed in other species after the creation of holes in the bullar wall (e.g. cat: Guinan & Peake 1967, Lynch 1981; and gerbil: Ravicz et al. 1992.) A more quantitative analysis of this putative hole-resonance occurs in sections 3.2.2 and 4.1.1.

3.2 Contributions of Different Middle-Ear Structures to the Measured Admittance

The admittances that we measured in our three structural conditions allow us to separate out the contributions of different structural components of the middle ear to its acousto-mechanical function.

3.2.1 Estimation of the admittance of the TM ossicles and cochlea, Y_TOC

The assumption that the admittance of the middle-ear air spaces is approximated by the admittance measured with a perforated TM $Y_{TM}^P$ allows us to investigate the effect of removing the middle-ear spaces on the intact admittance $Y_{TM}^I$. Others (Zwislocki 1962; Møller 1965; Guinan and Peake 1967; Lynch 1981; Huang et al. 1997) have suggested and tested the hypothesis that the middle-ear input admittance measured in the intact ear is the reciprocal of the “series” sum of the impedances of the middle-ear air spaces together with the impedance of the rest of the middle ear. In terms of admittances:

$$Y_{TM}^I=\frac{1}{\frac{1}{Y_{\mathit{MEair}}}+\frac{1}{Y_{\mathit{TOC}}}},$$ (Eqn. 1)

where Y_MEair is the admittance of the middle-ear air space, and Y_TOC is the admittance at the tympanic membrane produced by the TM, ossicles (and their ligaments) and the cochlea when the admittance of the middle-ear air spaces is made infinite (e.g. Huang et al. 1997). If we assume that the admittance measured with a perforated TM approximates Y_MEair, then, we can rearrange Eqn. 1 to solve for Y_TOC;

$$Y_{\mathit{TOC}}=\frac{1}{\frac{1}{Y_{TM}^I}-\frac{1}{Y_{TM}^P}}.$$ (Eqn. 2)

Estimates of Y_TOC computed for the nine ears of Figure 3 are illustrated in Figure 5. At frequencies below 500 Hz, the computed Y_TOC s have much in common with the admittances measured with an open bullar hole $Y_{TM}^H$ (Fig 3B): Both show angles that are generally consistent with compliant behavior at f < 100 Hz and the mean and a majority of the individual Y_TOC computations show a cluster of magnitude and angle maxima separated by minimum near 170 Hz (the lower-frequency arrow). Also, both the computed Y_TOC and the measured $Y_{TM}^H$ show an increased variance at the lowest frequencies; however below 200 Hz the variance in Y_TOC magnitude and angle at frequencies is larger than the variance in $Y_{TM}^H$. The increase in variance is probably introduced into the calculation of Y_TOC by the subtraction of quantities with similar magnitude and angle at frequencies less than 200 Hz, specifically, at f < 200 Hz $Y_{TM}^I\approx Y_{TM}^P$ (Figs 3 and 4).

Figure 5.

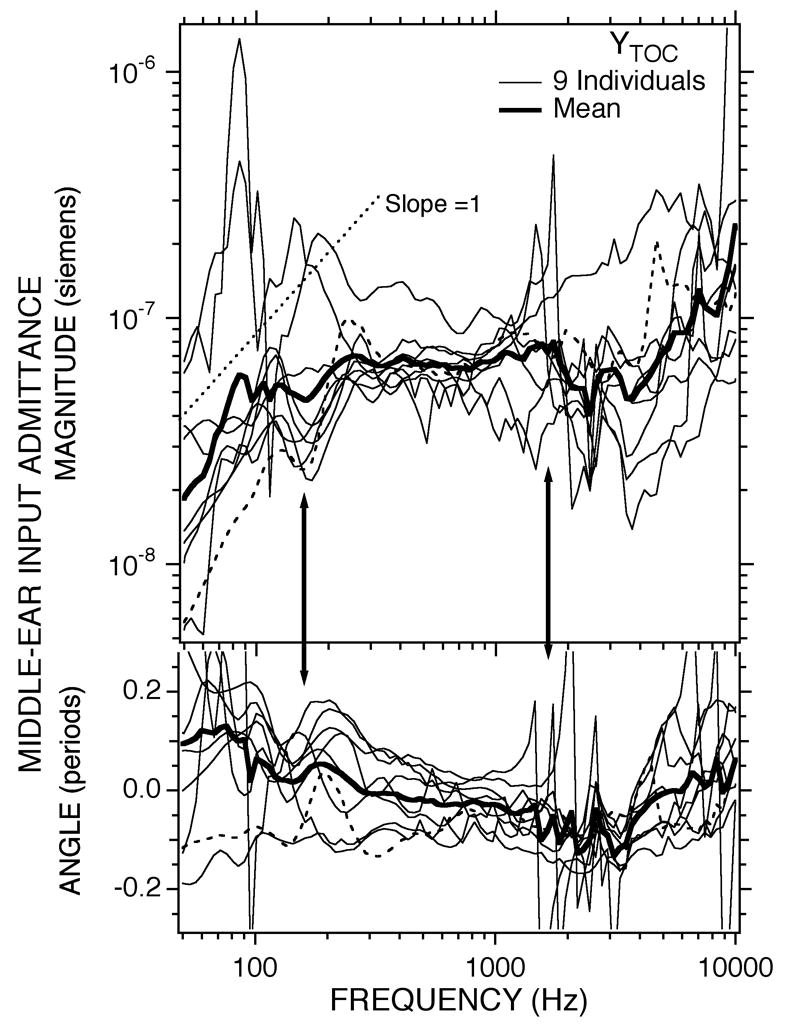
Estimates of the contribution of the TM, the ossicles (and their ligaments) and the cochlea to the middle-ear input admittance computed from the measurements with an intact middle ear and measurements with a perforated TM using Equation 2. The dashed data curve is ear 102, the ear that was an outlier in Fig 3B. The arrows point to the frequency regions of the low-frequency minimum and the region of significant variation in admittance.

In the middle frequencies 400 Hz < f < 4000 Hz there are significant differences between Y_TOC and $Y_{TM}^H$: The computed Y_TOC is less frequency-dependent with a nearly constant magnitude and an angle that is approximately zero, and the prominent notches seen in $Y_{TM}^H$ near 1200 Hz (the higher-frequency arrow) in Figure 3B and 4 are greatly reduced if not eliminated in Figure 5. There is, however, significant variation in the magnitude and angle of Y_TOC near 2000 Hz. We hypothesize that this variation results from errors in the approximation of Y_MEair by $Y_{TM}^P$ that result from small residual effects of the TM remnant in the perforated cases (Voss et al. 2001). These errors lead to errors in the denominator of Eqn. 2 at frequencies near the cavity-admittance extrema where the TM remnant effects are most prominent.

While the variance in the computed magnitude and angle of Y_TOC at low frequencies and the variance near 2000 Hz adds some uncertainty, Y_TOC and $Y_{TM}^H$ are generally similar, and the differences between the two are attributable to an air-space bullar-hole anti-resonance in the bullar-hole open case (Guinan and Peake 1967; Lynch 1981; Ravicz et al. 1992). This anti-resonance is described in the next section. The similarities between Y_TOC and $Y_{TM}^H$ together with the explanation of their differences by the air-space bullar-hole anti-resonance lead us to conclude that the computed Y_TOC are valid estimates of the contribution of the TM, ossicles and cochlea (the non-air space structures) to the middle-ear input admittance. We further conclude that the middle-ear input admittance in the chinchilla with an infinite airspace admittance (1) is compliant at f < 100 Hz with an equivalent volume of about 7 cc (Table 1); (2) is produced by an interaction of the mechanical features of multiple structures in the frequency range 100 < f < 300 leading to a cluster of maxima and a minimum in magnitude and angle; and (3) is dominated by a resistance at 300 <f< 10000 Hz. The magnitude of the resistance-dominated admittance in the 300 to 10000 Hz range is about 6×10⁻⁸ acoustic siemens (Table 1).

3.2.2 Estimation of the admittance of the air spaces and open bullar hole, Y_ASBH

We have argued that the admittance measured with an open-bullar hole includes the influence of an air-space bullar-hole anti-resonance. We can use the same series impedance model of the contribution of the middle-ear air spaces to the admittance evoked in Eqn. 1 and 2 to estimate the acoustic admittance of the air spaces with the 3–4 mm hole and see if it has characteristics of the hypothesized anti-resonance. This quantification of the admittance of the cavity hole will also enable us to understand how that hole contributes to the open-bullar-hole admittance.

The series model of middle-ear air space effects, suggests the middle-ear input admittance in the open-bullar-hole condition $Y_{TM}^H$ is the reciprocal of the sum of the impedances associated with Y_TOC and the air spaces and bullar hole admittance Y_ASBH, where:

$$Y_{TM}^H=\frac{1}{\frac{1}{Y_{\mathit{ASBH}}}+\frac{1}{Y_{\mathit{TOC}}}}\text{and}{Y}_{\mathit{ASBH}}=\frac{1}{\frac{1}{Y_{TM}^H}-\frac{1}{Y_{\mathit{TOC}}}}.$$ (Eqn. 3A&b)

Calculations of Y_ASBH from the nine ears with cavity manipulations using the measured $Y_{TM}^H$ and the calculated Y_TOC are illustrated in Figure 6. The estimates are most variable at frequencies less than 300 Hz, where the estimate of Y_ASBH is adversely affected by the small differences between the ratios in the denominator of Eqn. 2 and Eqn. 3B. Between 300 and 800 Hz Y_ASBH is roughly mass dominated; it has a magnitude that varies inversely with frequency (i.e. the magnitude vs. frequency has a log-log slope of − 1) and an angle between − 0.20 and − 0.4 periods³. This mass-like behavior is consistent with sound radiation from the open hole, which theoretically dominates the admittance at lower frequencies; the thick dashed lines in the magnitude and angle plots of Figure 6 are extrapolations of the mass-like behavior observed between 300 and 800 Hz to lower frequencies. Near 1500 Hz, the sharp magnitude minimum associated with a rapid change in angle from − 0.25 to 0.25 periods is consistent with an anti-resonance. The narrow frequency range between 1500 and 2500 Hz, where the admittance magnitude increases and the angle stays near 0.25 periods is also consistent with an anti-resonance, but the change in angle to − 0.25 periods and the nearly constant magnitude of the calculated admittance at frequencies above 3000 Hz are not. The similarity of the frequencies and the magnitudes of the admittance minima in Figure 6 and Figure 3B (see also Table 1) is consistent with the air-space hole interaction producing the minima in both $Y_{TM}^H$ and Y_ASBH. A quantitative comparison of the hole and bullar dimensions with the measured anti-resonance frequency is included in Section 4.1.1.

Figure 6.

Estimates of the acoustic admittance of the middle-ear air spaces with 4 mm or larger diameter hole in the superior bullar wall. The thick dashed lines at low frequencies are the extrapolated admittance magnitude and angle of a radiation mass through the hole. The dashed data curve is ear #102.

Comparisons of the magnitude of the measured $Y_{TM}^H$ (Figure 3B) and the estimates of Y_TOC (Figure 5) and Y_ASBH (Figure 6) in the context of Eqn. 3A suggests: (a) The air-space bullar-hole admittance has little effect on the open-hole middle ear input admittance at the lowest frequencies, f < 300 Hz, where the magnitude of Y_ASBH is greater than the magnitude of Y_TOC. This lack of effect results because the admittance of the acoustic mass of the hole is relatively large, and the air space admittance is effectively “shorted out”, such that $Y_{\mathit{TOC}}\approx Y_{TM}^H$. (b) The influence of the air-space bullar-hole admittance decreases the magnitude and angle of $Y_{TM}^H$ relative to Y_TOC at somewhat higher frequencies 300 < f < 1000 Hz where the magnitude of Y_ASBH is smaller than the magnitude of Y_TOC, and the admittance of the acoustic mass of the bullar hole begins to limit TM motion, (c) The air-space bullar-hole admittance introduces the admittance-magnitude minimum and phase-angle change in $Y_{TM}^H$ at the anti-resonance between the mass of the hole and the compliance of the air spaces where $Y_{TM}^H\approx Y_{\mathit{ASBH}}$.

3.3 The contribution of the inner ear to the middle-ear input admittance: Linear effects

In this section, we look at the results of manipulations that attempt to identify the contribution of the inner ear to the measured admittance. The manipulations we performed were to remove the cochlear load on the middle ear by (1) draining the cochlea (opening the superior semicircular canal and using a suction to remove the perilymph within the inner ear) or (2) interrupting the incudo-stapedial joint (ISJ) and pushing the stapes into the oval window. One of each of these manipulations was performed in two of the nine ears used to investigate middle-ear air-space effects with cut tensor tympani tendons (Figs. 7A&C). Both manipulations were performed in two additional ears that had both the tensor tendon and facial nerve sectioned (Figs. 7B&D).

Figure 7.

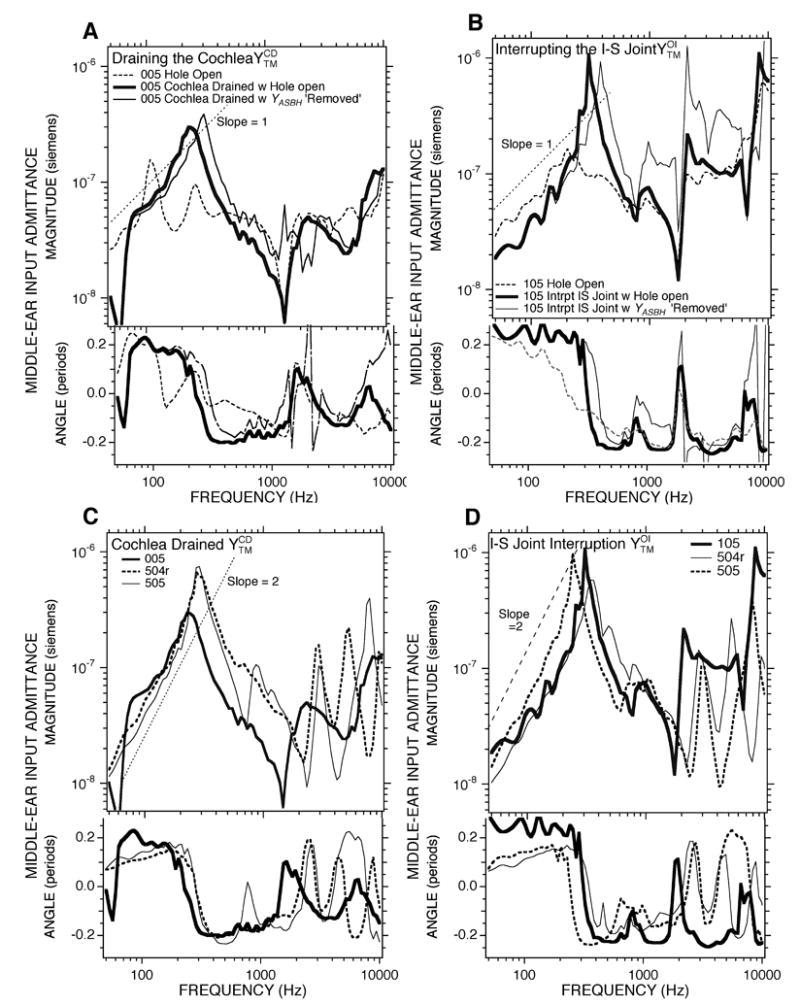
Effect of alterations in the cochlear load. A). Comparison of middle-ear input admittance before and after draining the cochlea, $Y_{TM}^{CD}$, measured with the bullar-hole open in Chinchilla 005. A version of $Y_{TM}^{CD}$ corrected for Y_ASBH (the air-space and bulla-hole admittance) is also shown. B). A similar comparisons of the admittance before and after interrupting the incudo-stapedial joint, $Y_{TM}^{OI}$, in Chinchilla 105. A version of $Y_{TM}^{OI}$ corrected for Y_ASBH is also shown. C). The admittance measured with an open-bullar hole and cochlea drained of perilymph $Y_{TM}^{CD}$ in three ears. D). The admittance measured with an open-bullar hole and the IS-joint interrupted $Y_{TM}^{OI}$ in three ears.

Panels A and B of Figure 7 compare the admittance after either cochlear draining $Y_{TM}^{CD}$ or ISJ interruption $Y_{TM}^{OI}$ (the thick solid data curves) with the admittance in the open bullar-hole state $Y_{TM}^H$ (the dashed data curve) in two ears. The most prominent change caused by these manipulations is the introduction of a resonance in the admittance near 250 Hz. The resonance is characterized by a relatively sharp admittance maximum, with a compliance-like admittance angle (near 0.25 periods) at frequencies below the resonance and a mass-like admittance angle (near − 0.25 periods) at frequencies above the resonance. The relatively sharp maximum and the rapid half-period change in phase angle is consistent with low resistance. The results illustrated in Figures 7A and 7B suggest that cochlear draining and ISJ interruption have little effect on the admittance in the open-bullar hole state at frequencies above 1000 Hz.

Figure 7A and B also include estimates of the admittance in the cochlear drained and ISJ interrupted states in which the admittance of the air-space and bullar hole have been removed (the thin solid data curves) by subtracting the appropriate individual estimate (Figure 6) of the impedance of the air-space-and bullar hole 1/Y_ASBH from the measured impedance $1/Y_{TM}^{CD}$ or $1/Y_{TM}^{OI}$ (analogous to the computation of Y_TOC in Equation 2). The differences in the resonant frequency near 250 Hz between the bullar-hole open measurements and Y_ASBH removed computations in 7A and B indicate that the acoustic mass of the bullar hole acts to decrease the resonant frequency in the bullar-hole open measurements. The increased admittance magnitude in the 300 to 2000 Hz range when Y_ASBH is removed is consistent with the removal of the radiation mass of the bullar hole.

The lower two panels (Figures 7C and 7D) illustrate the results of the two manipulations in three ears. All of these results illustrate the presence of a fairly sharp (low-resistance) resonance in the admittance near 250 Hz after cochlear draining or ISJ interruption. At frequencies above 500 Hz, the six admittance measurements in the two conditions all show a number of admittance magnitude minima and maxima accompanied by rapid shifts in phase angles. At least one of the prominent magnitude minimum (between 1000 and 3000 Hz) is the open bullar-hole anti-resonance; however, the other minima and maxima cannot be explained by the same mechanism. (As discussed later, the somewhat higher frequency of the airspace bullar-hole antiresonance in ears #504r and #505 can be attributed to a larger bullar hole in these measurements.) Cochlear draining and ISJ interruption have been demonstrated to produce at least one magnitude peak and rapid angle change in the admittance of cats (Møller 1965; Lynch 1981; Allen 1986; Puria and Allen 1998). The repeated admittance extrema observed in ears #504r and #505 have also been observed in the middle-ear admittance measured in cats after similar inner-ear and ossicular manipulations by some (Puria and Allen 1998), but not by others (Lynch 1981).

3.4 The contribution of the inner ear to the middle-ear input admittance: Nonlinear effects

Draining the cochlea and interrupting the ISJ affected another feature of the middle-ear admittance in the open bullar-hole state that we have yet to discuss, a stimulus-level dependence in our measurements of $Y_{TM}^H$ at frequencies less than 400 Hz. An example case (chinchilla #004) is illustrated in Figure 8. Variations in the sound pressure of the broad-band chirp from 69–94 dB SPL resulted in repeatable changes in the measured admittance at frequencies less than 400 Hz. Both the admittance magnitude and the angle generally decreased as stimulus level increased. However, some of the data at the lowest frequencies and lowest levels in Figure 8 are contaminated by noise, in part because of the small amount of low-frequency stimulus energy present in the broad-band chirp. To correct this problem, we also looked at the admittance measured in response to our low-pass chirps as a function of stimulus level.

Figure 8.

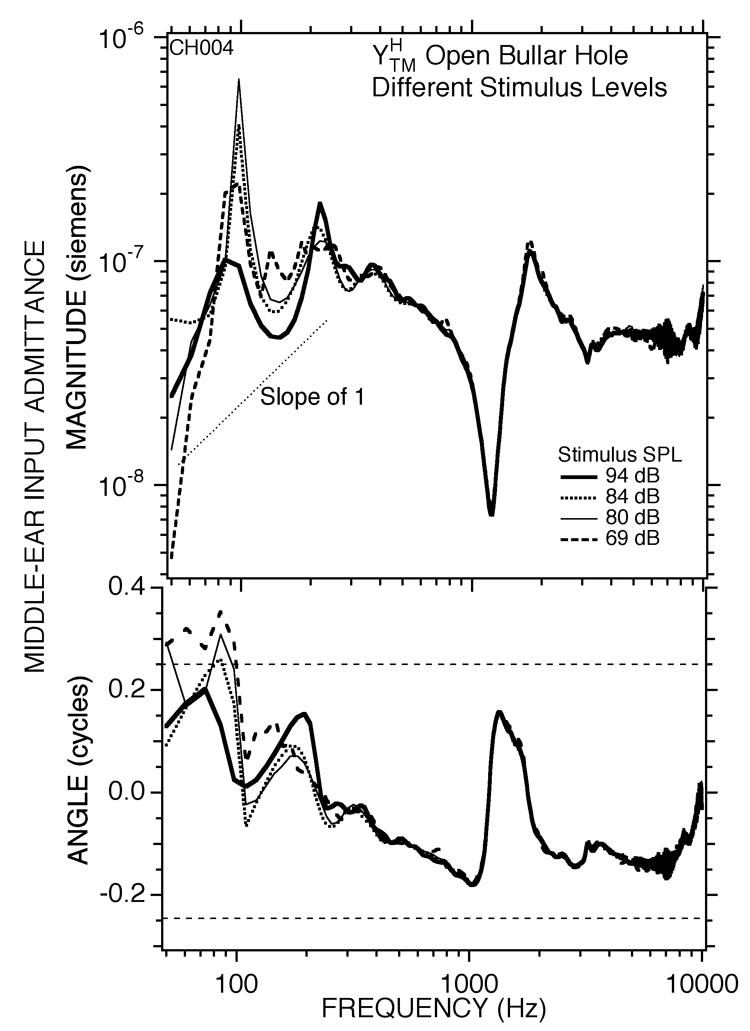
Measurements of middle ear input admittance measured in one ear (#004) using broad-band chirps. The hole in the bullar wall was opened. The rms level of the stimulus varied from 69 to 94 dB SPL.

Figure 9A shows low-pass chirp data for conditions analogous to Figure 8 measured in the same animal (#004). The concentration of stimulus energy in the low frequencies allowed a wider range of stimulus levels, and Figure 9a shows a regular decrease in admittance magnitude and angle in the 80 to 200 Hz range that occurred as the stimulus level increased from 70 to 105 dB SPL. In order to investigate the source of the nonlinear contribution to the admittance we performed several manipulations of the ear and the animal. Figure 9B shows that curarizing the animal to the point that it required artificial respiration had little effect on the frequency dependence and magnitude of the level dependence. The lack of effect of curare suggests that the middle-ear muscles are not the source of the low-frequency level dependence. On the other hand, the level dependence was reduced greatly after the animal was euthanized by anesthetic overdose (Figure 9C). Other manipulations were performed in a second animal. Figure 10A shows a level dependent admittance in the open bullar-hole state in chinchilla #005 that is comparable in frequency dependence and magnitude to that observed in #004 (Figure 9A). The level dependence persisted after sectioning the tendon of the tensor tympani (Figure 10B), but was greatly reduced after opening the superior canal and draining the cochlear lymphs (Figure 10C). The draining manipulation also greatly affected the frequency dependence of the admittance, producing a resonant peak near 240 Hz, similar to the results of Figs. 7A&C. These results are consistent with the view that both the level dependence and the multiple admittance extrema observed in the 80 to 300 Hz range in the open-hole condition (Fig. 3B) have their source in the inner ear. The level dependence in the admittance was best observed in the open bullar-hole condition. While the level dependence was also observable in the intact condition, it was greatly reduced in magnitude. This reduction in the level dependence in the intact cavity state is consistent with the middle-ear air space dominating the low-frequency admittance in the intact condition, and thereby obscuring the influence of the cochlear nonlinearity on the admittance.

Figure 9.

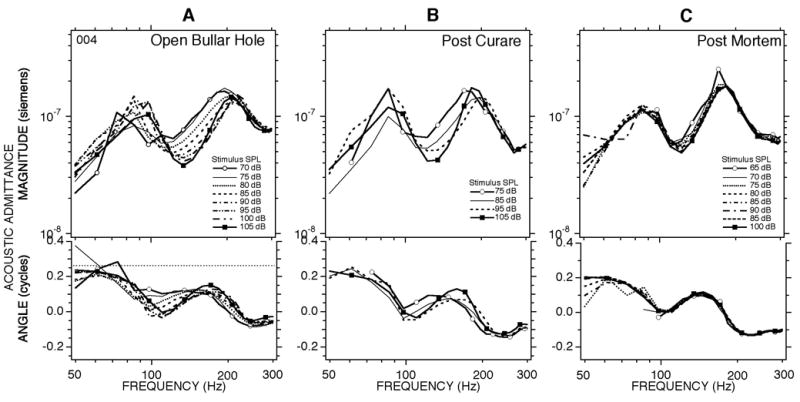
Measurements of middle-ear admittance with the bullar hole open made with low-pass chirps in ear #004. Measurements were made at multiple levels in three different ear conditions: (A) a pre-treatment control; (B) after the animal was curarized to the point that artificial respiration was necessary; (C) measurements made 20–30 minutes post-mortem.

Figure 10.

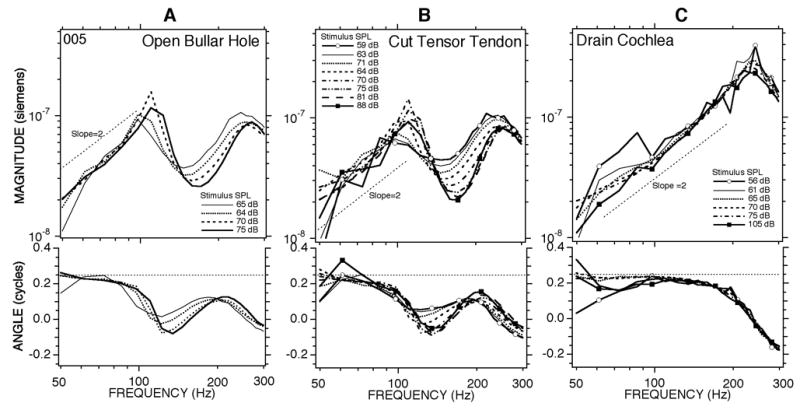
Measurements of middle-ear admittance with the bullar hole open made with the low-pass chirps in ear #005. Measurements were made at multiple levels in three different ear conditions: (A) a pre-treatment control; (B) after the tendon of the tensor tympani muscle was cut at the malleus; (C) after opening the posterior semicircular canal and draining the cochlear lymphs with a suction.

3.5 Contributions of the middle-ear muscles to the measured admittance

In our earliest measurements in deeply anesthetized chinchillas with open bullar hole and intact ossicular attachments to the middle-ear muscles, we occasionally saw periodic fluctuations of the microphone response that we found to be associated with spontaneous, rhythmic contractions of the tensor tympani. On one occasion we also saw rhythmic contractions of the tendon of the stapedius muscle. While the changes in the measured sound pressure (and the admittance computed from the sound measurements) produced by the rhythmically-contracting middle-ear muscles were fairly easy to detect, we would also occasionally see static changes in the middle-ear admittance. The changes were usually related to a decreased admittance at frequencies below 1000 Hz (e.g. the dotted curve in Figure 3B). In most cases these decreases in admittance persisted.

In a few cases where the tensor-tendon and facial nerve were intact, and the chinchilla was more lightly (though still deeply) anesthetized we saw occasional broad-band decreases in admittance that seemed to be correlated with high-level sound-stimuli. The data in Figure 11 are examples of such a temporal correlation of high-level stimuli and decreased admittance magnitudes. The first measurement in the series was an admittance comparable to most of the open-bullar measurements in Figure 3B made with a 100 dB SPL broadband chirp. The second measurement was made a few minutes later with a stimulus sound pressure of 105 dB SPL; this admittance is lower in magnitude at low frequencies and shows the low-frequency magnitude slope and angle of a compliance of about 1 cc in equivalent volume. Note the similarity of the stiffer low-frequency admittance and the sharp maximum near 800 Hz of this measurement to the outlier in Figure 3B. The third measurement made two minutes later with a stimulus level of 95 dB SPL was an admittance that was much like the initial measurement.

Figure 11.

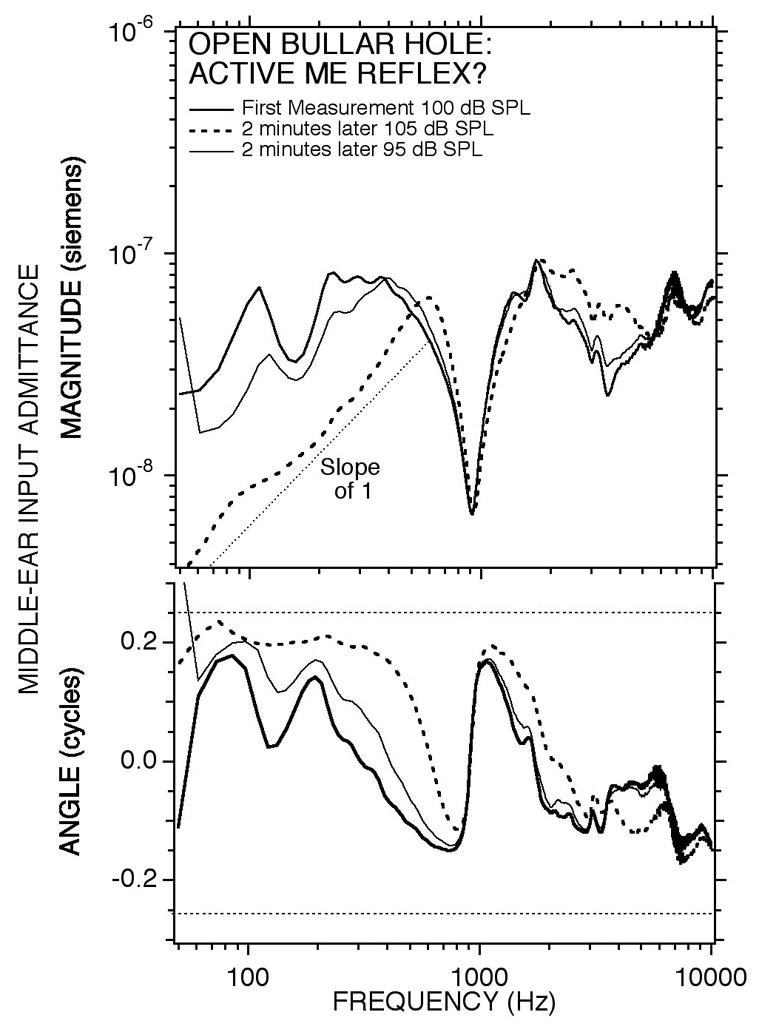
Changes in the admittance measured with the bullar-hole open with time and stimulus level. Measurements of middle-ear input admittance made in chinchilla #003 using high-level broad-band chirps. The first measurement with a 100 dB SPL chirp produced an admittance with low stiffness. The second measurement (with a 105 dB SPL chirp) produced a much higher stiffness (lower admittance) in the low frequencies. A few minutes later, a third measurement (with a 95 dB SPL chirp) produced an admittance much like the first.

Part way through this experimental series, we changed our surgical protocol in order to eliminate the possibility of middle-ear muscle contraction. The first change, which occurred after the first 4 animals in Figure 3, was to routinely section the tendon of the tensor tympani at the manubrium of the malleus. The second change, adapted after the initial nine-measurement set of Figure 3, was to section the tympanic branch of the facial nerve between its genu and the stapedius muscle. This procedure denervated the stapedius muscle but left it and its tendon intact. (This procedure was adapted because we were unable to reliably section the stapedial tendon without damaging the incudo-stapedial joint or the annular ligament.) After making both changes to the surgical protocol we saw no further evidence of spontaneous, sound-induced or long-term static decreases in admittance. Figure 12 compares the mean admittance measured in the nine ears of our initial measurement set with the bullar hole open (Figure 3B), with the mean and 95% confidence interval of a similar-sized sample with interrupted tensor tendon and denervated stapedius muscle. Below 300 Hz and above 3000 Hz the two data sets are quite similar.

Figure 12.

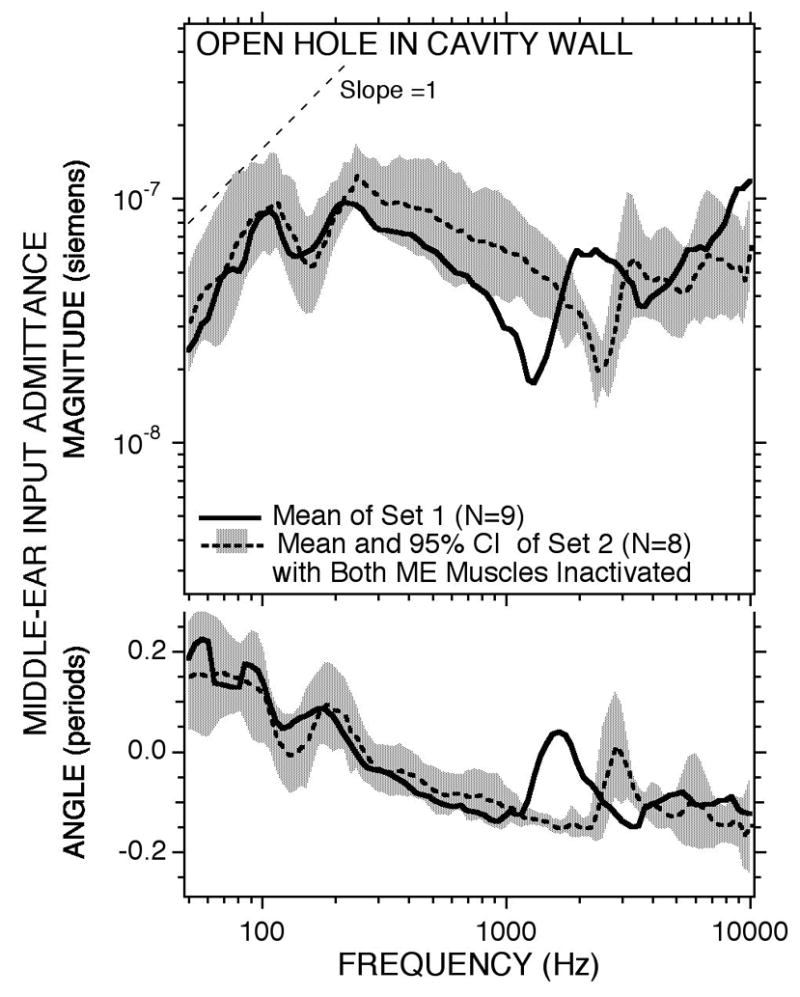
The means of two sets of measurements of middle-ear input admittance in the open bullar-hole condition. Set 1 includes the nine ears of Figure 3B in which five ears had the tendon of the tensor tympani muscle cut and no modification to the stapedius muscle. No manipulation of the muscles was performed in the other four ears of set 1. The tensor tendon was cut and the stapedius was denervated in all of the eight ears of set 2. The shading shows the 95% confidence interval around the set 2 mean. In order to allow transection of the facial nerve, the diameter of the superior bullar hole in set 2 was twice as large as that in set 1 and a second hole was opened for cochlear potential measurements (Songer & Rosowski 2006). This difference in hole size accounts for the difference in the frequency of the air-space and hole anti-resonance.

At frequencies between 300 and 3000 Hz the mean magnitude of the admittance measured in set 1 is generally lower and set 1 also displays a bullar-hole air-space anti-resonance centered at a lower frequency (1250 Hz as opposed to 2500 Hz in set 2). The higher admittance magnitude and the higher frequency of anti-resonance in set 2 are directly attributable to the smaller acoustic mass of the larger hole in the bullar wall (a diameter of 4 to 6 mm) that was needed to section the facial nerve and perform other manipulations of the superior semicircular canal as well as the presence of a smaller posterior bullar hole in these animals (Songer & Rosowski 2005). The acoustic mass of the bullar hole is inversely proportional to the area of the hole, and the frequency of the anti-resonance is proportional to the inverse square root of the acoustic mass of the hole. While the differences in bullar-hole configurations used in the two data sets prevents an exact match between the open bullar-hole admittances, the differences that are observed are consistent with the difference in bullar-hole dimensions. These minor procedural differences have little effect at the lowest frequencies (Figure 12) where we have observed the largest middle-ear muscle induced changes in admittance magnitude (Figure 11), and we therefore conclude that data set 1 (the nine ears in Figure 3) is little affected by middle-ear muscle contraction.

4. Discussion

4.1 The contribution of different middle-ear structures to the input admittance at the tympanic membrane

4.1.1 The middle-ear air spaces

The measurements we present of the middle-ear input admittance with large (greater than 4 mm diameter) perforations of the TM and sealed bullar walls $Y_{TM}^P$ are estimates of the admittance of the middle-ear air spaces (e.g. Voss et al. 2001). These admittances are compliance dominated at frequencies less than 1000 Hz with an average equivalent volume of 2 cc (Table 1). This volume falls well within the range of volume-filling estimates of chinchilla middle-ear air volume including: 1.5 cc (Vrettakos et al. 1988), 2.2 cc (Drescher and Eldredge 1974) and 2.8 cc (Teas and Nielsen 1975). At frequencies above 1000 Hz, the admittance in the perforated condition and, by inference, the admittance of the air spaces show a series of magnitude maxima and minima that are accompanied by rapid changes in phase angle. These extrema are consistent with resonances and anti-resonances produced by the separation of the chinchilla middle-ear air spaces into different subspaces by incomplete bony septa (Browning and Granich 1978). Such a structured air-space admittance has been observed in other species with similar segmentation of the middle-ear air space, e.g. domestic cats and other felids with two subspaces separated by an incomplete bony septum (Møller 1965; Guinan and Peake 1967; Peake et al. 1992; Huang et al. 1997) and humans with the separation of the mastoid air spaces from the tympanic air spaces by the narrow aditus ad antrum (Onchi, 1961; Zwislocki 1962; Stepp and Voss 2005).

Our measurements suggest that the air-space admittance has a significant effect on the admittance measured in the intact condition with sealed but vented bullar-walls $Y_{TM}^I$. Firstly, the low-frequency compliance in the intact condition is similar (but somewhat smaller) in magnitude to that measured in the perforated condition (1.6 cc vs. 2.0 cc on average; Table 1). Secondly the compliance of the middle ear is greatly increased (to ≈ 8.6 cc; Table 1) when the air-space admittance is “shorted” at low frequencies by opening the bullar hole.

Another indication of the contribution of the middle-ear air space admittance to the intact admittance is the sharp but shallow notch in $Y_{TM}^I$ magnitude near 2600 Hz (Figure 3A and 4). This frequency is similar to the mean of the frequency of the first anti-resonance in the perforated state $Y_{TM}^P$ (2450 ± 480 Hz: as defined by the mid-frequency admittance minimum and associated zero crossing ). Indeed, a paired Students t test shows the probability that the two sets of frequencies come from the same population is better than 10%. Also, the magnitude at the notch minimum in $Y_{TM}^I$ ([2.67 ± 1.2]×10⁻⁸ S) is 65% of the admittance magnitude at the anti-resonance in $Y_{TM}^P$ ([4.01 ± 1.48] × 10⁻⁸ S, Table 1). This relative difference in magnitudes is consistent with the anti-resonance in the segmented air-space playing a significant role at the notch seen in the admittance of the intact ear. It should be noted that while the cavity anti-resonance can be associated with a notch in the chinchilla intact admittance, the notch is much less prominent than the anti-resonance associated notch observed in cat (e.g. Guinan and Peake 1967).

The middle-ear air spaces also contribute to the admittance in the open bullar-hole state $Y_{TM}^H$. While the acoustic mass of the hole (Fig. 6) acts to reduce the magnitude and phase of $Y_{TM}^H$ relative to Y_TOC at frequencies between 300 and 1000 Hz, the most obvious effect of the hole and air space is the introduction of the hole-air-space anti-resonance near 1300 Hz in the $Y_{TM}^H$ of the first data set (Figures 3B and 12) and 2500 Hz in the second data set (Figure 12). The bullar-hole air-space anti-resonance is also the prominent feature in our estimates of the admittance of the open air spaces Y_ASBH (Figure 6).

The frequency of this anti-resonance in the different ears is roughly consistent with the dimensions of the bullar holes and the air space volume. A computation (Appendix 1) based on a Helmholtz resonator equation with the compliance of the middle-ear air (C_MEair) equivalent to 2 cc and the 1370 anti-resonance frequency defined from our $Y_{TM}^H$ data that results in an estimated bullar-hole radius of 2 mm, a little smaller than the 3–4 mm diameter of the hole we used. A similar calculation based on the average frequency of the anti-resonance in the second set of experiments (2500 Hz from Figure 12) yields a hole diameter of 5.2 mm, which is consistent with the larger superior bullar hole and the additional posterior bullar hole used in these animals (Songer & Rosowski 2005).

A complication in the above analysis is our assumption that the admittance of the middle-ear air spaces can be described in terms of the compliance of the total middle-ear air volume. This simplification is inconsistent with our measurements of middle-ear air space admittance, which demonstrate that air space admittance is complicated (with maxima and minima in magnitude and phase) in the 1000 to 4000 Hz range. These extrema reflect the separation of the chinchilla middle-ear air volume into multiple compartments joined together by narrow passages (Møller 1965; Browning and Granich 1978; Huang et al. 1997). This compartmentalization could reduce the effective compliance of the middle-ear air above 1000 Hz, while the effects of narrow connecting passages between the tympanic cavity (the air space immediately behind the TM) and the bullar hole could add acoustic mass.

4.1.2 The inner ear

Since the middle-ear air-space dominates the admittance measured in the intact middle ear (at least at frequencies below 800 Hz), one needs to reduce the influence of the air space influence – e.g. by opening the bullar hole (our measured $Y_{TM}^H$ in Figure 3B, 4 and 12), or calculating the middle-ear’s admittance when the air-space’s admittance is effectively infinite at all frequencies via Eqn. 2 (Y_TOC, Figure 5) – in order to see the contributions of other middle-ear structures and the inner ear to the middle-ear input admittance in that frequency range. The admittance revealed by computationally removing the cavity effects (Y_TOC) is of relatively high magnitude, only approximately compliant at the lowest frequencies (f < 100 Hz), complicated in frequency dependence between 100 and 300 Hz (Figure 3B and 5) where there are generally two maxima and a minimum in magnitude and angle, and dominated by resistance at frequencies between 300 and 10000 Hz (Figure 5). Also, the magnitude and angle of the admittance in the open-hole $Y_{TM}^H$ or infinite air-space state Y_TOC clearly depends on stimulus level in the 100–300 Hz range (Figures 8–10).

We assess the contributions of the inner ear to these features by comparing the admittance measured in the open-hole state with an intact inner ear, to measurements made in the open-hole state but with the cochlea drained or IS-joint interrupted. Figures 7A & C and Figure 10C together demonstrate that the largest effects of draining the cochlear fluids on the open-hole admittance are (1) to increase the admittance below 500 Hz by revealing a resonance centered near 250 Hz, and (2) to suppress the level-dependence of the admittance in that same frequency range. The first effect can be explained by the removal of a controlling low-admittance in series with the newly exposed resonant system. The second suggests that the inner ear is the source of the level dependence.

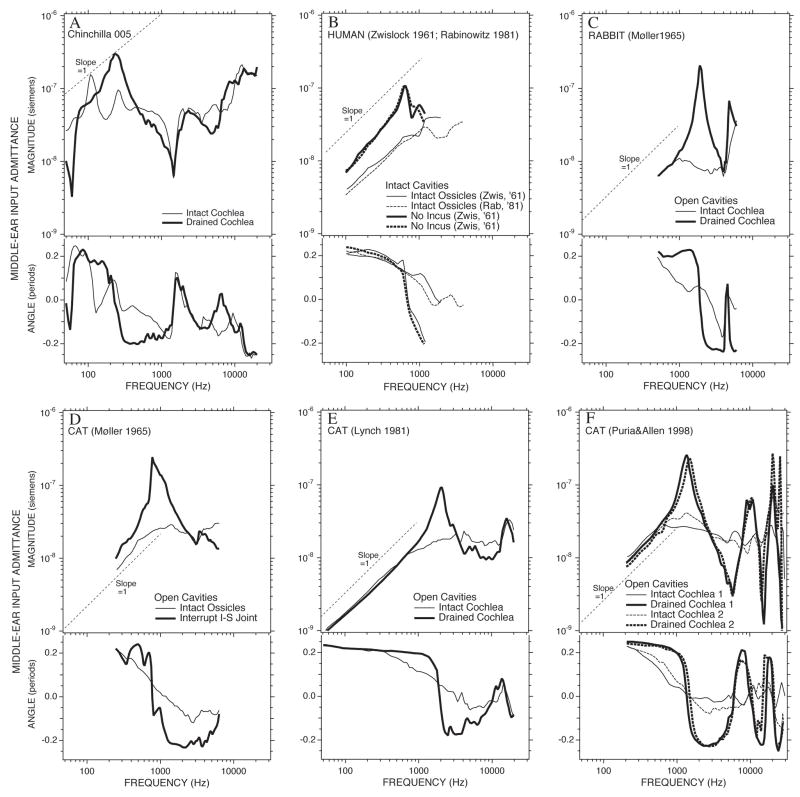
The appearance of a sharply resonant middle-ear input admittance after removal of the influence of the cochlea has been observed in other animals (Figure 13), including: rabbit (Møller 1965), cat (Møller 1965; Lynch 1981; Allen 1986; Puria and Allen 1998) and humans (Zwislocki 1962). These earlier results have generally been explained by the removal of cochlear damping from the middle ear, thereby exposing an underlying resonant system. While a similar explanation fits the resonant post-cochlear draining measurements in this study (Figure 7), the alterations produced by draining the cochlea while the cavity hole is open (Figure 7A) cannot be explained by the removal of a simple cochlear resistance. In particular, the presence of a simple resistance cannot account for the multiple maxima and the minima in admittance magnitude (and the accompanying phase changes) seen between 100 and 300 Hz in the open bullar-hole admittance (Fig 13A, as well as Figures 3B) or Y_TOC (Figure 5) when the cochlea is coupled to the middle ear. A more complicated cochlear model, which includes an acoustic mass and resistance to model the helicotrema (e.g. Dallos 1970; Lynch et al. 1982), can introduce a local maximum and a zero crossing in the middle-ear admittance near 200 Hz but is still too simple to explain the multiple extrema observed in the open bullar-hole admittance and Y_TOC in the 100 to 300 Hz range (Figures 3B and 5).

Figure 13.

Comparison of admittance measurements before and after removing the effect of the cochlea. (A) The admittance measured in Chinchilla 005 with an open cavity hole measured with an intact cochlea and after the cochlea is drained. (B) Comparisons of mean admittance measurements in normal (intact chain) human ears (Zwislocki 1962 & Rabinowitz 1981) and in the ears of two patients with missing inci (Zwislocki 1962). (C) and (D) Comparisons of admittance measured in individual rabbit and cat ears made with the middle-ear air spaces widely opened, before and after interrupting the ossicular chain (Møller 1965). (E) and (F) Comparisons of admittance measured in individual cat ears with the middle-ear air spaces widely opened, before and after draining the cochlear fluids (Lynch 1981; Puria and Allen 1998).

An inner-ear dependent level dependence in middle-ear signal transmission has been observed by others. Kim et al. (1980) described a low-frequency nonlinearity in the ear canals of chinchillas, that was decreased postmortem. Ruggero et al. (1996) described a nonlinear growth of sound pressure at low frequencies in chinchillas with open bullar holes. Of potential significance is the coincidence of the frequency range of non-linear admittance with the range where the multiple extrema in the middle-ear admittance are observed and the coincidence of those ranges with the frequency region of prominent helicotrema effects in chinchilla (Dallos 1970). A phenomenologically similar nonlinearity that is also prominent near the corner-frequency of helicotrema filtering exists in the input admittance of the alligator lizard (Rosowski et al. 1984; Rosowski et al. 1985). The suggestion that the admittance irregularity may be associated with a changeover from cochlear resistance to helicotrema-mass control of the cochlear input impedance implies that the nonlinear response is occurring at the apical most part of the cochlea.

4.1.3 The TM, ossicles and the ossicular ligaments

The admittance measured after draining the cochlea, with the bullar hole open, reflects the mechanics of the tympanic membrane and ossicles as well as the opened middle-ear air spaces. Figure 7A illustrates that the change in admittance produced by draining the inner ear is largest at frequencies below 500 Hz, where a fairly sharp resonance (admittance magnitude maximum and 0.5 cycle angle change) is exposed. The admittance after cochlear draining is much larger in magnitude than the admittance with the bullar hole opened, implying that this resonance results primarily from the mechanics of the TM and ossicles. We can use the admittance at the lowest frequencies (of Figures 7A and 13A to estimate a TM-ossicular acoustic compliance, C_TO, with an equivalent volume of about 12 cc (Table 2). This value is much higher than any other reported compliance for middle ears; in comparison, the compliance of the tympanic membrane and ossicular systems of humans, domestic cats and rabbits are all generally less than 2 cc (Table 2).

TABLE 2.

	Chinchilla	Human	Rabbit	Cat
State of ear	Cochlea Drained (Fig 13A)	No Incus (Fig 13B)	IS-Joint Interrupted (Fig 13C)	Cochlea Drained (Fig 13F)
CTO, Acoustic Compliance of TM and Ossicles (m3/Pa)	1.11×10−10	1.11×10−11	1.75×10−12	6.37×10−12
Equivalent Volume (cc)	12.3	1.56	0.25	0.89
First resonance (Hz)	300	620	2000	1300
MTO, Acoustic Mass of TM and Ossicles MTO =(CTO ω2)−1 (kg-m−4)	3215	5915	3617	2354
ATM, pars tensa Area* (mm2)	70	60	20	36
mTO, ‘Effective’ Mechanical Mass mTO= MTO ATM2 (mg)	15.75	21.29	1.45	3.05
Mass of TM† (mg)	(16.3)	14	(4.7)	(8.4)
Mass of ossicles †† (mg)	11.5	54.5	4.3	15.1
Total mass of TM and ossicles (mg)	27.8	68.5	9.0	23.5

Estimates of the acoustic compliance, acoustic mass and resonant frequency of the TM and ossicles in four species based on the data of Figure 13. These data allow computations of the ‘Effective’ mechanical mass of the TM and ossicles that is compared to published mass measurements.

^*From Rosowski (1994)

^†Mass of the human TM is from Wever & Lawrence (1954). The mass of the TM of the other animals is computed by scaling the human TM mass by the ratio of the TM areas of the other animals to the human TM area.

^††From Nummela (1995)

Once the compliance, C_TO, and the resonant frequency, f₀, are estimated from Figure 13, and assuming a simple series resonance, an acoustic mass of the tympanic membrane and ossicles can be determined where: M_TO =(C_TO (2πf₀)²)⁻¹. This acoustic mass reflects the ‘effective’ mechanical mass of the TM and ossicles normalized by the square of the area of the pars tensa of the tympanic membrane, where the effective mass is a measure of the mechanical inertia of the TM and ossicles. This inertance differs from the simple mass of these structures because the ossicles generally rotate rather than translate and only a fraction of the TM mass is effectively accelerated by sound. Table 2 shows estimates of both the acoustic mass and the effective mechanical mass computed from the data in Figure 13, along with published measurements of TM and ossicular mass in chinchilla, human, rabbit and cat (Wever and Lawrence 1954; Nummela 1995). In general the effective mass underestimates the actual mass of the TM and ossicles. In the chinchilla, the effective mass is 57% of the total mass; this percentage is only 31% in humans, 16% in rabbit and 13% in cat.

While it seems reasonable to ascribe the resonance observed in the admittance with the cochlea drained to an interaction between an acoustic compliance and some effective mass of the TM and ossicles, there is another viewpoint. Puria and Allen (1998) have reported measurements of middle-ear admittance after cochlear draining and ISJ interruption in cats that demonstrate a series of admittance magnitude maxima and minima that are associated with repeated half-period changes in angle (Fig. 13F). Puria & Allen interpret this pattern of repeated resonance (admittance magnitude maxima) and anti-resonance (a magnitude minima) in terms of waves traveling on the tympanic membrane. Such an interpretation is not necessarily inconsistent with the simple idea put forth above that the lowest TM-ossicular resonance reflects the interaction of TM and ossicular mass and stiffness.

Not all data support the presence of multiple minima and maxima in the drained-cochlear admittance. Lynch (1981) measured the admittance in 4 cat ears to frequencies higher than 20000 Hz before and after cochlear draining and ISJ interruption, yet the Lynch data (e.g. Figure 13E) show no signs of repeated resonances and anti-resonances. In our chinchilla admittance measurements (Figures 7C and 7D) after cochlear draining or ISJ interruption, two ears (#504r and #505) show clearly repeating admittance magnitude and minima with coincident half-cycle angle changes as frequency increases. Two other ears (#005 and #105) do not show such a pattern.

4.1.4 The middle-ear muscles

While the contributions of the middle-ear muscles to middle-ear mechanics have been described (Wever & Lawrence 1954; Møller 1965, 1974, 1983; Borg 1972) it is often assumed that anesthesia inactivates the middle-ear reflex. The data in Figure 11 (and possibly the outlier in Figure 3B) illustrate that we saw transient and on occasion sustained decreases in middle-ear impedance that we associate with phasic or tonic contractions of the tensor-tympani or stapedius muscle. (Similar phenomena have been observed in guinea pigs, e.g. Wiggers 1937; Nuttall 1974.) While auditory physiologist who work on chinchillas have known for a long time that it is necessary to cut the middle-ear muscles in order to reduce variability, we know of no previous quantification of the magnitude of the effect in this species. Figure 11 suggests that even in the anesthetized chinchillas, the muscles can contract enough to produce a factor of 5 to 10 decrease in middle-ear input admittance. The size of the decrease in middle-ear sound transmission produced by muscle contraction is probably larger (Lutman & Martin 1979; Avan et al. 2000).

It has been suggested that middle-ear muscles contract tonically in order to position the stiffness of the ear at some ‘optimal’ operating point (e.g. Henson 1974). The data in Figures 4, 11 and 12 argue against such a view. First, Figure 11 affirms that sound-induced contractions of the middle-ear muscle reduce the sensitivity of the ear to low-frequency sound and have little effects at higher frequencies. A similar conclusion can be draw from investigations in other mammalian ears (Wever and Lawrence 1954; Møller 1965; Nuttal 1974; Borg 1972). Second, Figure 12 points out that the low-frequency sensitivity of the TM, ossicles and cochlea is similar in cases with relaxed middle-ear muscles and cut muscles, i.e. the tension of the relaxed muscle is not significant to auditory function. Third, Figure 4 reveals that the primary determinant of stiffness in the intact chinchilla ear is the compliance of the middle-ear air spaces.

4.2 Comparisons to other measurements of middle-ear function in chinchilla as a measure of the frequency dependence of the middle ear

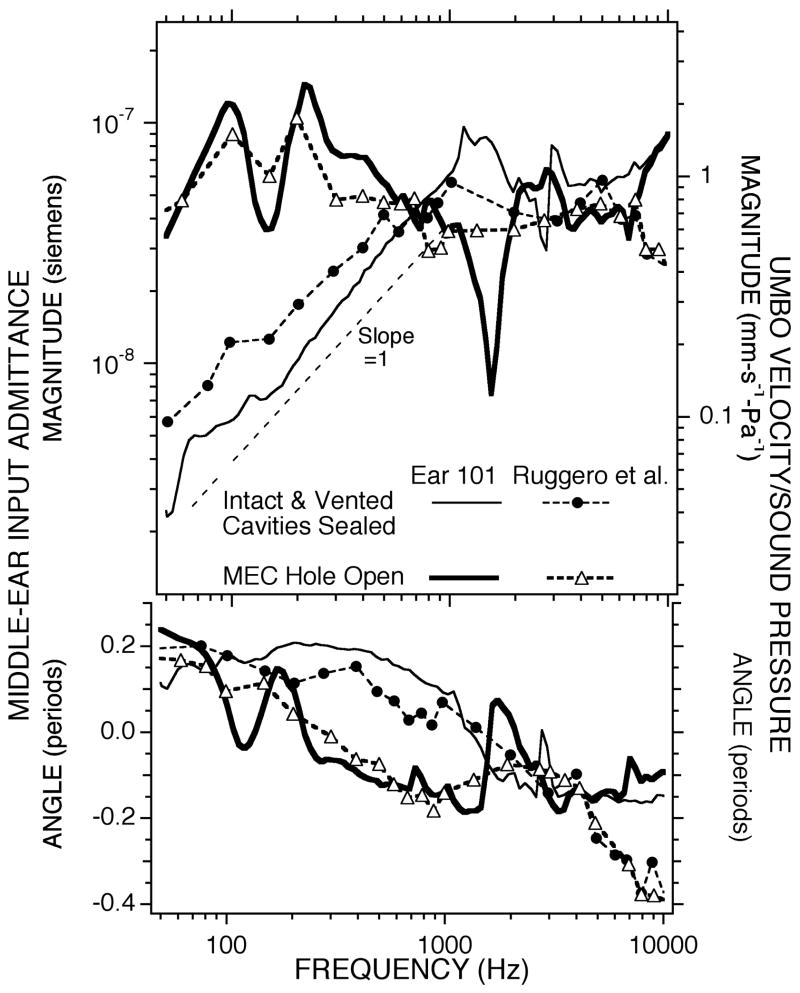
While there are no published measurements of middle-ear admittance in chinchilla in the different middle-ear conditions that we investigated, there are measurements of sound-induced umbo velocity in the chinchilla with the middle-ear air spaces sealed and with an open bullar hole (Ruggero et al. 1990). Our airspace sealed and hole-open measurements have many features in common with the umbo velocity measurements (Fig. 14) of Ruggero et al. (1990). The frequency dependence and the relative magnitudes of our intact air-space and open-bullar hole measurements are similar, although the finer frequency resolution of our measurements better defines the small notch associated with cavity resonances in the sealed and vented middle ear and the large minimum introduced by opening the hole in the cavity wall. Scaling of our admittance measurements (left axis) to match the velocity measurements of Ruggero et al. (1990) (right axis) leads to a suggested “effective area” of the chinchilla TM of 60 mm². The anatomical area of the chinchilla tympanic membrane is 70 mm² Table (2).

Figure 14.

Comparison between the admittance measurements in one of our chinchillas (#101), with the air-spaces intact and the bullar-hole open, and the average umbo-velocity measurements of Ruggero et al. (1990). The middle-ear input admittance is the area integral of the velocity of the tympanic membrane normalized by sound pressure. The admittance magnitude is plotted against the left-hand scale; the velocity/sound pressure data are scaled on the right hand side. The scales have been adjusted so that the admittance value equals the normalized velocity times an area of 60 mm².

4.3 Comparisons to other species

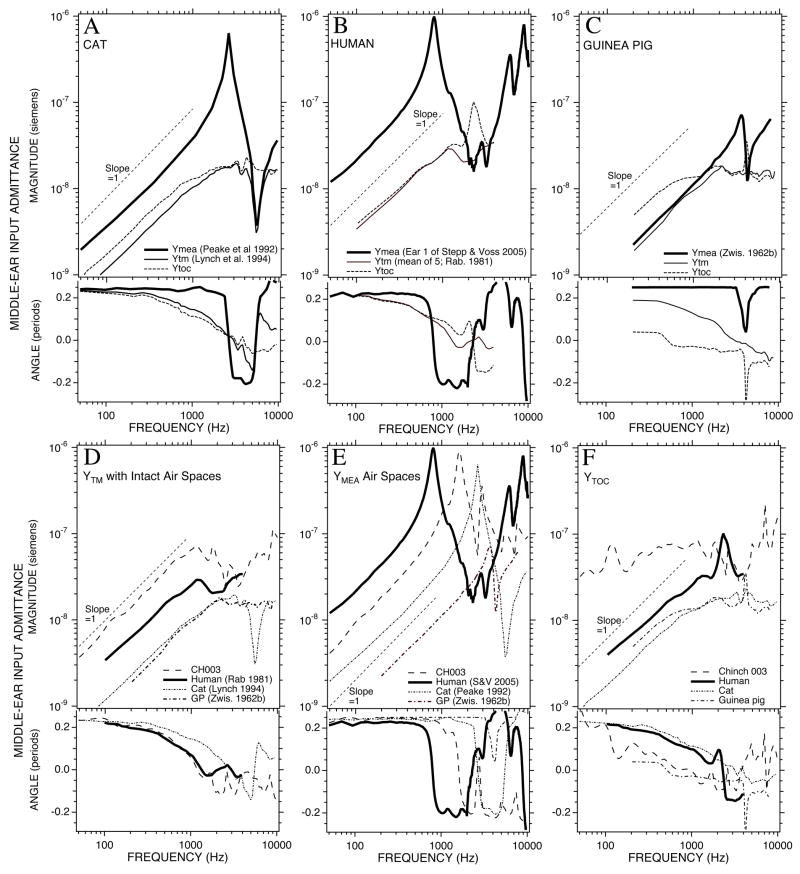
We compare published measurements of input admittance of the intact middle ear and the middle-ear air spaces in cat, human and guinea pig to our results in chinchilla (Figure 15). These measurements also allow us to calculate Y_TOC in the other species using Equation 2. Figure 15A–C point out that cat, human and guinea pig show different relative sizes of the intact and air-space admittances. In cat (Fig 15A) the admittance of the air spaces at low frequencies is about a factor of 2–3 larger than the admittance of the intact ear, such that making the admittance of the air spaces infinite (as seen in the computed Y_TOC) has a small but measurable effect on the admittance. In humans (Fig 15B) the air-space admittance at low frequencies is so large relative to the intact admittance that there is little difference between the intact admittance and Y_TOC. In guinea pigs (Fig. 15C) the air-space admittance at low frequencies approximates the admittance of the intact middle ear and Y_TOC is a factor of 2 larger than either the intact or air space admittance at frequencies below 1000 Hz. The relative size of the chinchilla air-space and intact middle-ear admittance (Figure 4) is more like the guinea pig, in that opening the cavity to increase the admittance produces a large (factor of 3 of greater) increase in the admittance measured at the tympanic membrane. This similarity in the magnitude of the effect of opening the cavities of chinchillas and guinea pigs has been observed previously (e.g. Dallos 1970).

Figure 15.

Comparison of admittance measurements of intact ears, middle-ear cavities and computations of Y_TOC. (A) The middle-ear admittance in cat: the intact middle ear (Ytm, Lynch et al. 1994), the middle-ear air space admittance (Ymea, Peake et al. 1992) and Y_TOC. (B) The middle-ear admittance in human: the intact middle ear (Ytm, Rabinowitz et al. 1981), the middle-ear air space admittance (Ymea, Stepp & Voss 2006) and Y_TOC. (C) The middle-ear admittance in guinea pig: the intact middle ear (Ytm, Zwislocki 1963), the middle-ear air space admittance (Ymea, Zwislocki 1963) and Y_TOC. (D-F) Comparisons of the three admittance types with measurements in Chinchilla #003.

Figures 15D-E compare the absolute magnitudes and the angles of the three different admittances in the four species. The chinchilla has the most admittant intact middle ear at all frequencies where we have measurements, while the admittance of the chinchilla middle-ear air spaces ranks second to the admittance of the large-volume human middle-ear spaces. With the cavities removed, the chinchilla middle ear is far and away the most admittant of the four.

The angles of the admittances in Figure 15D & E point out that in all of these four species, the admittance of the intact ears and of the air spaces are dominated by compliance at the lower frequencies. A similar compliance dominance at frequencies as high as 800 Hz is seen in the Y_TOC in cat and human. In chinchilla and guinea pig, however Y_TOC looks more resistive between 100 and 800 Hz, and the stiffness of the intact ears in this frequency range is a direct result of the smaller air-space admittance.

4.4 The adaptive value of the highly admittant middle ear in the chinchilla

Figure 15D points out that the chinchilla ear has a high middle-ear input admittance compared to other animals, especially at frequencies less than 2000 Hz. Figure 15F and 15E point out that this high admittance is the result of an unusually admittant tympanic membrane and ossicular chain (a large Y_TOC ) that is bounded by a middle-ear air volume that is large for an animal of the chinchilla’s size. Is this combination of large Y_TOC and large air space of any adaptive value in the arid open slopes of the high Andes that are the native habitat of these animals? There is a long history of the association of large middle-ear air spaces and open-arid environments (Heim de Balsac 1936; Legouix and Wisner 1955; Lay 1972; Webster and Webster 1975; Webster and Plassman 1992; Huang et al. 2002). The basic tenet of this association is that the atmospheric absorption of sounds of frequencies above 2000 Hz is greatly increased in low-humidity (see e.g., Huang et al. 2002) with the result that only sounds of lower frequencies carry for any distance. Coupled to this physical limitation on sound conduction is that the animals in question are nocturnal in their behavior and dependent on acoustic cues for conspecific localization and predator avoidance. The increased sensitivity to low-frequency sound that is associated with increased middle-ear admittance (Huang et al. 2002) would be of clear benefit under these circumstances.

4.5 The middle ear and auditory frequency response

There have been three common views of the action of the middle ear. One is the ideal transformer model of the ear, in which middle-ear sound transformation is reduced to the action of a coupled mechanical lever and an acoustical area ratio. This view has heuristic value for understanding the mechanisms of middle-ear action (Wever and Lawrence 1954; Dallos 1973; Rosowski 1994). The second is that the middle ear and external ear act as a filter that limits the sound energy available to the inner ear (Wever and Lawrence 1954; Dallos 1973; Zwislocki 1975; Rosowski et al. 1986; Rosowski 1991a&b). The third is that the middle ear acts as a transmission line that couples sound energy from the external ear to the inner ear in a relative frequency-independent manner (Olson 1998; Ruggero and Temchin 2002). While these views have their uses, they have also been misused in the literature. A common misuse of the ideal transformer model is the attempt to extrapolate auditory thresholds from measurements of ossicular lengths and tympanic-membrane areas in groups of species (e.g. Lay 1972; Webster and Webster 1975). To our knowledge no significant correlations between anatomical transformer measurements and auditory thresholds have been reported, though the lack of such correlations has been documented (Rosowski and Graybeal 1991). Another issue with the ideal transformer model is that, contrary to the second view, it assumes frequency-independent middle-ear function.

In support of the second view are reasonable matches between the frequency dependence of external- and middle-ear function with auditory thresholds in various animals (Dallos 1973; Zwislocki 1975; Khanna and Tonndorf 1978; Rosowski et al. 1986; Rosowski 1991a&b; Puria et al. 1997) at least to frequencies as high as 10000 Hz. Other lines of evidence supporting a role of the middle ear in determining hearing function are significant correlations between middle-ear dimensions and the low- and high-frequency limits of hearing in mammals (Rosowski & Graybeal 1991; Rosowski 1992, 1994), and that simple manipulations of middle-ear structures can have profound influences on hearing function, e.g. the 15 dB increase in the sensitivity of the chinchilla ear to low-frequency sound when a hole is placed in the bullar wall (Figs 3 & 4). However, one must be careful not to overstate the influence of the middle and external ear on limiting hearing function. Ruggero and Temchin (2002) have pointed out that one cannot discuss the factors that limit auditory sensitivity without including inner-ear mechanisms, such as the frequency range covered by the limited number of hair cells, frequency restrictions related to the finite length of the basilar membrane, and the action of the helicotrema in reducing the sensitivity to low-frequency sound. We must agree with these authors in that our own measurements (Fig 7) show the influence of the inner-ear impedance (including the helicotrema) on middle-ear function.

In support of the third view is data showing that when middle-ear transfer functions (either ossicular velocity or intra-cochlear sound-pressure normalized by ear-canal sound pressure) are plotted on linear frequency axes, the magnitude of the transfer functions tends to be fairly constant from a few thousand Hz to above the upper limit of hearing, and the phase angles of the transfer functions are approximately linearly related to frequency in the same frequency range (Olson 1998; Ruggero and Temchin 2002). However, such linear frequency plots greatly expand the few octaves of the audible range above 5000 Hz and suppress the 2-to-3 octaves of hearing range at frequencies less than 1000 Hz. Measurements of middle-ear transfer-function at frequencies below 1000 Hz and plots of these transfer functions on log-frequency axes, where equal weight is given to all of the octaves of the audible range, clearly show a large frequency dependence of the transfer-function magnitude at low audible frequencies as well as phase-angles that are inconsistent with simple delays (Figure 6 of Olson 1998; Figure 1 of Ruggero and Temchin 2002).

It seems clear that the transmission of sound from the environment to the inner ear depends on the acoustical and mechanical processes within the coupled external, middle and inner ear and that inner-ear sensory processes play a significant role in determining the hearing range. It is also clear that the external and middle ear help shape hearing sensitivity by filtering the sounds that reach the inner ear. A heuristic example of how the two processes work together is the mouse ear. Mice have small stiff middle ears that transmit little sound to the inner ear at frequencies less than 2000 Hz (Saunders and Summers 1982; Rosowski et al. 2003). At the same time they have short basilar membranes and a hair cell population that do not encode sounds of frequencies much less than 2000 Hz (Ehret and Frankenreiter 1977; Taberner and Liberman 2005). While the limitations of both the middle and inner ear act together to limit low-frequency hearing in the mouse, if one could produce a mouse hearing aid that is more effective at passing sound frequencies between 2000 and 10000 Hz it would increase the sensitivity of the mouse in that frequency range.

List of Symbols and Abbreviationss

β_A

The adiabatic bulk modulus of air which equals 1.4×10⁵ Pa at standard temperature and pressure

ρ₀, The density of air, at standard temperatur and pressure

1.2 kg-m⁻³

a

The effective radius of the bullar hole

A_TM

The area of the TM

C

An acoustic compliance with units of m³-Pa⁻¹

C_MEair

The acoustic compliance of the middle-ear air spaces

$C_{TM}^H$

The acoustic compliance measured lateral to the TM with 1 or 2 holes in the bullar walls

$C_{TM}^I$

The acoustic admittance lateral to the TM with the middle-ear air spaces intact or bullar-holes sealed

$C_{TM}^P$

The acoustic admittance lateral to the TM with bullar-holes sealed and the TM perforated

C_TOC

The acoustic compliance of the TM, ossicles and cochlea measured lateral to the TM

C_TO

The acoustic compliance of the TM and ossicles measured lateral to the TM

EqVol

The equivalent air volume that describes the magnitude of an acoustic compliance

f

frequency

ISJ

The incudo-stapedial joint

l

The thickness of the bon bullar wall

M^A

The acoustic mass associated with open the bullar hole with units of kg-m⁻⁴

m_TO

The effective mechanical mass of the TM and attached ossicles

M_TO

The acoustic mass of the TM and ossicles measured lateral to the TM

Pa

a pascal, the SI unit of pressure quivalent to 1 N-m⁻²

S

An acoustic siemen, a measure of acoustic admittance equivalent to 1 m-s⁻¹-Pa⁻¹

SPL, Sound Pressure Level a dB measure of sound level where X dB SPL

20 log10(Y rms Pa/2×10⁻⁵ Pa)

TM

The tympanic membrane or ear-drum membrane

Y

An acoustic admittance with units of siemens

Y_ASBH

The acoustic admittance of the middle-ear air spaces with an open bullar hole

Y_EC

The acoustic admittance measured at the entrance of the ear canal coupler

Y_TM

The acoustic admittance within the ear canal just lateral to the TM

$Y_{TM}^{CD}$

The acoustic admittance lateral to the TM with the cochlea drained of fluid

$Y_{TM}^H$

The acoustic admittance lateral to the TM with 1 or 2 holes in the bullar walls

$Y_{TM}^I$

The acoustic admittance lateral to the TM with the middle-ear air spaces intact or bullar-holes sealed

$Y_{TM}^{OI}$

The acoustic admittance lateral to the TM with the an interrupted ISJ

$Y_{TM}^P$

The acoustic admittance lateral to the TM with bullar-holes sealed and the TM perforated

Y_MEair

is the admittance of the middle-ear air space

Y_TOC

is the admittance at the tympanic membrane produced by the TM, ossicles (and their ligaments) and the cochlea when the admittance of the middle-ear air spaces is made infinite (Huang et al. 1997)

Appendix 1

The acoustic mass of the bullar hole M^A can be described in terms of the hole dimensions or the combination of the air-space compliance and the frequency of the anti-resonance:

$$M^A=\frac{{\rho }_0(l+1.6a)}{\pi a^2}=\frac{1}{C_{\mathit{MEair}}{(2\pi f_0)}^2},$$ Eqn. A1

where ρ₀ is the density of air, l is the thickness of the bony bullar wall (1 mm), a is the radius of the bullar hole, C_MEair is the acoustic compliance of the middle-ear air spaces (the equivalent volume divided by the adiabatic compressibility of air)², f₀ is the frequency of the anti-resonance and the factor of 1.6a represents the dual end-correction associated with flow through the bullar hole (e.g. Beranek 1986). We use the right-hand side of Equation A1 to solve for M^A using the data from our first set of 9 ears where f₀ =1370 Hz (Table 1). Rearranging the left-hand side equality of Equation A1 yields a quadratic relationship in a:

$$a^2-\frac{1.6{\rho }_o}{\pi M^A}a-\frac{{\rho }_{o}l}{\pi M^A}=0$$ Eqn. A2

that when solved produces one positive root such that the calculated hole diameter (2a) is 2 mm.