Abstract
Layer II stellate cells at different locations along the dorsal to ventral axis of medial entorhinal cortex show differences in the frequency of intrinsic membrane potential oscillations and resonance (Giocomo et al., 2007). The frequency differences scale with differences in the size and spacing of grid-cell firing fields recorded in layer II of the medial entorhinal cortex in behaving animals. To determine the mechanism for this difference in intrinsic frequency, we analyzed oscillatory properties in adult control mice and adult mice with a global deletion of the HCN1 channel. Data from whole-cell patch recordings show that the oscillation frequency gradient along the dorsal–ventral axis previously shown in juvenile rats also appears in control adult mice, indicating that the dorsal–ventral gradient generalizes across age and species. Knock-out of the HCN1 channel flattens the dorsal–ventral gradient of the membrane potential oscillation frequency, the resonant frequency, the time constant of the “sag” potential and the amplitude of the sag potential. This supports a role of the HCN1 subunit in the mechanism of the frequency gradient in these neurons. These findings have important implications for models of grid cells and generate predictions for future in vivo work on entorhinal grid cells.
Introduction
Single-unit recordings from rats and mice exploring open fields demonstrate that medial entorhinal cortex (mEC) “grid cells” fire in repeating spatial locations forming a hexagonal pattern (Hafting et al., 2005; Fyhn et al., 2008). In mEC layer II, the size and spacing of grid-cell firing fields increases from small to large along the dorsal–ventral axis (Sargolini et al., 2006; Fyhn et al., 2008). Whole-cell patch-clamp recordings of single mEC cells in rats indicate that intrinsic properties of layer II stellate cells systematically differ from dorsal to ventral mEC, correlating with the change in grid cell field size and spacing (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a,b). Biophysical properties dependent on the hyperpolarization activated cation current Ih, such as membrane potential oscillations (MPO) and resonant frequency, change from high to low frequencies along the dorsal–ventral axis (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a), correlating with a gradient in the time constant of Ih in rats (Giocomo and Hasselmo, 2008a). Models of grid cells (Burgess et al., 2007, 2008; Giocomo et al., 2007) have demonstrated that the differences in frequency properties could underlie the differences in size and spacing of grid-cell firing fields (Sargolini et al., 2006; Fyhn et al., 2008). Differences in Ih may depend on a gradient in the expression of hyperpolarization-activated cyclic nucleotide-gated (HCN) channels, specifically in the relative expression of HCN1, a subunit present in mEC (Notomi and Shigemoto, 2004) and characterized by its fast activation time constants (Chen et al., 2001). To test the role of HCN1, we examined dorsal–ventral differences in layer II stellate cells of adult control mice and compared them with the same cellular properties in adult mice with a global deletion of the HCN1 channel.
Materials and Methods
Slice physiology
Whole-cell patch-clamp recordings were performed on adult (21–56 d) mice, which were anesthetized and rapidly decapitated. All control mice were obtained directly from Jackson Laboratories (Strain: B6129SF2/J). Mice with global deletion of the HCN1 subunit were obtained from Jackson Laboratories and were bred using facilities at Boston University. All techniques were approved by the Institutional Animal Care and Use Committee at Boston University. After decapitation, the brain was removed under cold (4°C) artificial CSF (ACSF) (Sigma Aldrich) (ACSF concentrations in mm: 126.0 NaCl, 3 KCl, 2 MgSO4, 10.0 dextrose, 26.0 NaHCO3, 1.25 NaH2PO4, 2 CaCl2) oxygenated by bubbling 95% O2/5% CO2 through the ACSF. After removal, the brain was cut in half through the corpus callosum and the cut side glued to the slicing mount with the entorhinal cortex facing the blade, to allow for slicing of several sagittal sections of medial entorhinal cortex. Sagittal slices (400 μm thick) from both hemispheres were cut and placed in a holding chamber. After slicing, slices were stored at 31°C for 30 min followed by 30 min at room temperature. For whole-cell patch-clamp recordings, slices were placed in a submerged recording chamber with continuously flowing ACSF kept at 37.0 ± 0.5°C. An upright microscope (Axioskop, Zeiss) equipped with a 40× water-immersion objective lens (Zeiss) was used to visualize cells, allowing easy identification of the location and laminar distribution of EC cells. Recorded cells were first identified as stellate cells by choosing to record from cells located at the most superficial portion of layer II medial entorhinal cortex (near the border with layer I) and selecting to record only cells that displayed characteristics of stellate cells with multiple, thick branching dendrites (Klink and Alonso, 1997). For recordings, patch pipettes (4–7 mΩ) were pulled from 10 cm borosilicate glass capillary tubes (Sutter Instrument Company) with a Sutter Instrument model P-87 pipette puller and filled with the following (in mm): 120 K-gluconate, 10 HEPES, 0.2 EGTA, 20 KCl, 2 MgCl, 7 diTrisPhCr, 4 Na2ATP, and 0.3 Tris-GTP, pH adjusted to 7.3 with KOH. In addition, the intracellular recording solution contained 0.1% biocytin for later verification of cell morphology by staining of the cells. Tight seals (>1 GΩ) were formed between the recording pipette and cell membrane, and then ruptured with negative mouth pressure. At the end of recordings, cells were placed in 4% paraformaldehyde for later biocytin staining. All recordings were amplified by a Multiclamp 700B (Molecular Devices) and digitized by a Digidata 1440 at a sampling frequency of 20 kHz (50 μs). Capacitance neutralization and bridge balance were applied accordingly and current clamp data were filtered at 10 kHz. Signals were acquired using a Pentium-based computer running Clampex 10.0 software (Molecular Devices). The liquid junction potential was ∼5 mV, measured using the technique of Neher (1992). Membrane potentials reported throughout do not contain correction of this potential. The location of the cell along the dorsal–ventral axis was determined using the coordinates of a motorized manipulator (Sutter Instruments). The sagittal slice was placed in the dish perpendicular to the pipette tip attached to the manipulator. Immediately after recording, the coordinates of the pipette were noted using the manipulator's X and Y location (indicating the cell's location). The manipulator then moved the pipette to the dorsal tip of the hippocampal formation, which is located ∼300 micrometers above the postrhinal border according to the Allen Brain Atlas (Lein et al., 2007), and the X and Y locations were noted again. Based on these measurements, the distance of the cell relative to the postrhinal border could be determined and consistently compared between slices and experiments. In addition, the technique for locating the cell was confirmed by later morphological staining. The protocol for biocytin staining has been described in detail previously (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a). Examples of biocytin-filled stellate cells from control animals and knock-out animals are shown in supplemental Figure 5, available at www.jneurosci.org as supplemental material. In these experiments, 38 stellate cells were recorded from control animals and 48 stellate cells from knock-out animals. In some knock-out slices, layer V cells were also recorded to compare oscillatory properties between layer V and layer II (supplemental Fig. 6, available at www.jneurosci.org as supplemental material).
Data analysis
Analysis and statistics.
For data analysis, MATLAB, Clampfit 10.0 and Excel were used. Resistance was measured during recording by using the Multiclamp commander and injecting 1-s-long hyperpolarizing current steps. For a more detailed analysis of resistance (see supplemental Fig. 4, available at www.jneurosci.org as supplemental material), cells were held at –70 mV and a 3 s long hyperpolarizing current step applied. The resistance was calculated using built in Clampfit analysis protocols for steps resulting in a steady-state membrane potential near –85 mV (see supplemental Fig. 4, available at www.jneurosci.org as supplemental material). Overall, the distribution of data collected was not Gaussian [as determined by the Kolmogorov–Smirnov (ks) test in MATLAB]. Statistical tests that do not assume a Gaussian distribution of data were exclusively used to analyze the data. For correlation, the Spearman's rank correlation coefficient was determined for correlations using the “corr” function in MATLAB. To test the differences between two samples of data (knock-outs vs controls) the Kolmogorov–Smirnov test function “kstest2” in MATLAB was used. For analysis of power differences between controls and knock-outs a one-tailed Kruskal–Wallis test function “kruskalwallis” was used in MATLAB. Figures showing correlations were constructed in Excel using the least-squares method. For all statistical analysis a p value of <0.05 was considered significant and exact p values are reported for all analysis.
Membrane potential oscillation.
To measure membrane potential oscillations, current injections were applied in current-clamp mode at a variety of levels (1–1000 pA) until the cell began to spike rapidly. Large segments of data (< 10 s) were analyzed using two different techniques. An automated procedure in MATLAB analyzed 3 s long segments of membrane potential at a particular voltage (e.g., –50 mV). Multiple windows overlapping by 1.5 s were selected and windows containing spikes were removed from analysis. For the autocorrelation analysis, each window of data was zero centered and autocorrelations on the window were performed using the xcorr function of MATLAB. The frequency was determined as the inverse of the interval from the central peak to the first side peak. Frequencies of the three windows with the highest difference between the amplitude of the side peak and the trough between the two peaks were averaged and recorded as the results for the cell. For the initial analysis, the lower threshold was set at 2 Hz. If a cell did not show a peak before the end of the window, the window was extended to have a lower threshold of 0.5 Hz. For the power spectra analysis, a Hanning window was applied to each section of data and the fast Fourier transform (FFT) was calculated. The integral of the FFT for different frequency bins (0–2; 2–4; 4–6; 6–8; 8–10; 10–12 Hz) was measured on the five windows that showed the highest peak power. The average power integral for each frequency bin across the five windows was averaged and is reported as “power.”
Resonant frequency analysis.
Resonant frequency was measured with an impedance amplitude profile (ZAP), in which each cell was injected with a sinusoidal current that increased linearly from 0 to 20 Hz over the course of 20 s. This was generated in MATLAB using the chirp function. Cells were held near resting potential (at –70 mV) using a steady current injection if necessary. The initial amplitude of the ZAP was 100 pA. However, if the amplitude was too high (causing action potentials), the amplitude was decreased until the protocol could be run without causing action potentials. The power spectrum of the membrane voltage in response to the injection was divided by the power spectrum of the injected current to produce a function of input frequency versus impedance. An average of at least three trials in which there was no more than a 10 mV change in the membrane potential between the starting and ending points of the ZAP was used to determine the resonant frequency.
Sag analysis.
Observed in current-clamp with hyperpolarizing current steps, the sag potential is characterized by an initial strong hyperpolarization that decays to a more depolarized steady state potential. The sag observed depends on the presence and time course of Ih (Alonso and Klink, 1993) and has been shown to change from fast in dorsal to slow in ventral entorhinal cortex neurons (Giocomo et al., 2007; Giocomo and Hasselmo, 2008a). To analyze the sag, cells were held at –70 mV and 3 s long hyperpolarizing current injections were given at a range of amplitudes. To analyze the time contrast of the sag potential the “NonlinearLeastSquares” method in combination with the function “exp2” of MATLAB was used. The following double exponential function was used to fit the current-clamp data: F = A1e(−t/τ1) + A2e(−t/τ2), where A1 and A2 are the amplitude of the fast (τ1) and slow (τ2) component of the sag, respectively. The fit started from the trough of the sag response (+7 ms to exclude the trough) and ended 4 ms before the end of the current pulse. The fast time constant was used in subsequent analysis. Cells were used for subsequent analysis of the time constant if their sag trough reached –80.0 to –85.0 mV. The amplitude of the sag was measured from the same current-clamp data used to analyze the time constant of the sag. The peak trough membrane voltage and steady state membrane voltage (voltage reading 4 ms before the end of the hyperpolarizing current injection) were measured using analysis tools in Clampfit. The relative amplitude of the sag was determined by dividing the peak trough membrane voltage by the steady state membrane voltage. Traces which had a peak trough membrane potential between –95.0 and –90.0 mV as well as traces which had a peak trough membrane potential between –85.0 mV and –80.0 mV were used in subsequent analysis. For dorsal versus ventral measurements, dorsal was defined as cells from 0 to 1.59 mm from the postrhinal border whereas ventral was defined as cells at 1.6 mm or deeper.
Results
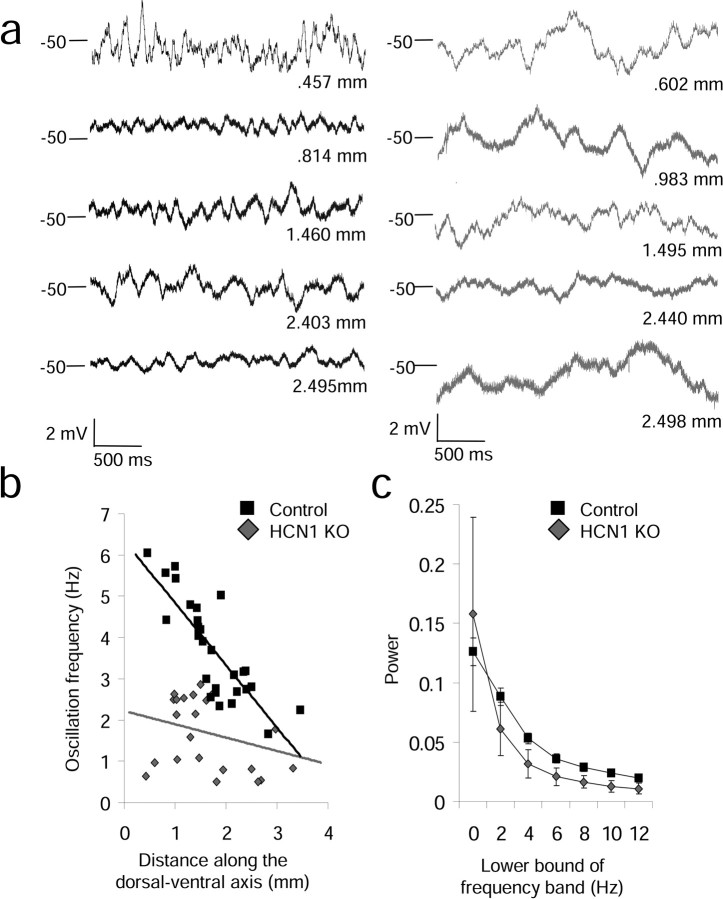
Physiological properties of stellate cells shown to differ in young rats (17–23 d) (Giocomo et al., 2007) also differ along the dorsal–ventral axis of mEC in adult mice, indicating that previously observed differences translate between species and ages. Comparing control and HCN1 knock-out (KO) mice, we observed a significant gradient of differences along the dorsal–ventral axis for MPO frequency, resonant frequency and characteristics of the sag potential. As shown in Figure 1, the frequency of MPOs at an approximate membrane potential of −50 mV showed a significant dorsal–ventral frequency gradient in control mice, as determined using autocorrelation analysis tested by the Spearman's rank correlation (SRC) (slope = −1.51, r = 0.82, p = 4.4 × 10−8 and n = 29). This difference is consistent with previous reports in rats (Giocomo et al., 2007; Giocomo and Hasselmo, 2008b). In contrast, the HCN1 KO mice did not show a significant dorsal–ventral gradient in MPO frequency (SRC: slope = −0.32, r = 0.28, p = 0.19 and n = 23) (Fig. 1a,b). In the HCN1 knock-out mice, MPOs at −50 mV were either not present or appeared with a low frequency similar to very ventral stellate cells in the control mice. These measurements of MPO frequency were made at the same holding potential of −50 mV to avoid differences in membrane potential oscillations caused by differences in holding membrane potential. Although knock-out of HCN1 can influence multiple properties of stellate cells, for example the resting potential (see supplemental Fig. 4, available at www.jneurosci.org as supplemental material), the firing threshold for cells analyzed for oscillatory activity at −50 mV was not significantly different (mean firing threshold ± SEM: control = −41.82 ± 0.55 and n = 29, KO = −40.47 ± 0.80 and n = 23, p = 0.08), consistent with previous research showing no significant difference between the firing threshold in control and HCN1 knock-out animals (Nolan et al., 2007).
Figure 1.
Effect of HCN1 knock-out on membrane potential oscillations at –50 mV. a, Examples of membrane potential oscillations at –50 mV in control (left) and HCN1 KO mice (right). b, The gradient of membrane potential oscillation frequency along the dorsal–ventral axis of control mice (black squares) is flattened by knock-out of HCN1 (gray diamonds). c, Power spectra analysis of oscillations show more power in higher-frequency ranges (> 4 Hz) in control (black) compared with HCN1 KO mice (gray) at –50 mV.
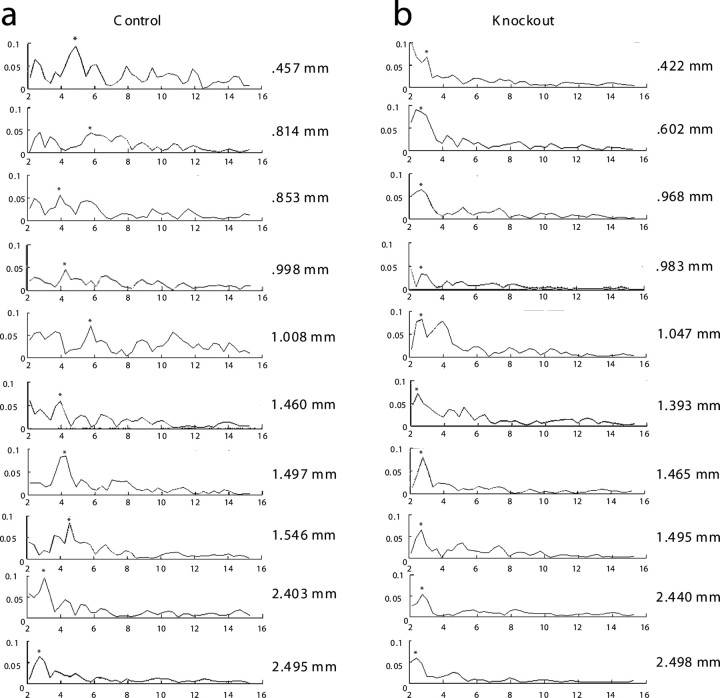
As shown in Figure 1c, binned power spectra analysis confirmed that MPOs in control cells showed significantly more power compared with MPOs in knock-out mice at higher-frequency ranges (> 4 Hz), as determined by a Kruskal–Wallis test (χ2 = 15.28, p = 9.3 × 10−5). Power spectra analysis revealed that, consistent with previous reports on HCN1 knock-out mice (Nolan et al., 2007), oscillation power was similar in controls and KO at more hyperpolarized membrane potentials (−60, −55 mV), where the dorsal–ventral gradient does not appear in control animals (Giocomo and Hasselmo, 2008a,b) (see supplemental Fig. 1, available at www.jneurosci.org as supplemental material). Individual examples of power spectra from controls and knock-out animals are shown in Figure 2, and power spectra from longer segments of membrane potential are shown in supplemental Figure 2, available at www.jneurosci.org as supplemental material. These examples of power spectra show differences in cells recorded at different anatomical locations along the dorsal to ventral axis in control mice (Fig. 2; supplemental Fig. 3, available at www.jneurosci.org as supplemental material), with greater power at higher frequencies in more dorsal cells. In addition, these examples show that the power spectra in knock-out animals has consistently lower power in the 5–12 Hz frequency band relative to the power in that band in cells from dorsal medial entorhinal cortex in control mice. These data suggests that the HCN1 subunit is critical for the dorsal–ventral gradient in MPO frequency observed at depolarized membrane potentials (−50 mV).
Figure 2.
Effect of HCN1 knock-out on membrane potential oscillations at −50 mV as shown with power spectra analysis. Examples of 20 power spectra from 3 s data segments are shown from 10 different control cells (left) and 10 HCN1 knock-out cells (right) located at different dorsal–ventral depths along the axis of medial entorhinal cortex. Asterisks indicate the frequency assigned for each data set. Individual depths of each cell are shown to the right of each plot. Dorsal cells tended to have peaks in their power spectra at higher frequencies in controls compared with knockouts. At more ventral locations, the frequency peaks were at low values in controls similar to those observed along the entire dorsal ventral axis of HCN1 knock-out mice.
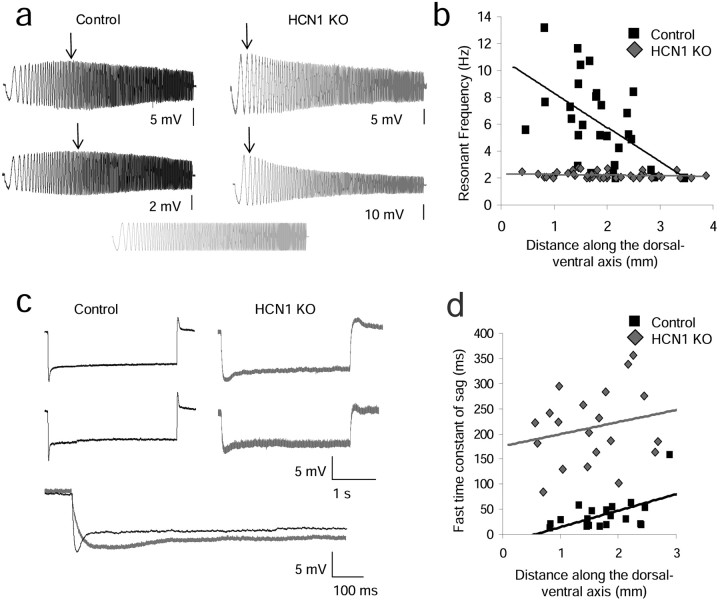
As shown in Figure 3, the resonant frequency observed when the cell is near rest (−70 mV) shows a significant dorsal–ventral gradient in adult control mice (SRC: slope = −2.54, r = 0.53, p = 0.003, n = 30), whereas knock-out of HCN1 abolishes the gradient, causing all cells to show very low resonant frequency (SRC: slope = −0.05, r = 0.16, p = 0.74, n = 40) (Fig. 3a,b). This is consistent with previous research reporting a correlation between the resonance frequency and oscillation frequency observed near threshold (Erchova et al., 2004) and indicates a role of the HCN1 subunit in the high resonant frequencies observed in dorsal mEC in controls.
Figure 3.
Effect of HCN1 knock-out on resonant frequency and the time constant of the sag potential. a, Examples of control (black) and HCN1 KO (gray) resonant frequencies in dorsal portions of mEC. b, Control animals show a dorsal–ventral gradient of resonant frequency that is flattened in HCN1 KO animals. c, Examples of sag potential from control and HCN1 KO stellate neurons. d, Control animals show a dorsal–ventral gradient of the time constant of the sag potential, whereas HCN1 KO animals do not.
As shown in Figure 3d, the time constant of the sag potential significantly differs along the dorsal–ventral axis in control mice (SRC: slope = 32.84, r = 0.56, p = 0.01, n = 20). This dorsal–ventral gradient is abolished in KO mice, consistent with the loss of the fast kinetics of Ih with the knock-out of the HCN1 subunit (SRC: slope = 24.03, r = 0.22, p = 0.35, n = 22). Figure 3c shows examples of the sag potential in control and knock-out mice. The loss of the fast component of the sag potential in HCN1 KO indicates an absence of the fast component of Ih and a role of the HCN1 subunit in the dorsal–ventral change in sag time constant.
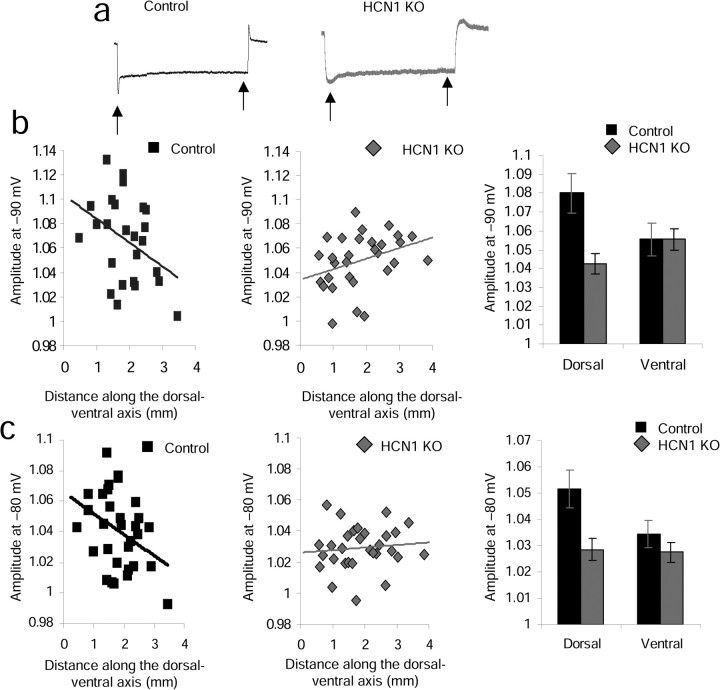
As shown in Figure 4, the amplitude of the sag potential decreased along the dorsal–ventral axis of medial entorhinal cortex stellate cells in control mice. When the trough of the sag equaled –95 to –90 mV (Fig. 4b), the amplitude of the sag relative to the steady-state membrane potential control cells showed a near significant decrease in amplitude from dorsal to ventral as determined by the Spearman's rank correlation (SRC) (slope = −0.02, r = 0.37, p = 0.058, n = 25), whereas the knock-outs showed a slight increase in amplitude from dorsal to ventral regions (slope = 0.009, r = 0.35, p = 0.06, n = 30). An increase in amplitude in the HCN1 KO animals would be consistent with a gradual dorsal–ventral increase in the number of non-HCN1 subunits (HCN2, HCN3, HCN4), all of which show slower kinetics compared with HCN1. When the trough of the sag equaled –85 to –80 mV (Fig. 4c), the amplitude of the sag relative to the steady-state membrane potential of control cells showed a significant decrease in amplitude from dorsal to ventral as determined by the SRC (slope = −0.01, r = 0.38, p = 0.04, n = 31), whereas the knock-outs showed no change in amplitude from dorsal to ventral regions (slope = 0.002, r = 0.11, p = 0.65, n = 31).
Figure 4.
Effect of HCN1 knock-out on the amplitude of the sag potential. a, Arrows indicate the approximate location of the sag trough measurement and steady-state amplitude measurement for a single example trace. b, Control mice show a dorsal–ventral gradient in sag amplitude that is flattened in HCN1 KO animals when the trough of the sag equaled –95 to –90 mV. c, Control mice show a dorsal–ventral gradient in sag amplitude that is flattened in HCN1 KO animals when the trough of the sag equaled –85 to –80 mV.
As shown in the right-hand histograms in Figure 4, b and c, for both ranges of membrane potential, dorsal cells (0–1.6 mm from the postrhinal border) showed significantly larger sag amplitudes in control versus HCN1 KO mice (mean amplitude ± SEM for −95 to –90 mV: control dorsal = 1.08 ± 0.01 and n = 9, KO dorsal = 1.04 ± 0.005 and n = 13, p = 0.01; mean amplitude ± SEM for −85 to –80: control dorsal = 1.05 ± 0.007 and n = 11, KO dorsal = 1.03 ± 0.004 and n = 12, p = 0.03). In contrast, for these membrane potentials, ventral cells showed no significant difference in sag amplitude between control and HCN1 KO mice (mean amplitude ± SEM for −95 to −90 mV: control ventral = 1.06 ± 0.009 and n = 13, KO ventral = 1.06 ± 0.006 and n = 17, p = 0.55; mean amplitude ± SEM for −85 to −80: control ventral = 1.03 ± 0.005 and n = 11, KO ventral = 1.03 ± 0.004 and n = 19, p = 0.16).
Discussion
In conclusion, adult control mice show a dorsal–ventral gradient in the biophysical properties of mEC neurons similar to young rats. The HCN1 subunit is critical for the dorsal–ventral gradient appearing in all reported biophysical characteristics: MPO frequency, resonance frequency, and the sag potential. The absence of HCN1 appears to result in predominant effects of other HCN subunits that may contribute to the slower frequency MPOs and slower sag potential still present in knockouts.
The current study presents data from HCN1 knock-out mice consistent with previous reports of changes in entorhinal stellate cells with the loss of the HCN1 subunit (Nolan et al., 2007). In that previous study, HCN1 knock-out was shown to reduce the resonance frequency and reduce the suppression of low-frequency membrane potential oscillations. Those results are consistent with our data showing loss of the gradient of resonance frequency and with our demonstration that HCN1 knock-out does not completely abolish subthreshold membrane potential oscillations but rather reduces dorsal, high-frequency oscillations and thus the dorsal–ventral gradient of oscillation frequency. In addition, this study complements other dorsal–ventral changes recently demonstrated in the adult mouse, such as differences in the temporal summation of synaptic potentials and differences in the amplitude of the h-current (Garden et al., 2008).
Membrane potential oscillations in entorhinal stellate cells have been modeled with deterministic biophysical simulations that generate oscillations at theta frequency dependent on h current (Dickson et al., 2000; Fransén et al., 2004; Rotstein et al., 2006), or with stochastic channel models that generate fluctuations in membrane potential (White et al., 1998, 2000; Dorval and White, 2005; Dudman and Nolan, 2009) with spectral properties shaped by the presence of HCN channels (Dudman and Nolan, 2009). Because the properties of the HCN current determine the frequency response in both types of models, anatomical differences in HCN1 subunit expression could cause an anatomical gradient of frequency response in both cases. Thus, our data are consistent with both models linking the frequency response of the HCN channel to membrane potential dynamics. Combined, all of these dorsal–ventral properties provide cellular mechanisms relevant to several computational models of grid-cell formation (Burgess et al., 2007; Hasselmo et al., 2007; Blair et al., 2008; Burgess, 2008; Kropff and Treves, 2008), which use specific dorsal–ventral changes in biophysical properties to simulate the gradient of field size and spacing of the grids (Sargolini et al., 2006; Fyhn et al., 2008). The results presented here, in combination with current computational models of grid cell formation, make the direct prediction that the dorsal–ventral gradient in grid cell field size and spacing will be lost in HCN1 knock-out mice.
Footnotes
This research was supported by National Institute of Mental Health (NIMH) Grants R01 MH61492 and R01 MH60013 and Silvio O. Conte Center Grant NIMH MH71702. We also thank Chris Andrews for programming assistance. Lisa M. Giocomo collected and analyzed data, created figures, and wrote this manuscript. Michael E. Hasselmo provided resources and comments on this manuscript. Both authors contributed ideas to the development of this project.
References
- Alonso A, Klink R. Differential electroresponsiveness of stellate and pyramidal-like cells of medial entorhinal cortex layer II. J Neurophysiol. 1993;70:128–143. doi: 10.1152/jn.1993.70.1.128. [DOI] [PubMed] [Google Scholar]
- Blair HT, Gupta K, Zhang K. Conversion of the phase- to a rate-coded position signal by a three-stage model of theta cells, grid cells, and place cells. Hippocampus. 2008;18:1239–1255. doi: 10.1002/hipo.20509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N. Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus. 2008;18:1157–1174. doi: 10.1002/hipo.20518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, O'Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Wang J, Siegelbaum SA. Properties of hyperpolarization-activated pacemaker current defined by coassembly of HCN1 and HCN2 subunits and basal modulation by cyclic nucleotide. J Gen Physiol. 2001;117:491–504. doi: 10.1085/jgp.117.5.491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson CT, Magistretti J, Shalinsky MH, Fransén E, Hasselmo ME, Alonso A. Properties and role if I(h) in the pacing of subthreshold oscillations in entorhinal cortex layer II neurons. J Neurophysiol. 2000;83:2562–2579. doi: 10.1152/jn.2000.83.5.2562. [DOI] [PubMed] [Google Scholar]
- Dorval AD, Jr, White JA. Channel noise is essential for perithreshold oscillations in entorhinal stellate neurons. J Neurosci. 2005;25:10025–10028. doi: 10.1523/JNEUROSCI.3557-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudman JT, Nolan MF. Stochastically gating ion channels enable patterned spike firing through activity-dependent modulation of spike probability. PLoS Comput Biol. 2009;5:e1000290. doi: 10.1371/journal.pcbi.1000290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erchova I, Kreck G, Heinemann U, Herz AV. Dynamics of rat entorhinal cortex layer II and III cells: characteristics of membrane potential resonance at rest predict oscillation properties near threshold. J Physiol. 2004;560:89–110. doi: 10.1113/jphysiol.2004.069930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransén E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME. Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus. 2004;14:368–384. doi: 10.1002/hipo.10198. [DOI] [PubMed] [Google Scholar]
- Fyhn M, Hafting T, Witter MP, Moser EI, Moser MB. Grid cells in mice. Hippocampus. 2008;18:1230–1238. doi: 10.1002/hipo.20472. [DOI] [PubMed] [Google Scholar]
- Garden DL, Dodson PD, O'Donnell C, White MD, Nolan MF. Tuning of synaptic integrtion in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron. 2008;60:875–889. doi: 10.1016/j.neuron.2008.10.044. [DOI] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Time constants of h current in layer II stellate cells differ along the dorsal to ventral axis of medial entorhinal cortex. J Neurosci. 2008a;28:9414–9425. doi: 10.1523/JNEUROSCI.3196-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Hasselmo ME. Computation by oscillations: implications of experimental data for theoretical models of grid cells. Hippocampus. 2008b;18:1186–1199. doi: 10.1002/hipo.20501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Zilli EA, Fransén E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, Giocomo LM, Zilli EA. Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus. 2007;17:1252–1271. doi: 10.1002/hipo.20374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klink R, Alonso A. Morphological characteristics of Layer II projection neurons in the rat medial entorhinal cortex. Hippocampus. 1997;7:571–583. doi: 10.1002/(SICI)1098-1063(1997)7:5<571::AID-HIPO12>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- Kropff E, Treves A. The emergence of grid cells: intelligent design or just adaptation? Hippocampus. 2008;18:1256–1269. doi: 10.1002/hipo.20520. [DOI] [PubMed] [Google Scholar]
- Lein ES, Hawrylycz MJ, Ao N, Ayres M, Bensinger A, Bernard A, Boe AF, Boguski MS, Brockway KS, Byrnes EJ, Chen L, Chen L, Chen TM, Chin MC, Chong J, Crook BE, Czaplinska A, Dang CN, Datta S, Dee NR, et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature. 2007;445:168–176. doi: 10.1038/nature05453. [DOI] [PubMed] [Google Scholar]
- Neher E. Correction for liquid junction potentials in patch clamp experiments. Meth Enzymol. 1992;207:123–131. doi: 10.1016/0076-6879(92)07008-c. [DOI] [PubMed] [Google Scholar]
- Nolan MF, Dudman JT, Dodson PD, Santoro B. HCN1 channels control resting and active integrative properties of stellate cells from layer II of the entorhinal cortex. J Neurosci. 2007;27:12440–12451. doi: 10.1523/JNEUROSCI.2358-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notomi T, Shigemoto R. Immunohistochemical localization of Ih channel subunits, HCN1–4, in the rat brain. J Comp Neurol. 2004;417:241–276. doi: 10.1002/cne.11039. [DOI] [PubMed] [Google Scholar]
- Rotstein HG, Oppermann T, White JA, Kopell N. The dynamic structure underlying subthreshold oscillatory activity and the onset of spikes in a model of medial entorhinal cortex stellate cells. J Comput Neurosci. 2006;21:271–292. doi: 10.1007/s10827-006-8096-8. [DOI] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- White JA, Klink R, Alonso A, Kay AR. Noise from voltage-gated ion channels may influence neuronal dynamics in the entorhinal cortex. J Neurophysiol. 1998;80:262–269. doi: 10.1152/jn.1998.80.1.262. [DOI] [PubMed] [Google Scholar]
- White JA, Rubinstein JT, Kay AR. Channel noise in neurons. Trends Neurosci. 2000;23:131–137. doi: 10.1016/s0166-2236(99)01521-0. [DOI] [PubMed] [Google Scholar]