Diagonal d′ does not (always) diagnose failure of separability: An addendum to

Abstract

Kingston, Diehl, Kirk, and Castleman (Journal of Phonetics, 2008) present a sophisticated experimental design and detection theoretic analysis of the internal auditory structure of phonological contrasts. However, a potentially important aspect of multidimensional detection theory – the covariance structure of assumed underlying multivariate Gaussian perceptual densities – was left unexplored. We discuss Kingston, et al.'s approach in the context of a general definition of multidimensional d′ and present a description of two distinct configurations of perceptual densities requiring fundamentally different interpretations that account equally well for the “mean-shift integrality” results reported by Kingston, et al. We end with a brief discussion of approaches to distinguishing these underlying configurations empirically.

1. Background

Kingston, Diehl, Kirk, and Castleman (2008; henceforth, KDKC) report an extremely interesting investigation of the internal auditory structure of phonological contrasts. We applaud this work, since we believe that this is an important and largely unexplored part of phonetics. KDKC's design is quite sophisticated, and their use of Signal Detection Theory (Green & Swets, 1966; henceforth SDT) in the study of auditory perception has much to recommend it.

This letter is intended to point out some additional subtleties of multidimensional SDT (also called General Recognition Theory, henceforth GRT; Ashby & Townsend, 1986, inter alia) which are left unexplored by KDKC (and which suggest interesting areas for future work). Specifically, their analyses rely on potentially unwarranted assumptions about underlying multidimensional perceptual distributions. Alternative explanations are possible for at least some of their findings.

The common (unidimensional) SDT measure of sensitivity – d′ – relies on the assumption that the random perceptual effects of interest are normally distributed. Central to KDKC's design, though, are stimuli situated in various two-dimensional acoustic spaces. Under the assumption that the acoustic dimensions correspond to distinct perceptual dimensions, the random perceptual effects of the two-dimensional stimuli will produce bivariate (normal) perceptual distributions. A unidimensional normal distribution is completely specified by two parameters – a mean and a variance. On the other hand, a bivariate normal distribution requires five parameters – two means, two variances, and a covariance.

Although KDKC's design is fairly complex, for our purposes the discussion may be limited to a subset of their stimuli without loss of generality. Consider the stimuli employed in KDKC's experiment 2a, which consist of a factorial combination of low and high F1 and short and long voicing continuation (see KDKC's Figure 5, p. 40). Because both low F1 and long voicing continuation are cues for [+ voice] and consist of relatively more energy at low frequencies, while high F1 and short voicing continuation are cues for [– voice] and consist of relatively less energy at low frequencies, KDKC hypothesize that F1 and voicing continuation will be perceptually integral.

If F1 and voicing continuation are perceptually integral, the perceptual effect of F1 will depend on the amount of voicing continuation, and the perceptual effect of voicing continuation will depend on the frequency of F1. The complement of perceptual integrality is perceptual separability. We would say that F1 is perceptually separable from voicing continuation if the perceptual effect of F1 did not depend on the amount of voicing continuation. Similarly, we would say that voicing continuation is perceptually separable from F1 if the perceptual effect of voicing continuation did not depend on the frequency of F1.

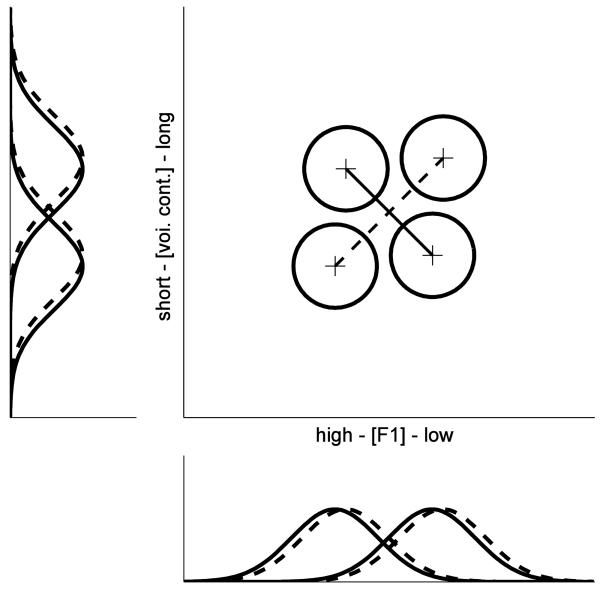
KDKC hypothesize that the pair of stimuli whose components vary in the same natural way (i.e., low F1, long continuation vs. high F1, short continuation), which, following KDKC, we will refer to as the positively correlated pair, will be easier to distinguish than the pair whose components vary in an opposing manner (i.e., high F1, long continuation vs. low F1, short continuation), which we will call the negatively correlated pair. In addition, they hypothesize that this pattern of relative discriminability will be due to perceptual integrality of a specific form, namely mean-shift integrality. Figure 1 depicts four equal likelihood contours (i.e., sets of points at constant height above the F1-voicing continuation plane) for four bivariate normal densities (i.e., modeled perceptual distributions) configured to illustrate mean-shift integrality. Each bivariate density has equal (unit) variance on each dimension and zero covariance (i.e., zero [perceptual] correlation). Figure 1 here is analogous to KDKC's Figure 2b (p. 32), but here the (co)variance structure of each perceptual distribution is explicitly represented (whereas in KDKC's Figure 2b, (co)variance is not illustrated).

Figure 1.

Example of Mean Shift Integrality. In the square panel (top right), the circles indicate equal likelihood contours of four bivariate normal densities. The plus signs indicate the means of the densities. The dashed line connects the positively correlated pair, and the solid line connects the negatively correlated pair. The bottom and left rectangular panels show the marginal (univariate normal) densities. In each marginal panel, solid-line densities correspond to the closer pair and dashed-line densities correspond to the more distant pair of bivariate densities.

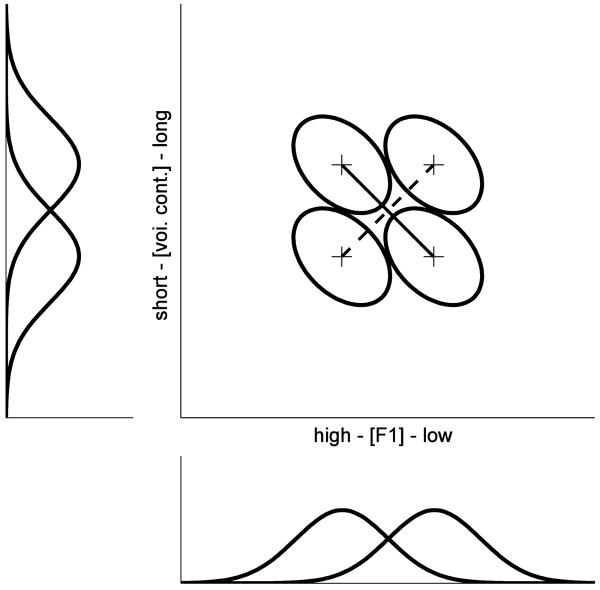
Figure 2.

Illustrative Example of Separability and Failure of Stochastic Independence. In the square panel (top right), the ellipses indicate equal likelihood contours of four bivariate normal densities with negative covariance. The plus signs indicate the means of the densities. The dashed line connects the positively correlated pair, and the solid line connects the negatively correlated pair. The bottom and left rectangular panels show the marginal (univariate normal) densities. Because perceptual separability holds here, there are only two (solid line) marginal densities visible in each marginal panel.

Note that other forms of integrality (i.e., failures of separability) are possible. This is because the definitions of separability and integrality are, in a sense, asymmetric. For example, F1 would be said to be separable from voicing continuation if, and only if, the perceptual effect of F1 were identical across levels of voicing continuation, regardless of whether or not the perceptual effects of voicing continuation are identical across levels of F1. Mutatis mutandis for the perceptual separability of voicing continuation from F1. On the other hand, perceptual integrality is anything other than this. To paraphrase Tolstoy, pairs of perceptually separable dimensions are all alike; every pair of perceptually integral dimensions are perceptually integral in their own way.

Failures of perceptual separability between F1 and voicing continuation are evident in the marginal panels of Figure 1. In the bottom panel, the dashed line marginal densities, which represent the perceptual effect of F1 for stimuli with long voicing continuation, are shifted relative to the solid line marginal densities, which represent the perceptual effect of F1 for stimuli with short voicing continuation. The same type of failure of perceptual separability on the other dimension is shown in the left panel. In this example, all marginal variances are the same.¹

The diagonal d′ values of interest to KDKC would, in this case, be measured along the dashed and solid lines in the main (square) panel of Figure 1. KDKC observed statistically significantly larger d′ values for the same sign pair than for the opposite sign pair in their experiment 2a (as well as 2b). Careful inspection of Figure 1 should make it clear that this configuration of perceptual distributions would produce exactly this pattern of results.² The positively correlated pair appear ‘farther apart’ from one another than do the negatively correlated pair.³

2. Generalized d′, separability, and independence

Unidimensional d′ is defined as the distance between the means of two univariate normal densities relative to their common or pooled standard deviation. When extended to a multidimensional situation, this d′ definition must take into account the complete covariance structure of both stimulus distributions. Thomas (1999, 2003) defined a generalization of the unidimensional d′, referred to as a generalized $d_g^{\prime }$ :

$$d_g^{\prime }(S_1,S_2)=\frac{{({\overrightarrow{\mu }}_2-{\overrightarrow{\mu }}_1)}^T({\overrightarrow{\mu }}_2-{\overrightarrow{\mu }}_1)}{\sqrt{\frac{1}{2}{({\overrightarrow{\mu }}_2-{\overrightarrow{\mu }}_1)}^T({\Sigma }_1+{\Sigma }_2)({\overrightarrow{\mu }}_2-{\overrightarrow{\mu }}_1)}}$$

where ${\overrightarrow{\mu }}_i$ and σ_i are the mean vector and covariance matrix for the density corresponding to the i^th stimulus, and superscript T indicates the vector transpose.

Conceptually, this $d_g^{\prime }$ measures a “distance” between the stimulus means relative to a pooled standard deviation from the univariate random variables that arise from projecting the multivariate densities onto a chord connecting the means of the two stimuli whose sensitivity is being scaled. This $d_g^{\prime }$ emanates from a decision strategy whereby the observer places an experienced percept into the response category whose perceptual mean is the closest in the Euclidean sense (Thomas, 2003) which is a reasonable strategy for the experimental condition typically used to compute a diagonal d′. Because of this, the pattern of d′ values observed by KDKC can also be produced by a configuration of perceptual densities wherein the two dimensions are mutually perceptually separable and statistical independence fails.

The parameters employed here were chosen to closely approximate the d′ values observed by KDKC, using Thomas' (1999, 2003) formula for generalized $d_g^{\prime }$. A configuration exhibiting perceptual separability and negative covariance within perceptual densities is illustrated in Figure 2. In this configuration of perceptual distributions, because perceptual separability holds across the board, the perceptual effect of F1 is identical across levels of voicing continuation (as can be seen in the bottom panel), and the perceptual effect of voicing continuation is identical across levels of F1 (as can be seen in the left panel). However, because there is negative covariance in each density, $d_g^{\prime }$ for the same sign pair 3.62, and $d_g^{\prime }$ for the opposite sign pair is 2.39. By way of comparison, for the illustrative parameters employed in generating Figure 1, $d_g^{\prime }$ for the same sign pair is 3.54, while $d_g^{\prime }$ for the opposite sign pair is 2.83 (cf. Figure 6, KDKC, p. 42, shaded bars).

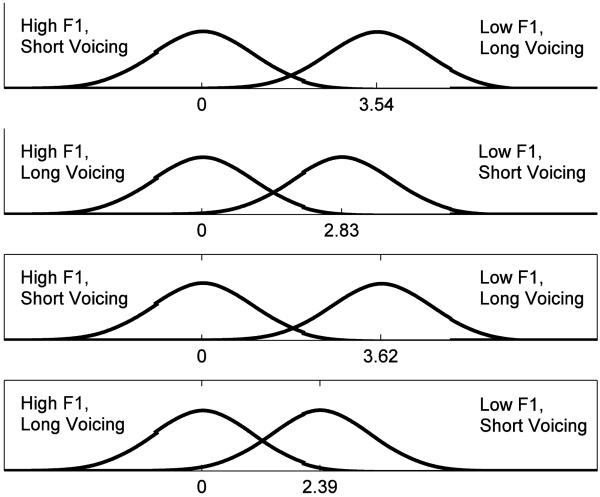
Figure 3 illustrates the univariate densities for the positively and negatively correlated pairs (i.e., the projections of the bivariate densities onto the chords connecting these pairs' means) for the mean-shift integrality and failure of stochastic independence examples illustrated in Figures 1 and 2, respectively. In each case, the x-axes are scaled by the common standard deviation of the two densities to facilitate comparisons across panels. As is readily apparent, diagonal d′ alone is unable to distinguish between mean shift integrality and separability with failure of stochastic independence. Furthermore, because d′ is not a metric, the marginal d′s do not bear any useful relationship to the diagonal d′s (cf. KDKC's discussion on p. 35); these two cases cannot be disambiguated even with knowledge of d′ for F1 at each level of voicing continuation and d′ for voicing continuation at each level of F1.

Figure 3.

Projected 'Diagonal' Univariate Densities. Each panel depicts projected univariate densities for 'diagonal' pairs of stimuli. The top panel shows projected densities for the positively correlated pair in the mean shift integrality case illustrated in Figure 1. The second panel from the top shows projected densities for the negatively correlated pair in the mean shift integrality case. The third panel from the top shows projected densities for the positively correlated pair in the failure of stochastic independence case illustrated in Figure 2. The bottom panel shows projected densities for the negatively correlated pair in the failure of stochastic independence case.

3. Discussion

To be clear, no claim is being made in this letter that the alternative explanation is correct or that the explanation proffered by KDKC is incorrect. The point here is simply that a potentially important aspect of the multidimensional SDT model – the covariance structure of the bivariate perceptual distributions – was left unexplored in KDKC's analyses. Importantly, the two configurations of model parameters illustrated above produce patterns of diagonal d′ essentially identical to those observed by KDKC, yet the interpretations of the underlying perceptual spaces differ substantially. As KDKC point out, if true mean-shift integrality underlies their data, this suggests that F1 and voicing continuation are mapped incompletely onto a single dimension. On the other hand, if the dimensions are separable but stochastic independence fails, this suggests that there is covarying perceptual noise in the (separable) processing channels for F1 and voicing continuation. Of course, it is also possible that both mean shift integrality and failure of independence underlie the data. The same basic argument applies to each case in which this particular pattern of diagonal d′s is observed.

It is important to note that these two theoretical possibilities – mean-shift integrality and (negative) within-stimulus perceptual covariance – are empirically indistinguishable using data obtained from a discrimination of the positively correlated pairs versus negatively correlated pairs, as they are mathematically equivalent in terms of predicted response probabilities. This fact may not be particularly important if one simply embraced one interpretation (e.g., mean-shift integrality) over the other (negatively covarying percepts) as the definition of perceptual interaction. However, in numerous publications, Ashby, Thomas, and their colleagues (Ashby & Townsend, 1986; Ashby, 1989, 2000; Thomas, 2001, 2002) have argued that these sources of interactions are conceptually different, and hence, are, in principle, empirically distinguishable when probed using designs of sufficient complexity.

One such successful attempt to disambiguate these two possibilities can be found in Olzak & Wickens (1997) who examined the nature of the perceptual interaction between components of compound sine-wave gratings in visual discrimination tasks. Using enough response categories and stimulus conditions, they were able to convincingly argue in favor of a true mean-shift integrality for one pair of stimulus dimensions (see Fig. 10, p. 1116). Their interpretation of this observed integrality was that information from the two stimulus attributes were combined in a summing circuit and that the observer's responses were actually made on the basis of the univariate result of that summing circuit. This conclusion is fundamentally different from a covarying noise conclusion, in which channels that process the stimulus dimensions remain separate but may experience cross-talk or be influenced by a common third mechanism.

Fortunately, recent developments in the GRT framework may be able to disambiguate these alternatives. For example, Thomas (2001, 2002), Wickens (1992), and Silbert, Townsend, and Lentz (2007) have developed parameter estimation techniques and comparative model fitting analyses of visual (Thomas and Wickens) and auditory perception experiments (Silbert, et al.) in which complete factorial combinations of stimulus attributes (i.e., not just pairs) are presented. Analysis of response times has also proven useful in this regard (Ashby & Maddox, 1994; Thomas, 2001).

To give a brief outline of one suggested method for disambiguating failure of perceptual independence and failure of perceptual separability, Silbert, et al., presented complete factorial sets of stimuli in multiple stimulus presentation base rate conditions (e.g., in terms of KDKC's dimensions, one base rate condition would have long voicing continuation stimuli presented more often than short voicing continuation stimuli, another would shift base rates in the opposite direction; analogous shifts in the presentation rate of high and low F1 stimuli could also be employed). Each base rate conditions produces a separate confusion matrix; the data aggregated across conditions then have degrees of freedom sufficient to constrain a fully general Gaussian GRT model (i.e., a model in which perceptual covariance and perceptual integrality may be modeled separately). In essence, multiple base rate conditions provide multiple observations of the shape and location of perceptual distributions. To the extent that negative covariance within distributions and shifts of means across distributions produce distinct patterns of identification confusions, they should be empirically distinguishable. We are currently carrying out simulations to test the ability of base rate manipulations and parameter estimation to distinguish between a large number of combinations of perceptual and decisional (failures of) independence and separability.

KDKC's work is, as it stands, exciting and very interesting; the role of auditory processing in speech perception deserves sophisticated study, which KDKC provide in generous measure. As the reader is undoubtedly aware, speech is an extremely complex signal, and the dimensions investigated by KDKC represent a small subset of the acoustic dimensions the could be profitably probed using GRT. We hope that everyone's interests will eventually be advanced through the application of more general, and more powerful, GRT tools to the perception of speech. KDKC's work shows the value of these tools in studying the structure within phonetic categories; they may also be productively applied to the structure between phonetic categories (e.g., Silbert, et al., 2007).

Appendix: Illustrative Parameter Values

Mean Shift Integrality	High F1 Short Voicing	High F1 Long Voicing	Low F1 Short Voicing	Low F1 Long Voicing
μx	0	0.25	2.25	2.5
μy	0	2.25	0.25	2.5
Failure of Independence	High F1 Short Voicing	High F1 Long Voicing	Low F1 Short Voicing	Low F1 Long Voicing
μx	0	0	2	2
μy	0	2	0	2

For mean shift integrality: $\Sigma =\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$; for failure of independence: $\Sigma =\left[\begin{array}{cc}\hfill 1\hfill & \hfill -0.4\hfill \\ \hfill -0.4\hfill & \hfill 1\hfill \end{array}\right]$