Modeling Nutrient Consumptions in Large Flow-Through Bioreactors for Tissue Engineering

Abstract

Flow-through bioreactors are utilized in tissue regeneration to ensure complete nutrient distribution and apply defined hydrodynamic stresses. The fundamental concepts in designing these bioreactors for regenerating large high aspect ratio tissues (large surface area relative to the thickness of the matrix such as skin, bladder, and cartilage) are not well defined. Further, tissue regeneration is a dynamic process where the porous characteristics change due to proliferation of cells, de novo deposition of matrix components, and degradation of the porous architecture. These changes affect the transport characteristics and there is an imminent need to understand the influence of these factors. Using computational fluid dynamic tools, changes in the pressure drop, shear stress distribution and nutrient consumption patterns during tissue regeneration were assessed in rectangular and circular reactors described by Lawrence et al (Lawrence et al. 2008). Further, six new designs with different inlet and outlet shapes were analyzed. The fluid flow was defined by the Brinkman equation on the porous regions using the pore characteristics of 85 μm and 120 pores/mm². The minimum flow requirements to satisfy nutrient (oxygen and glucose) requirements for three different cell types (SMCs, chondrocytes, and hepatocytes) was evaluated using convective diffusion equation. For consumption reaction, the Michaelis-Menten rate law was used, with constants (k_m and v_m values) extracted from literature. Simulations were performed by varying the flow rate as well as the cell number. One of the circular reactors with semicircular inlet and outlet shape decreased (i) non-uniformity in hydrodynamic stress within the porous structure and (ii) non-uniform nutrient distribution. All cell types showed increased consumption of oxygen than glucose. Hepatocytes needed a very high flow rate relative to other cell types. Increase in cell number suggested a need for increasing the flow in circular reactors.

INTRODUCTION

Regeneration of tissues outside the body utilizes a system where cells are populated in a porous biodegradable scaffolds in an optimum environment similar to the human body. Bioreactors of different shapes and flow systems have been utilized as a way to maintain optimum environmental conditions including sufficient amount of nutrients (Cummings and Waters 2007; Martin et al. 2004; Martin and Vermette 2005). To ensure complete nutrient distribution, flow-through configuration has been utilized as an approach to grow tissues (Botchwey et al. 2003; Goldstein et al. 2001; Jeong et al. 2005; Phillips et al. 2006; Sikavitsas et al. 2003; Sikavitsas et al. 2005). Apart from improving the distribution of the nutrients and replenishing the medium, the flow-through configuration stimulates mechanical stresses induced due to the nutrient flow which improves the proliferation, attachment and activity of some of the cell types.

Flow rate through the scaffold microarchitecture directly dictates the sufficiency of nutrients necessary for cellular activity and local shear stresses experienced by the cells. Very low flow rate could lead to nutrient deficiency and limited cell survivability. However, high flow rate leads to high shear stresses and cells respond to the level of hydrodynamic stress by remodeling their surrounding extracellular matrix and changing the tissue composition (Chatzizisis et al. 2007; Cooper et al. 2007). Further, high flow rates could deteriorate the quality of the regenerated tissues via washout of the de novo synthesized matrix elements prior to complete assembly. Flow conditions also affect scaffold degradation rates which in turn affect the structural and mechanical properties (Agrawal et al. 2000). Cellular constructs grown in vitro shrink, possibly as a result of contraction or as a result of hydrodynamic forces compressing the scaffold (Lo et al. 2000). Optimizing the flow rate of the nutrients is very important while designing a bioreactor for tissue regeneration.

Nutrient consumption and shear stress distribution in flow-through perfusion reactors have been widely investigated using computational fluid dynamic methodologies (Chung et al. 2008; Chung et al. 2007; Porter et al. 2005; Raimondi et al. 2006). The majority of these studies assess the flow patterns and shear stresses around small porous constructs. However, the fundamental concepts in developing these reactors for regenerating large tissues (for example skin, bladder, and cartilage) are not well defined. Many tissues have a high aspect ratio (large surface area relative to the thickness of the matrix) and contain multiple cell types. Effect of flow-through configuration within these systems has not been studied.

Previously, we reported the effect of the bioreactor shape and position of inlets and outlets on flow distribution and shear stress in high aspect ratio reactors containing porous structures (Lawrence BJ 2008). The non-ideal fluid distribution was characterized using the residence time distribution (RTD) analysis, which measures the amount of time different molecules present in the fluid spend within the reactor (Fogler 2006; Lawrence et al. 2004), allowing for consumption by the cellular components. The RTD analysis is independent of the metabolic reactions, although the total consumption of nutrients is determined by the residence time. Hence, simulations have to be performed with consumption to understand the nutrient distribution.

The objective of this study was to evaluate the nutrient distribution with consumption in high aspect ratio flow-through bioreactors containing porous structures. Since the previous circular reactors showed high shear stress regions at the inlet and outlet, six new reconfigured reactors with different extension shapes were analyzed for shear stress distribution. Simulations were performed using CFD packages CFX 11 (ANSYS Inc, Canonsburg, PA.) for flow distribution without porous structure and Comsol Multiphysics 3.4 (COMSOL, Inc., Burlington, MA) for flow distribution with nutrient consumption in the porous structure. One design was chosen depending on the pressure drop and shear stress distribution. Metabolic consumption for both oxygen and glucose was included using Michaelis-Menten type rate law for oxygen (and glucose consumption in some cell types). Nutrient transport and consumption was investigated in three different cell types based on the reaction rates reported in the literature (Alpert et al. 2002a; Fogler 2006; Motterlini et al. 1998a; Sengers et al. 2005b)

1. smooth muscle cells (SMCs) – present in various tissues, very responsive to stress levels

2. hepatocytes – metabolically very active, and very sensitive to nutrient levels

3. chondrocytes – anatomically located in a less metabolic demand area and it is less proliferative.

The shear stress and pressure drop analysis was also done and compared with the previous design. To understand the effects of changing porous characteristics during tissue regeneration attributed to de novo synthesis of matrix elements and cell colonization, simulations were also performed. These results show significant flow rate dependency on cell type used.

2. MATERIALS & METHODS

2.1. Sources of Materials

Chitosan with >310 kDa MW and 85% degree of deacetylation, and glacial acetic acid were obtained from Sigma Aldrich Chemical Co (St. Louis, MO). Ethanol (200 proof) was obtained from Aaper Alcohol and Chemical Company (Shelbyville, KY). All other reagents were purchased from Fisher Scientific (Waltham, MA).

2.2. Reactor Designs

Since flow rates are dependent on the size and shape of the bioreactor, simulations were performed in two different shaped reactors,

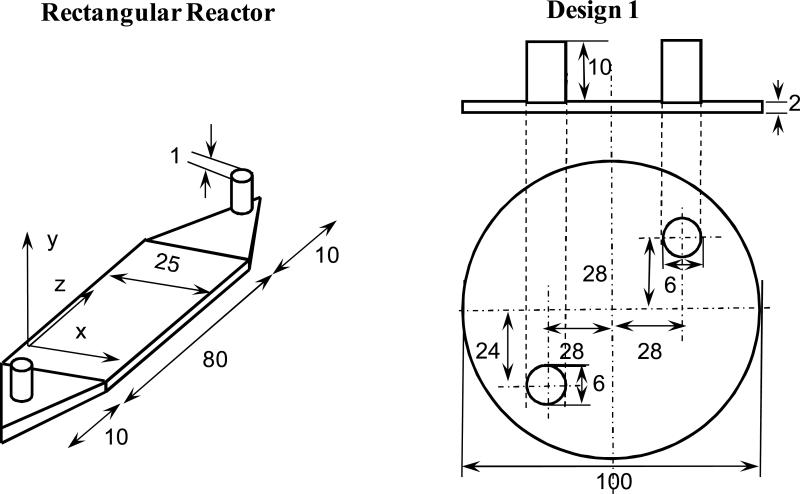
1. rectangular (8 cm long, 2.5 cm wide, and 0.2 cm high, with a 0.1cm inlet and outlet diameter) with inlet and outlet from the top, commonly used configuration in a variety of cell studies (Huang et al. 2005; Tilles et al. 2001);

2. circular (10 cm diameter and 0.2 cm high, with a 0.6 cm inlet and outlet diameter) reactor with different inlet and outlet designs. Design 1 was similar to the circular reactor previously reported (Lawrence BJ 2008) with inlet and outlet located directly on top of the porous structure. Six different designs with different inlet and outlet shapes and locations placed away from the region occupied by the scaffold inlet (Figure 1) were evaluated:

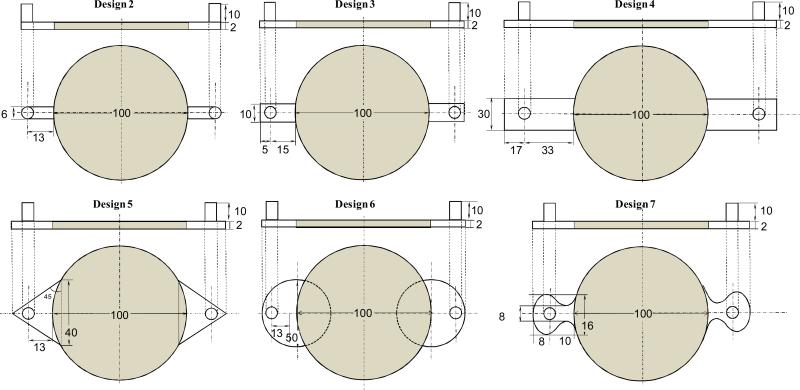
   • Design 2 had a 0.6 cm wide channel extension at the entrance and the exit. The center of the inlet and the outlet were at a distance of 1.3 cm away from the porous region.
   • In Design 3, the rectangular extensions were increased to a length of 1.8 cm and a breadth of 1cm. Further, a 2 mm region to the back of the inlet or outlet was also placed to allow the fluid to flow to the back of those regions with the idea of dispersing the stresses.
   • In Design 4, the rectangular extensions were further increased to a length of 5 cm and a breadth of 3 cm. The inlet and outlet were around 2.7 cm away from the porous region.
   • Design 5 had triangular extensions with an angle of 45 and a hypotenuse of 4 cm length. The inlet and outlet were at a distance of 8mm from the porous region.
   • Design 6 had semicircular extension of radius 2.5 cm for the inlet and the outlet. The center of the inlet and the outlet were at a distance of 1.3 cm away from the porous region.
   • Design 7 had curved extensions. The fluid at the inlet was forced to flow through a constricted area which expanded smoothly into the large area where the scaffold was placed. The outlet was the mirror replica of the inlet.

Figure 1.

Schematic of reactor designs used in this study. For circular reactors top view is shown along with the side view. All dimensions are in millimeters.

These reactor geometries were created using a CAD package (Solidworks™ or ANSYS Workbench 11). The CFX mesh was then created using ANSYS CAD2Mesh software. A critical challenge was overcoming problems associated with the aspect ratio i.e., very large surface area relative to the thickness of the channel. Maximum element size of 0.1 mm was chosen and a fine triangular mesh was created such that there were at least 10 nodes across the thickness of the reactor. The simulations were performed under steady state conditions. The outlet was set at atmospheric pressure and the walls were smooth with no slip condition. All the simulations in ANSYS were carried out at a flow rate of 5 mL/min or 1 mL/min.

2.3. Simulating fluid flow in the porous structure

Based on the pressure drop and shear stress distribution analysis, Design 6 was selected for further analysis in presence of porous structure along with Design 1. The steady state analysis of the fluid flow was performed using the COMSOL 3.4 Multiphysics (COMSOL, Inc., Burlington, MA). Three dimensional (3D) reactor models were created by extruding 2D reactor drawings using work plane settings option in the Draw tab and 3D Model View. Next, the subdomain and boundary conditions were set in the Physics tab. As the surface area is very large compared to the thickness of the reactor, a rectangular mesh was created to ensure that there were minimum 4 nodes across the 2mm thickness of the reactor by doing a swept mesh; rectangular mesh is more uniform than the regular triangular mesh and computationally less demanding. Initially the flow rate was set at 5 mL/min, which is the experimentally determined flow rate that can be used without affecting the chitosan porous structure. The flow rate was reduced to 1 mL/min and then to 0.001 mL/min to determine the minimum flow rate at which the nutrients were consumed fully. First, the simulations were performed to determine the velocity profiles by solving a) the Incompressible Navier –Stokes equation on the non-porous regions and b) the Brinkman equation on the porous regions. The nonporous sections of the reactor were modeled solving incompressible Navier-Stokes equation which is given by

$$\rho (u•\nabla )u=-\nabla •[-\tau +p{\delta }_{ij}]$$ (1)

$$\nabla •u=0$$ (2)

where η is the dynamic viscosity (Pa·s), ρ is the fluid's density (kg/m³), p is the pressure (Pa), δ_ij is the Kronecker delta function. The Brinkman equation is given by

$$\mu {\nabla }^2{u}_s-\frac{\mu }{\kappa }{u}_s=\nabla p$$ (3)

$$\nabla •u_s=0$$ (4)

where κ is the permeability of the porous medium (m²), u_s denotes the fluid superficial velocity vector (m/s), p is the fluid pressure (Pa), and μ is the effective viscosity in the porous medium (kg/m.s). The permeability (κ) of the porous medium is a geometric characteristic of the porous structure at several length scales. Based on the pore architecture of chitosan porous structures(Huang et al. 2005; Huang et al. 2006), the permeability was calculated using an average pore size of 85 μm and 120 pores/mm² in the equation

$$\kappa =\frac{\pi }{128}{n}_A{d}^4$$ (5)

where n_A is the number of pores per unit area and d is the average pore diameter. Both the permeability (κ, m²) and void fraction (ε_p, dimensionless) were incorporated into Eq.(3) in order to account for the porous characteristics of the matrix, yielding another form of the Brinkman Equation

$$\frac{\eta }{k}u=-\nabla •\left[\frac{-\tau }{{\epsilon }_p}+p{\delta }_{ij}\right]$$ (6)

The shear stress tensor is an integral part of the Navier-Stokes equations describing flow in a free channel. The shear stress was visualized as the viscous force per area in the z direction, as calculated by

$$\tau •n$$ (7)

where ε_p is the porosity of the porous media, taken as 85% based on the chitosan porous structure characteristics. While solving the incompressible Navier-Stokes equations, the perpendicular flow was given as 5 mL/min and the outlet boundary condition was set as pressure =0.

2.4. Simulating reaction in the porous region of the reactor

Using the steady state velocity profiles, the steady state concentration profiles of oxygen and glucose were obtained by solving the equation of continuity using the chemical reaction engineering module in COMSOL 3.4 Multiphysics. Nutrient consumption was included in the simulation via the rate law. The convective diffusion equation was used to obtain the concentration at varying position along the cross section of the reaction:

$$\nabla •(-D\nabla c)+u•\nabla c=r_A$$ (8)

where c_A is the concentration of the species (mol/m³), r_A is the rate of reaction of the species under consideration (mol/m³.s), D is the diffusivity of the species (m²/s), and u is velocity vector (m/s). Physical properties of water were used as it constitutes the bulk of the growth medium. The flow properties (i.e., viscosity and density) of the nutrient stream depend on the properties of the bulk fluid. Since the cells are present only in the porous scaffolds, nutrient consumption rate law was defined only in the porous region, the reaction term was zero in the non-porous regions.

Michaelis-Menten type rate law was used for both oxygen and glucose consumptions based on the reaction rates reported in the literature (Alpert et al. 2002a; Fogler 2006; Motterlini et al. 1998a; Sengers et al. 2005b). The rate law is given by the expression

$$-{\mathrm{r}}_{\mathrm{A}}=\frac{{\mathrm{v}}_{\mathrm{m}}{\mathrm{c}}_{\mathrm{A}}}{{\mathrm{k}}_{\mathrm{m}}+{\mathrm{c}}_{\mathrm{A}}}$$ (9)

where r_A is the reaction rate, v_m is the maximum reaction rate, and k_m is the Michaelis constant. For oxygen, C_A was replaceda by c₁ the oxygen concentration. In the case of glucose, C_A is replaced by c₂ the glucose concentration. Both the rate laws were defined in the COMSOL, enabling the visualization of both the oxygen and glucose profiles within the porous structure.

2.5. Determination of Michaelis-Menten parameters from Literature

Based on the reaction rates reported in the literature for cells cultured on tissue culture plastic surface (Alpert et al. 2002a; Motterlini et al. 1998a; Sengers et al. 2005b), the k_m and v_m values were obtained for three cell types. The kinetic parameters for oxygen and glucose consumption in chondrocytes reported by Sengers et al was used (Sengers et al. 2005a). For SMCs, the oxygen kinetic parameters were calculated from the partial pressure vs time plot reported by Motterlini et al (Motterlini et al. 1998a). Partial pressure of oxygen with respect to time was converted to concentration using Henrys law constant at 37°C and 1 atm. Then, Hanes-Woolf plot was developed to determine k_m and v_m values. The kinetic parameters reported by Alpert et al data was used (Alpert et al. 2002b) for glucose consumption in SMCs. For hepatocytes the kinetic parameters of oxygen were calculated from the partial pressure vs time reported by Balis et al (Balis et al. 1999). Table 1 shows the calculated kinetic parameters for three cell types. In all conditions, the v_m values were recalculated to the constant cell number used in the simulation. The simulations were performed at the same cell density (1.2×10¹² cells/m³). The changes in cell number were accomplished by scaling the v_m values. The concentration of oxygen and glucose at the inlet was given as:

$$c_i=c_{i0,inlet}$$ (10)

The initial concentration of oxygen in the growth medium was determined using the Henry's law constant at 37°C for each cell type (Table 1). Initial concentrations of glucose were based on the growth media (Table 1) formulations used for each cell type. Mass transport at the outlet was assumed to be dominated by convection with negligible contribution from diffusion i.e.,

$$n\cdot c_{i}u=R_A$$ (11)

At all other boundaries, insulating conditions were specified as

$$n\cdot (-D_i\nabla c_i+c_{i}u)=0$$ (12)

Table 1.

Rate Constants of oxygen and glucose for different cell types.

Cell type	Oxygen		Glucose		Inlet concentrations
	Km (mol/m3)	Vm (μmol/m3.s)	Km (mol/m3)	Vm (μmol/m3.s)	Oxygen (mol/m3)	Glucose (mol/m3)
Chondrocytes	6.0×10−3	2.47	0.35	45.1	0.205	5.1
SMCs	0.205	31.6	0.93	48.6	0.199	5.5
Hepatocytes	0.0263	41.1	-	-	0.214	-

3. RESULTS

3.1. Effect of Inlet and Outlet shape on pressure drop and shear stress

Assessment of shear stresses developed within the porous structures in Design 1 showed an increase in shear stress at the inlet and the outlet locations in circular reactors, unlike in rectangular reactor where the stresses were uniform. In addition, while performing experiments in circular reactors, it was observed that the porous structures were compressed at the inlet and the flow traveled over the top of the porous structures and along the walls with some infiltration into the porous structure. This bypass effect was minimized in the rectangular reactor by providing space at entry and exit, thereby ensuring that the flow entered the porous structure instead of bypassing it.

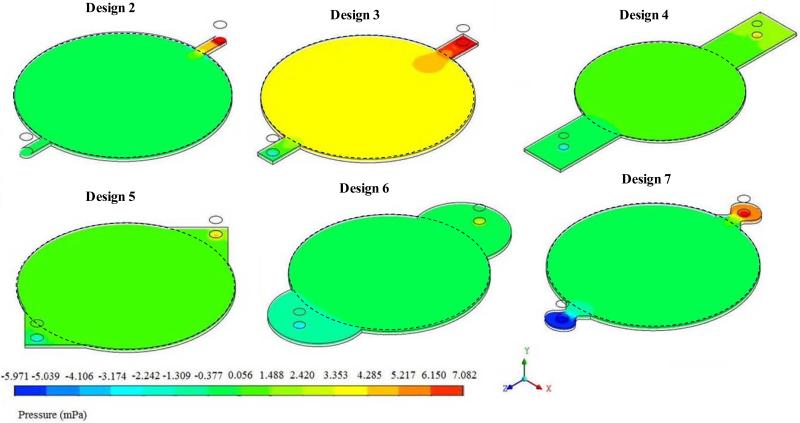
Based on these observations, the circular reactor was reconfigured by placing the inlets and outlets away from the porous structures, similar to rectangular reactor. When the pressure distribution across the porous region where the cells are grown was analyzed (Figure 2), Design 7 showed significant pressure drop across the reactor, probably due to the sudden expansion at the inlet and sudden reduction at the outlet. Design 3 operated at a higher pressure relative to other designs within the porous region. In Designs 2, 4, 5 and 6 the pressure distribution throughout the porous structure was uniform with high and low pressures near the entrance and exit respectively. Thus, from the pressure distribution analysis, Designs 2, 4, 5, and 6 were considered as potential designs useful in tissue regeneration.

Figure 2.

Variation in the distribution of pressure within the circular region due to inlet and outlet shapes.

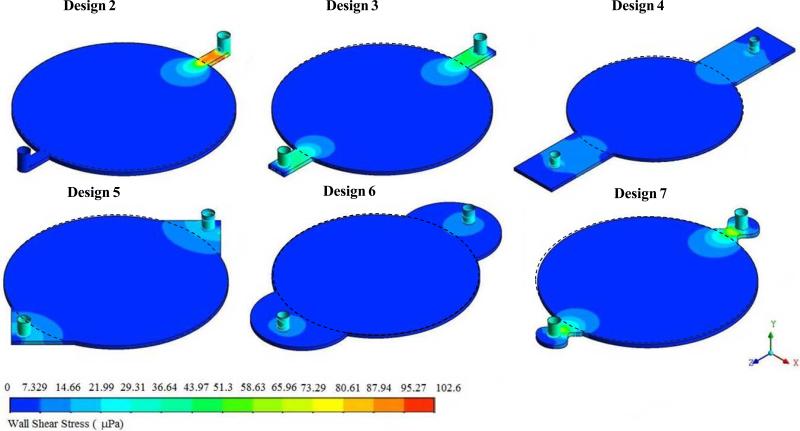
Next, the shear stress distribution was analyzed in all six designs. These results showed (Figure 3) that the shear stress was high near the entrance and the exit in designs 2, 3 and 7. In design 2, the shear stress was higher than in any other designs and it was higher near the entrance. Only Design 6 had uniform shear stress in the region where porous structure was present (indicated by the dotted circle). All other designs had some region with in the reactor area where shear stress varied. Based on these observations, Design 6 was considered for further analysis along with Design 1.

Figure 3.

Variation in the distribution of shear stress within the circular region due to inlet and outlet shapes.

3.2. Effect of flow rate on pressure drop and shear stress

Next, the pressure drop across different reactors and the shear stresses developed within the porous structures were assessed for different flow rates. Table 2A & 2B show the variation in the pressure drop and the shear stresses for chondrocytes and SMCs at different flow rate for each reactor design. Since these were based on Brinkman equation, without the effect of nutrient consumption, the pressure drop and shear stresses were not a function of the cell type (and their rate constants) but only the flow rate. Increase in flow rate increased the pressure drop and shear stresses in both the designs by similar magnitude; a 10-fold increase in flow rate increased the shear stresses and the pressure drop by 10-fold. However, Design 6 showed a marginal reduction in pressure drop at all the flow rates relative to Design 1. Importantly, the shear stress levels in Design 6 were lower by an order of magnitude relative to Design 1 at similar flow rates. Further, shear stress levels were uniform in the region where porous structure was present in Design 6, unlike Design 1 where significantly high level of shear stresses were observed at the inlet and outlet locations for the same flow rate.

Table 2.

Pressure Drop and Shear Stress within the reaction simulations at different flow rate for 85μm pore size, 120 pores/mm² and 154 μm² permeability

(A) Rectangular Reactor
	Chondrocytes		SMCs
Flowrate (mL/min)	ΔP (Pa)	Maximum Shear Stress (Pa)	ΔP (Pa)	Maximum Shear Stress (Pa)
0.001	0.126	4.77×10−6	0.126	4.77×10−6
0.003	0.378	1.43×10−5
0.005	0.631	2.39×10−5
0.01	1.26	4.77×10−5	1.26	4.77×10−5
0.03			3.79	1.43×10−4
0.05			6.31	2.39×10−4
1	126	4.77×10−3	126	4.77×10−3
5	631	0.0237	631	0.0237

(B) Circular Reactor
	Design 1						Design 6
	Chondrocytes			SMCs
Flow rate (mL/min)	ΔP (Pa)	Max.Shear Stress (dynes/cm2)		ΔP (Pa)	Max.Shear Stress (dynes/cm2)		ΔP (Pa)	Max.Shear Stress (dynes/cm2)
		x-direction	y-direction		x-direction	y-direction		x-direction	y-direction
5	276.105	0.0153	0.0174	276.105	0.0153	0.0174	212.612	3.785×10−3	7.513×10−4
1	55.248	3.055×10−3	3.481×10−3	55.248	3.055×10−3	3.481×10−3	42.542	7.573×10−4	1.431×10−5
0.1	5.525	3.055×10−4	3.481×10−4	5.525	3.055×10−4	3.481×10−4	4.254	7.573×10−5	1.431×10−6
0.01	0.552	3.055×10−5	3.481×10−5	0.552	3.055×10−5	3.481×10−5	0.425	7.573×10−6	1.431×10−7
0.001	0.055	3.055×10−6	3.481×10−6	0.055	3.055×10−6	3.481×10−6	0.042	7.573×10−7	1.431×10−8

3.3. Effect of permeability on pressure drop and shear stresses

During the course of tissue remodeling, cells proliferate and synthesize matrix elements which are deposited in the porous structures. These processes reduce the pore space available for fluid flow. Hence the pore size decreases but the number of pores per area does not. To understand the implications of these dynamic changes, simulations were carried out with decreasing pore sizes (from 85 μm to 10 μm) at constant number of pores per unit area determined experimentally (120 pores/mm²). Similar to our previous report (Lawrence BJ 2008), the pressure drop increased with reduced permeability (data not shown). The pressure drop was inversely proportional to 1/k as predicted by the Brinkman equation. The shear stresses were high in the circular reactor Design 1. Comparison of results from Design 1 with Design 6 showed (Table 3) that pressure drop in Design 1 was consistently higher than Design 6. Further, shear stress was uniform in the region containing porous structures (Figure 4A) of Design 6, unlike Design 1 where high shear stresses were observed at the inlet and the outlet (Lawrence BJ 2008).

Table 3.

Effect of permeability and void fraction on pressure drop, maximum shear stresses and the outlet oxygen consumption in circular reactors containing SMCs at 0.1 mL/min.

				Design 1				Design 6
Pore Size (μm)	Pores/ mm2	k (μm2)	ε	Pressure Drop (Pa)	Maximum Shear Stress (μPa)		Outlet Oxygen Concentration (mol/m3)	Pressure Drop (Pa)	Maximum Shear Stress (μPa)		Outlet Oxygen Concentration (mol/m3)
					x- direction	y- direction			x- direction	y- direction
85	120	154	0.85	5.525	305.5	348.1	0.084	4.254	75.73	14.31	0.07
50	120	18.4	0.85	46.077	308.1	351.6	0.084	35.472	76.23	15.24	0.07
37.5	120	5.82	0.85	145.606	308.3	352.0	0.084	112.114	76.29	16.8	0.07
25	120	1.15	0.85	737.236	373.6	336.8	0.084	567.322	76.325	17.57	0.07
17.5	120	0.276	0.85	3070.54	373.7	336.8	0.084	2363.79	76.33	17.73	0.07
10	120	0.029	0.85	28796.7	373.7	336.8	0.084	22150	76.33	17.78	0.07
85	120	154	0.42	5.534	302.8	344.2
50	120	18.4	0.086	46.154	305.2	347.5
37.5	120	5.82	0.036	145.802	305.9	348.6

Figure 4.

Effect of changed fluid distribution in two circular reactors. (A) Histogram profiles showing the shear stress distribution. (B) Oxygen concentration stream-lines with consumption by SMCs. Also shown are the location of the minimum points along with the corresponding oxygen concentration in mol/m³.

The shear stresses increased in a non-linear manner as the pore sizes decreased. However, the change was not as significant as the pressure drop. Based on Eq.(6), shear stress is a function of void fraction also, unlike pressure drop. Since, void fraction was kept constant at 85% in these simulations, reduced sensitivity of shear stress to altered pore structure could be attributed to the constant void fraction. To understand the role of void fraction, simulations were performed by decreasing the void fraction at constant pore size and pore numbers. These results showed (Table 3) a marginal increase in shear stress with nearly 50% reduction in void fraction.

3.4. Steady state concentration profile of nutrients

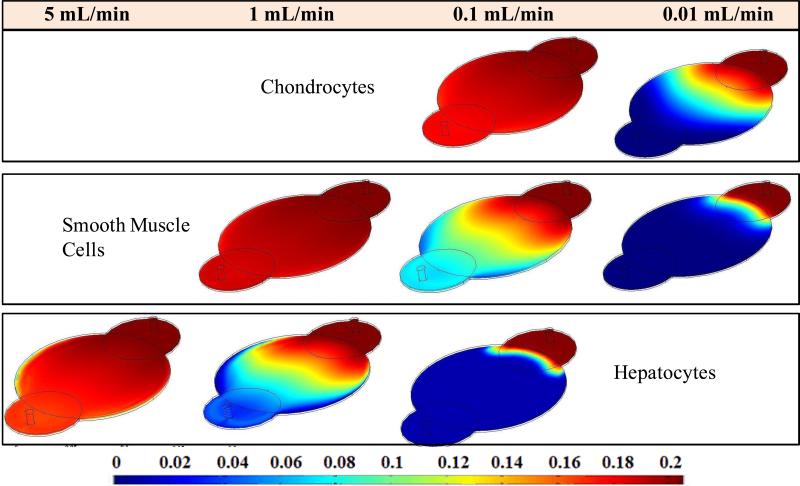
To understand the nutrient distribution with consumption, simulations were performed with defined rate laws using both oxygen and glucose rate law data for three cell types namely SMCs, chondrocytes and hepatocytes. The simulations were performed at the same cell density (1.2×10¹² cells/m³). These results showed increased consumption of oxygen (Figure 5) than glucose (Figure 6) for all cell types in both rectangular and circualr reactors. High oxygen consumption was observed in hepatocytes than in other two cell types. This can be attributed to the fact that hepatocytes are highly metabolic in nature compared to the other two cell types.

Figure 5.

Changes in oxygen concentration profile across the circular reactor Design 6 for different cell types at different flow rates.

Figure 6.

Changes in glucose concentration profile across the circular reactor for different cell types at different flow rates.

Next, effect of flow rate on nutrient consumption was investigated with the intention of determining the threshold flow rate at which the outlet oxygen concentration (and glucose) reached zero. Simulations were performed using flow rates ranging from 0.001 mL/min (very close to static culture) to 5 mL/min (experimental used flow rate for obtaining RTD). Flow rates were reduced in the increments of ten until a minimum flow rate was reached where the nutrients were completely consumed by the cells. These resultsa showed that oxygen limitation was reached at 0.05 mL/min and 0.1 mL/min in circular reactors (Design 1) containing SMCs, respectively. Chondrocytes needed very low flow rate (0.01 mL/min) and hepatocytes needed very high flow (1 mL/min). These flow rates were marginally higher for Design 6 because of increased holdup volume (Figure 4). Chondrocytes needed 0.1 to 0.01 mL/min flow rate, 1 to 0.1mL/min in case of SMCs and hepatocytes needed y 5 to 1 mL/min flow rate. Since rectangular reactor had significantly smaller holdup volume (4 mL) than circular reactors (15 mL), and shorter average residence time, oxygen and glucose consumptions were significantly less. Hence the minimum flow rate required for each cell type proportionally decreased for different cell types (data not shown).

3.5. Influence of residence time distribution on oxygen consumption for SMCs

The residence time distribution analysis is independent of the metabolic reactions, although the total consumption of nutrients is determined by the residence time. The contact time between cells and the nutrients depends on the residence time of the oxygen in the reactor and the residence time in turn depends on the volume of fluid distribution at constant flow rate. In rectangular reactor, minimum oxygen concentration in the entire corresponded to the outlet oxygen concentration, suggesting uniform fluid distribution (Figure 7). At 0.05 mL/min flow rate, the outlet oxygen concentration was 0.125 mol/m³ in presence of SMCs.

Figure 7.

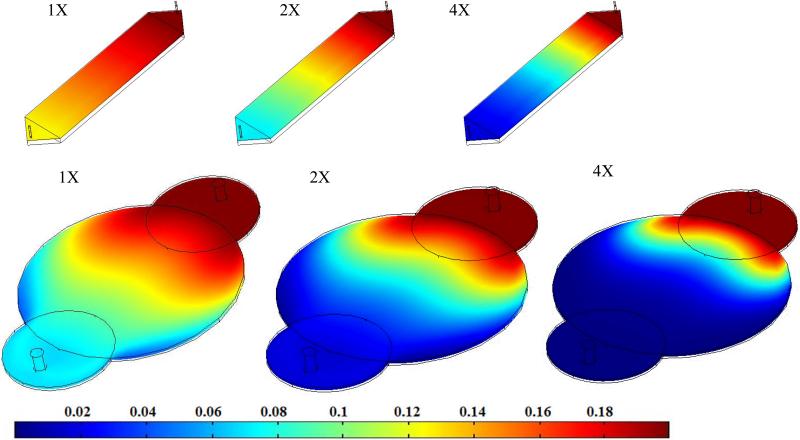
Effect of cell density on the oxygen consumption with 1X corresponding to 1.2 million cells per cm³.

To understand the improvements in fluid distribution in two circular reactors, concentration of oxygen at the outlet, C_mix, was calculated using

$$C_{mix}=\frac{\sum C_{avg}{V}_{arg}r\Delta r\Delta \theta }{\sum V_{arg}r\Delta r\Delta \theta }$$

where C_avg is the average oxygen concentration across the two finite elements and V_avg is the average velocity in the z-direction between those elements and r,θ were obtained using Cartesian coordinates relations $r=\sqrt{x^2+z^2}$ and $\theta =t{a}^{-1}n(x\mid z)$. Averaging was necessary as the concentration of the nutrients at the exit in Design 1 was not uniform due to the occurrence of reaction in the porous region. These results indicated that the consumption of oxygen was high in Design 6 relative to Design 1; the outlet oxygen concentration was 0.070 mol/m³ in Design 6 and 0.084 mol/m³ in Design 1.

Increased consumption could be attributed to improved fluid distribution i.e., with reduced channeling and dead volume. For example, presence of regions with decreased flow rate would reduce the replenishment of nutrients, creating a local minimum in the nutrient concentration. To assess whether the outlet oxygen concentration corresponds to the minimum concentration in the reactor i.e., the ideal fluid flow characteristics, stream line plots of oxygen concentration were generated. These results indicated that both Design 1(Figure 4B) and Design 6 had a minimum point near the exit of the reactor. There is a significant difference between the two designs in the minimum oxygen concentration and the outlet oxygen concentration: in Design1, the minimum oxygen concentration was 0.016 mol/m³ although the outlet concentration was 0.084 mol/m³ which implies that the medium has enough oxygen but not being utilized completely; in Design 6, the minimum oxygen concentration was 0.046mol/m³ which was very close to the outlet oxygen concentration of 0.070 mol/m³, implying better utilization of oxygen. Thus the low flow regions were reduced in Design 6, if not completely eliminated. This suggests a significant improvement in fluid flow although one needs to completely eliminate the low flow regions for generating a healthy tissue.

3.6. Effect of varying cell density on oxygen consumption

During tissue regeneration, cells grow and populate the porous structure. This increase in cell number could affect the fluid flow requirement. To understand the effect of increasing cell number on nutrient consumption, simulations were performed by assuming one and two doublings of initial cell seeding density. These results showed (Figure 7) that concentration of oxygen drastically decreased with increasing cell density of SMCs at the same flow rate. Regions with insufficient oxygen concentrations were observed in both circular reactor designs with two doublings in addition to the outlet concentration reaching zero, suggesting a need to increase the fluid flow rate. In the rectangular reactor, insufficient oxygen concentration regions were not observed although outlet oxygen concentration decreased to 0.071 mol/m³ with one doubling and 0.018 mol/m³ with two doublings. This suggests that dynamic changes in the cell population also affect the nutrient requirements. However, changes in cell number (Table 4) at constant permeability did not alter the pressure drop and shear stress at a constant flow rate. This could be explained by the fact that shear stresses and pressure drop were determined by the Navier-Stokes equation and Brinkman equation, independent of the reaction. Hence, change in cell number did not change shear stress and pressure drop.

Table 4.

Outlet oxygen concentration decreases as the number of SMCs increases with 120 Pores/mm² in Circular Reactors at 0.1 mL/min.

			Design 1		Design 6
Cell Multiplier	Pore Size (μm)	κ (μm2)	Minimum Oxygen Concentration (mol/m3)	Outlet Oxygen Concentrati on (mol/m3)	Minimum Oxygen Concentration (mol/m3)	Outlet Oxygen Concentration (mol/m3)
1×	85	154	0.0164	0.084	0.040	0.070
2×	85	154	9.679×10−4	0.036	0.005	0.017
4×	85	154	<0	0.006	7.605×10−5	0.001
1×	25	1.15	0.017	0.084	0.040	0.070
2×	25	1.15	9.677×10−4	0.036	0.005	0.017
4×	25	1.15	<0	0.006	7.794×10−5	0.001

4. Discussion

This study focused on understanding the fluid distribution with consumption in a flow-through bioreactor system useful in generating large pieces of high quality tissues. In a recent report from our laboratory, the effect of inlet and outlet locations on fluid distribution was demonstrated (Lawrence et al. 2008). These results showed that presence of inlet and outlet of the reactor directly on top of the porous structure compressed the porous structure. Further, simulation results confirmed a significant increase in shear stresses at the inlet and the outlet of the reactor while performing experiments. Since cells respond to hydrodynamic stresses by remodeling their surrounding ECM and change the tissue structure and composition to meet the functional demands (Gooch et al. 2001; Huang et al. 2005; Waters et al. 2006), it is important to have uniform shear stress distribution in the entire porous structure. To address the uneven shear stress distribution, semicircular reactor was reconfigured by altering the inlet and outlet of the reactor was investigating. Extensions were incorporated to the design by moving the inlet and outlet away from the porous structure region. Design 6 with circular inlet and outlet shape produced uniform shear stress in the porous region.

The pressure drop in the new design was less relative to the previous design (Design 1). Previously, experimentally measured pressure drop has been reported for the rectangular reactor. For rectangular reactors, pressure drop was 2−5 mmHg (0.267 −0.667 kPa) at 5 mL/min flowrate. The experimental pressure drop varied from 7−9 mmHg (0.930 − 1.20 kPa) for circular reactors which is slightly higher than the simulated value (0.570 kPa) at 5 mL/min flowrate. Nevertheless, these results validated the utility of the computational fluid dynamic simulation. Hence, the effect of nutrient consumption for three different cell types was effectively integrated into the simulations in the next step.

A number of different cell types have been studied under flow conditions in bioreactors to regenerate various tissues including bladder, cartilage, blood vessels, skin, and bone (Botchwey et al. 2003; Hoerstrup et al. 2000; Shito et al. 2001). These structures are located at various anatomical locations with variations in the blood flow rate. However, there is no comparison of physiological function to metabolic demand which determines the necessary minimum flow rates for each cell type. As such, three different cell types were analyzed via simulation using the rate constants data from literature. These results showed different minimum flow requirements before reaching the nutrient limiting conditions. Chondrocytes are the cells primarily responsible for maintaining cartilage, an avascular tissue whose function is to provide cushioning and lubrication at joints. SMCs expand and contract to ensure involuntary movement within the body. Hepatocytes form the metabolic hub of the body and there is significant blood circulation. Chondrocytes are far from the blood supply while SMCs are near the blood stream. Smaller Km values also suggest that the nutrient uptake rate is less sensitive to the local nutrient concentration. For example, the oxygen uptake rate by hepatocytes and chondrocytes are less sensitive to the local oxygen concentration relative to SMCs. Uptake rate is reduced by only 2 to 10% in chondrocytes and hepatocytes even with a fifty percent reduction in oxygen concentration, where as uptake rate is reduced by 35% in SMCs for 50% reduction in oxygen concentration.

The simulation data confirmed that chondrocytes consumed oxygen and glucose slower than SMCs, and that the minimum flow rate required for SMCs is an order of magnitude higher than for chondrocytes. Hepatocytes being highly metabolic consumed oxygen and glucose faster than chondrocytes and SMCs. To understand whether the rate calculated at the inlet condition to estimate flow rate, we performed calculations for oxygen using the Michealis-Menten rate law at the inlet concentration ${\phantom{\mid }-\mathrm{r}{}_{{\mathrm{O}}_2}\mid }_{\mathrm{inlet}}$. Then volumetric flow rate was calculated using the relation,

$${\phantom{\mid }-{\mathrm{r}}_{{\mathrm{o}}_2}\mid }_{\text{inlet}}=\frac{\upsilon \Delta {\mathrm{C}}_{{\mathrm{o}}_2}}{{\mathrm{V}}_{\mathrm{R}}}$$

where volume of the reactor (V_R with 0.85 void fraction), and medium concentration change (ΔC_O2). These results showed that the flow rate needed for the outlet concentration to be 0.07 mol/m³ is 0.076 mL/min for SMCs. Simulation results showed that at 0.1mL/min flow rate (Table 4), the outlet concentration is 0.07 mol/m³, which is in good agreement. Further, for complete utilization of oxygen, medium flow rate has to be 0.053 mL/min and the simulation results showed that 0.01 mL/min was not sufficient. Similarly for hepatocytes, minimum flow rate necessary for complete utilization of oxygen was 0.14 mL/min and simulation results showed that 0.1 mL/min was not sufficient. When cell numbers were doubled, 0.12 mL/min flow rate resulted in 0.017 mol/m³ oxygen outlet concentration for SMCs and simulation results with 0.1 mL/min showed same oxygen outlet concentration. This suggests that one could use the initial rate to estimate the minimum flow rate necessary to ensure sufficient nutrient supply.

Reconfigured circular reactor showed improvement in nutrient distribution with consumption. Local minimum was nearer to the outlet concentration. However, these simulations are based on the bulk phase fluid flow by considering diffusivity in water and indicate only the macroscopic gradient. Hence, they do not account for the transport across the cell membrane. Evaluating the microscopic concentration gradient at the cell wall necessary for oxygen to freely diffuse across the cell wall at a specific rate of diffusion as established by Fick's first law is necessary. Importantly, rate constants were obtained from literature which is based on either two-dimensional cultures or cells cultured on gels (Alpert et al. 2002b; Balis et al. 1999; Motterlini et al. 1998b; Sengers et al. 2005a). However, recent developments in tissue regeneration have demonstrated that cell growth kinetics in three-dimensional cultures is different than two-dimensional cultures (Cukierman et al. 2001; Stephens et al. 2007). Hence, to improve the simulation, one has to assess the glucose and oxygen consumption in three-dimensional cell cultures on substrates under investigation. Further, experimental validation in presence of cells to determine whether those minimum flow rates are sufficient to ensure nutrient distribution is necessary. In addition, one has to determine the effect of flow rate on the quality of the regenerated tissue. Evaluating the microscopic concentration gradient at the cell wall is necessary for oxygen to freely diffuse across the cell wall.

Results also showed a need for changing the flow rate or inlet pressure when tissue regeneration occurs either to ensure due to change in cell number or due to decreased permeability. Thus, one has to consider these factors during the regeneration process using flow-through reactor. Since flow rate is directly coupled to the shear stress cells would experience, one has to assess the utility of the flow-through configuration in tissue regeneration. Nevertheless, changes in permeability, void fraction, and rate of oxygen consumption were treated as completely independent phenomena in this study. However, these are interdependent factors which dynamically change during tissue regeneration. Therefore, future work should focus on providing a better understanding of the microscale phenomena that occur during tissue regeneration in order to better couple the changes in reaction rate to changes in the porous structure as cells colonize the scaffold material.

In summary, the new circular design decreased (i) non-uniformity in hydrodynamic stress within the porous structure and (ii) non-uniform nutrient distribution. One has to optimize the fluid flow rate based on the type of cell to be colonized. Further, flow rate and pressure drop have to be altered during the regeneration process to ensure uniform nutrient distribution without limitation.