Mössbauer, NMR, Geometric, and Electronic Properties in S = 3/2 Iron Porphyrins

Iron porphyrins with the intermediate spin S = 3/2 or admixed with S = 5/2 and 1/2 are models for a number of heme protein systems,^1,2 including cytochromes c'. They have been intensely investigated experimentally.^1-17 In particular, the ⁵⁷Fe Mössbauer quadrupole splittings and ¹H and ¹³C NMR chemical shifts were found to be useful probes for their electronic states. However, specific relationships between these spectroscopic properties and geometric parameters have not been reported. There are also no reports of quantum chemical calculations of these important spectroscopic probes in S = 3/2 iron porphyrins, except for our recent work on the Mössbauer properties of one of such complexes.¹⁸ In addition, their electronic states are under debate. While the early work suggested an electronic configuration of (d_xy)²(d_xz,d_yz)²(d_z2)¹(d_x2-y2)⁰ for S = 3/2 ferric porphyrins,¹ the more recent experimental work⁴ discovered two possibilities, with this early proposed electronic state for saddled iron porphyrins and a new electronic configuration of (d_xz,d_yz)³(d_xy)¹(d_z2)¹(d_x2-y2)⁰ for ruffled ones. However, a recent theoretical study proposed an opposite assignment of these two electronic states.¹⁹

Here, we present the results of the first quantum chemical calculations of the Mössbauer and NMR properties in various S = 3/2 iron porphyrins and their interesting new correlations with geometric and electronic properties. As shown in Table 1, the S = 3/2 complexes investigated here cover all possible coordination states of iron porphyrins: four, five, and six, as well as the commonly seen porphyrin conformations: planar, ruffled, and saddled.^{3-5,7,9-14,16,17} In addition to almost pure S = 3/2 complexes (1, 3, 4, 5), the one containing 20% S = 5/2 state (2) as well as the one related to those having spin crossover with S = 1/2 (6) were studied. A couple of spin admixed complexes with mostly S = 5/2 features (7, 8) were also calculated for comparison. Experimental x-ray structures were used in all calculations using the DFT method that previously gave accurate predictions of Mössbauer quadrupole splittings (ΔE_Q) and isomer shifts (δ_Fe)^18,20 and NMR ¹H and ¹³C hyperfine shifts²¹ for metalloproteins and models.²²

Table 1.

Mössbauer, NMR, Geometric, and Electronic Properties in S = 3/2 and 5/2 Iron Porphyrins ^a

Complex		S	RFeN (Å)	ΔEQ (mm/s)	δFe (mm/s)	δhfHβ (ppm)	δhfHCα (ppm)	δhfCα (ppm)	δhfCβ (ppm)	δhfCm (ppm)	Ref
1 [Fe(TipsiPP)]CB11H6Br6	Expt	3/2	1.944	5.16	0.33	−90.2					3
4-coordinate	Calc	3/2		4.97	0.24	−94.2	/	−509.9	−195.1	−100.6
Planar		5/2		4.10	0.27	−29.4	/	1795.1	1213.2	−350.5
2 FeOEP(3-ClPy)	Expt	3/2	1.979	3.23	0.36						16,17
5-coordinate	Calc	3/2		2.82	0.33	/	26.7, 6.3	−470.2	−38.4	89.7
Planar		5/2		1.98	0.34	/	56.3, 45.3	1304.6	1023.8	−46.8
3 FeTMCP(H2O)(EtOH)	Expt	3/2	1.950	3.79	0.35	−44.2					13
6-coordinate	Calc	3/2		3.65	0.32	−55.1	/	−313.7	−177.0	−28.4
Ruffled		5/2		3.16	0.34	27.1	/	1418.5	1185.8	−31.8
4 [Fe(TiPrP)(THF)2]ClO4	Expt	3/2	1.967	3.71	0.34	−61.1		−272.8	−110.5	−28.3	5,12
6-coordinate	Calc	3/2		3.33	0.35	−59.0	/	−299.7	−207.7	−44.4
Ruffled		5/2		2.81	0.35	25.2	/	1588.4	1013.5	−92.0
5 Fe(OETPP)ClO4	Expt	3/2	1.963				32.5, 2.8				4,11
5-coordinate	Calc	3/2		3.31	0.40	/	22.2, 0.0	117.3	17.4	−120.5
Saddled		5/2		3.27	0.40	/	205.5,25.7	1834.8	−371.7	−1854.5
6 [FeOETPP(4-CNPy)2]ClO4	Expt	3/2	1.975	3.03	0.57		31.6, 3.5	318.8	133.1	−388.9	4,7,9,10
6-coordinate	Calc	3/2		2.67	0.60	/	30.1,1.6	201.3	11.1	−252.1
Saddled		1/2		3.51	0.43	/	6.3,3.1	72.9	−50.8	158.5
7 [Fe(TipsiPP)]CF3SO3	Expt	5/2	2.053								3
5-coordinate	Calc	5/2		1.07	0.46	59.3	/	1171.5	1140.6	178.7
Planar		3/2		3.70	0.54	−10.4	/	−106.4	−226.5	60.6
8 Fe(OETPP)Cl	Expt	5/2	2.040	0.95	0.35		31.7, 15.9				4,14
5-coordinate	Calc	5/2		0.71	0.42	/	19.0, 10.1	602.8	1004.6	314.2
Saddled		3/2		1.88	0.48	/	3.1, 0.0	144.3	44.4	−87.2

^aTipsiPP = 5,10,15,20-tetrakis(2′,6′-bis(triisopropylsiloxy)phenylporphyrinato, OEP = 2,3,7,8,12,13,17,18-octaethylporphyrinato, TMCP = 5,10,15,20-tetramethylchiroporphyrinato, TⁱPrP = 5,10,15,20-tetraisopropylporphyrinato, OETPP = 2,3,7,8,12,13,17,18-octaethyl-5,10,15,20-tetraphenylporphy-rinato. Temperatures of Mössbauer and NMR results are listed in Table S1.

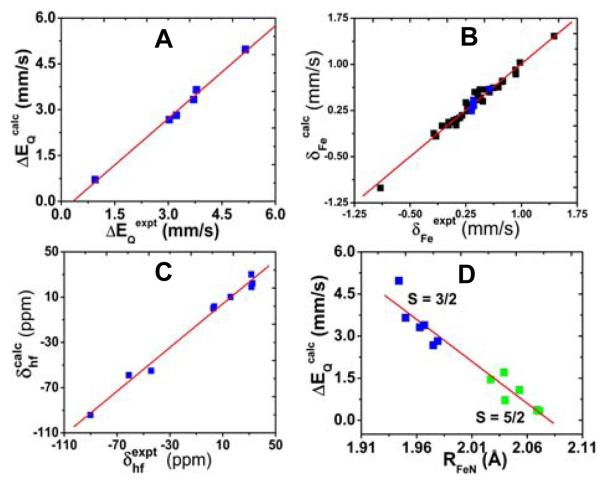
Clearly, as seen from Table 1, the computational results support experimental findings that the Mössbauer quadrupole splittings and ¹H and ¹³C NMR hyperfine shifts are sensitive probes of the spin states (S = 3/2 vs. 5/2 or 1/2), since for each of these complexes, only the calculated results from using the correct spin state for the x-ray structure are in good agreement with experimental spectroscopic data. As illustrated in Figure 1A, calculations of the experimental ΔE_Q results^{3,10,12-14,17} have a theory-versus-experiment correlation coefficient R² = 0.99 and a standard deviation of 0.12 mm/s or 2.9% of the whole experimental range from 0.95 mm/s to 5.16 mm/s. These results extend previous computational work on iron-containing proteins and models^18,20 to a total experimental range of 8.80 mm/s with R² = 0.98, Figure S1. The experimental Mössbauer isomer shifts were also well reproduced, Table 1. However, these data are insensitive to spin states and they only display a small range (see Figure 1B), which precludes its use as sensitive probes for these complexes. The ¹H NMR chemical shifts of pyrrole protons have long been recognized as good indicators of spin states in spin admixed 3/2, 5/2 complexes,^3,12,13,15 due to different spin density distributions between the intermediate and high spin states, which will affect the observed NMR hyperfine shift (δ_hf^Hβ), a major component of the NMR chemical shift that is proportional to spin densities.^21,22 For porphyrins with substituents on the pyrrole proton positions, such as OEP and OETPP, the experimental NMR hyperfine shifts of the −CH₂ group of the ethyl substituents^4,7,9,10 (δ_hf^HCα) were also investigated. As shown in Table 1 and Figure 1C, the experimental ¹H NMR hyperfine shifts covering a range of 122.7 ppm were accurately predicted with R² = 0.99. The predicted ¹³C NMR hyperfine shifts for porphyrin α-, β-, and meso-carbons (δ_hf^Cα, δ_hf^Cβ, δ_hf^Cm) are also in good agreement with experiment. Overall, the NMR predictions for these S = 3/2 systems are in the same trend line of previous calculations of proteins and models with other spin states,²¹ Figure S2. These results provide a solid basis for using DFT calculations in investigating S = 3/2 ferric porphyrin systems.

Figure 1.

A. Computed Mössbauer quadrupole splittings vs. experimental data. B. Calculated Mössbauer isomer shifts vs. experimental results. C. Calculated ¹H NMR hyperfine shifts vs. experimental data. D. Relationship between ΔE_Q and R_FeN. Blue and green data points are from this work and black data points are from previous work, refs 18 and 20.

Since these results represent the first successful calculations of experimental Mössbauer and NMR properties for a good variety of S = 3/2 iron porphyrins, we next investigated the relationships between these sensitive experimental probes and the structural features. Interestingly, the Mössbauer quadrupole splittings in these porphyrins (1-8) were found for the first time to have good correlations with the average bond lengths of iron and pyrrole nitrogen bonds, R_FeN. Although most complexes studied here have intermediate spins and only two are high spin species, this correlation can be extended to other high spin iron porphyrins and heme protein¹⁸ (9-12, Table S2) as well. As depicted in Figure 1D, large quadrupole splittings are correlated with smaller Fe-N bond lengths with R² = 0.93 and this correlation is independent of coordination states and porphyrin conformations. It should be noted that the Mössbauer quadrupole splittings are also correlated well with other useful experimental spectroscopic properties, such as pyrrole proton NMR shifts and the magnetic susceptibilities.¹⁵ Therefore, the quantitative relationship with Fe-N bond lengths may help structural investigations of the S = 3/2 and 5/2 heme proteins using a number of experimental techniques.

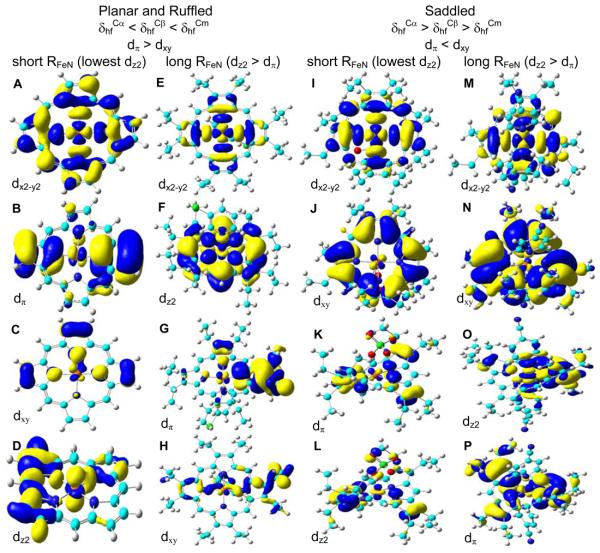
It is also interesting to note that among the S = 3/2 ferric porphyrins investigated here with three porphyrin coordination states (four, five, six) and three common porphyrin conformations (planar, ruffled, saddled), there are only two general trends of the porphyrin ¹³C NMR hyperfine shifts based on both experimental and computational results and the trends were found to depend on the porphyrin conformation, not the coordination state: δ_hf^Cα < δ_hf^Cβ < δ_hf^Cm for planar and ruffled complexes, and the opposite trend of δ_hf^Cα > δ_hf^Cβ > δ_hf^Cm for saddled ones (see Table 1). This indicates an important effect of the porphyrin conformation on the electronic structures as discussed below. Previous work^4,8,19 suggests that the relative ordering of d_xz/yz (or d_π) vs. d_xy can affect the ¹³C NMR hyperfine shift trends in the ruffled and saddled S = 3/2 iron porphyrins. Unfortunately, controversial results were obtained in the past.^4,8,19 To resolve this problem and understand the above new observations of the ¹³C NMR hyperfine shift trends in these intermediate spin ferric complexes with more varieties of porphyrin structures, we investigated all of the wavefunctions from above successful calculations. As shown in Figures 2A, 2E, 2I, 2M, S3A, and S4A, a common outcome of all these S = 3/2 complexes is that d_x2-y2 is of the highest energy, supporting previous work.^1,4,8,19 However, as a result of the current comprehensive investigation, more possibilities of frontier MO orderings were discovered than before:

• 1) d_x2-y2 > d_π > d_xy > d_z2 for complexes 1, 3, and 4, see Figures 2A-D, S3A-D, S4A-D, respectively

• 2) d_x2-y2 > d_z2 > d_π > d_xy for complex 2, see Figure 2E-H

• 3) d_x2-y2 > d_xy > d_π > d_z2 for complex 5, see Figure 2I-L

• 4) d_x2-y2 > d_xy > d_z2 > d_π for complex 6, see Figure 2M-P

Based on these results, it seems that the MO ordering does not depend on the coordination state. In contrast, the porphyrin conformation was found to play an important role as shown in Figures 2 and S3-4. This is consistent with the above observations of the ¹³C NMR results. Of particular interest is that, though altogether a number of different frontier MO orderings were discovered here, there are only two orderings concerning the iron d_π and d_xy orbitals:, d_π > d_xy in planar and ruffled complexes and the opposite trend of d_π < d_xy in the saddled ones, Figure 2. This kind of porphyrin conformation dependence is again the same as with the porphyrin ¹³C NMR hyperfine shifts, suggesting that the porphyrin conformation affects the relative ordering of d_π and d_xy orbitals, which are responsible for the observed porphyrin ¹³C NMR results. This is because among the three types of occupied iron d orbitals (d_π, d_xy, d_z2), only d_π and d_xy orbitals have significant contributions to the spin densities in the porphyrin ring, while the d_z2 orbital mainly influences axial ligands. Another interesting new observation is that the d_z2 ordering depends on the Fe-N distance. As shown in Figures 2 and S3-4, among the planar and ruffled S = 3/2 complexes, d_z2 is usually of the lowest energy when R_FeN is small, due to the weaker interaction along the z-axis compared to the stronger ones in the x-y plane from shorter Fe-N contacts. However, when R_FeN is long (≥ 1.975 Å), d_z2 is higher than d_π as usual. The same kind of dependence of d_z2 on R_FeN was also found with the saddled S = 3/2 porphyrins, see Figure 2.

Figure 2.

Summary of the structural dependence for porphyrin ¹³C NMR trends and MO orderings and the isosurface representations of α-LUMO (A), α-HOMO-2 (B), β-HOMO-3 (C), and α-HOMO-12 (D) for 1, α-LUMO (E), α-HOMO-1 (F), α-HOMO-2 (G), and α-HOMO-12 (H) for 2, α-LUMO+1 (I), β-HOMO (J), α-HOMO-2 (K), and α-HOMO-5 (L) for 5, α-LUMO+2 (M), α-HOMO (N), α-HOMO-2 (O), and α-HOMO-3 (P) for 6, with contour values = ± 0.02, 0.02, 0.04, 0.04, 0.02, 0.02, 0.02, 0.04, 0.02, 0.02, 0.04, 0.04, 0.02, 0.01, 0.02, and 0.02 au, respectively.

Overall, the results presented above should facilitate future investigations of related iron porphyrins and heme proteins.