Theoretical Bond Dissociation Energies of Halo-Heterocycles: Trends and Relationships to Regioselectivity in Palladium-Catalyzed Cross-Coupling Reactions

Abstract

Selectivity of the palladium-catalyzed cross-coupling reactions of heterocycles bearing multiple identical halogens is mainly determined by the relative ease of oxidative addition. This is related to both the energy to distort the carbon halogen bond to the transition-state geometry (related to the CX bond-dissociation energy) and to the interaction between the heterocycle π* (LUMO) and PdL₂ HOMO (J. Am. Chem. Soc. 2007, 129, 12664). The computed bond dissociation energies of a larger series of halo-heterocycles have been explored with B3LYP and higher accuracy G3B3 calculations. Quantitative trends in bond dissociation energies have been identified for five- and six-membered chloro and bromo substituted heterocycles with N, O, and S heteroatoms.

Introduction

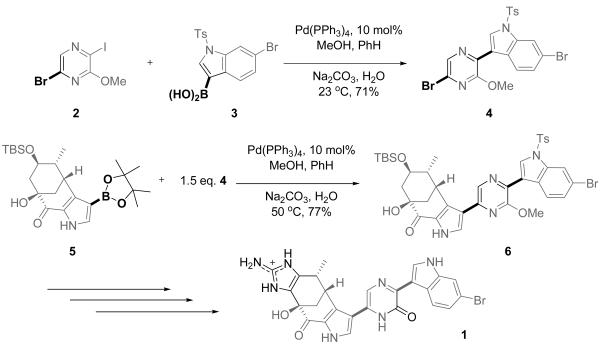
Polysubstituted heterocycles are important in pharmaceutical and manufacturing applications.¹ The synthesis of polysubstituted heterocycles frequently involves palladium-catalyzed cross-coupling reactions. Selective sequential cross-coupling reactions involving multihalogenated aromatics is a particularly attractive approach to poly-substituted heterocycles.² Several total syntheses involve such processes. For example, the Stoltz group employed two Suzuki reactions in the total synthesis of (+)-Dragmacidin F (1), an antiviral bromoindole alkaloid with in vitro activity against two viruses: HIV-1 and HSV-1 (Scheme 1).^3,4 The first palladium-catalyzed reaction which couples pyrazine 2 with indolyl boronic acid 3 was achieved through selective displacement of the iodine to produce dibromide, 4. To complete the backbone of (+)-Dragmacidin F (1), dibromide 4 was coupled to the pyrrole boronate ester 5. The selective cross-coupling with the bromide on the pyrazine ring is critical to achieve synthetic efficiency. Further functionalization affords 1.

Scheme 1.

Regioselective cross-coupling reactions in the total synthesis of (+)-Dragmacidin F.

What is the origin of this selectivity? Knowles et al. reported that one source of selectivity is the nature of the halogen that is being displaced; iodine reacts before bromine and bromine before chlorine.⁵ This originates from the significant differences in the carbon-halogen (C-X) bond strengths. However, for heterocycles bearing multiple identical halogens, the bond strengths should be very similar and other factors may become important. Some success in predicting the preferred cross-coupling position was achieved using NMR spectroscopy.⁶ Studies on the oxidative insertions of aryl monohalides by Pd(0) were undertaken by Ariafard and Lin,⁷ and a case study to investigate the selectivity in sonogashira couplings with 4,6-dichloro-2-pyrone was performed by Fairlamb and co-workers.⁸

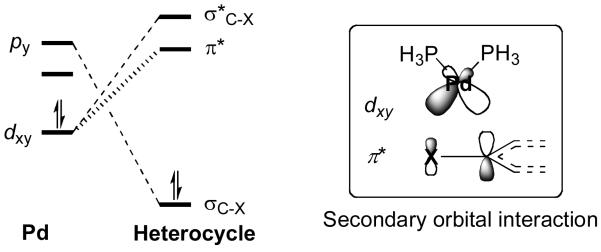
Generally, the the oxidative insertion step is considered to be the selectivity-determining step, even though recent studies suggest also the possibility of reversibility, highlighting the importance of the transmetallation step for regioselectivity.⁹ We recently reported that the regioselectivities in oxidative additions are controlled by (1) the energy to distort a C-X bond to the transition state geometry, a factor related to the bond dissociation energy (BDE), and (2) the interation between PdLL' and the aryl halide, which is controlled by the frontier molecular orbital (FMO) interactions.¹⁰ The orbital interactions involved in these interactions are shown in Figure 1.

Figure 1.

FMO interactions between PdLL' and Ar-X in an oxidative addition.

The distortion/interaction model is able to rationalize many interesting examples.¹⁰ When two different halogens, or halogens in very different chemical environments, are involved, the relative ease of C-X bond breaking often dictates the regioselectivity of oxidative addition. However, when the ease of C-X bond breaking (BDE) is about the same, then the interactions between PdLL' and the heteroaryl halide controls regioselectivity. Calculations of transition state geometries and energies were shown to be capable of reproducing relative activation energies.

We wish to develop sufficient understanding of the factors that control BDEs (and distortion energies) as well as interaction energies such that qualitative predictions can be made and the results of calculation can be understood. This paper reports a computational study of the bond dissociation energies of many common halo-heterocycles. Trends are identified so that the relative BDEs of different CX bonds can be predicted qualitatively, and the results of calculations can be understood.

Computational Details

Bond strengths of heterocycles with one to three chlorine or bromine substituents were studied. The Bond Dissociation Enthalpies (BDE) of carbon-halogen (C-X) bonds were computed using Gaussian03.¹¹ BDE is defined as change in enthalpy, ΔH, for homolysis of the C-X bond.

$$\Delta H\mathrm{A}-\mathrm{X}\left(\mathrm{g}\right)\to {\mathrm{A}}^{•}{\left(\mathrm{g}\right)}^{+}{\mathrm{X}}^{•}\left(\mathrm{g}\right)$$

The accuracies of three methods were evaluated: CBS-RAD (B3LYP,B3LYP),¹² G3B3,¹³ and UB3LYP/6-31G(d) (referred to as B3LYP). The CBS-RAD (Complete Basis Set-RADical) method was developed by the Radom group and is used for radicals, or open-shell systems, based on a modification of CBS-Q,¹⁴ a highly accurate, composite, ab initio method. The CBS-RAD (B3LYP,B3LYP) is a variation of CBS-RAD that uses B3LYP geometries and zero point energies, which are generally less computationally intensive. G3B3 is also a composite method based on G3,¹⁵ another highly accurate ab initio method, and utilizes B3LYP geometries and zero point energies. Recently, Zhao et al. published theoretical work on the BDEs of heterocycles using G3B3; the authors examined the BDEs of C-H bonds on methyl groups attached to five- and six-membered heterocycles.¹⁶ They were able to calibrate B3LYP to G3B3 by plotting a series of enthalpies found with both methods and using linear regression to determine an approximation of G3B3 energies using UB3LYP/6-31G(d) calculations. While the ab initio methods CBS-RAD and G3B3 are reported to give an MAD (mean average deviation) of 0.7¹⁷ and 0.9 kcal/mol,¹³ respectively, the utilities of these methods are limited by the number of heavy atoms (non-hydrogen atoms) in the molecule. B3LYP is significantly less computationally intensive, but has a MAD of 3.3 kcal/mol.¹⁸ We have found that CBS-RAD and G3B3 are practically limited to eight and ten heavy atoms, respectively. For this study, most of the halo-heterocycles contained between 6 and 9 heavy atoms. Fused heterocycles, however, contained at least 11 heavy atoms and are thus too large to compute practically with G3B3 and CBS-RAD.

Furthermore, while CBS-RAD has been shown to be highly accurate for small, acyclic systems, these results have not been reflected in our calculation of the BDE of chloro- and bromobenzene. The experimental BDE of bromobenzene is 82.6 kcal/mol¹⁹ and was calculated at 79.7 kcal/mol with CBS-RAD and 83.7 kcal/mol with B3LYP (G3B3 is only valid up to second row atoms). Chlorobenzene has an experimental BDE of 97.6 kcal/mol,¹⁹ while the calculated values are: 91.0 (B3LYP), 99.0 (G3B3), and 121.6 (CBS-RAD) kcal/mol. G3B3 is highly accurate and also has the fewest convergence problems. Due to these criteria, G3B3 and B3LYP were used to calculate BDEs.

Comparison of B3LYP and G3B3 BDEs

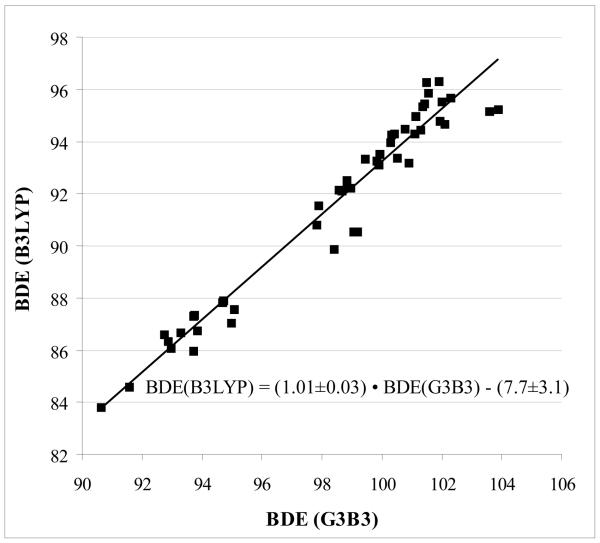
The BDEs of carbon-halogen bonds in 47 halo substituted heterocycles were calculated using both B3LYP and G3B3. Table S1 in the supporting information gives the data. Figure 2 is a plot of B3LYP BDEs versus G3B3 BDEs. There is a good linear relationship: BDE(B3LYP) = (1.01 ± 0.03) • BDE(G3B3) − (7.7 ± 3.1) ; R² = 0.975 ± 0.007. The UB3LYP/6-31G(d) method can thus be used with confidence to provide relative BDEs for the halo-heterocycles studied using this equation: BDE (G3B3) = (0.94 ± 0.03) •BDE (B3LYP) + (12.0 ± 2.6) ; R² = 0.975 ± 0.007.

Figure 2.

Comparison of BDEs computed using UB3LYP/6-31G(d) and G3B3 (kcal/mol). The correlation coefficint is R² = 0.975 ± 0.007.

Zhao et al. reported an analysis of the C-H BDEs on methyl groups attached to various heterocycles.¹⁶ They examined 69 different heterocycles and also found a linear correlation between B3LYP and G3B3 methods: BDE (G3B3) = 0.938 BDE (B3LYP) + 10.2. Both studies result in almost identical slopes (0.938 vs. 0.94), which indicates that the correlation between these two methods is the same even when different types of BDE are evaluated. The difference in y-intercept suggests that the nature of the atom is significant in evaluating BDEs.

Comparison of C-Cl and C-Br BDEs

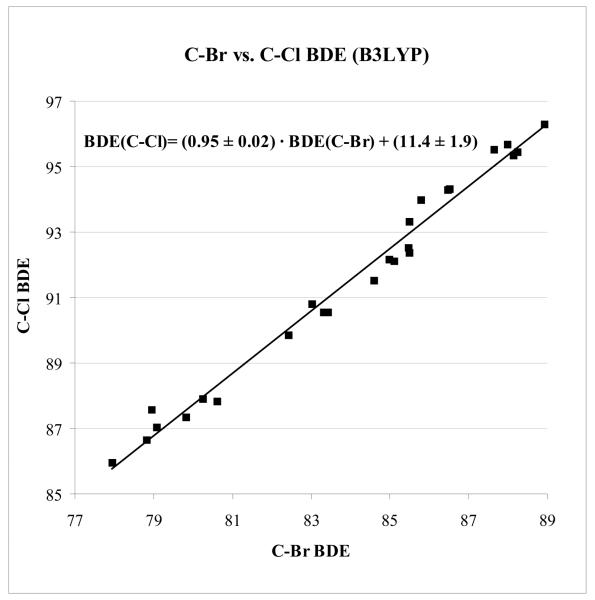
Given the limitation of G3B3 in calculating elements up to the second row only²⁰ and the fact that many of the palladium-catalyzed cross-coupling reactions occur with bromine and iodine, a comparison of C-Br and C-Cl BDEs computed at the UB3LYP/6-31G(d) level was conducted (Figure 3).

Figure 3.

Comparison of C-Cl and C-Br BDEs using UB3LYP/6-31G(d); BDEs in kcal/mol. The correlation coefficint is R² = 0.992 ± 0.002.

It was expected that the nature of the halogen would not affect the relative BDE in halogenated heterocycles. Indeed, calculations of 10 heterocycles that were monosubstituted with chlorine or bromine at different positions in the heterocycle using B3LYP show that there is very good correlation between C-Br and C-Cl BDEs (R² = 0.992 ± 0.002). Moreover, the slope is nearly one (m = 0.95 ± 0.02) and the y-intercept is 11.4 ± 1.9 (see Figure 3). This indicates that there is a nearly 1-to-1 correlation between C-Br and C-Cl BDEs; the C-Cl BDEs are (7.55 ± 0.42) kcal/mol higher than C-Br BDEs on average. Since the relative C-Cl BDEs reflect the relative BDEs of other halogens, calculations are only reported here for chlorinated heterocycles.

Results and Discussion

BDEs of 5-Membered Heterocycles with One Heteroatom

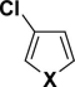
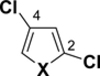
B3LYP and G3B3 were used to determine the BDEs of C-Cl bonds for 5-membered heterocycles bearing one heteroatom. Monochloro- and dichlorofurans, -thiophenes, and -pyrroles were studied (see Table 1). The G3B3 BDEs are 5 to 8 kcal/mol higher than the B3LYP BDEs. The BDEs for both 2-Cl and 3-Cl pyrrole, and furan are 101-102 kcal/mol, while for 2,4-dichloro pyrole and furan, the BDEs are 101-102 kcal/mol. In 2,3-dichloro pyrrole and furan, all BDEs are 103 kcal/mol.

Table 1.

C-Cl BDEs (in kcal/mol) of mono- and dichlorofuran, thiophene, and pyrrole using G3B3 (bold) and B3LYP (in parentheses).

			C2-Cl	C4-Cl	C2-Cl	C3-Cl
X = S	98.8 (92.5)	98.6 (92.2)	98.9 (91.9)	98.7 (91.4)	100.7 (92.8)	100.3 (92.1)
X = NH	101.9 (96.3)	101.5 (96.3)	101.9 (95.5)	101.4 (95.4)	103.0 (95.8)	102.6 (95.9)
X = O	102.0 (96.5)	101.4 (96.5)	102.1 (94.9)	101.4 (9.8)	103.9 (96.0)	102.8 (95.4)

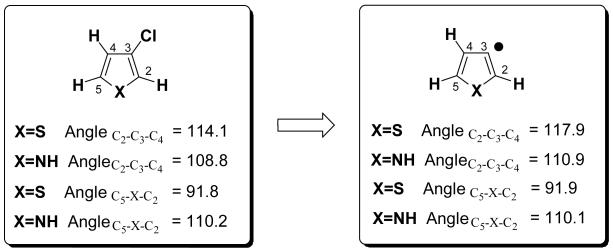
Thiophene has lower G3B3 BDEs, 99 kcal/mol for monochloro and 2,4-dichloro, and 100-101 kcal/mol for 2,4-dichloro thiophene. That thiophene shows lowest BDEs was also observed for the corresponding C-H BDEs that were studied by Hadad et al.²¹ Hadad et al. reported further that upon radical formation after C-H bond cleavage, a widening of the bond angle takes place at the site at which the radical is formed. They analyzed the bond angle changes at the radical site and found that the BDE of 5-membered rings is lower, the greater the bond angle change (the BDE of 6-membered rings is lower the smaller the bond angle change).²¹ They argued that the radical is more stable if the internal bond angles approach 120°. In the case of thiophene, the deviation from a regular pentagon (bond angle 108°) is largest among the series (C-S-C ca. 91°). At the same time upon radical formation via C-H bond cleavage, the increase of bond angle at the radical site is largest for thiophene derived radicals.²¹ We find an analogous relationship between bond angle change and BDE for the halogenated 5-membered heterocyles, i.e. the largest bond angle increase at the radical site is observed in the formation of chlorothiophene-derived radicals; an example is illustrated in Figure 4. 3-Chlorothiophene shows a larger bond angle increase (3.8°) than 3 chloropyrrole (2.1°), consistent with the lower BDE of chlorothiophene.

Figure 4.

Bond angles of G3B3 calculated structures of 3-chlorothiophene and 3-chloropyrrole and the corresponding radicals.

All three heterocycles show the same trend: if halogenation is in the 2 or 3 position [or 2 and 4] BDEs are nearly identical, but are raised by 1-2 kcal/mol if the substitution pattern is 2,3. The increase in BDE for the 2,3-substitution pattern is related to the dichloro starting material: 2,3-dichlorothiophene, for example, is 1 kcal/mol less stable than 2,4-dichlorothiophene [ΔH G3B3]. Furthermore, the bond angle encompassing the radical site (S-C₂-C₃ shown in Figure 5) is smaller if the chlorine is adjacent to the radical. This results in slightly less stabilization of the radical [spin-density is 1.00 for 3-chloro-2-radical and 0.98 for 4-chloro-2-radical] and overall in a 1.8 kcal/mol higher enthalpy [G3B3] of the thiophene radical that bears the chlorine ortho (see Figure 5).

Figure 5.

Bond angles of mono and dichlorothiophene and of the corresponding radicals.

Experimentally, cross-coupling reactions of 2,4-dibromofuran and dibromothiophene (2,3- and 2,4-) occur preferentially at the 2-position.^22,23 Computationally, the bond strengths are about the same at 2 and 3 or 2 and 4 in each of the heterocycles. Identical observations have been made with respect to the C-H BDE.²¹ Thus, in these cases, the selectivities in palladium cross-coupling reactions observed are not controlled by the bond strengths but originate instead from the FMO interactions between the heterocycle and the palladium catalyst.¹⁰

BDEs of 5-Membered Heterocycles with Two Heteroatoms

B3LYP and G3B3 predict the heterocycle containing sulfur, once again, to have the lowest BDE. For imidazole, thiazole and oxazole the 2-position has the lowest BDE, 1-3 kcal/mol lower than at the 4 or 5 positions, which have BDEs close to the 4 and 5 positions of pyrrole, thiophane, and furan, respectively. For chlorothiazoles, this difference is between 4-5 kcal/mol for both theory models.

These results are in line with experimental observations which show that the 2-position primarily reacts. For example, the Stille cross-coupling of 2,5-dibromothizaole with trimethyltin-thiazole affords the product of the substitution at the 2-position, in 76% yield.²⁴

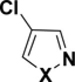
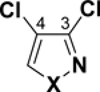
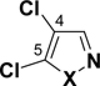
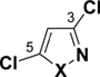
In the series of heterocycles containing the heteroatoms adjacent to one another (Table 3), the trend follows a similar pattern as for thiophene, imidazole and oxazole: the 3-position has the lowest BDE (95-96 for isothiazoles, and 99-100 for isoxazole and pyrrole), followed by the 5-position (98-99, 101), while the 4-position has the highest BDE (99-100, 102-104).

Table 3.

C-Cl BDEs (kcal/mol) of mono- and dichloroisothiazole, pyrazole, and isoxazole using G3B3 (bold) and B3LYP (in parentheses).

				C3-Cl	C4-Cl	C4-Cl	C5-Cl	C3-Cl	C5-Cl
X = S	94.7 (87.9)	98.6 (92.1)	97.9 (91.5)	96.3 (87.6)	99.3 (91.5)	100.2 (92.0)	99.7 (91.7)	94.6 (87.2)	97.6 (91.1)
X = NH	100.3 (94.3)	101.5 (95.9)	101.1 (95.0)	--	--	--	--	--	--
X = O	99.0 (92.2)	103.6 (95.2)	100.5 (93.4)	--	--	--	--	--	--

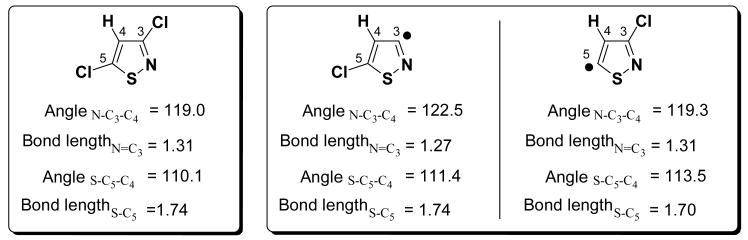
A halogen attached to a carbon α to an imine N has a lower BDE than a halogen attached to a carbon α to an O, S, or NH. This trend is seen across the heterocycles examined so far and is related to the resonance with the adjacent imine nitrogen lone pair. This is reflected in the bond angle differences. An analysis of 3,5-dichloroisothiazole to exemplify this is highlighted in Figure 6. The radical at 3-position has a bond angle larger than the radical in position 5. The larger angle results in greater stabilization (by 3.9 kcal/mol [ΔH calculated at G3B3]) of the radical in 3-position, which is confirmed by the spin densities: although the radical is located primarily in a σ-type orbital that is formally orthogonal to the π-system, the spin density is distributed over the other atoms also [see supporting information]. The spin density at the radical site is smaller for the radical in 3-position (0.798) than in 5-position (0.947) [calculated at B3LYP/6-31G(d)^25,21], consistent with the stability of the corresponding radical.

Figure 6.

Bond angle and bond length analysis of G3B3 calculated structures of chloroisothiophene and its radicals.

For chloroisothiazole and chloroisoxazole, both B3LYP and G3B3 predict that the 3-position has the lowest BDE. Much like the previous examples, B3LYP BDEs are 6 to 9 kcal/mol lower than G3B3 BDEs. For chloropyrazole, the 3-position has the lowest BDE, followed by the 5-position (1 kcal/mol higher); as expected, the 4-position has the highest BDE by 2 kcal/mol using both methods.

BDEs of Five-Membered Heterocycles with Three or More Heteroatoms

For 4-chloro- and 5-chloro- 1,2,3-triazole the BDEs are both 102 kcal/mol, the same as the BDEs of chloropyrroles (Figure 7). The 3- and 5-positions of 1,2,4-triazole have C-Cl BDEs of 101 and 100 kcal/mol, respectively. Pyrazole in contrast has a 1 kcal/mol lower C-Cl BDE at the 3-position than at the 5-position, having a nitrogen at the 4-position reverses this trend.

Figure 7.

C-Cl BDEs of 5-membered heterocycles with 3 or 4 heteroatoms using G3B3 (bold) and B3LYP (in parentheses), in kcal/mol.

The symmetric heterocycles, 1,2,5 and 1,3,4-oxadiazole have BDEs of 101 kcal/mol, like those found for the previous compounds. The 1,2,3,5-oxatriazole has a higher C-Cl BDE of 104 kcal/mol [although B3LYP BDE is similar to the other compounds]. The bond angle increase in this case is significant (3°), but the radical is hardly stabilized by the other atoms, showing a spin density of 0.953 at the radical site and thus explaining the relatively large BDE. For comparison 1,2,4 triazole shows an increase of only 2° in bond angle in the 5-position, but the radical is more stabilized [spin = 0.919] and the BDE is lower overall.

BDEs of 6-Membered Heterocycles

The BDEs of C-Cl bonds on 6-membered heterocycles are lowest at the position that is experimentally most reactive in cross-couplings; B3LYP and G3B3 BDEs are well correlated with reactivity.

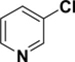
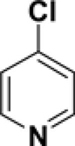
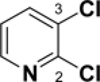
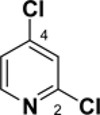
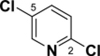
Pyridine reacts primarily α to the nitrogen. For example, a Suzuki cross-coupling reaction of 2,5-dibromopyridine with a functionalized borane gave the 2-position coupled product in 87% yield.²⁶ Calculations demonstrate that the 2-position has a lower C-Cl BDE (95-96 kcal/mol) than the other positions by 3-4 kcal/mol (see Table 4). This difference in BDEs is significant and above or very near the MAD of both methods [G3B3: 0.9 kcal/mol; B3LYP: 3.3 kcal/mol]. While G3B3 BDEs continue to be higher than B3LYP BDEs, the difference for 6-membered heterocycles can be larger; for pyridine, this difference is 8 to 11 kcal/mol. That the 2-position is of lowest BDE has also been found for the corresponding C-H BDE²¹ and it has been rationalized to be based on the neighboring N-C interaction that leads to stabilization via resonance.²⁷ Indeed the spin density of the 2-pyrridinyl radical is relatively low (0.829).

Table 4.

C-Cl BDEs (kcal/mol) of mono- and dichloropyridine using G3B3 (bold) and B3LYP (in parentheses).

			C2-Cl	C3-Cl	C2-Cl	C4-Cl	C2-Cl	C5-Cl
94.9 (87.1)	99.2 (90.6)	98.4 (89.9)	96.3 (84.9)	99.9 (88.6)	95.1 (86.3)	98.4 (89.5)	96.0 (87.1)	99.8 (90.8)

BDEs of Six-Membered Heterocycles with Two or More Heteroatoms

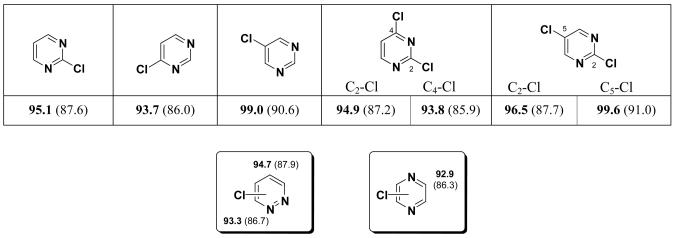
Concerning 6-membered heterocycles containing two or more heteroatoms, only pyrimidine has been studied experimentally in Pd-cross coupling reactions (examples are presented below). The mono- and disubstituted substrates were examined for their BDEs. Figure 8 shows that the 4-position has the lowest C-Cl BDE, followed by the 2-position and then the 5-position.

Figure 8.

C-Cl BDEs (kcal/mol) of mono and dichloropyrimidine, pyrazine and pyridazine using G3B3 (bold) and B3LYP (in parentheses).

In general, the C-Cl bonds α to one or two nitrogens have BDEs of 93-95 kcal/mol. The exception is 2,5-dichloro substitution with 1-1.6 kcal/mol greater BDE. The BDEs of the other positions are 95-100 kcal/mol. The B3LYP BDEs are lower than G3B3 BDEs by 7 to 9 kcal/mol. These computational results reflect the experimental findings that the order of reactivity for chloro pyrimidines is: 5 < 2 < 4.¹ When 2,4,5-trichloropyrimidine undergoes cross-coupling with tributyl-styryl-stannane via palladium catalysis, the 4-position is substituted in 71% yield. When 2,5-dichloropyrimidine undergoes the same reaction, the 2-position is substituted in 70% yield.²⁸ Both of these Suzuki cross-coupling reactions are regioselective for the position with the lowest computational C-Cl BDE. In contrast to 5-membered heterocycles, the position in between the heteroatoms is not the position of lowest BDE in the 6-membered heterocycles. The BDE of 3-chloropyridazine is lower than that of 4-chloropyridazine, once again pointing on the α-nitrogen effect.

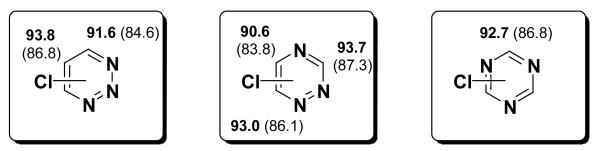
The pattern of BDEs in triazines is unusual, with BDEs of 91-94-kcal/mol there is no simple trend for the relative BDEs. 1,2,4-triazine (see Figure 9) shows a BDE pattern similar to pyrimidine (Figure 8); the position with the lowest BDE, the 5-position is α-aza instead of in-between the two nitrogens (3-position). The 5-position also has a lower BDE than the 6-position, but the difference is not as large; the BDE of the 5-position is lower than the 3-position by over 3 kcal/mol and the 6-position by over 2 kcal/mol utilizing both methods. The 4- and 6-positions of 1,2,3-triazine have a lower C-Cl BDE than the 5-position, being α to a nitrogen. Finally, pyrazine and 1,3,5-triazine show BDEs that are consistent with values of similar heterocycles (Figure 9).

Figure 9.

C-Cl BDEs of 6-membered heterocycles using G3B3 (bold) and B3LYP (parentheses); energies in kcal/mol.

BDEs of 6,5 Fused- Heterocycles

Due to the size of these fused ring systems and the limitations of G3B3 with respect to the number of heavy atoms, the BDEs were calculated at the B3LYP level of theory only. Therefore, B3LYP was calibrated to G3B3 to obtain theoretical G3B3 BDEs; the linear regression model used to obtain these values is shown later. For benzofuran (see Figure 10) the BDEs of the C-Cl bonds on the 6-membered ring are 98 kcal/mol (the experimental BDE of chlorobenzene is 97.6 kcal/mol¹⁹), while those on the furan ring are 102 kcal/mol, about the same as furan. These findings are in accord with the trend for C-H BDEs of benzofuran.²¹ Both furan and benzofuran react similarly when subjected to palladium-catalyzed cross-coupling conditions. For example, 2,3,5-tribromobenzofuran undergoes a Negishi coupling with an aryl zinc chloride selectively at the 2-position to afford the coupling product in 75 % yield.²⁹ This case is an example of a reaction clearly controlled by the FMO interactions between the heterocycle and the palladium catalyst, as explained in our previous communication.¹⁰

Figure 10.

C-Cl BDEs of 6,5 fused- heterocycles using estimated G3B3 values (bold) and B3LYP values (parentheses); energies in kcal/mol. G3B3 BDEs were estimated using a linear regression model.

Monosubstituted indoles have analogous C-Cl BDE patterns to benzofuran; the benzo C-Cl bond BDEs are 98-99 kcal/mol, and the pyrrole are 102-103 kcal/mol. The 2- and 3-positions have C-Cl BDEs that are significantly higher than the 6-position by 4 kcal/mol (Figure 10). Experimentally, 2,6-dibromoindole undergoes a Suzuki cross-coupling with thiophene boronic acid to give substitution at the 6-position of the indole.³⁰ The latter coupling thus seems controlled by the BDE (the 6-position is lower in BDE by 5 kcal/mol than the 2-position).

Much like benzofuran and indole, benzothiophene has the lowest C-Cl BDEs on the 6-membered ring; all these positions have identical B3LYP BDEs of 91 kcal/mol. The 2- and 3-position are higher in BDE similar to the other 5,6 fused systems, but the difference is not as significant (1 kcal/mol vs. > 4 kcal/mol for benzofuran and indole). These results are consistent with thiophene, which shows the lowest C-Cl BDE compared to furan and pyrrole. Moreover, benzothiophene reacts similarly to the aforementioned species: namely, the 2-position is more reactive than the 3-position despite similar C-Cl BDEs. For example, the Sonogashira cross-coupling reaction between 2,3-dibromobenzothiophene and t-butylacetylene yields the 2-substituted product in 84% yield.³¹

Benzothiazole has the lowest C-Cl BDE at the 2-position. The BDEs of the C-Cl bonds located on the fused 6 membered ring are 3 kcal/mol higher. This mirrors the situation in monocyclic rings: the G3B3 C-Cl BDE for the 2-position of chlorothiazole is 95 kcal/mol, while that for chlorobenzene is 99 kcal/mol. Experimentally, the 2-position on benzothiazole is also the most reactive. 2,4-Dibromobenzothiazole undergoes a Stille coupling with a vinyl triflate to give the 2-substituted product 63% yield.³²

BDEs of 6,6 Fused- Heterocycles

The 6,6 fused halo-heterocycles react in much the same way as their monocyclic counterparts. Computationally, the results are similar and also in line with the experimental cross-coupling findings. Quinoline, for example, is most reactive at the 2-position just like pyridine, and this position also has the lowest C-Cl BDE (94 kcal/mol). The remaining positions have BDEs of 96-98 kcal/mol. In addition, much like pyridine, the C-Cl BDE for quinoline is highest at the 3-position and slightly lower at the 4-position. The fused phenyl ring has C-Cl BDEs that are similar to that of chlorobenzene (97.6 kcal/mol¹⁹) and approximately 4 kcal/mol higher than the 2-position. A Negishi cross-coupling of 2,4-dichloroquinoline with phenylzinc chloride gives the product arising from substitution at the 2-position in 80% yield.³³ This substitution pattern can also be seen with a Suzuki or a Stille reaction.¹

Isoquinoline gives a distinctive C-Cl BDE pattern: the 3-position is 2 kcal/mol higher than the 1-position (95 vs. 93 kcal/mol at B3LYP). The remaining positions on isoquinoline (positions 4, 5, 6, 7, and 8) are 4-5 kcal/mol higher in BDE; these positions have C-Cl BDE of about 97 kcal/mol, the BDE of chlorobenzene. In a Suzuki coupling of 1,3-dichloroisoquinoline with an aryl boronic acid reaction was observed in the position of lowest BDE (1-position) to afford the product in 87% yield.³⁴

The 2- and 3-positions of the 6,6-fused system quinoxaline have the lowest C-Cl BDE at 93 kcal/mol, while the positions on the benzene fused ring have BDEs near that of chlorobenzene and about 4 kcal/mol higher. 2,6-Dichloroquinoxaline was found to undergo Sonogashira cross-coupling with tetrahydrofuran protected alcohol at the position of lowest BDE.³⁵

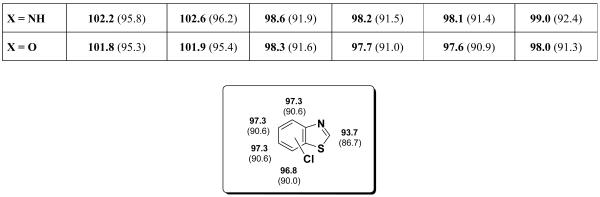
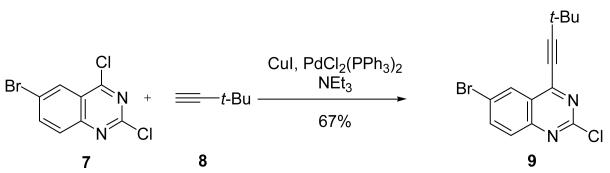
Quinazoline, much like its monocyclic counterpart pyrimidine, has the lowest C-Cl BDE at the 4-position, 92 kcal/mol, followed by the 2-position at 95 kcal/mol. Similar to the previous 6,6-fused systems, all of the positions on the phenyl ring have C-Cl BDEs that have mostly the same BDEs (96-97 kcal/mol) and, consequently, are 5-6 kcal/mol higher than the 2-position (Figure 11). In terms of reactivity, a Sonogashira coupling of 6-bromo 2,4-dichloroquinazoline 7 with t-butylacetylene 8 shows reaction at the 4-position (see Scheme 2).³⁶ In this case, the BDE of the C-Cl bond at the 4-position (84.8 kcal/mol at B3LYP) is larger than that of the C-Br at the 6-position (83 kcal/mol at B3LYP). The reaction is thus controlled by the FMO interactions between the heterocycle and the palladium catalyst, and actually favors the coupling with C-Cl at the 4-position instead of the weaker C-Br bond.

Figure 11.

C-Cl BDEs of 6,6 fused heterocycles using G3B3 (bold) and B3LYP (parentheses); energies in kcal/mol. G3B3 BDEs were estimated using a linear regression model.

Scheme 2.

Sonogashira cross-coupling reaction of 6-bromo 2,4-dichloroquinazoline 7.

Bond angle effect on BDE

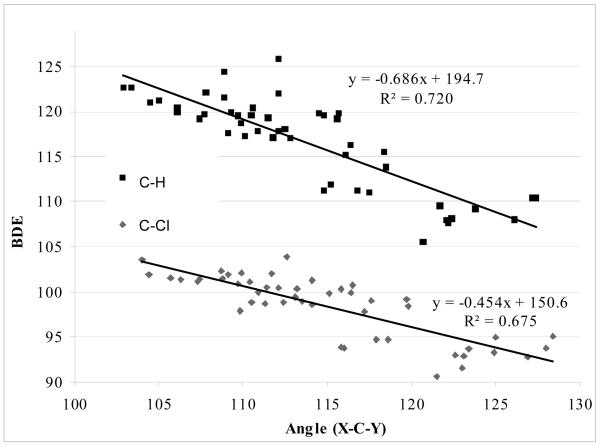
The BDEs computed show that the strength of C-Cl bonds on 5-membered rings is systematically stronger than for an equivalent bond on a 6-membered ring. This behavior has been found for C-H BDEs²¹ also and can be rationalized by looking more closely at the constraints of the carbon bearing the halogen. Feng et al. found that while 1,3-butadiene has a C₁-C₂-C₃ bond angle of 127° at its minimum, the 1,3-butadiene C₂-radical minimized structure presents a C₁-C₂-C₃ bond angle of 140°.¹⁸ They argued that six-membered rings result in lower BDEs compared to 5-membered rings since their intrinsic internal bond angles are larger (120° for 6-membered vs. 108° for 5-membered).¹⁸ As mentioned previously, Hadad et al. also studied the C-H BDEs of heterocycles and analyzed the bond angle changes that occur upon radical formation. They correlated these changes with BDEs and found a good linear relationship.²¹

Analysis of the BDEs computed in this study with respect to the internal bond angles of the corresponding carbon position in the halogenated heterocycle was done as a comparison to previous studies.¹⁸

Scheme 3 depicts the angle “X-C-Y”, where C is the carbon attached to the halogen (or hydrogen) where the BDE is being measured. X and Y refer to the adjacent atoms. A graph correlating the relationship of the bond angle to the BDE of the corresponding C-halogen(hydrogen) bond is illustrated in Figure 12. The heterocycles are for CH bond (□), and C-Cl BDEs appear below (◇). For each system there are 48 BDEs that have been calculated using G3B3 theory level. As can be seen, there is a qualitative correlation between bond angle and BDE. The correlation for the CH BDEs is marginally better (R² = 0.72) than for the halogenated system (R² = 0.68). As the bond angle gets larger, the BDE decreases in accord with the rationale proposed by Feng et al.¹⁸

Scheme 3.

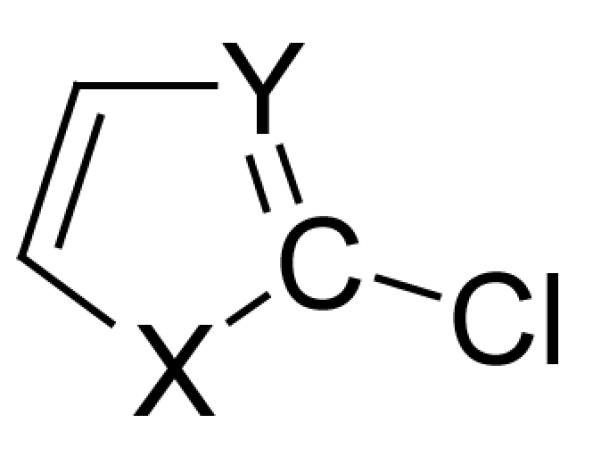
Definition of bond angle X-C-Y.

Figure 12.

Bond angle vs. C-Cl BDE of chloro heterocycles and C-H BDE of heterocycles using G3B3. (Results for C-H BDEs from Feng et al.¹⁸)

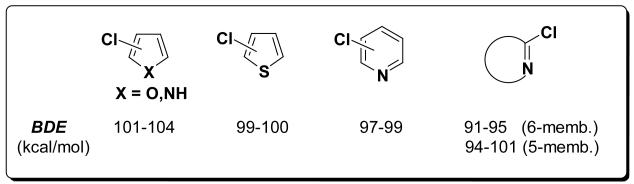
The C-Cl BDEs of various heterocycles are summarized in Figure 13. The 5-membered halogenated heterocycles have higher BDEs than their 6-membered analogues, also if fused with a benzene ring. The C-Cl bonds α to an imine N have lower BDEs than C-Cl bonds α to O, S or NH. This is due the higher stability of the radicals as a consequence of greater resonance stabilization for the radical α to the in-plane lone pair on N.

Figure 13.

Summary of C-Cl BDEs.

Conclusions

The bond dissociation enthalpies of various 5-membered, 6-membered, and fused ring heterocycles were calculated using B3LYP and G3B3. While the former is faster and more amenable to atoms of interest, the latter is more accurate. To establish the usefulness of these methods, B3LYP and G3B3 were compared and a benchmark was established. The BDEs are mainly determined by the ring size, and the internal angles, that are influenced by both ring size and distortion. For NH, O, and N, the BDEs vary little, being 101-104 kcal/mol for 5-membered and 97-99 kcal/mol for 6-membered heterocycles. The exception to these generalizations are (i) if sulfur is in the 5-membered ring: thiophenes have C-Cl BDE of 99-100 kcal/mol, and (ii) when the Cl is α to an imine. The BDEs for the latter cases drop to 94-101 kcal/mol for 5-membered rings, and to 91-95 kcal/mol for 6-membered rings, 2-8 kcal/mol lower than the usual C-Cl BDEs of 6-membered rings.

The implications for regioselective cross-couplings were alluded to, and will be described in more detail in future publications.

Table 2.

C-Cl BDEs (kcal/mol) of mono- and dichlorothiazole, imidazole, and oxazole using G3B3 (bold) and B3LYP (in parentheses).

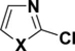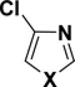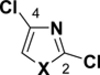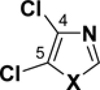				C2-Cl	C4-Cl	C2-Cl	C5-Cl	C4-Cl	C5-Cl
X = S	93.7 (87.4)	97.8 (90.8)	98.8 (92.4)	94.5 (87.4)	97.9 (90.3)	93.6 (86.4)	98.7 (91.8)	99.7 (90.7)	100.4 (92.5)
X = NH	99.4 (93.3)	100.4 (94.3)	101.3 (95.4)	99.9 (93.0)	100.5 (93.9)	99.1 (92.4)	101.2 (94.9)	101.6 (94.0)	103.0 (95.7)
X = O	100.3 (94.0)	101.1 (94.3)	102.3 (95.7)	--	--	--	--	--	--