Morpholino Monolayers: Preparation and Label-Free DNA Analysis by Surface Hybridization

Abstract

Surface hybridization, a reaction in which nucleic acid molecules in solution react with nucleic acid partners immobilized on a surface, is widely practiced in life science research. In these applications the immobilized partner, or "probe", is typically single-stranded DNA. Because DNA is strongly charged, high salt conditions are required to enable binding between analyte nucleic acids ("targets") in solution and the DNA probes. High salt, however, compromises prospects for label-free monitoring or control of the hybridization reaction through surface electric fields, as well as stabilizes secondary structure in target species that can interfere with probe-target recognition. In this work, initial steps toward addressing these challenges are taken by introducing Morpholinos, a class of uncharged DNA analogues, for surface-hybridization applications. Monolayers of Morpholino probes on gold supports can be fabricated with methods similar to those employed with DNA, and are shown to hybridize efficiently and sequence-specifically with target strands. Hybridization-induced changes in the interfacial charge organization are analyzed with electrochemical methods and compared for Morpholino and DNA probe monolayers. Molecular mechanisms connecting surface hybridization state to the interfacial capacitance are identified and interpreted through comparison to numerical Poisson Boltzmann calculations. Interestingly, positive as well as negative capacitive responses (contrast inversion) to hybridization are possible, depending on surface populations of mobile ions as controlled by the applied potential. Quantitative comparison of surface capacitance with target coverage (targets/area) reveals a near-linear relationship, and demonstrates sensitivities (limits of quantification) in the pg mm⁻² range.

1. Introduction

Surface hybridization, in which sequence-specific binding between polynucleic acid "probes" on a solid support and complementary "targets" from solution occurs at a solid-liquid interface, was introduced as a diagnostic method in the 1960's ^1,2. The technique continues to be widely exploited in modern DNA microarray and biosensor technologies for genotyping, transcriptome profiling, genetic identification, and related diagnostic applications³. When hybridization occurs at a surface, experiments show that the phenomenology of the reaction is more complex than in solution ^4–17. The crowded interfacial environment is characterized by nucleotide concentrations that approach the molar range, and the resultant amplification of interactions between nucleotides can have a dramatic impact on physical behavior manifesting, for example, in binding affinities orders of magnitude lower than those in solution ^{6,14,15,17,18}.

A consequence of molecular crowding is that a DNA probe layer presents a high, ~ 0.1 mol L⁻¹ concentration of immobilized negative charge. This charge density erects an electrostatic barrier to entry of like-charged would-be hybridization partners from solution. In order for hybridization to proceed, this barrier needs to be screened through the addition of salt such that the solution number density of mobile ions becomes comparable to that of the surface-bound DNA charge¹⁷. While this electrostatic screening benefits hybridization, it also suppresses electrostatic interactions between the probe layer and the underlying support that could be used to control or to monitor the surface hybridization state. As an alternative approach that avoids this drawback, electrostatic hindrance to surface hybridization can be tempered through the use of neutral (i.e. uncharged) probes, such as peptide nucleic acids (PNAs)^19,20 and Morpholinos²¹. Moreover, because the probe layer starts from an uncharged state, binding of charged nucleic acid targets is expected to elicit stronger structural changes, thus enhancing prospects for analysis of the hybridization reaction through purely electrostatic means.

From the selection of neutral probes, the high binding affinity of PNAs provides strong mismatch discrimination^19,22 that is expected to be well suited to genotyping and to resequencing. Applications of PNAs have typically relied on 16mer or shorter sequences^23–26 since longer strands, or ones containing long stretches of pyrimidines and purines, become increasingly challenging to prepare^27–29 and have greater potential for cross-reactivity with mismatched sequences. PNAs are thus expected to be less well suited to applications such as gene expression and pathogen detection which benefit from longer probe lengths, up to 70 nt,^30,31 to provide robust identification of a target's unique origin (i.e. a specific gene or biological entity). In such instances Morpholinos, which place few constraints on sequence design or length, are expected to be advantageous. Morpholinos also mitigate some of the difficult physicochemical properties of neutral DNA analogues; for example, they are about 100-fold more soluble than comparable PNAs and their relatively stiff backbone reduces propensity toward self-aggregation³².

The principal goal of the present study was to fundamentally understand origins of electrostatic signatures of hybridization on charge-neutral Morpholino layers, and to contrast this behavior with that of DNA probe films. The preparation of thiolate-anchored Morpholino films on gold supports is described first, based on adaptation of "mixed monolayer" methods used for production of molecularly precise DNA films consisting of the probe plus an alkanethiol surface-blocking agent ^33–36. The efficacy of the blocking-agent to passivate against surface-adsorption of the probe backbone is critical, and was confirmed with infrared spectroscopy. Electrochemical methods were used to study hybridization between Morpholino probes and DNA targets. Changes in layer organization, from probe-target binding, were related to the layer's capacitive (charging) response. The sensitivity and direction of the response, including observation of contrast inversion, were controllable by the surface potential, V_DC, at which the response was sampled. At the molecular level these relationships can be explained from the combined influence of V_DC and surface charge, stemming from hybridization of target strands, on the local populations of mobile ions, as further interpreted through Poisson-Boltzmann modeling. "Dual-color" redox labeling was used to simultaneously track surface populations of probe and target strands to derive a quantitative mapping between the capacitive response and the target occupancy. Viewed as a diagnostic tool for surface hybridization, these label-free capacitive measurements exhibit un-optimized sensitivities comparable to established methods such as surface plasmon resonance and quartz crystal microbalance techniques.

2. Materials and Methods

2.1. Materials

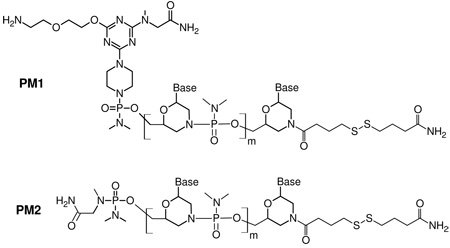
Morpholino oligomers, purified by precipitation, were purchased from Gene Tools LLC. HPLC purified DNA probes and targets were purchased from MWG Biotech. Table 1 lists the Morpholino and DNA sequences, their abbreviations, and experimental purpose.

Table 1.

Morpholino and DNA sequences.

sequence	abbreviation
5' NH2-TTT TAA ATT CTG CAA GTG AT-CO(CH2)3SS(CH2)3CONH2 3' A	PM1
Morpholino retinoblastoma RB1 marker probe; used for hybridization studies
5' NH2-TTT TAA ATT CTG CAA GTG AT-(CH2)3SS(CH2)3OH 3'	PD1
DNA probe; same sequence as PM1
5' TTT TTT TCC TTC CTT TTT TT-CO(CH2)3SS(CH2)3CONH2 3' A	PM2
Morpholino probe; used for subrared reflection-absorption spectroscopy (IRRAS) studies
5' ATC ACT TGC AGA ATT TAA 3'	TD1
DNA target; complementary to PM1 and PD1
5' AAA AAA AGG AAG GAA AAA 3'	TD2
DNA target; noncomplementary hybridization control

^AThe Morpholino PM1 and PM2 molecular structures are (m = 19):

N-(2-ferrocene-ethyl) maleimide ("F2") was synthesized as described¹⁷. Synthesis of ferrocene monocarboxylic acid N-hydroxy succinimide ester ("FC1") was similar to published methods ³⁷ and is detailed in the Supporting Information.

2.2. Bioconjugation of Ferrocene Tags

Electroactive tags F2 and FC1 were used to label target and probe molecules, respectively, to allow in-situ determination of strand surface coverage. Amine-terminated probes PM1 and PD1 were labeled with FC1 at the 5' end (Figure S2, Supporting Information) by combining 0.3 mmol L⁻¹ probe in 0.5 mol L⁻¹ pH 9.0 sodium carbonate buffer with a 150-fold excess of FC1, at room temperature for 16 hrs. Unreacted FC1 was removed on NAP-10 (GE Healthcare) and oligonucleotide purification cartridge (Applied Biosystems) prep columns, followed by reverse-phase HPLC (Beckman Coulter Gold® 125; Clarity 3 µm Oligo-RP column from Phenomenex®). HPLC conditions for ferrocene modified DNA probes were 50 °C, 0.5 ml min⁻¹, and a linear gradient of 12 to 60 % methanol in hexafluoroisopropanol/triethylamine buffer (HFIP-TEA; 100 mmol L⁻¹ HFIP, 4.5 mmol L⁻¹ TEA, pH 8.0) spread over 22 min. HPLC purification of Morpholinoferrocene conjugates proceeded identically but using a gradient of 12 to 100% methanol in HFIP-TEA over 20 min, followed by 5 min at 100% methanol. The dominant fraction of labeled material was collected, and a second run performed to confirm purity. Conjugates were dried in a vacuum centrifuge (Vacufuge®, Eppendorf) and stored dry at −14 °C until use. For experiments requiring labeled targets, additional TD1 and TD2 sequences (Table 1) were purchased that also included a 3' disulfide (−(CH₂)₃SS(CH₂)₃OH) end modification. Labeling of target oligonucleotides started with deprotection of the disulfide endgroup with dithiothreitol (DTT) to liberate the sulfhydryl moiety, in 10 mmol L⁻¹ DTT, 10 mmol L⁻¹ TRIS, 1 mmol L⁻¹ EDTA, pH 8.0, for 2 hrs. Excess DTT was removed on a NAP-10 column, followed by reacting the ~ 25 µmol L⁻¹ target solution with 30-fold excess of F2 (Figure S2, Supporting Information) in 150 mmol L⁻¹ pH 8.0 potassium phosphate buffer overnight. Final purification, collection, drying, and storage procedures were as for DNA probes.

2.3. Preparation of Probe Monolayers

Samples for electrochemical measurements were prepared on 1.6 mm diameter polycrystalline gold disk electrodes. The electrodes were first cleaned by mechanical polishing with 1 µm diamond suspension, rinsing with methanol and deionized (18.2 MΩ cm) water, and finally by potentiodynamic cycling in 0.5 mol L⁻¹ H₂SO₄ for 60 cycles from 0.24 V to 1.54 V (vs Ag/AgCl/3 mol L⁻¹ NaCl reference) at 0.1 V s⁻¹. The electrodes were again rinsed with deionized water and, without drying, the roughness factor r (r = actual area/geometric area) was determined from double layer capacitance.^38,39 Values of r ranged from 1.4 to 1.6. After a final rinse with deionized water, the still-wet electrodes were covered by probe deposition solution.

Probe solutions were pipetted directly onto cleaned supports. Probes were suspended at 0.25 µmol L⁻¹ probe in deionized water (Morpholino probes) or in 1 mol L⁻¹ MgCl₂ (DNA probes). Following immobilization of the probes, samples were rinsed with deionized water and then blocked in 1 mmol L⁻¹ mercaptopropanol (MCP; Sigma-Aldrich 95 % purity) in water for 90 min for DNA layers, or for 150 min for Morpholino layers. The longer blocking times for Morpholinos improved reproducibility of baselines in cyclic voltammetry experiments. The samples were rinsed again, and placed into target-free hybridization buffer (see below). All transfer steps were accomplished wet to minimize chances for adsorption of atmospheric contaminants.

Samples for infrared reflection-absorption spectroscopy (IRRAS) were prepared on standard size, float glass microscope slides coated with 5 nm of titanium and 100 nm of gold (EMF Corp., Ithaca, NY). The slides were cleaned for 10 min in 120 °C "piranha" solution consisting of 7:3 mixture of concentrated sulfuric acid and 30 % hydrogen peroxide solution in water (CAUTION: piranha solution is highly oxidizing and must not be stored in tightly capped containers on account of gas evolution). Following a rinse with deionized water the still-wet slides were covered with probe deposition solution. Conditions were as for preparation of electrochemical samples except that, in addition, slides were prepared also without the final MCP blocking step. After drying with a nitrogen stream, samples were used immediately for IRRAS measurements.

2.4. IRRAS Measurements

IRRAS spectroscopy was performed on a Perkin Elmer Spectrum 100 spectrometer equipped with an 80° specular reflectance accessory (PIKE Technologies). Spectra were collected from 900 cm⁻¹ to 4000 cm⁻¹ at 4 cm⁻¹ resolution, with software correction for presence of water vapor bands. Cleaned, but otherwise unmodified, gold-coated slides served as background.

2.5. Electrochemical Characterization

Electrochemical measurements were performed on a CHI660C workstation (CH Instruments) with a three electrode cell comprised of the modified Au working electrode, a platinum wire counter electrode, and an Ag/AgCl/3 mol L⁻¹ NaCl reference electrode (Bioanalytical Systems; 0.209 V vs NHE at 25 °C). All potentials are reported relative to this reference. A glass sleeve salt bridge was used to guard against leakage of NaCl from the reference electrode's reservoir into the electrolyte. The electrolyte, which also served as the hybridization buffer, was 0.2 mol L⁻¹ pH 7.0 sodium phosphate buffer. A fixed target concentration of 25 nmol L⁻¹ and probe coverages of about 5 × 10¹² probes cm⁻² were used. When data were not being collected the electrochemical cell was kept off.

Cyclic voltammetry (CV) measurements to determine the instantaneous coverage of ferrocene-labeled strands used a scan rate of 20 V s⁻¹ from 0 V to 0.6 V or to 0.65 V, requiring approximately 0.07 s per cycle. Probe and target surface coverages, S_P and S_T, were calculated from the charge Q associated with oxidation of their ferrocene tags:

$$S_{\mathrm{P}}=Q_{\text{FC}1}/(e{A}_{\mathrm{g}}r) S_{\mathrm{T}}=Q_{\mathrm{F}2}(e{A}_{\mathrm{g}}r)$$ (1)

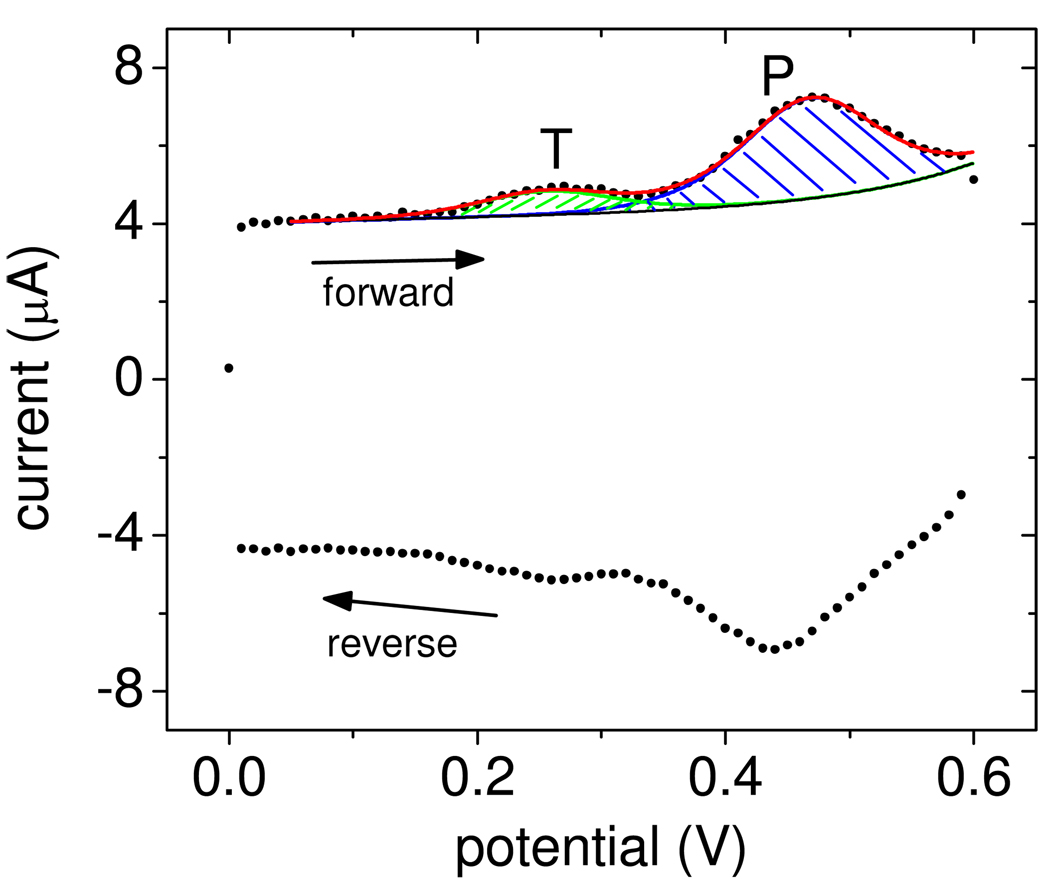
where e = 1.60 × 10⁻¹⁹ C is the elementary charge, A_g is the geometric area occupied by the probe layer, and r is the measured roughness factor. Q_FC1 and Q_F2 are total charges from the oxidation FC1 → FC1⁺ + e⁻ and F2 → F2⁺ + e⁻, respectively, corresponding to integration of the blue and green areas in Figure 1 after converting the potential axis to time. Each probe and target possesses one ferrocene tag. The "T" peak near 0.25 V represents increased current due to oxidation of F2, and confirms presence of surface-bound target molecules. The probe FC1 signal, labeled "P", is observed near 0.45 V. On the reverse scan the tags are reset back to the neutral ferrocene state. The figure also shows fits to the data from which Q_FC1 and Q_F2 were determined. Fits were calculated by an automated computer routine described in the Supporting Information.

Figure 1.

Points (•): Experimental data. The CV scan starts from 0 V, moves along the forward trace to 0.6 V, and returns to 0 V along the reverse trace. The "T" and "P" peaks are from oxidation of target F2 and probe FC1 tags. The curves are computer-generated fits used to calculate Q_FC1 and Q_F2 (Supporting Information). Black line (–): baseline current I_B (equation S2, Supporting Information); green line (): current I_T,F2 from target tags (equation S3); blue line (): current I_T,FC1 from probe tags (equation S3); red line (): total current I_tot = I_B + I_T,F2 + I_T,FC1.

In AC impedance (ACI) measurements, (1) a steady bias, V_DC, is imposed to set up the surface environment (e.g. distribution of mobile ions) and, (2) the charge-flow (current) response of this environment to perturbations in potential is sampled using a weak sinusoidal read-out function added to V_DC. Under the experimental conditions used, the response consisted only of charging currents, with the electrochemical cell behaving as a series combination of a resistance, R, representing the electrolyte, and a differential capacitance per area, C_d, representing the probe-modified working electrode. C_d characterizes the surface organization of the probe layer and, for a series RC arrangement, is calculated from the measured out-of-phase impedance Z" using |Z"| = 1/(2πfA_grC_d). f is the read-out frequency. Z" is related to experimental quantities via Z" = − V_acI_op/(I_ip² + I_op²) with V_ac the magnitude of the imposed read-out function, and I_ip and I_op the magnitudes of the measured in-phase and out-of-phase current components, respectively. A useful interpretation of C_d is as a metric of the near-surface screening of electric fields: more effective screening correlates with higher capacitance because greater charge dσ₀ must be placed on the electrode to achieve a potential increment dV (see equation 2 below). Screening can be provided by polarization of the surface environment, as governed by the local dielectric properties, and/or by redistribution of mobile ionic charge.

An ACI measurement consisted of stepping the surface bias V_DC from 0.25 V to - 0.2 V in 0.025 V steps, and back, with C_d determined at each step. A full C_d-loop took 1 min, and was performed once every 5 min during the course of hybridization. A read-out frequency f = 5435 Hz and ac potential magnitude of 5 mV rms were used. This frequency corresponded to a phase angle of 45 ° to 50 °, and was sufficiently low to avoid secondary capacitive charging observed in the presence of the salt bridge at high frequencies, yet high enough to minimize contributions from spurious interfacial charge transfer that become more prominent at low frequencies.

2.6. Theoretical Calculation of C_d

Theoretical predictions of the behavior of C_d were used to guide interpretation of observed experimental trends. C_d is defined by the derivative of the surface charge per area of the electrode, σ₀, with respect to the electrode potential V

$$C_{\mathrm{d}}=\frac{d{\sigma }_0}{dV}$$ (2)

$${\sigma }_0=-\epsilon {\epsilon }_0{\frac{dV}{dx}|}_{0+\leftarrow x}$$ (3)

where equation 3 follows from Gauss' Law. Here ε is the material dielectric constant (relative static permittivity), ε₀ is the permittivity of vacuum, and x is the perpendicular distance from the electrode surface. V(x) was calculated by numerical integration of the Poisson-Boltzmann equation,

$$\frac{d^{2}V}{d{x}^2}=\frac{\rho (x)}{\epsilon (x){\epsilon }_0}$$ (4)

$$\rho (x)=z_{\mathrm{I}}e{c}_{\mathrm{I}}(x)+{\displaystyle \sum _j{z}_{\mathrm{j}}}e{c}_{\mathrm{j}\infty }\text{exp}(-z_{\mathrm{j}}eV(x)/\mathit{\text{kT}})\text{exp}(-{\beta }_{\mathrm{j}}(x))$$ (5)

ρ(x) is the concentration of charge at x, e is the unit charge (1.60 × 10⁻¹ C), z_I and c_I are the valence and concentration of immobile charged sites (e.g. c_I might represent concentration of DNA backbone phosphate residues), T is absolute temperature, k is the Boltzmann constant, and z_j, c_j∞, and β_j are the valence, solution concentration, and partitioning penalty of species j, where j ranges over all ions free to partition between solution and the probe layer. For example, if in the probe layer β_Na+ = 1, then there is a 1 kT penalty to transport a Na⁺ cation from solution to the layer (e.g. from changes in solvation interactions) in addition to the eV term.

Equations 4 and 5 were solved for V(x) by modeling the MCP/probe film/electrolyte structure as a multilayer inside of which each layer k, of width t_k, was specified by constant values of ε_k, c_Ik, and β_k. Runge-Kutta-Verner fifth and sixth order methods were used to integrate equation 4, expressed as two ordinary differential equations dy₁/dx = −ρ_k/(ε_kε₀) and dy₂/dx = y₁, where y₂ = V(x). The integration was performed from the probe layer/electrolyte interface at $x_{\mathrm{B}}={\displaystyle \sum _k{t}_{\mathrm{k}}}$ to the electrode surface at x = 0, with continuity of the potential V(x) and electric displacement ε dV/dx at boundaries between layers. The two required initial conditions were (1) a specified value for V(x_B) and (2) the corresponding potential gradient dV/dx at x = x_B. The gradient can be calculated by integrating equation 4 analytically once; if x₁ and x₂ are two positions within layer k, then

$${\frac{\mathit{\text{dV}}}{\mathit{\text{dx}}}|}_{x2}={\left({\left(\frac{\mathit{\text{dV}}}{\mathit{\text{dx}}}\right)}_{x1}^2-\frac{2e{N}_{\mathrm{A}}}{{\epsilon }_{\mathrm{k}}{\epsilon }_0}\left[z_{\text{Ik}}{c}_{\text{Ik}}(V_2-V_1)+\frac{\mathit{\text{kT}}}{e}{\displaystyle \sum _j{c}_j\text{exp}(-z_j{\mathit{\text{eV}}}_2/\mathit{\text{kT}}-{\beta }_{\text{jk}})\{\text{exp}(z_{j}e(V_2-V_1)/\mathit{\text{kT}}-1\}}\right]\right)}^{}$$ (6)

For the semi-infinite electrolyte with x₂ = x_B, x₁ = ∞, c_I = 0, and β_j = 0, and with dV/dx and V going to 0 as x → ∞, equation 6 simplifies to

$${\frac{dV}{dx}|}_{x_{\mathrm{B}}}={\left(-\frac{2\mathit{\text{kT}}{N}_{\mathrm{A}}}{\epsilon {\epsilon }_0}{\displaystyle \sum _j{c}_{\mathrm{j}}}\left\{1-\text{exp}(-z_{\mathrm{j}}\mathit{\text{eV}}(x_{\mathrm{B}})/\mathit{\text{kT}})\right\}\right)}^{1/2}$$ (7)

which served as the second initial condition. C_d was obtained from the calculated V(x) by numerical differentiation, according to equation 2 and equation 3.

The electrolyte was modeled as containing sodium cations and three types of phosphate anions with relative concentrations governed by acid-base equilibria: H₂PO₄⁻, HPO₄²⁻, and PO₄³⁻. For the experimental 0.2 mol L⁻¹ pH 7.0 phosphate buffer, the concentrations used are 0.315 mol L⁻¹ Na⁺, 0.0846 mol L⁻¹ H₂PO₄⁻, 0.115 mol L⁻¹ HPO₄²⁻, and 5.54 × 10⁻⁷ mol L⁻¹ PO₄³⁻. The electrolyte dielectric constant was taken to be 80, and the temperature was 295 °K.

3. Results and Discussion

3.1. IRRAS Studies of MCP Passivation

Direct contact of probes with the solid support can be detrimental to hybridization activity; for example, single-stranded DNA probes are known to adsorb to gold through base-surface interactions^40,41 that result in surface-bound conformations with poor hybridization activity ^11,33,36. Hybridization activity can be restored by treatment, or passivation, of the surface with alkanethiols such as mercaptohexanol or mercaptopropanol (MCP) with a hydrophilic surface chemistry to which the probes do not strongly adsorb. These displacer molecules assemble into a monolayer coating that lifts the probe backbone off the support, leaving the strands attached through their thiolate bond only, in an end-tethered geometry favorable to hybridization.

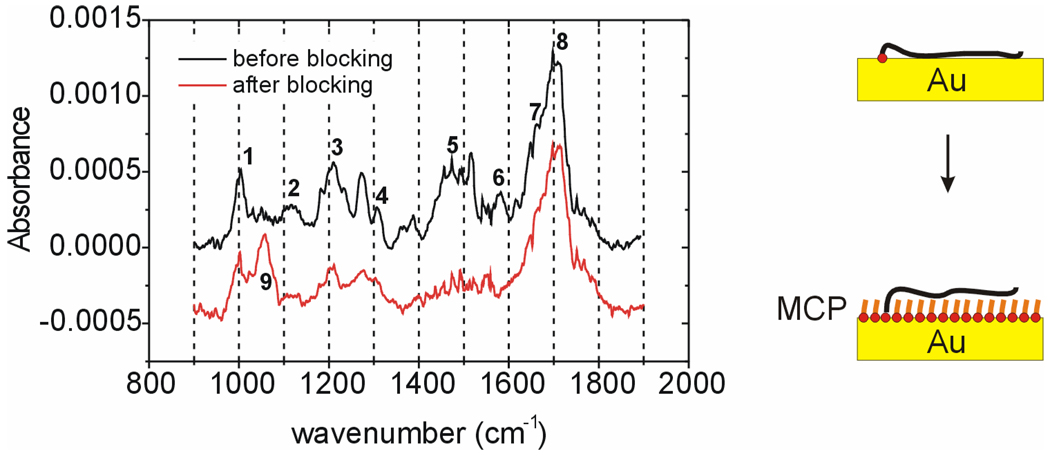
Morpholino probes, through their bases, were similarly expected to exhibit an affinity for gold, motivating examination of whether MCP is able to successfully displace these interactions. The thymine-rich probe PM2 was selected for these experiments because thymine-gold interactions yield an IR marker band in the region 1580 to 1600 cm^−142,43, attributed to C=O stretches of chemisorbed thymine ⁴². A successful passivation of the surface with MCP, in which the probe backbone is displaced from direct contact with the support, should be accompanied by a disappearance of this marker band.

Figure 2 compares IRRAS spectra of a PM2 monolayer before and after MCP blocking. The assignments for the dominant spectral bands are given in Table 2. The disappearance of the marker band, corresponding to peak 6, after MCP passivation indicates that displacement of adsorptive contacts between thymine bases and the support was successful. In parallel, the appearance of the C-OH stretch at 1060 cm⁻¹ (peak 9) confirms the surface presence of MCP.

Figure 2.

IRRAS spectra before (–) and after () blocking of a PM2 monolayer with mercaptopropanol (MCP). Assignments for numbered peaks are provided in Table 2. Peak 6 is diagnostic of contact between thymine bases and the Au support.

Table 2.

IRRAS spectral assignments for Morpholino monolayers.

peak # (Fig. 2)	position (cm−1)	primary attribution	reference
1	1000	P–O–C asymmetric stretch	44
2	1120	C–O–C asymmetric stretch	44
3	1210	P=O stretch	44
4	1310	phosphoroamidate (CH3)2N–P vibration	45
5	1420–1520	various bands (thymine, phosphoroamidate)	42,45
6	1580	C=O stretch of chemisorbed thymine	42
7	1670	C4=O stretch of thymine	42
8	1705	C2=O stretch of thymine	42
9	1060	C–OH stretch of mercaptopropanol	44

3.2. Charge Organization of Hybridized Morpholino Monolayers

A specific state of surface hybridization defines a unique combination of immobilized and mobile ion concentrations at the surface. The response of this environment to an applied potential can be used to characterize the state of hybridization and in principle provides for a convenient, label-free approach to diagnostics. However, significant challenges arise in quantitatively relating a label-free electrochemical response (e.g. surface capacitance, surface potential, field-effect transduction) with molecular coverage of analyte. The underlying relationships between surface organization and the measured response are obscure and at times counter-intuitive; for example, both decreases ^46–50 and increases^51–53 in surface capacitance due to hybridization have been reported, illustrating that even the direction of change can be unpredictable. Similarly, orders of magnitude disparities exist in estimated sensitivities of field-effect transduction, despite similar mechanisms of contrast⁵⁴.

In this section, the aim is to fundamentally understand the physical changes induced in charge organization of Morpholino films undergoing hybridization, and to compare these to when DNA probes are used. Optimization of Morpholino assays, which perform best at low salt concentrations where DNA probes do not function, will be reported separately. At the buffer strength (0.2 mol L⁻¹ pH 7.0 sodium phosphate) used for the present experiments both probe types hybridize well. In the experiments that will be described, the surface state was characterized at a point in time during the course of hybridization as a function of applied surface potential, V_DC, through the change in surface capacitance, ΔC_d(V_DC), brought on by probe-target binding. In turn, ΔC_d can be interpreted in terms of the near-surface ionic concentrations and dielectric strength. All of the experiments of this section used unlabeled targets in order to extend the positive limit on V_DC up to 0.25 V without interference from tag electroactivity in the determination of C_d, at the cost of foregoing quantification of target coverage (quantitative comparison of target coverage with ΔC_d is postponed to section 3.3). Control experiments showed that (1) target coverage was not significantly perturbed by changes in surface potential during C_d measurements (Supporting Information, Figure S3) and (2) hybridization of Morpholino films was sequence-specific, with binding of non-complementary TD2 targets below detection (Supporting Information, Figure S4).

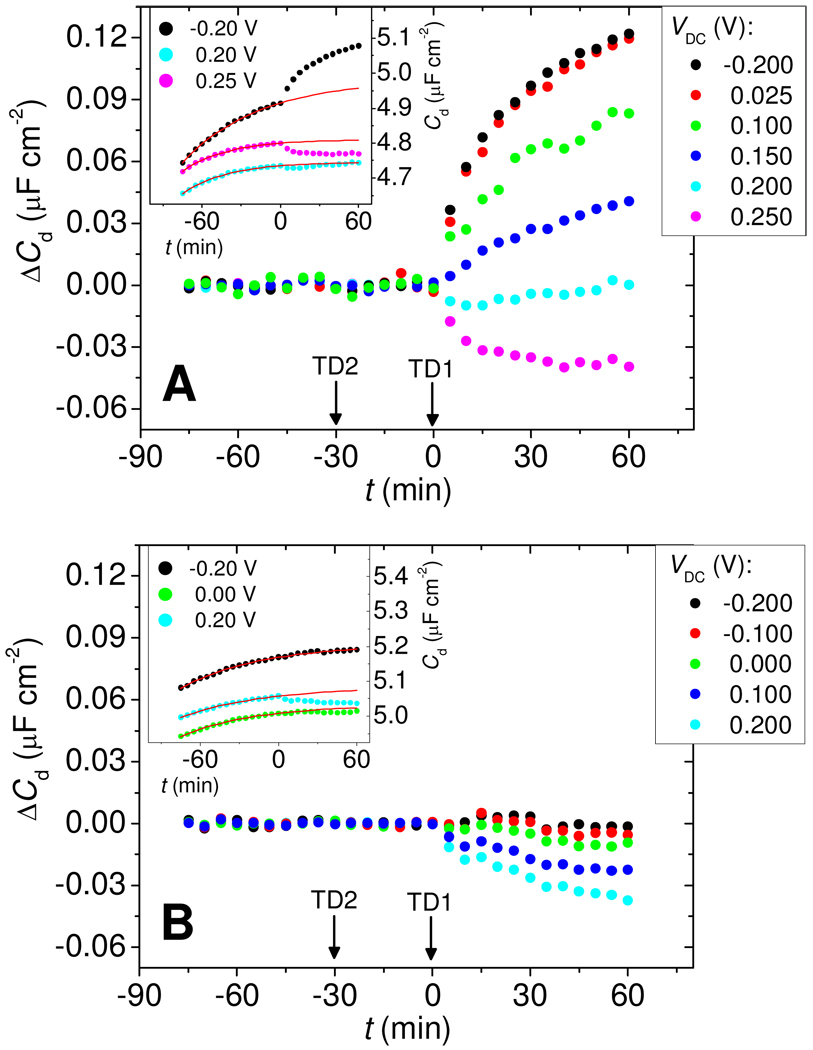
Figure 3 compares the evolution of ΔC_d for Morpholino (Figure 3A) and DNA (Figure 3B) probe films in the presence of target molecules. The insets show raw data in the form of traces of C_d vs time. Prior to addition of complementary target TD1 at time t = 0, only a featureless increase in the baseline, on the order of 1 % per hour, was observed in the raw data. The source of this increase is not known with certainty but is suspected to reflect gradual loss of MCP. Empirically, the shape of the baseline could be represented by a first order process; that is, the baseline function f_B was modeled as f_B = A₁ – A₂exp(−A₃t), with A₁, A₂, and A₃ determined from a least squares fit to data prior to hybridization, −75 min < t < 0 min (see insets to Figures 3A and 3B). ΔC_d, attributed to binding of target molecules, follows from ΔC_d = C_d - f_B. For each run, probe layers were first measured under target-free buffer, next under 25 nmol L⁻¹ non-complementary TD2 target for 30 min (−30 min < t < 0 min), and finally under a TD1:TD2 mixture with each target present at 25 nmol L⁻¹. Addition of non-complementary TD2 at t = −30 min did not produce a resolved response at any of the potentials, whereas addition of the complementary TD1 target at t = 0 min immediately led to a change in ΔC_d.

Figure 3.

(A) Main panel: Change in capacitance ΔC_d for Morpholino layers undergoing hybridization as a function of measurement bias V_DC. Arrows indicate addition of non-complementary TD2 and complementary TD1 targets. Inset: Examples of raw C_d vs time data (points) and fitted baselines f_B (red solid lines), at three settings of V_DC. ΔC_d was calculated as the difference between C_d and the baseline. Conditions: 4.9 × 10¹² probes cm⁻², 25 nmol L⁻¹ target, pH 7.0 0.2 mol L⁻¹ sodium phosphate buffer. (B) Same as (A) but for DNA probe layers at 5.1 × 10¹² probes cm⁻² and otherwise identical conditions.

Strikingly, as shown in the main panel of Figure 3A, the response of Morpholino films to hybridization was tunable, with a change in sign (contrast inversion) from positive to negative as V_DC increased past 0.2 V. Moreover, in the range from −0.2 V to 0.025 V the response was nearly independent of V_DC, making this range attractive for diagnostic applications. Above 0.025 V, ΔC_d started to decrease with V_DC and became negative beyond the contrast inversion point at 0.2 V. In comparison, hybridization of DNA targets to DNA probes produced ΔCd ≈ 0 when measured at negative biases, below −0.1 V. As V_DC increased, contrast improved and an increasingly negative (ΔCd < 0) response to hybridization was observed.

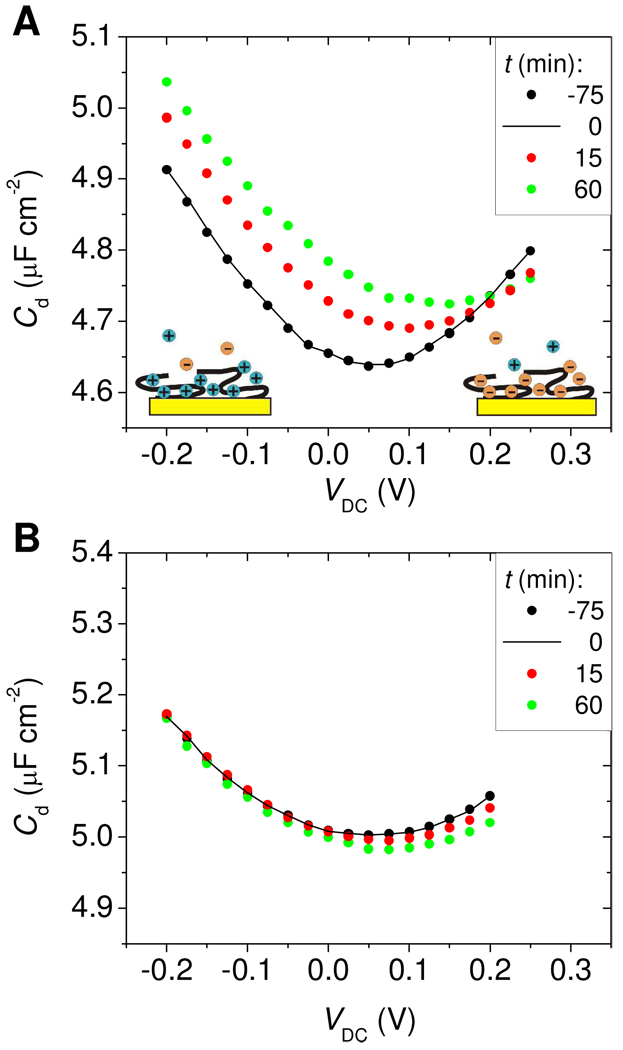
The data in Figure 3 show that, depending on V_DC and probe type, binding of target molecules can manifest as an increase, a decrease, or a null response. Understanding the origins of this diversity of trends provides insight into the physical changes that accompany surface hybridization. In Figure 4, the data are replotted to show the full dependence of C_d on V_DC at selected time points, for Morpholino (Figure 4A) and DNA (Figure 4B) probe layers. Between t = −75 min (black points) and t = 0 min (black trace) the probe films were kept under buffer and non-complementary TD2 target, with little if any change taking place. Introduction of complementary TD1 target at t = 0 produced horizontal and vertical displacements of the C_d(V_DC) trace. As illustrated by the cartoons in Figure 4A, the ubiquitous increase in C_d at the extremes of V_DC is attributed to potential-driven accumulation of solution ions near the surface: phosphate anions at more positive potentials and sodium cations when V_DC is swept negatively. The elevation in surface concentration of mobile ions provides for more efficient ionic screening, and hence higher capacitance⁵⁵.

Figure 4.

C_d(V_DC) traces as a function of time for (A) Morpholino and (B) DNA probe films. t = 0 (black line) corresponds to introduction of complementary TD1 target and onset of hybridization. Shift in C_d due to baseline drift was corrected relative to t = 0 by plotting C_d(t) = C_d,raw(t) – ( f_B(t) - f_B(0) ), where f_B(t) - f_B(0) is the change in baseline between t and 0 min, and C_d,raw(t) is the unprocessed data.

The displacements of the C_d(V_DC) traces in Figure 4 were interpreted with the help of the Poisson-Boltzmann (PB) model, described by equation 2 through equation 7. The MCP layer was modeled using a width t_MCP = 0.67 nm⁵⁶, a dielectric constant ε_MCP = 4.4, and β = 1000 for all solution ions. These settings reproduced the experimental capacitance of about 5.6 µF cm⁻² for a pure MCP monolayer. Setting the partitioning penalty β to 1000 effectively renders the MCP layer impermeable to ions. The description of the Morpholino layer proved more complex. One expectation is that unhybridized probes are in a collapsed, desolvated state. The principal reason for this suspicion is that the surface concentration of ~ 0.1 to 1 mol L⁻¹ significantly exceeds the bulk solubility of ~ 1 mmol L⁻¹⁵⁷, implying that the probes exist as a precipitated film. As a first approximation, therefore, the layer thickness t_P was set to the collapsed "dry" value of 0.52 nm, derived from the measured probe coverage and a volume of 0.53 nm³ per nucleotide⁵⁸.

In order to capture the experimental upturn in C_d at positive and negative biases (Figure 4A), it was necessary to allow sodium Na⁺ and monovalent phosphate H₂PO₄⁻ ions to partition into the probe film under the influence of V_DC. This condition was met by keeping the partitioning penalty β small for these ions (Figure 5 caption). However, partitioning of divalent phosphate (HPO₄²⁻) led to an overly exaggerated upturn at positive V_DC; thus, only monovalent phosphate was assumed to penetrate.⁵⁹ Finally, it is important to note that experiments express V_DC relative to a reference electrode, with an unknown absolute potential, whereas calculations express V_DC relative to solution. This leads to an offset in V_DC between calculated and experimental curves⁶⁰.

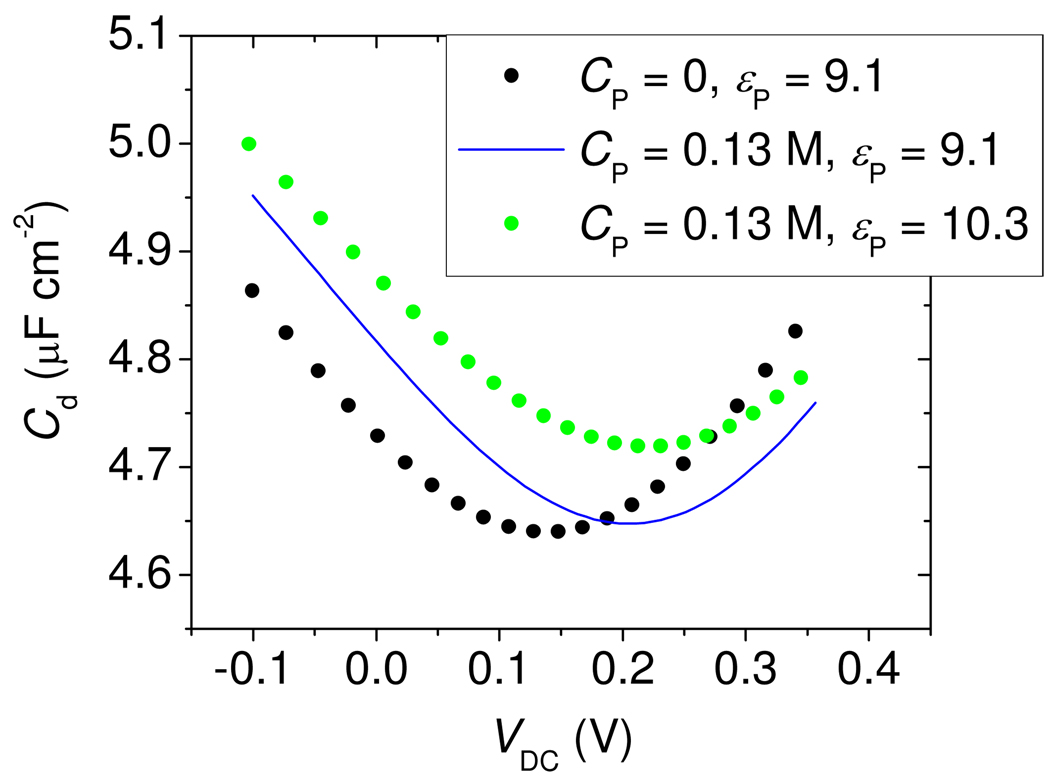
Figure 5.

PB theory calculations, illustrating the effect of (1) an increase in immobilized negative charge C_P of the probe layer from 0 (black points) to 0.13 mol L⁻¹ (blue line), and (2) an increase in dielectric constant ε_P of the probe layer from 9.1 (blue line) to 10.3 (green points). The shape of the curve traced out by the black points corresponds, approximately, to t = 0 data in Figure 4A, while the green trace can be compared to the t = 60 min data. MCP layer parameters: t_mcp = 0.67 nm, ε _mcp = 4.4, β_j,mcp = 1000 for all ions. Morpholino probe layer parameters:$t_{\mathrm{P}}=0.52\text{nm},{\beta }_{{\text{Na}}^{+},\mathrm{P}}=0,{\beta }_{{\mathrm{H}}_2{\text{PO}}_4^{-},\mathrm{P}}=1.8,{\beta }_{{\text{HPO}}_4^{2-},\mathrm{P}}=1000,{\beta }_{{\text{PO}}_4^{3-},\mathrm{P}}=1000$. Electrolyte parameters: T = 295 °K, 0.2 mol L⁻¹ pH = 7.0 phosphate buffer.

Figure 5 shows that two simple adjustments in model parameters were able to qualitatively reproduce experimentally observed changes in C_d due to hybridization. The first type of adjustment consists of addition of immobile charge sites to the Morpholino layer (c_I term in equation 5), the predominant outcome of which is a horizontal shift of the C_d(V_DC) curve parallel to the potential axis. In Figure 5 this is illustrated by the black and blue traces representing, respectively, a neutral film and a layer with 0.13 mol L⁻¹ concentration of immobile negative charge⁶¹. The horizontal shift arises because of an altered permselectivity of the film. The effect can be recast in hybridization terms as follows. Binding of targets introduces immobile, negatively charged sites to the probe layer. The presence of these sites depletes anions and accumulates cations in the film, and alters the value of C_d. In order to restore C_d and the cation-to-anion balance at the surface to their pre-hybridization values, a more positive V_DC must be applied to compensate for the effect of the negatively charged sites. This positive offset in V_DC manifests as a translation of the entire C_d(V_DC) curve toward positive potentials.

The above explanation and the PB model present a simplified description in that the charge of hybridized targets was assumed to be strictly immobile. This approximation is partly justified by the observation that, at the high frequency (5435 Hz) used for measurement, surface-tethered DNA oligonucleotide chains do not respond significantly to oscillating surface fields⁶²; thus, the main contribution to C_d is expected to be from movement of small ions whose mobility is not impaired by backbone connectivity, or the large mass-to-charge ratio of DNA.

The second type of adjustment illustrated in Figure 5 is a change in the dielectric constant profile. In general, such a change could result from variation in composition, thickness, homogeneity, or other structural rearrangement of the probe layer brought on by hybridization. The local dielectric constant represents capacity of the surface environment to screen electric fields through polarization: higher values correspond to more effective screening, allowing greater surface charge to build up in response to an increment in potential, and increasing C_d (equation 2). A change in dielectric constant thus raises or lowers C_d;⁶³ causing a vertical displacement of the C_d(V_DC) curve. This is illustrated in Figure 5, where an upward displacement was produced by increasing the dielectric constant of the probe film from 9.1 (blue curve) to 10.3 (green trace).

For Morpholino films, the impact of hybridization on the C_d(V_DC) curve can be summarized as a rightward and an upward translation (Figure 4A). The rightward displacement signifies a change in permselectivity that favors cations and expels anions; as discussed above, this outcome is expected from hybridization of negatively charged targets. The upward displacement indicates improved dielectric screening. These dielectric changes are expected to reflect various effects, difficult if not impossible to disentangle. For example, hybridization may improve solvent compatibility of the probe layer, elevating the local dielectric constant through increased water content, and concomitantly leave a thinner underlayer of unhybridized, collapsed probes on the surface. It is the cumulative effect of such changes that would be reflected in the observed, upward displacement in C_d.

Hybridization to DNA probes resulted in a rightward displacement of the C_d(V_DC) curve (Figure 4B) indicating that, also in this case, binding of target molecules shifted the cation:anion balance in favor of cations. The qualitative impact of hybridization on permselectivity was therefore same for Morpholino as for DNA probe layers. However, in contrast to the Morpholino results, the C_d(V_DC) curve shifted slightly downward. Decrease in capacitance for hybridized DNA probe films was previously attributed to lowering of polarization screening because of volumetric displacement of solvent molecules by DNA targets,^46–48 whose dielectric constant is lower. This explanation also agrees with the present observations. Compared to Morpholino films, target hybridization to a DNA probe layer should have little impact on the layer's solvent compatibility because of the good solubility of DNA probes.

The origins of the contrast inversion reported in Figure 3A for Morpholino hybridization are now clear. When ΔC_d is measured at a V_DC negative of the C_d minimum, the unhybridized and uncharged layer is initiated in a cation-rich state. In this scenario, subsequent binding of target strands is accompanied by additional accumulation of cations, rather than expulsion of anions of which there are very few in proximity of the surface. The extra cations are needed to ensure electroneutrality. In this cascade of events, hybridization elevates the local concentration of small ions, ionic screening is enhanced, and thus C_d increases - leading to positive contrast (ΔC_d > 0). However, as shown by data positive of V_DC = 0.2 V in Figure 4A, contrast can be also negative (ΔC_d < 0). Since the C_d(V_DC) curve is also translated upward, the decrease in C_d cannot be attributed to a lowering of the dielectric constant (e.g. from displacement of water molecules by targets). Rather, the explanation is sought in a lowering of the local ionic strength. A diminished ionic strength would imply that hybridization of targets causes a drop in concentration of mobile ions at the surface. This outcome is expected if, as targets bind, electroneutrality is satisfied by expulsion of anions from the surface. Indeed, at sufficiently positive biases the surface concentration of anions will greatly exceed that of cations, making anion-expulsion the default mechanism used to satisfy electroneutrality; i.e. the surface ionic strength will drop as targets bind, leading to a negative contrast. The target countercharge, in this case, must then be mostly provided by positive charge on the electrode.

3.3. Mapping ΔC_d to Target Coverage

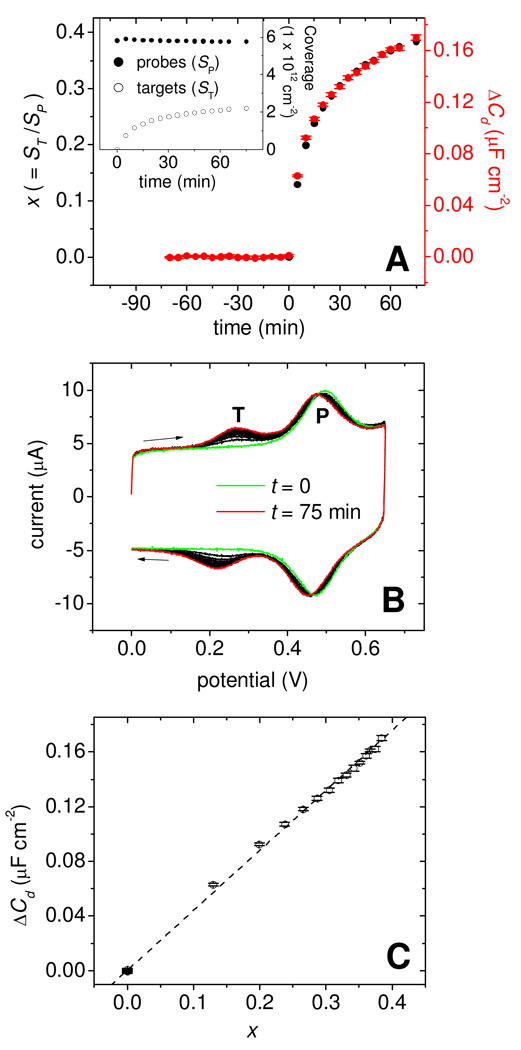
The experiments in Figure 3 and Figure 4 helped elucidate physical mechanisms of surface hybridization on Morpholino monolayers, but did not provide quantitative dependence of ΔC_d on the extent of hybridization. This dependence was explored in a separate series of measurements using F2-labeled targets, probe coverage of 5.8 × 10¹² probes cm⁻², and six V_DC settings: 0, −0.01, −0.02, −0.03, −0.04, and −0.05 V. These potentials fall within the diagnostically optimal window in which contrast was strongest and largely potential-independent (Figure 4A). C_d was determined every 5 minutes at all six potentials and, immediately following, probe coverage S_P and target coverage S_T were measured using cyclic voltammetry (CV). The combined C_d and CV measurement required 30 s to complete. After subtraction of the f_B baseline, the six ΔC_d values from each time point were averaged and standard deviations were calculated. Target and probe coverages were combined into the hybridization conversion x, defined by x = S_T/S_P.

Figure 6A plots x (black points) and ΔC_d (red points; error bars are standard deviations) as a function of time, with t = 0 corresponding to addition of complementary TD1 target. The inset shows target and probe coverages calculated from the CV scans shown in Figure 6B. The ~ 2 % decrease in probe coverage is attributed in part to gradual tag degradation via the ferricinium state ^64,65. In Figure 6B, the peak near 0.24 V is from targets while that near 0.48 V is from the probes. Surface, as opposed to solution, origins of the target signal were confirmed by noting that the peak current, measured from the baseline, scaled linearly with scan rate dV/dt⁶⁶. During hybridization the probe CV peak shifted negatively by about −20 mV and slightly broadened (cf. green and red CV traces in Figure 6B). This shift reflects the creation of a membrane potential ^67,68 at the surface from the binding of negatively-charged targets, which facilitates oxidation of ferrocene by stabilizing the positively charged ferricinium state. Figure 6C shows that ΔC_d and x were strongly correlated, with a near-linear relationship between the two quantities.

Figure 6.

(A) Main panel: Time traces of surface conversion x = S_T/S_P (black points) and of ΔC_d signal (red points) for hybridization of TD1 targets to PM1 probes. Plotted ΔC_d values are averages of measurements at V_DC of 0, −0.01, −0.02, −0.03, −0.04, and −0.05 V. Error bars give the standard deviations. Buffer: 0.2 mol L⁻¹ pH 7.0 sodium phosphate. Inset: Probe (filled points) and target (open points) coverages determined from cyclic voltammetry. (B) Cyclic voltammograms used for calculation of probe and target coverages. First (t = 0) and last (t = 75 min) scans are highlighted in green and red, respectively. "T" marks the target peak, "P" marks the probe peak. (C) Dependence of ΔC_d on x. Dashed line: least-squares linear fit (R² = 0.9992).

The label-free limit of quantification, l_Q, is defined as ten times s_B where s_B is the standard deviation of the background prior to hybridization (i.e. for −70 < t < 0). Performing this calculation on the data in Figure 6A yields s_B = 2.2 × 10⁻¹⁰ F cm⁻² and l_Q = 10s_B = 2.2 × 10⁻⁹ F cm⁻². The capacitance units can be converted to more informative units of target coverage by multiplying l_Q by dS_T/dΔC_d, where dS_T/dΔC_d = 1.3 × 10¹⁹ targets F⁻¹ follows from dS_T/dΔC_d = S_P (dΔC_d/dx)⁻¹, with dΔC_d/dx given by the slope of the line in Figure 6C. This yields l_Q = 2.9 × 10¹⁰ targets cm⁻², representing 0.5 % hybridization of the probe layer, or about 2.5 pg mm⁻² of target. This limit is comparable to or exceeds that of surface plasmon resonance and quartz crystal microbalance techniques^69–71, two popular methods for label-free monitoring of surface bioaffinity reactions.

4. Conclusions

Morpholino monolayers on gold can be prepared through direct adaptation of known chemistries for DNA monolayers, in which a thiolate bond serves to anchor Morpholino strands through one terminus to the surface, and the rest of the surface is passivated against nonspecific adsorption with a short chain alkanethiol. Hybridization of Morpholino monolayers, which are uncharged, with charged nucleic acid targets alters the dielectric and ionic strength characteristics of the surface environment. Hybridization of target molecules adds negative charge to the probe layer which has to be compensated by changes in local concentrations of small ions; i.e. by accumulation of cations and/or by expulsion of anions. Which adjustment mechanism dominates is tunable by the applied surface potential; e.g. at negative biases, when surface concentration of anions is small, accumulation of cations is the primary response mechanism. At positive potentials, expulsion of anions is dominant. These signatures of hybridization can be monitored through the surface differential capacitance C_d, where they lead to increases or decreases in C_d depending on the relative surface populations of cations and anions. Similar phenomena would be expected to arise in electrostatic monitoring of surface hybridization using other uncharged probe molecules, such as PNAs ^72–74 or nylon nucleotides ^75,76. The described physical processes are also analogous to those in other systems driven by charge effects; e.g. in metal-oxide-semiconductor structures, where semiconductor dopant sites take the place of immobile target charges and the phenomena of charge carrier inversion and accumulation correspond to accumulation of anions or cations in the probe layer.

A central motivation for the present study of Morpholino surface hybridization is prospects of label-free DNA or RNA analysis. Based on a 10:1 signal-to-noise criterion, C_d measurements demonstrated limits of quantification down to 3 × 10¹⁰ targets cm⁻², corresponding to several pg of material per mm². This performance matches that of other label-free methods, including surface plasmon resonance⁶⁹ and quartz crystal microbalance⁷¹ techniques, that could be used for analysis of nucleic acids by surface hybridization. In the case of capacitive transduction, sensitivity is expected to improve at lower ionic strengths, under conditions more dilute than the 0.2 mol L⁻¹ phosphate buffer used. These and related performance issues will be analyzed separately. If label-free capacitive diagnostics are found promising, they can be adopted to microelectronic biochip platforms, in the spirit of recent efforts to develop fully-integrated chip hardware for label-based electrochemical nucleic acid assays.^47,77–79

Supplementary Material

1_si_001. Supporting Information Available.

Description of the synthesis of the FC1 tag; Figure S2 illustrating conjugation of ferrocene tags to probe and target strands; description of equations and methods used to fit cyclic voltammetry data to extract peak areas; control experiments examining impact of surface potential variation during C_d measurement; cyclic voltammetry control experiments for nonspecific adsorption of target strands. Complete Ref. 30. This material is available free of charge via the Internet at http://pubs.acs.org.