Summary
The local field potential (LFP) is increasingly used to measure the combined activity of neurons within a region of tissue. Yet, available estimates of the size of this region are highly disparate, ranging from a few hundred microns to several millimeters. To measure the size of this region directly, we used a combination of multielectrode recordings and optical imaging. We determined the orientation selectivity of stimulus-evoked LFP signals in cat area V1 and were able to predict it on the basis of the surrounding map of orientation preference. The results show that LFP signals originate within ~250 μm of the recording electrode. This quantitative estimate of spatial scale indicates that LFPs are more local than often recognized, and provides a guide to the interpretation of the increasing number of studies that rest on LFP recordings.
Introduction
The local field potential (LFP) is a measure of combined electrical activity within a volume of neural tissue (Mitzdorf, 1985). A growing number of studies record it to investigate mechanisms of cortical sensory processing, motor planning, and higher-level cognitive functions such as memory, decision-making, and attention (Henrie and Shapley, 2005; Kreiman et al., 2006; Liu and Newsome, 2006; Pesaran et al., 2002; Scherberger et al., 2005; Womelsdorf et al., 2006). LFP activity appears to be the electrical signal that corresponds most closely to fMRI measurements (Logothetis et al., 2001), and may even be a promising candidate to guide robotic prostheses (Andersen et al., 2004).
In visual cortex, LFP signals driven by visual stimuli have been extensively investigated. A number of studies have concentrated on the evoked response, i.e. the average response time-locked to the presentation of a visual stimulus (e.g., Kitano et al., 1994; Mitzdorf, 1985; Schroeder et al., 1991; Victor et al., 1994). Another body of literature has concentrated on induced activity, i.e. ongoing oscillations whose amplitude is modulated by the stimulus (e.g., Eckhorn et al., 1988; Frien et al., 2000; Gray et al., 1989; Kruse and Eckhorn, 1996).
Despite their increasing popularity, LFP signals present a problem of interpretation: it is not known whether they reflect the activity of a small and localized population, or of a large and distributed one. In the cerebral cortex, disparate estimates are available for the extent over which the underlying signals are integrated. These estimates range from several hundred micrometers (Berens et al., 2008; Engel et al., 1990; Kruse and Eckhorn, 1996; Liu and Newsome, 2006) to a few millimeters (Kreiman et al., 2006; Logothetis et al., 2001; Mitzdorf, 1985). These discordant estimates, moreover, are rather qualitative, and are not accompanied by a definition of what is meant by “size”. The region of integration is not expected to have sharp boundaries.
Complicating this matter is the debate about whether the various frequency components of the LFP have different spatial footprints. It has been proposed that the higher frequencies (in the gamma range, around 25–90 Hz) may carry information that is more local than the lower frequencies, perhaps because of capacitive properties of brain tissue (Liu and Newsome, 2006). This interpretation is problematic, however, because brain tissue has been shown to transmit high frequencies equally well as low frequencies, i.e. to act largely as a resistive network (Logothetis et al., 2007; Mitzdorf, 1985; Nicholson and Freeman, 1975; Ranck, 1963).
We sought to characterize quantitatively the area of integration underlying LFP signals by relating the functional properties of these signals to the functional properties of the underlying population. We focused on primary visual cortex (V1), and relied on its highly-organized map of orientation preference, which can be imaged in fine spatial detail. We drove V1 neurons with visual stimuli that evoke strong LFP responses. These LFP responses showed clear orientation tuning. By comparing the tuning of LFPs recorded at multiple sites with quantitative predictions based on the map of orientation preference we obtained a quantitative estimate of the extent of neural tissue contributing to the LFP at those sites.
Results
To evoke strong LFP responses we chose visual stimuli that drive transient and coherent, i.e. synchronous, neuronal responses (Regan and Regan, 1988; Victor et al., 1994; Zemon and Ratliff, 1982). The coherence of responses across space is important because the LFP represents a sum over a volume of neural tissue, and incoherent responses across neurons would cancel each other out. The transient nature of responses over time is also important because the brain’s ongoing activity (which here represents noise) decreases in amplitude as 1/frequency, so it is easiest to detect evoked responses that have power at higher frequencies (Benucci et al., 2007).
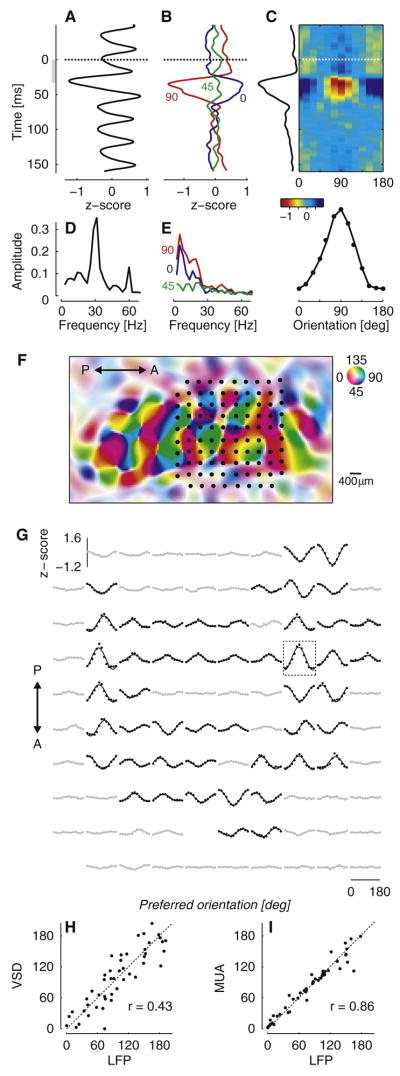
Following this approach we evoked LFP responses that were strongly orientation selective (Figure 1A–E). We recorded LFP signals in area V1 of anesthetized cats in response to pseudo-random sequences of gratings of varying orientation and spatial phase (Ringach et al., 1997), each flashed for 32 ms (‘orientation noise stimulus’). As expected, stimulus-triggered LFPs strongly oscillated at 31 Hz, the stimulus update frequency; this oscillation is clearly visible when averaging across stimulus orientations (Figure 1A,D). Its origins lie in the membrane potential responses of individual neurons (Gillespie et al., 2001). We isolated the tuned component of the evoked LFPs by triggering on the presentation of individual orientations and subtracting the mean across orientations. The resulting responses are clearly tuned for orientation (Figure 1B). The time course of these tuned responses is slower than that of the untuned response (Figure 1A); indeed, their power is concentrated well below the stimulus update frequency of 31 Hz (Figure 1E). LFP responses to different orientations followed the same time course, allowing us to assign to the recording site a single orientation tuning curve (Figure 1C).
Figure 1.
Orientation selectivity of LFPs evoked by orientation noise stimuli in primary visual cortex. (A) Mean across orientations of the LFP response. Responses were aligned to grating onset (dashed line), and averaged across grating orientations. The oscillation ~30 ms after stimulus onset is largest because it is aligned with the occurrence of grating stimuli (excluding blank stimuli). (B) Tuned components of the LFP response for three stimulus orientations. Responses were aligned to the onset of a single orientation (dashed line), and the mean across orientations (shown in A) was subtracted. (C) Estimate of the orientation tuning curve. We applied Singular Value Decomposition to the responses and obtained the orientation tuning curve and the response time course plotted at the margins. (D) Amplitude of the frequency spectrum for the mean across orientations of the LFP response shown in A. (E) Same, for the tuned components of the LFP response shown in B. (F) Layout of the 10×10 electrode array (dots), aligned with the map of orientation preference measured with voltage-sensitive dyes. Hue indicates preferred orientation and saturation indicates tuning strength (legend). (G) Orientation tuning of LFP responses measured in the electrode array. Half of the sites were classified as strongly tuned (black) and the other half as weakly tuned (gray) based on the standard deviation across orientations. Rectangle: recording site shown in A–E. (H) Relation between orientation preference of LFPs and of the corresponding pixels in orientation preference map. (I) Relation between orientation preference of LFPs and simultaneously recorded multi-unit spike activity. To remove outliers, only sites with strong LFP tuning (shown in G) contributed to these scatter plots.
To relate the orientation tuning of LFPs to the underlying population of neurons, we combined multielectrode recordings with optical imaging (Figure 1F–I). We first used voltage-sensitive dye (VSD) imaging to obtain high-resolution maps of orientation preference (Benucci et al., 2007). We subsequently implanted an array of 10×10 electrodes (400 μm grid spacing) in the same cortical patch, and determined its precise location within the orientation map (Figure 1F). This location is the one that maximizes the correlation between the orientation preference measured optically and the orientation preference of multi-unit spike activity (Nauhaus and Ringach, 2007). Such alignments are very reliable, with a typical precision of ~30 μm. At most of the recording sites, LFP signals revealed a pronounced selectivity for orientation (Figure 1G). Reassuringly, their orientation preference was strongly correlated (r = 0.43, p<0.0001) with the orientation preference previously measured optically (Figure 1H) and with that of the multiunit spike activity (r = 0.86, p < 0.0001), which was acquired simultaneously (Figure 1I).
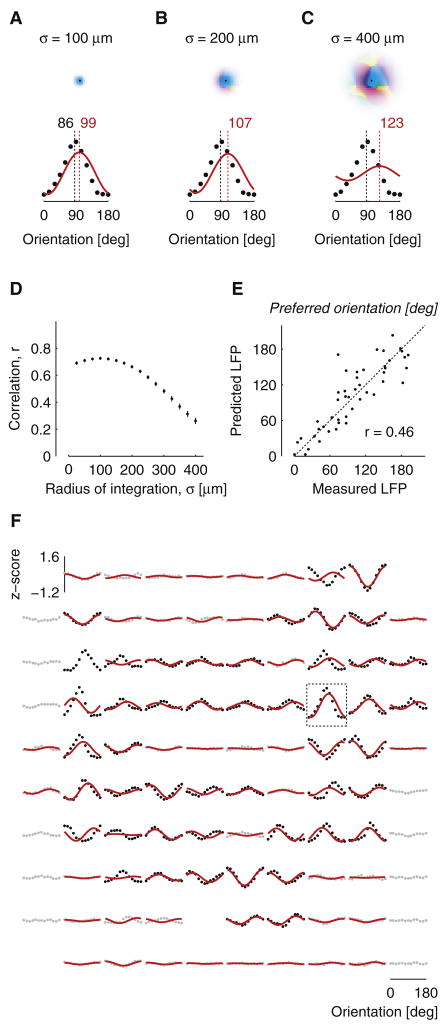
Next, we compared the orientation selectivity of the evoked LFP responses with quantitative predictions based on the map of orientation preference (Figure 2A–C). We considered that: (a) Electrical fields are a weighted sum of contributions from a local volume; (b) LFP signals reflect the membrane potential of neurons rather than their spike responses (Freeman, 1975); (c) the orientation preference of V1 neurons does not vary along the vertical dimension. To predict the orientation tuning of LFPs, therefore, we computed weighted sums of tuning curves with preferred orientations given by the orientation preference map, and a constant tuning width of 32 degrees, the average tuning width of membrane potentials recorded intracellularly in cat V1 (Carandini and Ferster, 2000). The weights in this summation were given by a two-dimensional Gaussian centered on the electrode position. We compared the LFP tuning curves predicted by this model to the actual LFP tuning curves for different values of the radius of integration (the standard deviation σ of the two-dimensional Gaussian). For small values of the radius (σ = 100 μm) the model performed well: its predictions resembled the measured LFP tuning curves both in preferred orientation and in amplitude (Figure 2A). Increasing the radius to larger values led to predicted tuning curves with increasing deviations in preferred orientation and with progressively shallower tuning (Figure 2B,C).
Figure 2.
Predicting the orientation selectivity of LFPs based on the orientation preference map. (A–C) LFP tuning curves predicted from the map of orientation preference, for three values of σ, the radius of integration. For each value of σ, the region of integration is shown (top) together with the LFP tuning curves (bottom) predicted by the model (red). The measured LFP tuning curve is plotted for comparison (black). Dashed lines indicate preferred orientation determined by a cosine fit. (D) Correlation between predicted and measured LFP responses, across all orientations and recording sites, as a function of σ. Error bars indicate standard error of the mean (bootstrap tests). (E) Relation between orientation preference of predicted and measured LFPs at the optimal radius of integration (σ = 100 μm). To remove outliers, only sites with strong LFP tuning (defined in Figure 1) contributed to this analysis. (F) Predicted LFP orientation tuning curves (red) superimposed on measured LFP orientation tuning curves (gray and black) in the electrode array. Predictions were restricted to recording sites with reliable signal/noise ratios in the map of orientation preference. Rectangle indicates the recording site of panels A–C and of Figure 1A–E.
Similar results were obtained across the array: the orientation preference of the evoked LFP responses could be closely predicted from the map of orientation preference, but only if the area of integration was small (Figure 2D–F). To determine the optimal area of integration, we varied the radius σ and examined the overall correlation (computed across stimulus orientations and electrodes) between the predicted and the measured LFP tuning curves (Figure 2D). This correlation peaks at a radius of σ = 100 μm (r = 0.73, p<0.0001), beyond which it decreases rapidly. At the optimal radius, the predicted tuning curves resemble the measured ones rather well (Figure 2F), yielding a high correlation between the predicted and the measured LFP orientation preferences (r = 0.46, p<0.0001, Figure 2E). The quality of the fits was roughly equal across the array, but there was a tendency for the model to perform best in orientation domains, i.e. away from pinwheels (Supplementary Figure 1).
We confirmed these results in two other animals. Just as in the data from cat 1, the quality of the prediction in cats 2 and 3 deteriorated when the radius of integration σ grew much beyond 100 μm. At this value of σ, the overall correlation between measured and predicted LFP tuning curves was r = 0.79 (cat 2) and r = 0.60 (cat 3); the correlation between measured and predicted orientation preferences was r = 0.62 in cat 2 and r = 0.34 in cat 3 (p<0.0001 in all cases). These correlations decreased steadily as σ increased beyond 100 μm. The optimal value of σ represents an estimate of the tissue volume over which the signals contributing to the LFP are integrated.
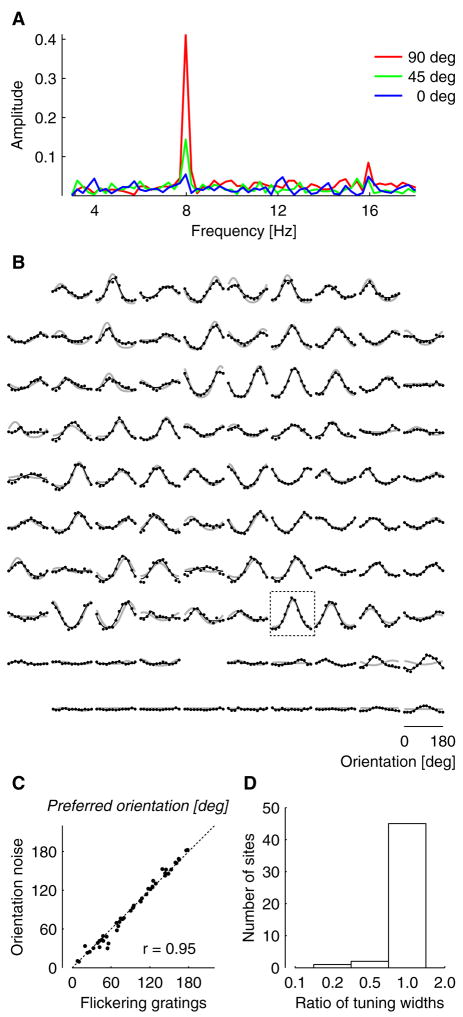
Our estimate of spatial integration concerns summation of activity across coherently active neurons and propagation of electrical signals in cortex, and should therefore be valid regardless of the stimulus that gives rise to these signals. To test this prediction, we performed additional experiments in which we recorded responses to a different visual stimulus, a contrast-reversing grating (Figure 3). We first presented orientation noise stimuli and determined tuning curves for the evoked LFP responses. We then recorded LFP responses evoked by standing gratings that reversed in contrast at a frequency of 4 Hz, and asked if the orientation tuning of these responses is similar to that obtained with orientation noise. Contrast-reversing stimuli evoke responses that oscillate at twice the reversal frequency (Benucci et al., 2007; Regan and Regan, 1988; Zemon and Ratliff, 1982). We determined the amplitude of this second harmonic response as a function of stimulus orientation (Figure 3A,B). The resulting tuning curves are very similar to those obtained with orientation noise, both in preferred orientation (Figure 3C) and in tuning width (Figure 3D). In summary, the orientation tuning of LFP signals, and consequently the spatial scale of such signals, is the same regardless of which of the two stimuli elicits the responses.
Figure 3.
Comparison of LFP selectivity determined with orientation noise stimuli and contrast-reversing gratings. (A) Amplitude spectra of the responses to contrast-reversing gratings for three stimulus orientations, recorded at a single electrode. Stimuli reversed in contrast at 4 Hz, leading to LFP responses at 8 Hz (second harmonic, or F2 component). (B) The orientation tuning curves of F2 responses measured across the electrode array (black). The tuning curves for orientation noise stimuli are provided for comparison (gray). Rectangle indicates the recording site of panel A. (C) Relation between orientation preferences determined with orientation noise and with contrast-reversing gratings. To remove outliers, only well-tuned sites are compared in this analysis (top 75%, based on the standard deviation across orientations). (D) Distribution of ratios of tuning widths for the same set of sites. For each site, the width of the F2 tuning curve was divided by the width of the tuning curve obtained with orientation noise stimuli.
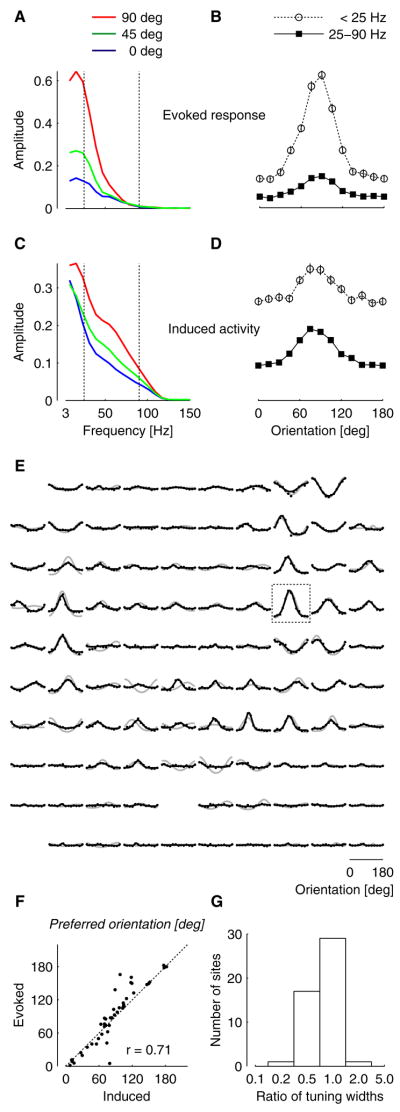
Similarly, our estimates of spatial integration should be valid regardless of whether the signals being integrated are evoked responses or modulations of ongoing oscillations. To test this prediction, we determined LFP selectivity not only for the evoked responses, time-locked to a visual stimulus, but also for the induced activity, ongoing oscillations modulated by the presence of the stimulus (Figure 4). Induced activity has much of its power at high frequencies, in the gamma range (Eckhorn et al., 1988; Gray et al., 1989). This activity may be hard to measure during our rapid stimulation regime, since it can be reduced by stimulus-evoked responses (Kruse and Eckhorn, 1996). We therefore concentrated on brief intervals in the stimulus sequence where gratings were followed by blanks. These intervals were sufficiently long to allow gamma power analysis (see Supplementary Figure 2 for an analysis of the time course of induced gamma activity). We first analyzed the evoked responses, which are simply measured by averaging the LFP signals across intervals (Figure 4A,B). As expected, the results are very similar to those seen when analyzing the full stimulus sequences (Figure 1E), with the evoked response having most of its power and orientation tuning at frequencies below 25 Hz. We then analyzed the induced activity. We removed the evoked response from the LFP measured in each interval, and computed the amplitude spectrum before averaging across intervals. We found the induced activity to be tuned for orientation, and to have substantial power and orientation tuning at frequencies in the gamma range (Figure 4C,D). Across sites, the induced gamma activity had similar tuning as the evoked responses (Figure 4E); indeed, the two had very similar orientation preference (Figure 4F) and fairly similar tuning width, with the gamma induced activity showing somewhat sharper tuning (Figure 4G). We conclude that the orientation tuning of LFP signals, and consequently the spatial footprint of such signals, is similar whether the signals constitute evoked responses or induced activity.
Figure 4.
Comparison of tuning curves for evoked LFP responses and induced LFP activity. We examined brief intervals in the stimulus sequence, where gratings were followed by a blank. (A) Amplitude of the frequency spectrum for the evoked response. Vertical lines indicate the gamma band (25–90 Hz) (B) Selectivity of the evoked response, determined by averaging spectral amplitudes below (open circles) and within (filled squares) the gamma range. Error bars represent 95% bootstrap confidence intervals for the mean. (C–D) Same, for induced activity, i.e. oscillations whose amplitude is modulated by the stimulus. (E) Comparison of selectivity for induced LFP activity in the gamma band (black) and for evoked LFP responses (gray, same as in Figure 1G). Rectangle indicates the recording site shown in A–D. (F) Relation between orientation preferences of evoked responses obtained with random noise stimuli and orientation preferences of induced gamma band activity. Weakly-tuned recording sites were excluded from the comparison (conventions as in Figure 1). (G) Distribution of ratios of tuning widths for the same set of sites. For each site, the width of the tuning curve for induced activity was divided by the width of the tuning curve for evoked responses.
Discussion
Our findings indicate that the origin of field potentials in the cerebral cortex is local, within 250 μm of the recording electrode. A simple weighted summation model allowed us to predict the orientation tuning of LFPs in V1 from the map of orientation preference. The appropriate area of integration was given by a Gaussian with a radius σ of up to ~100 μm. Most of the volume (96%) under a Gaussian surface lies within a radius of σ times 2.5, i.e. within a radius of ~250 μm. This estimate indicates that the origin of LFPs is more local than often recognized. Indeed, a number of other studies had reported the spread of LFP signals to range from about 400 micrometers to several millimeters (Berens et al., 2008; Engel et al., 1990; Kreiman et al., 2006; Kruse and Eckhorn, 1996; Liu and Newsome, 2006; Logothetis et al., 2001; Mitzdorf, 1985).
Though smaller than previous estimates, our quantitative measurement of LFP spatial scale, ~250 μm, is consistent with some earlier observations. Eckhorn and collaborators studied LFPs in cat V1 and found them to be orientation selective, suggesting that the area of integration is on a scale comparable to the maps of orientation preference (Eckhorn et al., 1988; Frien et al., 2000). Liu and Newsome (2006) reached similar conclusions in macaque area MT, but only for LFP signals in the gamma range; for these signals they proposed a footprint extending up to a few hundred micrometers. In a more direct test, Engel and collaborators (1990) suggested an upper bound at 400 microns: they cut the cortex between pairs of electrodes separated by this distance and found correlations in the two LFP traces to decrease dramatically.
Our estimates, however, apply only to LFPs recorded with microelectrodes. Field potentials are often measured with a silver ball that is substantially larger than the typical microelectrode tip. Due to its size, the ball is typically placed subdurally or even epidurally. The resulting field potentials are likely to originate from a larger region of tissue than those recorded with microelectrodes penetrating the cortex.
Our estimate of spatial scale of LFP signals should be considered an upper limit, achieved when the stimulus evokes membrane potential modulations that are coherent across large numbers of neurons. Because LFP signals represent the sum of transmembrane currents in the neighborhood of the recording electrode, they act like a spatiotemporal filter, emphasizing coherent inward or outward currents and suppressing incoherent currents. During the responses to arbitrary stimuli, including natural stimuli, the group of coherently active neurons is likely to be smaller; if these neurons are near each other, the LFP recorded in their vicinity could reflect the activity of a smaller region of space than the one we have estimated.
Our combination of imaging with multielectrode recordings proved to be useful for estimating the spatial scale of LFP signals, but it cannot deliver an estimate of the layers from which the signals originate nor of the cellular types and compartments that give rise to most of the signal. To answer these questions the most appropriate techniques remain those of current-source density estimates (Mitzdorf, 1985) and of intracellular recordings in vivo (Lampl et al., 1999).
It has been proposed by multiple authors that LFP signals in the gamma range (in the region of 25–90 Hz) may be more sharply selective (Frien et al., 2000; Henrie and Shapley, 2005; Liu and Newsome, 2006; Siegel and König, 2003), and may originate from a smaller region, than those in lower frequencies (Liu and Newsome, 2006). These findings may seem at odds with our analysis, which indicates that low frequencies carry clear information about stimulus orientation. We found that induced activity in the gamma range was only slightly more selective for orientation than signals measured at lower frequencies, whether evoked or induced (Figure 4).
At least two factors may contribute to this apparent discrepancy.
First, the aforementioned studies largely concern induced activity, whereas the strong selectivity we found in low-frequency LFP signals is due to evoked responses. Some studies concentrated purposefully on induced activity (Frien et al., 2000; Siegel and König, 2003). Others used stimuli that evoke a tonic response in the neuronal population under study (Henrie and Shapley, 2005; Liu and Newsome, 2006). Tonic LFP responses are hard to distinguish from ongoing activity, which has most of its power at the low frequencies. Only the transients caused by stimulus onset and offset would provide strong evoked responses, and there were perhaps too few of them in the data to provide good signal/noise ratios. By comparison, both of our stimuli evoke a large number of transient responses, enabling a better measurement of evoked responses.
Second, our own results indicate that the untuned component of induced activity measured in the gamma range is much smaller than the untuned component measured at lower frequencies (Figure 4D). While the tuned components have similar amplitude for the two frequency bands, the ratio of tuned to untuned components is much larger in the gamma range than at lower frequencies. In this sense, therefore, it is entirely legitimate to consider gamma band induced activity to be more selective for orientation than activity induced at lower frequencies.
These considerations resolve the apparent conflict between the capacitive filtering hypothesis, which proposed that high frequencies travel less far in brain tissue than low frequencies (Liu and Newsome, 2006) and the observation that the impedance of cortical tissue is independent of frequency (Logothetis et al., 2007; Mitzdorf, 1985; Nicholson and Freeman, 1975; Ranck, 1963). The issue is moot, because selectivity for stimulus features in the LFP is high even at lower frequencies.
To conclude, our quantitative estimate of spatial scale indicates that LFPs are more local than often recognized. LFP signals can faithfully report the selectivity of cortical populations but only if the underlying map varies on a similar or larger scale. In addition to cat V1, there may well be other instances of such a match. For example, if movement encoding maps in the human motor cortex were to vary on a similar scale, then LFP recordings could indeed constitute a promising source of signals to drive a motor prosthesis (Andersen et al., 2004). These considerations and our quantitative estimate provide a guide to the interpretation of the increasing number of studies that rest on LFP recordings.
Experimental procedures
Animal preparation and Visual stimulation
Procedures were approved by the Animal Care and Use Committee of the Smith-Kettlewell Eye Research Institute.
Maps of orientation preference and multielectrode recordings of extracellular activity were obtained from anesthetized cats as explained previously (Benucci et al., 2007)(Nauhaus and Ringach, 2007). Briefly, maps of orientation preference were obtained from anesthetized cats by staining the cortex with the voltage-sensitive dye (VSD) RH-1692 and imaging its fluorescence with a digital camera. Microelectrode arrays (10×10 electrodes) were subsequently inserted into the imaged region of cortex. Stimuli were 30-deg sine-wave gratings at 50 % contrast. Orientation noise stimuli consisted of a sequence of gratings flashed for 32 ms each, randomly varying in orientation and spatial phase. Standing gratings contrast-reversed at 4 Hz, lasted 4 s, and had one of 12 orientations and one of 4 spatial phases. Specific details of these experimental procedures and of parameters of visual stimulation are provided in the Supplemental Material.
Analysis of stimulus-evoked LFP signals
To analyze stimulus-evoked LFP responses we filtered the recordings between 3 Hz and 100 Hz (lowering the cutoff to 15 Hz yielded similar tuning curves). We computed z-scores by averaging responses across trials and dividing this average by the standard deviation across trials.
To analyze responses to orientation noise stimuli, we performed the following steps. (1) We removed variations in activity common to all sites by subtracting the mean response across all sites from the response obtained at each recording site; skipping this step yielded noisier data but did not change the overall results (Supplementary Figure 3), (2) We computed the stimulus-triggered average response for each grating orientation, pooling across phases. (3) We subtracted the mean across orientations, i.e. the untuned component of the response (this untuned component varied from site to site with no apparent relation to the map; most likely its strength depends on electrode depth, which we do not control). (4) We determined the best separable approximation for the effects of orientation and time using Singular Value Decomposition, which yielded the orientation tuning profile and the temporal waveform. The preferred orientation of each site was estimated by fitting the orientation tuning profile with a cosine function.
To analyze responses to contrast reversing gratings, we computed the amplitude of the second harmonic response (F2) for each stimulus orientation, and averaged these amplitudes across stimulus spatial phases. For the analysis in Figure 3 we scaled the F2 tuning curves by a factor that minimized the mean squared distance between responses to contrast-reversing gratings and responses to orientation noise. We compared the tuning curves in the two sets of responses by fitting them with Gaussian functions (Carandini and Ferster, 2000), whose parameters indicate preferred orientation and tuning width for each site.
Prediction of the LFP tuning curve from the orientation preference map
To estimate the integration radius of the LFP response, we performed the following steps. (1) We constructed a tuning curve for every pixel in the orientation map. This tuning curve models the membrane potential responses of the neurons in that pixel. For its preferred orientation, we took the value indicated by the orientation preference map. For its tuning width, we took the average value measured for membrane potential in cat V1 by intracellular measurements, which is 32 degrees (Carandini and Ferster, 2000). We also tried different values for this tuning width and obtained very similar results. (2) We computed the responses of every pixel to the set of orientations used in the experiment. (3) For each electrode, we multiplied the computed responses with a 2-dimensional Gaussian weighting function of a given radius, centered on the electrode site. The resulting values, plotted as a function of stimulus orientation, represent the predicted LFP tuning curve for that electrode. We scaled each predicted tuning curve by the standard deviation of the measured tuning curve, and examined the overall correlation between measured and predicted LFP responses, across all orientations and recording sites, as a function of the radius σ of the Gaussian weighting function. We then rescaled all predicted LFP responses by the factor that minimized the mean squared distance between predicted and measured LFP responses (at all orientations and at all sites).
Supplementary Material
Acknowledgments
We thank Laura Busse and Robert Frazor for help in the experiments. This work was supported by National Eye Institute grants 17396 (MC), 12816 (DLR), and 18322 (DLR), by DARPA FA-8650-06-C-7633 (DLR) and by a Scholar Award from the McKnight Endowment Fund for Neuroscience (MC). MC holds the GlaxoSmithKline/Fight for Sight Chair in Visual Neuroscience.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andersen RA, Musallam S, Pesaran B. Selecting the signals for a brain-machine interface. Curr Opin Neurobiol. 2004;14:720–726. doi: 10.1016/j.conb.2004.10.005. [DOI] [PubMed] [Google Scholar]
- Benucci A, Frazor RA, Carandini M. Standing Waves and Traveling Waves Distinguish Two Circuits in Visual Cortex. Neuron. 2007;55:103–117. doi: 10.1016/j.neuron.2007.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P, Keliris GA, Ecker AS, Logothetis NK, Tolias AS. Comparing the feature selectivity of the gamma-band of the local field potential and the underlying spiking activity in primate visual cortex. Frontiers in systems neuroscience. 2008 doi: 10.3389/neuro.06.002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carandini M, Ferster D. Membrane Potential and Firing Rate in Cat Primary Visual Cortex. J Neurosci. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckhorn R, Bauer R, Jordan W, Brosch M, Kruse W, Munk M, Reitboeck HJ. Coherent oscillations: a mechanism of feature linking in the visual cortex? Multiple electrode and correlation analyses in the cat. Biol Cybern. 1988;60:121–130. doi: 10.1007/BF00202899. [DOI] [PubMed] [Google Scholar]
- Engel AK, König P, Gray CM, Singer W. Stimulus-Dependent Neuronal Oscillations in Cat Visual Cortex: Inter-Columnar Interaction as Determined by Cross-Correlation Analysis. Eur J Neurosci. 1990;2:588–606. doi: 10.1111/j.1460-9568.1990.tb00449.x. [DOI] [PubMed] [Google Scholar]
- Freeman WJ. Mass action in the nervous system. New York: Academic Press; 1975. [Google Scholar]
- Frien A, Eckhorn R, Bauer R, Woelbern T, Gabriel A. Fast oscillations display sharper orientation tuning than slower components of the same recordings in striate cortex of the awake monkey. Eur J Neurosci. 2000;12:1453–1465. doi: 10.1046/j.1460-9568.2000.00025.x. [DOI] [PubMed] [Google Scholar]
- Gillespie DC, Lampl I, Anderson JS, Ferster D. Dynamics of the orientation-tuned membrane potential response in cat primary visual cortex. Nat Neurosci. 2001;4:1014–1019. doi: 10.1038/nn731. [DOI] [PubMed] [Google Scholar]
- Gray CM, Konig P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- Henrie JA, Shapley R. LFP Power Spectra in V1 Cortex: The Graded Effect of Stimulus Contrast. J Neurophysiol. 2005;94:479–490. doi: 10.1152/jn.00919.2004. [DOI] [PubMed] [Google Scholar]
- Kitano M, Niiyama K, Kasamatsu T, Sutter EE, Norcia AM. Retinotopic and nonretinotopic field potentials in cat visual cortex. Visual Neurosci. 1994;11:953–977. doi: 10.1017/s0952523800003904. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Hung CP, Kraskov A, Quiroga RQ, Poggio T, DiCarlo JJ. Object selectivity of local field potentials and spikes in the macaque inferior temporal cortex. Neuron. 2006;49:433–445. doi: 10.1016/j.neuron.2005.12.019. [DOI] [PubMed] [Google Scholar]
- Kruse W, Eckhorn R. Inhibition of sustained gamma oscillations (35–80 Hz) by fast transient responses in cat visual cortex. Proc Natl Acad Sci USA. 1996;93:6112–6117. doi: 10.1073/pnas.93.12.6112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lampl I, Reichova I, Ferster D. Synchronous membrane potential fluctuations in neurons of the cat visual cortex. Neuron. 1999;22:361–374. doi: 10.1016/s0896-6273(00)81096-x. [DOI] [PubMed] [Google Scholar]
- Liu J, Newsome WT. Local Field Potential in Cortical Area MT: Stimulus Tuning and Behavioral Correlations. J Neurosci. 2006;26:7779–7790. doi: 10.1523/JNEUROSCI.5052-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Kayser C, Oeltermann A. In Vivo Measurement of Cortical Impedance Spectrum in Monkeys: Implications for Signal Propagation. Neuron. 2007;55:809–823. doi: 10.1016/j.neuron.2007.07.027. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Nauhaus I, Ringach DL. Precise Alignment of Micromachined Electrode Arrays With V1 Functional Maps. J of Neurophysiol. 2007;97:3781–3789. doi: 10.1152/jn.00120.2007. [DOI] [PubMed] [Google Scholar]
- Nicholson C, Freeman JA. Theory of current source-density analysis and determination of conductivity tensor for anuran cerebellum. J Neurophysiol. 1975;38:356–368. doi: 10.1152/jn.1975.38.2.356. [DOI] [PubMed] [Google Scholar]
- Pallas SL, Wenner P, Gonzalez-Islas C, Fagiolini M, Razak KA, Kim G, Sanes D, Roerig B. Developmental Plasticity of Inhibitory Circuitry. J Neurosci. 2006;26:10358–10361. doi: 10.1523/JNEUROSCI.3516-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–811. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Ranck JB. Specific impedance of rabbit cerebral cortex. Exp Neurol. 1963;7:144–152. doi: 10.1016/s0014-4886(63)80005-9. [DOI] [PubMed] [Google Scholar]
- Regan D, Regan MP. Objective evidence for phase-independent spatial frequency analysis in the human visual pathway. Vision Res. 1988;28:187–191. [PubMed] [Google Scholar]
- Ringach DL, Hawken MJ, Shapley R. Dynamics of orientation tuning in macaque primary visual cortex. Nature. 1997;387:281–284. doi: 10.1038/387281a0. [DOI] [PubMed] [Google Scholar]
- Scherberger H, Jarvis MR, Andersen RA. Cortical Local Field Potential Encodes Movement Intentions in the Posterior Parietal Cortex. Neuron. 2005;46:347–354. doi: 10.1016/j.neuron.2005.03.004. [DOI] [PubMed] [Google Scholar]
- Schroeder CE, Tenke CE, Givre SJ, Arezzo JC, Vaughan JHG. Striate cortical contribution to the surface-recorded pattern-reversal vep in the alert monkey. Vision Res. 1991;31:1143–1157. doi: 10.1016/0042-6989(91)90040-c. [DOI] [PubMed] [Google Scholar]
- Siegel M, König P. A Functional Gamma-Band Defined by Stimulus-Dependent Synchronization in Area 18 of Awake Behaving Cats. J Neurosci. 2003;23:4251–4260. doi: 10.1523/JNEUROSCI.23-10-04251.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victor JD, Purpura K, Katz E, Mao B. Population encoding of spatial frequency, orientation, and color in macaque V1. J Neurophysiol. 1994;72:2151–2166. doi: 10.1152/jn.1994.72.5.2151. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Mitra PP, Desimone R, Fries P. Gamma-band synchronization in visual cortex predicts speed of change detection. Nature. 2006;439:733–736. doi: 10.1038/nature04258. [DOI] [PubMed] [Google Scholar]
- Zemon V, Ratliff F. Visual evoked potentials: evidence for lateral interactions. Proc Natl Acad Sci USA. 1982;79:5723–5726. doi: 10.1073/pnas.79.18.5723. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.