Irregular Firing of Isolated Cortical Interneurons in Vitro Driven by Intrinsic Stochastic Mechanisms

Abstract

Pharmacologically isolated GABAergic irregular spiking and stuttering interneurons in the mouse visual cortex display highly irregular spike times, with high coefficients of variation ≈0.9–3, in response to a depolarizing, constant current input. This is in marked contrast to cortical pyramidal cells, which spike quite regularly in response to the same current injection. We applied time-series analysis methods to show that the irregular behavior of the interneurons was not a consequence of low-dimensional, deterministic processes. These methods were also applied to the Hindmarsh and Rose neuronal model to confirm that the methods are adequate for the types of data under investigation. This result has important consequences for the origin of fluctuations observed in the cortex in vivo.

1 Introduction

Certain classes of cortical γ-aminobutric acid (GABA)-ergic interneurons have been observed to emit highly irregular spike trains in vitro (Kawaguchi, 1993; Gupta, Wang, & Markram, 2000; Toledo-Rodriguez et al., 2004; Stiefel, Englitz, & Sejnowski, 2004) in response to a constant current injection. This irregular firing is commonly characterized (e.g., Markram et al., 2004) by a high coefficient of variation (CV) (≈0.9–3) and burst-like spike sequences interrupted by interburst intervals of unpredictable length in response to a constant current. In contrast, other classes of interneurons and pyramidal cells show highly regular responses with respect to the same stimulus. The essential question of how this variable output results from the nonvariable input, that is, what the underlying process of generation or transduction is, has not been investigated.

Although irregular firing has frequently been described (Kawaguchi, 1993, 1995; Kawaguchi & Kubota, 1996; Cauli et al., 1997, 2000; Gupta et al., 2000; Kawaguchi & Kondo, 2002; Toledo-Rodriguez et al., 2004), it mainly served as a physiological indicator to classify the diverse population of interneurons into several subpopulations. In particular, primarily physiological criteria have been used for defining the top-level classes, for example, the neuronal response to a constant current in vitro served to define the respective classes in the widely used classification schemes by Kawaguchi (1993) or Gupta et al. (2000). In these schemes, irregular current responses served to define the irregular spiking (IS) class (Kawaguchi, 1993) and the stuttering (ST) cells (Gupta et al., 2000), which have recently been confirmed as separate classes (Markram et al., 2004). Although this demonstrated the usefulness of the irregular response for classification purposes, no satisfactory explanation has been proposed for it so far. A number of experimental studies have provided candidate currents relevant for the irregular firing (Porter et al., 1998; Bennett & Wilson, 1998, 1999; Bennett, Callaway, & Wilson, 2000), but no models have been proposed that implement these currents and reproduce the phenomenon.

The observed irregular behavior is in principle compatible with both stochastic and nonlinear, deterministic (e.g. chaotic) processes. A stochastic process would indicate that interneurons react strongly to certain fluctuations (Wilson, Chang, & Kitai, 1990; Bennett & Wilson, 1999). These could be intrinsic, stochastic fluctuations, most likely channel noise, which would also be present in in vitro recordings with blocked synaptic transmission. Nonetheless, in vivo they could as well be caused by synaptic input. Thus, in vitro, the spike patterns would resemble noise, yet in vivo they could possibly be a temporally precise function of the input or a mixture of both. In contrast, if the origin of the irregular firing in vitro arose from a nonlinear deterministic process in the interneurons, the complex, cortical rhythm could be a by-product. A number of examples of such processes in neurons are known from experimental (Hayashi, Nakao, & Hirakawa, 1982; Hayashi, Ishizuka, & Ohta, 1982; Hayashi, Ishizuka, & Hirakawa, 1983; Canavier, Perla, & Shepard, 2004; Jeong, Kwak, Kim, & Lee, 2005) and theoretical studies (Hindmarsh & Rose, 1984; Chay & Rinzel, 1985; Canavier, Clark, & Byrne, 1990; Schweighofer et al., 2004). This possibility is intriguing since interneurons have been shown to generate the gamma rhythms (35–80 Hz) found in the cortical network (Buhl, Tams, & Fisahn, 1998; Fisahn, Pike, Buhl, & Paulsen, 1998). Knowing which type of process is actually present is at the heart of any explanatory model. Advances in nonlinear time series analysis (see Kantz & Schreiber, 1999, or Abarbanel, 1996, for reviews) in the past decade have given researchers the tools needed to address this question. For the present context, the time-series analysis of interspike intervals (Longtin, 1993; Sauer, 1994; Racicot & Longtin, 1997; Castro & Sauer, 1997; Hegger & Kantz, 1997) based on methods for nonlinear prediction (e.g., Farmer & Sidorowich, 1987) is a central topic.

This study provides a starting point for characterizing the nature of the underlying irregular process. We recorded extended spike trains from interneurons (and, for comparison, some pyramidal cells) from the visual cortex of mice and applied various methods of linear and nonlinear time-series analysis to them. With the help of benchmarking tests against surrogate data, we show that based on the data available, a low-dimensional, deterministic process is unlikely. This leaves a high-dimensional or, for all practical purposes, a stochastic process as the most likely source. Based on these results we have devised and analyzed a single-cell model that is able to reproduce super- and subthreshold findings of various preparations (Stiefel, Englitz, & Sejnowski, 2004).

2 Methods

2.1 Electrophysiological Recordings

Recordings from rat cortical interneurons were analyzed in this study, the same data set as in a recent related, study (Stiefel et al., 2004). Briefly, continuous suprathreshold voltage traces were recorded with the patch-clamp technique from layer II/III pyramidal neurons and interneurons in slices of the mouse visual cortex. The neurons were pharmacologically isolated by blocking excitatory synaptic transmission (DNQX, 10 μM, APV, 20 μM) in all and inhibitory synaptic transmission (Bicuculline, 10 μM) in the majority of cases. The neurons were driven above firing threshold by injection of constant DC depolarizing currents, and the voltage was recorded continuously from 16 to 500 seconds. Spikes trains were constructed from the voltage recordings by noting an event at the time of each positive threshold crossing of the voltage signal. Subsequently, interspike interval (ISI) series were constructed by taking the temporal difference between successive spikes. ISI series are denoted as S_ISI or as S_ISI (n) where n denotes the nth ISI in the respective series. Altogether, about 24,000 spikes (out of approximately 38,000 totally recorded) were analyzed.

2.2 Data Analysis

Analog voltage and spike time data were analyzed with software custom written in LabView 6.2 (National Instruments, Austin, TX), Mathematica 4.2 (Wolfram Research, Champaign, IL), and Matlab 6 (The Mathworks, Natick, MA).

For the time-series analysis we used mostly algorithms from the TISEAN package (Hegger, Kantz, & Schreiber, 1999; Schreiber & Schmitz, 2000), because it is well tested and freely available. We describe them briefly below, but refer readers to the TISEAN authors' Web site (http://www.mpipks-dresden.mpg.de/tisean/TISEAN_2.1/index.html) for a more detailed description and the C/Fortran source code.

The general outline of the analysis is as follows (details for each method are provided with the results). After testing for weak stationarity, we performed a number of simple analyses (spike-triggered averages, delay representations, time-dependent mutual information) to detect regularities in the data. Next we used more sophisticated time-series analysis algorithms to test for determinism (three nonlinear prediction algorithms and a linear, autoregressive approach). All tests were conducted on the actual data, appropriate surrogate data (Theiler, Eubank, Longtin, Galdrikian, & Farmer, 1992), and benchmarking data generated by the Hindmarsh and Rose model (Hindmarsh & Rose, 1984). The results of all tests for determinism are given with respect to the null hypothesis of a naive prediction based on global statistical quantities, that is, relative to the standard deviation of the ISIs. A forecast error of 1 indicates that the prediction is only as good as a prediction based on the mean itself. A relative forecast error of 0 indicates perfect prediction.

3 Results

3.1 Raw Data and Statistics

We recorded from 16 interneurons, out of which 8 showed nonadapting, irregular patterns, 4 cells showed IS patterns, and 4 cells showed ST patterns. Further subclassification according to the initial response behavior (classical, delayed, bursting; see Gupta et al., 2000) was omitted, since we were interested in continuous spiking. Multiple, long (1–10 minutes) recordings containing several hundred to thousands of spikes each were obtained from the irregularly spiking cells. Cells were chemically isolated by blocking GABAergic and glutamatergic transmission (see sections 2 and 4 concerning electrical synapses) to study their intrinsic dynamics. Recordings were considered for time-series analysis only if they fulfilled weak stationarity and their length exceeded 500 spikes (see section 3.3 for details).

Sample voltage traces for IS and ST cells are shown in Figure 1A and corresponding ISI series and histograms in Figures 1B and 1C, respectively. IS and ST behaviors were easily discernible on the basis of the ISI histogram shapes, where IS cells showed a moderate peak at the lowest ISIs, directly followed by an exponentially decreasing distribution of ISIs. ST cells exhibited a dominant peak around the lowest ISIs, followed by a broad, unimodal distribution at larger ISIs around the mean interburst interval. The CV (see Figure 1D) for ST cells was significantly higher (p < 0.005 (n = 4), using two group t-tests) than for IS cells. CVs of these groups were significantly higher (ST (n = 4): p < 0.001; IS (n = 4): p < 0.04) than for regular and fast-spiking cells (n = 3). The burst index (BI; percentage of ISIs shorter than two times the minimal ISI) for ST cells was significantly higher (p < 0.004, n = 4) than for IS cells (see Figure 1E). These spike statistics persisted over a range of different input currents, where the exact amplitudes depended on the individual cell (data not shown; see also Markram et al., 2004).

Figure 1.

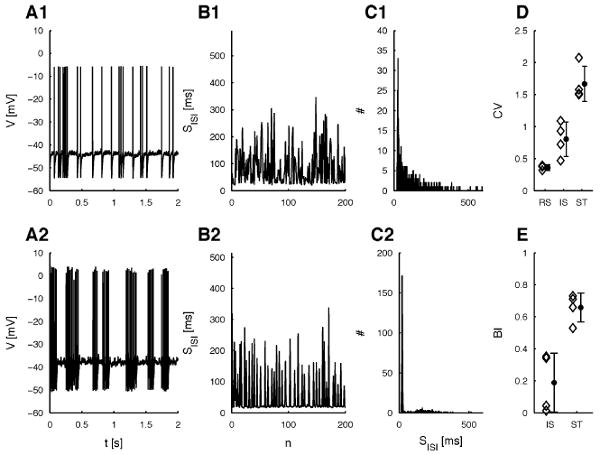
Raw voltage and ISI data and global statistics for both irregular cell types. (A) Sample traces for typical IS (A1, c0314) and ST (A2, c0625) cells. (B) Small part (<20%) of the ISI sequences corresponding to the IS (B1) and ST (B2) cell shown in A. (C) ISI histograms for spike trains of the IS (C1) and ST (C2) cell in A (>1000 spikes each). (D) CVs of the three cell types recorded. Diamonds show averages for a number of recordings from each cell. The star indicates the average over the cells in this class. Although CVs vary in each group, the bursts in ST cells lead to distinctively higher CVs 1.5–3. (E) Burst indices for IS and ST cell types. Diamonds show averages for a number of recordings from each cell. The filled circle indicates the average over the cells in this class. Note that the BI is mainly useful for distinguishing IS and ST cells, whereas regular spiking cells would have BIs almost equal to 1. Error bars in D and E indicate two SEM around the mean.

From the subthreshold voltage traces and many other experiments, it is clear that neurons are noisy systems. Note, however, that this does not necessarily imply that the high variability of the ISIs is a direct consequence of this noise (especially the ST pattern would require additional explanation). One could imagine an intrinsic, deterministic process that interacts only with the membrane potential V_m after passing some threshold, analogous to the rapid activation of Na-channels, directly causing a spike. Distinguishing between these possibilities is the aim of the following sections.

3.2 Construction of Surrogate and Benchmark Data

The ISI series can be used to reconstruct the underlying dynamics (Sauer, 1994) or at least partially predict the ISI series (Racicot & Longtin, 1997), even when the dynamics are chaotic. The main challenge in the context of patch-clamp recordings is the limited number of spikes (≈10,000 met all the criteria; see section 3.3) and thus the need to validate the analysis using custom surrogate data. Surrogate data share certain properties with the original data set (e.g., distribution or power spectrum) but with a systematic variation of the property under investigation. We used three types of surrogate data (Theiler et al., 1992):

1. To test for any deterministic features in a time series, we created surrogate data from the original ISI data by shuffling the ISIs, denoted as randomly shuffled (RS) surrogates. This procedure retains all statistical properties that do not depend on the temporal sequence (e.g., characteristic statistical properties like mean, variance, and distribution).

2. To test for nonlinear features in a time series, we created surrogate data from the original data that retain their linear properties; that is, an amplitude-scaled, stationary, linear process is the null hypothesis. These iterative amplitude adjusted Fourier transform (IAAFT) surrogates (Hegger et al., 1999; Schreiber & Schmitz, 2000) were generated using the TISEAN routine “surrogates.” IAAFT surrogates were employed only if any deterministic structure had been detected with the first set of surrogate data.

3. To test our data analysis routines on time series generated by a model with known nonlinear, deterministic dynamics, we used voltage traces and ISI series generated by a neuronal model (Hindmarsh & Rose, 1984). The Hindmarsh and Rose (HR) neuron model is governed by the equations:

   $$\begin{array}{l}\frac{dV(t)}{dt}=y+3V^2-V^3-z-I\\ \frac{dy(t)}{dt}=1+5V^2-y\\ \frac{dz(t)}{dt}=-r\left(z-4\left(V+1.6\right)\right).\end{array}$$

The parameters used for obtaining the chaotic regime were r = 0.006 and I ε [3.01, 3.08]. For each of these values, noisy versions were simulated, where white gaussian noise was added to I. The standard deviation of this current noise was adjusted to match the experimentally measured subthreshold standard deviation in voltage σ(V) relative to the total range of values, that is, the spike height. For recorded cells, σ(V)/h_spike≈0.5 mV/50 mV = 1%. Three levels of noise, leading to 0%, 1%, and 2% subthreshold noise, were simulated in the HR model.

If the time-series analysis algorithms are unable to detect the presence of determinism in time series generated by this noisy model, they cannot be expected to successfully detect determinism in the experimental data sets. Since the statistics of the HR data set and the experimental data do not match in all respects, we included results for both RS and IAAFT surrogates for the HR data.

The HR model was chosen since it can deterministically generate highly irregular ISI sequences in response to constant input, which are reminiscent of the ST pattern (see Figure 4). Although the HR's ISI distribution captures some aspects of the ISI distributions—both IS and STcells—this confluence on the level of the ISI distributions is unlikely to render the model more easily predictable on a dynamical level; for example, Racicot and Longtin (1997) conclude that for high enough firing rates, ISI histogram shapes different from the original shape can nonetheless lead to good reconstructions. Consequently, other deterministic models could well have the same ISI histogram as either IS or ST cells and still show the same level of predictability as the HR data.

Figure 4.

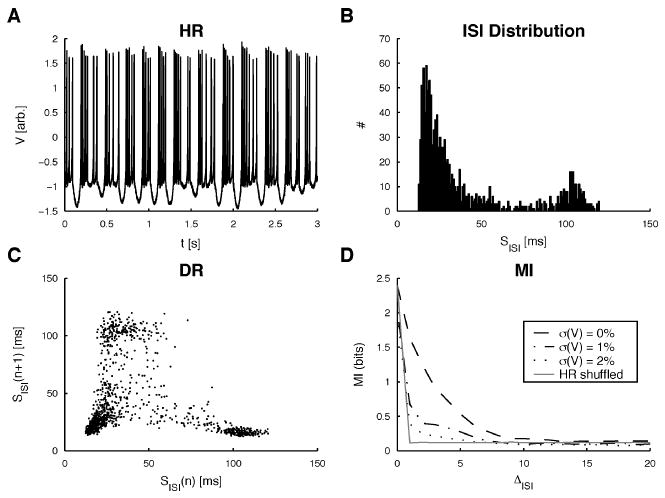
Surrogate data sets from the HR model. (A) Voltage-variable traces from the HR model for 1% noise are shown (voltage value in arbitrary units). (B) ISI histogram for the data in A containing 1200 ISIs. It contains components of IS (broadly decaying) and ST (second interburst ISI peak) histograms. (C) DR of the ISI sequence from A. Some bijective structures, especially in the range of 60 to 120 ms, can be observed, but there are also regions (<60 ms) where no clear dependence is observed. (D) MI of the ISI sequences for three different levels of noise (see section 2 for details) and their RS surrogates. Clearly the ISIs in the original sequences contain more information about the following ISIs than the RS surrogates and the physiologically recorded ISI sequences (see Figure 3C). The first minimum was reached between 8 and 15 ISIs, depending on the noise level. These delays were used for embedding.

Comparison with surrogate data can be turned into a significance test (Kantz & Schreiber, 1999). To attain a desired significance level p, one draws N = 1/p samples from the surrogate distribution. Then a quantity of interest computed from the given data set is statistically different from this distribution with probability p if its value lies below or above all N values computed from the surrogates. Since we chose p = 0.05, 20 surrogates of each kind were created and analyzed.

Note that the surrogate data sets were designed to contain the same number of spikes as the data sets under investigation. By keeping this number constant, we can view the results of the algorithms modulo their dependence on the number of data points, that is, if the algorithms can detect determinism in the ISI series generated by the HR model based on only 1000 spikes but fail to do so in the experimental data, then the source of variability in the neuron should have greater complexity. Clearly this approach is incomplete in the sense that ISI series from higher-dimensional dynamics would not be detected, but it can at least provide a weak lower limit.

3.3 Stationarity

ISI series S_ISI were considered stationary or non-stationary based on the standard criterion of weak stationarity (Kantz & Schreiber, 1999), that is, constant mean and standard deviation (SD) over the recording period. Additionally, we compared the spectral content of the first and second half of each recording. To assess the first criterion, the standard error of the mean (SEM),

$$\text{SEM}\left(S_{\text{ISI}}\right)=\frac{\sqrt{{\sum }_{n=1}^N(S_{\text{ISI}}{(n)-\langle S_{\text{ISI}}\rangle )}^2)}}{\sqrt{(N-1)N}}=\frac{\text{sd}(S_{\text{ISI}})}{\sqrt{N}},$$

and the standard error of the standard deviation,

$$\text{SES}\left(S_{\text{ISI}}\right)=\frac{\sqrt{{\sum }_{n=1}^N{(|S_{\text{ISI}}(n)-\langle S_{\text{ISI}}\rangle |-\text{sd}(S_{\text{ISI}}))}^2)}}{\sqrt{N}}=\frac{\text{sd(sd}(S_{\text{ISI}}))}{\sqrt{N}},$$

were computed for stretches of N = 100 consecutive ISIs. If the distance between the running mean and the global mean stayed below 2 SEM (= 95% confidence interval), the null hypothesis of constant mean was maintained, analogously for the SD (not shown). Data were trimmed or excluded entirely if they failed to match either the mean or SD constancy.

Figure 2B shows the mean, the SD, and the respective running quantities for the four typical ISI sequences from two IS cells (1,2) and two ST (3,4) cells shown in the respective plots of Figure 2A. Overall, 14 of 26 recordings (containing more than 500 spikes each) from five (two IS, three ST) cells (totaling 10,205 spikes) fulfilled weak stationarity and were used in the following analyses. In 12 of the 14 recordings, bicuculline and DNQX were both applied; in the remaining two recordings, only DNQX was applied. Power spectra were computed using the Matlab function spectrum, which uses Welch's averaged periodogram method. As shown in Figure 2C, the spectra of the first (circles) and second (triangles) half of each data set agree with each other for almost all frequencies. Results for the other weakly stationary time series were comparable. Assessing strong stationarity requires quantitative comparison of the empirically determined probability transition matrices (Kantz & Schreiber, 1999). Due to the limited number of data, this type of analysis did not yield conclusive results (data not shown).

Figure 2.

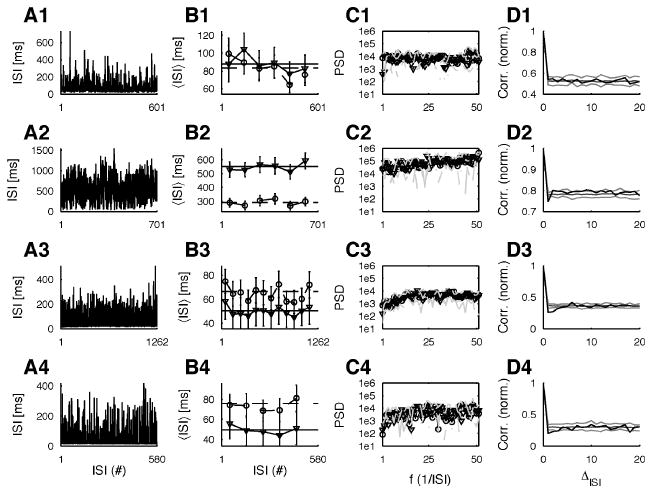
Weak stationarity can be assumed for most ISI sequences. (A) The sequence of ISIs for typical recordings from the cells (A1) c0314, (A2) c0903, (A3) c0310, and (A4) c0625. (B) The running mean (triangles, solid) and SD (circles, dashed) (points represent averages over 100 consecutive samples) are graphed, where the error bars indicate their respective standard errors. The horizontal lines show the global mean (solid) and SD (dashed), respectively, for visual comparison. (C) Compares the frequency content of the first (circles, solid) and second (triangles, dotted) half of each data set. (D) The autocorrelation (normalized to the correlation for 0 shift) of the original time series (black) and the mean (dark gray) surrounded by the envelope (light gray) of 20 shuffled surrogates.

Figure 2D shows the autocorrelation of the respective ISI sequences (black) and the average (dark gray) surrounding the envelope of 20 RS surrogates (light gray). For one of the IS cell data (1/2) and all of the ST cell (3/3) data, there exists a small yet significant negative correlation (with respect to the average at higher separations) for one or two steps. Due to the duality between autocorrelation and power spectrum, this explains the depression at low frequencies for Figures 2C2 to 2C4.

3.4 Spike-Triggered Averages, Delay Representations, and Mutual Information

We computed spike-triggered averages (STAs) for isolated and first-in-a-burst spikes to detect characteristic voltage kernels in the prespike phase. As shown in Figure 3A, for most cells, the prespike phase was on average flat, with the exception of an increase in voltage in the last few milliseconds before the spike. In addition some cells (3/8) showed a slight hyperpolarization about 10 ms before the spike. This type of kernel is also obtained in cortical neurons responding to a noisy current (Mainen & Sejnowski, 1995). For each cell class, STAs of two typical cells are shown, where base voltages were normalized for easier comparison.

Figure 3.

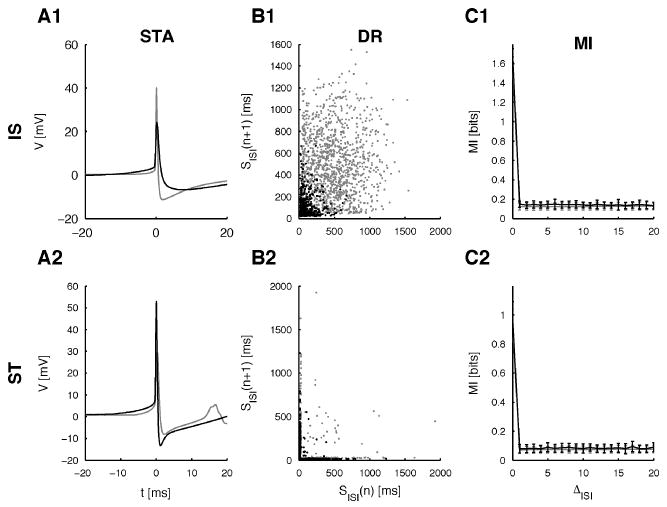
Spike-triggered averages, delay representations, and mutual information for IS and ST cells. (A) STAs for two IS (A1, c0903 (gray), c0314 (black)) and two ST (A2, c0625 (gray), 0310 (black)) cells. Note the increase in voltage during the last few milliseconds before the spike and for some cells (3/8) a decrease about 10 ms before the spike. (B) Delay representations of the ISIs for two IS (B1) and two ST (B2) cells. IS cells show a wide distribution for all ISIs. ST cells show a regular region for the interburst intervals due to the lack of isolated spikes. However, for the intraburst ISI length, one-step predictability is very low due to the irregular sequence of interburst intervals. (C) Average mutual information (MI) of the ISIs for all cells and permuted ISIs. Remarkably the MI of the original ISIs and of the permuted ISIs are practically identical. The small error bars (SD) indicate that this property is well conserved across cells.

Delay representations (DR), often termed “ISI return maps,” are a simple yet effective way to identify deterministic mapping rules within a time series. A DR is created by simply mapping the nth versus the n+1th data point. If the time series depends on only the last step, the resulting 2D plot should resemble a functional graph; one-to-many mappings should not occur. This graph can be disturbed by various sources of noise, which would lead to a fuzzy mapping—for the nth data point, a limited distribution of n+1th data points occurs. But the influence of noise is not expected to broaden the distribution of n + 1th data points for a given nth data point to a flat distribution over the whole range of possible values, which would correspond to a total loss of predictability. This method can be extended to a greater number of previous steps. We applied this method to all irregular spiking cells. Corresponding DRs for two IS and two ST cells are shown in Figure 3. IS cells (see Figure 3B1) show a wide distribution for all ISIs with an increasing density toward smaller ISIs, owing to the distribution of ISIs (see Figure 1C1). ST cells (see Figure 3B2) show an extremely broad distribution for short ISIs, owing to the ISI following a burst. In addition, the interval preceding a short interval (horizontal part) is broadly distributed for both cell types, severely violating the criterion of one-to-many mappings and indicating only limited one-step functional dependence. Although the HR model shows more structure in the region from 60 to 120 ms (see Figure 4C), variability dominates for shorter ISIs. Hence, the character of the process underlying the real and the simulated cells is not distinguishable at this level of analysis. DRs for two consecutive steps were similarly analyzed, but no succinct regularities were observed. For the ST cells, a modified DR was computed that shows the next ISI as a function of the number of spikes in the preceding burst. No clear functional dependence could be observed (data not shown); however, the number of data points (i.e., interburst intervals) becomes comparably small.

The mutual information, MI, between points of a time series separated by a certain distance in time can help to uncover deterministic regularities in a time series by computing the amount of information about a future data point contained at a current point (Abarbanel, 1996). Adapted for ISI series, the mutual information at a distance of k ISIs is defined as

$$MI(k)=\sum _{S_{\text{ISI}}(n),S_{\text{ISI}}(n+k)}P(S_{\text{ISI}}(n),S_{\text{ISI}}(n+k)){log}_2\left(\frac{P(S_{\text{ISI}}(n),S_{\text{ISI}}(n+k))}{P(S_{\text{ISI}}(n))P(S_{\text{ISI}}(n+k))}\right).$$

The MI of the individual ISI series from both cell types and their respective RS surrogates were practically indistinguishable. In Figure 3 the MI for ISI series and their RS surrogates are shown as averages over the cells for both IS and ST cells. The vanishingly small error bars indicate that this reflects the MI on the level of the individual cells. Based on the surrogate statistics described above, this means that with respect to the mutual information, neither of the ISI series differed from their permuted counterparts. These results contrast with the MI of the HR model and its RS surrogates, where a clear difference was observed (see Figure 4D). Hence, at the level of the mutual information, the irregular patterns can be distinguished from the deterministic HR model, even when the latter includes additive white noise. The MI is superior to the autocorrelation function since it is sensitive to linear and nonlinear correlations (Abarbanel, 1996).

3.5 Linear and Nonlinear Prediction

In order to assess the presence of determinism in the time series, we applied four different time-series prediction methods on each of the data sets and compared their prediction errors. Three of the methods—the local linear (Farmer & Sidorowich, 1987; Longtin, 1993), simple nonlinear, and the radial basis function methods—rely on a prior embedding of the time series in a reconstructed phase space. An embedding of an ISI series S_ISI turns it into a trajectory in D-dimensional space by assigning data points S_ISI (t), S_ISI (t + k), S_ISI (t + 2k), …, S_ISI (t + (D − 1)k) of the time series to the coordinates in the 1st, 2nd, …, Dth dimension of a new D-dimensional time series $S_{\text{ISI}}^D$. The first step of this procedure is to select a suitable embedding delay, k, and an embedding dimension, D. Briefly, the local linear method (TISEAN onestep) uses a linear approximation based on neighbors of the current point and their successors to predict the following point within the phase space. The simple nonlinear prediction method (TISEAN zeroth) computes an average over the successors of points in a neighborhood of the current point to predict the next point by taking the mean of all the neighbors' successors. The radial basis function method (TISEAN rbf) is a global nonlinear method that fits the coefficients of localized basis functions to the reconstructed dynamics and uses the linear combination of these to predict the next point in the reconstructed phase space. (See Kantz & Schreiber, 1999, for more detailed descriptions.)

Finally, we used standard autoregressive models (TISEAN ar-model) of various orders in which a weighted, linear sum of previous data points predicts the next point. No phase space embedding is required in this case. Note that the weights are optimized globally; hence, that is the same relationship, the same weights, holds for the whole time series.

In order to determine k of each ISI series, we selected the first discernible minimum of the mutual information as a function of the number of ISIs (see Figure 3C; Abarbanel, 1996). For the recorded ISI series and all the RS surrogates, this minimum lay between 1 and 4 ISIs. The first zero crossing of the autocorrelation always yielded k = 1 ISI (see Figure 2D). In contrast k's between 9 and 15 ISIs (depending on the noise level) were found for the HR neuron (see Figure 4D). As expected, the mutual information degraded faster for stronger noise amplitudes. Averages over the given ranges of k's were used in the following to reduce the bias of an inappropriate choice of k. From the original work of Takens (1981), the reconstruction should be stable under (small) variations of k. The positions of the minima were largely independent of the number of boxes used in estimating the mutual information. No significant increases of the mutual information were observed for k's beyond the range shown.

The appropriate D for the embedding is often chosen by the false nearest-neighbor method (FNN; Kennel, Brown, & Abarbanel, 1992). We applied this method to all time series using the range of k's found. Although significant quantitative differences were seen, none of the time series, except for the noise-free HR model, fulfilled the criterion of dropping below 1% to 5% of false nearest neighbors. Using low plateaus (<20% FNNs; Kennel et al. 1992) as a criterion for the correct embedding dimension under the influence of noise, the noisy HR models embedded in dimensions 4 to 6. The recorded ISI series did not reach lower plateaus (≈40% FNNs) than their RS surrogates, which can taken as an indication that no further deterministic dynamics were separated by increasing D. A marked difference was already apparent at D = 1: the clean HR data started at only 50% FNNs, whereas the recorded ISIs started at about 98% FNNs.

Since we were not able to confidently determine Ds for most of the data sets, we performed the tests for determinism with a range of relevant Ds. Figure 5 shows the results for all data sets and all algorithms. All average forecast errors are given with respect to the standard deviation of the respective ISI series. A relative forecast error of 1 corresponds to trivially guessing the mean every time. To avoid overloading the graphs with curves, only the error bars, rather than individual predictions for each record and embedding delay, are shown. These averages and the error bars were computed over the individual recordings and the relevant range of k (see above).

Figure 5.

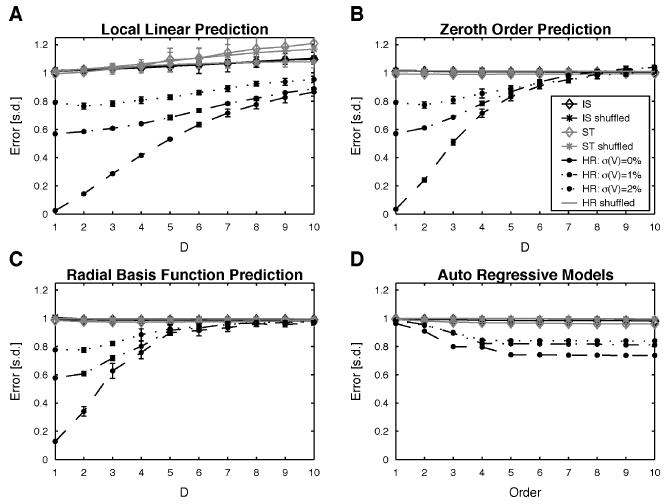
Tests for determinism in the spike trains. Relative forecast errors based on one-step-ahead predictions by (A) the local linear approach, (B) the zeroth-order approach, (C) the radial basis functions, and (D) autoregressive model of various order. Predictions for spike trains recorded from interneurons (diamonds: IS: black, ST: gray), their RS surrogates (asterisks: IS: black, ST: gray) and the HR data are shown (legend in B applies to all plots). Error bars always indicate two SEMs, except for the surrogates, where they are envelopes over 20 realizations. The mostly small SEMs indicate that all analyzed recordings behaved alike.

Both the phase-space prediction methods (local linear, see Figure 5A; 0th order, see Figure 5B; radial basis function, see Figure 5C) and the linear method (autoregressive model, see Figure 5D) detected determinism in the HR ISI series. Of the nonlinear methods, the local linear method performed best and showed the shallowest dependence on the embedding dimension. The simple nonlinear and radial basis function methods performed similarly, having analogous dependencies on the embedding dimension, which is again a consequence of the sparseness for higher D.

The AR model performed, even for quite high orders, markedly poorer than the embedding methods for lower dimensions, and the quality of its predictions was weakly negatively correlated with the model order used. The slightly negative autocorrelation of the ST records (see Figure 2D3 or 2D4) is reflected here in a 4% reduction of the prediction error. We computed the Akaike information criterion (AIC) (Akaike, 1974) (i.e., AIC(S_ISI, k) = 2 σ(S_ISI)²k – 2 MSE, where k is the order of the AR model and MSE is the mean squared error of the prediction). The AIC is already minimal for k = 1, indicating that increasing the model order is not recommended given the decrease in MSE.

With regard to the results for the HR model, the successful prediction by embedding methods (for D = 1) is a consequence of the stereotypic increase of the ISIs within a burst and the similarity of interburst intervals after certain intraburst intervals. The chaotic nature does not limit one-step prediction, since chaos manifests itself in the variable number of spikes within a burst and the distance between bursts. Consequently, the embedding methods can successfully use information gained from neighbors in phase space, that is, examples from previous bursts. As noted in the description of the FNN results, such behavior could have been expected, since the FNNs at D = 1 are much lower for the HR than for the IS/ST data. Interestingly, this dependence of the prediction error on D has been observed before: a Fitzhugh-Nagumo system driven by the x component of the chaotic Rössler system gave similar results, especially in the high-firing-rate regime, where more faithful reconstruction & expected (see Racicot & Longtin, 1997, Fig. 10). Conversely the AR method performed poorly since it estimates a global, linear model. For low orders, it fails because a linear model cannot capture the nonlinear change in the ISIs. With increasing orders, the shortcomings of linearity can be overcome partially, since linear combinations of intraburst ISIs can be used to predict the following intraburst ISIs. This explains the agreement between the average number of spikes in a burst (4–5) and the order of the AR method at which the decrease of the error levels off (4–5). Nonetheless, the global nature of the AR method in the end prevents it from reducing the error further, since the sequence of ISIs changes so abruptly between interburst and intraburst intervals that both types of intervals can hardly be predicted by the same coefficients. To test directly whether the predictions were based on linear or nonlinear properties of the HR data, we compared these to predictions based on the IAAFT surrogates (see Figure 6), which retain the linear properties of the time series (see section 2). For the embedding methods (see Figures 6A to 6C) prediction of the IAAFT surrogates is significantly impoverished mostly up to D = 4, indicating that the removed nonlinear features were effective in predicting the following ISI. Conversely, in the AR method, prediction results hardly differ between original data and IAAFT surrogates (see Figure 6D), indicating that the AR method used only the linear properties of the data for prediction.

Figure 6.

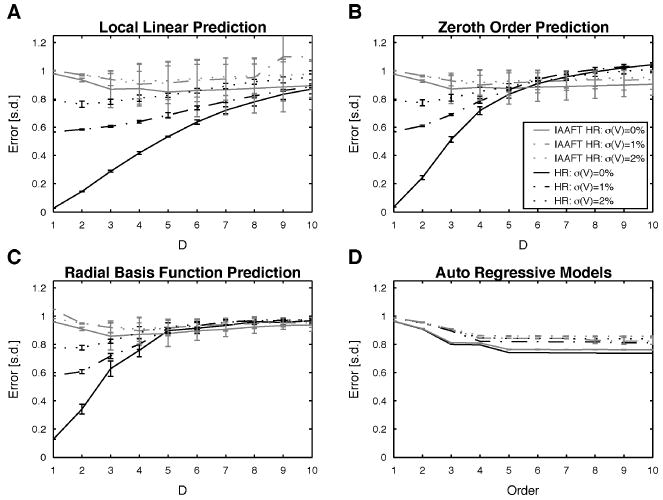
Tests for nonlinear determinism in the spike trains. Relative forecast errors based on one-step-ahead predictions by (A) the local linear approach, (B) the zeroth-order approach, (C) the radial basis functions, and (D) autoregressive model of various order. Predictions for the HR data and the IAAFT surrogates of the HR data are shown (legend in B applies to all plots). Error bars denote two SEMs.

Significantly, however, these results indicate that reducing uncertainty in prediction based on ISI series from a nonlinear, even chaotic process is possible, given as few as 1000 ISIs.

In contrast, none of the prediction methods detected any predictability in any of the ISI time series recorded from interneurons (relative forecast error ≈1) and their RS surrogates. Although this was expected for all RS surrogates, for the experimental data, especially due to the occurrence of bursts, at least some predictability might be expected. The wide range of interburst intervals and the variable number of spikes per burst leads to the observed chance level in prediction (given the mean).

4 Discussion

The irregular firing patterns of cortical GABAergic interneurons we analyzed did not show any sign of determinism. Based on the number of data analyzed and the benchmarking tests, we conclude that a low-dimensional, deterministic process is highly unlikely to be the source of the variable discharges. Consequently, a high-dimensional or, for practical purposes equivalently, a stochastic process is the most likely explanation for the high variability of consecutive ISIs. Such a mechanism, however, renders endogenous pacemaking an unlikely function for these classes of interneurons, which would require an autonomous, deterministic process.

The lack of evidence for a low-dimensional, deterministic process is tempered by a number of possible limitations: First, the sampling (i.e., spike rate) might not have been sufficiently high. Simulations have shown that the relation between the timescales of an underlying process and the rate at which the underlying process is sampled is a critical determinant for successful reconstruction of the original system dynamics (Racicot & Longtin, 1997). Higher sampling rates typically lead to better quality of reconstruction, although lower rates also resulted in a considerable reduction in prediction error. Whether the sampling rate, that is, the mean firing rate, was adequate for the (potentially) underlying timescales cannot be known unless prediction is (at least partially) achieved.

A second possible limitation for the lack of evidence of determinism could be the existence of a large, slow noise source. If some noise source exists, which influences the dynamics rarely but severely, the potentially detectable determinism would be seriously disturbed. The footprints of this source could be hidden at certain spike onsets and thus remain undetected in the STA.

A final, and probably the most important, limitation of our analysis is that neither the number of spike trains nor the number of spikes is adequate to reach precise conclusions. Unfortunately, obtaining longer, stationary data has proven to be extremely difficult due to the fragile nature of interneurons under the required recording conditions (extended stimulation and penetration). In this context, patch clamp recordings had to be preferred over extracellular recordings in order to stimulate the (otherwise silent) cells and check for isolation. We attempted to compensate the low spike counts by the use of appropriate surrogate data and selecting the longest and most stationary spike trains only. Thus, although it is difficult to reach precise conclusions, the complete lack of predictability for the experimental data is indicative of the lack of a low-dimensional, deterministic process. At the same time, it should be emphasized that the rapid decline of predictability with increasing D for the HR data indicates that for higher dimensions, the number of spikes is too low to distinguish determinism from randomness.

In the case of a stochastic process, it remains to be explained why the distribution of the ISIs does not resemble the distribution of the underlying noise sources; neither follows a Poisson or a gamma distribution. A specific mechanism needs to exist that transforms the distribution of the underlying process into the observed distribution. It is known that this cell class exhibits a high responsiveness with respect to certain weak inputs (Wilson et al., 1990), that is, some input fluctuations are gated into eliciting spikes or even burst sequences.

A plausible general candidate mechanism would be a subcritical Hopf bifurcation, that is, stochastic switching between a stable fixed point (resting potential) and a stable limit cycle (repetitive spiking) as detailed in Ermentrout (1998) and Brown, Feerick, and Feng (2001). This mechanism and the reported results are incorporated in our recently proposed model (Stiefel, Englitz, & Sejnowski, 2007) which details how interneurons could transform voltage noise into irregular spike times. This Hodgkin-Huxley type model (Hodgkin & Huxley, 1952) includes a fast K⁺-conductance, which creates a substantial region of bistability in phase space (switching region; Rowat, 2007) between the rest state and continuous spiking. Noise can easily transfer the neuron between these modes, thus exhibiting stochastic switching between burst firing, single spikes, and quiescence. For different parameter ranges, the model resembles the IS and the ST behavior in terms of CV and also ISI distribution.

The observed variability could also arise as a superposition of many deterministic processes, especially electrically coupled interneurons. This would mean that the observed variability would derive from network activity rather than single-neuron dynamics. We did not use pharmacological blockers of gap junctions as they show limited specificity and thus also interfere with other intracellular mechanisms and are therefore inadequate for studying endogenous dynamics (Rozental, Srinivas, & Spray, 2001). Several factors speak against a contribution of gap junctions to our data. First, we did not observe any potentials that could have originated in other neurons (spikelets) in any of our recordings. This was true for both near-threshold potentials (used for the time series analysis) and recordings at hyperpolarized potentials. The later recording conditions make a detection of gap-junction-mediated potentials much more likely due to the voltage difference between coupled cells and the quiescence of the membrane potential. Second, gap junctions mostly couple interneurons of the same class (Amitai et al., 2002). Because all recorded cells were not spontaneously active, other coupled cells are unlikely to be spontaneously active. Thus, we can be reasonably sure of the absence of gap-junction-mediated potentials in our recordings.

The main source of noise in isolated neurons is channel noise, generated by the stochastic opening and closing of individual ion channels (Hille, 2001). The existence of irregular activity is indicative of a high sensitivity to noise and fluctuations, which becomes functionally important in vivo when massive barrages of synaptic potentials arrive at the dendrite (Destexhe, Rudolph, & Par, 2003). Interneurons should be strongly driven by this highly irregular input and may introduce additional variability. This sensitivity of the spike initiation dynamics of ST and IS interneurons to voltage noise is thus likely to preserve or even enhance the discharge variability of all neurons in the cortical network.