Detecting directional influence in fMRI connectivity analysis using PCA based Granger causality

Abstract

A fMRI connectivity analysis approach combining both principal component analysis (PCA) and Granger causality method (GCM) is proposed to study directional influence between functional brain regions. Both simulated data and human fMRI data obtained during behavioral tasks were used to validate this method. If PCA is first used to reduce number of fMRI time series, then more energy and information features in the signal can be preserved than using averaged values from brain regions of interest. Subsequently, GCM can be applied to principal components extracted in order to further investigate effective connectivity. The simulation demonstrated that by using GCM with PCA, between-region causalities were better represented than using GCM with average values. Furthermore, after localizing an emotion task-induced activation in the anterior cingulate cortex, inferior frontal sulcus and amygdala, the directional influences among these brain regions were resolved using our new approach. These results indicate that using PCA may improve upon application of existing GCMs in study of human brain effective connectivity.

1. Introduction

A neural system is composed of complex networks with a large amount of correlated variables. In the past decade, fMRI using the blood oxygen level dependent (BOLD) effect has been successful in identifying functional brain circuits underlying neural computations (Varela et al., 2001). Nowadays, most interest in system neuroscience has switched from mapping sites of activation towards identifying the interconnectivity that weave them together into dynamic systems (Goebel et al., 2003; Lee et al., 2003). Impressive methodological progress has been made since the first description of the BOLD effect (Ogawa et al., 1990) and functional integration (Friston et al., 2002) has been proposed to investigate changes in the correlation between brain areas under different task conditions. Recently, a Granger causality mapping (GCM) method based on vector autoregressive (VAR) modeling of fMRI time series (Goebel et al., 2003; Roebroeck et al., 2005; Sato et al., 2006; Londei et al., 2007) was proposed to examine effective connectivity over the human brain. This is an apparent methodological advance in functional connectivity research using data driven approaches. Identifying causal relationships among simultaneously acquired signals has been a challenge in computational modeling of temporal processes and has a wide variety of applications such as time series analysis in economics (Granger et al., 1969) and in dynamic EEG analysis (Kaminski et al., 2001; Hesse et al., 2003; Brovelli et al., 2004).

However, in previous fMRI studies using Granger causality method (GCM), the analyses were always based on values in a single voxel or average values from regions of interest (ROIs) (Goebel et al., 2003). However, this averaging approach may lose part of information in the time series. For multivariate time series data, there is often the need to examine causal relationships involving blocks of time series. In fMRI analyses, a ROI may be treated as a source from which a group of time series can be extracted, and principal component analysis (PCA) may be employed to identify clustering within this vector of time series and more efficiently extract the signal energy and information features (Jolliffe et al., 1986; Polat et al., 2007). PCA is a multivariate analytical technique which can be applied to measurements that are continuous or binary. In the current study, PCA is employed to reduce the dimensionality of BOLD signal data in certain ROIs by combining correlated features into a set of new orthogonal variables called principal components (PCs), and the complete set of signals can then be represented as a vector of time series with a few PCs. Furthermore, the more efficient representation of signals generated by PCA is, the more information on causal relationship can be obtained in GCM analyses so as to identify a brain network and its connectivity with directional influence.

In this article, we introduced PCA and Granger causality theories and the results based on simulated data were also presented to illustrate the advantage of the proposed method. For an immediate application of our new approach, human data from a fMRI study of emotional tasks were analyzed to clarify the directional relationship among the brain regions activated during the tasks.

2. Results

Significant differences in modeled signal activations are summarized in Table 1. Emotion specific activations found using the conjunction of the contrast [emotion vs. identity] and [emotion vs. control] occurred at the left inferior frontal sulcus. The pregenual cingulate BOLD response showed a greater decrease from baseline during emotion matching than the identity matching. The BOLD response at the subgenual cingulate gyrus and amygdala was not specific to either the emotion or identity conditions and appeared when contrasting either face matching condition against the control. The activation was more statistically significant at the right amygdala (peak t(11) = 7.25 for emotion). The main four activated brain ROIs were displayed in Fig. 1. Directional causality in emotion related brain pathways was investigated by looking for changes over time in BOLD responses in Fig. 2. Note that the ACC response increased over time and was reported associated with the amygdala. We further investigated the interactions among the pACC, sACC, inferior frontal sulcus and right amygdala using Granger causality analysis. Both subgenual and pregenual cingulate gyrus send projections to the amygdala (Mayberg et al., 2003; Vogt, 2005), and DTI fiber tracking was recently used to show connections between the sACC and amygdale (Johansen-Berg et al., 2006). Inferior frontal sulcus could be considered as part of the dorsolateral prefrontal cortex, which is associated with working memory and executive functions. Ochsner et al. (Ochsner et al., 2005) have described this region of the prefrontal cortex as involvement in indirect emotional regulation since there is no strong anatomic connection between this region and amygdala. We investigated the local brain network based on the conclusions described above and used the pairwise vector Granger causality analysis on the PCs vectors to clarify the relationship among these mentioned regions.

Table 1.

Clusters of activation

Region	Hemisphere	Brodmann area	Talairach coordinates	Size (mm3)	T score
Emotion > Identity and Control
Inferior frontal sulcus	L	9/44	−44, 17, 30	208	5.1
Precentral gyrus	R	4	51, −3, 53	162	5.0
Pregenual cingulate gyrus	L	24/32	−3, 38, 9	180	−4.8
Transverse temporal gyrus	L	41	−45, −26, 15	79	−4.7
Emotion and Identity > Control
Amygdala	R	N/A	23, −6, −9	510	6.2
Subgenual cingulate gyrus	R	32	4,38, −7	120	5.3
Fusiform gyrus	R	37	40, −41, −18	248	5.1
Inferior temporal sulcus	R	37	49, −70, −3	293	6.2
Middle temporal gyrus	R	39	54, −58, 11	1005	8.6
Posterior cingulate gyrus	R	23	2, −55, 25	1770	6.0

Minimum cluster size: 50mm³. “Emotion > Identity and Control” was a conjunction of “Emotion > Identity” and “Emotion > Control”. . “Emotion and Identity > Control” was a conjunction of “Emotion > Control” and “Identity > Control”.

Fig. 1.

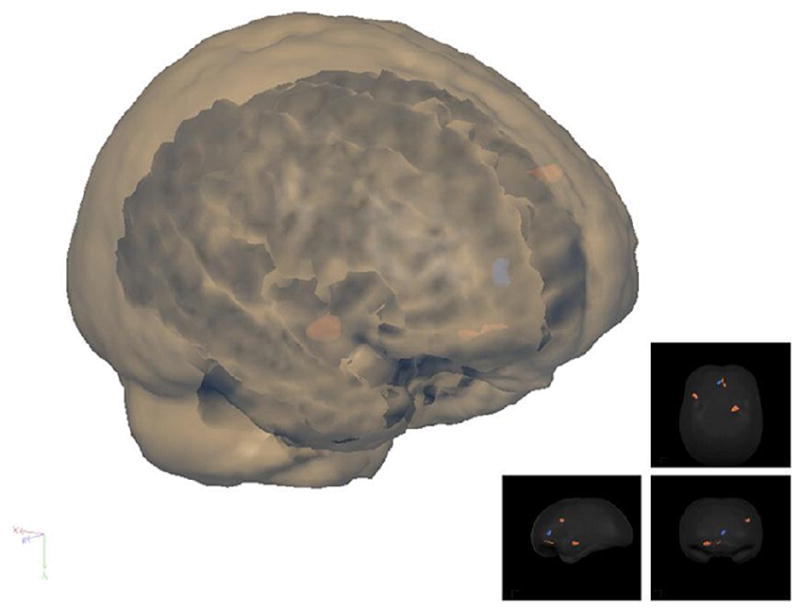
“Glass brain” showing main clusters of activation with a threshold of t(11) > 4.0. Left inferior prefrontal sulcus, right amygdala, and anterior cingulate cortex activations for the group illustrated on this rendered 3D brain.

Fig. 2.

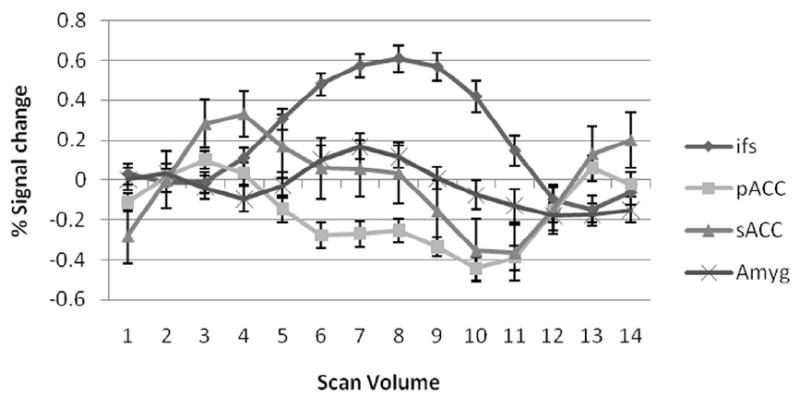
Mean BOLD response. Error bars denote standard error of mean. Pregenual cingulate gyrus BOLD response is negative for the condition with a significantly greater decrease; subgenual cingulate gyrus and amygdala BOLD response remain at baseline during the emotional task; inferior frontal sulcus BOLD response is always positive.

The selected four activated brain ROIs include sACC, pACC, right amygdala and inferior frontal sulcus. The pregenual cingulate gyrus BOLD response is negative with a significantly greater decrease in the emotion condition compared to the other conditions. The subgenual cingulate gyrus BOLD response remained at baseline during the emotion and identity conditions and decreased during the control condition. The right amygdalar BOLD response increased during the emotion and identity conditions and the inferior frontal sulcus BOLD response was seen only during the emotion condition. The Granger causality analysis indicates that both the sACC and pACC have a strong directional influence upon the right amygdala during the emotion task (Fig. 3). The inferior frontal sulcus has an indirect influence upon the right amygdala via the sACC, and the right amygdala receives a direct drive from the inferior frontal sulcus, which may be caused by the indirect influence for the limitation of pairwise Granger causality method. Coupling Granger causality for directional intrinsic connectivity was shown in the temporal domain in Table 2. The only significant instantaneous interactions were among a triangular network consisting of the amygdala, sACC, and pACC. The instantaneous influence between the pACC and sACC is 0.283 with a threshold value of 0.135, the instantaneous influence between pACC and amygdala is 0.326 with the threshold value 0.113 and the one between the sACC and amygdala is 0.227 with the threshold value 0.130 (p < 0.05). Low sample resolution makes it hard to clarify directional causality, but these regions may have such a relationship in such a brain network. Fig. 3 shows only the significant interactions within the four-node brain network (p < 0.05). In previous studies, Etkin et al. (Etkin et al., 2006) concluded that emotional conflict is resolved through top-down inhibition of amygdalar activity by the rostral cingulate cortex (rACC) and Johanssen-Berg et al. (Johansen-Berg et al., 2006) used DTI fiber tracking to show connections between the sACC and amygdala, and between the pACC and medial prefrontal cortex. Our results are almost consistent with previous human brain studies (Mayberg et al., 2003; Johansen-Berg et al., 2006; Etkin et al., 2006) and animal studies of medial prefrontal-amygdalar interactions (Quirk et al., 2003; Delgado et al., 2006). No significant causality was found when Granger causality method was applied to the average values of activated clusters in our study.

Fig. 3.

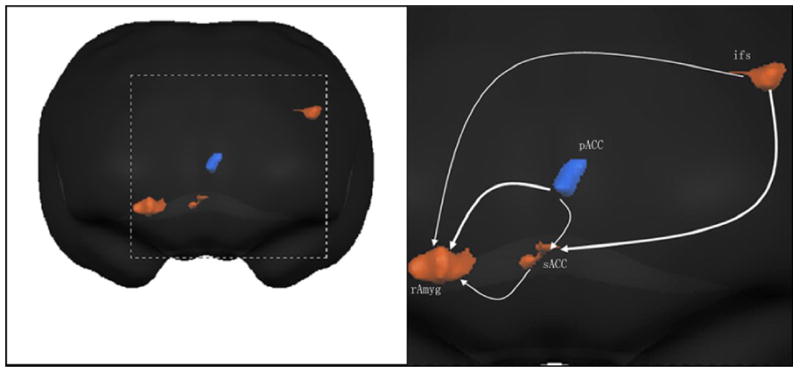
Graphical description of human brain network across conditions. The lines in the Granger causality graphs have arrowheads, indicating the direction of Granger causal influence. Lines between region pairs not reaching significance in the Granger causality measures are not shown. Ifs, inferior frontal sulcus; pACC, pregenual cingulate gyrus; sACC, subgenual cingulate gyrus; rAmyg, right amygdale.

Table 2.

Granger causality values

Granger causality
Brain regions	Inferior frontal sulcus	Right Amygdala	Pregenual cingulate gyrus	Subgenual cingulate gyrus
Inferior frontal sulcus	-	0.260*	0.184	0.338*
Right Amygdala	0.210	-	0.180	0.126
Pregenual cingulate gyrus	0.230	0.360*	-	0.216*
Subgenual cingulate gyrus	0.148	0.270*	0.218	-

Direction of influence is from the activated region at the left to the region at the top. Values are shown for temporal interactions determined to be significant by the permutation procedure described in Method. -, the pairing of a region with itself, because the Granger causality is measured only between different regions;

^*are shown the significant Granger causality between brain regions (p< 0.05).

Finally, in order to verify the Granger causality results of the emotion task study, the ROIs of pACC, sACC, inferior frontal sulcus and right amygdala were presented by 3, 2, 4, and 10 cubic voxel time series values at the original scanned resolution, respectively. Subsequently, each region’s BOLD data were transformed into a vector consisting of original vectors and 123 functional volumes with no information loss, for subsequent Granger causality analysis comparison. Coupling Granger causality for directional intrinsic connectivity based on different strategies was shown in the temporal domain in Table 3.

Table 3.

Effective Granger causalities among ROIs using different strategies.

Causal\Method	M1	M2	M3	M4
IFS → rAmyg	0.260	0.344	0.0173	0.0514
IFS → sACC	0.338	0.485	0.0198	0.0620
pACC → sACC	0.216	0.308	0.0160	0.0493
pACC → rAmyg	0.360	0.511	0.0206	0.0653
sACC → rAmyg	0.270	0.393	0.0184	0.0494

M1 is Granger causality analysis using PCA based on the data of highly interpolated resolution directly output from the Brain Voyager QX; M2 is the strategy of vector GCM analysis based on the data of highly interpolated resolution directly output from Brain Voyager QX; M3 is based on the average values and M4 only used the first component for the Granger causality analysis.

From the results shown in Table 3, we can find that the proposal method results are consistent with the full blockwise GCM, and both methods have better results than the Granger causality analysis based on the average values or only first component (cover about 65% energy) of PCs. Specialty, the PCA+GCM method could take fewer computation time cost than using the original ROI vectors when the ROIs contain lots of voxels, mapping the entire brain or analysis based on conditional Granger causality (Zhou et al., 2009). More energy (over 85%) needs to be covered when choosing the number of PCs, the Granger causality analysis based on only one component is not enough for the brain connectivity study.

3. Discussion

It has been widely recognized that clarifying neural connectivity is essential for understanding of brain function. Recently, effective connectivity between brain regions has been extracted from fMRI data based on the indirect BOLD signals instead of neural activity signals (Goebel et al., 2003; Roebroeck et al., 2005; Valdés-Sosa et al., 2005). The classical pairwise Granger causality method is a data driven approach mostly based on single voxel values or an average value of ROIs time series (Goebel et al., 2003; Roebroeck et al., 2005). This approach may lose parts of useful information for the Granger causality analysis. The Granger causality analysis is performed on the time series vectors in selected ROIs. The original vectors are decomposed into several PCs, which cover most of the energy with less information loss. This method appears valid and it can be used to the numeric simulation and the fMRI dataset. Although these are preliminary observations, it is evident that the modified procedure may provide more accurate information in the brain network for Granger causality analysis relative to the classic methods. The studies are aimed at combining two widely used techniques and they confirm greater accuracy using the modified methodology than using traditional Granger causality mapping (Goebel et al., 2003). Due to the limited temporal resolution and the method itself (Geweke, 1984), our expected direct influence is always hard to be distinguished from instantaneous causality and indirect causality. In the simulation, we interpret such kinds of direct influence as the theoretical values. But as for the fMRI data analysis, the directional Granger causality might be hard differentiated from the instantaneous causality for we only performed the influence analysis on the neural correlates of emotional conflict with 123 functional volumes scanned using a normal TR value for each subject.

Our results indicate that the direct influence from ACC to right amygdala and the indirect influence from inferior frontal sulcus to right amygdala via sACC. These influences have been found in agreement with the results from previous studies (Mayberg, 2003; Johansen-Berg et al., 2006; Etkin et al., 2006). The most important contribution of this paper is that the integration of PCA and Granger causality method is proposed as a powerful tool for identifying large scale functional connectivity patterns from a relatively short time series of functional neuroimaging data. The technique of brain connectivity analysis based on PCA and Granger causality is a potentially valuable tool to be used in the investigation of causality relations in brain connectivity studies. It would be useful in measuring brain effective connectivity and finding a correlation between such measurements and behavioral or physiological parameters of research populations.

4. Experimental Procedure

4.1 Methods

Either PCA or GCM alone has been successfully used in fMRI studies. But GCM has never been applied to the PCs of vector time series except for averaged ROI time series. Furthermore, most previous studies using the GCM tested only one or two human subjects with a large number of functional scan volumes. Here, we employed PCA and Granger causality for analyzing data from multiple simulations as well fMRI data from 12 subjects with fewer scan volumes.

Principal component analysis (PCA)

PCA (Jolliffe et al., 1986) is a multivariable statistical analysis technique for data compression and feature extraction. PCA seeks the linear combinations of the original variables such that the derived variables capture maximal variance. In detail, for a given n-dimensional matrix n×m, where n and m are the number of observations and the number of variables respectively, the p principal axes (p= n ) are orthogonal axes onto which the retained variance is maximum in the projected space. Reducing the dimensionality of the n-dimensional input space by projecting input data onto a reduced number of p directions can facilitate subsequent Granger causality analysis based on vector time series. The PCA describes the original data space in a base of eigenvectors. The corresponding eigenvalues account for the energy of the process in the eigenvector directions. An assumption is made for such feature extraction and dimensionality reduction by PCA that has the most information of the observation vectors contained in the subspace spanned by the first p PCs. Considering data projection restricted to the p eigenvectors with highest eigenvalues, an effective reduction in dimensionality of the original data input space can be achieved with minimum information loss (Soares-Filho et al., 2001). The details of calculations used in PCA can be found in Song et al. (Song et al., 1997).

Granger causality

Granger causality analysis was performed on the block time series of two brain regions activated following decomposition into PCs. As Geweke (Geweke, 1982) has proposed, a measure of linear influence F_{X, Y} between two time series of discrete zero-mean stochastic processes x_t = (x_1t, ⋯ , x_Mt)^T and y_t = (y_1t, ⋯ , y_Nt)^T, define w_t =(x_t^T, y_t^T) ^T, where T stands for matrix transposition, and M, N are the number of PCs of x_t, y_t, respectively. The influence measure F_{X, Y} is the sum of three components: the linear influence from x to y (F_{X → Y}), linear influence from y to x (F_{Y → X}) and the instantaneous influence F_X.Y defined as below, where Σ₁ = var(x_t|X_t−1), Σ₂ = var(x_t|X_t−1,Y_t−1), T₁ = var(y_t|Y_t−1), T₂=var(y_t|X_t−1,Y_t−1) and ϒ = var(w_t|W_t−1). The conditional variance is taken to be the variance of the residual about the linear projection which accounts for the prediction.

$$\begin{array}{l}{F}_{Y\to X}=ln(\mid {\mathrm{\sum }}_1\mid /\mid {\mathrm{\sum }}_2\mid ),\\ F_{X\to Y}=ln(\mid T_1\mid /\mid T_2\mid ),\\ F_{X·Y}=ln(\mid {\mathrm{\sum }}_2\mid ·\mid T_2\mid /\mid \mathrm{\Upsilon }\mid ),\\ F_{X·Y}=ln(\mid {\mathrm{\sum }}_1\mid ·\mid T_1\mid /\mid \mathrm{\Upsilon }\mid )=F_Y\end{array}$$

It is important to note that these temporal measures can be decomposed into the frequency domain under general conditions. The existence of these equalities gives credence and convenience to studying Granger causality in both frequency and temporal domains. In the simulation part of this paper, the frequency domain result of causality is also shown as an obvious contrast.

$$\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{f}_{Y\to X}(\lambda )$$

There are two main obstacles and limitations to the application of GCM in fMRI studies. Although indirect information on dynamic interactions and low temporal resolution of data acquisition are potential problems, this analysis has been successfully applied in brain causal connectivity studies using fMRI (Goebel et al., 2003; Valdés-Sosa et al., 2005; Londei et al., 2007). With the assumptions of the finite order of AR-models and wide sense stationary w_t, PCA and Granger causality algorithm can be performed on the selected activated ROIs for the relevant task to investigate the causal relationship between different human brain regions.

4.2 Simulation

Previous non-invasive fMRI studies have shown that statistical techniques based on VAR-modeling and Granger causality are capable of detecting an effective connectivity map of the human brain without considering any inclusion of exogenous variables or subjective assumptions. We consider a simple five-node oscillatory network structurally connected with different delays. The network involves four variables each representing an autoregressive process:

$$\begin{array}{l}{x}_1(t)=0.55x_1(t-1)-0.7x_1(t-2)+{\epsilon }_1(t)\\ x_2(t)=0.56x_2(t-1)-0.75x_2(t-2)+0.6x_1(t-1)+{\epsilon }_2(t)\\ x_3(t)=0.57x_3(t-1)-0.8x_3(t-2)+0.4x_1(t-2)+{\epsilon }_3(t)\\ x_4(t)=0.58x_4(t-1)-0.85x_4(t-2)+0.5x_1(t-3)+{\epsilon }_4(t)\\ x_5(t)=0.59x_5(t-1)-0.9x_5(t-2)+0.8x_1(t-4)+{\epsilon }_5(t)\end{array}$$

where ε₁, ε₂, ε₃, ε₄, ε₅ are independent Gaussian white noise processes with zero means and variances of σ₁², σ₂², σ₃², σ₄², σ₅² respectively. Define P(t) = (x₂(t); x₃(t); x₄(t); x₅(t)) and Q(t) = (x₁(t)), considering such a simple system consisting of two vector variables and using Granger causality to investigate the influence between P(t) and Q(t). The configuration of the system is illustrated that Q(t) drives P(t) after different time unit delays via x₁(t).

The sample rate is set to 200 Hz and the network model was simulated with σ₁²= 1.0, σ₂²= 2.0, σ₃²= 0.8, σ₄²= 1.0, and σ₅²= 1.5 to generate a data set of 500 realizations each with 1000 time points. Assuming no knowledge of the model, a second order MVAR model (Ding et al., 2000) based on Bayesian Information Criterion was fitted to the generated data set to perform within each pair of interest Granger causality analysis in the frequency domain and temporal domain, as shown in Fig. 4.

Fig. 4.

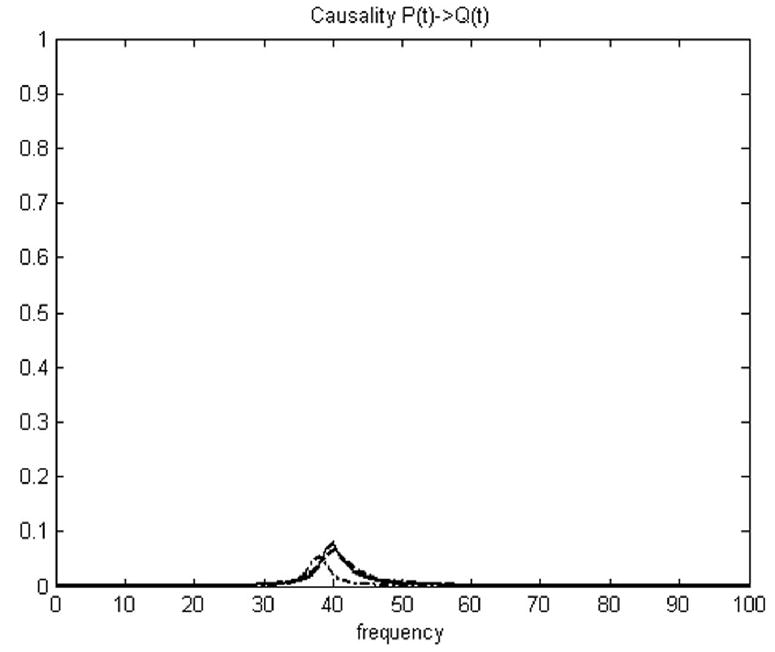
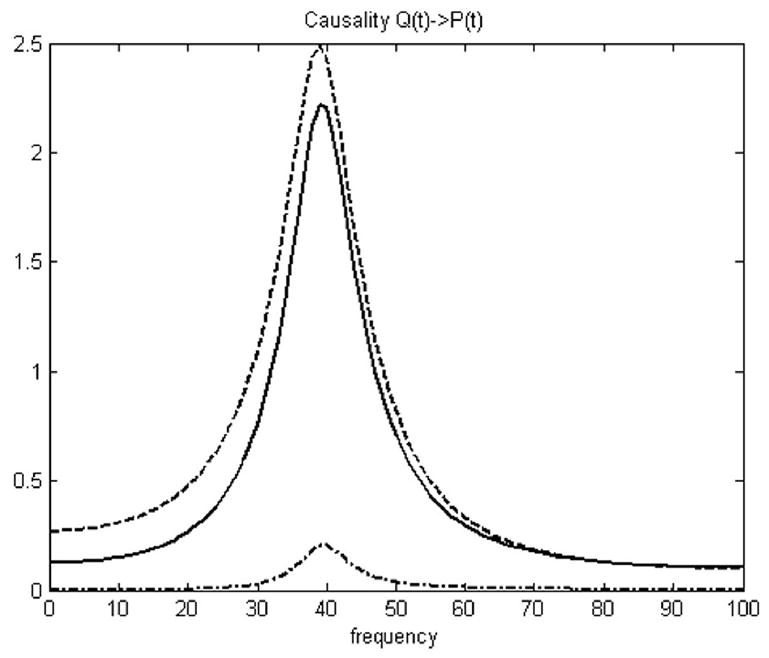
Granger causality analysis of simulation. Causality between P(t) and Q(t) in frequency domain. Dashdot line is based on average value; Dashed line is based on vector Granger causality method; Solid line is based on PCA (over 95% energy) and vector Granger causality method.

The numeric simulation dataset is composed with 500 realizations each with 1000 time points, there are totally 500,000 points in each time series. In the permutation test, these significance thresholds were determined using a permutation procedure that involved creating 500 permutations of the numeric simulation dataset by random rearrangement of the realization order independently for both vectors P and Q. The Granger causality spectrum was computed for each permutation, and then the maximum causality value over the frequency range was identified. Then we can calculate the Granger causality in time domain under general conditions by integral. After 500 permutation steps, a distribution of Granger causality values in time domain was created. Choosing a p-value at p = 0.002 for this distribution gave the threshold of the results. The Granger causalities under the thresholds were not significant and the very small causality can be further eliminated to zero if less than the threshold. In Fig. 4, little influence was found from P(t) to Q(t) but strong influence from Q(t) to P(t) was detected using both methods. Furthermore, the PCA + Granger causality analysis gave a stronger result than standard Granger analysis using average values. Only frequency Granger causality results were shown in Fig. 4. The temporal causality F_Q→P calculated based on average values is 0.0193, and the new temporal causality F_Q→P calculated using the proposal method is 0.421, which is displayed next to the theoretical value 0.529 calculated based on the original vectors (p<0.002). The simulation result in Table 4 shows that the Granger causality analysis based on vectors PCs instead of average value is much closer to the theoretical result value calculated based on the original vectors. Activated clusters of real fMRI data always include large number of voxels. It is hard to use vector Granger causality method directly, but the PCA + Granger causality analysis can solve this problem. The between-region causalities can be better represented using PCA + GCM than using GCM based on average values. This modified method is applied to real fMRI data in next section.

Table 4.

Granger causalities between P and Q based on different strategies.

Methods	FQ→P	FP→Q	FP.Q
GCM+Avg	0.0193	0.0108	0.00177
GCM+Original	0.529*	0.00820	0.00302
GCM+PCA	0.421*	0.0120	0.0230

Values are shown for temporal interactions determined to be significant by the permutation procedure described in Method. F_Q→P means the causality from Q to P; F_P→Q means the causality from P to Q; F_P.Q means the instantaneous causality between P and Q.

^*are shown the significant Granger causality (p< 0.002).

4.3 Application to Human fMRI data

Cognitive task and Participants

Three conditions were used in our behavioral task, namely face-matching task: (1) “Emotion”, in which participants were asked to match the faces by their expressed emotion (happiness, fear, or anger) from a target face to two probe faces below; (2) “Identity”, in which participants were asked to match neutral faces by identity; (3) “Control”, in which participants were asked to match pixilated patterns derived from neutral face pictures. The task was ordered in blocks of six 3 s trials of the same condition, preceded by a 3 s instruction screen. The block condition was varied in a fixed sequence that repeated four times and was counterbalanced across participants. The entire run consisted of twelve 21 s tasks blocks interspersed with thirteen 9 s rest blocks and lasted 189s. During rest, a fixation cross was displayed. A total of 48 grayscale face portraits were presented from the series “Pictures of Facial Affect” (Ekman et al., 1976). Twelve control patterns were created by shrinking, randomizing and enlarging neutral face pictures as previously described (Wright et al., 2006). In the emotion condition, one actor was selected for the probe face and a second actor for both of the target faces. The pictures subtended approximately 3.6° × 5.4° (target) and 2.9° × 4.3° (probes) of the visual field. Subjects made a decision to select the left or right target by pressing a button under their index or middle finger respectively. The subjects practiced each condition inside the scanner before the experimental run.

Twelve right-handed volunteers (6 females, 18–53 years old) with normal or corrected to normal vision, consisting of comparable ages (mean [S.D.]: 29.42±12.44) were recruited as approved by the University of Florida’s Institutional Review Board. No participant reported any neurological or psychiatric history or use of psychoactive medications for the previous 6 months.

MR scanning and Data preprocessing

The experiment was performed on a Siemens Allegra 3.0 Tesla MR scanner (Siemens, Munich, Germany) with a dome-shaped standard head coil. Structural images were acquired using a T1 MPRAGE sequence in the sagittal plane at 1.0 mm³ resolution, TR = 1780 ms, TE = 4.38 ms, flip angle = 8°. Functional images acquired T2* weighted echo planar imaging BOLD sequence in the axial orientation (parallel to the AC–PC line), covering the whole brain with 36 slices, 3.8 mm thick with no gap using TR = 3000 ms, TE = 30 ms, flip angle = 90°, a 240 mm² FOV and a 64×64 voxels matrix, giving 3.75 mm in-plane resolution. A total of 125 volumes were scanned during the matching task experiment and the first two volumes were discarded before analysis to allow for T1 equilibration. Stimulus presentation, response registration, and synchronization to the scanner acquisition were performed using the software program E-Prime (Psychology Software Tools, Pittsburgh, PA). Responses were collected with a MRI-compatible button glove attached to the participant’s right hand.

Imaging data were analyzed using Brain-Voyager QX (Brain Innovation, Maastricht, Holland). The anatomic and functional images were coregistered and normalized to Talairach space for each subject. Functional images underwent 3D motion correction, linear trend removal, and slice timing correction. Spatial smoothing was applied using a Gaussian filter of 6.00 mm full-width half maximum and no temporal smoothing was applied to the functional data. Regional activations were estimated using a multiple subject general linear model (GLM). A reference function was built for each condition by convolving the block presentation time series with an estimated HRF (Boynton et al., 1996). Three predictor functions reflecting the main stimulation in the task were least squares filtered. Statistical maps were created using random effects analysis. Individual voxel time series were regressed onto the model combined with these predictors, and clusters of voxels with significant differences between predictors were analyzed with a statistical threshold of t(11)>4.0 (p<0.002) and a minimum cluster size of 50 mm³. The two experimental conditions (Emotion and Identity) were contrasted with the control condition in order to identify activation within specific brain regions, and we validated the GLM results by drawing the average BOLD response to each condition for each cluster of significant voxels (Wright et al., 2004). To investigate the brain network connectivity, the BOLD response to emotion condition was calculated separately for four repetitions and averaged across blocks and subjects.

PCA and Granger causality method (GCM)

The PCA method is widely used to make large measurement more effective in many fields. Here, PCA was used for dimensionality reduction within the large number of voxels activated in each ROI by performing a covariance analysis between factors and was based on the hypotheses that most of the information and energy within the ROIs is included in a few PCs. The activated regions in brain imaging within emotion task were represented by a vector consisting of hundreds of attributes. After selecting the activated brain regions with Brain-Voyager QX, the ROI voxel time series were decomposed into a simple vector time course by the PCA method. In our study, ROIs included pregenual cingulate gyrus (pACC), subgenual cingulate gyrus (sACC), inferior frontal sulcus and right amygdala, which were represented by 180, 120, 208, and 510 cubic voxel values, respectively with 123 volumes (time points) for each subject. Subsequently, each region’s BOLD data were transformed into a vector consisting of 5 PCs and 123 functional volumes with minimum information loss (less than 5%), for subsequent Granger causality analysis.

The Granger causality approach allows the determination of the causal relations among these activated brain regions with the GLM analysis. It extracts three parameters with a different functional meaning, F_{X → Y}, F_{Y → X}, and F_X·Y, which stands for causality from region x to region y, influence from region y to region x, and instantaneous influence between these two regions. According to a previous study (Roebroeck et al., 2005), the low temporal resolution of fMRI may not provide enough information for inferring directional causality, but most of the causality effects still differentiate from the instantaneous ones. Despite this problem, the method is also useful in Granger causality mapping and most brain connectivity studies. The Granger causality method was applied to the complete run from the emotion experiment to calculate values for the influence between the preselected activated brain regions using a first order autoregressive model.

Hence, Granger causality between two regions was considered looking for one TR (Goebel et al., 2003). Such sub-TR delayed influences can be captured by this level of directional Granger causality (our TR is 3.0 s). Furthermore, to assign significance levels to the computed measures a permutation procedure was applied (Nichols et al., 2002; Chen et al., 2006). These significance thresholds were determined using a permutation procedure that involved creating 500 permutations of the fMRI data by random rearrangement of the subject order independently for each ROI region (vector time series). The Granger causality spectrum was computed for each permutation, and then the Granger causality in temporal domain was calculated by integral for each permutation. The resulting significance level is the proportion of values in this nulldistribution that are larger than the value computed for the original signal. After 500 permutation steps, a distribution of causality values in temporal domain was created. Choosing a p-value for this distribution gave the thresholds of the fMRI results. Here, the causality results were reported using a significance threshold of p < 0.05.