Nonequilibrium separation of short DNA using nanoslit arrays

Abstract

A nonequilibrium regime of size-based separation was observed experimentally for double-stranded deoxyribonucleic acid (DNA) molecules with lengths below 1 kbp moving electrokinetically through nanofluidic nanoslit arrays. The breakdown of Ogston sieving was supplanted at higher electric fields to recover rapid separation with a reversed elution order and elution times one to two orders of magnitude faster than with Ogston sieving at lower fields. A simple kinetic model describes the experimental results.

INTRODUCTION

Nanofluidic devices have enabled new methods for the manipulation and analysis of biomolecules,^{1, 2, 3, 4, 5, 6} and the potential of these devices for separating biomolecular mixtures is of broad technological and scientific interest.^{1, 3, 7, 8} A simple and appealing geometry with complex functionality is the nanoslit array, or nanofilter array, produced by etching alternating deeper wells and shallower nanoslits into a rigid substrate. This fundamentally interesting geometry mimics the topology employed in analytical models of polyacrylamide gels,⁹ arguably the most successful platform for biomolecular separations. Experimentally, the incorporation of conventional gels on-chip is nontrivial, and the demonstration of reusable, sieving nanostructures fabricated directly within channels, such as nanoslit arrays, marks important progress toward the realization of lab on a chip instruments. Proteins and short DNA molecules have been separated in nanoslit arrays using relatively low applied average electric field values, E_ave, where Ogston¹⁰ or electrostatic sieving are the dominant separation mechanisms, and more compact species elute first.^{7, 8}

Recent theoretical studies predict that new physical processes could be exploited for the rapid separation of DNA molecules in nanoslit arrays at high electric fields. Brownian dynamics (BD) simulations of long DNA molecules suggest a trapping mechanism whereby larger, more slowly diffusing molecules enter regions of diminished electric field strength in wells less frequently than smaller molecules and consequently elute more quickly.¹¹ A separate simulation study shows greater mobility for larger charged spheres at high electric fields, because smaller spheres diffuse to and follow electric field lines that penetrate more deeply into the wells.¹² In another BD study, Laachi et al.¹³ report faster elution of longer rodlike DNA, because the electric field gradient at the interface between wells and nanoslits exerts a length-dependent torque on the molecules, assisting rotation into orientations that permit entry into a nanoslit.

Consistent with predictions, this study experimentally observed a recovery of resolution after the breakdown of Ogston sieving and a reversal of elution order with increasing E_ave values in nanoslit arrays, followed by a maximum in recovered resolution and emergence of a new plateau in mobility. Short DNA molecules with lengths below 1 kbp were separated in nanoslit arrays with nanoslit depths shallower than those previously reported^{7, 8, 14} and approximately the same size or smaller than the molecules themselves. Experimental results were compared across a comprehensive collection of additional nanofluidic geometries for controlled and detailed interrogation of the system. The engineered, nanofabricated geometries of the nanofluidic devices facilitated theoretical modeling of this previously unexplored separation behavior. A simple activated transport model, accounting for electrostatic energy and orientation entropy changes during transit between wells and nanoslits, accurately describes the experimental data.

EXPERIMENTAL RESULTS AND DISCUSSION

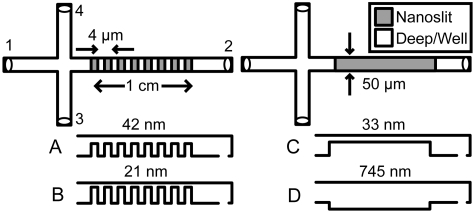
Four nanofluidic geometries were constructed from fused silica (Fig. 1), using contact and reduction photolithography, reactive ion etching, and fusion bonding. Devices were characterized using atomic force microscopy and a tip with a <10 nm specified radius. Root-mean-square surface roughness values were <1 nm. Nanoslit array devices A and B had respective nanoslit depths of (42±1) and (21±1) nm, respective well depths of (690±5) and (688±8) nm, and nanoslit and well lengths of approximately 2 μm. These geometries allowed study of the influence of changing nanoslit depth on the elution of short DNA molecules. Individual nanoslit devices C and D had separation regions with respective depths of (33±1) and (745±15) nm, which corresponded to a single nanoslit or well of devices A and B. Channels were 50 μm wide.

Figure 1.

Top-down schematics of nanoslit array (A and B) and individual nanoslit (C and D) device geometries with side-view schematics (not to scale).

55 bp DNA was formed by hybridizing complementary synthetic oligonucleotides, while 259 and 753 bp samples were prepared as polymerase chain reaction products. DNA molecules were labeled fluorescently at five base pairs to one molecule of YOYO-1. The contour and persistence lengths were assumed to increase by approximately 24% due to the dye.¹⁵ This gave approximate dyed contour lengths of 24, 109, and 317 nm for the 55, 259, and 753 bp DNA, respectively, and an approximate increased persistence length from 51 to 63 nm.¹⁶

Prior to experiments, devices were flushed with 5X tris borate-EDTA (TBE, T4415, Sigma) buffer [or 5X tris acetate-EDTA (TAE, T9650, Sigma)] with 2% polyvinylpyrrolidone (PVP, 10 kDa, 81390, Fluka) (w∕w) that had been diluted using 18 MΩ cm water and filtered to 100 nm. PVP suppressed electro-osmotic flow.¹ 753 or 259 bp DNA were loaded with 55 bp DNA into reservoir 3 (Fig. 1), with typical concentrations between approximately 1 and 3 μg∕ml. A custom voltage divider toggled between one set of dc voltages on gold electrodes in each reservoir to load DNA molecules electrophoretically from reservoirs 3 to 4 and a second set of voltages to inject a plug toward reservoir 2. Video capture began upon switching voltages, with asynchronism leading to an estimated error of ±0.25 s in the determination of peak elution times. Experiments were carried out at a nominal temperature of 25 °C.

Electrical current through the separation regions was measured using a current preamplifier and custom computer software. Current values were corrected for a measured leakage current. For experiments using TBE buffer, additional uncertainty was estimated from linear interpolations between current measurements to map applied voltages to current values. TBE and TAE buffer conductivities measured at 25 °C were (3.16±0.01) and (7.49±0.02) mS∕cm, respectively. The bulk conductivity was used, because the smallest device dimension (21 nm) was much larger than the approximate Debye length of 5X TBE buffer (0.6 nm). E_ave values were calculated from average currents, conductivities, and device geometries.

Epifluorescence video microscopy was performed with an inverted microscope, 40× 1.15 numerical aperture water immersion objective, bandpass filter set suited to YOYO-1, metal halide lamp, and electron-multiplying charge-coupled device camera. Images were acquired and processed using custom computer software. Videos were taken 0.5 cm or 1 cm down the separation region with exposure times of 50 ms (data at 0.5 cm) or 100 ms (data at 1 cm). Frame by frame background subtraction corrected for intensity fluctuations of the light source. Pixel intensities were summed across the channel width for each frame in an approximately 16×52 μm² area. The resulting electropherograms were fit to Gaussian functions. Measured times included the time to elute through a 195 μm long deep region (effectively another well) before the start of each separation region. DNA lengths were distinguished readily by the spatial extent of the fluorescence from individual molecules.

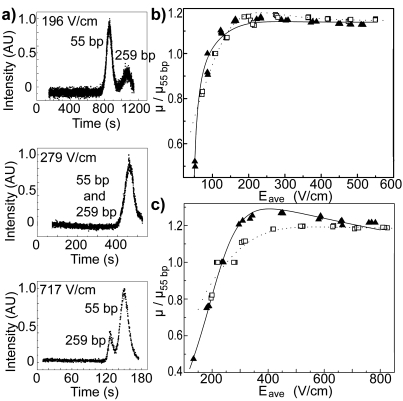
Representative electropherograms of DNA molecules eluting from a nanoslit array are shown in Fig. 2a. Figures 2b, 2c present the mobilities, μ, of 259 and 753 bp DNA normalized by the mobility of the 55 bp DNA, μ_{55 bp}, for each elution and plotted versus E_ave. Ogston sieving is evident at lower E_ave values, where smaller DNA molecules elute first. As E_ave increases, a crossover from Ogston sieving to a new regime is marked by the return of resolution with rapid separation in which larger DNA molecules elute first. This is the first experimental evidence for the field-induced reversal of DNA elution order in a nanoslit array. Upon further increase in E_ave, these relative mobilities approach plateau values, limiting the maximum resolution recovered in the nonequilibrium separation regime.

Figure 2.

(a) Electropherograms of 55 and 259 bp DNA taken in nanoslit array device B. Elution order changed with increasing values of E_ave. μ for 259 bp DNA (open squares) and 753 bp DNA (closed triangles) is normalized by μ_{55 bp} for each elution and plotted against E_ave for geometries A (b) and B (c). Theoretical fits to the data are shown for 259 bp (dotted line) and 753 bp DNA (solid line). Errors of one standard deviation are smaller than the data symbols.

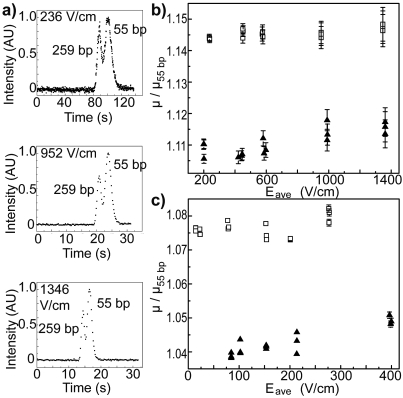
To demonstrate that this field-induced reversal is characteristic of the nanoslit array, similar experiments were performed in geometries C and D containing individual nanoslits. Representative electropherograms are provided in Fig. 3a, and the corresponding relative mobility is plotted as a function of E_ave in Figs. 3b, 3c. Unlike results for the nanoslit arrays, these plots give no evidence for a reversal of elution order.

Figure 3.

(a) Electropherograms of 55 and 259 bp DNA taken in nanofluidic device C. Elution order did not change for all investigated values of E_ave. μ for 259 bp DNA (open squares) and 753 bp DNA (closed triangles) is normalized by μ_{55 bp} for each elution and plotted against E_ave for geometries C (b) and D (c). Errors are one standard deviation and where not visible are smaller than the data symbol. Errors are larger for (b) than for (c), Fig. 2b, or Fig. 2c, due to shorter elution times.

The elution order in devices C and D is consistently 259 bp DNA first, then 753 bp DNA, and 55 bp DNA last, in contrast with μ values that increase with DNA length as reported by Stellwagen et al.¹⁷ Measurements of the electrophoretic separation of other polyelectrolytes also identified a maximum in free solution mobility, in which the flexibility of the polymer backbone was speculated to have played an important role.¹⁸ To determine whether this elution order was caused by the formation of borate complexes between DNA and TBE buffer components,¹⁹ experiments in device A were repeated substituting TAE for the TBE buffer. These measurements showed no significant variations in DNA behavior (data not shown). The elution order also cannot be attributed to differences in DNA composition, entrance effects, DNA-DNA interactions, sieving due to PVP, or steric interactions with channel surfaces, given the similar base pair composition of the DNA, lack of resolution 0.5 cm down the separation region for all E_ave values using TBE buffer (data not shown), reproducible peak shapes,¹⁷ low concentration of PVP,¹ and similar elution behavior in devices C and D, respectively. However, taking the ratio of DNA charge to its friction coefficient as an estimate for the free solution mobility, while allowing for differences in flexibility¹⁸ by treating the 259 bp DNA as a rigid rod and the 753 bp DNA as a series of Kuhn step sized spheres, it can be shown that μ of 259 bp DNA is larger that of 753 bp DNA. Additionally, the upward trends visible in Figs. 3b, 3c may indicate increased orientation of DNA molecules along the direction of the electric field with larger E_ave values.

THEORETICAL RESULTS AND DISCUSSION

To gain insight into the physical process responsible for the reversal in elution order in the nanoslit arrays, Peclet numbers were calculated for E_ave values at which Ogston sieving failed, E^∗. The rotational Peclet number, which compares electric field-induced torque to rotational diffusion, is given by Pe_r=∣Q∣E^∗l(1−δ)∕[k_bT(1+δ)] for a molecule of contour length l and charge Q, where k_b represents Boltzmann’s constant, T is the absolute temperature, and δ≡d_s∕d_w for arrays with nanoslit depths of d_s and well depths of d_w.¹³ Table 1 lists experimental values of Pe_r for devices A and B. Discrepancies with the value of unity predicted by Laachi et al.¹³ suggest that the physics of their theory incorporating torque assistance cannot fully describe the observed behavior. Disregarding torque assist, separation by Ogston sieving should disappear at a translational Peclet number, which compares electrophoresis to translational diffusion and is given by ${\mathrm{Pe}}_t=2{\mu }_w\delta d_w^2{E}^{\ast }∕\left[D{l}_w\left(1+\delta \right)\right]$,¹³ of order unity. Here, μ_w represents the mobility in a well, l_w is the well length, and D is the translational diffusivity calculated using expressions for a rod (55 and 259 bp DNA) or wormlike chain (753 bp DNA). To estimate values for μ_w, the weighted average of μ_{55 bp} was computed for experiments in geometry D. Elution times were then corrected for the offset between each experiment and the time associated with the weighted average of μ_{55 bp}. This allowed comparison between μ for the 259 and 753 bp DNA. Experimental Pe_t values are also summarized in Table 1. Because the longer DNA lengths are increasingly less retarded by their diffusive motion in the nanoslit array with increasing E_ave values up to E^∗, as indicated by Pe_t values approaching unity, they begin to overtake the 55 bp DNA, which retain Pe_t values well below one. Considering also the uncertainty in δ, D, μ_w, and E^∗, experimental Pe_t values support this conventional explanation for the breakdown of Ogston sieving. The separation that re-emerges for E_ave larger than E^∗ is therefore called “nonequilibrium.”

Table 1.

Rotational (Pe_r) and translational (Pe_t) Peclet numbers calculated at E^∗.

DNA (bp)	Device
	A		B
	Per	Pet	Per	Pet
55	0.5	0.04	1.5	0.05
259	13	0.14	32	0.18
753	17	0.63	250	0.92

Existing theories do not adequately represent the experimental results for the nanoslit arrays presented here, and a simple kinetic model is therefore proposed for the activated transport of DNA molecules through a nanoslit array in the nonequilibrium sieving regime. Consider an analyte moving under isothermal conditions from a well to a nanoslit in an electric field E_ave. The electrical potential energy change can be estimated as 2QE_aveR(1−δ)∕(1+δ), where R is the radius of gyration. The transition also exacts an entropy cost, ΔS_w→s=k_b ln(K_s∕K_w), where K_s and K_w are the partition coefficients calculated theoretically in the nanoslit and well, respectively.²⁰ The energy barrier for the transition is

$$\Delta G=2Q{E}_{\text{ave}}R\left(1-\delta \right)∕\left(1+\delta \right)-k_{b}T\text{\hspace{0.17em}ln}\left(K_s∕K_w\right).$$ (1)

Assuming an activated process, the forward and reverse rates are, respectively, k_f=A exp[−ΔG∕k_bT] and k_r=A exp[ΔG∕k_bT], where A is an attempt frequency that is estimated as D(2∕L)² for an array with period L. The overall transition rate, k, from the well to nanoslit is

$$k=k_f-k_r=2A\text{\hspace{0.17em}sinh}\left\{-2Q{E}_{\text{ave}}R\left(1-\delta \right)∕\left[k_{b}T\left(1+\delta \right)\right]+\text{ln}\left(K_s∕K_w\right)\right\}.$$ (2)

The total elution time, t, through the nanoslit array is a sum of three terms: the time to transit the (i) wells and (ii) nanoslits in response to E_ave and (iii) the average time that the analyte is trapped by the N periods in the nanoslit array, t_trap, which is inversely proportional to k.¹¹ Using μ=NL∕tE_ave, t is rewritten in terms of E_ave, the geometries of the array and analyte, and the maximum mobility, μ_max (which occurs when t_trap=0):

$$\mu ={\mu }_{\text{max}}{\left[1+\left({\mu }_{\text{max}}{E}_{\text{ave}}\right)∕\left(\alpha \text{\hspace{0.17em}sinh}\left[\beta E_{\text{ave}}+\text{ln}\left(K_s∕K_w\right)\right]\right)\right]}^{-1},$$ (3)

where β=−2QR(1−δ)∕[k_bT(1+δ)], α=8D∕L, and μ_max=[4∕(1+δ)][(1∕μ_wδ)+(1∕μ_s)]⁻¹. The mobility in the nanoslit μ_s is calculated similarly to μ_w but using experimental results from device C.

Equation 3 was fit to experimental μ values for each DNA length to determine theoretical curves for the relative mobilities, which are shown in Figs. 2b, 2c. Qualitative experimental results are accurately captured by Eq. 3, including the initial reversal of elution order, the appearance of an optimal field for maximal recovered resolution, and the plateau at still higher E_ave values. Fit curves for the 753 bp DNA deviate slightly from the data, perhaps due to the need for data at still higher E_ave values to better fit the plateau for μ_{55 bp} and the assumption of rodlike DNA by the model.

The values of μ_max, α, and β predicted using the theoretical expressions are compared in Table 2 with experimental values, showing remarkable consistency considering the simplicity of the model and complexity of the experimental system. Although the model neglects nanofluidic phenomena, such as finite double layer thickness, that impact shallower devices more than deeper devices, similar overall agreement is seen between theoretical and experimental values for devices A and B. μ_max represents the plateau in relative mobility for high E_ave values at which the convection of the 55 bp DNA begins to dominate over its diffusion, with all DNA lengths migrating without being retarded by the array geometry. μ_max values calculated theoretically using data from devices C and D agree well with values obtained from the fits to the experimental data from devices A and B. α relates the attempts of a DNA molecule to transit between a well and nanoslit to translational diffusion and also shows good overall agreement between theory and experiment. Electro-osmotic flow, which has not been included in the model, reduces experimental values for α relative to theoretical predictions, manifesting as theory to fit ratios that tend toward values >1, as seen in Table 2. β concerns the change in electrical potential energy as a molecule transits the interface between a well and nanoslit. This parameter exhibits less accord than the other fit parameters between theory and experiment, perhaps due to assumptions in theoretical calculations neglecting charge condensation along the DNA in solution and estimating R by treating the 55 and 259 bp DNA as rigid rods and the 753 bp DNA as a wormlike chain.

Table 2.

Comparison of theoretical and fit values of the model parameters.

Device		A			B
DNA (bp)		55	259	753	55	259	753
μmax (cm2∕V s)	Theory	(1.7698±0.0003)×10−5	(1.9002±0.0005)×10−5	(1.8102±0.0004)×10−5	(9.368±0.002)×10−6	(1.0040±0.0002)×10−5	(9.566±0.002)×10−6
	Fit	(2.22±0.02)×10−5	(2.15±0.02)×10−5	(2.92±0.03)×10−5	(1.11±0.03)×10−5	(1.12±0.01)×10−5	(1.20±0.01)×10−5
	Theory∕fit	0.8±0.007	0.9±0.008	0.6±0.006	0.8±0.02	0.9±0.008	0.8±0.07
α (cm∕s)	Theory	1.0×10−2	3.3×10−3	5.4×10−4	1.0×10−2	3.3×10−3	5.4×10−4
	Fit	(4±2)×10−3	(1±0.3)×10−3	(5±2)×10−3	(8±2)×10−3	(1.3±0.5)×10−3	(4±2)×10−4
	Theory∕fit	2.5±1.3	3.3±1.0	0.11±0.04	1.3±0.3	2.5±1.0	1.4±0.7
β (cm∕V)	Theory	3.2×10−3	6.7×10−2	3.9×10−1	3.4×10−3	7.2×10−2	4.2×10−1
	Fit	(1.8±0.3)×10−2	(2.8±0.3)×10−2	(2.4±0.2)×10−2	(6.1±0.8)×10−3	(1.3±0.1)×10−2	(2.2±0.2)×10−2
	Theory∕fit	0.2±0.03	2.4±0.3	16.3±2.0	0.6±0.08	5.5±0.4	19.1±1.7

These findings indicate that the model provides a good basic representation for the physical mechanisms at work during high electric field separations of short DNA in nanoslit arrays. Ogston sieving failed and the elution order reversed, when electric field-induced convection became the dominant transport process for larger DNA and the transport of smaller DNA remained dominated by diffusion. Separation persisted for very high E_ave, although with diminished resolution, as the trapping effects of the array became negligible, causing all molecules to migrate at μ_max. The reversal in elution order can be induced at lower E_ave via increased δ [for example, compare Figs. 2b, 2c] or by increasing the effective DNA charge with a low ionic strength buffer. The onset of μ_max can be shifted to higher E_ave by reducing δ or the analyte charge to size ratio, q. While smaller δ augments trapping overall, reduced q slows the approach to μ_max, expanding the range of E_ave values over which enhanced resolution is achieved in the nonequilibrium regime.

CONCLUDING REMARKS

Operation in the nonequilibrium sieving mode offers practical advantages, such as elution times one to two orders of magnitude more rapid than with Ogston sieving, increasing throughput and minimizing diffusive and heating problems, although admittedly sacrificing some separation resolution as compared to Ogston sieving at very low E_ave values. The proposed kinetic model could aid in the design of optimized nanoslit array experiments for improved separation in the important tasks of analyzing short DNA and biomolecules with complex shapes, such as proteins, and help illuminate the physical behavior of biomolecules during conventional gel separations. However, DNA behavior observed in the nonequilibrium separation regime may yet be unique to engineered fluidic nanostructures, due to the precise relationship required between analyte properties and channel geometry. The physical intuition captured by the simple model is expected to form the foundation for future investigations of a more sophisticated theory and numerical simulations.